Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 9 ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ Ex 9.1 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 7 Maths Chapter 9 ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ Exercise 9.1
1. ਹੇਠ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਦੇ ਤੁੱਲ (equivalent) ਦੋ ਪਰਿਮੇਯ ਸੰਖਿਆ ਲਿਖੋ :
ਪ੍ਰਸ਼ਨ (i).
\(\frac{4}{5}\)
ਉੱਤਰ:

∴ \(\frac{4}{5}\) ਦੇ ਤੁੱਲ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਹਨ \(\frac{8}{10}\) ਅਤੇ \(\frac{12}{15}\) |
ਪ੍ਰਸ਼ਨ (ii).
\(\frac{-5}{9}\)
ਉੱਤਰ:
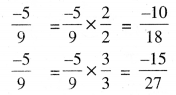
∴ \(\frac{-5}{9}\) ਦੇ ਤੱਲ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਹਨ \(\frac{-10}{18}\) ਅਤੇ \(\frac{-15}{27}\)
ਪ੍ਰਸ਼ਨ (iii).
\(\frac{3}{-11}\)
ਉੱਤਰ:
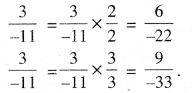
∴ \(\frac{3}{11}\) ਡੁੱਲ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਹਨ : \(\frac{6}{-22}\) ਤੇ \(\frac{9}{-33}\)
![]()
2. ਹੇਠ ਲਿਖੀਆਂ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਦਾ ਮਿਆਰੀ ਰੂਪ
ਪ੍ਰਸ਼ਨ (i)
\(\frac{35}{49}\)
ਉੱਤਰ:
\(\frac{35}{49}\)
∵ 35 ਅਤੇ 49 ਦਾ ਮ.ਸ.ਵ. 7 ਹੈ ।

ਇਸ ਲਈ ਅੰਸ਼ ਅਤੇ ਹਰ ਦੋਵਾਂ ਨੂੰ 7 ਨਾਲ ਭਾਗ ਕਰਨ ‘ਤੇ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ ।
\(\frac{35}{49}\) = \(\frac{35 \div 7}{49 \div 7}\) = \(\frac{5}{7}\)
∴ \(\frac{35}{49}\) ਦਾ ਮਿਆਰੀ ਰੂਪ \(\frac{5}{7}\) ਹੈ ।
ਪ੍ਰਸ਼ਨ (ii)
\(\frac{-42}{56}\)
ਉੱਤਰ:
\(\frac{-42}{56}\)
∵ – 42 ਅਤੇ 56 ਦਾ ਮ.ਸ.ਵ. = 14
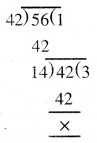
ਇਸ ਲਈ ਅੰਸ਼ ਅਤੇ ਹਰ ਦੋਵਾਂ ਨੂੰ 14 ਨਾਲ ਭਾਗ ਕਰਨ ‘ਤੇ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ ।
\(\frac{-42}{56}\) = \(\frac{-42 \div 14}{56 \div 14}\) = \(\frac{-3}{4}\)
∴ \(\frac{-42}{56}\) ਦਾ ਮਿਆਰੀ ਰੂਪ \(\frac{-3}{4}\) ਹੈ ।
ਪ੍ਰਸ਼ਨ (iii).
\(\frac{19}{-57}\)
ਉੱਤਰ:
\(\frac{19}{-57}\)
∵ 19 ਅਤੇ 57 ਦਾ ਮ.ਸ.ਵ. 19 ਹੈ ।

∴ ਅੰਸ਼ ਅਤੇ ਹਰ ਦੋਵਾਂ ਨੂੰ 19 ਨਾਲ ਭਾਗ ਕਰਨ ‘ਤੇ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ ।
\(\frac{19}{-57}\) = \(\frac{-19 \div 19}{-57 \div 19}\) = \(\frac{1}{-3}\)
∴ \(\frac{-42}{56}\) ਦਾ ਮਿਆਰੀ ਰੂਪ \(\frac{1}{-3}\) ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ (iv).
\(\frac{-12}{-36}\)
ਉੱਤਰ:
\(\frac{-12}{-36}\)
∵ 12 ਅਤੇ 36 ਦਾ ਮ.ਸ.ਵ. 12 ਹੈ ।
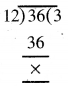
ਅੰਸ਼ ਅਤੇ ਹਰ ਦੋਵਾਂ ਨੂੰ 12 ਨਾਲ ਭਾਗ ਕਰਨ ‘ਤੇ
\(\frac{-12}{-36}\) = \(\frac{-12 \div 12}{-36 \div 12}\) = \(\frac{1}{3}\)
∴ \(\frac{-12}{36}\) ਦਾ ਮਿਆਰੀ ਰੂਪ \(\frac{1}{3}\) ਹੈ ।
3. ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਹੜੇ ਜੋੜੇ ਇੱਕ ਹੀ ਪਰਿਮੇਯ ਸੰਖਿਆ ਨੂੰ ਦਰਸਾਉਂਦੇ ਹਨ :
ਪ੍ਰਸ਼ਨ (i)
\(\frac{-15}{25}\) ਅਤੇ \(\frac{18}{-30}\)
ਉੱਤਰ:
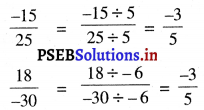
∴ \(\frac{-15}{25}\) ਅਤੇ \(\frac{18}{-30}\) ਇੱਕ ਹੀ ਪਰਿਮੇਯ ਸੰਖਿਆ ਨੂੰ ਦਰਸਾਉਂਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ (ii)
\(\frac{2}{3}\) ਅਤੇ \(\frac{-4}{6}\)
ਉੱਤਰ:
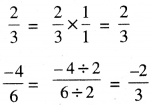
∴ \(\frac{2}{3}\) ਅਤੇ \(\frac{-4}{6}\) ਇੱਕ ਹੀ ਪਰਿਮੇਯ ਸੰਖਿਆ ਨੂੰ ਨਹੀਂ ਦਰਸਾਉਂਦੇ ਹਨ ।
![]()
ਪ੍ਰਸ਼ਨ (iii).
\(\frac{-3}{4}\) ਅਤੇ \(\frac{-12}{16}\)
ਉੱਤਰ:
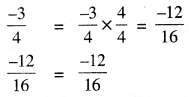
∴ \(\frac{-3}{4}\) ਅਤੇ \(\frac{-12}{16}\) ਇੱਕ ਹੀ ਪਰਿਮੇਯ ਸੰਖਿਆ ਨੂੰ ਦਰਸਾਉਂਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ (iv).
\(\frac{-3}{-7}\) ਅਤੇ \(\frac{3}{7}\)
ਉੱਤਰ:
\(\frac{-3}{-7}\) = \(\frac{-3 \div -1}{-7 \div -1}\) = \(\frac{3}{7}\)
∴ \(\frac{-3}{-7}\) ਅਤੇ \(\frac{3}{7}\) ਇੱਕ ਹੀ ਪਰਿਮੇਯ ਸੰਖਿਆ ਨੂੰ ਦਰਸਾਉਂਦੇ ਹਨ ।
4. ਹੇਠ ਲਿਖੀਆਂ ਵਿੱਚੋਂ ਕਿਹੜੀ ਪਰਿਮੇਯ ਸੰਖਿਆ ਵੱਡੀ ਹੈ ?
ਪ੍ਰਸ਼ਨ (i).
\(\frac{3}{7}\), \(\frac{4}{5}\)
ਉੱਤਰ:
(i) ਦਿੱਤੀਆਂ ਹੋਈਆਂ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਹਨ
\(\frac{3}{7}\) ਅਤੇ \(\frac{4}{5}\)
7 ਅਤੇ 5 ਦਾ ਲ.ਸ.ਵ. 35 ਹੈ ।
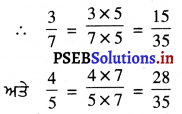
∵ ਦੂਸਰੇ ਦਾ ਅੰਸ਼ ਪਹਿਲੇ ਦੇ ਅੰਸ਼ ਤੋਂ ਵੱਡਾ ਹੈ ।
ਜਿਵੇਂਕਿ ਆਪ 28 > 15
ਇਸ ਲਈ \(\frac{4}{5}\) > \(\frac{3}{7}\)।
![]()
ਪ੍ਰਸ਼ਨ (ii).
\(\frac{-4}{12}\), \(\frac{-8}{12}\)
ਉੱਤਰ:
ਦਿੱਤੀਆਂ ਹੋਈਆਂ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਹਨ :
\(\frac{-4}{12}\) ਅਤੇ \(\frac{-8}{12}\)
∵ ਪਹਿਲੇ ਦਾ ਅੰਸ਼ ਦੂਸਰੇ ਤੋਂ ਵੱਡਾ ਹੈ ।
ਜਿਵੇਂ ਕਿ -4 > – 8
∴ \(\frac{-4}{12}\) > \(\frac{-8}{12}\)
ਪ੍ਰਸ਼ਨ (iii).
\(\frac{-3}{9}\), \(\frac{4}{-18}\)
ਉੱਤਰ:
ਦਿੱਤੀਆਂ ਹੋਈਆਂ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ : \(\frac{-3}{9}\), \(\frac{4}{-18}\)
\(\frac{-3}{9}\) = \(\frac{-3 \times 2}{9 \times 2}\) = \(\frac{-6}{18}\)
\(\frac{4}{-18}\) = \(\frac{4 \times -1}{-18 \times -1}\) = \(\frac{-4}{18}\)
ਜਿਵੇਂ ਕਿ 4 > – 6.
∴ \(\frac{4}{-18}\) > \(\frac{-3}{9}\)
ਪ੍ਰਸ਼ਨ (iv).
\(-2\frac{3}{5}\), \(-3\frac{5}{8}\)
ਉੱਤਰ:
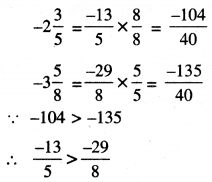
ਇਸ ਲਈ \(-2\frac{3}{5}\) > \(-3\frac{5}{8}\)
![]()
5. ਹੇਠ ਲਿਖੀਆਂ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਨੂੰ ਵੱਧਦੇ ਕ੍ਰਮ ਵਿੱਚ ਲਿਖੋ ।
ਪ੍ਰਸ਼ਨ (i).
\(\frac{-5}{7}\), \(\frac{-3}{7}\), \(\frac{-1}{7}\)
ਉੱਤਰ:
\(\frac{-5}{7}\), \(\frac{-3}{7}\), \(\frac{-1}{7}\)
ਇੱਥੇ -5 < 3 < -1
ਇਸ ਲਈ \(\frac{-5}{7}\) < \(\frac{-3}{7}\) < \(\frac{-1}{7}\)
ਵੱਧਦਾ ਕ੍ਰਮ ਹੈ :
\(\frac{-5}{7}\), \(\frac{-3}{7}\), \(\frac{-1}{7}\)
ਪ੍ਰਸ਼ਨ (ii).
\(\frac{-1}{5}\), \(\frac{-2}{15}\), \(\frac{-4}{5}\)
ਉੱਤਰ:
\(\frac{-1}{5}\), \(\frac{-2}{15}\), \(\frac{-4}{5}\)
5, 15, 5 ਦਾ ਲ.ਸ.ਵ. 15 ਹੈ ॥
∴ \(\frac{1}{5}\) = \(\frac{-1×3}{5×3}\) = \(\frac{-3}{15}\)

ਪ੍ਰਸ਼ਨ (iii).
\(\frac{-3}{8}\), \(\frac{-2}{4}\), \(\frac{-3}{2}\)
ਉੱਤਰ:
8, 4, 2 ਦਾ ਲ.ਸ.ਵ. 8 ਹੈ ।
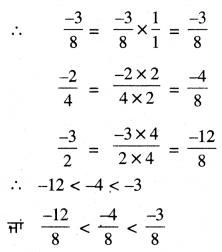
ਵੱਧਦਾ ਰੂਮ ਹੈ : \(\frac{-3}{2}\), \(\frac{-2}{4}\), \(\frac{-3}{8}\)
![]()
6. ਹੇਠ ਲਿਖੀਆਂ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਦੇ ਵਿਚਕਾਰ ਪੰਜ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਲਿਖੋ ।
ਪ੍ਰਸ਼ਨ (i).
-2 ਅਤੇ 1
ਉੱਤਰ:
ਦਿੱਤੀਆਂ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ -2 ਅਤੇ 1 ਹਨ
ਅਸੀਂ -2 ਅਤੇ -1 ਨੂੰ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਦੇ ਰੂਪ ਵਿੱਚ ਲਿਖਦੇ ਹਾਂ, ਜਿੱਥੇ ਹਰ 5 + 1 = 6 ਹੋਵੇ ।
ਸਾਡੇ ਕੋਲ ਹੈ : -2 = 2 × \(\frac{6}{6}\) = \(\frac{-12}{6}\)
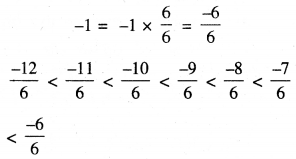
ਇਸ ਲਈ -2 ਅਤੇ -1 ਵਿਚਕਾਰ ਪੰਜ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ \(\frac{-11}{6}\), \(\frac{-10}{6}\), \(\frac{-9}{6}\), \(\frac{-8}{6}\), \(\frac{-7}{6}\) ਹਨ ।
ਜੋ ਕਿ \(\frac{-11}{6}\), \(\frac{-5}{3}\), \(\frac{-3}{2}\), \(\frac{-4}{3}\), \(\frac{-7}{6}\)
ਪ੍ਰਸ਼ਨ (ii).
\(\frac{-4}{5}\) ਅਤੇ \(\frac{-2}{3}\)
ਉੱਤਰ:
(ii) ਦਿੱਤੀਆਂ ਹੋਈਆਂ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਹਨ \(\frac{-4}{5}\) ਅਤੇ \(\frac{-2}{3}\)
ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਅਸੀਂ ਇੱਕ ਸਮਾਨ ਹਰ ਵਾਲੀਆਂ ਡੁੱਲ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਪਤਾ ਕਰਾਂਗੇ ।
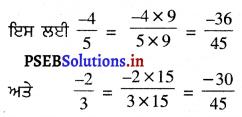
ਹੁਣ ਅਸੀਂ ਅੰਸ਼ -36 ਅਤੇ -30 ਦੇ ਵਿਚਕਾਰ ਪੰਜ ਸੰਪੂਰਨ ਸੰਖਿਆਵਾਂ -35, 34, -33, -32, 31 ਚੁਣਦੇ ਹਾਂ ।
ਇਸ ਲਈ \(\frac{-36}{45}\) ਅਤੇ \(\frac{-30}{45}\) ਵਿਚਕਾਰ ਪੰਜ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਹਨ
\(\frac{-35}{45}\), \(\frac{-34}{45}\), \(\frac{-33}{45}\), \(\frac{-32}{45}\), \(\frac{-31}{45}\)
ਇਸ ਲਈ \(\frac{-4}{5}\) ਅਤੇ \(\frac{-2}{3}\) ਵਿਚਕਾਰ ਪੰਜ ਪਰਿਮੇਯ | ਸੰਖਿਆਵਾਂ ਹਨ :
\(\frac{-35}{45}\), \(\frac{-34}{45}\), \(\frac{-33}{45}\), \(\frac{-32}{45}\), \(\frac{-31}{45}\)
ਜਿਵੇਂ ਕਿ \(\frac{-7}{9}\), \(\frac{-34}{45}\), \(\frac{-11}{15}\), \(\frac{-32}{45}\), \(\frac{-31}{45}\)
![]()
ਪ੍ਰਸ਼ਨ (iii).
\(\frac{1}{3}\) ਅਤੇ \(\frac{5}{7}\)
ਉੱਤਰ:
ਦਿੱਤੀਆਂ ਹੋਈਆਂ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਹਨ \(\frac{1}{3}\) ਅਤੇ \(\frac{5}{7}\)
ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਅਸੀਂ ਇਕ ਸਮਾਨ ਹਰ ਵਾਲੀਆਂ ਤੱਲ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਪਤਾ ਕਰਦੇ ਹਾਂ ।

ਇਸ ਲਈ \(\frac{1}{3}\) ਅਤੇ \(\frac{5}{7}\) ਵਿਚਕਾਰ ਪੰਜ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਹਨ :
\(\frac{8}{21}\), \(\frac{3}{7}\), \(\frac{10}{21}\), \(\frac{4}{7}\), \(\frac{13}{21}\)
7. ਹੇਠ ਲਿਖੇ ਹਰੇਕ ਵਿੱਚ, ਚਾਰ ਹੋਰ ਤੁੱਲ ਪਰਿਯ ਸੰਖਿਆਵਾਂ ਲਿਖੋ ।
ਪ੍ਰਸ਼ਨ (i).
\(\frac{-1}{5}\), \(\frac{-2}{10}\), \(\frac{-3}{15}\), \(\frac{-4}{20}\)……………..
ਉੱਤਰ:
\(\frac{-1}{5}\), \(\frac{-2}{10}\), \(\frac{-3}{15}\), \(\frac{-4}{20}\)……………..
\(\frac{-1}{5}\) ਸਰਲਤਮ ਰੂਪ ਵਿੱਚ ਇੱਕ ਪਰਿਮੇਯ ਸੰਖਿਆ ਹੈ ਹੁਣ, ਅਸੀਂ ਲਿਖ ਸਕਦੇ ਹਾਂ ।
\(\frac{-2}{10}\) – \(\frac{-1}{-5}\) × \(\frac{2}{2}\)
\(\frac{-3}{15}\) = \(\frac{-1}{5}\) × \(\frac{3}{3}\) ਅਤੇ \(\frac{-1}{5}\) = \(\frac{-1}{5}\) × \(\frac{4}{4}\)
ਅਸੀਂ ਇਨ੍ਹਾਂ ਸੰਖਿਆਵਾਂ ਵਿੱਚ ਅਸੀਂ ਇੱਕ ਪੈਟਰਨ ਦੇਖਦੇ ਹਾਂ | ਅਗਲੀਆਂ 4 ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਹੋਣਗੀਆਂ ।

![]()
ਪ੍ਰਸ਼ਨ (ii).
\(\frac{-1}{7}\), \(\frac{2}{-14}\), \(\frac{3}{-21}\), \(\frac{4}{-28}\) …………
ਉੱਤਰ:
ਦਿੱਤੀਆਂ ਹੋਈਆਂ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਹਨ
\(\frac{-1}{7}\), \(\frac{2}{-14}\), \(\frac{3}{-21}\), \(\frac{4}{-28}\) …………
\(\frac{-1}{7}\) ਸਰਲਤਮ ਰੂਪ ਵਿੱਚ ਇੱਕ ਪਰਿਮੇਯ ਸੰਖਿਆ ਹੈ।
ਹੁਣ ਅਸੀਂ ਲਿਖ ਸਕਦੇ ਹਾਂ
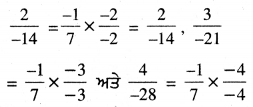
ਇਸ ਲਈ ਅਸੀਂ ਸੰਖਿਆਵਾਂ ਨੂੰ ਇਕ ਪੈਟਰਨ ਵਿਚ ਦੇਖਦੇ ਹਾਂ ।
ਅਗਲੀਆਂ ਚਾਰ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਹਨ :
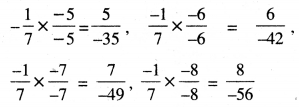
ਇਸ ਲਈ ਲੋੜੀਂਦੀਆਂ ਚਾਰ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਹਨ :
\(\frac{5}{-35}\), \(\frac{6}{-42}\), \(\frac{7}{-49}\), \(\frac{8}{-56}\)
8. ਹੇਠ ਲਿਖੀਆਂ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਨੂੰ ਸੰਖਿਆ ਰੇਖਾ ‘ਤੇ ਅੰਕਿਤ ਕਰੋ ।
ਪ੍ਰਸ਼ਨ (i).
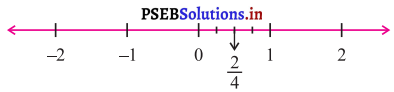
\(\frac{2}{4}\)
ਉੱਤਰ:
ਇੱਕ ਸੰਖਿਆ ਰੇਖਾ ਖਿੱਚੋ ਅਤੇ ਇਸ ਉੱਤੇ ਇੱਕ ਬਿੰਦ O ਚੁਣੋ ਜੋ ਕਿ ਪਰਿਮੇਯ ਸੰਖਿਆ) ਨੂੰ ਨਿਰਪਿਤ ਕਰਦਾ ਹੈ | ਅਸੀਂ 0 ਦੇ ਸੱਜੇ ਪਾਸੇ ਇੱਕ ਬਿੰਦ A ਚੁਣਦੇ ਹਾਂ ਜੋ ਕਿ 1 ਨੂੰ ਨਿਰੂਪਿਤ ਕਰਦਾ ਹੈ । ਹੁਣ ਰੇਖਾ ਖੰਡ OA ਨੂੰ ਚਾਰ ਬਰਾਬਰ ਭਾਗਾਂ ਵਿੱਚ ਵੰਡੋ । 0 ਤੋਂ ਸੱਜੇ ਪਾਸੇ ਦੂਸਰਾ ਭਾਗ ਪਰਿਮੇਯ ਸੰਖਿਆ \(\frac{2}{4}\) ਨੂੰ ਨਿਰੂਪਿਤ ਕਰਦਾ ਹੈ ਜਿਵੇਂ ਕਿ ਹੇਠਾਂ ਦਿੱਤੇ ਚਿੱਤਰ ਵਿੱਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ (ii).
\(\frac{-3}{4}\)
ਉੱਤਰ:ਇੱਕ ਸੰਖਿਆ ਰੇਖਾ ਖਿੱਚੋ ਅਤੇ ਇਸ ਉੱਤੇ ਇੱਕ ਬਿੰਦੁ O ਚੁਣੋ ਜੋ ਕਿ ਪਰਿਮੇਯ ਸੰਖਿਆ 0 ਨੂੰ ਨਿਰਪਿਤ ਕਰਦਾ ਹੈ । 0 ਤੋਂ ਖੱਬੇ ਪਾਸੇ ਅਸੀਂ ਇੱਕ ਬਿੰਦੂ A ਚੁਣਾਂਗੇ ਜੋ -1 ਨੂੰ ਦਰਸਾਏਗਾ | OA ਨੂੰ 4 ਬਰਾਬਰ ਭਾਗਾਂ ਵਿੱਚ ਵੰਡੋ । O ਤੋਂ ਖੱਬੇ ਪਾਸੇ ਵਾਲਾ ਤੀਸਰਾ ਭਾਗ ਪਰਿਮੇਯ ਸੰਖਿਆ \(\frac{-3}{4}\) ਨੂੰ ਨਿਰੂਪਿਤ ਕਰਦਾ ਹੈ । ਜਿਵੇਂ ਕਿ ਚਿੱਤਰ ਵਿਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iii).
\(\frac{5}{8}\)
ਉੱਤਰ:
ਇੱਕ ਸੰਖਿਆ ਰੇਖਾ ਖਿੱਚੋ ਅਤੇ ਇਸ ਉੱਤੇ ਇੱਕ ਬਿੰਦੂ O ਚੁਣੋ ਜੋ ਕਿ ਪਰਿਯ ਸੰਖਿਆ ਸਿਫ਼ਰ ਨੂੰ ਨਿਰੂਪਿਤ ਕਰਦਾ ਹੈ । ਸਿਫਰ ਦੇ ਸੱਜੇ ਪਾਸੇ ਇੱਕ ਬਿੰਦ A ਨਿਰੂਪਿਤ ਕਰੋ ।OA ਨੂੰ 8 ਬਰਾਬਰ ਭਾਗਾਂ ਵਿੱਚ ਵੰਡੋ । O ਤੋਂ ਸੱਜੇ ਪਾਸੇ ਪੰਜਵਾਂ ਹਿੱਸਾ ਪਰਿਮੇਯ ਸੰਖਿਆ \(\frac{5}{8}\) ਨੂੰ ਨਿਰੂਪਿਤ ਕਰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iv).
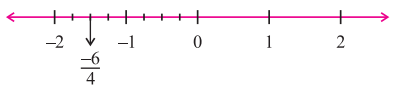
\(\frac{-6}{4}\)
ਉੱਤਰ:
ਇੱਕ ਸੰਖਿਆ ਰੇਖਾ ਖਿੱਚੋ ਅਤੇ ਇਸ ਉੱਤੇ ਇੱਕ ਬਿੰਦ O ਚੁਣੋ ਜੋ ਕਿ ਪਰਿਮੇਯ ਸੰਖਿਆ ਸਿਫਰ ਨੂੰ ਨਿਰੂਪਿਤ ਕਰਦਾ ਹੈ । 0 ਤੋਂ ਖੱਬੇ ਪਾਸੇ ਇੱਕ ਬਿੰਦੂ A ਚੁਣੋ ਜੋ ਕਿ – 2 ਨੂੰ ਨਿਰੂਪਿਤ ਕਰਦਾ ਹੈ ।
OA ਨੂੰ ਅੱਠ ਬਰਾਬਰ ਭਾਗਾਂ ਵਿੱਚ ਵੰਡੋ । O ਤੋਂ ਖੱਬੇ ਪਾਸੇ ਛੇਵਾਂ ਭਾਗ ਪਰਿਮੇਯ ਸੰਖਿਆ \(\frac{-6}{4}\) ਨੂੰ ਨਿਰੂਪਿਤ ਕਰਦਾ ਹੈ । ਜਿਵੇਂ ਕਿ ਚਿਤਰ ਵਿਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ ।
![]()
9. ਬਹੁਵਿਕਲਪੀ ਪ੍ਰਸ਼ਨ :
ਪ੍ਰਸ਼ਨ (i).
\(\frac{3}{4}\) = \(\frac{?}{12}\), ਤਾਂ ? =
(a) 3
(b) 6
(c) 9
(d) 12.
ਉੱਤਰ:
(c) 9
ਪ੍ਰਸ਼ਨ (ii).
\(\frac{-4}{7}\) = \(\frac{?}{14}\), ਤਾਂ ? =
(a) -4
(b) -8
(c) 4
(d) 8
ਉੱਤਰ:
(b) -8
ਪ੍ਰਸ਼ਨ (iii).
ਪਰਿਮੇਯ ਸੰਖਿਆ \(\frac{-21}{28}\) ਦਾ ਮਿਆਰੀ ਰੂਪ ……. ਹੈ ।
(a) \(\frac{-3}{4}\)
(b) \(\frac{3}{4}\)
(c) \(\frac{3}{7}\)
(d) \(\frac{-3}{7}\)
ਉੱਤਰ:
(a) \(\frac{-3}{4}\)
![]()
ਪ੍ਰਸ਼ਨ (iv).
ਹੇਠ ਲਿਖੀਆਂ ਵਿੱਚੋਂ ਕਿਹੜੀ ਪਰਿਮੇਯ ਸੰਖਿਆ \(\frac{7}{4}\) ਦੇ ਬਰਾਬਰ ਨਹੀਂ ਹੈ ?
(a) \(\frac{14}{-8}\)
(b) \(\frac{21}{-12}\)
(c) \(\frac{28}{-16}\)
(d) \(\frac{7}{-8}\)
ਉੱਤਰ:
(d) \(\frac{7}{-8}\)
ਪ੍ਰਸ਼ਨ (v).
ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਹੜਾ ਸਹੀ ਹੈ ?
(a) 0 > \(\frac{-4}{9}\)
(b) 0 < \(\frac{-4}{9}\) (c) 0 = \(\frac{4}{9}\) (d) ਕੋਈ ਨਹੀਂ । ਉੱਤਰ: (a) 0 > \(\frac{-4}{9}\)
ਪ੍ਰਸ਼ਨ (vi).
ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਹੜਾ ਸਹੀ ਹੈ ?
(a) \(\frac{-4}{5}\) > \(\frac{-3}{10}\)
(b) \(\frac{-4}{5}\) > \(\frac{3}{-10}\)
(c) \(\frac{-4}{5}\) = \(\frac{3}{-10}\)
(d) ਕੋਈ ਨਹੀਂ ।
ਉੱਤਰ:
(a) \(\frac{-4}{5}\) > \(\frac{-3}{10}\)
