Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 10 ਪ੍ਰਯੋਗਿਕ ਰੇਖਾ ਗਣਿਤ Ex 10.3 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 7 Maths Chapter 10 ਪ੍ਰਯੋਗਿਕ ਰੇਖਾ ਗਣਿਤ Exercise 10.3
ਪ੍ਰਸ਼ਨ 1.
ਤ੍ਰਿਭੁਜ ABC ਦੀ ਰਚਨਾ ਕਰੋ ਜਿਸ ਵਿਚ AB = 4 cm, ∠B = 30° BC=4 cm ਹੋਵੇ । ਭੁਜਾਵਾਂ ਦੇ ਆਧਾਰ ਤੇ ਇਸ ਤਿਭੁਜ ਦੀ ਕਿਸਮ ਵੀ ਦੱਸੋ ।
ਹੱਲ :
ਦਿੱਤਾ ਹੈ : △ABC ਦੀਆਂ ਦੋ ਭੁਜਾਵਾਂ AB = 4 cm, BC = 4 cm ਅਤੇ ∠B = 30° ਹਨ ।
ਰਚਨਾ ਦੇ ਪਗ :
ਪਗ 1. ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਅਸੀਂ ABC ਦੀ ਰਫ ਆਕ੍ਰਿਤੀ | ਬਣਾਵਾਂਗੇ ਅਤੇ ਦੋ ਭੁਜਾਵਾਂ ਅਤੇ ਦਿੱਤੇ ਹੋਏ ਕੋਣ ਦਾ ਮਾਪ ਅੰਕਿਤ ਕਰਾਂਗੇ ।
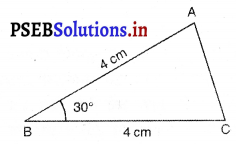
ਪਗ 2. 4 cm ਦੀ ਲੰਬਾਈ ਦਾ ਰੇਖਾਖੰਡ BC ਖਿੱਚੋ ।
![]()
ਪਗ 3. B ਤੋਂ ਕਿਰਨ BX ਖਿੱਚੋ ਜੋ BC ਨਾਲ 30° ਦਾ ਕੋਣ ਬਣਾਵੇ । ਬਿੰਦੂ A ਕਿਰਨ BX ਉੱਤੇ ਕਿਤੇ ਸਥਿਤ ਹੋਵੇਗਾ।)
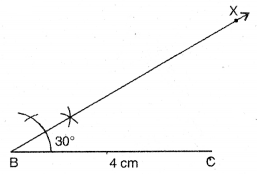
ਪਗ 4. (A ਨੂੰ ਨਿਸ਼ਚਿਤ ਕਰਨ ਦੇ ਲਈ ਦੂਰੀ AB ਦਿੱਤੀ ਹੋਈ ਹੈ) B ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ 4 cm ਅਰਧ ਵਿਆਸ ਵਾਲੀ ਇੱਕ ਚਾਪ ਲਗਾਓ ਜੋ BX ਨੂੰ ਬਿੰਦੂ A ਤੇ ਕੱਟਦੀ ਹੈ ।
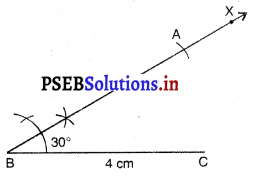
ਪਗ 5. AC ਨੂੰ ਮਿਲਾਓ ।
ਇਸ ਤਰ੍ਹਾਂ ਲੋੜੀਂਦੀ △ABC ਪ੍ਰਾਪਤ ਹੋ ਜਾਂਦੀ ਹੈ ।
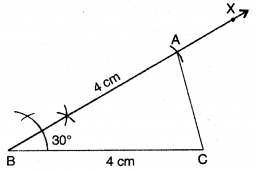
ਕਿਉਂਕਿ ਤ੍ਰਿਭੁਜ ਦੀਆਂ ਦੋ ਭੁਜਾਵਾਂ ਬਰਾਬਰ ਹਨ ।
ਇਸ ਲਈ △PQR ਇੱਕ ਸਮਦੋਭੁਜੀ ਤਿਭੁਜ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 2.
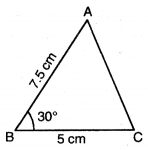
△ABC ਦੀ ਰਚਨਾ ਕਰੋ ਜਿਸ ਵਿਚ AB = 7.5 cm, BC = 5 cm ਅਤੇ ∠B = 30° ਹੋਵੇ ।
ਹੱਲ :
ਦਿੱਤਾ ਹੈ : △ABC ਦੀਆਂ ਦੋ ਭੁਜਾਵਾਂ AB =7.5 cm, BC = 5 cm ਅਤੇ ∠B = 30° ਹਨ ।
ਰਚਨਾ ਦੇ ਪਗ :
ਪਗ 1. ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਅਸੀਂ △ABC ਦੀ ਰਫ ਆਕ੍ਰਿਤੀ ਬਣਾਵਾਂਗੇ ਅਤੇ ਭੁਜਾਵਾਂ ਦੇ ਮਾਪ ਅਤੇ ਦਿੱਤੇ ਕੋਣ ਦਾ ਮਾਪ ਅੰਕਿਤ ਕਰਾਂਗੇ ।
ਪਗ 2. 5 cm ਦੀ ਲੰਬਾਈ ਦਾ ਰੇਖਾਖੰਡ BC ਖਿੱਚੋ ।
![]()
ਪਗ 3. ਬਿੰਦੁ B ਤੋਂ ਕਿਰਨ BX ਖਿੱਚੋ ਜੋ BC ਨਾਲ 30° ਦਾ ਕੋਣ ਬਣਾਵੇ । ਬਿੰਦੁ ਨ ਕੋਣ ਦੀ ਕਿਰਨ BX ਉੱਤੇ ਕਿਤੇ ਸਥਿਤ ਹੋਵੇਗਾ।)
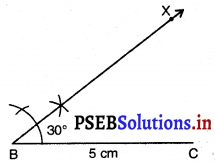
ਪਗ 4. (A ਨੂੰ ਨਿਸ਼ਚਿਤ ਕਰਨ ਦੇ ਲਈ ਦੂਰੀ AB ਦਿੱਤੀ ਹੋਈ ਹੈ।) B ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ 7.5 cm ਅਰਧ ਵਿਆਸ ਵਾਲੀ ਇੱਕ ਚਾਪ ਲਗਾਓ ਜੋ BX ਨੂੰ ਬਿੰਦੂ A ਉੱਤੇ ਕੱਟਦੀ ਹੈ ।
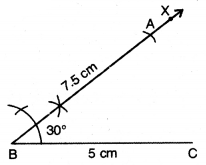
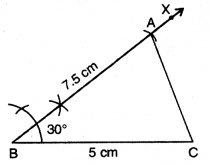
ਪਗ 5. AC ਨੂੰ ਮਿਲਾਓ ।
ਇਸ ਤਰ੍ਹਾਂ ਲੋੜੀਂਦੀ △ABC ਪ੍ਰਾਪਤ ਹੋ ਜਾਂਦੀ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 3.
△XYZ ਦੀ ਰਚਨਾ ਕਰੋ ਜਿਸ ਵਿਚ XY = 6 cm, YZ = 6 cm ਅਤੇ ∠Y = 60° ਹੋਵੇ । ਤ੍ਰਿਭੁਜ ਦੀ ਕਿਸਮ ਵੀ ਦੱਸੋ ।
ਹੱਲ :
ਰਚਨਾ ਦੇ ਪਗ :
ਪਗ 1. ਦਿੱਤੇ ਹੋਏ ਮਾਪ ਦੇ ਨਾਲ XYZ ਦੀ ਰਫ ਆਕ੍ਰਿਤੀ ਬਣਾਉ ।
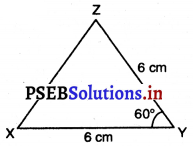
ਪਗ 2. 6 cm ਦੀ ਲੰਬਾਈ ਦਾ ਇੱਕ ਰੇਖਾਖੰਡ XY ਖਿੱਚੋ ।
![]()
ਪਗ 3. ਪਰਕਾਰ ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਬਿੰਦੂ Y ਤੇ, ਕਿਰਨ YA ਖਿੱਚੋ, ਜੋ XY ਨਾਲ 60° ਦਾ ਕੋਣ ਬਣਾਏ ।
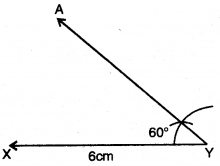
ਪਗ 4. Y ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ ਅਰਧ ਵਿਆਸ 6 cm ਦੀ । ਇੱਕ ਚਾਪ ਲਗਾਓ ਜੋ ਕਿਰਨ YA ਨੂੰ Z ਤੇ ਕੱਟੇ ।
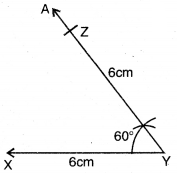
ਪਗ 5. XZ ਨੂੰ ਮਿਲਾਓ । ਲੋੜੀਂਦੀ ਤ੍ਰਿਭੁਜ △XYZ ਹੈ । ਤੀਸਰੀ ਭੁਜਾ ਨੂੰ ਮਾਪੋ | ਅਸੀਂ ਦੇਖਦੇ ਹਾਂ ਕਿ ZX = 6 cm ਹੈ ।
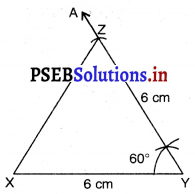
∴ △ XYZ ਵਿਚ
XY = YZ = ZX = 6 cm ਹੈ ।
ਇਸ ਲਈ XYZ ਇੱਕ ਸਮਭੁਜੀ ਤਿਭੁਜ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 4.
ਹੇਠ ਲਿਖੀਆਂ ਵਿਚੋਂ ਕਿਹੜੀ ਤਿਭੁਜ ਦੀ ਰਚਨਾ SAS ਨਿਯਮ ਦੀ ਵਰਤੋਂ ਕਰਕੇ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ ?
(a) AB = 5 cm, BC = 5 cm, CA = 6 cm
(b) AB = 5 cm, BC = 5 cm, ∠B = 40°
(c) ∠A = 60°, ∠B = 60°, ∠C = 60°
(d) BC = 5 cm, ∠B = ∠C = 45°
ਉੱਤਰ :
(b) AB = 5 cm, BC = 5 cm, ∠B = 40°
