Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 9 ਬੀਜਗਣਿਤਕ ਵਿਅੰਜਕ ਅਤੇ ਤਤਸਮਕ InText Questions and Answers.
PSEB 8th Class Maths Solutions Chapter 9 ਬੀਜਗਣਿਤਕ ਵਿਅੰਜਕ ਅਤੇ ਤਤਸਮਕ InText Questions
ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
ਇਕ ਚਲ ਵਾਲੇ ਅਤੇ ਦੋ ਚਲਾਂ ਵਾਲੇ ਵਿਅੰਜਕਾਂ ਦੀਆਂ ਪੰਜ-ਪੰਜ ਉਦਾਹਰਨਾਂ ਦਿਓ ।
ਹੱਲ:
ਇਕ ਚਲ ਵਾਲੇ ਵਿਅੰਜਕਾਂ ਦੀਆਂ ਉਦਾਹਰਨਾਂ :
(i) 4x2 – 4x + 5
(ii) 9x
(iii) – 6x3
(iv) 2x5 + 3x2 + 4x
(v) 5a2 + 6a + 3
ਦੋ ਚਲਾਂ ਵਾਲੇ ਵਿਅੰਜਕਾਂ ਦੀਆਂ ਉਦਾਹਰਨਾਂ :
(i) 5xy + \(\frac{5}{11}\)xy2
(ii) \(-\frac{7}{10}\)ab + \(\frac{1}{3}\)ab2
(iii) 7xy + 5x2y + 3xy2
(iv) 3xy
(v) – 8xy + 9x2y.
ਪ੍ਰਸ਼ਨ 2.
x, x – 4, 2x + 1, 3x – 2 ਨੂੰ ਸੰਖਿਆ ਰੇਖਾ ‘ਤੇ ਦਰਸਾਉ ।
ਹੱਲ:
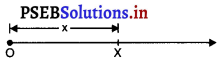
x
ਸੰਖਿਆ ਰੇਖਾ ਉੱਤੇ ਚਲ x ਦੀ ਸਥਿਤੀ X ਹੈ ।
x – 4
ਸੰਖਿਆ ਰੇਖਾ ਉੱਤੇ x – 4 ਦਾ ਮੁੱਲ X ਦੇ ਖੱਬੇ ਪਾਸੇ ਵੱਲ 4 ਇਕਾਈ ਦੀ ਦੂਰੀ ਉੱਤੇ ਬਿੰਦੂ P ਦੇ ਦੁਆਰਾ ਦਰਸਾਇਆ ਜਾਂਦਾ ਹੈ ।
![]()
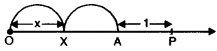
2x + 1
ਸੰਖਿਆ ਰੇਖਾ ਉੱਤੇ 2 ਦੀ ਸਥਿਤੀ ਬਿੰਦੂ A ਉੱਤੇ ਹੋਵੇਗੀ ।
ਮੂਲ ਬਿੰਦੂ ਤੋਂ 8 ਦੀ ਦੂਰੀ X ਦੀ ਦੂਰੀ ਤੋਂ ਦੁੱਗਣੀ ਹੋਵੇਗੀ । 2x + 1 ਦੀ ਸਥਿਤੀ B, A ਦੇ ਸੱਜੇ ਪਾਸੇ 1 ਇਕਾਈ ਦੀ ਦੂਰੀ ਤੇ ਹੋਵੇਗੀ ।
3x – 2
ਸੰਖਿਆ ਰੇਖਾ ਉੱਤੇ 31 ਦੀ ਸਥਿਤੀ ਬਿੰਦੂ B ਉੱਤੇ ਹੋਵੇਗੀ ।
ਲ ਬਿੰਦੂ ਤੋਂ B ਦੀ ਦੁਰੀ ਦੀ ਦੁਰੀ ਤੋਂ ਤਿਗੁਨੀ ਹੋਵੇਗੀ । 3x – 2 ਦੀ ਸਥਿਤੀ P ਦੀ ਸਥਿਤੀ B ਦੇ ਖੱਬੇ ਪਾਸੇ 2 ਇਕਾਈ ਦੀ ਦੂਰੀ ਤੇ ਹੋਵੇਗੀ ।

![]()
ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
ਵਿਅੰਜਕ x2y2 – 10x2y + 5xy2 – 20 ਦੇ ਹਰੇਕ ਪਦ ਦੇ ਗੁਣਜ ਪਹਿਚਾਣੋ ।
ਹੱਲ:
x2y2 ਦਾ ਗੁਣਜ 1 ਹੈ ।
x2y ਦਾ ਗੁਣਜ – 10 ਹੈ ।
xy2 ਦਾ ਗੁਣਜ 5 ਹੈ ।
ਅਚਲ ਪਦ- 20 ਹੈ ।
ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
ਹੇਠਾਂ ਲਿਖੇ ਬਹੁਪਦਾਂ ਨੂੰ ਇਕ ਪਦੀ, ਦੋ ਪਦੀ ਅਤੇ ਤਿੰਨ ਪਦੀ ਦੇ ਰੂਪ ਵਿਚ ਵਰਗੀਕਰਨ ਕਰੋ :
– z + 5, x + y + z, x + y + z + 100, ab – ac, 17.
ਹੱਲ:
ਇਕ ਪਦੀ : 17
ਦੋ ਪਦੀ : – z + 5, ab – ac
ਤਿੰਨਪਦੀ : x + y + z
ਬਹੁਪਦ : x + y + z + 100.
![]()
ਪ੍ਰਸ਼ਨ 2.
ਬਣਾਓ :
(a) ਤਿੰਨ ਇਸ ਤਰ੍ਹਾਂ ਦੇ ਦੋ ਪਦੀ ਜਿਸ ਵਿਚ ਕੇਵਲ ਇਕ ਚਲ x ਹੋਵੇ ।
(b) ਤਿੰਨ ਇਸ ਤਰ੍ਹਾਂ ਦੇ ਦੋ ਪਦੀ ਜਿਸ ਵਿੱਚ x ਅਤੇ y ਚਲ ਹੋਣ ।
(c) ਤਿੰਨ ਇਕ ਪਦੀ ਜਿਸ ਵਿਚ x ਅਤੇ y ਚਲ ਹੋਣ ।
(d) ਚਾਰ ਜਾਂ ਜ਼ਿਆਦਾ ਪਦਾਂ ਵਾਲੇ 2 ਬਹੁਪਦ ।
ਹੱਲ:
(a) ਦੋ ਪਦੀ ਜਿਸ ਵਿਚ ਕੇਵਲ ਇਕ ਚਰ x ਹੋਵੇ
(i) 3x2 + 5x
(ii) 6x3 + 2x
(iii) 9x + 4x3
(b) ਦੋ ਪਦੀ ਜਿਸ ਵਿਚ 1 ਅਤੇ y ਚ ਹੋਵੇ :
(i) 3x2y + 4xy
(ii) 9xy + 6xy2
(iii) 5xy + 8x2y
(c) ਇਕ ਪਦੀ ਜਿਸ ਵਿਚ 1 ਅਤੇ y ਹੋਵੇ :
(i) 4x2y
(ii) 5xy2
(iii) 3xy
(d) ਚਾਰ ਅਤੇ ਜ਼ਿਆਦਾ ਪਦਾਂ ਵਾਲੇ ਬਹੁਪਦ :
(i) a + b + c + d
(ii) 2x3 + 5x2 + 3x + 18
(iii) 3x2 + 4xy + y2 + y + x + 9.
ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
ਹੇਠਾਂ ਲਿਖਿਆਂ ਵਿਚ ਹਰੇਕ ਦੇ ਦੋ ਸਮਾਨ ਪਦ ਲਿਖੋ :
(i) 7xy
(ii) 4 mn2
(iii) 2l.
ਹੱਲ:
(i) 7xy ਦੇ ਸਮਾਨ ਪਦ :
3xy, 9xy ਆਦਿ ।
(ii) 4mn2 ਦੇ ਸਮਾਨ ਪਦ :
9mn2, mnv ਆਦਿ ।
(iii) 2l ਦੇ ਸਮਾਨ ਪਦ :
6l, 9l, 5l ਆਦਿ ।
![]()
ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
4x × 5y × 7z ਪਤਾ ਕਰੋ ।
ਸਭ ਤੋਂ ਪਹਿਲਾਂ 4 × 5y ਪਤਾ ਕਰੋ ਅਤੇ ਫਿਰ ਉਸ ਨੂੰ 7z ਨਾਲ ਗੁਣਾ ਕਰੋ, ਜਾਂ
ਪਹਿਲਾਂ 5y × 7z ਪਤਾ ਕਰੋ, ਅਤੇ ਇਸ ਨੂੰ 4 ਨਾਲ ਗੁਣਾ ਕਰੋ ।
ਕੀ ਨਤੀਜਾ ਇਕੋ ਜਿਹਾ ਹੋਵੇਗਾ ? ਤੁਸੀਂ ਕੀ ਵਿਚਾਰ ਕਰ ਸਕਦੇ ਹੋ ?
ਕੀ ਗੁਣਾ ਕਰਦੇ ਸਮੇਂ ਕ੍ਰਮ ਦਾ ਮਹੱਤਵ ਹੈ ?
ਹੱਲ:
4x × 5y × 7z
= (4x × 5y) × 7z
= [(4 × 5) × (xy}} × 7z
= 20xy × 7z = (20 × 7)
(xy) (z) = 140xyz
= 4x × 5y × 7z
= 4x × (5y × 7z)
= 4x × (5 × 7) (yz)
= 4x × 35yz
= (4 × 35) (xyz)
= 140 xyz
ਨਹੀਂ, ਗੁਣਾ ਕਰਦੇ ਸਮੇਂ ਕੁਮ ਨਤੀਜੇ ਨੂੰ ਪਰਿਵਰਤਿਤ ਨਹੀਂ ਕਰਦਾ ।
ਦੋਨੋਂ ਸਥਿਤੀਆਂ ਵਿਚ ਨਤੀਜਾ ਸਮਾਨ ਹੈ ।
ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
ਗੁਣਨਫਲ ਪਤਾ ਕਰੋ :
(i) 2x (3x + 5xy)
(ii) a2(2ab – 5c).
ਹੱਲ:
(i) (2x) × (3x + 5xy)
= (2x) × (3x) + (2x) × (5xy)
= 6x2 + 10x2y.
(ii) a2(2ab – 5c) = a2 × 2ab – a2 × 5c.
= 2a3b – 5a2c.
![]()
ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
(4p2 + 5p + 7) × 3p ਦਾ ਗੁਣਨਫਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
(4p2 + 5p + 7) × 3p = 4p2 × 3p + 5p × 3p + 7 × 3p
= 12p3 + 15p2 + 21p
ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
ਤਤਸਮਕ (I) ਵਿਚ b ਦੇ ਸਥਾਨ ‘ਤੇ – b ਰੱਖੋ । ਕੀ ਤੁਹਾਨੂੰ ਤਤਸਮਕ (II) ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ ?
ਹੱਲ:
ਤਤਸਮਕ (I) ਹੈ :
(a + b)2 = a2 + 2ab + b2
ਇਸ ਵਿੱਚ b ਦੇ ਸਥਾਨ ਉੱਤੇ -b ਰੱਖਣ ਤੇ, ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
[a +(-b)]2 = a2 + 2a(-b) + (-b)2
ਜੋ (a – b)2 = a2 – 2ab + b
ਜੋ ਕਿ ਤਤਸਮਕ (II) ਹੈ ।
ਇਸ ਲਈ ਤਤਸਮਕ (I) ਵਿਚ b ਦੇ ਸਥਾਨ ਉੱਤੇ b. ਰੱਖਣ ਤੇ ਸਾਨੂੰ ਤਤਸਮਕ (II) ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
![]()
ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
a = 2, b = 3, x= 5 ਦੇ ਲਈ ਤਤਸਮਕ (IV) ਦੀ ਪੜਤਾਲ ਕਰੋ ।
ਹੱਲ:
ਤਤਸਮਕ (IV) ਹੈ।
(x + a) (x + b) = x2 + (a + b)x + ab
L.H.S. = (x + a) (x + b)
= (5 + 2) (5 + 3)
= (7) (8)
= 56
ਅਤੇ R.H.S. = x2 + (a + b) x + ab
= (5)2 + (2 + 3) 5 + 2 × 3
= 25 + 6 × 5 + 6
= 25 + 25 + 6
= 56
∴ L.H.S. = R.H.S. = 56.
ਇਸ ਲਈ ਤਤਸਮਕ ਦੇ ਕੋਣਾਂ ਪੱਖਾਂ ਦੇ ਮੁੱਲ a = 2, b = 3, x = 5 ਦੇ ਲਈ ਸਮਾਨ ਹੈ ।
ਪ੍ਰਸ਼ਨ 2.
ਤਤਸਮਕ (IV) ਵਿਚ a = b ਲੈਣ ‘ਤੇ, ਤੁਸੀਂ ਕੀ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹੋ ? ਕੀ ਇਹ ਤਤਸਮਕ (I) ਨਾਲ ਸੰਬੰਧਿਤ ਹੈ ?
ਹੱਲ:
ਤਤਸਮਕ (IV) ਹੈ :
(x + a) (x + b) = x2 + (a + b)x + ab
ਇਸ ਵਿਚ a = b ਲੈਣ ਤੇ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ :
(x + a) (x + a) = x2 + (a + a) x + a.a
⇒ (x + a)2 = x2 + 2ax + a2
ਹਾਂ, ਇਹ ਤਤਸਮਕ (I) ਨਾਲ ਸੰਬੰਧਿਤ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 3.
ਤਤਸਮਕ (IV) ਵਿਚ a = – c ਅਤੇ b = – c ਲੈਣ ਤੇ, ਤੁਸੀਂ ਕੀ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹੋ ? ਕੀ ਇਹ ਤਤਸਮਕ (II) ਨਾਲ ਸੰਬੰਧਿਤ ਹੈ ?
ਹੱਲ:
ਤਤਸਮਕ (IV) ਹੈ :
(x + a) (x + b) = x2 + (a + b)x + ab
ਇਸ ਵਿਚ a = – c ਅਤੇ b = – c ਲੈਣ ਤੇ, ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ :
[x + (-c)] [x + (-c)] = x2 + [- c) +(-c)]x +(-c) (-c)
⇒ (x – c) (x – c) = x2 + (-2c)x + c2
⇒ (x – c)2 = x2 – 2cx + c2
ਹਾਂ, ਇਹ ਤਤਸਮਕ (II) ਨਾਲ ਸੰਬੰਧਿਤ ਹੈ ।
ਪ੍ਰਸ਼ਨ 4.
ਤਤਸਮਕ (IV) ਵਿਚ b = – a ਲਵੋ । ਤੁਸੀਂ ਕੀ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹੋ ? ਕੀ ਇਹ ਤਤਸਮਕ (III) ਨਾਲ ਸੰਬੰਧਿਤ ਹੈ ?
ਹੱਲ:
ਤਤਸਮਕ (IV) ਹੈ :
(x + a) (x + b) = x2 + (a + b)x + ab
ਇਸ ਵਿਚ b = – a ਲੈਣ ਤੇ, ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ :
(x + a) [x + (-a)] = x2 + [a + (-a)]x + a. (-a)
⇒ (x + a) (x – a) = x2 + (a – a)x – a2
⇒ (x + a) (x – a) = x2 – a2
ਹਾਂ, ਇਹ ਤਤਸਮਕ (III) ਨਾਲ ਸੰਬੰਧਿਤ ਹੈ ।
