Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 13 ਸਿੱਧਾ ਅਤੇ ਉਲਟ ਸਮਾਨ ਅਨੁਪਾਤ InText Questions and Answers.
PSEB 8th Class Maths Solutions Chapter 13 ਸਿੱਧਾ ਅਤੇ ਉਲਟ ਸਮਾਨ ਅਨੁਪਾਤ InText Questions
ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
ਹੇਠ ਲਿਖੀਆਂ ਸਾਰਣੀਆਂ ਨੂੰ ਦੇਖੋ ਤੇ ਪਤਾ ਕਰੋ ਕਿ ਕੀ x ਅਤੇ y ਸਿੱਧੇ ਸਮਾਨ ਅਨੁਪਾਤ ਵਿੱਚ ਹਨ ।
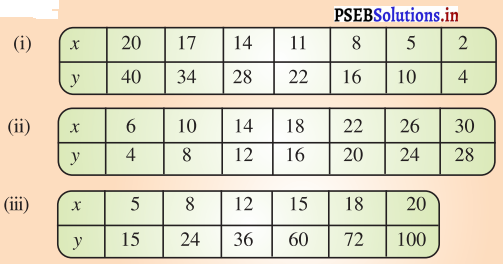
ਹੱਲ:
(i) ਦਿੱਤੀ ਗਈ ਸਾਰਣੀ ਹੈ :
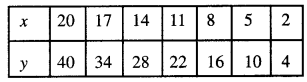
ਇੱਥੇ, ਅਸੀਂ ਦੇਖਦੇ ਹਾਂ ਕਿ ਹਰੇਕ ਸਥਿਤੀ ਵਿਚ \(\frac{x}{y}\) ਵਿਚ ਅਨੁਪਾਤ ਸਮਾਨ ਅਰਥਾਤ ਨੂੰ \(\frac{1}{2}\) ਹੀ ਹੈ । ਇਸ ਲਈ x ਅਤੇ y ਸਮਾਨਅਨੁਪਾਤੀ ਹਨ !
(ii) ਦਿੱਤੀ ਗਈ ਸਾਰਣੀ ਹੈ :
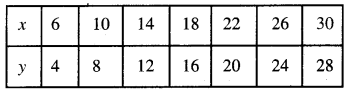
ਇੱਥੇ ਅਸੀਂ ਦੇਖਦੇ ਹਾਂ ਕਿ ਹਰੇਕ ਸਥਿਤੀ ਵਿਚ ਅਨੁਪਾਤ \(\frac{x}{y}\) ਸਮਾਨ ਨਹੀਂ ਹਨ ।
ਇਸ ਲਈ x ਅਤੇ y ਸਮਾਨਅਨੁਪਾਤੀ ਨਹੀਂ ਹਨ ।
![]()
(iii) ਦਿੱਤੀ ਗਈ ਸਾਰਣੀ ਹੈ :
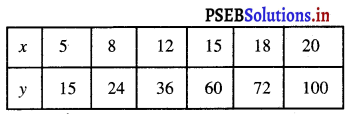
ਇੱਥੇ ਅਸੀਂ ਦੇਖਦੇ ਹਾਂ ਕਿ ਹਰੇਕ ਸਥਿਤੀ ਵਿਚ ਅਨੁਪਾਤ \(\frac{x}{y}\) ਸਮਾਨ ਨਹੀਂ ਹਨ ।
ਇਸ ਲਈ x ਅਤੇ y ਸਮਾਨ ਅਨੁਪਾਤੀ ਨਹੀਂ ਹਨ ।
ਪ੍ਰਸ਼ਨ 2.
ਮੂਲਧਨ = ₹ 1000, ਵਿਆਜ ਦਰ = 8% ਸਲਾਨਾ । ਹੇਠ ਲਿਖੀ ਸਾਰਣੀ ਨੂੰ ਭਰੋ ਅਤੇ ਪਤਾ ਕਰੋ ਕਿ, ਕਿਸ ਤਰ੍ਹਾਂ ਦਾ ਵਿਆਜ (ਸਧਾਰਨ ਜਾਂ ਮਿਸ਼ਰਿਤ ਸਮਾਂ ਅੰਤਰਾਲ ਦੇ ਨਾਲ ਸਿੱਧੇ ਅਨੁਪਾਤ ਵਿਚ ਬਦਲਦਾ ਹੈ ।
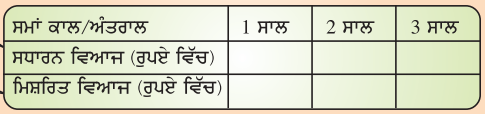
ਹੱਲ:
ਮੁਲਧਨ (P) = ₹ 1000
ਦਰ (R) = 8% ਸਲਾਨਾ
ਸਮਾਂ (t) = 1 ਸਾਲ ਦੇ ਲਈ
ਸਧਾਰਨ ਵਿਆਜ (S.I.) = \(\frac{P×R×T}{100}\)
= ₹ \(\frac{1000×8×1}{100}\) = ₹ 80
ਸਮਾਂ (t) = 2 ਸਾਲ ਦੇ ਲਈ
ਸਧਾਰਨ ਵਿਆਜ (S.I.) = \(\frac{P×R×T}{100}\)
= ₹ \(\frac{1000×8×2}{100}\) = ₹ 160
ਸਮਾਂ (t) = 3 ਸਾਲ ਦੇ ਲਈ
ਸਧਾਰਨ ਵਿਆਜ (S.I.) = \(\frac{P×R×T}{100}\)
= ₹ \(\frac{1000×8×3}{100}\) = ₹ 240
1 ਸਾਲ ਦੇ ਲਈ ਮਿਸ਼ਰਿਤ ਵਿਆਜ
A = P(1 + \(\frac{R}{100}\))t
= ₹ 1000(1 + \(\frac{8}{100}\))1
= ₹ 1000(1 + \(\frac{2}{25}\))1
= ₹ 1000(\(\frac{25+2}{25}\))1
= ₹ 1000(\(\frac{27}{25}\))1
ਕੁੱਲ ਰਾਸ਼ੀ (A) = 1000 × \(\frac{27}{25}\) = ₹ 1080
∴ ਮਿਸ਼ਰਿਤ ਵਿਆਜ = A – P
= 1080 – 1000 = ₹ 80
ਦੋ ਸਾਲ ਦੇ ਲਈ :
A = 1000(\(\frac{27}{25}\))2
= 1000 × \(\frac{27}{25}\) × \(\frac{27}{25}\)
ਕੁੱਲ ਰਾਸ਼ੀ (A) = ₹ 1166.40
∴ ਮਿਸ਼ਰਿਤ ਵਿਆਜ = A – P
= ₹ 66.40 – ₹ 1000
= ₹ 166,40
ਤਿੰਨ ਸਾਲ ਦੇ ਲਈ :
A = 1000(\(\frac{27}{25}\))3
= 1000 × \(\frac{27}{25}\) × \(\frac{27}{25}\) × \(\frac{27}{25}\)
= ₹ 1259.712
∴ ਮਿਸ਼ਰਿਤ ਵਿਆਜ = A – P
= ₹ 1259,712 – ₹ 1000
= ₹ 259.712
ਲੋੜੀਂਦੀ ਸਾਰਣੀ ਹੈ :
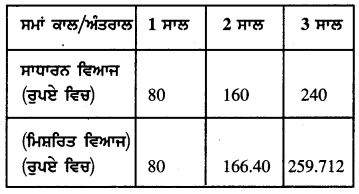
ਸਾਰਣੀ ਤੋਂ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਸਧਾਰਨ ਵਿਆਜ ਸਮਾਂ ਅਵਧੀ ਦੇ ਨਾਲ ਪ੍ਰਤੱਖ ਅਨੁਪਾਤ ਵਿਚ ਬਦਲਦਾ ਹੈ ।
![]()
ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
ਹੇਠ ਲਿਖੀ ਸਾਰਣੀਆਂ ਨੂੰ ਦੇਖੋ ਅਤੇ ਪਤਾ ਕਰੋ ਕਿ ਕਿਹੜੇਕਿਹੜੇ ਚਲਾਂ ( ਇੱਥੇ x ਅਤੇ y) ਦੇ ਜੋੜੇ ਆਪਸ ਵਿਚ ਉਲਟ ਸਮਾਨ ਅਨੁਪਾਤ ਵਿਚ ਹਨ :
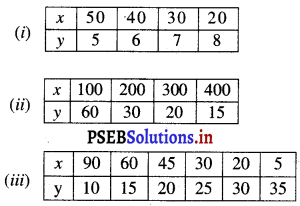
ਹੱਲ:
(i) ਇੱਥੇ, ਦਿੱਤੀ ਗਈ ਸਾਰਣੀ ਵਿਚ ਗੁਣਨਫਲxy ਅਚੱਲ ਨਹੀਂ ਹੈ ।
∴ x ਅਤੇ y ਉਲਟ ਸਮਾਨ ਅਨੁਪਾਤ ਵਿਚ ਨਹੀਂ ਹੈ ।
(ii) ਇੱਥੇ ਦਿੱਤੀ ਗਈ ਸਾਰਣੀ ਵਿਚ ਗੁਣਨਫਲ xy ਅਰਥਾਤ 6000 ਅਚੱਲ ਹੈ ।
∴ x ਅਤੇ y ਉਲਟ ਸਮਾਨ ਅਨੁਪਾਤ ਵਿਚ ਨਹੀਂ ਹੈ ।
(iii) ਇੱਥੇ, ਦਿੱਤੀ ਗਈ ਸਾਰਣੀ ਵਿਚ ਗੁਣਨਫਲ xy ਅਚੱਲ ਨਹੀਂ ਹੈ ।
∴ x ਅਤੇ y ਉਲਟ ਸਮਾਨ ਅਨੁਪਾਤ ਨਹੀਂ ਹੈ ।
