Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 16 ਸੰਖਿਆਵਾਂ ਦੇ ਨਾਲ ਖੇਡਣਾ InText Questions and Answers.
PSEB 8th Class Maths Solutions Chapter 16 ਸੰਖਿਆਵਾਂ ਦੇ ਨਾਲ ਖੇਡਣਾ InText Questions
ਕੋਸ਼ਿਸ਼ ਕਰੋ :
1. ਹੇਠ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਨੂੰ ਵਿਆਪਕ ਰੂਪ ਵਿਚ ਲਿਖੋ :
ਪ੍ਰਸ਼ਨ (i).
25
ਹੱਲ:
25 = 20 + 5 = (10 × 2) + 5
ਪ੍ਰਸ਼ਨ (ii).
73
ਹੱਲ:
73 = 70 + 3 = (10 × 7) + 3
ਪ੍ਰਸ਼ਨ (iii).
129
ਹੱਲ:
129 = 100 + 20 +9 = (100 × 1) + (10 × 2) + 9 × 1
![]()
ਪ੍ਰਸ਼ਨ (iv).
302.
ਹੱਲ:
302 = 300 + 2 = (100 × 3) + (10 × 0) + 2 × 1.
ਪ੍ਰਸ਼ਨ 2.
ਹੇਠਾਂ ਲਿਖਿਆਂ ਨੂੰ ਸਧਾਰਨ ਰੂਪ ਵਿਚ ਲਿਖੋ :
(i) 10 × 5 + 6
(ii) 100 × 7 + 10 × 1 + 8
(iii) 100a + 10c + b.
ਹੱਲ:
(i) 10 × 5 + 6 = 50 + 6 = 56
(ii) 100 × 7 + 10 × 1 + 8 = 700 + 10 + 8
= 718
(iii) 100a + 10c + b = 100 × a + 10 × c + 1 × b = acb
ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪੜਤਾਲ ਕਰੋ ਕਿ ਜੇ ਸੁੰਦਰਮ ਨੇ ਹੇਠ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਚੁਣੀਆਂ ਹੁੰਦੀਆਂ, ਤਾਂ ਕੀ ਨਤੀਜੇ ਪ੍ਰਾਪਤ ਹੁੰਦੇ :
ਪ੍ਰਸ਼ਨ (i).
27
ਹੱਲ:
27 ਅੰਕ ਉਲਟਾਉਣ ਤੇ ਸੰਖਿਆ = 72
ਦੋਵਾਂ ਦਾ ਜੋੜ 27 + 72 = 99
ਭਾਗ = 99 ÷ 11 = 9, ਬਾਕੀ = 0
ਨਾਲ ਹੀ ; 2 +7 = 9
ਐਰਥਾਤ ਭਾਗਫਲ ਉਸਦੇ ਦੁਆਰਾ ਚੁਣੀ ਗਈ ਸੰਖਿਆ ਦੇ ਅੰਕਾਂ ਦੇ ਜੋੜਫਲ ਬਰਾਬਰ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ (ii).
39
ਹੱਲ:
39 ਅੰਕ ਉਲਟਾਉਣ ਤੇ ਸੰਖਿਆ = 93
ਦੋਵਾਂ ਦਾ ਜੋੜ 39 + 93 = 132
ਭਾਗ = 132 ÷ 11 = 12, ਬਾਕੀ = 0
ਨਾਲ ਹੀ ; 3 + 9 = 12
ਅਰਥਾਤ ਭਾਗਫਲ ਉਸਦੇ ਦੁਆਰਾ ਚੁਣੀ ਗਈ ਸਿਖਿਆ ਦੇ ਜੋੜਫਲ ਦੇ ਬਰਾਬਰ ਹੈ ।
ਪ੍ਰਸ਼ਨ (iii).
64
ਹੱਲ:
64 ਅੰਕ ਉਲਟਾਉਣ ਤੇ ਸੰਖਿਆ = 46
ਦੋਵਾਂ ਦਾ ਜੋੜ 64 + 46 = 110
ਭਾਗ = 110 ÷ 11 = 10, ਬਾਕੀ = 0.
ਨਾਲ ਹੀ; 6 + 4 = 10
ਅਰਥਾਤ ਭਾਗਫਲ ਉਸਦੇ ਦੁਆਰਾ ਚੁਣੀ ਗਈ ਸੰਖਿਆ ਦੇ ਅੰਕਾਂ ਦੇ ਜੋੜਫਲ ਦੇ ਬਰਾਬਰ ਹੈ ।
ਪ੍ਰਸ਼ਨ (iv).
17.
ਹੱਲ:
17 ਅੰਕ ਉਲਟਾਉਣ ਤੇ ਸੰਖਿਆ = 71
ਦੋਵਾਂ ਦਾ ਜੋੜ 17 + 71 = 88
ਭਾਗ = 88 ÷ 1 = 8, ਬਾਕੀ = 0
ਨਾਲ ਹੀ : 1 + 7 = 8
ਅਰਥਾਤ ਭਾਗਵਲ ਉਸਦੇ ਦੁਆਰਾ ਚੁਣੀ ਗਈ ਸੰਖਿਆ ਦੇ ਅੰਕਾਂ ਦੇ ਜੋੜਫਲ ਦੇ ਬਰਾਬਰ ਹੈ ।
![]()
ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪੜਤਾਲ ਕਰੋ ਕਿ ਜੇ ਸੁੰਦਰਮ ਨੇ ਉਪਰੋਕਤ ਦੇ ਲਈ ਹੇਠ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਚੁਣੀਆਂ ਹੁੰਦੀਆਂ, ਤਾਂ ਕੀ ਨਤੀਜੇ ਮਿਲਦੇ :
ਪ੍ਰਸ਼ਨ (i).
17
ਹੱਲ:
17
ਅੰਕਾਂ ਨੂੰ ਪਲਟਣ ਤੇ, ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ : 71
ਅੰਤਰ = 71 – 17 = 54
ਭਾਗ = 54 ÷ 9 = 6, ਬਾਕੀ = 0
ਨਾਲ ਹੀ ; 7 – 1 = 6.
ਅਰਥਾਤ ਭਾਗਫਲ ਉਸਦੇ ਦੁਆਰਾ ਚੁਣੀ ਗਈ ਸੰਖਿਆ ਦੇ ਅੰਕਾਂ ਦਾ ਅੰਤਰ ਹੈ ।
ਪ੍ਰਸ਼ਨ (ii).
21
ਹੱਲ:
21
ਅੰਕਾਂ ਨੂੰ ਪਲਟਣ ਤੇ, ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ : 12
ਅੰਤਰ = 21 – 12 = 9
ਭਾਗ = 9 ÷ 9 = 1, ਬਾਕੀ = 0
ਨਾਲ ਹੀ ; 2 – 1 = 1
ਅਰਥਾਤ ਭਾਗਫਲ ਉਸਦੇ ਦੁਆਰਾ ਚੁਣੀ ਗਈ ਸੰਖਿਆ ਦੇ ਅੰਕਾਂ ਦਾ ਅੰਤਰ ਹੈ ।
ਪ੍ਰਸ਼ਨ (iii).
96
ਹੱਲ:
96
ਅੰਕਾਂ ਨੂੰ ਪਲਟਣ ਤੇ, ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ : 69
ਅੰਤਰ = 96 – 69 = 27
ਭਾਗ = 27 ÷ 9 = 3, ਬਾਕੀ = 0
ਨਾਲ ਹੀ ; 9 – 6 = 3
ਅਰਥਾਤ ਭਾਗਫਲ ਉਸਦੇ ਦੁਆਰਾ ਚੁਣੀ ਗਈ ਸੰਖਿਆ ਦੇ ਅੰਕਾਂ ਦਾ ਅੰਤਰ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ (iv).
37.
ਹੱਲ:
37
ਅੰਕਾਂ ਨੂੰ ਪਲਟਣ ਤੇ, ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ : 73.
ਅੰਤਰ = 73 – 37 = 36
ਭਾਗ = 36 ÷ 9 = 4, ਬਾਕੀ = 0
ਨਾਲ ਹੀ ; 7 – 3 = 4
ਅਰਥਾਤ ਭਾਗਫਲ ਉਸਦੇ ਦੁਆਰਾ ਚੁਣੀ ਗਈ ਸੰਖਿਆ ਦੇ ਅੰਕਾਂ ਦਾ ਅੰਤਰ ਹੈ ।
ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪੜਤਾਲ ਕਰੋ ਕਿ ਜੇ ਮੀਨਾਕਸ਼ੀ ਨੇ ਹੇਠਾਂ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਚੁਣੀਆਂ ਹੁੰਦੀਆਂ, ਤਾਂ ਨਤੀਜਾ ਕੀ ਮਿਲਦਾ ? ਹਰੇਕ ਸਥਿਤੀ ਵਿਚ, ਅੰਤ ਵਿਚ ਪ੍ਰਾਪਤ ਹੋਏ ਭਾਗਫਲ ਦਾ ਇਕ ਰਿਕਾਰਡ (record) ਰੱਖੋ ।
ਪ੍ਰਸ਼ਨ (i).
132
ਹੱਲ:
132
ਅੰਕਾਂ ਨੂੰ ਪਲਟਣ ਤੇ, ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ : 231
∴ ਅੰਤਰ = 231 – 132 = 99
ਹੁਣ; 99 ÷ 99 = 1, ਭਾਗਫਲ = 1, ਬਾਕੀ = 0
ਨਾਲ ਹੀ; 2 – 1 = 1
ਅਰਥਾਤ ਭਾਗਫਲ ਸੈਂਕੜੇ ਦੇ ਅੰਕ ਅਤੇ ਇਕਾਈ ਦੇ ਅੰਕ ਦੇ ਅੰਤਰ ਦੇ ਬਰਾਬਰ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ (ii).
469
ਹੱਲ:
469
ਅੰਕਾਂ ਨੂੰ ਪਲਟਣ ਤੇ, ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ : 964.
∴ ਅੰਤਰ = 964 – 469 = 495
ਹੁਣ; 495 ÷ 99 = 5, ਭਾਗਫਲ = 5, ਬਾਕੀ = 0
ਨਾਲ ਹੀ; 9 – 4 = 5
ਅਰਥਾਤ ਭਾਗਵਲ ਸੈਂਕੜੇ ਦੇ ਅੰਕ ਅਤੇ ਇਕਾਈ ਦੇ ਅੰਕ ਦੇ ਅੰਤਰ ਦੇ ਬਰਾਬਰ ਹੈ ।
ਪ੍ਰਸ਼ਨ (iii).
737
ਹੱਲ:
737
ਅੰਕਾਂ ਨੂੰ ਉਲਟਣ ਤੇ, ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ : 737
∴ ਅੰਤਰ = 737 – 737 = 0
ਹੁਣ; 0 ÷ 99 = 0, ਭਾਗਫਲ = 0, ਬਾਕੀ = 0
ਨਾਲ ਹੀ; 7 – 7 = 0
ਅਰਥਾਤ ਭਾਗਫਲ ਸੈਂਕੜੇ ਦੇ ਅੰਕ ਅਤੇ ਇਕਾਈ ਦੇ ਅੰਕ ਦੇ ਅੰਤਰ ਦੇ ਬਰਾਬਰ ਹੈ ।
ਪ੍ਰਸ਼ਨ (iv).
901.
ਹੱਲ:
901
ਅੰਕਾਂ ਨੂੰ ਉਲਟਣ ਤੇ, ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ : 109.
∴ ਅੰਤਰ. = 901 – 109 = 792
ਹੁਣ; 792 ÷ 99 = 8, ਭਾਗਫਲ = 8, ਬਾਕੀ = 0
ਨਾਲ ਹੀ; 9 – 1 = 8
ਅਰਥਾਤ ਭਾਗਫਲ ਸੈਂਕੜੇ ਦੇ ਅੰਕ ਅਤੇ ਇਕਾਈ ਦੇ ਅੰਕ ਦੇ ਅੰਤਰ ਦੇ ਬਰਾਬਰ ਹੈ ।
![]()
ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪੜਤਾਲ ਕਰੋ ਕਿ ਜੇ ਸੁੰਦਰਮ ਨੇ ਹੇਠਾਂ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਸੋਚੀਆਂ ਹੁੰਦੀਆਂ, ਤਾਂ ਨਤੀਜਾ ਕੀ ਮਿਲਦਾਂ :
ਪ੍ਰਸ਼ਨ (i).
417
ਹੱਲ:
417
ਇੱਥੇ: 417
ਹੁਣ; 741 ਲਵੋ
[ਅਰਥਾਤ ਇਕਾਈ ਦਾ ਅੰਕ ਉਸ ਸੰਖਿਆ ਦੇ ਸਭ ਤੋਂ ਖੱਬੇ ਸਿਰੇ ਉੱਤੇ ਪਹੁੰਚ ਗਿਆ ਹੈ] ਤਾਂ; 174
[ਅਰਥਾਤ ਸੈਂਕੜੇ ਦਾ ਅੰਕ ਉਸ ਸੰਖਿਆ ਦੇ ਸਭ ਤੋਂ ਸੱਜੇ ਸਿਰੇ ਤੇ ਪਹੁੰਚ ਗਿਆ ਹੈ |]
ਇਨ੍ਹਾਂ ਸਾਰੀ ਤਿੰਨਾਂ ਸੰਖਿਆਵਾਂ ਨੂੰ ਜੋੜਨ ਤੇ, ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :

ਇਸ ਸੰਖਿਆ ਨੂੰ 37 ਨਾਲ ਭਾਗ ਦੇਣ ਤੇ, ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
ਅਰਥਾਤ 1332 ÷ 37 = 36 (ਕੋਈ ਬਾਕੀ ਨਹੀਂ)
ਪ੍ਰਸ਼ਨ (ii).
632
ਹੱਲ:
632
ਇੱਥੇ; 632
ਹੁਣ; 263 ਲਵੋ ।
ਅਰਥਾਤ ਇਕਾਈ ਦਾ ਅੰਕ ਉਸ ਸੰਖਿਆ ਦੇ ਸਭ ਤੋਂ ਖੱਬੇ ਸਿਰੇ ਉੱਤੇ ਪਹੁੰਚ ਗਿਆ ਹੈ। ਹੁਣ; 326
[ਅਰਥਾਤ ਸੈਂਕੜੇ ਦਾ ਅੰਕ ਉਸ ਸੰਖਿਆ ਦੇ ਸਭ ਤੋਂ ਸੱਜੇ ਸਿਰੇ ਤੇ ਪਹੁੰਚ ਗਿਆ ਹੈ ]
ਇਨ੍ਹਾਂ ਸਾਰੀ ਤਿੰਨਾਂ ਸੰਖਿਆਵਾਂ ਨੂੰ ਜੋੜਨ ਤੇ, ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
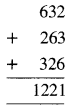
ਇਸ ਸੰਖਿਆ ਨੂੰ 37 ਨਾਲ ਭਾਗ ਦੇਣ ਤੇ, ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
ਅਰਥਾਤ 1221 ÷ 37 = 33 (ਕੋਈ ਬਾਕੀ ਨਹੀਂ)
![]()
ਪ੍ਰਸ਼ਨ (iii).
117
ਹੱਲ:
117
ਇਹ; 117
ਹੁਣ; 711 ਲਵੋ
[ਅਰਥਾਤ ਇਕਾਈ ਦਾ ਅੰਕ ਉਸ ਸੰਖਿਆ ਦੇ ਸਭ ਤੋਂ ਖੱਬੇ ਸਿਰੇ ਉੱਤੇ ਪਹੁੰਚ ਗਿਆ ਹੈ।]
ਹੁਣ; 171
[ਅਰਥਾਤ ਸੈਂਕੜੇ ਦਾ ਅੰਕ ਉਸ ਸੰਖਿਆ ਦੇ ਸਭ ਤੋਂ ਸੱਜੇ ਸਿਰੇ ਤੇ ਪਹੁੰਚ ਗਿਆ ਹੈ |]
ਇਨ੍ਹਾਂ ਸਾਰੀ ਸੰਖਿਆਵਾਂ ਨੂੰ ਜੋੜਨ ਤੇ, ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
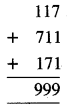
ਇਸ ਸੰਖਿਆ ਨੂੰ 37 ਨਾਲ ਭਾਗ ਦੇਣ ਤੇ, ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ
ਅਰਥਾਤ 999 ÷ 37 = 27 (ਕੋਈ ਬਾਕੀ ਨਹੀਂ)
ਪ੍ਰਸ਼ਨ (iv).
937.
ਹੱਲ:
937
ਇੱਥੇ; 937
ਹੁਣ; 793 ਲਵੋ
[ਅਰਥਾਤ ਇਕਾਈ ਦਾ ਅੰਕ ਉਸ ਸੰਖਿਆ ਦੇ ਸਭ ਤੋਂ ਖੱਬੇ ਸਿਰੇ ਉੱਤੇ ਪਹੁੰਚ ਗਿਆ ਹੈ।]
ਹੁਣ; 379
[ਅਰਥਾਤ ਸੈਂਕੜੇ ਦਾ ਅੰਕ ਉਸ ਸੰਖਿਆ ਦੇ ਸਭ ਤੋਂ ਸੱਜੇ ਸ਼ਿਰੇ ਤੇ ਪਹੁੰਚ ਗਿਆ ਹੈ |]
ਇਨ੍ਹਾਂ ਸਾਰੇ ਤਿੰਨ ਸੰਖਿਆਵਾਂ ਨੂੰ ਜੋੜਨ ਤੇ, ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
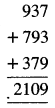
ਇਸ ਸੰਖਿਆ ਨੂੰ 37, ਨਾਲ ਭਾਗ ਕਰਨ ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
ਅਰਥਾਤ 2109 ÷ 37 = 57 (ਕੋਈ ਬਾਕੀ ਨਹੀਂ)
![]()
ਇਸ ਨੂੰ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
ਦੋ ਅੰਕਾਂ ਦੀ ਇਕ ਸੰਖਿਆ ab ਲਿਖੋ ਅਤੇ ਇਸਦੇ ਅੰਕਾਂ ਨੂੰ ਪਲਟਣ ਤੇ ਪ੍ਰਾਪਤ ਸੰਖਿਆ ba ਲਿਖੋ ।
ਇਹਨਾਂ ਦਾ ਜੋੜ ਪਤਾ ਕਰੋ । ਮੰਨ ਲਉ ਇਹ ਜੋੜ ਇਕ | ਤਿੰਨ ਅੰਕਾਂ ਦੀ ਸੰਖਿਆ dad ਹੈ ।
ਭਾਵ ab + ba = dad
(10 a + b) + (10 b + a) = dad
11(a + b) = dad
ਜੋੜ (a + b) ਸੰਖਿਆ 18 ਤੋਂ ਜ਼ਿਆਦਾ ਨਹੀਂ ਹੋ ਸਕਦਾ (ਕਿਉਂ ?)
ਕੀ dad, 11 ਦਾ ਇਕ ਗੁਣ ਹੈ ?
ਕੀ dad, 198 ਤੋਂ ਘੱਟ ਹੈ ? 198 ਤਕ ਤਿੰਨ ਅੰਕਾਂ ਦੀਆਂ ਅਜਿਹੀ ਸਾਰੀਆਂ ਸੰਖਿਆਵਾਂ ਲਿਖੋ, ਜੋ 11 ਦਾ ਗੁਣ ਹਨ ? a ਅਤੇ d ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਦੋ-ਅੰਕਾਂ ਦੀ ਸੰਖਿਆ ab ਹੈ । ਇਸ ਦੇ ਅੰਕਾਂ ਨੂੰ ਪਲਟਣ ਤੇ ਪ੍ਰਾਪਤ ਸੰਖਿਆ ba ਹੈ ।
ਮੰਨ ਲਉ ab ਅਤੇ ba ਦਾ ਜੋੜ ਇਕ ਤਿੰਨ ਅੰਕਾਂ ਦੀ ਸੰਖਿਆ dad ਹੈ ।
ab + ba = dad
⇒ (10 + b) + (10b + a) = dad
⇒ 11(a + b) = dad ਜੋੜ
(a + b), 18 ਤੋਂ ਜ਼ਿਆਦਾ ਨਹੀਂ ਹੋ ਸਕਦੀ ਕਿਉਂਕਿ ਦੋ ਅੰਕਾਂ ਦੀ ਸਭ ਤੋਂ ਵੱਡੀ ਸੰਖਿਆ 99 ਹੋ ਸਕਦੀ ਹੈ, ਜਦਕਿ 99 + 99 = 198 ਹੁੰਦਾ ਹੈ ।
ਅੰਤ ਸੰਖਿਆ dad, 11 ਦਾ ਇਕ ਗੁਣਜ ਹੈ ।
ਸੰਖਿਆ 198 ਤੱਕ ਤਿੰਨ ਅੰਕਾਂ ਦੀ ਅਜਿਹੀਆਂ ਸਾਰੀਆਂ ਸੰਖਿਆਵਾਂ, ਜੋ 11 ਦੀ ਗੁਣਜ ਹੈ ।
110, 121, 132, 43, 154, 165, 176, 187 ਅਤੇ 198 ਹੈ ।
ਸਪੱਸ਼ਟ ਹੈ ਕਿ dad = 121
⇒ a = 2, d = 1.
ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪਹਿਲਾ ਪ੍ਰਸ਼ਨ ਤੁਹਾਡੀ ਸਹਾਇਤਾ ਦੇ ਲਈ ਕੀਤਾ ਹੋਇਆ ਹੈ ।
ਪ੍ਰਸ਼ਨ 1.
ਜਦ ਭਾਗ N ÷ 5 ਤੋਂ ਬਾਕੀ 3 ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ਤਾਂ N ਦੀ ਇਕਾਈ ਦਾ ਅੰਕ ਕੀ ਹੋ ਸਕਦਾ ਹੈ ?
ਹੱਲ:
ਇਕਾਈ ਦੇ ਅੰਕ ਨੂੰ 5 ਨਾਲ ਭਾਗ ਦੇਣ ਤੇ ਬਾਕੀ 3 ਆਉਣਾ ਚਾਹੀਦਾ ਹੈ । ਇਸ ਲਈ ਇਕਾਈ ਦਾ ਅੰਕ ਜਾਂ ਤਾਂ 3 ਜਾਂ 8 ਹੋਵੇਗਾ ।
![]()
ਪ੍ਰਸ਼ਨ 2.
ਜਦ ਭਾਗ N ÷ 5 ਤੋਂ ਬਾਕੀ 1 ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ, ਤਾਂ N ਦੀ ਇਕਾਈ ਦਾ ਅੰਕ ਕੀ ਹੋ ਸਕਦਾ ਹੈ ?
ਹੱਲ:
ਇਕਾਈ ਦੇ ਅੰਕ ਨੂੰ ਜਦੋਂ5 ਨਾਲ ਭਾਗ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਤਾਂ ਬਾਕੀ 1 ਆਉਣਾ ਚਾਹੀਦਾ ਹੈ । ਇਸ ਲਈ ਇਕਾਈ ਦਾ ਅੰਕ ਜਾਂ ਤਾਂ 1 ਜਾਂ 6 ਹੋਵੇਗਾ ।
ਪ੍ਰਸ਼ਨ 3.
ਜਦ ਭਾਗ N ÷ 5 ਤੋਂ ਬਾਕੀ4 ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ, ਤਾਂN ਦੀ ਇਕਾਈ ਦਾ ਅੰਕ ਕੀ ਹੋ ਸਕਦਾ ਹੈ ?
ਹੱਲ:
ਇਕਾਈ ਦੇ ਅੰਕ ਨੂੰ ਜਦੋਂ 5 ਨਾਲ ਭਾਗ ਕੀਤਾ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਬਾਕੀ 4 ਆਉਣਾ ਚਾਹੀਦਾ ਹੈ । ਇਸ ਲਈ ਇਕਾਈ ਦਾ ਅੰਕ ਜਾਂ ਤਾਂ 4 ਜਾਂ 9 ਹੋਵੇਗਾ ।
ਕੋਸ਼ਿਸ਼ ਕਰੋ :
(ਪਹਿਲਾ ਪ੍ਰਸ਼ਨ ਤੁਹਾਡੀ ਸਹਾਇਤਾ ਦੇ ਲਈ ਕੀਤਾ ਹੋਇਆ ਹੈ।)
ਪ੍ਰਸ਼ਨ 1.
ਜਦ ਭਾਗ N ÷ 2 ਤੋਂ ਬਾਕੀ 1 ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ, ਤਾਂ N ਦੀ ਇਕਾਈ ਦਾ ਅੰਕ ਕੀ ਹੋ ਸਕਦਾ ਹੈ ?
ਹੱਲ:
N ਇਕ ਟਾਂਕ ਸੰਖਿਆ ਹੈ । ਇਸ ਲਈ ਇਸ ਇਕਾਈ ਦਾ ਅੰਕ ਵੀ ਟਾਂਕ ਸੰਖਿਆ ਹੋਵੇਗਾ ।
ਇਸ ਲਈ N ਦੀ ਇਕਾਈ ਦਾ ਅੰਕ 1, 3, 5, 7 ਜਾਂ 9 ਹੋਵੇਗਾ ।
![]()
ਪ੍ਰਸ਼ਨ 2.
ਜਦ ਭਾਗ N ÷ 2 ਤੋਂ ਕੋਈ ਬਾਕੀ ਪ੍ਰਾਪਤ ਨਹੀਂ ਹੁੰਦਾ ( ਭਾਵ ਬਾਕੀ 0 ਹੈ), ਤਾਂ ਕਿ ਦੀ ਇਕਾਈ ਦਾ ਅੰਕ ਕੀ ਹੋ ਸਕਦਾ
ਹੈ ?
ਹੱਲ:
N ਇਕ ਜਿਸਤ ਸੰਖਿਆ ਹੈ ਇਸ ਲਈ ਇਸਦੀ ਇਕਾਈ ਦਾ ਅੰਕ ਵੀ ਜਿਸਤ ਸੰਖਿਆ ਹੋਵੇਗਾ । ਇਸ ਲਈ ਇਕਾਈ ਦਾ ਅੰਕ 2, 4, 8 ਜਾਂ 0 ਹੋਵੇਗਾ ।
ਪ੍ਰਸ਼ਨ 3.
ਮੰਨ ਲਵੋ ਕਿ ਭਾਗ N ÷ 5 ਨਾਲ ਬਾਕੀ 4 ਅਤੇ ਭਾਗ N ÷ 2 ਨਾਲ ਬਾਕੀ 1 ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ । N ਦੀ ਇਕਾਈ ਦਾ ਅੰਕ ਕੀ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ?
ਹੱਲ:
ਆਪ
ਕੋਸ਼ਿਸ਼ ਕਰੋ ।
ਹੇਠਾਂ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਨੂੰ 9 ਨਾਲ ਭਾਜਯੋਗਤਾ ਦੀ ਪੜਤਾਲ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
108
ਹੱਲ:
108.
108 ਦੇ ਅੰਕਾਂ ਦਾ ਜੋੜ = 1 + 0 + 8 = 9.
ਕਿਉਂਕਿ ਇਹ ਸੰਖਿਆ 9 ਨਾਲ ਭਾਜਯੋਗ ਹੈ ।
∴ ਸੰਖਿਆ 108, 9 ਨਾਲ ਭਾਜਯੋਗ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 2.
616
ਹੱਲ:
616.
616 ਦੇ ਅੰਕਾਂ ਦਾ ਜੋੜ = 6 + 1 + 6 = 13.
ਕਿਉਂਕਿ ਇਹ ਸੰਖਿਆ 9 ਨਾਲ ਭਾਜਯੋਗ ਨਹੀਂ ਹੈ ।
∴ ਸੰਖਿਆ 616, 9 ਨਾਲ ਭਾਜਯੋਗ ਨਹੀਂ ਹੈ ।
ਪ੍ਰਸ਼ਨ 3.
294
ਹੱਲ:
294.
294 ਦੇ ਅੰਕਾਂ ਦਾ ਜੋੜ= 2 + 9 + 4 = 15.
ਕਿਉਂਕਿ ਇਹ ਸੰਖਿਆ 9 ਨਾਲ ਭਾਜਯੋਗ ਨਹੀਂ ਹੈ ।
∴ ਸੰਖਿਆ 294, 9 ਨਾਲ ਭਾਜਯੋਗ ਨਹੀਂ ਹੈ ।
ਪ੍ਰਸ਼ਨ 4.
432
ਹੱਲ:
432.
432 ਦੇ ਅੰਕਾਂ ਦਾ ਜੋੜ = 4 + 3 + 2 = 9.
ਕਿਉਂਕਿ ਇਹ ਸੰਖਿਆ 9 ਨਾਲ ਭਾਜਯੋਗ ਹੈ ।
∴ ਸੰਖਿਆ 432, 9 ਨਾਲ ਭਾਜਯੋਗ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 5.
927
ਹੱਲ:
927.
927 ਦੇ ਅੰਕਾਂ ਦਾ ਜੋੜ = 9 + 2 + 7 = 18
ਕਿਉਂਕਿ ਇਹ ਸੰਖਿਆ 9 ਨਾਲ ਭਾਜਯੋਗ ਹੈ ।
∴ ਸੰਖਿਆ 92, 9 ਨਾਲ ਭਾਜਯੋਗ ਹੈ ।
ਸੋਚੋ, ਚਰਚਾ ਕਰੋ ਅਤੇ ਲਿਖੋ
ਪ੍ਰਸ਼ਨ 1.
ਤੁਸੀਂ ਦੇਖ ਚੁੱਕੇ ਹੋ ਕਿ 450, 10 ਨਾਲ ਭਾਜਯੋਗ ਹੈ । ਇਹ 2 ਅਤੇ 5 ਨਾਲ ਵੀ ਭਾਜਯੋਗ ਹੈ, ਜੋ 10 ਦੇ ਗੁਣਨਖੰਡ ” ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਸੰਖਿਆ 135, 9 ਨਾਲ ਭਾਜਯੋਗ ਹੈ । ਇਹ 3 ਨਾਲ ਵੀ ਭਾਜਯੋਗ ਹੈ, ਜੋ 9 ਦਾ ਇਕ ਗੁਣਨਖੰਡ ਹੈ ।
ਕੀ ਤੁਸੀਂ ਕਹਿ ਸਕਦੇ ਹੋ ਕਿ ਜਦੋਂ ਕੋਈ ਸੰਖਿਆ ਕਿਸੇ | ਸੰਖਿਆ ਅ ਨਾਲ ਭਾਜਯੋਗ ਹੋਵੇ, ਤਾਂ ਇਹ ਅ ਦੇ ਹਰੇਕ ਗੁਣਨਖੰਡ ਨਾਲ ਵੀ ਭਾਜਯੋਗ ਹੋਵੇਗੀ ?
ਹੱਲ:
ਹਾਂ, ਅਸੀਂ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਜੇਕਰ ਕੋਈ ਸੰਖਿਆ ਕਿਸੇ ਸੰਖਿਆ ਅ ਨਾਲ ਭਾਜਯੋਗ ਹੋਵੇ, ਤਾਂ ਇਹ m ਦੇ ਹਰੇਕ ਗੁਣਨਖੰਡ ਨਾਲ ਵੀ ਭਾਜਯੋਗ ਹੋਵੇਗੀ ।
![]()
ਪ੍ਰਸ਼ਨ 2.
(i) ਇਕ ਤਿੰਨ ਅੰਕਾਂ ਦੀ ਸੰਖਿਆ abc ਨੂੰ 100 a + 10b + c ਦੇ ਰੂਪ ਵਿਚ ਲਿਖੋ । ਹੁਣ
100 a + 10b + c = 99 a + 11b + (a – b + c)
= 11 (9a +b) + (a – b + c)
ਜਦ ਸੰਖਿਆ abc, 11 ਨਾਲ ਭਾਜਯੋਗ ਹੋਵੇ, ਤਾਂ ਤੁਸੀਂ (a – b + c) ਦੇ ਬਾਰੇ ਵਿਚ ਕੀ ਕਹਿ ਸਕਦੇ ਹੋ ? ਕੀ ਇਹ ਜ਼ਰੂਰੀ ਹੈ ਕਿ (a + c – b), 11 ਨਾਲ ਭਾਜਯੋਗ ਹੋਵੇ ?
(ii) ਇਕ ਚਾਰ ਅੰਕਾਂ ਦੀ ਸੰਖਿਆ abcd ਨੂੰ ਇਸ ਪ੍ਰਕਾਰ ਲਿਖੋ
1000a + 100b + 10c + d
= (1001 a + 99b + 11c) – (a – b + c – d)
= 11(91a + 9b + c) – [(b + d – a + c)]
ਜੇਕਰ ਸੰਖਿਆ abcd, 11 ਨਾਲ, ਭਾਜਯੋਗ ਹੈ, ਤਾਂ (b + d) – ( a + c) ਦੇ ਬਾਰੇ ਵਿਚ ਤੁਸੀਂ ਕੀ ਕਹਿ ਸਕਦੇ ਹੋ ?
(iii) ਉਪਰੋਕਤ (i) ਅਤੇ (ii) ਨਾਲ, ਕੀ ਤੁਸੀਂ ਕਹਿ ਸਕਦੇ ਹੋ, ਕਿ ਉਹ ਸੰਖਿਆ 11 ਨਾਲ ਭਾਜਯੋਗ ਹੋਵੇਗੀ, ਜਦ ਇਸਦੇ ਟਾਂਕ ਸਥਾਨਾਂ ਦੇ ਅੰਕਾਂ ਦੇ ਜੋੜ ਅਤੇ ਜਿਸਤ ਸਥਾਨਾਂ ਦੇ ਅੰਕਾਂ ਦੇ ਜੋੜ ਦਾ ਅੰਤਰ 11 ਨਾਲ ਭਾਜਯੋਗ ਹੋਵੇਗਾ ?
ਹੱਲ:
(i) ਹਾਂ, ਇਹ ਜ਼ਰੂਰੀ ਹੈ ਕਿ (a + c – b), 11 ਨਾਲ ਭਾਜਯੋਗ ਹੋਵੇ ।
(ii) ਜੇਕਰ ਸੰਖਿਆ abcd, 11 ਨਾਲ ਭਾਜਯੋਗ ਹੋਵੇ, ਤਾਂ (b + d) – (a + c), 11 ਨਾਲ ਭਾਜਯੋਗ ਹੋਣੀ ਚਾਹੀਦੀ ।
(iii) ਹਾਂ, ਅਸੀਂ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਕੋਈ ਸੰਖਿਆ 11 ਨਾਲ ਭਾਜਯੋਗ ਹੋਵੇਗੀ ।
ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਹੇਠਾਂ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਦੀ 3 ਨਾਲ ਭਾਜਯੋਗਤਾ ਦੀ ਪੜਤਾਲ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
108
ਹੱਲ:
108.
108 ਦੇ ਅੰਕਾਂ ਦਾ ਜੋੜ = 1 + 0 + 8 = 9.
ਇਹ ਸੰਖਿਆ 3 ਨਾਲ ਭਾਜਯੋਗ ਹੈ ।
∴ ਸੰਖਿਆ 108 ਵੀ 3 ਨਾਲ ਭਾਜਯੋਗ ਹੈ ।
ਭਾਵ = \(\frac{108}{3}\) = 36.
![]()
ਪ੍ਰਸ਼ਨ 2.
616
ਹੱਲ:
616.
616 ਦੇ ਅੰਕਾਂ ਦਾ ਜੋੜ = 6 + 1 + 6 = 13.
ਇਹ ਸੰਖਿਆ 8 ਨਾਲ ਭਾਜਯੋਗ ਨਹੀਂ ਹੈ ।
∴ ਸੰਖਿਆ 616, 3 ਨਾਲ ਭਾਜਯੋਗ ਨਹੀਂ ਹੈ ।
ਭਾਵ \(\frac{616}{3}\) = 205\(\frac{1}{3}\).
ਪ੍ਰਸ਼ਨ 3.
294
ਹੱਲ:
294.
294 ਦੇ ਅੰਕਾਂ ਦਾ ਜੋੜ = 2 + 9 + 4 = 15
ਇਹ ਸੰਖਿਆ 3 ਨਾਲ ਭਾਜਯੋਗ ਹੈ ।
∴ ਸੰਖਿਆ 294 ਵੀ 3 ਨਾਲ ਭਾਜਯੋਗ ਹੈ ।
ਭਾਵ \(\frac{294}{3}\) = 98.
![]()
ਪ੍ਰਸ਼ਨ 4.
432
ਹੱਲ:
432.
432 ਦੇ ਅੰਕਾਂ ਦਾ ਜੋੜ = 4 + 3 + 2 = 9.
ਇਹ ਸੰਖਿਆ 3 ਨਾਲ ਭਾਜਯੋਗ ਹੈ ।
∴ ਸੰਖਿਆ 432, ਵੀ 3 ਨਾਲ ਭਾਜਯੋਗ ਹੈ !
ਭਾਵ \(\frac{432}{3}\) = 144
ਪ੍ਰਸ਼ਨ 5.
927.
ਹੱਲ:
927.
927 ਦੇ ਅੰਕਾਂ ਦਾ ਜੋੜ = 9 + 2 + 7 = 18
ਇਹ ਸੰਖਿਆ 3 ਨਾਲ ਭਾਜਯੋਗ ਹੈ ।
∴ ਸੰਖਿਆ 927, ਵੀ 3 ਨਾਲ ਭਾਜਯੋਗ ਹੈ ।
ਭਾਵ \(\frac{927}{3}\) = 309.
