PSEB 10th Class Science Important Questions Chapter 12 ਬਿਜਲੀ

Punjab State Board PSEB 10th Class Science Important Questions Chapter 12 ਬਿਜਲੀ Important Questions and Answers.

PSEB 10th Class Science Important Questions Chapter 12 ਬਿਜਲੀ

ਵੱਡੇ ਉੱਚਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Long Answer Type Questions)

ਪ੍ਰਸ਼ਨ 1.
(ਕ) ਬਿਜਲ ਕਰੰਟ ਦੇ ਤਾਪੀ ਪ੍ਰਭਾਵ ਸੰਬੰਧੀ ਲਿਖੋ ।
(ਖ) ਬਿਜਲੀ ਸ਼ਕਤੀ ਦੀ ਪਰਿਭਾਸ਼ਾ ਦਿਓ। ਇਸ ਦੀ ਇਕਾਈ ਵਾਟ ਦੀ ਵੀ ਪਰਿਭਾਸ਼ਾ ਦਿਓ।
(ਗ) ਬਿਜਲੀ ਉਰਜਾ ਕੀ ਹੈ ? ਇਸ ਦੀਆਂ ਇਕਾਈਆਂ ਦੀ ਪਰਿਭਾਸ਼ਾ ਦਿਓ ।
ਉੱਤਰ-
(ਕ) ਤਾਪੀ ਪ੍ਰਭਾਵ ਦੇ ਨਿਯਮ – ਜਦੋਂ ਕਿਸੇ ਚਾਲਕ ਵਿਚੋਂ ਬਿਜਲ ਕਰੰਟ ਲੰਘਦਾ ਹੈ, ਤਾਂ ਇਹ ਗਰਮ ਹੋ ਜਾਂਦਾ ਹੈ । ਇਸ ਤੱਥ ਦਾ ਅਧਿਐਨ ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਜੁਲ ਨੇ ਕੀਤਾ। ਇਸ ਲਈ ਇਸ ਨੂੰ ਜੁਲ ਦਾ ਤਾਪਨ ਨਿਯਮ (Joule’s heating effect) ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਇਸ ਨਿਯਮ ਦੇ ਅਨੁਸਾਰ ਜਦੋਂ ਚਾਲਕ ਵਿਚੋਂ ਕਰੰਟ ਲੰਘਦਾ ਹੈ, ਤਾਂ ਪੈਦਾ ਹੋਇਆ ਤਾਪ :
(i) ਕਰੰਟ ਦੇ ਵਰਗ ਦੇ ਸਿੱਧਾ ਅਨੁਪਾਤੀ ਹੁੰਦਾ ਹੈ ।
H ∝ I² (ਜਦੋਂ ਪ੍ਰਤਿਰੋਧ R, ਸਮਾਂ t ਹੋਣ)
(ii) ਚਾਲਕ ਦੇ ਪ੍ਰਤਿਰੋਧ ਦੇ ਸਿੱਧਾ ਅਨੁਪਾਤੀ ਹੈ ।
H ∝ R (ਜਦੋਂ ਧਾਰਾ I, ਸਮਾਂ ਵੀ t ਹੋਣ)
(iii) ਸਮੇਂ ਦੇ ਸਿੱਧਾ ਅਨੁਪਾਤੀ ਹੁੰਦਾ ਹੈ ਜਿੰਨੇ ਸਮੇਂ ਲਈ ਕਰੰਟ ਲੰਘਾਈ ਜਾਂਦੀ ਹੈ ।
H ∝ t (ਜਦੋਂ ਤਿਰੋਧ R ਅਤੇ ਕਰੰਟ I ਹੋਣ)
(i), (ii) ਅਤੇ (iii) ਤੋਂ
H ∝ I² Rt
ਸਮਾਨੁਪਾਤੀ ਨਿਯੰਤਰਕ ਦਾ ਮਾਨ ਮਾਤਕਾਂ ਦੀ ਪ੍ਰਣਾਲੀ ‘ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ। S.I. ਪ੍ਰਣਾਲੀ ਵਿੱਚ ਇਸ ਦਾ ਮਾਨ 1 ਹੈ ।
∴ H = I² Rt (ਜੂਲ ਵਿੱਚ)

(ਖ) ਬਿਜਲਈ ਸ਼ਕਤੀ – ਬਿਜਲੀ ਦੁਆਰਾ ਕਾਰਜ ਕਰਨ ਦੀ ਦਰ ਨੂੰ ਬਿਜਲਈ ਸ਼ਕਤੀ ਕਹਿੰਦੇ ਹਨ ।
ਮੰਨ ਲਓ ਕਿ ਆਪਣੇ ਸਿਰਿਆਂ ਦੇ ਪਾਰ V ਟੈਂਸ਼ਲ ਅੰਤਰ ਵਾਲੇ ਚਾਲਕ ਵਿਚੋਂ ਸਮੇਂ t ਦੇ ਲਈ ਧਾਰਾ I ਲੰਘਦੀ ਹੈ ਤਾਂ ਕਾਰਜ ਇਸ ਤਰ੍ਹਾਂ ਹੋਵੇਗਾ-
W = VIt
ਪਰ ਸਰਕਟ ਦੀ ਸ਼ਕਤੀ ਇਸ ਤਰ੍ਹਾਂ ਦਿੱਤੀ ਜਾਵੇਗੀ

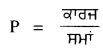
= \(\frac{\mathrm{W}}{t}\)
= \(\frac{\mathrm{VI} t}{t}\)
= VI
ਓਹਮ ਦੇ ਨਿਯਮ ਅਨੁਸਾਰ
I = \(\frac{\mathrm{V}}{\mathrm{R}}\)
∴ P = V × I
= \(\frac{V^{2}}{R}\)
ਅਤੇ P = I²R
ਬਿਜਲ ਸ਼ਕਤੀ ਦੀ ਇਕਾਈ – ਜੇ v ਨੂੰ ਵੋਲਟ ਅਤੇ I ਨੂੰ ਐਮਪੀਅਰ ਵਿੱਚ ਮਾਪਿਆ ਜਾਵੇ, ਤਾਂ ਸ਼ਕਤੀ ਵਾਟ ਵਿੱਚ ਹੋਵੇਗੀ।
ਵਾਟ ਦੀ ਪਰਿਭਾਸ਼ਾ – ਬਿਜਲਈ ਸਰਕਟ ਵਿੱਚ ਇੱਕ ਵਾਟ ਬਿਜਲਈ ਸ਼ਕਤੀ ਉਦੋਂ ਕਹੀ ਜਾਵੇਗੀ ਜਦੋਂ ਇੱਕ ਐਮਪੀਅਰ ਕਰੰਟ ਕਿਸੇ ਚਾਲਕ ਦੇ ਸਿਰਿਆਂ ਵਿੱਚ ਇੱਕ ਵੋਲਟ ਦੇ ਟੈਂਸ਼ਲ ਅੰਤਰ ਹੋਣ ਤੇ ਵਗਦਾ ਹੈ ।
1 ਵਾਟ = 1 ਵੋਲਟ × ਐਮਪੀਅਰ
ਸ਼ਕਤੀ ਦੀ ਵੱਡੀ ਇਕਾਈ ਕਿਲੋਵਾਟ (KW) ਹੈ ।
1 ਕਿਲੋਵਾਟ = 1000 ਜੂਲ

(ਗ) ਬਿਜਲਈ ਊਰਜਾ – ਕਿਸੇ ਨਿਸਚਿਤ ਸਮੇਂ ਵਿੱਚ ਕਰੰਟ ਦੁਆਰਾ ਕੁੱਲ ਕੀਤੇ ਗਏ ਕਾਰਜ ਦੀ ਮਾਤਰਾ, ਬਿਜਲਈ ਊਰਜਾ ਕਹਾਉਂਦੀ ਹੈ ।
ਮੰਨ ਲਓ, ਕਿਸੇ ਚਾਲਕ ਵਿੱਚ 1 ਐਮਪੀਅਰ ਕਰੰਟ ਸਮੇਂ ਲਈ ਲੰਘਦਾ ਹੈ, ਜਦੋਂ ਇਸ ਦੇ ਸਿਰਿਆਂ ਵਿਚਕਾਰ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ ਹੁੰਦਾ ਹੈ, ਉਦੋਂ ਵਰਤੀ ਗਈ ਉਰਜਾ ਜਾਂ ਕੀਤਾ ਗਿਆ ਕਾਰਜ ਇਸ ਤਰ੍ਹਾਂ ਹੁੰਦਾ ਹੈ-
W = VIt
ਬਿਜਲਈ ਊਰਜਾ ਦੀ ਇਕਾਈ ਜੂਲ ਜਾਂ ਵਾਟ ਸੈਕਿੰਡ ਹੈ। ਪਰ ਇਹ ਇੱਕ ਛੋਟੀ ਇਕਾਈ ਹੈ। ਬਿਜਲਈ ਊਰਜਾ ਦੀ ਵੱਡੀ ਇਕਾਈ ਵਾਟ ਘੰਟਾ ਹੈ ।

ਵਾਟ ਘੰਟੇ ਦੀ ਪਰਿਭਾਸ਼ਾ – ਬਿਜਲਈ ਊਰਜਾ ਇੱਕ ਵਾਟ ਘੰਟਾ ਕਹੀ ਜਾਂਦੀ ਹੈ, ਜਦੋਂ ਚਾਲਕ ਵਿਚੋਂ ਇੱਕ ਐਮਪੀਅਰ ਕਰੰਟ ਇੱਕ ਘੰਟੇ ਲਈ ਲੰਘਦਾ ਹੈ ਅਤੇ ਜਦੋਂ ਇਸ ਦੇ ਸਿਰਿਆਂ ਦੇ ਵਿਚਕਾਰ ਇੱਕ ਵੋਲਟ ਦਾ ਟੈਂਸ਼ਲ ਅੰਤਰ ਹੁੰਦਾ ਹੈ ।
1 ਵਾਟ ਘੰਟਾ = 1 ਵਾਟ × 1 ਘੰਟਾ
= 1 ਵੋਲਟ × 1 ਐਮਪੀਅਰ × 1 ਘੰਟਾ
1 ਕਿਲੋਵਾਟ ਘੰਟਾ = 1000 ਵਾਟ ਘੰਟਾ
ਬਿਜਲਈ ਊਰਜਾ ਦੀ ਵੱਡੀ ਇਕਾਈ ਕਿਲੋਵਾਟ ਘੰਟਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਕਿਸੇ ਚਾਲਕ ਦੇ ਪ੍ਰਤਿਰੋਧ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ? ਕਿਸੇ ਚਾਲਕ ਦਾ ਪ੍ਰਤਿਰੋਧ ਕਿਨ੍ਹਾਂ ਕਾਰਕਾਂ ‘ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ ? (ਮਾਡਲ ਪੇਪਰੇ)
ਉੱਤਰ-
ਚਾਲਕ ਦਾ ਪ੍ਰਤਿਰੋਧ – ਕਿਸੇ ਚਾਲਕ ਦੇ ਸਿਰਿਆਂ ਵਿੱਚ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ ਅਤੇ ਉਸ ਵਿੱਚ ਪ੍ਰਵਾਹਿਤ ਹੋ ਰਹੇ ਕਰੰਟ ਦੀ ਮਾਤਰਾ ਦੇ ਅਨੁਪਾਤ ਨੂੰ ਚਾਲਕ ਦਾ ਤਿਰੋਧ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
ਜੇ ਚਾਲਕ ਦੇ ਸਿਰਿਆਂ ਵਿਚਕਾਰ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ vਹੋਵੇ ਅਤੇ ਇਸ ਵਿਚੋਂ ਲੰਘ ਰਹੀ ਕਰੰਟ ਦੀ ਮਾਤਰਾ 1 ਹੋਵੇ ਤਾਂ ਪ੍ਰਤਿਰੋਧ (R)
ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ (V) ਪ੍ਰਤਿਰੋਧ (R)

ਪ੍ਰਤਿਰੋਧ ਦਾ ਮਾਤ੍ਰਿਕ-S.I. ਪ੍ਰਣਾਲੀ ਵਿੱਚ ਪ੍ਰਤਿਰੋਧ ਦਾ ਮਾਤ੍ਰਿਕ ਓਹਮ ਹੈ ਜਦਕਿ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ ਵੋਲਟ ਅਤੇ ਬਿਜਲੀ ਕਰੰਟ ਨੂੰ ਐਮਪੀਅਰ ਵਿੱਚ ਮਾਪਿਆ ਜਾਂਦਾ ਹੈ ।

ਓਹਮ (Ohn) – ਕਿਸੇ ਚਾਲਕ ਦਾ ਤਿਰੋਧ ਇੱਕ ਓਹਮ ਹੋਵੇਗਾ ਜੇ ਉਸਦੇ ਸਿਰਿਆਂ ਵਿਚਕਾਰ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ ਇੱਕ ਵਲਟ ਹੋਵੇ ਅਤੇ ਉਸ ਵਿਚੋਂ ਲੰਘ ਰਹੇ ਕਰੰਟ ਦੀ ਮਾਤਰਾ ਇੱਕ ਐਮਪੀਅਰ ਹੋਵੇ ।

ਚਾਲਕ ਦੇ ਪ੍ਰਤਿਰੋਧ ਦੀ ਨਿਰਭਰਤਾ – ਕਿਸੇ ਚਾਲਕ ਦਾ ਤਿਰੋਧ ਹੇਠ ਲਿਖੇ ਕਾਰਕਾਂ ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ-
(i) ਚਾਲਕ ਦੀ ਲੰਬਾਈ (l)-ਕਿਸੇ ਚਾਲਕ ਦਾ ਪ੍ਰਤਿਰੋਧ ਚਾਲਕ ਦੀ ਲੰਬਾਈ (l) ਦੇ ਸਿੱਧਾ ਅਨੁਪਾਤੀ ਹੁੰਦਾ ਹੈ ।
ਅਰਥਾਤ R ∝ l ………(1)

(ii) ਚਾਲਕ ਦੀ ਪਰਿਖੇਤਰ ਕਾਟ ਦਾ ਖੇਤਰਫਲ (A)-ਕਿਸੇ ਚਾਲਕ ਦਾ ਤਿਰੋਧ ਉਸਦੀ ਪਰਿਖੇਤਰ ਕਾਟ (A) ਦੇ ਖੇਤਰਫਲ ਦਾ ਉਲਟ ਅਨੁਪਾਤੀ ਹੁੰਦਾ ਹੈ ।
ਅਰਥਾਤ R ∝ \(\frac{1}{\mathrm{~A}}\) ………(2)

(iii) ਚਾਲਕ ਦੇ ਪਦਾਰਥ ਦੀ ਪ੍ਰਕਿਰਤੀ-ਕਿਸੇ ਚਾਲਕ ਦਾ ਪ੍ਰਤਿਰੋਧ ਉਸ ਚਾਲਕ ਦੇ ਪਦਾਰਥ ਦੀ ਪ੍ਰਕਿਰਤੀ ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ ।
ਇਨ੍ਹਾਂ ਸਾਰੇ ਕਾਰਕਾਂ ਨੂੰ ਜੋੜਨ (ਸੰਯੋਜਿਤ) ਨਾਲ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
R ∝ \(\frac{l}{\mathrm{~A}}\)
ਜਾਂ R = ρ × \(\frac{l}{\mathrm{~A}}\) ਜਿੱਥੇ ਏ ਅਨੁਪਾਤੀ ਸਥਿਰ ਅੰਕ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਪ੍ਰਯੋਗ ਦੁਆਰਾ ਗਿਆਤ ਕਰੋ ਕਿ ਕਿਸੇ ਚਾਲਕ ਦੇ ਲਈ ਪ੍ਰਤਿਰੋਧ ਦਾ ਮਾਨ ਕਿਨ੍ਹਾਂ-ਕਿਨ੍ਹਾਂ ਕਾਰਕਾਂ ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ ?
ਉੱਤਰ-

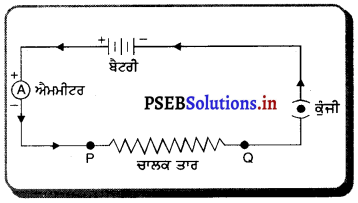
ਕਿਸੇ ਧਾਤੂ ਚਾਲਕ ਦਾ ਪ੍ਰਤਿਰੋਧ ਜਿਨ੍ਹਾਂ ਕਾਰਕਾਂ ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ, ਉਹ ਹੇਠ ਲਿਖੇ ਪ੍ਰਯੋਗ ਦੁਆਰਾ ਦਰਸਾਇਆ ਜਾ ਸਕਦਾ ਹੈ :
ਪ੍ਰਯੋਗ – ਇੱਕ ਬੈਟਰੀ, ਐਮਮੀਟਰ, ਪ੍ਰਤਿਰੋਧਕ ਤਾਰ ਅਤੇ ਸਵਿੱਚ ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਬਿਜਲਈ ਸਰਕਟ ਬਣਾਓ। ਸਵਿੱਚ ਨੂੰ ਦਬਾ ਕੇ ਸਰਕਟ ਵਿੱਚੋਂ ਬਿਜਲਈ ਧਾਰਾ ਪ੍ਰਵਾਹਿਤ ਕਰੋ । ਐਮਮੀਟਰ ਨਾਲ ਬਿਜਲਈ ਧਾਰਾ ਦਾ ਮਾਨ ਨੋਟ ਐਮੀਟਰ ਕਰੋ । ਹੁਣ ਇਸ ਤਾਰ ਦੀ ਥਾਂ ਤੇ ਉਸੇ ਲੰਬਾਈ ਅਤੇ ਮੋਟਾਈ ਦੀ ਕਿਸੇ ਹੋਰ ਧਾਤੂ ਦੀ ਤਾਰ ਦੁਆਰਾ ਜੋੜੋ ਅਤੇ ਐਮਮੀਟਰ ਦੁਆਰਾ ਬਿਜਲਈ ਧਾਰਾ ਦਾ ਮਾਨ ਨੋਟ ਕਰੋ । ਤਾਰ ਤੁਸੀਂ ਵੇਖਦੇ ਹੋ ਕਿ ਬਿਜਲਈ ਧਾਰਾ ਦਾ ਮਾਨ ਬਦਲ ਜਾਂਦਾ ਹੈ । ਇਸ ਪ੍ਰਯੋਗ ਤੋਂ ਇਹ ਸਿੱਧ ਹੁੰਦਾ ਹੈ ਕਿ ਚਾਲਕ ਦਾ ਪ੍ਰਤਿਰੋਧ ਉਸ ਦੀ ਪ੍ਰਕਿਰਤੀ ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ ਅਰਥਾਤ ਇੱਕ ਹੀ ਤਾਪ ਤੇ ਸਮਾਨ ਲੰਬਾਈ ਅਤੇ ਮੋਟਾਈ ਵਾਲੇ ਭਿੰਨਭਿੰਨ ਧਾਤੂਆਂ ਦੇ ਚਾਲਕਾਂ ਦਾ ਪ੍ਰਤਿਰੋਧ ਭਿੰਨ-ਭਿੰਨ ਹੁੰਦਾ ਹੈ ।

ਹੁਣ ਪਹਿਲੇ ਤਾਰ ਦੇ ਵਿਆਸ ਬਰਾਬਰ ਅਤੇ ਉਸ ਧਾਤੂ ਤੋਂ ਬਣੀ ਹੋਈ ਇੱਕ ਤਾਰ ਲਓ ਜਿਸ ਦੀ ਲੰਬਾਈ ਪਹਿਲੀ ਤਾਰ ਨਾਲੋਂ ਦੁੱਗਣੀ ਹੋਵੇ। ਇਸ ਤਾਰ ਨੂੰ ਸਰਕਟ ਵਿੱਚ ਜੋੜੋ ਅਤੇ ਇਸ ਵਿਚੋਂ ਬਿਜਲਈ ਧਾਰਾ ਪ੍ਰਵਾਹਿਤ ਕਰੋ। ਤੁਸੀਂ ਦੇਖੋਗੇ ਕਿ ਧਾਰਾ ਦਾ ਇਹ ਮਾਪ ਪਹਿਲੇ ਮਾਪ ਤੋਂ ਅੱਧਾ ਹੋ ਗਿਆ ਹੈ ਜਾਂ ਪ੍ਰਤਿਰੋਧ ਦੁੱਗਣਾ ਹੋ ਗਿਆ ਹੈ। ਇਸ ਤੋਂ ਸਿੱਧ ਹੁੰਦਾ ਹੈ ਕਿ ਤਿਰੋਧ ਲੰਬਾਈ ਦੇ ਸਮਾਨੁਪਾਤੀ ਹੁੰਦਾ ਹੈ। ਜੇਕਰ ਚਾਲਕ ਦਾ ਪ੍ਰਤਿਰੋਧ R ਅਤੇ ਤਾਰ ਦੀ ਲੰਬਾਈ l ਹੋਵੇ ਤਾਂ
R ∝ l ………..(1)

ਹੁਣ ਇੱਕ ਧਾਤੂ ਦੀਆਂ ਬਣੀਆਂ ਹੋਈਆਂ ਦੋ ਤਾਰਾਂ ਲਓ, ਜਿਨ੍ਹਾਂ ਦੀ ਲੰਬਾਈ ਇੱਕ ਸਮਾਨ ਹੋਵੇ, ਪਰੰਤੂ ਕਾਟ ਦਾ ਖੇਤਰਫਲ ਵੱਖ-ਵੱਖ ਹੋਵੇ। ਪਹਿਲਾਂ ਘੱਟ ਕਾਟ ਦੇ ਖੇਤਰਫਲ ਵਾਲੀ ਤਾਰ ਨੂੰ ਸਰਕਟ ਵਿੱਚ ਜੋੜੋ ਅਤੇ ਬਾਅਦ ਵਿੱਚ ਵੱਧ ਕਾਟ ਵਾਲੇ ਖੇਤਰਫਲ ਦੀ ਤਾਰ ਨੂੰ ਸਰਕਟ ਵਿੱਚ ਜੋੜੋ। ਤੁਸੀਂ ਦੇਖੋਗੇ ਕਿ ਤਾਰ ਵਿੱਚ ਬਿਜਲਈ ਧਾਰਾ ਦਾ ਮਾਨ ਪਹਿਲਾਂ ਦੀ ਤੁਲਨਾ ਵਿੱਚ ਅਧਿਕ ਪ੍ਰਵਾਹਿਤ ਹੋ ਰਿਹਾ ਹੈ। ਇਸ ਤੋਂ ਸਪੱਸ਼ਟ ਹੁੰਦਾ ਹੈ ਕਿ ਦੂਸਰੇ ਤਾਰ ਦਾ ਪ੍ਰਤਿਰੋਧ ਪਹਿਲੇ ਤਾਰ ਦੇ ਮੁਕਾਬਲੇ ਵਿੱਚ ਘੱਟ ਹੈ। ਇਸ ਤੋਂ ਸਿੱਧ ਹੁੰਦਾ ਹੈ ਕਿ ਚਾਲਕ ਦਾ ਪ੍ਰਤਿਰੋਧ ਉਸਦੇ ਕਾਟ ਦੇ ਖੇਤਰਫਲ ਦੇ ਵਿਲੋਮ ਅਨੁਪਾਤੀ ਹੁੰਦਾ ਹੈ। ਜੇਕਰ ਚਾਲਕ ਦਾ ਤਿਰੋਧ R ਅਤੇ ਤਾਰ ਦੀ ਕਾਟ ਦਾ ਖੇਤਰਫਲ A ਹੈ, ਤਾਂ
R ∝ \(\frac{1}{A}\) …………….. (2)
(1) ਅਤੇ (2) ਨੂੰ ਜੋੜਨ ਨਾਲ, R ∝ \(\frac{l}{\mathrm{~A}}[latex]
ਜਾਂ R = ρ × [latex]\frac{l}{a}\)

ਜਿੱਥੇ ρ ਸਥਿਰ ਅੰਕ ਹੈ ਅਤੇ ਇਸ ਨੂੰ ਚਾਲਕ ਦੀ ਪ੍ਰਤਿਰੋਧਕਤਾ ਕਹਿੰਦੇ ਹਨ। ਇਸ ਦਾ ਮਾਨ ਚਾਲਕ ਦੇ ਪਦਾਰਥ ਦੀ ਕਿਰਤੀ ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਓਹਮ ਦਾ ਨਿਯਮ ਕੀ ਹੈ ? ਤੁਸੀਂ ਪ੍ਰਯੋਗਸ਼ਾਲਾ ਵਿੱਚ ਇਸ ਦੀ ਕਿਵੇਂ ਪੁਸ਼ਟੀ ਕਰੋਗੇ ?
ਜਾਂ
ਓਹਮ ਦਾ ਨਿਯਮ ਲਿਖੋ । ਚਿੱਤਰ ਬਣਾ ਕੇ ਸਮਝਾਓ ਕਿ ਇਸ ਦੀ ਪ੍ਰਯੋਗਸ਼ਾਲਾ ਵਿਚ ਵਿਆਖਿਆ ਕਿਵੇਂ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ?
ਜਾਂ
ਓਹਮ ਦਾ ਨਿਯਮ ਲਿਖੋ । ਇਸ ਨੂੰ ਪ੍ਰਯੋਗਸ਼ਾਲਾ ਵਿੱਚ ਪ੍ਰਯੋਗਾਤਮਕ ਤੌਰ ਤੇ ਸਿੱਧ ਕਰਨ ਲਈ ਸਰਕਟ ਚਿੱਤਰ ਬਣਾਓ ।
ਉੱਤਰ-

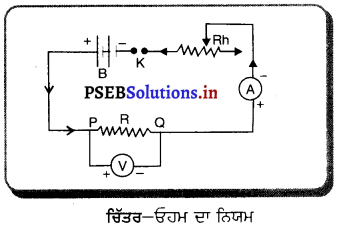
ਓਹਮ ਦਾ ਨਿਯਮ (Ohm’s Law) – ਓਹਮ ਦੇ ਨਿਯਮ ਅਨੁਸਾਰ “ਕਿਸੇ ਚਾਲਕ ਦੇ ਸਿਰਿਆਂ ਦੇ ਵਿੱਚ ਪੁਟੈਂਸ਼ਲ ਅੰਰy ਅਤੇ ਉਸ ਵਿੱਚ ਪ੍ਰਵਾਹਿਤ ਹੋ ਰਹੀ ਕਰੰਟ ਦੀ ਮਾਤਰਾ 1 ਦਾ ਅਨੁਪਾਤ ਸਦਾ ਸਥਿਰ ਰਹਿੰਦਾ ਹੈ, ਸ਼ਰਤ ਚਾਲਕ ਦੀਆਂ ਭੌਤਿਕ ਹਾਲਤਾਂ ਤਾਪਮਾਨ ਅਤੇ ਦਬਾਅ ਆਦਿ ਨਾ ਬਦਲਣ ।”
ਜਾਂ = \(\frac{\mathrm{V}}{\mathrm{I}}\) = ਸਥਿਤ ਅੰਕ (R)
ਇਸ ਸਥਿਰ ਅੰਕ (R) ਨੂੰ ਚਾਲਕ ਦਾ ਪ੍ਰਤਿਰੋਧ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
ਓਹਮ ਦੇ ਨਿਯਮ ਦੀ ਪੁਸ਼ਟੀ-ਦਿੱਤੇ ਗਏ ਚਾਲਕ PQ ਨੂੰ ਬੈਟਰੀ (B), ਇੱਕ ਕਰੰਟ ਨਿਯੰਤਰਕ (Rh), ਇੱਕ ਐਮਮੀਟਰ (A) ਅਤੇ ਇਕ ਕੁੰਜੀ (K) ਨੂੰ ਦਿੱਤੇ ਗਏ ਸਰਕਟ ਵਿੱਚ ਜੋੜੇ । ਚਾਲਕ PQ ਦੇ ਸਿਰਿਆਂ ਦੇ ਵਿਚਕਾਰ ਵੋਲਟ ਮੀਟਰ V ਲਗਾਓ, ਜਿਵੇਂ ਕਿ ਚਿੱਤਰ ਵਿੱਚ ਵਿਖਾਇਆ ਗਿਆ ਹੈ ।

ਹੁਣ ਕੁੰਜੀ ਵਿੱਚ ਪਲੱਗ ਲਗਾ ਕੇ ਚਾਲਕ PQ ਵਿੱਚ ਪ੍ਰਵਾਹਿਤ ਹੋ ਰਹੇ ਕਰੰਟ ਦੀ ਪੜ੍ਹਤ ਐਮਮੀਟਰ ਵਿੱਚ ਅਤੇ ਚਾਲਕ
ਕਰੋ ।

ਦੇ ਸਿਰਿਆਂ ਵਿਚਕਾਰ ਦਾ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ V ਵੋਲਟਮੀਟਰ ਵਿੱਚ ਨੋਟ ਕਰੋ। ਹੁਣ V ਅਤੇ I ਦਾ ਅਨੁਪਾਤ (\(\frac{\mathrm{V}}{\mathrm{I}}\)) ਪਤਾ ਕਰੋ ।

ਹੁਣ ਨਿਯੰਤਰਕ ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਸਰਕਟ ਵਿੱਚ ਕਰੰਟ ਦਾ ਮੁੱਲ ਬਦਲੋ ਅਤੇ ਵੋਲਟਮੀਟਰ ਅਤੇ ਐਮਮੀਟਰ ਦੀ ਨਵੀਂ ਪੜ੍ਹਤ ਨੋਟ ਕਰੋ। ਫਿਰ ਤੋਂ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ ਅਤੇ ਧਾਰਾ ਦੇ ਅਨੁਪਾਤ (\(\frac{V_{1}}{I_{1}}\)) ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ । ਕਰੰਟ ਨਿਯੰਤਰਕ ਦੇ ਸੰਪਰਕ ਦੀ ਸਥਿਤੀ ਬਦਲ ਕੇ ਇਸ ਯੋਗ ਨੂੰ ਦੁਹਰਾਓ। ਮੰਨ ਲਓ ਇਸ ਵਾਰ ਐਮੀਟਰ ਦੀ ਪੜ੍ਹਤ I₂ ਅਤੇ ਵੋਲਟਮੀਟਰ ਦੀ ਪੜ੍ਹਤ V₂ ਹੈ । ਹੁਣ ਫਿਰ \(\frac{V_{2}}{I_{2}}\) ਦਾ ਅਨੁਪਾਤ ਕੱਢੋ। ਤੁਸੀਂ ਦੇਖੋਗੇ ਕਿ ਹਰ ਵਾਰ ਟੈਂਸ਼ਲ ਅੰਤਰ ਅਤੇ ਧਾਰਾ ਦਾ ਅਨੁਪਾਤ ਸਥਿਰ ਹੈ ।
ਅਰਥਾਤ \(\frac{\mathrm{V}}{\mathrm{I}}=\frac{\mathrm{V}_{1}}{\mathrm{I}_{1}}=\frac{\mathrm{V}_{2}}{\mathrm{I}_{2}}\) = ….R (ਸਥਿਰ ਅੰਕ)
ਇਸ ਸਥਿਰ ਅੰਕ ਨੂੰ ਪ੍ਰਤਿਰੋਧ ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਇਸ ਤਰ੍ਹਾਂ ਓਮ ਦੇ ਨਿਯਮ ਦੀ ਪੁਸ਼ਟੀ ਹੋ ਜਾਂਦੀ ਹੈ। ਹੁਣ ਚਾਲਕ PQ ਦੇ ਟੈਂਸ਼ਲ ਅੰਤਰ ਦੇ ਵੱਖ-ਵੱਖ ਮੁੱਲਾਂ ਅਤੇ ਇਸ ਅਨੁਸਾਰ ਕਰੰਟ ਦੇ ਵੱਖ-ਵੱਖ ਮਾਨ ਦੇ ਵਿਚਾਲੇ ਗਰਾਫ਼ ਖਿੱਚੋ ।

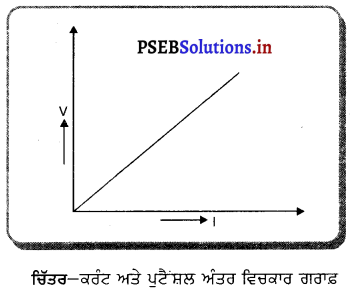
ਗਰਾਫ਼ ਇਕ ਸਿੱਧੀ ਰੇਖਾ ਹੈ, ਇਹ ਓਹਮ ਦੇ ਨਿਯਮ ਦੀ ਪੁਸ਼ਟੀ ਕਰਦਾ ਹੈ, ਜਿਵੇਂ ਕਿ ਚਿੱਤਰ ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ । ਗਰਾਫ਼ ਤੋਂ ਪਤਾ ਲਗਦਾ ਹੈ ਕਿ, ਜਿਵੇਂ-ਜਿਵੇਂ ਚਾਲਕ ਵਿੱਚ ਟੈਂਸ਼ਲ ਅੰਤਰ ਵੱਧਦਾ ਹੈ, ਕਰੰਟ ਵਿੱਚ ਰੇਖੀ ਵਾਧਾ ਹੁੰਦਾ ਹੈ, ਜੋ ਕਿ ਓਹਮ ਦਾ ਨਿਯਮ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਲੜੀ ਵਿੱਚ ਜੋੜੇ ਗਏ ਕਈ ਪ੍ਰਤਿਰੋਧਾਂ ਦਾ ਡੁੱਲ-ਪ੍ਰਤਿਰੋਧ ਕਿੰਨਾ ਹੁੰਦਾ ਹੈ ? ਇਸ ਲਈ ਇੱਕ ਸੰਬੰਧ ਦਾ ਵਿਉਂਤਪਤ ਪਤਾ ਕਰੋ ।
ਜਾਂ
ਲੜੀ ਵਿੱਚ ਜੋੜੇ ਗਏ ਕਈ ਪ੍ਰਤੀਰੋਧਾਂ ਦਾ ਤੁੱਲ-ਪ੍ਰਤੀਰੋਧ ਕਿੰਨਾ ਹੁੰਦਾ ਹੈ ? ਚਿੱਤਰ ਬਣਾਓ ਅਤੇ ਸੰਬੰਧ ਸਥਾਪਿਤ ਕਰੋ ।
ਉੱਤਰ-
ਜਦੋਂ ਪ੍ਰਤਿਰੋਧਾਂ ਨੂੰ ਲੜੀ ਵਿਚ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਸੰਯੋਜਨ ਦਾ ਤੁੱਲ-ਪ੍ਰਤਿਰੋਧ ਇਕੱਲੇ-ਇਕੱਲੇ ਪ੍ਰਤਿਰੋਧਾਂ ਦੇ ਜੋੜ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ ।

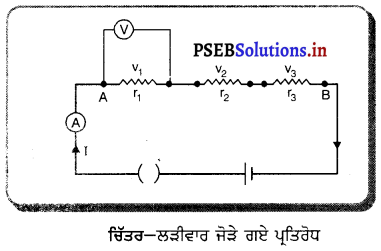
ਲੜੀ ਵਿੱਚ ਜੋੜੇ ਗਏ ਪ੍ਰਤਿਰੋਧਾਂ ਦਾ ਉਨ੍ਹਾਂ ਦੇ ਡੁੱਲ – ਤਿਰੋਧਾਂ ਨਾਲ ਸੰਬੰਧ ਦਾ ਵਿਉਂਤਪੱਤ-ਲੜੀ ਵਿੱਚ ਜੁੜੇ ਹਿੱਸੇ ਤਿੰਨ ਵਿਰੋਧਾਂ r₁,r₂ ਅਤੇ r₃ ਤੇ ਵਿਚਾਰ ਕਰੋ ਜਿਵੇਂ ਕਿ ਚਿੱਤਰ ਵਿੱਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ। ਮੰਨ ਲਓ, ਹਰੇਕ ਵਿੱਚ ਕਰੰਟ I ਲੰਘ ਰਿਹਾ ਹੈ। ਪ੍ਰਤਿਰੋਧ ਦੇ ਸਿਰਿਆਂ ਵਿਚਕਾਰ ਟੈਂਸ਼ਲ ਅੰਤਰ ਇਸਦੇ ਪ੍ਰਤਿਰੋਧ ਦੇ ਸਮਾਨੁਪਾਤੀ ਹੈ ।
ਮੰਨ ਲਓ,
V₁ = r₁ ਦੇ ਸਿਰਿਆਂ ਦੇ ਵਿਚਕਾਰ ਟੈਂਸ਼ਲ ਅੰਤਰ
V₂ = r₂ ਦੇ ਸਿਰਿਆਂ ਦੇ ਵਿਚਕਾਰ ਟੈਂਸ਼ਲ ਅੰਤਰ
V₃ = r₃ ਦੇ ਸਿਰਿਆਂ ਦੇ ਵਿਚਕਾਰ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ
V = V₁ + V₂ + V₃
ਮੰਨ ਲਓ, R_S ਪੂਰੀ ਲੜੀ ਦਾ ਤਿਰੋਧ ਹੈ ।
ਓਹਮ ਦੇ ਨਿਯਮ ਅਨੁਸਾਰ,
V = IR_S
ਇਸ ਤਰ੍ਹਾਂ
V₁ = Ir₁
V₂ = Ir₂
V₂ = Ir₃

(i) ਵਿੱਚ ਮਾਨ ਰੱਖਣ ਤੇ
IR_S = Ir₁ + Ir₂ + Ir₃
ਇਸ ਲਈ ਜਦੋਂ ਪ੍ਰਤਿਰੋਧ ਲੜੀ ਵਿੱਚ ਜੋੜੇ ਜਾਂਦੇ ਹਨ ਤਾਂ ਇਨ੍ਹਾਂ ਦਾ ਕੁੱਲ ਤਿਰੋਧ ਸਾਰੇ ਪ੍ਰਤਿਰੋਧਾਂ ਦੇ ਜੋੜਾਂ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਜਦੋਂ ਤਿੰਨ ਪ੍ਰਤਿਰੋਧਕਾਂ ਨੂੰ ਸਮਾਨਾਂਤਰ ਕੂਮ ਵਿੱਚ ਜੋੜ ਕੇ ਇੱਕ ਬੈਟਰੀ ਨਾਲ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ ਤਾਂ ਇਨ੍ਹਾਂ ਤੱਲਪ੍ਰਤਿਰੋਧ ਦੇ ਲਈ ਇਕ ਸੰਬੰਧ ਮਾਲੂਮ ਕਰੋ।
ਜਾਂ
ਸਮਾਨਾਂਤਰਬੱਧ ਜੋੜੇ ਗਏ ਕੁੱਝ ਪ੍ਰਤੀਰੋਧਾਂ ਦਾ ਡੁੱਲ-ਪ੍ਰਤੀਰੋਧ ਕਿੰਨਾ ਹੋਵੇਗਾ ? ਚਿੱਤਰ ਬਣਾਓ ਅਤੇ ਸੰਬੰਧ ਸਥਾਪਿਤ ਕਰੋ।
ਜਾਂ ਬਿਜਲੀ ਸਰਕਟ ਵਿੱਚ ਜਦ ਦੋ ਜਾਂ ਵੱਧ ਤਿਰੋਧਾਂ (R₁, R₂, R₃, ………) ਨੂੰ ਸਮਾਨਾਂਤਰ ਕੂਮ ਵਿੱਚ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ ਤਾਂ ਪਰਿਣਾਮੀ ਤਿਰੋਧ (R) ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ V ਅਤੇ ਬਿਜਲੀਧਾਰਾ (I) ਲਈ ਸੰਬੰਧ/ਸੂਤਰ ਸਥਾਪਿਤ ਕਰੋ । ਅੰਕਿਤ ਚਿੱਤਰ ਵੀ ਬਣਾਓ ।
ਉੱਤਰ-
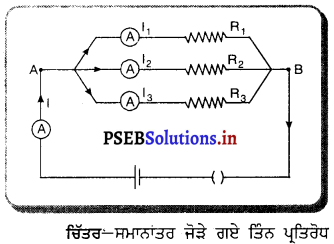
ਸਮਾਨਾਂਤਰ ਵਿੱਚ ਪ੍ਰਤਿਰੋਧ – ਮੰਨ ਲਓ, ਤਿੰਨ ਪ੍ਰਤਿਰੋਧ R₁, R₂, R₃, ਬਿੰਦੁ A ਅਤੇ B ਦੇ ਵਿਚਕਾਰ ਸਮਾਨਾਂਤਰ ਕੂਮ ਵਿੱਚ ਜੋੜੇ ਗਏ ਹਨ। ਹੁਣ ਜੇ ਬਿੰਦੁ A ਅਤੇ B ਦੇ ਵਿਚਕਾਰ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ ਲਗਾਉਣ ਤੇ ਮੁੱਖ ਸਰਕਟ ਵਿੱਚ ਬਿਜਲੀ ਕਰੰਟ I ਪ੍ਰਵਾਹਿਤ ਹੋ ਰਹੀ ਹੋਵੇ ਤਾਂ ਬਿੰਦੁ A ਤੇ ਇਹ ਬਿਜਲੀ ਕਰੰਟ ਤਿੰਨ ਹਿੱਸਿਆਂ ਵਿੱਚ ਵੰਡਿਆ ਜਾਂਦਾ ਹੈ। ਮੰਨ ਲਓ ਤਿਰੋਧ R₁, R₂, ਅਤੇ R₃, ਵਿੱਚੋਂ ਲੰਘਣ ਵਾਲਾ ਕਰੰਟ I₁, I₂, I₃ ਹੈ ।
ਤਾਂ
I = I₁ + I₂ + I₃

ਜੇ ਦੋਵੇਂ ਸਿਰਿਆਂ ਦੇ ਵਿਚਕਾਰ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ v ਹੈ, ਤਾਂ ਓਹਮ ਨਿਯਮ ਅਨੁਸਾਰ,
I₁ = \(\frac{\mathrm{V}}{\mathrm{R}_{1}}\)
I₂ = \(\frac{\mathrm{V}}{\mathrm{R}_{2}}\)
I₃ = \(\frac{\mathrm{V}}{\mathrm{R}_{3}}\)
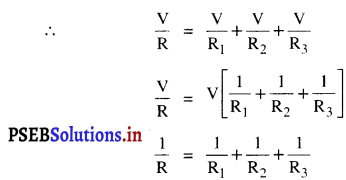
I = \(\frac{\mathrm{V}}{\mathrm{R}}\) , ਜਿੱਥੇ ਕਿ ਸੰਯੋਜਨ ਦਾ ਡੁੱਲ-ਤਿਰੋਧ ਹੈ ।
(1) ਵਿੱਚ ਮਾਨ ਰੱਖਣ ਤੇ

ਪ੍ਰਸ਼ਨ 7.
ਬਿਜਲਈ-ਊਰਜਾ ਅਤੇ ਬਿਜਲਈ-ਸ਼ਕਤੀ ਦੀ ਪਰਿਭਾਸ਼ਾ ਦਿਓ ਅਤੇ ਇਨ੍ਹਾਂ ਦੀਆਂ ਮਾੜਾਂ ਦੱਸੋ ।
ਜਾਂ
ਬਿਜਲਈ ਸ਼ਕਤੀ ਦੀ ਪਰਿਭਾਸ਼ਾ ਲਿਖੋ। ਇਸ ਦੀ ਇਕਾਈ ਵਾਟ ਦੀ ਵੀ ਪਰਿਭਾਸ਼ਾ ਲਿਖੋ ।
ਉੱਤਰ-
ਬਿਜਲਈ ਸ਼ਕਤੀ – ਕਾਰਜ ਕਰਨ ਦੀ ਦਰ ਨੂੰ ਬਿਜਲਈ ਸ਼ਕਤੀ ਕਹਿੰਦੇ ਹਨ ।
ਮੰਨ ਲਓ, ਇਕ ਚਾਲਕ ਦੇ ਸਿਰਿਆਂ ਵਿੱਚ V ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ ਲਗਾਇਆ ਹੈ ਅਤੇ I ਕਰੰਟ ਲੰਘਦਾ ਹੈ । t ਸਮੇਂ ਦੇ ਲਈ I ਕਰੰਟ ਪ੍ਰਵਾਹਿਤ ਕਰਨ ਲਈ ਕੀਤਾ ਗਿਆ ਕਾਰਜ ਇਸ ਪ੍ਰਕਾਰ ਹੋਵੇਗਾ-
W = VIt
ਪਰ ਸਰਕਟ ਦੀ ਸ਼ਕਤੀ ਇਸ ਪ੍ਰਕਾਰ ਪ੍ਰਗਟ ਕੀਤੀ ਜਾਂਦੀ ਹੈ-

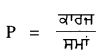
= \(\frac{\mathrm{W}}{t}\)
= \(\frac{\mathrm{VI} t}{t}\)
= VI
P = VI
ਓਹਮ ਦੇ ਨਿਯਮ ਅਨੁਸਾਰ,
P = \(\frac{\mathrm{V}^{2}}{\mathrm{R}}\) [∵ I = \(\frac{\mathrm{V}}{\mathrm{R}}\)]
ਅਤੇ P = I²R [ ∵ V = IR]
ਬਿਜਲਈ-ਸ਼ਕਤੀ ਦੀ ਇਕਾਈ-
∵ P = V × I

ਜੇ V ਨੂੰ ਵੋਲਟ ਵਿੱਚ ਅਤੇ I ਨੂੰ ਐਮਪੀਅਰ ਵਿੱਚ ਮਾਪਿਆ ਜਾਵੇ ਤਾਂ ਸ਼ਕਤੀ ਵਾਟ ਵਿੱਚ ਹੋਵੇਗੀ ।
ਵਾਟ ਦੀ ਪਰਿਭਾਸ਼ਾ – ਬਿਜਲਈ ਸਰਕਟ ਵਿੱਚ ਇੱਕ ਵਾਟ ਬਿਜਲਈ-ਸ਼ਕਤੀ ਤਦ ਹੁੰਦੀ ਹੈ ਜਦੋਂ ਕਿਸੇ ਚਾਲਕ ਦੇ ਸਿਰਿਆਂ ਵਿਚਕਾਰ ਇੱਕ ਵੋਲਟ ਦਾ ਟੈਂਸ਼ਲ ਅੰਤਰ ਹੋਵੇ ਅਤੇ ਉਸ ਵਿਚੋਂ ਇੱਕ ਐਮਪੀਅਰ ਕਰੰਟ ਲੰਘ ਰਿਹਾ ਹੋਵੇ ।
1 ਵਾਟ = 1 ਵੋਲਟੋ × 1 ਐਮਪੀਅਰ ਸ਼ਕਤੀ ਦੀ ਵੱਡੀ ਇਕਾਈ ਕਿਲੋਵਾਟ (kw) ਹੈ ।
1 ਕਿਲੋਵਾਟ = 1000 ਵਾਟ
ਬਿਜਲਈ ਊਰਜਾ – ਕਿਸੇ ਨਿਸਚਿਤ ਸਮੇਂ ਵਿੱਚ ਧਾਰਾ ਦੁਆਰਾ ਕੁੱਲ ਕੀਤੇ ਗਏ ਕਾਰਜ ਦੀ ਮਾਤਰਾ, ਬਿਜਲਈ ਊਰਜਾ ਕਹਾਉਂਦੀ ਹੈ ।
1 ਕਿਲੋਵਾਟ = 1000 ਵਾਟ
ਮੰਨ ਲਓ ਕਿਸੇ ਚਾਲਕ ਵਿਚੋਂ I ਐਮਪੀਅਰ ਧਾਰਾ t ਸਮੇਂ ਲੰਘਦੀ ਹੈ, ਜਦਕਿ ਇਸ ਦੇ ਸਿਰਿਆਂ ਵਿਚਕਾਰ V ਵੋਲਟ ਟੈਂਸ਼ਲ ਅੰਤਰ ਹੁੰਦਾ ਹੈ। ਵਰਤੀ ਗਈ ਉਰਜਾ ਜਾਂ ਕੀਤਾ ਗਿਆ ਕਾਰਜ ਇਸ ਤਰ੍ਹਾਂ ਪ੍ਰਗਟ ਕੀਤਾ ਜਾਂਦਾ ਹੈ-
W = QV
W = VIt ਹੁਣ, ਓਹਮ ਨਿਯਮ ਤੋਂ
V = IR
W = I²Rt
ਇਸ ਤਰ੍ਹਾਂ ਬਿਜਲ-ਊਰਜਾ (W) ਇਨ੍ਹਾਂ ਦੇ ਸਿੱਧਾ ਅਨੁਪਾਤੀ ਹੁੰਦਾ ਹੈ-
(i) ਕਰੰਟ ਦਾ ਵਰਗ (I²)
(ii) ਤਾਰ ਦਾ ਪ੍ਰਤਿਰੋਧ (R)
(iii) ਸਮਾਂ (1) ਜਿਸ ਲਈ ਕਰੰਟ ਤਾਰ ਵਿਚੋਂ ਲੰਘਦਾ ਹੈ ।
ਬਿਜਲਈ ਊਰਜਾ ਦੀ ਮਾਣਕ ਇਕਾਈ ਜੂਲ ਜਾਂ ਵਾਟ ਸੈਕਿੰਡ ਹੈ ਪਰ ਇਹ ਇੱਕ-ਛੋਟੀ ਇਕਾਈ ਹੈ। ਬਿਜਲਈ ਊਰਜਾ ਦੀ ਵੱਡੀ ਇਕਾਈ ਵਾਟ ਘੰਟਾ ਹੈ ।

ਵਾਟ ਘੰਟਾ – ਬਿਜਲਈ ਊਰਜਾ ਇੱਕ ਵਾਟ ਘੰਟਾ ਹੁੰਦੀ ਹੈ ਜੇਕਰ ਚਾਲਕ ਵਿਚੋਂ ਇੱਕ ਐਮਪੀਅਰ ਕਰੰਟ ਇੱਕ ਘੰਟੇ ਲਈ ਪ੍ਰਵਾਹਿਤ ਹੋਵੇ ਅਤੇ ਜਦੋਂ ਇਸ ਦੇ ਸਿਰਿਆਂ ਵਿਚਕਾਰ ਇੱਕ ਵੋਲਟ ਦਾ ਟੈਂਸ਼ਲ ਅੰਤਰ ਹੋਵੇ।
1 ਵਾਟ ਘੰਟਾ = 1 ਵਾਟ × 1 ਘੰਟਾ
= 1 ਵੋਲਟ × 1 ਐਮਪੀਅਰ × 1 ਘੰਟਾ
ਬਿਜਲ ਊਰਜਾ ਦੀ ਵੱਡੀ ਇਕਾਈ ਨੂੰ ਕਿਲੋਵਾਟ ਘੰਟਾ (kWh) ਕਹਿੰਦੇ ਹਨ ।
1 ਕਿਲੋਵਾਟ ਘੰਟਾ = 1000 ਵਾਟ ਘੰਟਾ
ਕਿਲੋਵਾਟ ਘੰਟਾ ਇਕਾਈ ਵਪਾਰਕ ਬੋਰਡ ਵਲੋਂ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਹੈ। ਇਸ ਲਈ ਇਸ ਨੂੰ B.O.T. ਇਕਾਈ ਵੀ ਕਹਿੰਦੇ ਹਨ। ਘਰੇਲੂ ਉਪਯੋਗ ਲਈ ਇਹ ਬਿਜਲ ਊਰਜਾ ਦੀ ਵਪਾਰਕ ਇਕਾਈ ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਕਿਸੇ ਚਾਲਕ (ਤਾਰ ਵਿੱਚੋਂ ਚਾਰਜ ਦੇ ਪ੍ਰਵਾਹ ਲਈ ਇਲੈਂਨਾਂ ਦਾ ਪ੍ਰਵਾਹ ਕਿਸ ਤਰ੍ਹਾਂ ਹੁੰਦਾ ਹੈ ? ਸਪੱਸ਼ਟ ਕਰੋ।
ਉੱਤਰ-
ਕਿਸੇ ਧਾਤਵੀਂ ਚਾਲਕ ਵਿੱਚ ਪਰਮਾਣੂ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਹੁੰਦੇ ਹਨ। ਇਨ੍ਹਾਂ ਵਿੱਚ ਉਪਸਥਿਤ ਸੁਤੰਤਰ ਇਲੈੱਕਟੁਨ ਸਾਰੀਆਂ ਦਿਸ਼ਾਵਾਂ ਵਿੱਚ ਗਤੀ ਕਰਦੇ ਹਨ। ਭਿੰਨ-ਭਿੰਨ ਦਿਸ਼ਾਵਾਂ ਵਿੱਚ ਗਤੀ ਕਰਨ ਦੇ ਕਾਰਨ ਇਲੈੱਕਵਾਂਨਾਂ ਦਾ ਬਹਾਓ ਕਿਸੇ ਨਿਸਚਿਤ ਦਿਸ਼ਾ ਵਿੱਚ ਨਹੀਂ ਹੁੰਦਾ ਹੈ, ਇਸ ਲਈ ਕਿਸੇ ਚਾਰਜ ਦਾ ਪ੍ਰਵਾਹ ਨਹੀਂ
ਹੁੰਦਾ ਹੈ ।

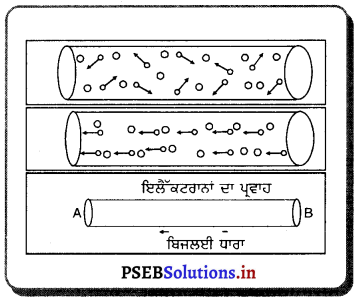
ਜਦੋਂ ਇਸ ਚਾਲਕ (ਤਾਰ) ਨੂੰ ਬੈਟਰੀ ਦੇ ਨਾਲ ਜੋੜ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ਤਾਂ ਚਾਲਕ ਦਾ ਇੱਕ ਸਿਰਾ ਧਨ ਅਤੇ ਦੂਜਾ ਸਿਰਾ ਰਿਣ ਬਣ ਜਾਂਦਾ ਹੈ। ਇਲੈੱਕਟ੍ਰਨ ਧਨ ਖੇਤਰ ਵੱਲ ਖਿੱਚੇ ਜਾਂਦੇ ਹਨ ਜਿਸਦੇ ਫਲਸਰੂਪ ਉਹ ਖੱਬੇ ਪਾਸੇ ਵੱਲ ਨੂੰ ਗਤੀਸ਼ੀਲ ਹੋ ਜਾਂਦੇ ਹਨ। ਇਲੈੱਕਟ੍ਰਾਨਾਂ ਦੀ ਗਤੀ ਸੱਜੇ ਤੋਂ ਖੱਬੀ ਦਿਸ਼ਾ ਵੱਲ ਹੋਣ ਕਾਰਨ ਚਾਰਜ ਦਾ ਪ੍ਰਵਾਹ ਸੱਜੇ ਤੋਂ ਖੱਬੇ ਦਿਸ਼ਾ ਵੱਲ ਹੁੰਦਾ ਹੈ। ਇਸ ਵਰਤਾਰੇ ਨੂੰ ਦਿੱਤੇ ਗਏ ਚਿੱਤਰ ਦੁਆਰਾ ਦਰਸਾਇਆ ਜਾ ਸਕਦਾ ਹੈ ।

ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Short Answer Type Questions)

ਪ੍ਰਸ਼ਨ 1.
ਬਿਜਲੀ ਦਾ ਸਾਡੇ ਰੋਜ਼ਾਨਾ ਜੀਵਨ ਵਿੱਚ ਕੀ ਰੋਲ ਹੈ ?
ਉੱਤਰ-
ਬਿਜਲੀ ਦਾ ਸਾਡੇ ਜੀਵਨ ਵਿਚ ਰੋਲ-ਬਿਜਲੀ ਦਾ ਸਾਡੇ ਜੀਵਨ ਵਿੱਚ ਬਹੁਤ ਵੱਡਾ ਯੋਗਦਾਨ ਹੈ। ਇਸ ਨਾਲ ਜੀਵਨ ਵਿੱਚ ਕਈ ਸਹੂਲਤਾਂ ਮਿਲਦੀਆਂ ਹਨ, ਜਿਵੇਂ ਰਾਤ ਨੂੰ ਹਨੇਰਾ ਦੂਰ ਕਰਨ ਲਈ ਇਸਦਾ ਉਪਯੋਗ ਬਿਜਲੀ ਦੇ ਬੱਲਬ ਅਤੇ ਟਿਊਬ ਲਾਈਟ ਵਿੱਚ ਕੀਤਾ ਜਾਂਦਾ ਹੈ, ਗਰਮੀਆਂ ਵਿੱਚ ਡੇਜ਼ਰਟ ਕੂਲਰ, ਏਅਰ ਕੰਡੀਸ਼ਨਰ ਆਦਿ ਨਾਲ ਬਿਜਲੀ ਦਾ ਉਪਯੋਗ ਕਰ ਕੇ ਘਰਾਂ ਨੂੰ ਠੰਡਾ ਅਤੇ ਸਰਦੀਆਂ ਵਿੱਚ ਹੀਟਰ ਆਦਿ ਨਾਲ ਗਰਮ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਤੋਂ ਛੁੱਟ ਬਿਜਲੀ ਦਾ ਉਪਯੋਗ ਕਰਕੇ ਟੈਲੀਵਿਜ਼ਨ, ਰੇਡੀਓ, ਸਿਨੇਮਾ ਅਤੇ ਸੰਗੀਤ ਆਦਿ ਦੁਆਰਾ ਮਨੋਰੰਜਨ ਹੁੰਦਾ ਹੈ। ਖੇਤੀ, ਆਵਾਜਾਈ ਅਤੇ ਉਦਯੋਗਾਂ ਵਿੱਚ ਮਸ਼ੀਨਾਂ ਆਦਿ ਨੂੰ ਚਲਾਉਣ ਲਈ ਵੀ ਬਿਜਲੀ ਦਾ ਉਪਯੋਗ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਇਲੈਕਟ੍ਰੋਸਟੈਟਿਕਸ ਤੋਂ ਤੁਹਾਡਾ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਇਲੈੱਕਟ੍ਰੋਸਟੈਟਿਕਸ (Electrostatics) – ਜਦੋਂ ਦੋ ਵਸਤੂਆਂ ਨੂੰ ਆਪਸ ਵਿੱਚ ਇੱਕ ਦੂਜੇ ਨਾਲ ਰਗੜਿਆ ਜਾਂਦਾ ਹੈ ਤਾਂ ਉਨ੍ਹਾਂ ਦੋਨਾਂ ਵਿੱਚ ਛੋਟੀਆਂ-ਛੋਟੀਆਂ ਅਤੇ ਹਲਕੀਆਂ ਵਸਤੂਆਂ ਨੂੰ ਆਪਣੇ ਵੱਲ ਆਕਰਸ਼ਿਤ ਕਰਨ ਦਾ ਗੁਣ ਆ ਜਾਂਦਾ ਹੈ । ਅਜਿਹਾ ਰਗੜ ਦੁਆਰਾ ਪੈਦਾ ਹੋਈ ਬਿਜਲੀ ਦੇ ਕਾਰਨ ਹੁੰਦਾ ਹੈ, ਜਿਸ ਨੂੰ ਰਗੜ ਬਿਜਲੀ ਜਾਂ ਸਥਿਰ ਬਿਜਲੀ ਵੀ ਕਹਿੰਦੇ ਹਨ। ਸਥਿਰ ਚਾਰਜਾਂ ਦੇ ਅਧਿਐਨ ਨੂੰ ‘ਇਲੈੱਕਟ੍ਰੋਸਟੈਟਿਕਸ’ ਕਹਿੰਦੇ ਹਨ ।

ਉਦਾਰਹਨ-ਜਦੋਂ ਕਿਸੇ ਪੈਂਨ ਨੂੰ ਸੁੱਕੇ ਵਾਲਾਂ ਦੇ ਨਾਲ ਰਗੜਿਆ ਜਾਂਦਾ ਹੈ ਤਾਂ ਇਹ ਕਾਗ਼ਜ਼ ਦੇ ਛੋਟੇ-ਛੋਟੇ ਟੁਕੜਿਆਂ ਨੂੰ ਆਪਣੇ ਵੱਲ ਖਿੱਚ ਲੈਂਦਾ ਹੈ। ਇਹ ਰਗੜ ਦੁਆਰਾ ਪੈਦਾ ਹੋਈ ਬਿਜਲੀ ਦੇ ਕਾਰਨ ਸੰਭਵ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਧਨ ਅਤੇ ਰਿਣ ਚਾਰਜ ਕੀ ਹੁੰਦਾ ਹੈ ? ਇਹ ਕਿਵੇਂ ਪੈਦਾ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਧਨ ਚਾਰਜ (Positive Charge) – ਰੇਸ਼ਮ ਦੇ ਕੱਪੜੇ ਦੇ ਨਾਲ ਰਗੜਨ ਤੇ ਕੱਚ ਦੀ ਛੜ ਤੇ ਪੈਦਾ ਹੋਏ ਚਾਰਜ ਨੂੰ ਧਨ ਚਾਰਜ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
ਰਿਣ ਚਾਰਜ (Negative Charge) – ਬਿੱਲੀ ਦੀ ਖੱਲ ਨਾਲ ਰਗੜਨ ਤੇ ਆਬਨੂਸ (ਐਨਾਈਟ ਦੀ ਛੜ ’ਤੇ ਪੈਦਾ ਹੋਏ ਚਾਰਜ ਨੂੰ ਰਿਣ ਚਾਰਜ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਚਾਲਕਾਂ ਅਤੇ ਰੋਧਕਾਂ ਵਿਚਕਾਰ ਅੰਤਰ ਸਪੱਸ਼ਟ ਕਰੋ।
ਜਾਂ
ਚਾਲਕ ਅਤੇ ਰੋਧਕ ਦੀ ਪਰਿਭਾਸ਼ਾ ਦਿਓ ।
ਉੱਤਰ-
ਚਾਲਕ ਅਤੇ ਰੋਧਕ (Conductors and insulators)-
ਚਾਲਕ-ਚਾਲਕਾਂ ਵਿੱਚ ਬਹੁਤ ਸਾਰੇ ਸੁਤੰਤਰ ਇਲੈੱਕਵਾਂਨ ਹੁੰਦੇ ਹਨ ਜੋ ਬਿਜਲ ਕਰੰਟ ਦੇ ਪ੍ਰਭਾਵ ਅਧੀਨ ਗਤੀ ਕਰਦੇ ਹਨ। ਜਦੋਂ ਚਾਲਕ ਨੂੰ ਬੈਟਰੀ ਨਾਲ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ ਤਾਂ ਇਹ ਇਲੈੱਕਟਾਂ ਇਸ ਦੇ ਧਨ ਟਰਮੀਨਲ ਵੱਲ ਆਕਰਸ਼ਿਤ ਹੁੰਦੇ ਹਨ ਅਤੇ ਰਿਣ ਟਰਮੀਨਲ ਤੋਂ ਪ੍ਰਤਿਕਰਸ਼ਿਤ ਹੁੰਦੇ ਹਨ। ਇਸ ਲਈ ਚਾਲਕ ਵਿੱਚ ਇਨ੍ਹਾਂ ਇਲੈੱਕਟ੍ਰਾਨਾਂ ਦੀ ਗਤੀ ਦੇ ਕਾਰਨ ਚਾਰਜ ਦਾ ਸਥਾਨਾਂਤਰਨ ਹੁੰਦਾ ਹੈ। ਇਸ ਲਈ ਚਾਲਕ ਅਜਿਹੇ ਪਦਾਰਥ ਹਨ ਜਿਨ੍ਹਾਂ ਵਿੱਚੋਂ ਆਸਾਨੀ ਨਾਲ ਬਿਜਲ ਕਰੰਟ ਲੰਘਦਾ ਹੈ।
ਉਦਾਹਰਨ – ਤਾਂਬਾ, ਚਾਂਦੀ, ਐਲੂਮੀਨੀਅਮ ਆਦਿ ।

ਰੋਧਕ – ਅਜਿਹੇ ਪਦਾਰਥ ਜਿਨ੍ਹਾਂ ਵਿੱਚ ਸੁਤੰਤਰ ਇਲੈੱਕਵਾਂਨ ਬਹੁਤ ਘੱਟ ਹੁੰਦੇ ਹਨ। ਇਨ੍ਹਾਂ ਪਦਾਰਥਾਂ ਵਿੱਚ ਇਲੈੱਕਟਾਂਨ ਆਸਾਨੀ ਨਾਲ ਗਤੀ ਨਹੀਂ ਕਰ ਸਕਦੇ ਹਨ ਅਰਥਾਤ ਜਿਨ੍ਹਾਂ ਪਦਾਰਥਾਂ ਵਿੱਚੋਂ ਬਿਜਲ ਕਰੰਟ ਨਹੀਂ ਲੰਘਦਾ ਉਹ ਰੋਧਕ ਕਹਾਉਂਦੇ ਹਨ ।
ਉਦਾਹਰਨ-ਰਬੜ, ਕੱਚ, ਪਲਾਸਟਿਕ ਆਦਿ ।

ਪ੍ਰਸ਼ਨ 5.
ਬਿਜਲਈ ਪੁਟੈਂਸ਼ਲ ਦਾ ਕੀ ਅਰਥ ਹੈ ? ਧਨ ਪੁਟੈਂਸ਼ਲ ਅਤੇ ਰਿਣ ਪੁਟੈਂਸ਼ਲ ਵਿੱਚ ਅੰਤਰ ਸਪੱਸ਼ਟ ਕਰੋ।
ਉੱਤਰ-
ਬਿਜਲਈ ਟੈਂਸ਼ਲ – ਇਹ ਚਾਲਕ ਦੀ ਇੱਕ ਵਿਸ਼ੇਸ਼ ਬਿਜਲਈ ਅਵਸਥਾ ਹੈ ਜੋ ਸਾਨੂੰ ਇਹ ਦੱਸਦੀ ਹੈ ਕਿ ਕਿਸੇ ਦੂਸਰੇ ਚਾਲਕ ਦੇ ਸੰਪਰਕ ਵਿੱਚ ਆਉਣ ਨਾਲ ਬਿਜਲਈ ਚਾਰਜ ਦਾ ਬਹਾਓ ਕਿਸ ਦਿਸ਼ਾ ਵਿੱਚ ਹੋਵੇਗਾ। ਕਿਸੇ ਚਾਲਕ ਦਾ ਪੁਟੈਂਸ਼ਲ ਧਰਤੀ ਦੇ ਸਾਪੇਖ ਮਾਪਿਆ ਜਾਂਦਾ ਹੈ ।

ਧਨ ਪੁਟੈਂਸ਼ਲ – ਜੇਕਰ ਧਨ ਚਾਰਜ ਵਸਤੂ ਤੋਂ ਧਰਤੀ ਵੱਲ ਵਹਿੰਦਾ ਜਾਂ ਇਲੈਕਟ੍ਰਾਨ ਧਰਤੀ ਤੋਂ ਵਸਤੂ ਵੱਲ ਪ੍ਰਵਾਹਿਤ ਹੋਣ ਤਾਂ ਉਸ ਵਸਤੂ ਦੇ ਟੈਂਸ਼ਲ ਨੂੰ ਧਨ ਟੈਸ਼ਲ ਕਹਿੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 6.
ਕਿਸੇ ਸੈੱਲ ਦੇ ਬਿਜਲਈ ਵਾਹਕ ਬਲ ਦਾ ਕੀ ਅਰਥ ਹੈ ?
ਉੱਤਰ-
ਸੈੱਲ ਦਾ ਬਿਜਲਈ ਵਾਹਕ ਬਲ – ਇਕਾਈ ਚਾਰਜ ਨੂੰ ਪੂਰੇ ਸਰਕਟ ਵਿੱਚੋਂ ਪ੍ਰਵਾਹਿਤ ਕਰਾਉਣ ਵਿੱਚ ਸਰਕਟ ਵਿੱਚ ਸੈੱਲ ਦੁਆਰਾ ਖ਼ਰਚ ਕੀਤੀ ਜਾਣ ਵਾਲੀ ਊਰਜਾ ਨੂੰ ਸੈੱਲ ਦਾ ਬਿਜਲਈ ਵਾਹਕ ਬਲ ਕਹਿੰਦੇ ਹਨ। ਇਸ ਨੂੰ E ਦੁਆਰਾ ਦਰਸਾਇਆ ਜਾਂਦਾ ਹੈ। ਬਿਜਲਈ ਵਾਹਕ ਬਲ ਦੀ S.I ਇਕਾਈ ਵੋਲਟ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਇਲੈੱਕਟ੍ਰੋਸਟੈਟਿਕਸ ਵਿੱਚ ਕੂਲਾਂਮ ਦਾ ਨਿਯਮ ਬਿਆਨ ਕਰੋ ਅਤੇ ਇਸ ਦੀ ਵਿਆਖਿਆ ਕਰੋ ।
ਜਾਂ
ਸਥਿਰ ਬਿਜਲਈ ਵਿੱਚ ਕੂਲਾਂਮ ਦੇ ਨਿਯਮ ਦੀ ਪਰਿਭਾਸ਼ਾ ਦਿਓ ।
ਜਾਂ
ਸਥਿਰ ਬਿਜਲਈ ਵਿੱਚ ਕੂਲਾਂਮ ਦਾ ਨਿਯਮ ਬਿਆਨ ਕਰੋ ਅਤੇ ਇਸ ਦੀ ਵਿਆਖਿਆ ਕਰੋ ।
ਉੱਤਰ-
ਇਲੈੱਕਟ੍ਰੋਸਟੈਟਿਕਸ ਵਿੱਚ ਕੂਲਾਮ ਦਾ ਨਿਯਮ – ਕੂਲਾਂਮ ਦੇ ਨਿਯਮ ਅਨੁਸਾਰ ਦੋ ਸਮਜਾਤੀ ਰੂਪ ਵਿੱਚ ਚਾਰਜਿਤ ਵਸਤੁਆਂ ਦੇ ਵਿਚਕਾਰ ਅਪਕਰਸ਼ਨ ਬਲ ਜਾਂ ਦੋ ਅਸਮਜਾਤੀ ਚਾਰਜ ਵਾਲੀਆਂ ਵਸਤੂਆਂ ਦੇ ਵਿਚਕਾਰ ਆਕਰਸ਼ਣ ਬਲ ਉਨ੍ਹਾਂ ਚਾਰਜਾਂ ਦੀ ਮਾਤਰਾ ਦੇ ਗੁਣਾਂ ਦੇ ਸਿੱਧਾ ਅਨੁਪਾਤੀ ਅਤੇ ਉਨ੍ਹਾਂ ਵਿਚਕਾਰ ਦੂਰੀ ਦੇ ਵਰਗ ਦੇ ਉਲਟ ਸਮਾਨੁਪਾਤੀ ਹੁੰਦਾ ਹੈ ।

ਮੰਨ ਲਓ ਦੋ ਬਿੰਦੂਆਂ ਤੇ ਚਾਰਜ ਦੀ ਮਾਤਰਾ q₁ ਅਤੇ q₂ ਹੈ ਅਤੇ ਇਨ੍ਹਾਂ ਵਿਚਕਾਰ ਦੂਰੀ ‘d’ ਹੈ। ਜੇ ਇਨ੍ਹਾਂ ਵਿਚਕਾਰ ਕਿਰਿਆ ਕਰ ਰਿਹਾ ਬਲ F ਹੋਵੇ, ਤਾਂ
F ∝ q₁q₂ ……….(i)
ਅਤੇ
F ∝ \(\frac{1}{d^{2}}\) ………(ii)
ਸਮੀਕਰਨ (1) ਅਤੇ (ii) ਨੂੰ ਮਿਲਾ ਕੇ,
F ∝ \(\frac{q_{1} q_{2}}{d^{2}}\)
ਜਾਂ
F = \(\frac{q_{1} q_{2}}{d^{2}}\)
ਜਿੱਥੇ K ਅਨੁਪਾਤ ਅੰਕ ਹੈ ਜਿਸਦਾ ਮੁੱਲ ਚਾਰਜਾਂ ਦੇ ਮਾਧਿਅਮ ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ । ਜੇਕਰ ਇਨ੍ਹਾਂ ਚਾਰਜਾਂ ਨੂੰ ਕੂਲਾਂਮ ਵਿੱਚ ਅਤੇ ਦੂਰੀ ਨੂੰ ਮੀਟਰਾਂ ਵਿੱਚ ਲਿਆ ਜਾਵੇ, ਤਾਂ ਹਵਾ ਜਾਂ ਨਿਰਵਾਯੂ ਲਈ K = 9 × 10⁹ ਹੈ ।
F = 9 × 10⁹ × \(\) ਨਿਊਟਨ

ਪ੍ਰਸ਼ਨ 8.
ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ ਕਿਸ ਨੂੰ ਕਹਿੰਦੇ ਹਨ ?
ਜਾਂ
ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ ਕਿਸਨੂੰ ਕਹਿੰਦੇ ਹਨ ? ਇਸ ਦੀ ਇਕਾਈ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ-ਇੱਕ ਬਿਜਲੀ ਖੇਤਰ ਵਿੱਚ ਦੋ ਬਿੰਦੂਆਂ ਦੇ ਵਿਚਕਾਰ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ ਉਸ ਖੇਤਰ ਕਾਰਨ ਸਥਿਰ ਬਿਜਲੀ ਦਲ ਦੇ ਉਲਟ ਇੱਕ ਇਕਾਈ ਧਨ ਚਾਰਜ ਨੂੰ ਇੱਕ ਬਿੰਦੂ ਤੋਂ ਦੂਜੇ ਬਿੰਦੂ ਤਕ ਲੈ ਜਾਣ ਲਈ ਕੀਤੇ ਗਏ ਕਾਰਜ ਦੀ ਮਾਤਰਾ ਹੈ । ਪੁਟੈਂਥਲ ਅੰਤਰ ਦੀ ਇਕਾਈ ਵੋਲਟ ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਵੋਲਟ ਦੀ ਪਰਿਭਾਸ਼ਾ ਲਿਖੋ। ਇਹ ਕਿਸ ਦੀ ਇਕਾਈ ਹੈ ?
ਉੱਤਰ-
ਵੋਲਟ-ਬਿਜਲੀ ਖੇਤਰ ਦੇ ਦੋ ਬਿੰਦੂਆਂ ਦੇ ਵਿਚਕਾਰ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ ਇੱਕ ਵੋਲਟ ਹੁੰਦਾ ਹੈ, ਜਦੋਂ ਇੱਕ ਕੂਲਾਮ ਦੇ ਚਾਰਜ ਨੂੰ ਇਕ ਬਿੰਦੂ ਤੋਂ ਦੂਜੇ ਬਿੰਦੂ ਤਕ ਲੈ ਜਾਣ ਵਿੱਚ 1 ਜੂਲ ਕਾਰਜ ਕੀਤਾ ਗਿਆ ਹੋਵੇ

ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ ਦੀ ਇਕਾਈ ਵੋਲਟ ਹੈ ।

ਪ੍ਰਸ਼ਨ 10.
ਅਸੀਂ ਕਿਵੇਂ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਬਿਜਲ ਕਰੰਟ ਚਾਰਜ ਦੇ ਪ੍ਰਵਾਹ ਕਾਰਨ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਜੇ ਅਸੀਂ ਇੱਕ ਚਾਰਜਿਤ ਬਿਜਲਦਰਸ਼ੀ ਨੂੰ ਤਾਰਾਂ ਦੁਆਰਾ ਅਣਚਾਰਜਿਤ ਬਿਜਲਦਰਸ਼ੀ ਦੇ ਨਾਲ ਜੋੜੀਏ, ਤਾਂ ਚਾਰਜ ਚਾਰਜਿਤ ਬਿਜਲਦਰਸ਼ੀ ਤੋਂ ਅਣਚਾਰਜਿਤ ਬਿਜਲਦਰਸ਼ੀ ਵੱਲ ਪ੍ਰਵਾਹਿਤ ਕਰਨਾ ਸ਼ੁਰੂ ਕਰ ਦੇਵੇਗਾ। ਇਸ ਨਾਲ ਅਸਚਾਰਜਿਤ ਬਿਜਲਦਰਸ਼ੀ ਦੇ ਪੱਤਰੇ ਵਧੇਰੇ ਫੈਲ ਕੇ ਇੱਕ ਦੂਜੇ ਤੋਂ ਵੱਖ ਹੋ ਜਾਣਗੇ ਅਤੇ ਖੁੱਲ੍ਹ ਜਾਣਗੇ। ਕਰੰਟ ਦਾ ਇਹ ਵਾਹ ਓਨੀ ਦੇਰ ਤਕ ਚਲਦਾ ਰਹੇਗਾ ਜਦੋਂ ਤੱਕ ਕਿ ਦੋਵੇਂ ਬਿਜਲਦਰਸ਼ੀਆਂ ਦੇ ਪੱਤਰੇ ਇੱਕ ਨਹੀਂ ਹੋ ਜਾਂਦੇ। ਬਰਾਬਰੀ ਆਉਣ ‘ਤੇ ਬਿਜਲਦਰਸ਼ੀ ਤੇ ਪੱਤਰੇ ਇੱਕ ਸਾਰ ਖੁੱਲ੍ਹਣਗੇ। ਚਾਰਜ ਦੇ ਇਸ ਪ੍ਰਵਾਹ ਨੂੰ ਹੀ ਬਿਜਲਈ ਧਾਰਾ ਕਹਿੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 11.
ਬਿਜਲ ਕਰੰਟ ਕੀ ਹੈ ?
ਜਾਂ
ਬਿਜਲ ਕਰੰਟ ਕਿਸ ਨੂੰ ਕਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਬਿਜਲ ਕਰੰਟ (Electric Current) – ਜਦੋਂ ਦੋ ਬਿੰਦੂ, ਜੋ ਕਿ ਵੱਖ-ਵੱਖ ਟੈਂਸ਼ਲਾਂ ਤੇ ਹੋਣ, ਨੂੰ ਇੱਕ ਤਾਂਬੇ ਦੀ ਤਾਰ ਦੁਆਰਾ ਜੋੜ ਦਿੱਤਾ ਜਾਵੇ ਤਾਂ ਚਾਰਜ ਵੱਧ ਪੁਟੈਂਸ਼ਲ ਤੋਂ ਘੱਟ ਪੁਟੈਂਸ਼ਲ ਵਾਲੇ ਚਾਲਕ ਵੱਲ ਪ੍ਰਵਾਹ ਸ਼ੁਰੂ ਕਰ ਦਿੰਦਾ ਹੈ । ਇਹ ਕਿਰਿਆ ਉਦੋਂ ਤੱਕ ਚਲਦੀ ਰਹਿੰਦੀ ਹੈ, ਜਦੋਂ ਤਕ ਕਿ ਦੋਨੋਂ ਬਿੰਦੂਆਂ ਦਾ ਪੁਟੈਂਸ਼ਲ ਬਰਾਬਰ ਨਹੀਂ ਹੋ ਜਾਂਦਾ । ਜੇ ਦੋਨਾਂ ਬਿੰਦੂਆਂ ਵਿੱਚ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ ਬਣਿਆ ਰਹੇ, ਤਾਂ ਚਾਰਜ ਦਾ ਪ੍ਰਵਾਹ ਜਾਰੀ ਰਹਿੰਦਾ ਹੈ। ਇਸ ਤਰ੍ਹਾਂ ਚਾਰਜ ਦੇ ਲਗਾਤਾਰ ਪ੍ਰਵਾਹ ਨੂੰ ਕਰੰਟ ਕਹਿੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 12.
ਬਿਜਲਈ ਧਾਰਾ ਕਿਵੇਂ ਊਸ਼ਮਾ ਉਤਪੰਨ ਕਰਦੀ ਹੈ ?
ਉੱਤਰ-
ਕਿਸੇ ਧਾਤਵੀ ਚਾਲਕ ਵਿੱਚ ਬਹੁਤ ਵੱਡੀ ਸੰਖਿਆ ਵਿੱਚ ਮੁਕਤ ਇਲੈੱਕਵਾਂਨ ਗਤੀ ਕਰਦੇ ਹਨ। ਜਦੋਂ ਚਾਲਕ ਨੂੰ ਬਿਜਲਈ ਸਰੋਤ ਨਾਲ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਮੁਕਤ ਇਲੈੱਕਫੁੱਟ ਉੱਚੇ ਪੁਟੈਂਸ਼ਲ ਤੋਂ ਨੀਵੇਂ ਟੈਂਸ਼ਲ ਵੱਲ ਪ੍ਰਵਾਹਿਤ ਹੁੰਦੇ ਹਨ ਜਿਸ ਤੋਂ ਇਲੈਂਕਨ ਪਰਮਾਣੂਆਂ ਨਾਲ ਟਕਰਾਉਂਦੇ ਹਨ । ਇਸ ਟਕਰਾਓ ਕਾਰਨ ਮੁਕਤ ਇਲੈੱਕਟ੍ਰਾਨਾਂ ਦੀ ਗਤਿਜ ਉਰਜਾ ਚਾਲਕ ਦੇ ਪਰਮਾਣੁਆਂ ਵਿੱਚ ਸਥਾਨਾਂਤਰਿਤ ਹੋ ਜਾਂਦੀ ਹੈ । ਪਰਮਾਣੂਆਂ ਦੀ ਗਤਿਜ ਉਰਜਾ ਵੱਧ ਜਾਂਦੀ ਹੈ, ਜਿਸ ਕਾਰਨ ਚਾਲਕ ਦੇ ਤਾਪ ਦੀ ਧੀ ਹੋ ਜਾਂਦੀ ਹੈ ਅਤੇ ਊਸ਼ਮਾ ਉਤਪੰਨ ਹੋ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 13.
ਕਿਸੇ ਚਾਲਕ ਵਿੱਚ ਪ੍ਰਵਾਹਿਤ ਬਿਜਲਈ ਧਾਰਾ ਤੋਂ ਉਤਪੰਨ ਹੋਈ ਊਸ਼ਮਾ ਦਾ ਸੰਬੰਧ ਸਥਾਪਿਤ ਕਰੋ ।
ਉੱਤਰ-
ਬਿਜਲੀ ਅਤੇ ਊਸ਼ਮਾ ਵਿਚਕਾਰ ਸੰਬੰਧ – ਜਦੋਂ ਕਿਸੇ ਚਾਲਕ ਵਿੱਚੋਂ ਬਿਜਲਈ ਧਾਰਾ ਲੰਘਾਈ ਜਾਂਦੀ ਹੈ, ਤਾਂ ਉਹ ਗਰਮ ਹੋ ਜਾਂਦਾ ਹੈ। ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਜੂਲ ਨਾਂ ਦੇ ਵਿਗਿਆਨਿਕ ਨੇ ਸਾਨੂੰ ਇਹ ਦੱਸਿਆ ਸੀ । ਇਸ ਲਈ ਇਸ ਨੂੰ ਜੂਲ ਦਾ ਤਾਪਨ ਪ੍ਰਭਾਵ ਦਾ ਨਿਯਮ ਕਹਿੰਦੇ ਹਨ। ਕਿਉਂਕਿ ਚਾਲਕ ਬਿਜਲਈ ਧਾਰਾ ਦੇ ਪ੍ਰਵਾਹ ਦਾ ਤਿਰੋਧ ਕਰਦਾ ਹੈ, ਇਸ ਲਈ ਚਾਲਕ ਵਿੱਚ ਲਗਾਤਾਰ ਬਿਜਲਈ ਧਾਰਾ ਦੇ ਪ੍ਰਵਾਹ ਹੋਣ ਵਿੱਚ ਕਾਰਜ ਕਰਨਾ ਪੈਂਦਾ ਹੈ ਜੋ ਉਸ਼ਮਾ ਦੇ ਰੂਪ ਵਿੱਚ ਪ੍ਰਗਟ ਹੁੰਦਾ ਹੈ ।

ਮੰਨ ਲਓ ਕਿਸੇ R ਤਿਰੋਧ ਵਾਲੇ ਚਾਲਕ ਵਿੱਚ t ਸੈਕਿੰਡ ਤੱਕ I ਬਿਜਲਈ ਧਾਰਾ, V ਪੁਟੈਂਸ਼ਲ ਤੇ ਪ੍ਰਵਾਹਿਤ ਹੋ ਰਹੀ ਹੈ ਅਤੇ t ਸਮਾਂ ਲਈ I ਧਾਰਾ Q ਚਾਰਜ ਕਾਰਨ ਹੋਵੇ ਤਾਂ,
I = \(\frac{\mathrm{Q}}{t}\)
ਜਾਂ Q = I × t
Q ਚਾਰਜ ਲਈ ਕੀਤਾ ਗਿਆ ਕਾਰਜ W = Q × V
= It × V
= It × I × R
= I² Rt (∵ V = I × R)
ਜੇਕਰ ਉਤਸਰਜਿਤ ਊਰਜਾ ਨੂੰ ਮ ਨਾਲ ਪ੍ਰਦਰਸ਼ਿਤ ਕੀਤਾ ਜਾਵੇ ਤਾਂ
H = W
∴ H = I²Rt ਜੂਲ

ਪ੍ਰਸ਼ਨ 14.
ਚਾਲਕ ਦੇ ਪ੍ਰਤਿਰੋਧ ਦੀ ਪਰਿਭਾਸ਼ਾ ਦਿਓ । ਇਸ ਦਾ ਮਾਤ੍ਰਿਕ ਦੱਸੋ ।
ਜਾਂ
ਚਾਲਕ ਦੇ ਪ੍ਰਤਿਰੋਧ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ? ਇਸ ਦੇ ਨਿਯਮ ਦੀ ਪਰਿਭਾਸ਼ਾ ਲਿਖੋ ।
ਉੱਤਰ-
ਚਾਲਕ ਦਾ ਪ੍ਰਤਿਰੋਧ – ਕਿਸੇ ਚਾਲਕ ਦੇ ਸਿਰਿਆਂ ਵਿੱਚ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ ਅਤੇ ਉਸ ਵਿੱਚ ਪ੍ਰਵਾਹਿਤ ਹੋ ਰਹੇ ਕਰੰਟ ਦੀ ਮਾਤਰਾ ਦੇ ਅਨੁਪਾਤ ਨੂੰ ਚਾਲਕ ਦਾ ਤਿਰੋਧ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
ਜੇ ਚਾਲਕ ਦੇ ਸਿਰਿਆਂ ਵਿਚਕਾਰ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ vਹੋਵੇ ਅਤੇ ਇਸ ਵਿਚੋਂ ਲੰਘ ਰਹੀ ਕਰੰਟ ਦੀ ਮਾਤਰਾ 1 ਹੋਵੇ ਤਾਂ ਪ੍ਰਤਿਰੋਧ (R)
ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ (V) ਪ੍ਰਤਿਰੋਧ (R)

ਪ੍ਰਤਿਰੋਧ ਦਾ ਮਾਤ੍ਰਿਕ-S.I. ਪ੍ਰਣਾਲੀ ਵਿੱਚ ਪ੍ਰਤਿਰੋਧ ਦਾ ਮਾਤ੍ਰਿਕ ਓਹਮ ਹੈ ਜਦਕਿ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ ਵੋਲਟ ਅਤੇ ਬਿਜਲੀ ਕਰੰਟ ਨੂੰ ਐਮਪੀਅਰ ਵਿੱਚ ਮਾਪਿਆ ਜਾਂਦਾ ਹੈ ।

ਓਹਮ (Ohn) – ਕਿਸੇ ਚਾਲਕ ਦਾ ਤਿਰੋਧ ਇੱਕ ਓਹਮ ਹੋਵੇਗਾ ਜੇ ਉਸਦੇ ਸਿਰਿਆਂ ਵਿਚਕਾਰ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ ਇੱਕ ਵਲਟ ਹੋਵੇ ਅਤੇ ਉਸ ਵਿਚੋਂ ਲੰਘ ਰਹੇ ਕਰੰਟ ਦੀ ਮਾਤਰਾ ਇੱਕ ਐਮਪੀਅਰ ਹੋਵੇ ।

ਪ੍ਰਸ਼ਨ 15.
ਪ੍ਰਤਿਰੋਧਕਤਾ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ? ਇਸ ਦਾ S.I. ਮਾਤ੍ਰਿਕ ਲਿਖ ਕੇ ਮਹੱਤਤਾ ਦੱਸੋ ।
ਉੱਤਰ-
ਪ੍ਰਤਿਰੋਧਕਤਾ – ਕਿਸੇ ਇਕਾਈ ਲੰਬਾਈ ਅਤੇ ਇਕਾਈ ਪਰਿਖੇਤਰਫਲ ਵਾਲੇ ਚਾਲਕ ਦਾ ਪ੍ਰਤਿਰੋਧ ਉਸ ਚਾਲਕ ਦੀ ਪ੍ਰਤਿਰੋਧਕਤਾ ਕਹਾਉਂਦੀ ਹੈ। ਇਸ ਦਾ S.I. ਮਾਤ੍ਰਿਕ Ω m (ਓਹਮ-ਮੀਟਰ ਹੈ ।
ਮਹੱਤਤਾ-

1. ਇਹ ਤਾਪਮਾਨ ਦੇ ਨਾਲ ਪਰਿਵਰਤਿਤ ਹੁੰਦਾ ਹੈ ।
2. ਜਿਨ੍ਹਾਂ ਪਦਾਰਥਾਂ ਦੀ ਪ੍ਰਤਿਰੋਧਕਤਾ ਵੱਧ ਹੁੰਦੀ ਹੈ ਉਹ ਬਿਜਲੀ ਦੇ ਕੁਚਾਲਕ ਜਾਂ ਘੱਟ ਚਾਲਕ ਹੁੰਦੇ ਹਨ ।
3. ਜਿਨ੍ਹਾਂ ਪਦਾਰਥਾਂ ਦੀ ਪ੍ਰਤਿਰੋਧਕਤਾ ਘੱਟ ਹੁੰਦੀ ਹੈ, ਉਹ ਬਿਜਲਈ ਧਾਰਾ ਦੇ ਚੰਗੇ ਚਾਲਕ ਹੁੰਦੇ ਹਨ। ਜਿਵੇਂ-ਧਾਤਾਂ, ਮਿਸ਼ਰਧਾਤਾਂ ਆਦਿ ।
4. ਕਿਸੇ ਮਿਸ਼ਰਧਾਤੂ ਦੀ ਪ੍ਰਤਿਰੋਧਕਤਾ ਉਸਦੀਆਂ ਘਟਕ ਧਾਤਾਂ ਤੋਂ ਅਧਿਕ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 16.
ਤਾਪੀ ਉਪਕਰਨਾਂ ਵਿੱਚ ਧਾਤਾਂ ਅਤੇ ਮਿਸ਼ਰਤ ਧਾਤਾਂ ਦਾ ਉਪਯੋਗ ਕਿਸ ਕਾਰਨ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਉੱਚ ਪ੍ਰਤਿਰੋਧਕਤਾ ਦੇ ਗੁਣਾਂ ਵਾਲੀਆਂ ਧਾਤਾਂ ਅਤੇ ਮਿਸ਼ਰਤ ਧਾਤਾਂ ਦਾ ਉਪਯੋਗ ਤਾਪਨ ਉਪਕਰਨਾਂ ਵਿੱਚ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਕਿਉਂਕਿ-

1. ਇਹ ਉੱਚੇ ਤਾਪਮਾਨ ਤੇ ਆਕਸੀਕ੍ਰਿਤ ਨਹੀਂ ਹੁੰਦੇ ਹਨ ।
2. ਇਹ ਅਧਿਕ ਪ੍ਰਤਿਰੋਧ ਕਰਦੇ ਹਨ ।
3. ਇਹ ਉੱਚੇ ਤਾਪਮਾਨ ਤੇ ਨਹੀਂ ਜਲਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 17.
ਬਿਜਲ ਸਰਕਟ ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ?
ਉੱਤਰ-
ਇਹ ਇੱਕ ਬੰਦ ਸਰਕਟ ਹੁੰਦਾ ਹੈ, ਜਿਸ ਵਿੱਚ ਇਲੈੱਕਟ੍ਰਾਨ ਬਹੁਤ ਤੇਜ਼ੀ ਨਾਲ ਲੰਘਦੇ ਹਨ। ਜਦੋਂ ਕਿਸੇ ਚਾਲਕ ਨੂੰ ਬੈਟਰੀ ਨਾਲ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਇਲੈੱਕਟਾਂਨ ਰਿਣ ਟਰਮੀਨਲ ਤੋਂ ਧਨ ਟਰਮੀਨਲ ਵੱਲ ਪ੍ਰਵਾਹਿਤ ਹਨ। ਪਰ ਕਰੰਟ (I) ਦੀ ਪਰੰਪਰਿਕ ਦਿਸ਼ਾ ਇਲੈਂਕਨ ਦੇ ਪ੍ਰਵਾਹ ਦੀ ਦਿਸ਼ਾ ਤੋਂ ਉਲਟ ਲਈ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 18.
ਬਿਜਲਈ ਕਰੰਟ ਕੀ ਹੈ ? ਇਸ ਦੀਆਂ ਮਾਤ੍ਰਿਕਾਂ ਦੱਸੋ।
ਜਾਂ
ਬਿਜਲਈ ਕਰੰਟ ਕੀ ਹੈ ? ਇਸਦੀ S.I. ਪ੍ਰਣਾਲੀ ਵਿੱਚ ਇਕਾਈ ਦੀ ਪਰਿਭਾਸ਼ਾ ਲਿਖੋ ।
ਉੱਤਰ-
ਬਿਜਲਈ ਕਰੰਟ (Current) – ਜੇ ਦੋ ਚਾਰਜਿਤ ਵਸਤੂਆਂ ਨੂੰ ਇੱਕ ਚਾਲਕ ਦੁਆਰਾ ਜੋੜਿਆ ਜਾਵੇ ਤਾਂ ਇਲੈੱਕਵਾਂਨ ਇੱਕ ਵਸਤੂ ਤੋਂ ਦੂਜੀ ਵਸਤੂ ਵੱਲ ਪ੍ਰਵਾਹਿਤ ਹੁੰਦੇ ਹਨ। ਇਲੈਂਕਟਾਂਨਾਂ ਦੇ ਪ੍ਰਵਾਹ ਦੀ ਦਰ ਨੂੰ ਬਿਜਲ ਈਧਾਰਾ (I) ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਦੂਜੇ ਸ਼ਬਦਾਂ ਵਿੱਚ, ਇਕਾਈ ਸਮੇਂ ਵਿੱਚ ਪ੍ਰਵਾਹਿਤ ਹੋ ਰਹੇ ਚਾਰਜ ਨੂੰ ਬਿਜਲਈ ਕਰੰਟ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।

= 6.25 × 10¹⁸ ਇਲੈੱਕਟ੍ਰਾਨ

ਐਮਪੀਅਰ (Ampere) – ਜਦੋਂ ਕਿਸੇ ਚਾਲਕ ਵਿੱਚੋਂ ਇੱਕ ਸੈਕਿੰਡ ਲਈ ਇੱਕ ਕੂਲਾਂ ਚਾਰਜ ਪ੍ਰਵਾਹਿਤ ਹੁੰਦਾ ਹੈ, ਤਾਂ ਉਸ ਨੂੰ ਇੱਕ ਐਮਪੀਅਰ ਕਿਹਾ ਜਾਂਦਾ ਹੈ।
ਕਰੰਟ ਦੀ ਛੋਟੀ ਇਕਾਈ ਮਿਲੀ-ਐਮਪੀਅਰ ਹੈ ।
1 ਮਿਲੀ-ਐਮਪੀਅਰ = \(\frac{1}{1000}\) ਐਮਪੀਅਰ
= 10^-3 ਐਮਪੀਅਰ

ਪ੍ਰਸ਼ਨ 19.
ਕਰੰਟ ਮਾਪਣ ਲਈ ਕਿਸ ਯੰਤਰ ਦਾ ਉਪਯੋਗ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ? ਸਰਕਟ ਵਿੱਚ ਇਸ ਨੂੰ ਕਿਵੇਂ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਸਰਕਟ ਵਿੱਚ ਪ੍ਰਵਾਹਿਤ ਕਰੰਟ ਨੂੰ ਮਾਪਣ ਲਈ ਐਮਮੀਟਰ ਦਾ ਉਪਯੋਗ ਕੀਤਾ ਜਾਂਦਾ ਹੈ। ਇਹ ਸਰਕਟ ਵਿੱਚ ਹਮੇਸ਼ਾ ਇਸ ਢੰਗ ਨਾਲ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ ਕਿ ਸੰਪੂਰਨ ਕਰੰਟ ਇਸ ਵਿੱਚੋਂ ਪ੍ਰਵਾਹਿਤ ਹੋਵੇ ਅਰਥਾਤ ਲੜੀਵਾਰ ਕੂਮ ਵਿਚ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ। ਐਮਮੀਟਰ ਦਾ ਪ੍ਰਤਿਰੋਧ ਬਹੁਤ ਘੱਟ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 20.
ਬਿਜਲੀ ਊਰਜਾ ਦੀ ਇਕਾਈ ਦੀ ਪਰਿਭਾਸ਼ਾ ਲਿਖੋ।
ਜਾਂ
ਇਕ ਵਾਟ = ਘੰਟਾ ਦੀ ਪਰਿਭਾਸ਼ਾ ਦਿਓ । ਉੱਤਰ-ਬਿਜਲੀ ਊਰਜਾ ਦੀ ਇਕਾਈ ਜੂਲ/ਵਾਟ-ਸੈਕਿੰਡ/ਵਾਟ-ਘੰਟਾ ਹੈ।
ਵਾਟ-ਘੰਟਾ-ਬਿਜਲੀ ਊਰਜਾ ਇੱਕ ਵਾਟ-ਘੰਟਾ ਹੁੰਦੀ ਹੈ ਜੇ ਇਕ ਐਮਪੀਅਰ ਕਰੰਟ ਚਾਲਕ ਵਿੱਚੋਂ ਇੱਕ ਘੰਟੇ ਲਈ ਪ੍ਰਵਾਹਿਤ ਹੋਵੇ ਅਤੇ ਜਦੋਂ ਉਸਦੇ ਸਿਰਿਆਂ ਵਿੱਚ ਇੱਕ ਵੋਲਟ ਦਾ ਟੈਂਸ਼ਲ ਅੰਤਰ ਹੋਵੇ !
1 ਵਾਟ ਘੰਟਾ = 1 ਵਾਟ × 1 ਘੰਟਾ
= 1 ਵੋਲਟ × 1 ਐਮਪੀਅਰ × 1 ਘੰਟਾ
ਬਿਜਲੀ ਦੀ ਵੱਡੀ ਇਕਾਈ ਨੂੰ ਕਿਲੋਵਾਟ ਘੰਟਾ ਕਹਿੰਦੇ ਹਨ ।
1 ਕਿਲੋਵਾਟ ਘੰਟਾ = 1000 ਵਾਟ ਘੰਟਾ ।

ਪ੍ਰਸ਼ਨ 21.
ਇਕ ਕਿਲੋਵਾਟ ਘੰਟਾ ਵਿੱਚ ਕਿੰਨੇ ਜੂਲ ਹੁੰਦੇ ਹਨ ?
ਜਾਂ
ਇਕ ਕਿਲੋਵਾਟ ਘੰਟਾ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕਰੋ ।
ਉੱਤਰ-
ਕਿਲੋਵਾਟ ਘੰਟਾ – ਜੇਕਰ ਇੱਕ ਕਿਲੋਵਾਟ ਬਿਜਲਈ ਸ਼ਕਤੀ ਨੂੰ 1 ਘੰਟੇ ਤਕ ਪ੍ਰਯੋਗ ਕੀਤਾ ਜਾਵੇ, ਤਾਂ ਖਪਤ ਹੋਈ ਊਰਜਾ ਇੱਕ ਕਿਲੋਵਾਟ ਘੰਟਾ (kWh) ਹੁੰਦੀ ਹੈ ।
∴ 1 kWh = 1 kW × 1 ਘੰਟਾ
= 1000 ਵਾਟ × 3600 ਸੈਕਿੰਡ
= 1000 × 3600 ਸੈਕਿੰਡ
∴ 1 ਕਿਲੋਵਾਟ ਘੰਟਾ (1 kWh) = 36 × 10⁵ ਜੂਲ ।

ਪ੍ਰਸ਼ਨ 22.
ਕੀ ਕਾਰਨ ਹੈ ਕਿ ਬਿਜਲਈ ਵਾਹਕ ਤਾਰਾਂ ਵਿੱਚ ਬਹੁਤ ਘੱਟ ਤਾਪਮਾਨ ਉਤਪੰਨ ਹੁੰਦਾ ਹੈ, ਜਦਕਿ ਬਿਜਲਈ ਬੱਲਬ ਦੇ ਫਿਲਾਮੈਂਟ ਵਿੱਚ ਉੱਚ ਤਾਪਮਾਨ ਪੈਦਾ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਬਿਜਲਈ ਵਾਹਕ ਤਾਰਾਂ ਦੇ ਪ੍ਰਤਿਰੋਧ ਦੀ ਤੁਲਨਾ ਬਿਜਲਈ ਬੱਲਬ ਦੇ ਫਿਲਾਮੈਂਟ ਦਾ ਪ੍ਰਤਿਰੋਧ, ਵਿੱਚ ਬਹੁਤ ਜ਼ਿਆਦਾ ਹੁੰਦਾ ਹੈ । ਇਸ ਲਈ ਬਿਜਲਈ ਧਾਰਾ ਪ੍ਰਵਾਹਿਤ ਕਰਨ ਤੇ ਬਿਜਲਈ ਬੱਲਬ ਦੇ ਫਿਲਾਮੈਂਟ ਵਿੱਚ ਵਧੇਰਾ ਉੱਚਾ ਉਤਪੰਨ ਹੁੰਦਾ ਹੈ, ਪਰੰਤੂ ਬਿਲਜਈ ਵਾਹਕ ਤਾਰਾਂ ਵਿੱਚ ਨਹੀਂ ।

ਪ੍ਰਸ਼ਨ 23.
ਹੇਠ ਲਿਖਿਆਂ ਦੇ ਕਾਰਨ ਸਪੱਸ਼ਟ ਕਰੋ :-
(i) ਜੇਕਰ ਤੁਸੀਂ ਐਮਮੀਟਰ ਨੂੰ ਸਮਾਨੰਤਰ ਕ੍ਰਮ ਵਿੱਚ ਸੰਯੋਜਿਤ ਕਰਦੇ ਹੋ ਤਾਂ ਐਮਮੀਟਰ ਕਿਉਂ ਸੜ ਜਾਂਦਾ ਹੈ ?
(ii) ਇੱਕ ਨਿਸ਼ਚਿਤ ਤਾਪ ਤੋਂ ਕੁੱਝ ਹੇਠਾਂ ਕੁੱਝ ਪਦਾਰਥਾਂ ਦੀ ਪ੍ਰਤਿਰੋਧਕਤਾ ਘੱਟ ਕੇ ਜ਼ੀਰੋ ਕਿਉਂ ਹੋ ਜਾਂਦੀ ਹੈ ?
ਉੱਤਰ-
(i) ਸਰਕਟ ਦੇ ਹੋਰ ਉਪਕਰਨਾਂ ਦੀ ਤੁਲਨਾ ਵਿੱਚ ਐਮਮੀਟਰ ਦਾ ਪ੍ਰਤਿਰੋਧ ਨਾ ਹੋਣ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ। ਜਦੋਂ ਐਮਮੀਟਰ ਨੂੰ ਸਰਕਟ ਵਿੱਚ ਸਮਾਨੰਤਰ ਕੂਮ ਵਿੱਚ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਸਰਕਟ ਦਾ ਕੁੱਲ ਪੁਟੈਂਸ਼ਲ ਐਮਮੀਟਰ ਦੇ ਸਿਰਿਆਂ ਵਿੱਚ ਕਾਰਜ ਕਰਦਾ ਹੈ ਜਿਸ ਤੋਂ ਐਮਮੀਟਰ ਵਿੱਚ ਉੱਚ ਬਿਜਲਈ ਧਾਰਾ ਪ੍ਰਵਾਹਿਤ ਹੁੰਦੀ ਹੈ ਅਤੇ ਉਸ ਕਾਰਨ ਵਧੇਰੇ ਤਾਪ ਦੇ ਉਤਪੰਨ ਹੋਣ ਕਾਰਨ ਐਮਮੀਟਰ ਸੜ ਜਾਂਦਾ ਹੈ ।

(ii) ਜਦੋਂ ਕਿਸੇ ਚਾਲਕ ਪਦਾਰਥ ਦਾ ਤਾਪ ਭਾਂਤਿਕ ਤਾਪ ਤੋਂ ਘੱਟ ਹੋ ਜਾਂਦਾ ਹੈ ਤਾਂ ਪਦਾਰਥ ਅਤਿਚਾਲਕ ਵਿੱਚ ਪਰਿਵਰਤਿਤ ਹੋ ਜਾਂਦਾ ਹੈ ਜਿਸ ਤੋਂ ਉਸਦਾ ਪ੍ਰਤਿਰੋਧ ਅਚਾਨਕ ਜ਼ੀਰੋ ਹੋ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 24.
ਬਿਜਲਈ ਉਪਕਰਨਾਂ ਨੂੰ ਸਮਾਨਾਂਤਰ ਕ੍ਰਮ ਵਿੱਚ ਜੋੜਨਾ ਕਿਉਂ ਲਾਭਦਾਇਕ ਹੈ ?
ਉੱਤਰ-
ਸਮਾਨਾਂਤਰ ਸੰਯੋਜਨ ਦੇ ਲਾਭ-

1. ਪ੍ਰਤਿਰੋਧਾਂ ਨੂੰ ਸਮਾਨਾਂਤਰ ਕੂਮ ਵਿੱਚ ਜੋੜਨ ਨਾਲ ਕਿਸੇ ਵੀ ਚਾਲਕ ਵਿੱਚ ਸਵਿੱਚ ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਬਿਜਲਈ ਧਾਰਾ ਸੁਤੰਤਰਤਾ ਪੂਰਵਕ ਭੇਜੀ ਜਾਂ ਰੋਕੀ ਜਾ ਸਕਦੀ ਹੈ ।
2. ਅਜਿਹਾ ਕਰਨ ਨਾਲ ਸਾਰੀਆਂ ਸਮਾਨਾਂਤਰ ਸ਼ਾਖ਼ਾਵਾਂ ਦੇ ਸਿਰਿਆਂ ਵਿਚਕਾਰ ਟੈਂਸ਼ਲ ਅੰਤਰ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ। ਇਸ ਲਈ ਬੱਲਬ, ਬਿਜਲਈ ਐੱਸ, ਰੈਫ਼ਰੀਜ਼ੇਟਰ, ਰੇਡੀਓ ਅਤੇ ਟੈਲੀਵਿਜ਼ਨ ਆਦਿ ਨੂੰ ਇੱਕ ਹੀ ਟੈਂਸ਼ਲ ਤੇ ਚੱਲਣ ਯੋਗ ਬਣਾਇਆ ਜਾ ਸਕਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 25
ਪ੍ਰਤਿਰੋਧ ਤੇ ਕੀ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ, ਜੇਕਰ-
(i) ਤਾਰ ਦੀ ਲੰਬਾਈ ਵਧਾ ਦਿੱਤੀ ਜਾਵੇ ।
(ii) ਪਰਿਖੇਤਰਫਲ ਵਧਾ ਦਿੱਤਾ ਜਾਵੇ ।
ਉੱਤਰ-
(i) ਪ੍ਰਤਿਰੋਧ, ਤਾਰ ਦੀ ਲੰਬਾਈ ਦੇ ਸਿੱਧਾ ਸਮਾਨੁਪਾਤੀ ਹੁੰਦਾ ਹੈ । ਇਸ ਲਈ ਤਾਰ ਦੀ ਲੰਬਾਈ ਵਧਾਉਣ ਨਾਲ ‘ ਪ੍ਰਤਿਰੋਧ ਅਧਿਕ ਹੋ ਜਾਂਦਾ ਹੈ ।

(ii) ਮੋਟੇ ਤਾਰ ਦਾ ਪ੍ਰਤਿਰੋਧ ਬਾਰੀਕ ਤਾਰ ਦੇ ਮੁਕਾਬਲੇ ਵਿੱਚ ਘੱਟ ਹੁੰਦਾ ਹੈ ਕਿਉਂਕਿ ਤਾਰ ਦੀ ਮੋਟਾਈ ਕਾਰਨ ਉਸ ਦਾ ਪਰਿਖੇਤਰਫਲ ਵੱਧ ਜਾਂਦਾ ਹੈ ਜਿਸ ਤੋਂ ਪ੍ਰਤਿਰੋਧ ਘੱਟ ਹੋ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 26.
ਸੰਯੋਜਕ ਤਾਰਾਂ ਤਾਂਬੇ ਦੀਆਂ ਹੀ ਕਿਉਂ ਬਣਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ ? ਇਹ ਤਾਰਾਂ ਮੋਟੀਆਂ ਕਿਉਂ ਹੁੰਦੀਆਂ
ਹਨ ?
ਉੱਤਰ-
ਚਾਂਦੀ ਤੋਂ ਬਾਅਦ ਤਾਂਬਾ (ਕਾਪਰ) ਹੀ ਬਿਜਲੀ ਦਾ ਵਧੀਆ ਚਾਲਕ ਹੈ। ਇਸ ਦਾ ਪ੍ਰਤਿਰੋਧ ਘੱਟ ਹੋਣ ਕਾਰਨ ਇਸ ਵਿੱਚੋਂ ਬਿਜਲਈ ਧਾਰਾ ਅਸਾਨੀ ਨਾਲ ਪ੍ਰਵਾਹ ਕਰ ਸਕਦੀ ਹੈ। ਸੰਯੋਜਕ ਤਾਰਾਂ (ਬਿਜਲੀ ਵਾਹਕ ਤਾਰਾਂ) ਮੋਟੀਆਂ ਰੱਖੀਆਂ ਜਾਂਦੀਆਂ ਹਨ, ਕਿਉਂਕਿ ਕਿਸੇ ਤਾਰ ਦਾ ਪ੍ਰਤਿਰੋਧ ਉਸਦੀ ਮੋਟਾਈ ਦੇ ਉਲਟ (ਵਿਲੋਮ) ਅਨੁਪਾਤੀ ਹੁੰਦਾ ਹੈ। ਜਿਹੜੀ ਤਾਰ ਜਿੰਨੀ ਮੋਟੀ ਹੋਵੇਗੀ ਓਨਾ ਹੀ ਉਸ ਦਾ ਪ੍ਰਤਿਰੋਧ ਘੱਟ ਹੋਵੇਗਾ। ਇਸ ਦੇ ਸਿੱਟੇ ਵਜੋਂ ਬਿਜਲਈ ਧਾਰਾ ਅਸਾਨੀ ਨਾਲ ਉਸ ਵਿਚੋਂ ਪ੍ਰਵਾਹਿਤ ਹੋ ਸਕੇਗੀ ।

ਪ੍ਰਸ਼ਨ 27.
ਬਿਜਲੀ ਦੇ ਚਾਲਕ ਕੀ ਹੁੰਦੇ ਹਨ ? ਦੋ ਉਦਾਹਰਣਾਂ ਦਿਓ ।
ਉੱਤਰ-
ਬਿਜਲੀ ਦੇ ਚਾਲਕ-ਅਜਿਹੇ ਪਦਾਰਥ ਜਿਨ੍ਹਾਂ ਵਿੱਚੋਂ ਬਿਜਲਈ ਧਾਰਾ ਦਾ ਪ੍ਰਵਾਹ ਸੌਖਾ ਹੋ ਜਾਂਦਾ ਹੈ, ਬਿਜਲੀ ਦੇ ਚਾਲਕ ਅਖਵਾਉਂਦੇ ਹਨ ।
ਉਦਾਹਰਣ-

1. ਤਾਂਬਾ
2. ਐਲੂਮੀਨੀਅਮ
3. ਤੇਜ਼ਾਬ ਯੁਕਤ ਪਾਣੀ ।

ਸੰਖਿਆਤਮਕ ਪ੍ਰਸ਼ਨ (Numerical Questions)

ਪ੍ਰਸ਼ਨ 1.
ਦੋ ਛੋਟੇ ਚਾਰਜਿਤ ਗੋਲਿਆਂ ਤੇ 2 × 10^-7 ਕੂਲਾਂਮ ਅਤੇ 3 × 10^-7 ਕੂਲਾਂਮ ਦੇ ਚਾਰਜ ਹਨ ਅਤੇ ਇਹ ਹਵਾ ਵਿੱਚ 30 cm ਦੀ ਦੂਰੀ ‘ਤੇ ਰੱਖੇ ਗਏ ਹਨ। ਇਨ੍ਹਾਂ ਵਿਚਕਾਰ ਲੱਗ ਰਿਹਾ ਬਲ ਮਾਲੂਮ ਕਰੋ ।
ਹੱਲ :
ਪਹਿਲੇ ਗੋਲੇ ਦਾ ਚਾਰਜ q₁ × 10^-7 ਕੂਲਾਂਮ
ਦੂਜੇ ਗੋਲੇ ਦਾ ਚਾਰਜ q₂ = 3 × 10^-7 ਕੂਲਾਂਮ
ਗੋਲਿਆਂ ਵਿਚਕਾਰ ਦੂਰੀ d = 30 cm
= \(\frac{30}{100}\)m
= 0.30 cm
ਹਵਾ ਮਾਧਿਅਮ ਲਈ K = 9 × 10⁹
ਦੋਨੋਂ ਗੋਲਿਆਂ ਵਿਚਕਾਰ ਬਿਜਲੀ ਬਲ F = ?

ਪ੍ਰਸ਼ਨ 2.
ਇੱਕ ਚਾਲਕ ਦੀ ਲੰਬਾਈ 3.0 m, ਪਰਿਖੇਤਰਫਲ 0.02 mm² ਅਤੇ ਪ੍ਰਤਿਰੋਧ 2 ਓਹਮ ਹੈ। ਇਸ ਦੀ ਪ੍ਰਤਿਰੋਧਕਤਾ ਮਾਲੂਮ ਕਰੋ ।
ਹੱਲ :
ਚਾਲਕ ਦੀ ਲੰਬਾਈ (l) = 3.0 m
ਚਾਲਕ ਦਾ ਪਰਿਖੇਤਰਫਲ (a) = 0.02 m²
= \(\frac{0.02}{10^{6}}\)m²
ਚਾਲਕ ਦਾ ਪ੍ਰਤਿਰੋਧ (R) = 2 ਓਹਮ
ਚਾਲਕ ਦੀ ਪ੍ਰਤਿਰੋਧਕਤਾ (ρ) = ?
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ, R = ρ × \(\frac{l}{a}\)
2 = ρ × \(\frac{3}{0.02 \times 10^{-6}}\)
∴ ρ = \(\frac{2 \times 0.02 \times 10^{-6}}{3}\)
ρ = \(\frac{2 \times 2}{3 \times 10^{2}}\) × 10^-6
= \(\frac{4}{3}\) × 10^-8
= 1.33 × 10^-8 ਓਹਮ-ਮੀਟਰ ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 3.
30 Ω, 50 Ω ਅਤੇ 80 Ω, ਦੇ ਲੜੀ ਵਿੱਚ ਜੋੜੇ ਗਏ ਤਿੰਨ ਤਿਰੋਧਕਾਂ ਦਾ ਤੱਲ-ਤਿਰੋਧ ਮਾਲੂਮ ਕਰੋ ।
ਹੱਲ :
ਇੱਥੇ r₁ = 30 Ω
r₂ = 50 Ω
r₃ = 80 Ω
ਹੁਣ, ਕਿਉਂਕਿ ਤਿੰਨਾਂ ਪ੍ਰਤਿਰੋਧਾਂ r₁, r₂, r₃ ਨੂੰ ਲੜੀਬੱਧ ਜੋੜਿਆ ਗਿਆ ਹੈ, ਇਸ ਲਈ ਉਨ੍ਹਾਂ ਦੇ ਡੁੱਲ-ਪ੍ਰਤਿਰੋਧ (R) ਤਿੰਨਾਂ ਦੇ ਜੋੜ ਬਰਾਬਰ ਹੈ ।
R = r₁ + r₂ + r₃ )
= 30 Ω + 50 Ω + 80 Ω
R = 160 Ω

ਪ੍ਰਸ਼ਨ 4.
40 Ω, 60 Ω, ਅਤੇ 90 Ω ਦੇ ਤਿੰਨ ਪ੍ਰਤਿਰੋਧਕਾਂ ਨੂੰ ਸਮਾਨਾਂਤਰਬੱਧ ਵਿੱਚ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ। ਇਸ ਸੰਯੋਜਨ ਦਾ ਪ੍ਰਭਾਵਸ਼ਾਲੀ ਪ੍ਰਤਿਰੋਧ ਕਿੰਨਾ ਹੈ ?
ਹੱਲ :
ਇੱਥੇ r₁ = 40 Ω
r₂ = 60 Ω
r₃ = 90 Ω
ਮੰਨ ਲਓ ਤਿੰਨਾਂ ਦਾ ਪ੍ਰਭਾਵਸ਼ਾਲੀ ਪ੍ਰਤਿਰੋਧ R ਹੈ
ਕਿਉਂਕਿ ਤਿੰਨਾਂ ਪ੍ਰਤਿਰੋਧਕਾਂ ਨੂੰ ਸਮਾਨਾਂਤਰ ਵਿੱਚ ਸੰਯੋਜਿਤ ਕੀਤਾ ਗਿਆ ਹੈ, ਇਸ ਲਈ
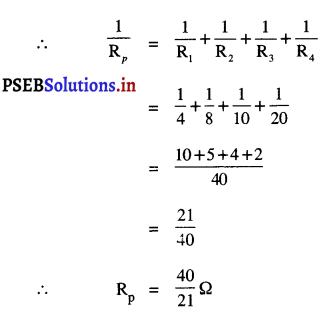
\(\frac{1}{R}\) = \(\frac{1}{r_{1}}+\frac{1}{r_{2}}+\frac{1}{r_{3}}\)
= \(\frac{1}{40}+\frac{1}{60}+\frac{1}{90}\)
\(\frac{1}{R}\) = \(\frac{9+6+4}{360}\)
\(\frac{1}{R}\) = \(\frac{19}{360}\)
∴ R = \(\frac{360}{19}\) = 18.95 Ω

ਪ੍ਰਸ਼ਨ 5.
6 Ω, 8 Ω, ਅਤੇ 10 Ω ਦੇ ਤਿੰਨ ਪ੍ਰਤਿਰੋਧ ਲੜੀ ਬੱਧ ਜੋੜੇ ਗਏ ਹਨ । ਪਰਿਪੱਖ ਦਾ ਕੁੱਲ ਤਿਰੋਧ ਪਤਾ ਕਰੋ ।
ਹੱਲ :
ਦਿੱਤਾ ਹੈ,
R₁ = 6 Ω , R₂ = 8 Ω, R₃ = 10 Ω
ਮੰਨ ਲਓ ਪਰਿਪੱਖ ਦਾ ਕੁੱਲ ਪ੍ਰਤਿਰੋਧ R ਹੈ, ਤਾਂ
ਲੜੀ ਬੱਧ ਸੰਯੋਜਨ ਦਾ ਕੁੱਲ ਤਿਰੋਧ, R = R₁ + R₂ + R₃
= 6Ω + 8Ω + 10Ω
= 24Ω

ਪ੍ਰਸ਼ਨ 6.
5 Ω, 8 Ω, ਅਤੇ 12 Ω ਪ੍ਰਤਿਰੋਧਾਂ ਵਾਲੇ ਤਿੰਨ ਪ੍ਰਤਿਰੋਧ ਲੜੀਵਾਰ ਕੌਮ ਵਿਚ ਜੋੜੇ ਗਏ ਹਨ । ਪਰਿਪੱਖ ਦਾ ਪਰਿਣਾਮੀ ਤਿਰੋਧ ਪਤਾ ਕਰੋ ।
ਹੱਲ :
ਦਿੱਤਾ ਹੈ,
R₁ = 5 Ω, R₂ = 8 Ω , R₃ = 12 Ω
ਮੰਨ ਲਓ ਪਰਿਪੱਖ ਦਾ ਪਰਿਣਾਮੀ ਪ੍ਰਤਿਰੋਧ R ਹੈ, ਤਾਂ
ਲੜੀਵਾਰ ਕੂਮ ਵਿਚ ਜੋੜੇ ਗਏ ਤਿਰੋਧਾਂ ਦਾ ਪਰਿਣਾਮੀ ਤਿਰੋਧ, R = R₁ + R₂ + R₃
= 5Ω + 8Ω + 12Ω
= 25Ω

ਪ੍ਰਸ਼ਨ 7.
4 Ω, 8 Ω, 12 Ω ਅਤੇ 24 Ω ਕਿਸ ਤਰਤੀਬ ਵਿਚ ਜੋੜੇ ਜਾਣ ਤਾਂ ਜੋ ਵੱਧ ਤੋਂ ਵੱਧ ਪ੍ਰਤਿਰੋਧ ਪ੍ਰਾਪਤ ਹੋਵੇਗਾ ? ਪਰਿਣਾਮੀ ਪ੍ਰਤਿਰੋਧ ਵੀ ਪਤਾ ਕਰੋ ।
ਹੱਲ : ਦਿੱਤਾ ਹੈ,
R₁ = 4 Ω , R₂ = 8 Ω , R₃ = 12 Ω , R₄ = 24 Ω
ਮੰਨ ਲਓ ਪਰਿਣਾਮੀ ਪ੍ਰਤਿਰੋਧ R ਹੈ,
ਜੇਕਰ ਇਨ੍ਹਾਂ ਚਹੁੰ ਤਿਰੋਧਾਂ ਨੂੰ ਲੜੀਕੂਮ ਵਿਚ ਜੋੜਿਆ ਜਾਏਗਾ ਤਾਂ ਵੱਧ ਤੋਂ ਵੱਧ ਪ੍ਰਤਿਰੋਧ ਪ੍ਰਾਪਤ ਹੋਵੇਗਾ । ਪਰਿਣਾਮੀ ਪ੍ਰਤਿਰੋਧ, R = R₁ + R₂ + R₃ + R₄.
= 4Ω + 8Ω + 12Ω + 24Ω
= 48Ω

ਪ੍ਰਸ਼ਨ 8.
4 Ω, 8 Ω, 10 Ω ਅਤੇ 20 Ωਪ੍ਰਤਿਰੋਧ ਦੀਆਂ ਚਾਰ ਕੁੰਡਲੀਆਂ ਨੂੰ ਜੋੜਨ ਤੇ (1) ਅਧਿਕਤਮ (2) ਨਿਊਨਤਮ ਤਿਰੋਧ ਕਿੰਨਾ ਪ੍ਰਾਪਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ਅਤੇ ਕਿਵੇਂ ਪ੍ਰਾਪਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ? (ਮਾਂਡਲ ਪੇਪਰ)
ਹੱਲ :
1. ਅਧਿਕਤਮ ਤਿਰੋਧ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਸੰਯੋਜਨ – ਇਨ੍ਹਾਂ ਚਹੁੰ ਪ੍ਰਤਿਰੋਧਾਂ ਨੂੰ ਲੜੀਮ ਵਿਚ ਜੋੜਨ ਨਾਲ ਅਧਿਕਤਮ ਪਰਿਣਾਮੀ ਪ੍ਰਤਿਰੋਧ ਪ੍ਰਾਪਤ ਹੋਵੇਗਾ ।
∴ R_S = R₁ + R₂ + R₃ + R₄
= 4Ω + 8Ω + 10Ω + 20Ω
= 42Ω

2. ਨਿਊਨਤਮ ਪ੍ਰਤਿਰੋਧ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਸੰਯੋਜਨ-ਜੇਕਰ ਦਿੱਤੇ ਗਏ ਤਿਰੋਧਾਂ ਨੂੰ ਸਮਾਨਾਂਤਰ ਕੂਮ ਵਿਚ ਜੋੜਿਆ ਜਾਵੇਗਾ ਤਾਂ ਪਰਿਣਾਮੀ ਤਿਰੋਧ ਨਿਊਨਤਮ ਪ੍ਰਤਿਰੋਧ ਹੋਵੇਗਾ ।

ਪ੍ਰਸ਼ਨ 9.
ਬਿਜਲੀ ਦੇ ਪੰਜ ਬੱਲਬਾਂ ਨੂੰ, ਜਿਨ੍ਹਾਂ ਵਿਚੋਂ ਹਰੇਕ ਦਾ ਪ੍ਰਤਿਰੋਧ 400 ਓਹਮ ਹੈ, 220 V ਦੀ ਸਪਲਾਈ ਨਾਲ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ। (ੳ) ਹੋਰ ਲੈਂਪ ਦੀ ਵੋਲਟੇਜ (ਅ) ਜੇ ਬੱਲਬਾਂ ਨੂੰ ਪ੍ਰਤੀਦਿਨ 5 ਘੰਟੇ ਲਈ 30 ਦਿਨਾਂ ਵਾਸਤੇ ਜਲਾਇਆ ਜਾਵੇ ਤਾਂ ਬਿਜਲੀ ਦਾ ਖ਼ਪਤ ਬਿਲ ਮਾਲੂਮ ਕਰੋ, ਜਦੋਂ ਕਿ ਇਕ ਯੂਨਿਟ ਦਾ ਮੁੱਲ 3 ਰੁਪਏ ਹੋਵੇ।
ਹੱਲ :
ਹਰ ਬੱਲਬ ਦਾ ਪ੍ਰਤਿਰੋਧ= 440 ਓਹਮ
5 ਬੱਲਬ ਸਮਾਨਅੰਤਰ ਜੋੜੇ ਗਏ ਹਨ ਤੇ ਉਨ੍ਹਾਂ ਦਾ ਡੁੱਲ-ਤਿਰੋਧ R ਹੈ ।

= 88 ਓਹਮ
ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ V = 220 V
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ, P = \(\frac{\mathrm{V}^{2}}{\mathrm{R}}\)
= \(\frac{220 \times 220}{88}\)
= \(\frac{5 \times 220}{2}\) = 550 W
ਹਰੇਕ ਲੈਂਪ ਦੀ ਵਾਟੇਜ (ਸ਼ਕਤੀ) = \(\frac{550}{5}\) = 110 ਵਾਟ
ਸਮਾਂ = 30 × 5 ਘੰਟੇ
= 150 ਘੰਟੇ
ਊਰਜਾ ਦੀ ਖ਼ਪਤ (E) = p × t
= 550 ਘੰਟੇ × 150 ਘੰਟੇ
= 82500 ਵਾਟ-ਘੰਟੇ
= \(\frac{82500}{1000}\) ਕਿਲੋਵਾਟ ਘੰਟੇ
= \(\frac{825}{10}\) ਯੂਨਿਟ
ਊਰਜਾ ਸਪਲਾਈ ਦੀ ਦਰ = 3 ਰੁ: ਪ੍ਰਤੀ ਯੂਨਿਟ
ਬਿਜਲੀ ਦੇ ਬਿੱਲ ਦੀ ਰਕਮ =\(\frac{825}{10}\) × 3
= 247.50 ਰੁਪਏ ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 10.
ਦੋ ਤਾਰਾਂ ਜਿਨ੍ਹਾਂ ਨੂੰ ਸਮਾਨਅੰਤਰ ਬੱਧ ਜੋੜਿਆ ਗਿਆ ਹੈ ਦਾ ਪ੍ਰਤਿਰੋਧ 12 Ω ਹੈ ਲੜੀ ਵਿੱਚ ਜੋੜਨ ਤੇ ਇਨ੍ਹਾਂ ਦਾ ਪ੍ਰਤਿਰੋਧ 50 Ω , ਹੋ ਜਾਂਦਾ ਹੈ। ਪ੍ਰਤਿਰੋਧਾਂ ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ :
ਮੰਨ ਲਓ ਕਿ ਦੋ ਪ੍ਰਤਿਰੋਧ R₁ ਅਤੇ , ਹਨ
ਜਦੋਂ ਇਨ੍ਹਾਂ ਨੂੰ ਲੜੀ ਵਿੱਚ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ ਤਾਂ ਕੁੱਲ ਪ੍ਰਤਿਰੋਧ-
R_S = R₁ + R₂ = 50 Ω ……….(i)
ਸਮਾਨਅੰਤਰ ਬੱਧ ਵਿੱਚ ਜੋੜਨ ‘ਤੇ ਇਨ੍ਹਾਂ ਦਾ ਸਮੂਚਾ ਪ੍ਰਤਿਰੋਧ-

(i) ਅਤੇ (ii) ਤੋਂ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ
R₁ + \(\) = 50

ਜਾਂ R₁² – 50 R₁ + 600 = 0
ਜਾਂ R₁² – 30 R₁ – 20 R₁ + 600 = 0
ਜਾਂ R₁(R₁ – 30) – 20 (R₁ – 30) = 0
ਜਾਂ (R₁ – 30) (R₁ – 20) = 0
∴ R₁ – 30 = 0 ਜਾਂ R₁ – 20 = 0
∴ ਅਰਥਾਤ R₁ = 30 Ω ਅਤੇ R₁ = 20 Ω
ਇਸ ਲਈ ਪਹਿਲਾ ਤਿਰੋਧ R₂ = 30 Ω
ਅਤੇ ਦੂਜਾ ਤਿਰੋਧ R₂ = 20 Ω
ਇਸ ਲਈ ਪਹਿਲਾ ਪ੍ਰਤਿਰੋਧ R₁ = 20 ਅਤੇ ਦੂਜਾ ਤਿਰੋਧ R₂ = 30 Ω ਲੈ ਸਕਦੇ ਹਾਂ ।

ਪ੍ਰਸ਼ਨ 11.
ਇੱਕ ਸਰਕਟ A ਆਕਾਰ ਦਾ ਹੈ ਜਿਸ ਵਿੱਚ ਓਹਮ ਪ੍ਰਤਿ ਸਮ ਦੇ ਪੰਜ ਪ੍ਰਤਿਰੋਧ ਜੁੜੇ ਹੋਏ ਹਨ। ਇਸ ਦੀਆਂ ਦੋ ਭੁਜਾਵਾਂ 20 ਸਮ ਦੀਆਂ ਹਨ ਅਤੇ ਵਿੱਚ ਵਾਲੀ ਲੰਬਾਈ 10 ਸਮ ਹੈ ਜਦਕਿ ਸ਼ੀਰਸ਼ ਕੋਣ 60° ਹੈ। ਇਸ ਦਾ ਪ੍ਰਤਿਰੋਧ ਗਿਆਤ ਕਰੋ ।

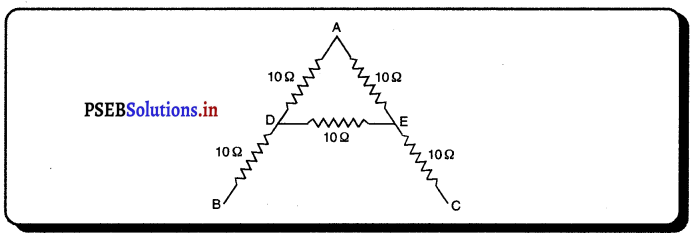
ਹੱਲ :
ਪ੍ਰਸ਼ਨ ਵਿੱਚ ਦਿੱਤਾ ਗਿਆ ਸੰਯੋਜਨ ਅਸਲ ਵਿੱਚ ਇਸ ਪ੍ਰਕਾਰ ਹੈ ।

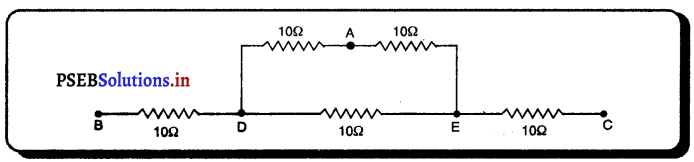
DA ਅਤੇ AE ਸ਼੍ਰੇਣੀਕੂਮ ਵਿੱਚ ਜੁੜੇ ਹਨ
∴ DA ਅਤੇ AE ਦਾ ਕੁੱਲ ਤਿਰੋਧ = 10 + 10
= 20 Ω
ਹੁਣ DE ਅਤੇ AE ਦਾ ਕੁੱਲ ਤਿਰੋਧ 20 Ω DE ਦੇ ਸਮਾਨੰਤਰ ਹੈ, ਇਸ ਲਈ
DAED ਦਾ ਪ੍ਰਭਾਵੀ ਪ੍ਰਤਿਰੋਧ \(\frac{1}{r}\) = \(\frac{1}{10}+\frac{1}{20}\)
= \(\frac{2+1}{20}\)
∴ r = \(\frac{20}{3}\)Ω
ਹੁਣ BD, DAED ਅਤੇ EC ਲੜੀਕੂਮ ਵਿਵਸਥਾ ਵਿੱਚ ਸੰਯੋਜਿਤ ਹਨ
∴ B ਅਤੇ C ਦੇ ਵਿੱਚ ਕੁੱਲ ਤਿਰੋਧ = 10 + \(\frac{20}{3}\) + 10
= \(\frac{30+20+30}{3}\)
= \(\frac{80}{3}\)
= 26.67 Ω

ਪ੍ਰਸ਼ਨ 12.
ਇੱਕ ਬੱਲਬ 200 v ਅਤੇ 100 wਦਾ ਹੈ। ਇਸ ਦਾ ਪ੍ਰਤਿਰੋਧ ਕੀ ਹੋਵੇਗਾ ? ਇਹ ਬੱਲਬ 4 ਘੰਟੇ ਲਈ ਦੀਪਤ ਹੁੰਦਾ ਹੈ। ਇਸ ਨੇ ਕਿੰਨੀ ਊਰਜਾ ਖਪਤ ਕੀਤੀ ਹੈ ? ਇਸ ਦਾ 2.50 ਰੁ: ਪ੍ਰਤਿ ਯੂਨਿਟ ਦੀ ਦਰ ਨਾਲ ਖ਼ਰਚ ਪਤਾ ਕਰੋ ।
ਹੱਲ :
P = \(\frac{\mathrm{V}^{2}}{\mathrm{R}}\)
ਜਾਂ R = \(\frac{\mathrm{V}^{2}}{\mathrm{P}}\)
∴ ਪ੍ਰਤੀਰੋਧ R = \(\frac{(200)^{2}}{100}\)
= \(\frac{200 \times 200}{100}\)
= 400 Ω
ਖ਼ਪਤ ਹੋਈ ਊਰਜਾ E = \(\frac{100 \times 4}{1000}\)
= 0.4 Kwh
ਕੁੱਲ ਖ਼ਰਚਾ = 0.4 × 2.50
= 1 ਰੁਪਏ

ਪ੍ਰਸ਼ਨ 13.
220 V ਦੇ ਬਿਜਲਈ ਸਰੋਤ ਨੂੰ ਚਾਰ 40 W, 220 V ਦੇ ਬੱਲਦਾਂ ਨੂੰ ਸ਼ੇਣੀਬੱਧ ਵਿਵਸਥਾ ਵਿੱਚ ਸੰਯੋਜਿਤ ਕਰਨ ਤੇ ਹਰੇਕ ਵਿੱਚੋਂ ਪ੍ਰਵਾਹਿਤ ਹੋਣ ਵਾਲੀ ਧਾਰਾ ਦਾ ਮਾਨ ਪਤਾ ਕਰੋ। ਜੇਕਰ ਇੱਕ ਬੱਲਬ ਫਿਊਜ਼ ਹੋ ਜਾਵੇ ਤਾਂ 220 v ਸਰੋਤ ਤੋਂ ਪ੍ਰਵਾਹਿਤ ਹੋਣ ਵਾਲੀ ਧਾਰਾ ਤੇ ਕੀ ਪ੍ਰਭਾਵ ਪਏਗਾ ?
ਹੱਲ :
40 ਵਾਟ ਦੇ ਬੱਲਬ ਦਾ ਪ੍ਰਤਿਰੋਧ = \(\frac{\mathrm{V}^{2}}{\mathrm{P}}\)
= \(\frac{(220)^{2}}{40}\)
40 ਵਾਟ ਦੇ ਚਾਰ ਬੱਲਬਾਂ ਦਾ ਕੁੱਲ ਪ੍ਰਤਿਰੋਧ = \(\frac{4 \times(220)^{2}}{40}\)
= 4840 Ω
ਪ੍ਰਵਾਹਿਤ ਧਾਰਾ I = \(\frac{\mathrm{V}}{\mathrm{R}}\)
= \(\frac{220}{4840}\)
= 0.045A
ਇੱਕ ਬੱਲਬ ਦੇ ਫਿਊਜ਼ ਹੋਣ ਨਾਲ ਉਸ ਵਿੱਚ ਧਾਰਾ ਦਾ ਪ੍ਰਵਾਹ ਨਹੀਂ ਹੋਵੇਗਾ ।

ਪ੍ਰਸ਼ਨ 14.
12V ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ ਦੇ ਦੋ ਬਿੰਦੂਆਂ ਦੇ ਵਿੱਚ 20 ਚਾਰਜ ਨੂੰ ਲਿਜਾਣ ਵਿੱਚ ਕਿੰਨਾ ਕਾਰਜ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ?
ਹੱਲ :
ਟੈਂਸ਼ਲ ਅੰਤਰ (V) = 12 ਵੋਲਟ ਦੇ ਦੋ ਬਿੰਦੂਆਂ ਵਿੱਚ ਪ੍ਰਵਾਹਿਤ ਚਾਰਜ ਦਾ ਮਾਨ Q = 2 ਕੂਲਾਂਮ ।
ਇਸ ਲਈ ਚਾਰਜ ਨੂੰ ਸਥਾਨੰਤਰਿਤ ਕਰਨ ਵਿੱਚ ਕੀਤਾ ਗਿਆ ਕਾਰਜ W = V × Q
= 12 V × 2 C
= 24 J (ਜੂਲ) ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 15.
ਇੱਕ 20 Ω ਪ੍ਰਤਿਰੋਧ ਬਿਜਲਈ ਬੱਲਬ ਅਤੇ ਇੱਕ 4 Ω ਪ੍ਰਤਿਰੋਧ ਦਾ ਚਾਲਕ 6V ਦੀ ਬੈਟਰੀ ਨਾਲ ਚਿੱਤਰ ਅਨੁਸਾਰ ਜੁੜੇ ਹਨ । ਗਣਨਾ ਕਰੋ : (a) ਸਰਕਟ ਦਾਕੁੱਲ ਤਿਰੋਧ (b) ਸਰਕਟ ਵਿੱਚ ਪ੍ਰਵਾਹਿਤ ਧਾਰਾ।
ਹੱਲ :

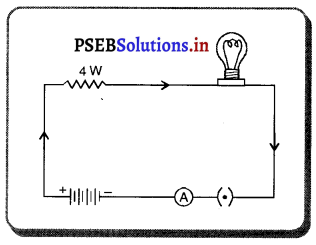
ਦਿੱਤਾ ਹੈ, ਬੱਲਬ ਦਾ ਪ੍ਰਤਿਰੋਧ R₁ = 20 Ω
ਅਤੇ ਚਾਲਕ ਦਾ ਪ੍ਰਤਿਰੋਧ R₂ = 4 Ω
ਬੈਟਰੀ ਦਾ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ V = 6 V
(a) ∵ ਦੋਨੋਂ ਪ੍ਰਤਿਰੋਧ ਸ਼੍ਰੇਣੀਕੂਮ ਵਿੱਚ ਜੁੜੇ ਹਨ,
∴ ਸਰਕਟ ਦਾ ਕੁੱਲ ਤਿਰੋਧ R = R₁ + R₂
= 20Ω + 4Ω
= 24Ω

(b) ਸਰਕਟ ਵਿੱਚ ਲੱਗਿਆ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ V = 6 V
ਕੁੱਲ ਪ੍ਰਤਿਰੋਧ R = 24 Ω
∴ ਸਰਕਟ ਵਿੱਚ ਪ੍ਰਵਾਹਿਤ ਹੋ ਰਹੀ ਧਾਰਾ I = \(\frac{\mathrm{V}}{\mathrm{R}}\)
= \(\frac{6 \mathrm{~V}}{24 \Omega}\)
= 0.25 A

ਪ੍ਰਸ਼ਨ 16.
ਇੱਕ 4 Ω ਦੇ ਤਿਰੋਧਕ ਵਿੱਚ 100.J ਊਸ਼ਮਾ ਪ੍ਰਤਿ ਸੈਕਿੰਡ ਦੀ ਦਰ ਨਾਲ ਉਤਪੰਨ ਹੋ ਰਹੀ ਹੈ। ਪ੍ਰਤਿਰੋਧਕ ਦੇ ਸਿਰਿਆਂ ਦੇ ਵਿੱਚ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ ਗਿਆਤ ਕਰੋ। ਹੱਲ :
ਦਿੱਤਾ ਹੈ, ਊਸ਼ਮਾ H = 100 J
ਸਮਾਂ t = 1s
ਤਿਰੋਧ R = 4 Ω
ਸੂਤਰ H = I² Rt ਦੀ ਵਰਤੋਂ ਕਰਨ ਤੇ
ਬਿਜਲਈ ਧਾਰਾ I = \(\sqrt{\frac{\mathrm{H}}{\mathrm{R} t}}\)
= \(\sqrt{\frac{100 \mathrm{~J}}{4 \Omega \times 1 \mathrm{~s}}}\)
= 5A
ਪਰੰਤੂ V = I × R
∴ ਤਿਰੋਧਕ ਦੇ ਸਿਰਿਆਂ ਵਿਚਾਲੇ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ V = 5 A × 4 Ω
= 20 V

ਪ੍ਰਸ਼ਨ 17.
ਨਾਲ ਦਿੱਤੇ ਗਏ ਚਿੱਤਰ ਵਿੱਚ R₁ = 10 Ω, R₂ = 40 Ω, R₃ = 30 Ω, R₄ = 20 Ω ਅਤੇ Rs = 60 ਹੈ ਅਤੇ 12 v ਦੀ ਬੈਟਰੀ ਇਸ ਸੰਯੋਜਨ ਵਿੱਚ ਜੁੜੀ ਹੋਈ ਹੈ। ਪਰਿਕਲਨ ਕਰੋ : – (a) ਸਰਕਟ ਦਾ ਕੁੱਲ ਤਿਰੋਧ ਅਤੇ (b) ਸਰਕਟ ਵਿੱਚ ਪ੍ਰਵਾਹਿਤ ਧਾਰਾ।

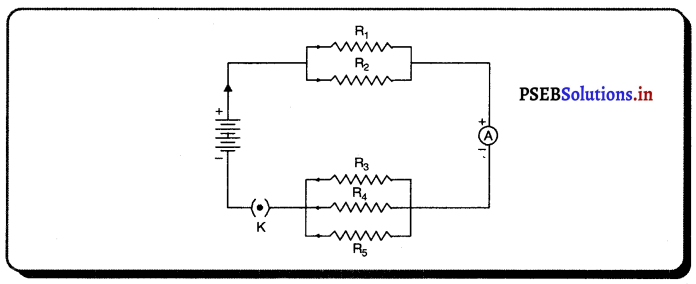
ਹੱਲ :
(a) ਮੰਨ ਲਓ R₁ ਅਤੇ R₂ ਪ੍ਰਤਿਰੋਧਕਾਂ ਦਾ ਸਮਾਨਅੰਤਰ ਬੱਧ ਸੰਯੋਜਨ ਦਾ ਡੁੱਲ-ਪ੍ਰਤਿਰੋਧ R’ ਹੈ, ਤਾਂ

∴ R’ = 8 Ω
ਹੁਣ R₃, R₄ ਅਤੇ R₅ ਸਮਾਨਅੰਤਰ ਸੰਯੋਜਨ ਹਨ । ਜੇਕਰ ਇਨ੍ਹਾਂ ਦਾ ਕੁੱਲ ਪ੍ਰਤਿਰੋਧ R” ਹੈ, ਤਾਂ

∴ R” = 10 Ω

ਸਪੱਸ਼ਟ ਹੈ ਕਿ R’ ਅਤੇ R” ਨੂੰ ਸ਼੍ਰੇਣੀਬੱਧ ਵਿੱਚ ਸੰਯੋਜਿਤ ਕੀਤਾ ਗਿਆ ਹੈ ਅਤੇ ਇਨ੍ਹਾਂ ਦਾ ਕੁੱਲ ਤਿਰੋਧ R ਹੈ, ਤਾਂ
R = R’ + R”
= 8 Ω + 10 Ω
∴ R = 18 Ω

(b)ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ V = 12 V
ਸਰਕਟ ਦਾ ਕੁੱਲ ਪ੍ਰਤਿਰੋਧ R = 18 Ω
∴ ਸਰਕਟ ਵਿੱਚ ਪ੍ਰਵਾਹਿਤ ਹੋ ਰਹੀ ਬਿਜਲਈ ਧਾਰਾ I = \(\frac{\mathrm{V}}{\mathrm{R}}\)
= \(\frac{12 \mathrm{~V}}{18 \Omega}\)
= 0.67 A

ਪ੍ਰਸ਼ਨ 18.
ਜਦੋਂ ਇੱਕ ਬਿਜਲਈ ਹੀਟਰ ਕਿਸੇ ਸਰੋਤ ਤੋਂ 4A ਦੀ ਧਾਰਾ ਲੈਂਦਾ ਹੈ ਤਾਂ ਇਨ੍ਹਾਂ ਦੇ ਸਿਰਿਆਂ ਵਿਚ 60 y ਦਾ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ ਹੈ ਜੇਕਰ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ ਨੂੰ ਵਧਾ ਕੇ 120 V ਕਰ ਦਿੱਤਾ ਜਾਵੇ ਤਾਂ ਹੀਟਰ ਕਿੰਨੀ ਬਿਜਲਈ ਧਾਰਾ ਪ੍ਰਾਪਤ ਕਰੇਗਾ ?
ਹੱਲ :
ਪਹਿਲੀ ਅਵਸਥਾ ਵਿੱਚ ਦਿੱਤਾ ਹੈ, ਬਿਜਲਈ ਹੀਟਰ ਦੁਆਰਾ ਲਈ ਗਈ ਬਿਜਲਈ ਧਾਰਾ I₁ = 4 A
ਬਿਜਲਈ ਹੀਟਰ ਦੇ ਸਿਰਿਆਂ ਵਿਚਕਾਰ ਟੈਂਸ਼ਲ ਅੰਤਰ V₁ = 60 V
ਬਿਜਲਈ ਹੀਟਰ ਦੀ ਕੁੰਡਲੀ ਦਾ ਪ੍ਰਤਿਰੋਧ R = \(\frac{\mathrm{V}_{1}}{\mathrm{I}_{1}}\)
= \(\frac{60 \mathrm{~V}}{4 \mathrm{~A}}\)
= 15 Ω
ਓਹਮ ਦੇ ਨਿਯਮ ਅਨੁਸਾਰ ਹੀਟਰ ਦੀ ਕੁੰਡਲੀ ਦਾ ਪ੍ਰਤਿਰੋਧ R ਸਥਿਰ ਰਹੇਗਾ ।
ਦੂਜੀ ਅਵਸਥਾ ਵਿੱਚ
ਟੈਂਸ਼ਲ ਅੰਤਰ V₂ = 120 V
ਕੁੰਡਲੀ ਦਾ ਪ੍ਰਤਿਰੋਧ R = 15 Ω
∴ ਬਿਜਲਈ ਹੀਟਰ ਵਿੱਚ ਪ੍ਰਵਾਹਿਤ ਧਾਰਾ I₂ = \(\frac{V_{2}}{R}\)
= \(\frac{120 \mathrm{~V}}{15 \Omega}\)
= 8 A

ਬਹੁਤ ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Very Short Answer Type Questions)

ਪ੍ਰਸ਼ਨ 1.
ਕਿਸੇ ਬਿੰਦੂ ਤੇ ਬਿਜਲ ਟੈਂਸ਼ਲ ਕੀ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਇਕਾਈ ਚਾਰਜ ਅਨੰਤ ਤੋਂ ਕਿਸੇ ਬਿੰਦੂ ਤਕ ਲੈ ਜਾਣ ਵਿੱਚ ਕੀਤੇ ਗਏ ਕਾਰਜ ਨੂੰ ਉਸ ਬਿੰਦੂ ਤੇ ਬਿਜਲ ਪੁਟੈਂਸ਼ਲ ਕਹਿੰਦੇ ਹਨ ।
W = QV

ਪੁਟੈਂਸ਼ਲ ਨੂੰ ਵੋਲਟ ਵਿੱਚ ਮਾਪਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 2.
ਬਿਜਲਈ ਚੁੰਬਕ ਦੀ ਧਰੁਵਤਾ ਵਿੱਚ ਤਬਦੀਲੀ ਕਿਸ ਤਰ੍ਹਾਂ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ ?
ਉੱਤਰ-
ਬਿਜਲਈ ਚੁੰਬਕ ਦੀ ਧਰੁਵਤਾ ਵਿੱਚ ਤਬਦੀਲੀ ਬਿਜਲਈ ਧਾਰਾ ਦੀ ਦਿਸ਼ਾ ਬਦਲ ਕੇ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਕਿਹੜੇ ਚਾਰਜ ਆਪਸ ਵਿੱਚ ਆਕਰਸ਼ਣ ਕਰਦੇ ਹਨ ਤੇ ਕਿਹੜੇ ਅਪਕਰਸ਼ਣ ?
ਉੱਤਰ-
ਸਮਾਨ ਚਾਰਜ ਆਪਸ ਵਿੱਚ ਪ੍ਰਤਿਕਰਸ਼ਣ ਕਰਦੇ ਹਨ ਅਤੇ ਅਸਮਾਨ ਚਾਰਜ ਆਪਸ ਵਿੱਚ ਆਕਰਸ਼ਣ ਕਰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 4.
ਕਿਸੇ ਚਾਲਕ ਦਾ ਪ੍ਰਤਿਰੋਧ ਕਿਹੜੀਆਂ-ਕਿਹੜੀਆਂ ਗੱਲਾਂ ‘ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ ?
ਉੱਤਰ-
ਚਾਲਕ ਦਾ ਪ੍ਰਤਿਰੋਧ ਨਿਰਭਰ ਕਰਦਾ ਹੈ-

1. ਲੰਬਾਈ ਦੇ ਸਿੱਧਾ ਅਨੁਪਾਤੀ ।
2. ਖੇਤਰਫਲ ਦੇ ਉਲਟ ਅਨੁਪਾਤੀ ।

ਪ੍ਰਸ਼ਨ 5.
ਕਿਸਦਾ ਪ੍ਰਤਿਰੋਧ ਘੱਟ ਹੈ-100 w ਦੇ ਬੱਲਬ ਦਾ ਜਾਂ 60 w ਦੇ ਬੱਲਬ ਦਾ ?
ਉੱਤਰ-
P = \(\frac{V^{2}}{R}\)
ਕਿਉਂਕਿ P ∝ \(\frac{1}{R}\)
∴ ਵਧੇਰੇ ਸ਼ਕਤੀ ਵਾਲੇ ਬੱਲਬ ਦਾ ਪ੍ਰਤਿਰੋਧ ਘੱਟ ਹੋਵੇਗਾ ।
ਇਸ ਲਈ 100 W ਵਾਲੇ ਬੱਲਬ ਦਾ ਪ੍ਰਤਿਰੋਧ ਘੱਟ ਹੋਵੇਗਾ ।

ਪ੍ਰਸ਼ਨ 6.
ਜੇ ਤਾਰ ਦੀ ਲੰਬਾਈ ਦੁੱਗਣੀ ਅਤੇ ਖੇਤਰਫਲ ਅੱਧਾ ਕਰ ਦਿੱਤਾ ਜਾਵੇ ਤਾਂ ਪ੍ਰਤਿਰੋਧ ‘ਤੇ ਕੀ ਪ੍ਰਭਾਵ ਪਵੇਗਾ ?
ਹੱਲ :
R₁ = ρ\(\frac{l_{1}}{\mathrm{~A}_{1}}\), R₂ = ρ\(\frac{l_{2}}{\mathrm{~A}_{2}}\)
R₂ = \(\frac{\frac{\rho 2 l_{1}}{\mathrm{~A}_{1}}}{2}\)
= \(\frac{2 \times 2 \times \rho \times l_{1}}{\mathrm{~A}_{1}}\)
= 4 R₁
ਇਸ ਲਈ ਤਿਰੋਧ ਚਾਰ ਗੁਣਾ ਹੋ ਜਾਵੇਗਾ।

ਪ੍ਰਸ਼ਨ 7.
ਬਿਜਲ ਪੁਟੈਂਸ਼ਲ ਦੀ ਇਕਾਈ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਵੋਲਟ ।

ਪ੍ਰਸ਼ਨ 8.
ਤਿਰੋਧ ਦਾ ਮਾਤ੍ਰਿਕ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਓਹਮ ।

ਪ੍ਰਸ਼ਨ 9.
ਬਿਜਲ ਸ਼ਕਤੀ ਦੀ ਇਕਾਈ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਵਾਟ ।

ਪ੍ਰਸ਼ਨ 10.
40 W ਅਤੇ 100 w ਦੇ ਦੋ ਬੱਲਬਾਂ ਵਿਚੋਂ ਕਿਸ ਬੱਲਬ ਦੇ ਤੰਤੂ ਦਾ ਪ੍ਰਤਿਰੋਧ ਵੱਧ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
40 W ਬੱਲਬ ਦਾ ।

ਪ੍ਰਸ਼ਨ 11.
ਇੱਕ ਕਿਲੋਵਾਟ ਘੰਟਾ ਵਿੱਚ ਕਿੰਨੇ ਜੂਲ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ-
1 ਕਿਲੋਵਾਟ ਘੰਟਾ (Kwh) = 3.6 × 10⁶ ਜੂਲ ।

ਪ੍ਰਸ਼ਨ 12.
ਸਾਡੇ ਘਰਾਂ ਵਿੱਚ ਬਿਜਲੀ ਦੀ ਸਪਲਾਈ ਕਿੰਨੀ ਹੈ ?
ਉੱਤਰ-
220V – 230V.

ਪ੍ਰਸ਼ਨ 13.
ਓਹਮ ਦਾ ਨਿਯਮ ਲਿਖੋ ਅਤੇ ਇਸ ਨੂੰ ਗਣਿਤਿਕ ਰੂਪ ਵਿੱਚ ਪ੍ਰਦਰਸ਼ਿਤ ਕਰੋ।
ਉੱਤਰ-
ਓਹਮ ਦਾ ਨਿਯਮ-ਕਿਸੇ ਚਾਲਕ ਵਿੱਚੋਂ ਪ੍ਰਵਾਹਿਤ ਹੋਣ ਵਾਲੀ ਬਿਜਲਈ ਧਾਰਾ (I) ਉਸ ਦੇ ਸਿਰਿਆਂ ਵਿਚਕਾਰ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ (V) ਦੇ ਸਮਾਨੁਪਾਤੀ ਹੁੰਦੀ ਹੈ ।
ਗਣਿਤਿਕ ਰੂਪ ਵਿੱਚ, V ∝ I
ਜਾਂ \(\frac{\mathrm{V}}{\mathrm{I}}\) = R (ਚਾਲਕ ਲਈ ਸਥਿਰ ਅੰਕ)

ਪ੍ਰਸ਼ਨ 14.
ਚਾਂਦੀ ਦੀ ਪ੍ਰਤਿਰੋਧਕਤਾ 1.6 × 10^-8 Ωm ਹੈ । ਇਸ ਕਥਨ ਦਾ ਕੀ ਅਰਥ ਹੈ ?
ਉੱਤਰ-
ਇਸ ਕਥਨ ਦਾ ਅਰਥ ਹੈ ਕਿ 1m ਲੰਬੇ ਅਤੇ 1m²-ਕਾਟ ਦੇ ਖੇਤਰਫਲ ਵਾਲੇ ਚਾਂਦੀ ਦੇ ਤਾਰ ਦਾ ਪ੍ਰਤਿਰੋਧ 1.6 × 10^-8 Ω ਹੋਵੇਗਾ ।

ਪ੍ਰਸ਼ਨ 15.
ਐਮਮੀਟਰ ਨੂੰ ਸਰਕਟ ਵਿੱਚ ਕਿਵੇਂ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਸਰਕਟ ਦੇ ਜਿਸ ਘਟਕ ਵਿੱਚੋਂ ਪ੍ਰਵਾਹਿਤ ਹੋਣ ਵਾਲੀ ਬਿਜਲਈ ਧਾਰਾ ਦਾ ਮਾਪ ਲੈਣਾ ਹੁੰਦਾ ਹੈ, ਐਮਮੀਟਰ ਨੂੰ ਉਸ ਘਟਕ ਨਾਲ ਸ਼ੇਣੀਕੂਮ ਵਿੱਚ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 16.
ਕਿਸ ਦਾ ਪ੍ਰਤਿਰੋਧ ਅਧਿਕ ਹੋਵੇਗਾ – 50 w ਦੇ ਬੱਲਬ ਦਾ ਜਾਂ 25 w ਦੇ ਬੱਲਬ ਦਾ ਅਤੇ ਕਿੰਨੇ ਗੁਣਾ ਹੋਵੇਗਾ ?
ਉੱਤਰ-
ਮੰਨ ਲਓ ਬੱਲਦਾਂ ਦੇ ਪ੍ਰਤਿਰੋਧ R₁ ਅਤੇ R₂ ਹਨ ਅਤੇ ਲੱਗਿਆ ਪੁਟੈਂਸ਼ਲ V ਹੈ, ਤਾਂ
P₁ = 50 = \(\frac{V^{2}}{R_{1}}\)
ਅਤੇ p₂ = 25 = \(\frac{\mathrm{V}^{2}}{\mathrm{R}_{2}}\)
∴ \(\frac{P_{1}}{P_{2}}\) = \(\frac{50}{25}=\frac{V^{2}}{R_{1}} \times \frac{R_{2}}{V^{2}}\)
⇒ 2 = \(\frac{\mathrm{R}_{2}}{\mathrm{R}_{1}}\)
⇒ R₂ = 2 × R₁

ਪ੍ਰਸ਼ਨ 17.
ਕਿਸੇ ਬਿਜਲਈ ਸਰਕਟ ਵਿੱਚ ਚਾਬੀ ਜਾਂ ਸਵਿੱਚ (Plug) ਦੇ ਚਿੰਨ੍ਹ ਦੱਸੋ ਜਦੋਂ ਸਰਕਟ
(i) ਖੁੱਲ੍ਹਾ ਹੋਵੇ
(ii) ਬੰਦ ਹੋਵੇ ।
ਉੱਤਰ-
(i) ਖੁੱਲ੍ਹੇ ਬਿਜਲਈ ਸਰਕਟ ਵਿੱਚ ਚਾਬੀ ਜਾਂ ਸਵਿੱਚ-()-
(ii) ਬੰਦ ਬਿਜਲਈ ਸਰਕਟ ਵਿੱਚ ਚਾਬੀ ਜਾਂ ਸਵਿੱਚ-(.)-

ਪ੍ਰਸ਼ਨ 18.
ਦੋ ਬਿਜਲਈ ਸੁਚਾਲਕਾਂ ਦੇ ਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ-

1. ਕਾਪਰ
2. ਐਲੂਮੀਨੀਅਮ।

ਪ੍ਰਸ਼ਨ 19.
ਬਿਜਲੀ ਊਰਜਾ ਦੀ ਪਰਿਭਾਸ਼ਾ ਲਿਖੋ ।
ਉੱਤਰ-
ਬਿਜਲੀ ਊਰਜਾ – ਕਿਸੇ ਨਿਸਚਿਤ ਸਮੇਂ ਵਿਚ ਧਾਰਾ ਦੁਆਰਾ ਕੀਤੇ ਗਏ ਕਾਰਜ ਦੀ ਮਾਤਰਾ ਨੂੰ ਬਿਜਲੀ ਊਰਜਾ ਕਹਿੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 20.
ਬਿਲਜਈ ਸਰਕਟ ਵਿੱਚ ਵੋਲਟਮੀਟਰ ਨੂੰ ਕਿਵੇਂ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਸਮਾਨਅੰਤਰ ਕੁਮ ਵਿੱਚ ।

ਪ੍ਰਸ਼ਨ 21.
ਕਰੰਟ ਦੀ ਇਕਾਈ ਦੱਸੋ ।
ਉੱਤਰ-
ਐਮਪੀਅਰ ।

ਪ੍ਰਸ਼ਨ 22.
ਬਿਜਲਈ ਸਮਰੱਥਾ (ਸ਼ਕਤੀ) ਦੀ ਵੱਡੀ ਇਕਾਈ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਕਿਲੋਵਾਟ (kw) ।

ਪ੍ਰਸ਼ਨ 23.
ਧਾਤਾਂ ਵਿੱਚ ਬਿਜਲਈ ਧਾਰਾ ਦਾ ਪ੍ਰਵਾਹ ਕਿਸ ਪਰਮਾਣੂ ਕਣ ਦੇ ਕਾਰਨ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਇਲੈੱਕਟਾਂਨ ।

ਪ੍ਰਸ਼ਨ 24.
ਇੱਕ ਇਲੈੱਕਟ੍ਰਾਨ ਤੇ ਕਿੰਨੇ ਕੂਲਾਂਮ ਚਾਰਜ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
1.6 × 10^-19C

ਪ੍ਰਸ਼ਨ 25.
ਇੱਕ ਕੂਲਾਂਮ ਚਾਰਜ ਕਿੰਨੇ ਇਲੈੱਕਨਾਂ ਦੇ ਚਾਰਜ ਦੇ ਬਰਾਬਰ ਹੈ ?
ਉੱਤਰ-
6.25 × 10¹⁸ ਇਲੈੱਕਟ੍ਰਾਨਾਂ ਦੇ ਚਾਰਜ ਦੇ ਬਰਾਬਰ ।

ਪ੍ਰਸ਼ਨ 26.
ਸਭ ਤੋਂ ਵਧੀਆ ਬਿਜਲਈ ਚਾਲਕ ਦਾ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਚਾਂਦੀ ।

ਪ੍ਰਸ਼ਨ 27.
ਤਾਂਬੇ ਅਤੇ ਲੋਹੇ ਵਿੱਚੋਂ ਬਿਜਲੀ ਦਾ ਕਿਹੜਾ ਚੰਗਾ ਚਾਲਕ ਹੈ ?
ਉੱਤਰ-
ਤਾਂਬਾ ।

ਪ੍ਰਸ਼ਨ 28.
ਬਿਜਲਈ ਬੱਲਬ ਦਾ ਫਿਲਾਮੈਂਟ ਕਿਸ ਧਾਤੂ ਦਾ ਬਣਾਇਆ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਟੰਗਸਟਨ ਧਾਤ ਦਾ ।

ਪ੍ਰਸ਼ਨ 29.
ਬਿਜਲਈ ਐੱਸ ਅਤੇ ਟੋਸਟਰ ਦੇ ਫਿਲਾਮੈਂਟ ਕਿਸ ਧਾਤੂ ਦੇ ਬਣੇ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਨਾਈਟ੍ਰੋਮ ਮਿਸ਼ਰਤ ਧਾਤੂ ਦੇ ।

ਪ੍ਰਸ਼ਨ 30.
ਬਿਜਲਈ ਪੁਟੈਂਸ਼ਲ ਦਾ S.I. ਮਾਤ੍ਰਿਕ ਦੱਸੋ ।
ਉੱਤਰ-
ਐਮਪੀਅਰ ।

ਪ੍ਰਸ਼ਨ 31.
ਬਿਜਲਈ ਪ੍ਰਤਿਰੋਧ ਦਾ S.I. ਮਾਤ੍ਰਿਕ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਓਹਮ ।

ਪ੍ਰਸ਼ਨ 32.
ਕਿਸੇ ਪਦਾਰਥ ਦੀ ਪ੍ਰਤਿਰੋਧਕਤਾ ਦਾ S.I. ਮਾਤ੍ਰਿਕ ਲਿਖੋ ।
ਉੱਤਰ-
ਓਹਮ-ਮੀਟਰ (Ωm) ।

ਪ੍ਰਸ਼ਨ 33.
ਬਿਜਲਈ ਚਾਰਜ ਦਾ S.I. ਮਾਤ੍ਰਿਕ ਲਿਖੋ ।
ਉੱਤਰ-
ਕੂਲਾਂਮ ।

ਪ੍ਰਸ਼ਨ 34.
ਤਿਰੋਧ ਦੇ ਸ਼੍ਰੇਣੀ ਸੰਯੋਜਨ ਅਤੇ ਸਮਾਨ ਅੰਤਰ ਸੰਯੋਜਨ ਵਿੱਚੋਂ ਕਿਸਦਾ ਪ੍ਰਤਿਰੋਧ ਅਧਿਕਤਮ ਹੁੰਦਾ ਹੈ ਅਤੇ ਕਿਸਦਾ ਨਿਊਨਤਮ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਸ਼੍ਰੇਣੀ ਸੰਯੋਜਨ ਦਾ ਅਧਿਕਤਮ ਪ੍ਰਤਿਰੋਧ ਅਤੇ ਸਮਾਨਅੰਤਰ ਦਾ ਨਿਊਨਤਮ ਪ੍ਰਤਿਰੋਧ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 35.
ਕਿਲੋਵਾਟ ਘੰਟਾ (kwh) ਕੀ ਹੈ ?
ਉੱਤਰ-
ਕਿਲੋਵਾਟ ਘੰਟਾ ਬਿਜਲਈ ਊਰਜਾ ਦੀ ਵਪਾਰਕ ਇਕਾਈ ਹੈ ।

ਪ੍ਰਸ਼ਨ 36.
1kwh ਕਿੰਨੇ ਜੂਲ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
1kwh = 3.6 × 10⁶ ਜੂਲ ।

ਪ੍ਰਸ਼ਨ 37.
ਘਰਾਂ ਵਿੱਚ ਬਿਜਲਈ ਉਪਕਰਨ ਕਿਸ ਵਿਵਸਥਾ ਵਿੱਚ ਜੁੜੇ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਸਮਾਨਅੰਤਰ ਸੰਯੋਜਨ ਵਿਵਸਥਾ ਵਿੱਚ ।

ਪ੍ਰਸ਼ਨ 38.
ਇੱਕ ਦਿਸ਼ਾਈ (D.C.) ਬਿਜਲਈ ਧਾਰਾ ਦੇ ਸਰੋਤ ਦਾ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਬਿਜਲਈ ਸੈੱਲ ਜਾਂ ਬੈਟਰੀ ।

ਪ੍ਰਸ਼ਨ 39.
ਬਿਜਲੀ ਸੈੱਲ ਅਤੇ ਬਿਨਾਂ ਜੋੜ ਤੋਂ ਤਾਰ ਕਰਾਸਿੰਗ ਲਈ ਸੰਕੇਤ ਲਿਖੋ ।
ਉੱਤਰ-
ਬਿਜਲੀ ਸੈੱਲ ਦਾ ਸੰਕੇਤ :
ਬਿਨਾਂ ਜੋੜ ਤੋਂ ਤਾਰ ਕਰਾਸਿੰਗ ਲਈ ਸੰਕੇਤ :

ਪ੍ਰਸ਼ਨ 40.
(i) ਪ੍ਰਤਿਰੋਧ ਅਤੇ
(ii) ਐਮਮੀਟਰ ਲਈ ਸੰਕੇਤ ਲਿਖੋ ।
ਉੱਤਰ-
(i) ਪ੍ਰਤਿਰੋਧ ਲਈ ਸੰਕੇਤ :
(ii) ਐਮਮੀਟਰ ਲਈ ਸੰਕੇਤ :

ਪ੍ਰਸ਼ਨ 41.
ਬਿਜਲੀ ਲਈ ਬੈਟਰੀ ਜਾਂ ਸੈੱਲਾਂ ਦਾ ਸੰਯੋਜਨ ਅਤੇ ਤਾਰ ਜੋੜ ਦੇ ਸੰਕੇਤ ਲਿਖੋ ।
ਉੱਤਰ-
ਬਿਜਲੀ ਲਈ ਬੈਟਰੀ ਜਾਂ ਸੈੱਲਾਂ ਦੇ ਸੰਯੋਜਨ ਲਈ ਸੰਕੇਤ :
ਤਾਰ ਜੋੜ ਦਾ ਸੰਕੇਤ :

ਵਸਤੂਨਿਸ਼ਠ ਪ੍ਰਸ਼ਨ (Objective Type Questions)

ਪ੍ਰਸ਼ਨ 1.
V ∝ I ਦਾ ਨਿਯਮ ਪ੍ਰਤਿਪਾਦਿਤ ਕੀਤਾ ਹੈ-
(a) ਫੈਰਾਡੇ ਨੇ
(b) ਵਾਟ ਨੇ
(c) ਓਹਮ ਨੇ
(d) ਕੂਲਾਂਮ ਨੇ ।
ਉੱਤਰ-
(c) ਓਹਮ ਨੇ ।

ਪ੍ਰਸ਼ਨ 2.
ਪੁਟੈਂਸ਼ਲ ਦਾ ਮਾਤਕ ਹੈ-
(a) ਐਮਪੀਅਰ
(b) ਵੋਲਟ
(c) ਓਹਮ
(d) ਵਾਟ ।
ਉੱਤਰ-
(b) ਵੋਲਟ ।

ਪ੍ਰਸ਼ਨ 3.
ਬਿਜਲੀ ਸ਼ਕਤੀ ਦਾ ਮਾਕ ਹੈ-
(a) ਐਮਪੀਅਰ
(b) ਵੋਲਟ
(c) ਓਹਮ
(d) ਵਾਟ ।
ਉੱਤਰ-
(d) ਵਾਟ ।

ਪ੍ਰਸ਼ਨ 4.
\(\frac {1}{3}\) Ω ਦੇ ਤਿੰਨ ਤਿਰੋਧਕਾਂ ਨੂੰ ਕਿਸੇ ਤਰ੍ਹਾਂ ਸੰਯੋਜਿਤ ਕਰਕੇ ਕਿੰਨਾ ਵੱਧ ਤੋਂ ਵੱਧ ਪ੍ਰਤਿਰੋਧ ਪ੍ਰਾਪਤ ਕਰ ਸਕਦੇ ਹਾਂ ?
(a) \(\frac {1}{3}\) Ω
(b) 1 Ω
(c) \(\frac {1}{9}\) Ω
(d) 3 Ω
ਉੱਤਰ-
(b) 1 Ω

ਪ੍ਰਸ਼ਨ 5.
ਫਿਊਜ਼ ਨੂੰ ਕਿਸੇ ਯੁਕਤੀ ਨਾਲ ਕਿਸ ਕੂਮ ਵਿੱਚ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ ?
(a) ਸਮਾਨਾਂਤਰ ਕੁਮ
(b) ਸ਼੍ਰੇਣੀਕੂਮ
(c) ਸਮਾਨਾਂਤਰ ਅਤੇ ਸ਼੍ਰੇਣੀਕੂਮ ਦੋਨਾਂ ਵਿੱਚ
(d) ਇਹਨਾਂ ਵਿੱਚੋਂ ਕੋਈ ਨਹੀਂ ।
ਉੱਤਰ-
(b) ਸ਼੍ਰੇਣੀਕੁਮ ।

ਪ੍ਰਸ਼ਨ 6.
ਬਿਜਲਈ ਚਾਰਜ ਦਾ SI ਮਾਕ ਹੈ-
(a) ਵਾਟ
(b) ਕਿਲੋਵਾਟ
(c) ਕੂਲਾਂਮ
(d) ਐਮਪੀਅਰ ।
ਉੱਤਰ-
(c) ਕੂਲਾਂਮ ।

ਪ੍ਰਸ਼ਨ 7.
ਬਿਜਲੀ ਧਾਰਾ ਨੂੰ ਕਿਸ ਮਾਕ ਵਿੱਚ ਦਰਸਾਇਆ ਜਾਂਦਾ ਹੈ ?
(a) ਕੂਲਾਮ
(b) ਐਮਪੀਅਰ
(c) ਵਾਟ
(d) ਕਿਲੋਵਾਟ ।
ਉੱਤਰ-
(b) ਐਮਪੀਅਰ ।

ਪ੍ਰਸ਼ਨ 8.
ਪਰਿਪੱਬਾਂ ਵਿੱਚ ਪ੍ਰਵਾਹਿਤ ਹੋ ਰਹੀ ਬਿਜਲੀ ਧਾਰਾ ਨੂੰ ਕਿਸ ਯੰਤਰ ਦੁਆਰਾ ਮਾਪਿਆ ਜਾਂਦਾ ਹੈ ?
(a) ਐਮਮੀਟਰ
(b) ਵੋਲਟਮੀਟਰ
(c) ਗੈਲਵੇਨੋਮੀਟਰ
(d) ਬਿਜਲੀ ਮੀਟਰ ।
ਉੱਤਰ-
(a) ਐਮਮੀਟਰ ।

ਪ੍ਰਸ਼ਨ 9.
ਐਮਮੀਟਰ ਨੂੰ ਪਰਿਪੱਬ ਵਿੱਚ ਕਿਵੇਂ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ ?
(a) ਸ਼੍ਰੇਣੀਕ੍ਰਮ ਵਿੱਚ
(b) ਸਮਾਨਾਂਤਰ ਕੂਮ ਵਿੱਚ
(c) ਸ਼੍ਰੇਣੀਕੂਮ ਅਤੇ ਸਮਾਨਾਂਤਰ ਕੂਮ ਦੋਨਾਂ ਵਿੱਚ
(d) ਇਨ੍ਹਾਂ ਵਿੱਚੋਂ ਕੋਈ ਨਹੀਂ ।
ਉੱਤਰ-
(a) ਸ਼੍ਰੇਣੀਕ੍ਰਮ ਵਿੱਚ ।

ਪ੍ਰਸ਼ਨ 10.
ਟੈਂਸ਼ਲ ਅੰਤਰ ਨੂੰ ਕਿਸ ਯੰਤਰ ਨਾਲ ਮਾਪਿਆ ਜਾਂਦਾ ਹੈ ?
(a) ਐਮਮੀਟਰ
(b) ਵੋਲਟਮੀਟਰ
(c) ਗੈਲਵੇਨੋਮੀਟਰ
(d) ਬਿਜਲੀ ਮੀਟਰ ।
ਉੱਤਰ-
(b) ਵੋਲਟਮੀਟਰ ।

ਖ਼ਾਲੀ ਥਾਂਵਾਂ ਭਰਨਾ

ਪ੍ਰਸ਼ਨ-ਹੇਠ ਲਿਖੀਆਂ ਖ਼ਾਲੀ ਥਾਂਵਾਂ ਭਰੋ :

(i) ਸਮਾਨਾਂਤਰ ਕੂਮ ਵਿੱਚ ਸੰਯੋਜਿਤ ਹਰੇਕ ਤਿਰੋਧਕ ਵਿੱਚ ਵਹਿ ਰਹੀ ਬਿਜਲਈ ਧਾਰਾ ਦੀ ਮਾਤਰਾ …………………….. ਹੁੰਦੀ ਹੈ ।
ਉੱਤਰ-
ਵੱਖ-ਵੱਖ

(ii) ਓਹਮ ਦੇ ਨਿਯਮ ਅਨੁਸਾਰ ਕਿਸੇ ਚਾਲਕ ਤਾਰ ਦੇ ਲਈ V ਅਤੇ I ਦੇ ਵਿਚਕਾਰ ਦਾ ਸੰਬੰਧ …………………….. ਹੈ ।
ਉੱਤਰ-
R

(iii) ਕਿਸੇ ਬਿਜਲਈ ਪਰਿਪੱਖ ਵਿੱਚ ਬਿਜਲਈ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ ਦਾ ਮਾਪ ………………………….. ਦੁਆਰਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
ਉੱਤਰ-
ਵੋਲਟਮੀਟਰ

(iv) ਇੱਕ ਕਿਲੋਵਾਟ ਘੰਟਾ (Kwh) ………………………….. ਦਾ ਮਾਤਕ ਹੈ ।
ਉੱਤਰ-
ਬਿਜਲਈ ਊਰਜਾ

(v) ਕਿਸੇ ਬਿਜਲਈ ਪਰਿਪੱਥ ਵਿੱਚ ਬਿਜਲਈ ਧਾਰਾ ਨੂੰ ਮਾਪਣ ਵਾਲਾ ਯੰਤਰ …………………….. ਹੈ ।
ਉੱਤਰ-
ਐਮਮੀਟਰ ।