Punjab State Board PSEB 6th Class Science Book Solutions Chapter 14 पानी Textbook Exercise Questions, and Answers.
PSEB Solutions for Class 6 Science Chapter 14 पानी
PSEB 6th Class Science Guide पानी Textbook Questions, and Answers
1. खाली स्थान भरें
(i) पानी से वाष्पों में बनने की क्रिया को ………………….. कहते हैं।
उत्तर-
वाष्पीकरण
(ii) जलवाष्पों से पानी के परिवर्तन की प्रक्रिया ………………….. कहलाती है।
उत्तर-
संघनन
(iii) एक या अधिक साल से वर्षा के न होने को …………………… कहा जाता है।
उत्तर-
सूखा
(iv) …………………….. बहुत अधिक वर्षा के कारण होते हैं।
उत्तर-
बाढ़
(v) पानी की तीन अवस्थाएं ………………….., …………………….. तथा ………………… हैं।
उत्तर-
ठोस, तरल और गैस
(vi) पौधों में वाष्प के उत्सर्जन …………….. द्वारा से होता है।
उत्तर-
स्टौमेटा ।

2. सही या ग़लत बताएं
(i) बर्फ ठंडी होने से भाप में बदलती है।
उत्तर-
ग़लत
(ii) सूरज की रोशनी में पानी का वाष्पीकरण होता है।
उत्तर-
सही
(iii) पानी की पाइप में लीकेज होने से मरम्मत न करें।
उत्तर-
ग़लत
(iv) महासागरों का पानी पीने योग्य होता है।
उत्तर-
ग़लत
(v) खेती-बाड़ी के लिए तुपका प्रणाली द्वारा सिंचाई लाभदायक है।
उत्तर-
सही
3. कॉलम ‘क’ का कॉलम ‘ख’ से उचित मिलान करें
| कॉलम ‘क’ |
कॉलम ‘ख’ |
| (i) पानी का संरक्षण |
(क) पानी की ठोस अवस्था |
| (ii) बर्फ |
(ख) धूप वाला दिन |
| (iii) वर्षा/जल कण |
(ग) वर्षा के पानी का संचयन |
| (iv) वाष्पीकरण |
(घ) भौम (भूमिगत) पानी |
| (v) ताज़ा पानी |
(ङ) बादलों से वर्षा |
उत्तर-
| कॉलम ‘क’ |
कॉलम ‘ख’. |
| (i) पानी का संरक्षण |
(ग) वर्षा के पानी का संचयन |
| (ii) बर्फ |
(क) पानी की ठोस अवस्था |
| (iii) वर्षा/जल कण |
(ङ) बादलों से वर्षा |
| (iv) वाष्पीकरण |
(ख) धूप वाला दिन |
| (v) ताज़ा पानी |
(घ) भौम (भूमिगत) पानी |

4. सही विकल्प चुनें
प्रश्न (i)
धरती का कितना हिस्सा पानी के साथ ढका हुआ है ?
(क) दो तिहाई
(ख) एक तिहाई
(ग) आधा
(घ) तीन चौथाई।
उत्तर-
(घ) तीन चौथाई।
प्रश्न (ii)
सर्दियों की ठंडी सुबह में धुंध के होने का कारण है-
(क) संघनन
(ख) वर्षा
(ग) वाष्पन
(घ) कोई नहीं।
उत्तर-
(क) संघनन।
प्रश्न (ii)
कौन-से पानी का स्रोत पीने के लिए नहीं प्रयोग कर सकते ?
(क) नदी
(ख) बांध
(ग) महासागर
(घ) झीलें।
उत्तर-
(ग) महासागर।
प्रश्न (iv)
तरल से गैस में बदलने की प्रक्रिया को कहते हैं-
(क) वाष्पन
(ख) संघनन
(ग) पिघलना
(घ) उबाल।
उत्तर-
(क) वाष्पन।
प्रश्न (v)
मानवीय शरीर में कितने प्रतिशत पानी होता है ?
(क) 60%
(ख) 80%
(ग) 70%
(घ) 90%।
उत्तर-
(ख) 80%
5. अति लघूत्तर प्रश्न
प्रश्न (i)
पानी के दो मुख्य स्रोत कौन-कौन से हैं ?
उत्तर-
जल के दो प्रमुख स्रोत सतही जल और भूजल हैं।

प्रश्न (ii)
तुपका प्रणाली द्वारा सिंचाई का क्या महत्त्व है ?
उत्तर-
तुपका या ड्रिप सिंचाई का लाभ यह है कि पानी और अन्य पोषक तत्व सीधे पौधों तक पहुंचते हैं।
प्रश्न (iii)
तामान का वाष्पीकरण पर क्या प्रभाव पड़ता है ?
उत्तर-
तापमान में वृद्धि के साथ वाष्पीकरण की दर बढ़ जाती है।
प्रश्न (iv)
भौम जल और सतह जल में अंतर स्पष्ट करें।
उत्तर-
भौम जल पृथ्वी की सतह के नीचे होता है और पीने के लिए सुरक्षित है। सतही जल झीलों, नदियों, कुओं और जलाशयों में पाया जाता है।
प्रश्न (v)
वाष्प उत्सर्जन की परिभाषा लिखें। उत्तर-वह प्रक्रिया जिसके द्वारा पौधे हवा में पानी खो देते हैं, वाष्प उत्सर्जन कहलाती है।
6. लघूत्तर प्रश्न
प्रश्न (i)
बाढ़ किसे कहते हैं ? उसके साथ पैदा होने वाले प्रभाव बताएं।
उत्तर-
अपनी सामान्य सीमा से अधिक मात्रा में पानी के अतिप्रवाह को बाढ़ के रूप में जाना जाता है।
बाढ़ के प्रभाव-
- बहुत से लोग और जानवर मर जाते हैं।
- कुछ लोग बेघर हो जाते हैं।
- संचारी रोगों का व्यापक प्रसार।
प्रश्न (ii)
संघनन की परिभाषा लिखकर दो उदाहरण भी बताएं।
उत्तर-
गैसीय रूप को वापस तरल रूप में बदलने की प्रक्रिया संघनन कहलाती है।
उदाहरण हैं-
- कार के अगले अथवा पिछले शीशे पर धुंध जमना ।
- सर्दी की सुबह में घास की पत्तियों पर ओस।

प्रश्न (iii)
बादल किस तरह बनते हैं ?
उत्तर-
जब हम पृथ्वी की सतह से ऊपर जाते हैं, तो तापमान गिर जाता है। हवा इतनी ठंडी हो जाती है कि जल वाष्प संघनित होकर पानी की बूंदों का निर्माण करती है। हवा में एक साथ ये पानी की बूंदें बादल कहलाती हैं।
प्रश्न (iv)
पानी के संरक्षण के कोई तीन ढंग लिखें।
उत्तर-
पानी के संरक्षण के कोई तीन तरीके हैं-
- वर्षा जल संचयन
- पानी का पुनर्चक्रण
- उपयोग में न होने पर नल बंद करना।
प्रश्न (v)
सूखा क्या है ? इसके साथ क्या प्रभाव पड़ते हैं ?
उत्तर-
जिस अवधि में बहुत कम या कोई वर्षा नहीं होती है उसे सूखा कहा जाता है।
सूखे का प्रभाव-
- पानी की कमी के कारण मिट्टी शुष्क और उपजाऊ हो जाती है।
- तालाब सूख जाते हैं और कुओं में पानी का स्तर नीचे चला जाता है।
7. निबंधात्मक प्रश्न
प्रश्न (i)
पानी के उपयोग की सूची बनाएं।
उत्तर-
पानी एक बहुत ही महत्त्वपूर्ण संसाधन है और इसका उपयोग कई उद्देश्यों के लिए किया जाता है। पानी के कुछ उपयोगों का उल्लेख नीचे किया गया है
पानी के उपयोग-
- यह पृथ्वी पर तापमान बनाए रखता है।
- इसका उपयोग पीने, स्नान करने, कपड़े तथा बर्तन आदि धोने आदि के लिए किया जाता है।
- बिजली पैदा करने के लिए बहते पानी का उपयोग किया जाता है।
- इसका उपयोग फसलों की सिंचाई के लिए किया जाता है।
- इसका उपयोग सफाई, खाना पकाने, सिंचाई आदि के लिए भी किया जाता है।
प्रश्न (ii)
जल चक्र को चित्र की सहायता से स्पष्ट करें।
उत्तर-
प्रकृति में जल चक्र – जल वर्षा, ओस, हिम आदि के रूप में पृथ्वी पर गिरता है। यह जल तालाबों, जलधाराओं, महासागरों में गिरता है और कुछ जल पृथ्वी के नीचे चला जाता है। सूर्य की गर्मी से झीलों, तालाबों, नदीयों, महासागरों आदि से पानी वाष्पित हो जाता है और वातावरण को जलवाष्पों से भर देता है। ये जलवाष्प ठंडा होने पर संघनित होकर बादल बन जाते हैं। ये बादल जब बरसते हैं तो जल पृथ्वी पर वापस आ जाता है। इस प्रकार यह सिलसिला अर्थात जल चक्र चलता रहता है।
प्रश्न (iii)
पानी के संरक्षण की क्या आवश्यकता है ? वर्षा के पानी का संग्रहण करने की विधियों की व्याख्या करें।
उत्तर-
पृथ्वी पर ताजा पानी केवल 2.59% है और बहुत कम मात्रा में है जिसका उपयोग पीने या मानव उपभोग के लिए किया जा सकता है। इसलिए हमें पानी का संरक्षण करना चाहिए।
वर्षा के पानी का संचयन-
यह एक ऐसी तकनीक है जिसमें वर्षा के पानी का संग्रह और भंडारण और उसका पुन-उपयोग शामिल है। यह सबसे सरल और सबसे पुराना तरीका है।
वर्षा के पानी के संचयन की तकनीक-
वर्षा के पानी के संचयन के लिए सबसे अधिक इस्तेमाल की जाने वाली तकनीक छत के ऊपर वर्षा के पानी का संचयन है।
रूफ टॉप रेन वाटर हार्वेस्टिंग-
इसमें बारिश का पानी घर की छत पर इकट्ठा किया जाता है और फिर पाइप के जरिए भंडारण टैंक में जमा किया जाता है। इस संचित जल का उपयोग किसी भी कार्य में किया जा सकता है।
Science Guide for Class 6 PSEB पानी Intext Questions and Answers
सोचें तथा उत्तर दें (पेज 145)
प्रश्न 1.
क्या हर व्यक्ति एक जैसी पानी की मात्रा का प्रयोग करता है ?
उत्तर-
नहीं, हर व्यक्ति एक जैसी पानी की मात्रा में जल का प्रयोग नहीं करता है।

सोचें तथा उत्तर दें (पेज 146)
प्रश्न 1.
जब हम फ्रिज में से आइसक्रीम बाहर निकालते हैं तो क्या होता है ?
उत्तर-
यह पिघल जाती है।
प्रश्न 2.
आइसक्रीम किस अवस्था में होती है ?
उत्तर-
ठोस।
सोचें तथा उत्तर दें (पेज 147)
प्रश्न 1.
गर्मियों के दिनों में पानी फर्श पर फैलाने से क्या होता है ?
उत्तर-
यह वाष्पित हो जाता है।
प्रश्न 2.
उपले (Cow dung cake) धूप में क्यों रखे जाते हैं ?
उत्तर-
उपले धूप में सुखाने के लिए रखे जाते हैं। पानी के वाष्पीकरण के परिणामस्वरूप यह शुष्क हो जाते हैं ।
सोचें तथा उत्तर दें (पेज 148)
प्रश्न 1.
ठंडे पानी की बोतल को फ्रिज में से निकालने के बाद आप पानी की बूंदें बोतल की सतह पर क्यों देखते
उत्तर-
रेफ्रिजरेटर के बाहर का तापमान अधिक गर्म होता है और जब बोतल रेफ्रिजरेटर से बाहर आती है, तो हवा में मौजूद वाष्प संघनित हो जाती है और बोतल की सतह पर पानी की बूंदों का निर्माण करती है। इस प्रक्रिया को संघनन के रूप में जाना जाता है।
PSEB Solutions for Class 6 Science पानी Important Questions and Answers
1. बहुविकल्पीय प्रश्न
प्रश्न (i)
जल-चक्र एक प्रक्रिया है-
(क) तीव्र
(ख) धीमी
(ग) मध्यम
(घ) इनमें से कोई नहीं।
उत्तर-
(ख) धीमी।
प्रश्न (ii)
एक किलो गेहूँ प्राप्त करने के लिए गेहूँ के पौधों से …………………… लीटर जल का वाष्पोत्सर्जन होता है।
(क) 100
(ख) 200
(ग) 400
(घ) 500।
उत्तर-
(घ) 500।

प्रश्न (iii)
अधिक वर्षा का कारण होता है-
(क) सूखा
(ख) बाढ़
(ग) आंधी
(घ) इनमें से कोई नहीं।
उत्तर-
(ख) बाढ़।
प्रश्न (iv)
पृथ्वी का ……………… भाग जल से घिरा हुआ है।
(क) \(\frac{1}{3}\)
(ख) \(\frac{2}{3}\)
(ग) \(\frac{1}{4}\)
(घ) इनमें से कोई नहीं।
उत्तर-
(ख) \(\frac{2}{3}\)
प्रश्न (v)
बहुत अधिक मात्रा में जल उपलब्ध होता है-
(क) दरिया
(ख) कुँआ
(ग) समुद्र
(घ) वर्षा ।
उत्तर-
(ग) समुद्र।
प्रश्न (vi)
जल का इसके वाष्यों में परिवर्तित होना है-
(क) वाष्पन
(ख) वाष्पोत्सर्जन
(ग) संघनन ।
(घ) इनमें से कोई नहीं।
उत्तर-
(क) वाष्पन।
प्रश्न (vii)
जलवाष्पों का जल में परिवर्तित होना कहलाता है-
(क) वाष्पन
(ख) वाष्पोत्सर्जन
(ग) संघनन
(घ) इनमें से कोई नहीं।
उत्तर-
(ग) संघनन।
2. खाली स्थान भरें
(i) जल पृथ्वी का सबसे अधिक ……………………. संसाधन है।
उत्तर-
आवश्यक
(ii) हमे वर्षा जल …………………… करना चाहिए ।
उत्तर-
संरक्षण
(iii) पानी की बूंदों के संग्रह को …………………….. कहा जाता है।
उत्तर-
बादल
(iv) बारिश और हिमपात के आने को ………………. कहा जाता है।
उत्तर-
अवक्षेपण ।

3. सही या ग़लत चुनें
(i) पौधे की पत्तियों में छोटे-छोटे छिद्र रंध्र कहलाते हैं।
उत्तर-
सही
(ii) जल चक्र एक चक्रीय प्रक्रिया नहीं है।
उत्तर-
ग़लत
(iii) बाढ़ में संक्रामक रोग होने का भय रहता है।
उत्तर-
सही
(iv) पानी का पुनः उपयोग नहीं किया जाना चाहिए।
उत्तर-
ग़लत
(v) वर्षा जल एकत्र होने पर भूजल का स्तर अधिक रहेगा।
उत्तर-
सही
4. कॉलम ‘क’ और कॉलम ‘ख’ का उचित मिलान करें
| कॉलम ‘क’ |
कॉलम ‘ख’ |
| (i) पीने का पानी |
(a) हवा में जलवाष्प का संचय |
| (ii) खारा पानी |
(b) वर्षा की लंबे समय तक अनुपस्थिति |
| (iii) वाष्पीकरण का उत्क्रमण |
(c) बारिश का पानी |
| (iv) बादल |
(d) महासागरों का जल |
| (v) सूखा |
(e) संघनन |
उत्तर-
| कॉलम ‘क’ |
कॉलम ‘ख’ |
| (i) पीने का पानी |
(c) बारिश का पानी |
| (ii) खारा पानी |
(d) महासागरों का जल |
| (iii) वाष्पीकरण का उत्क्रमण |
(e) संघनन |
| (iv) बादल |
(a) हवा में जलवाष्प का संचय |
| (v) सूखा |
(b) वर्षा की लंबे समय तक अनुपस्थिति |

5. अति लघूत्तर प्रश्न
प्रश्न 1.
रोज़ाना जीवन में जल से हम क्या कार्य करते हैं ?
उत्तर-
जल से हम रोज़ाना खाना पकाते, कपड़े धोते, बर्तन साफ़ करते और स्नान करते हैं।
प्रश्न 2.
क्या विभिन्न क्षेत्रों में रहने वाले लोगों को समान मात्रा में जल उपलब्ध होता है ?
उत्तर-
विभिन्न क्षेत्रों में रहने वाले लोगों को समान मात्रा में जल उपलब्ध नहीं होता।
प्रश्न 3.
क्या उद्योगों में वस्तुओं के उत्पादन के लिए जल का उपयोग होता है ?
उत्तर-
हाँ, वस्तुओं के उत्पादन में उद्योगों में जल का उपयोग होता है।
प्रश्न 4.
हमें जल कहाँ से प्राप्त होता है ?
उत्तर-
हमें जल नदियों, झरनों, तालाबों, कुँओं अथवा हैंड पंप से प्राप्त होता है।
प्रश्न 5.
पृथ्वी का कितना भाग जल से घिरा है ?
उत्तर-
लगभग 2/3 भाग।
प्रश्न 6.
वाष्पन किसे कहते हैं ?
उत्तर-
वाष्पन-जल का वाष्पों में परिवर्तित होना वाष्पन कहलाता है।

प्रश्न 7.
वाष्पन के लिए क्या अनिवार्य है ?
उत्तर-
वाष्पन के लिए ऊष्मा अनिवार्य है। यह ऊष्मा मुख्यतः सूर्य से प्राप्त होती है।
प्रश्न 8.
कौन-सी अवस्थाएँ वाष्पन को तेज़ करती हैं ?
उत्तर-
खुली सतह, ऊष्मा और चलती वायु वाष्पन को तेज़ करती हैं।
प्रश्न 9.
वाष्पोत्सर्जन किसे कहते हैं ?
उत्तर-
वाष्पोत्सर्जन – पौधों के पत्तों की सतह से जल के वाष्पों के उत्सर्जन को वाष्पोत्सर्जन कहते हैं। यह लगातार चलता है। दिन के समय यह अधिक होता है।
प्रश्न 10.
जल का पृथ्वी के पृष्ठ पर पुनः वापिस लाने में किस प्रक्रम की महत्त्वपूर्ण भूमिका है ?
उत्तर-
संघनन प्रक्रम।
प्रश्न 11.
वायुमंडल में संघनन कब होता है ?
उत्तर-
जब वायु पर्याप्त ऊँचाई पर जाकर ठंडी हो जाती है उसमें उपस्थित जलवाष्प संघनित होने लगते हैं।
प्रश्न 12.
सर्दियों में प्रातःकाल धरती के पास कोहरा क्यों दिखाई देता है ?
उत्तर-
धरती ठंडी होने के कारण जलवाष्प संघनित हो जाते हैं जो कोहरे के रूप में दिखाई देते हैं।

प्रश्न 13.
किन क्रियाओं के द्वारा जल वायु में जाता है ?
उत्तर-
वाष्पन और वाष्पोत्सर्जन के कारण।
प्रश्न 14.
जल पुनः धरती पर वापिस किस रूप में आता है ?
उत्तर-
वर्षा, ओले तथा हिम के रूप में।
प्रश्न 15.
वर्षा और हिम के रूप में पृथ्वी पर गिरा अधिकांश जल कहाँ वापिस चला जाता है ?
उत्तर-
वर्षा तथा हिम के रूप में भूमि पर गिरा अधिकांश जल अंततः महासागरों में वापिस चला जाता है।
प्रश्न 16.
भौम जल किसे कहते हैं ?
उत्तर-
भौम जल-भूमिगत पानी को भौम जल कहते हैं।
प्रश्न 17.
हैंड पंप या नल कूप से खींचा जल कहाँ से आता है ?
उत्तर-
भौम जल से।
प्रश्न 18.
भूमि पर जल की आपूर्ति कौन बनाए रखता है ?
उत्तर-
जलचक्र।

प्रश्न 19.
हमारे देश में अधिकांश वर्षा कौन-से मौसम में होती है ?
उत्तर-
मानसून में।
प्रश्न 20.
बाढ़ आने का मुख्य कारण क्या है ?
उत्तर-
अत्यधिक वर्षा ।
प्रश्न 21.
बाढ़ मे क्या हानि होती है ?
उत्तर-
बाढ़ से फसलें, पालतू जानवर, संपदा तथा मानव जीवन की अपार क्षति होती है।
प्रश्न 22.
जल की मांग बढ़ने का क्या कारण है ?
उत्तर-
जनसंख्या वृद्धि।
प्रश्न 23.
हम जल को कैसे सुरक्षित कर सकते हैं ?
उत्तर-
हमें जल का विवेकपूर्ण उपयोग करना चाहिए। जल को व्यर्थ न होने दें।
प्रश्न 24.
वर्षा जल संग्रहण का मूल मंत्र क्या है ?
उत्तर-
वर्षा जल संग्रहण का मूल मंत्र यह है कि जल जहां गिरे वहीं एकत्र कीजिए।

प्रश्न 25.
वर्षा जल संग्रहण की दो तकनीकें लिखें।
उत्तर-
- छत के ऊपर वर्षा संग्रहण।
- सड़क के किनारे बनी नालियों द्वारा एकत्रित वर्षा का जल भूमि में सीधे पहुंचने दिया जाना।
प्रश्न 26.
वर्षा जल संग्रहण किसे कहते हैं ?
उत्तर-
वर्षा के जल को एकत्र करना और उसका भंडारण करना जल संग्रहण कहलाता है।
6. लघूत्तर प्रश्न
प्रश्न 1.
हम घरेलू कार्य के अतिरिक्त जल और कहाँ उपयोग करते हैं ?
उत्तर-
हम गेहूँ, चावल, दालें, सब्जियाँ तथा अन्य बहुत सी खाने की वस्तुओं को उगाने के लिए जल का उपयोग करते हैं। हमारे उपयोग की लगभग सभी वस्तुओं के उत्पादन में जल का उपयोग, उद्योगों में किया जाता है।
प्रश्न 2.
किसी झील, नदी अथवा कुएँ से जल की आपूर्ति कैसे करते हैं ?
उत्तर-
हम अपने घरों में टोंटियों में एकत्र किये जल का प्रयोग करते हैं। टूटियों के द्वारा जो जल हम प्राप्त करते हैं वह जल भी किसी झील, नदी या किसी कुएँ से प्राप्त किया जाता है जिसकी आपूर्ति फिर पाइपों के नेटवर्क द्वारा की जाती है।

प्रश्न 3.
यदि किसी दिन आपको जल की आपूर्ति टोंटियों द्वारा नहीं हो रही हो तो आप क्या करोगे ?
उत्तर-
जिस दिन हमें जल की आपूर्ति टोंटियों द्वारा नहीं होती, तब हमें बहुत दूर से जल लाना पड़ता है। तब हम जल की कम मात्रा का उपयोग करेंगे, जितना हम अन्य दिनों में करते हैं। क्योंकि जल की कमी के कारण हमें कम जल से ही गुज़ारा करना पड़ता है।
प्रश्न 4.
हम समुद्रों तथा महासागरों का उपयोग क्यों नहीं कर सकते ?
उत्तर-
समुद्रों और महासागरों के जल में बहुत-से लवण घुले होते हैं जिससे जल खारा होता है। इसलिए, यह पीने के लिए अनुपयुक्त तथा अन्य घरेलू, कृषि तथा उद्योगों की आवश्यकता की पूर्ति के लिए उचित नहीं है।
प्रश्न 5.
महासागरों का जल तालाबों, झीलों, नदियों तथा कुँओं में कैसे पहुँचता है ?
उत्तर-
सूर्य की गर्मी के कारण महासागरों की सतह से जल वाष्पित होकर जलवाष्पों के रूप में वायु में चला जाता है। यह जलवाष्प संघनित होकर बादलों में परिवर्तित हो जाते हैं और इन बादलों में वर्षा के रूप में बरसते हैं। यह वर्षा का पानी नदियों, झीलों, तालाबों और कुओं में आता है। इस प्रकार महासागरों से पानी इन जल स्रोतों में आता है।

प्रश्न 6.
एक क्रियाकलाप द्वारा दर्शाओ कि जल का वाष्पन धूप और छाया दोनों में होता है।
उत्तर-
क्रियाकलाप-दो एक जैसी प्लेट लीजिए। एक प्लेट को सूर्य के प्रकाश (धूप) में तथा दूसरी को छाया वाले स्थान पर रखिए। अब इन दोनों प्लेट में बराबर मात्रा में जल भरिए। प्रत्येक 15 मिनट पश्चात् दोनों प्लेटों का निरीक्षण करें। तुम देखोगे कि छाया वाले स्थान पर रखी हुई प्लेट से भी जल विलुप्त होता है, यद्यपि इसमें अधिक समय लगता है। सूर्य के प्रकाश की ऊष्मा यहाँ भी पहुंच जाती है, ऐसा इसलिए होता है क्योंकि दिन के समय हमारे चारों ओर की वायु भी गर्म हो जाती है। गर्म वायु छाया में रखे जल को वाष्पित करने के लिए ऊष्मा प्रदान करती है। इस प्रकार जल के सभी खुले पृष्ठों से वाष्पन की क्रिया होती रहती है।

प्रश्न 7.
क्या पौधों द्वारा भी जल की क्षति होती है ?
उत्तर-
हाँ, पौधों द्वारा भी जल की क्षति होती है। सभी पौधों को वृद्धि के लिए जल की आवश्यकता होती है। पौधे इस जल की कुछ मात्रा का उपयोग अपना भोजन बनाने में करते हैं तथा कुछ मात्रा को अपने विभिन्न भागों में सुरक्षित रखते हैं। इस जल का शेष भाग, पौधों की पत्तियों द्वारा वाष्पोत्सर्जन प्रक्रम द्वारा जलवाष्प के रूप में वायु में मुक्त हो जाता है।
प्रश्न 8.
एक क्रियाकलाप द्वारा दर्शाओ कि वायु में जलवाष्प उपस्थित होते हैं ?
उत्तर-
जल से आधा भरा एक गिलास लीजिए। गिलास को बाहर से सूखे कपड़े से पोंछिए। जल में कुछ बर्फ़ डालिए। एक या दो मिनट तक प्रतीक्षा कीजिए।

कुछ समय बाद गिलास की बाहरी सतह पर जल की बूंदें दिखाई देंगी। बर्फ़ युक्त जल भरे गिलास की बाहरी सतह, बाहर की हवा को ठंडा कर देती है और वायु में विद्यमान जलवाष्प गिलास की सतह पर संघनित हो जाते हैं।
प्रश्न 9.
सर्दियों में प्रातःकाल घास की पत्तियों पर ओस की बूंदें दिखाई देती हैं। इसका क्या कारण है ? क्या यह ओस की बूंदें गर्मियों में भी प्रातःकाल दिखाई देती हैं ?
उत्तर-
सर्दियों में प्रात:काल घास की ओस की बूंदें पत्तियों पर संघनन के कारण दिखाई देती हैं। क्योंकि वायु में उपस्थित जलवाष्प घास की पत्तियाँ ठंडी होने के कारण उन पर संघनित हो जाते हैं।
गर्मियों में यह बूंदें कम दिखाई देती हैं। केवल ठंडी रात वाली सुबह ही यह दिखाई देती हैं।
प्रश्न 10.
जल को पृथ्वी के पृष्ठ पर पुनः वापिस लाने में संघनन प्रक्रम कैसे भूमिका निभाती है ?
अथवा
वर्षा, ओले और हिम कैसे गिरती है ?
उत्तर-
हम जैसे-जैसे पृथ्वी के पृष्ठ से ऊपर जाते हैं, ताप कम हो जाता है। जैसे-जैसे वायु ऊपर उठती जाती है वह ठंडी होती जाती है। पर्याप्त ऊँचाई पर यह वायु इतनी ठंडी हो जाती है कि इसमें उपस्थित जलवाष्प संघनित होकर छोटी-छोटी जल की बूंदों, जिन्हें जलकणिका कहते हैं, में परिवर्तित हो जाता है। ये छोटी जलकणिकाएँ, जो वायु में तैरती रहती हैं, हमें बादलों के रूप में दिखाई देती हैं।
इस प्रकार बनी हुई बहुत सी जलकणिकाएँ आपस में मिलकर एक बड़े माप की जल की बूंदें बनाती हैं। इसमें से कुछ जल की बूंदें इतनी भारी हो जाती हैं कि वे नीचे की ओर गिरने लगती हैं। इन गिरती हुई बूंदों को ही हम वर्षा कहते हैं। विशेष परिस्थितियों में यह ओले या हिम के रूप में भी गिर सकती है।

प्रश्न 11.
जल कैसे वायु में जाता है और पुनः धरती पर कैसे आता है ?
उत्तर-
वाष्पन तथा वाष्पोत्सर्जन द्वारा जल वायु में जाता है। यह जलवाष्प संघनित होकर बादल बनते हैं और वर्षा, ओले तथा हिम के रूप में यह जल पुनः धरती पर वापिस आ जाते हैं।
प्रश्न 12.
वर्षा के जल से भौम जल में कैसे बढ़ौत्तरी होती है ?
उत्तर-
वर्षा का जल झीलों तथा तालाबों को भर देता है। इस जल का कुछ भाग भूमि द्वारा सोख लिया जाता है। मृदा में से जल धीरे-धीरे भूमि के नीचे रिसता रहता है। यह जल हमें भौम जल के रूप में उपलब्ध होता है। कुओं का भरण भौम जल से ही होता हैं।
प्रश्न 13.
किन क्षेत्रों में वर्षा का जल व्यर्थ जाता है अथवा भूमिगत नहीं होता ?
उत्तर-
उन क्षेत्रों में, जहाँ भूमि पर वनस्पति बहुत कम है या बिल्कुल ही नहीं है वहाँ वर्षा का जल शीघ्र बह जाता है। बहुत से ऐसे भी क्षेत्र हैं जहाँ पर अधिकांश ज़मीन सीमेंट के फर्श से ढकी होती है। ऐसी भूमि में जल का रिसाव बहुत कम होता है जिससे अंतत: भौम-जल की उपलब्धता प्रभावित हो जाती है।
प्रश्न 14.
बाढ़ क्या है ? इससे क्या क्षति होती है ?
उत्तर-
बाढ़ – भारी वर्षा से नदियों, झीलों तथा तालाबों का जल स्तर बढ़ सकता है। ऐसा होने पर जल एक बड़े क्षेत्र में फैल कर बाढ़ का कारण बन सकता है। यह खेतों, वनों, गाँवों और शहरों को जलमग्न कर सकता है। हमारे देश में बाढ़ से फसलें, पालतू जानवर, संपदा तथा मानव जीवन की अपार क्षति होती है। बाढ़ के समय जल में रहने वाले जीव भी बह जाते हैं। प्रायः जब बाढ़ का जल उतरता है तो ये जल जीव थल भाग में फंस कर मर जाते हैं।

प्रश्न 15.
सूखा किसे कहते हैं ? सूखे में क्या कठिनाइयाँ आती हैं ?
उत्तर-
सूखा – यदि किसी क्षेत्र में एक वर्ष या उससे भी अधिक समय तक वर्षा न हो तो सूखा पड़ता है। वाष्पन एवं वाष्पोत्सर्जन द्वारा मृदा से लगातार जल की क्षति होती रहती है। मृदा सूख जाती है। उस क्षेत्र के तालाबों और कुँओं में जल का स्तर गिर जाता है और उनमें से कुछ सूख भी जाते हैं। भौम-जल की भी कमी हो जाती है।
सूखे की स्थिति में खाद्यान्न और चारा प्राप्त करना दुर्लभ हो जाता है। आपने हमारे देश या संसार के कुछ भागों में पड़े सूखे के बारे में सुना होगा। सूखे वाले क्षेत्रों में रहने वाले लोगों को कई कठिनाइयों का सामना करना पड़ता है।

प्रश्न 16.
जल की माँग क्यों बढ़ रही है ? जल को कैसे सुरक्षित कर सकते हैं ?
उत्तर-
जल की माँग दिन-प्रतिदिन बढ़ रही है। जनसंख्या वृद्धि के साथ-साथ जल का उपयोग करने वाले लोगों की संख्या भी बढ़ रही है। बहुत-से नगरों में जल भरने के लिए लंबी कतारों का दिखना एक साधारण दृश्य है। खाने की वस्तुओं के उत्पादन और उद्योगों में भी जल की अधिकाधिक मात्रा का प्रयोग हो रहा है। इन्हीं कारणों से संसार के बहुत-से भागों में जल की कमी हो गयी है।
जल का संरक्षण-
- जल के संरक्षण के लिए आवश्यक है कि जल का विवेकपूर्ण उपयोग किया जाए।
- हमें जल को सावधानी से प्रयोग करना चाहिए।
- हमें जल व्यर्थ नहीं करना चाहिए।
प्रश्न 17.
वर्षा के जल का संग्रहण कैसे करते हैं ?
उत्तर-
वर्षा के जल को एकत्र करना और उसका भंडारण करके बाद में प्रयोग करना, जल की उपलब्धता में वृद्धि करने का एक उपाय है। इस उपाय द्वारा वर्षा का जल एकत्र करने को वर्षा जल संग्रहण कहते हैं। वर्षा जल संग्रहण का मूल मंत्र यह है कि “जल जहाँ गिरे वहीं एकत्र कीजिए।”
7. निबंधात्मक प्रश्न
प्रश्न 1.
जल के भिन्न-भिन्न स्रोतों की व्याख्या करो।
उत्तर-
जल का स्रोत – जल भिन्न-भिन्न स्रोतों से प्राप्त होता है। जल के मुख्य स्रोत हैं-
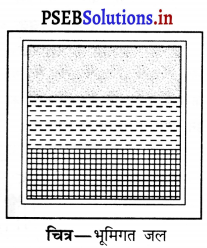
(i) भूमिगत जल (Underground Water)
(ii) सतह जल (Surface Water)
(i) भूमिगत जल (Underground Water) – मानसून मौसम के दौरान वर्षा का कुछ जल मिट्टी के नीचे चला जाता है। यह एक विशेष स्तर पर जाकर एकत्रित हो जाता है। धरती के नीचे छिद्रयुक्त चट्टानों (Impervious Rocks) से ऊपर, जल के इस भंडार को भूमिगत जल कहते हैं। देखें चित्र।
भूमिगत जल में निलंबित (Suspended) अशुद्धियां नहीं होती। भूमिगत जल मुख्य रूप से दो प्रकार का होता है-

(a) कुएँ का जल (Well water)
(b) चश्मे का जल (Spring water)
(a) कुएँ का जल – तहदार चट्टानों के ऊपर एकत्रित हुए जल भंडार को कुएँ कहते हैं तथा इसमें उपस्थित जल को कुएँ का जल कहते हैं। कुएँ के जल में कई घुलनशील अशुद्धियाँ मिल जाती हैं।
आजकल शहरों तथा गाँव में ट्यूबवैल में बोर करके हम कुओं की अपेक्षा अधिक जल निकाल सकते हैं।
(b) चश्मों का जल-वर्षा का जल तहदार चट्टानों से ऊपर भूमिगत के
रूप में एकत्रित हो जाता है। धरती के नीचे कमज़ोर भाग पर दाब डालकर कई
बार यह जल चश्मा बन कर धरती की सतह से बाहर फूट पड़ता है। जल की ऐसी धारा को चश्मा का जल कहते हैं। चश्मे के जल में आमतौर पर खनिज तथा कई तरह के लवण घुले होते हैं। यह पानी निलंबित अशुद्धियों से रहित होता है। कभी-कभी खनिज चश्मे के जल को विशेष रोगनाशक (Curable) गुण प्रदान करते हैं तथा औषधि के रूप में प्रयुक्त होता है।
(ii) सतह जल (Surface Water) – धरती की सतह के ऊपर स्थित जल को सतह जल कहा जाता है। यह जल तीन प्रकार का होता है-
(a) वर्षा का जल (Rain Water)
(b) नदी तथा झीलों का जल (River and Lake Water)
(c) समुद्रीय जल (Sea Water)।
(a) वर्षा का जल – प्राकृतिक जल का यह सबसे अधिक शुद्ध रूप है। परंतु वर्षा के कुछ छराटों से पूर्व वातावरण में से धूल, रोगाणु, कीटाणु तथा कई तरह की घुलनशील गैसें मिल जाती हैं।
(b) नदी तथा झीलों का जल – नदियाँ भी जल का एक मुख्य स्रोत हैं। कुछ नदियों में सारा वर्ष ही जल बहता रहता है। परंतु कुछ नदियों का जल गर्मियों में बहुत कम हो जाता है या वे सूख जाती हैं। यह जल पहाड़ियों से बहता हुआ नदियों में गिरता है। इस जल में कीटाणु, गारा, मिट्टी, रेत तथा अन्य कई घुलनशील लवण होते हैं।
(c) समुद्रीय जल-नदियाँ अंत में समुद्र में गिरती हैं। इसलिए समुद्र प्राकृतिक जल का सबसे बड़ा भंडार है। इसके जल में नदियों के जल वाली सभी अशुद्धियाँ शामिल होती हैं। इससे बड़ी मात्रा में लवण घुले होने के कारण समुद्र का जल खारा होता है।
समुद्रीय जल पीने तथा सिंचाई करने योग्य नहीं होता।
प्रश्न 2.
प्रकृति में जलचक्र का संक्षेप में वर्णन कीजिए।
उत्तर-
प्रकृति में जलचक्र – सूर्य की गर्मी के कारण महासागरों की सतह से जल वाष्पित होकर जल-वाष्पों के रूप में वायु में चला जाता है। यह जलवाष्प संघनित होकर बादलों में परिवर्तित हो जाते हैं और इन बादलों से वर्षा के रूप में बरसते हैं। यह वर्षा का पानी नदियों, झीलों, तालाबों और कुओं में आता है। इस प्रकार महासागरों से पानी इन पानी के स्रोतों में आता है।
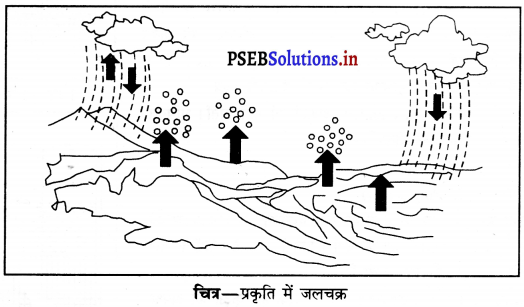
वर्षा तथा हिम के रूप में भूमि पर गिरा अधिकांश जल, अंततः महासागरों में वापिस चला जाता है। यह विभिन्न ढंगों से होता है।
पर्वतों पर हिम पिघलकर जल बन जाती है। यह जल पहाड़ों से झरनों तथा नदियों के रूप में नीचे गिरता है। कुछ जल जो वर्षा के रूप में भूमि पर गिरता है, वह भी नदियों और झरनों के रूप में बह जाता है। अधिकांश नदियाँ भूमि पर लंबी दूरी तय करती हैं और अंततः किसी समुद्र या महासागर में गिर जाती हैं तथापि कुछ नदियों का जल झीलों में बह जाता है।
वर्षा का जल भी झीलों तथा तालाबों को भर देता है। वर्षा के जल का कुछ भाग भूमि द्वारा सोख लिया जाता है
और मृदा में विलुप्त हुआ प्रतीत होता है। इस जल का कुछ भाग वाष्पन तथा वाष्पोत्सर्जन द्वारा वापिस वायु में चला जाता है। शेष जल धीरे-धीरे भूमि के नीचे रिसता रहता है। इस जल का अधिकांश भाग हमें भौम-जल के रूप में उपलब्ध हो जाता है।

प्रश्न 3.
वर्षा जल संग्रहण की कौन-सी तकनीकें हैं ? उनका उल्लेख कीजिए।
उत्तर-

वर्षा जल संग्रहण की दो तकनीकें हैं-
(i) छत के ऊपर वर्षा जल संग्रहण जिन्हें इस प्रणाली में भवनों की छत पर एकत्रित वर्षा के जल को भंडारण टैंक में पाइपों द्वारा पहुँचाया जाता है। इस जल में, छत पर उपस्थित मिट्टी के कण हो सकते हैं जिन्हें उपयोग करने से पहले निस्यंदित करना आवश्यक होता है। इस जल को भंडारण टैंक में एकत्रित करने के स्थान पर सीधे ही पाइपों द्वारा ज़मीन में बने किसी खड्डे तक ले जाया जा सकता है। जहाँ से यह मिट्टी में रिसाव द्वारा भौमजल की पुनः पूर्ति करेगा।
(ii) अन्य विकल्प के तौर पर सड़क के किनारे बनी नालियों द्वारा एकत्रित वर्षा का जल भूमि में सीधे पहुँचने दिया जाए।

![]()
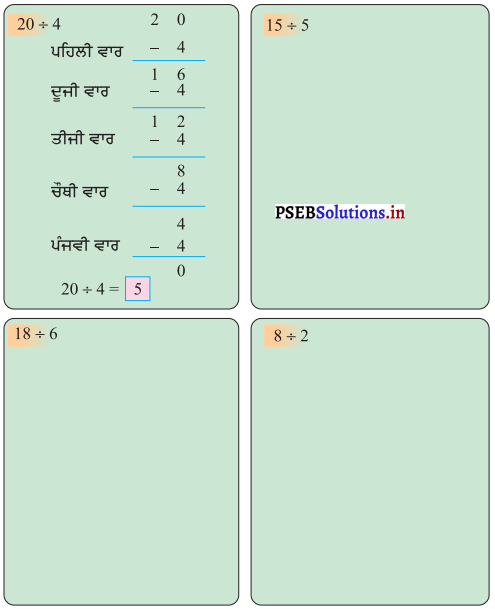
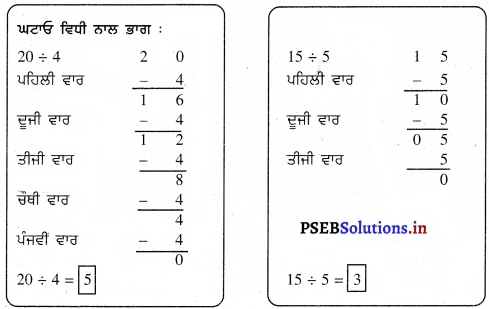
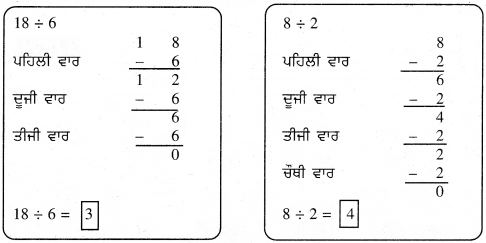
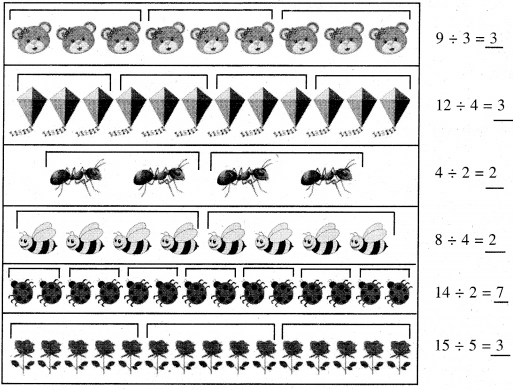
![]()

![]()
![]()
![]()


![]()





![]()
![]()

![]()

![]()
![]()



![]()
![]()



![]()
![]()
![]()
![]() = 1
= 1![]() ÷ 42 = 0
÷ 42 = 0![]()
![]()

![]()
![]()