Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 10 ਪ੍ਰਯੋਗਿਕ ਰੇਖਾ ਗਣਿਤ Ex 10.1 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 7 Maths Chapter 10 ਪ੍ਰਯੋਗਿਕ ਰੇਖਾ ਗਣਿਤ Exercise 10.1
ਪ੍ਰਸ਼ਨ 1.
ਇੱਕ ਰੇਖਾ l ਲਓ, ਇਸਦੇ ਬਾਹਰ ਸਥਿਤ ਕੋਈ ਬਿੰਦੂ p ਲਉ, ਸਿਰਫ਼ ਫੁੱਟੇ ਅਤੇ ਪਰਕਾਰ ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਵਿਚੋਂ ਲੰਘਦੀ ਹੋਈ ) ਦੇ ਸਮਾਂਤਰ ਇੱਕ ਰੇਖਾ ਖਿੱਚੋ ।
ਹੱਲ :
ਰਚਨਾ ਦੇ ਪਗ :
ਪਗ 1. ਸਹੀ ਲੰਬਾਈ ਦੀ ਇੱਕ ਰੇਖਾ ਖਿੱਚੋ ਅਤੇ ਇਸ ਦੇ ਬਾਹਰ ਬਿੰਦੂ ‘p` ਲਵੋ । [ਚਿੱਤਰ (i) ਦੇਖੋ]

ਪਗ 2. ਰੇਖਾ 1 ਉੱਪਰ ਕੋਈ ਬਿੰਦੂ ‘ੴ’ ਲਓ ਅਤੇ ੧ ਨੂੰ p ਨਾਲ ਮਿਲਾਓ [ਚਿੱਤਰ (ii) ਦੇਖੋ]
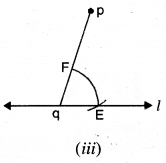
ਪਗ 3. q ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ ਅਤੇ ਕੋਈ ਸੁਵਿਧਾ | ਅਨੁਸਾਰ ਅਰਧ ਵਿਆਸ ਲੈ ਕੇ ਇੱਕ ਚਾਪ ਲਗਾਉ ਜੋ ਨੂੰ E ਉੱਤੇ ਅਤੇ pq ਨੂੰ F ਉੱਤੇ ਕੱਟੇ । [ਚਿੱਤਰ (iii) ਦੇਖੋ]
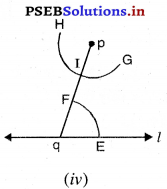
ਪਗ 4. ਹੁਣ ਬਿੰਦੂ p ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ ਅਤੇ ਪਗ 3 ਵਾਲਾ ਹੀ ਅਰਧ ਵਿਆਸ ਲੈ ਕੇ pq ਨੂੰ ਕੱਟਦੇ ਹੋਏ ਚਾਪ GH ਖਿੱਚੋ ਜੋ pq ਨੂੰ 1 ਉੱਤੇ + ਕੱਟੇ ।[ਚਿੱਤਰ (iv) ਦੇਖੋ]
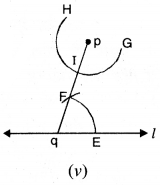
ਪਗ 5. ਪਰਕਾਰ ਦੇ ਤਿੱਖੇ ਸਿਰੇ ਨੂੰ E ਉੱਤੇ ਰੱਖੋ ਅਤੇ ਇਸ ਨੂੰ ਖੋਲ੍ਹ ਕੇ ਇਸ ਤਰ੍ਹਾਂ ਰੱਖੋ ਕਿ ਪੈਨਸਿਲ ਦੀ ਨੋਕ F ਉੱਪਰ ਰਹੇ । [ਚਿੱਤਰ (v) ਦੇਖੋ].
ਪਗ 6. Iਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ ਅਤੇ ਪਰਕਾਰ ਦਾ ਅਰਧ · ਵਿਆਸ ਪਗ 5 ਵਾਲਾ ਹੀ ਰੱਖਦੇ ਹੋਏ ਇੱਕ ਚਾਪ ਲਗਾਓ ਜੋ ਚਾਪ GH ਨੂੰ ! ਉੱਪਰ ਕੱਟੇ । [ਚਿੱਤਰ (vi) ਦੇਖੋ.
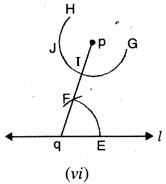
ਪਗ 7. ਹੁਣ p ਅਤੇ ਹ ਨੂੰ ਮਿਲਾ ਕੇ ਰੇਖਾ ‘ਖਿੱਚੋ । [ਚਿੱਤਰ (vii) ਦੇਖੋ]
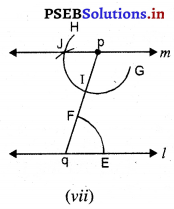
ਨੋਟ : ਧਿਆਨ ਦਿਓ ਕਿ ∠Jpg ਅਤੇ ∠pqE ਅੰਦਰਲੇ ਇਕਾਂਤਰ ਕੋਣ ਹਨ ਅਤੇ ∠pqE = ∠qpJ
∴ m || l.
![]()
ਪ੍ਰਸ਼ਨ 2.
ਰੇਖਾ ਤੋਂ 3.5 cm ਦੀ ਦੂਰੀ ਤੇ ਇੱਕ ਸਮਾਂਤਰ ਰੇਖਾ ਖਿੱਚੋ ।
ਹੱਲ :
ਰਚਨਾ ਦੇ ਪਗ :
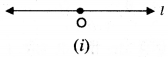
ਪਗ 1. ਇੱਕ ਰੇਖਾ ‘l’ ਅਤੇ ਇਸ ਦੇ ਉੱਪਰ ਬਿੰਦੂ O ਲਵੋ । [ਚਿੱਤਰ (1) ਦੇਖੋ]
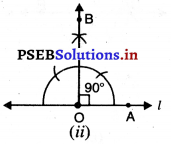
ਪਗ 2.0 ਤੇ ∠AOB = 90° ਖਿੱਚੋ ਚਿੱਤਰ (ii) ਦੇਖੋ]
ਪਗ 3. ਪਰਕਾਰ ਦੇ ਤਿੱਖੇ ਸਿਰੇ ਨੂੰ ‘0’ (zero) ਜ਼ੀਰੋ ਤੇ ਰੱਖੋ, ਫੁੱਟੇ ਤੇ ਦਿਖਾਓ ਅਤੇ ਇਸ ਨੂੰ ਖੋਲ੍ਹ ਕੇ ਇਸ ਤਰ੍ਹਾਂ ਰੱਖੋ ਕਿ ਪੈਨਸਿਲ ਦੀ ਨੋਕ 3.5 cm ਤੇ ਰਹੇ । [ਚਿੱਤਰ (iii) ਦੇਖੋ]
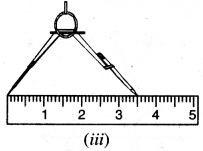
ਪਗ 4: 0 ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ ਪਰਕਾਰ ਨੂੰ ਪਗ 3 ਵਾਲਾ ਹੀ ਰੱਖਦੇ ਹੋਏ ਇੱਕ . ਚਾਪ ਲਗਾਓ ਜੋ ਕਿਰਨ OB ਨੂੰ X ਉੱਤੇ ਕੱਟੇ । [ਚਿੱਤਰ (iv) ਦੇਖੋ]
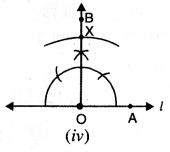
ਪਗ 5. X ਉੱਤੇ ਇੱਕ ਰੇਖਾ m’, OB ਦੇ ਲੰਬਕਾਰ . ਖਿੱਚੋ । ਦੂਜੇ ਸ਼ਬਦਾਂ ਵਿਚ ∠CXO = 90° [ਚਿੱਤਰ (v) ਦੇਖੋ]
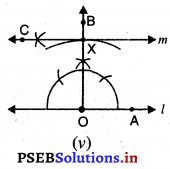
ਇਸ ਤਰੀਕੇ ਨਾਲ ਆ ਰੇਖਾ 1 ਦੇ ਸਮਾਂਤਰ ਹੈ ।
ਧਿਆਨ ਦਿਓ : ∠AOX ਅਤੇ ∠CXO ਅੰਦਰਲੇ | ਇਕਾਂਤਰ ਕੋਣ ਹਨ ਅਤੇ ∠AOX = ∠ (ਹਰੇਕ = 90).
∴ m || l.
ਨੋਟ : ਅਸੀਂ ਕਾਟਵੀਂ ਰੇਖਾ OX ਅਤੇ ਸਮਾਂਤਰ ਰੇਖਾਵਾਂ 1 ਅਤੇ ਅ ਦੇ ਮਾਮਲੇ ਵਿਚ ਤਿੰਨਾਂ ਵਿਚੋਂ ਕਿਸੇ ਵੀ ਵਿਸ਼ੇਸ਼ਤਾ ਦਾ ਇਸਤੇਮਾਲ ਕਰ ਸਕਦੇ ਹਾਂ ।
![]()
ਪ੍ਰਸ਼ਨ 3.
ਮੰਨ ਲਉ l ਇੱਕ ਰੇਖਾ ਹੈ ਅਤੇ P ਇੱਕ ਬਿੰਦ ਹੈ ਜੋ l ਉੱਪਰ ਸਥਿਤ ਨਹੀਂ ਹੈ । P ਤੋਂ ਹੋ ਕੇ l ਦੇ ਸਮਾਂਤਰ ਇੱਕ ਰੇਖਾ m ਖਿੱਚੋ | ਹੁਣ P ਨੂੰ l ਤੇ ਕਿਸੇ ਬਿੰਦੁ Q ਨਾਲ ਜੋੜੋ । m ਉੱਪਰ ਕੋਈ ਹੋਰ ਬਿੰਦੂ R ਚੁਣੋ । R ਤੋਂ ਹੋ ਕੇ, PQ ਦੇ ਸਮਾਂਤਰ ਇੱਕ ਰੇਖਾ ਖਿੱਚੋ । ਮੰਨ ਲਉ ਇਹ ਰੇਖਾ, ਰੇਖਾ l ਦੇ ਬਿੰਦੂ S ਉੱਪਰ ਮਿਲਦੀ ਹੈ । ਸਮਾਂਤਰ ਰੇਖਾਂਵਾ ਦੇ ਇਹਨਾਂ ਦੋਹਾਂ ਸਮੂਹਾਂ ਤੋਂ ਕਿਹੜੀ ਆਕ੍ਰਿਤੀ ਬਣਦੀ ਹੈ ?
ਹੱਲ :
ਰਚਨਾ ਦੇ ਪਗ :
ਪਗ 1. ਇੱਕ ਰੇਖਾ ‘l’ ਅਤੇ ਇਸ ਦੇ ਬਾਹਰ ਬਿੰਦੁ ‘P ਲਓ । ਚਿੱਤਰ (i) ਦੇਖੋ]
ਪਗ 2. ਰੇਖਾ l ਉੱਤੇ ਕੋਈ ਬਿੰਦੂ A ਲਵੋ ਅਤੇ P ਨੂੰ A ਨਾਲ ਮਿਲਾਓ । [ਚਿੱਤਰ (ii) ਦੇਖੋ]
ਪਗ 3. A ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ ਅਤੇ ਸੁਵਿਧਾ ਅਨੁਸਾਰ ਅਰਧ ਵਿਆਸ ਲੈ ਕੇ l ਨੂੰ B ਉੱਪਰ ਅਤੇ AP ਨੂੰ C ਉੱਪਰ ਕੱਟਦਾ ਹੋਇਆ ਇੱਕ ਚਾਪ ਖਿੱਚੋ । [ਚਿੱਤਰ (iii) ਦੇਖੋ]
ਪਗ 4. ਹੁਣ P ਬਿੰਦੂ ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ ਅਤੇ ਪਗ 3 | ਵਾਲਾ ਹੀ ਅਰਧ ਵਿਆਸ ਲੈ ਕੇ ਇੱਕ ਚਾਪ DE, PA ਨੂੰ ਕੱਟਦੇ ਹੋਏ F ਉੱਤੇ ਖਿੱਚੋ । [ਚਿੱਤਰ (iv) ਦੇਖੋ].
ਪਗ 5. ਪਰਕਾਰ ਦੇ ਤਿੱਖੇ ਸਿਰੇ ਨੂੰ B ਉੱਪਰ ਰੱਖੋ ਅਤੇ ਇਸ ਨੂੰ ਖੋਲ੍ਹ ਕੇ ਇਸ ਤਰ੍ਹਾਂ ਰੱਖੋ ਕਿ ਪੈਨਸਿਲ ਦੀ ਨੋਕ C ਉੱਪਰ ਰਹੇ । [ਚਿੱਤਰ (v) ਦੇਖੋ].
ਪਗ 6. F ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ ਅਤੇ ਅਰਧ ਵਿਆਸ ਪਗ 5 ਵਾਲਾ ਹੀ ਰੱਖਦੇ ਹੋਏ ਇੱਕ ਚਾਪ ਲਗਾਓ ਜੋ DE ਨੂੰ G ਉੱਪਰ ਕੱਟੇ । [ਚਿੱਤਰ (vi) ਦੇਖੋ].
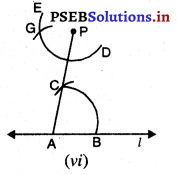
ਪਗ 7. ਹੁਣ PG ਨੂੰ ਮਿਲਾ ਕੇ ਰੇਖਾ m’ ਖਿੱਚੋ । ਚਿੱਤਰ (vii) ਦੇਖੋ].
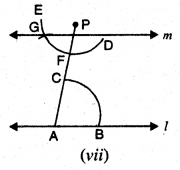
ਧਿਆਨ ਦਿਓ ਕਿ ∠PAR ਅਤੇ ∠APG ਅੰਦਰਲੇ ਇਕਾਂਤਰ ਕੋਣ ਹਨ ਅਤੇ ∠PAB = ∠APG
∴ m || l.
ਪਗ 8. l ਉੱਤੇ ਬਿੰਦੂ Q ਲਓ | PQ ਨੂੰ ਮਿਲਾਓ । [ਚਿੱਤਰ (viii) ਦੇਖੋ]
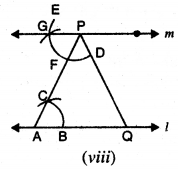
ਪਗ 9. m ਉੱਤੇ ਹੋਰ ਬਿੰਦੂ R ਲਓ । [ਚਿੱਤਰ (ix) ਦੇਖੋ]
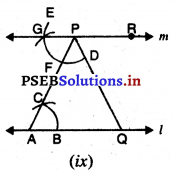
ਪਗ 10. P ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ ਉਹੀ ਅਰਧ ਵਿਆਸ ਰੱਖਦੇ ਹੋਏ ਇੱਕ ਚਾਪ ਲਗਾਉ ਜੋ ਰੇਖਾ m ਨੂੰ H ਉੱਤੇ ਅਤੇ | PQ ਨੂੰ 1 ਉੱਤੇ ਕੱਟੇ । [ਚਿੱਤਰ (x) ਦੇਖੋ]
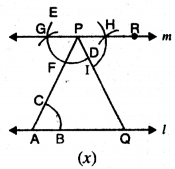
ਪਗ 11. ਹੁਣ R ਬਿੰਦੂ ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ ਅਤੇ ਪਗ 10 ਵਾਲਾ ਹੀ ਅਰਧ ਵਿਆਸ ਲੈ ਕੇ ਚਾਪ JK ਬਣਾਓ ।[ਚਿੱਤਰ (xi) ਦੇਖੋ]
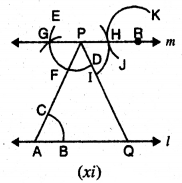
ਪਗ 12. ਪਰਕਾਰ ਦੇ ਤਿੱਖੇ ਸਿਰੇ ਨੂੰ H ਉੱਤੇ ਰੱਖੋ ਅਤੇ | ਇਸ ਤਰ੍ਹਾਂ ਖੋਲ੍ਹ ਕੇ ਰੱਖੋ ਕਿ ਪੈਨਸਿਲ ਦੀ ਨੋਕ 1 ਉੱਪਰ | ਰਹੇ । [ਚਿੱਤਰ (xii) ਦੇਖੋ]
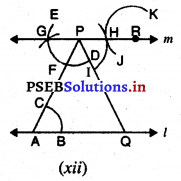
ਪਗ 13. R ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ ਅਤੇ ਪਰਕਾਰ ਨੂੰ ਪਗ 12 ਵਾਂਗ ਹੀ ਖੋਲ੍ਹਦੇ ਹੋਏ, ਇੱਕ ਚਾਪ ਲਗਾਓ ਜੋ ਚਾਪ JK ਨੂੰ Lਉੱਤੇ ਕੱਟੇ । [ਚਿੱਤਰ (xiii) ਦੇਖੋ]
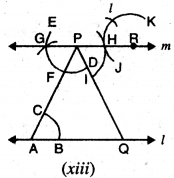
ਪਗ 14. ਹੁਣ PQ ਦੇ ਸਮਾਂਤਰ ਰੇਖਾ ਖਿੱਚਦੇ ਹੋਏ RL ਨੂੰ ਮਿਲਾਓ । ਮੰਨ ਲਉ ਇਹ ਰੇਖਾ ‘l’ ਨੂੰ S ਤੇ ਮਿਲਦੀ ਹੈ । [ਚਿੱਤਰ (xiv) ਦੇਖੋ]
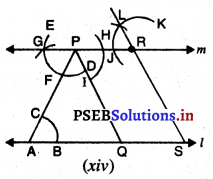
ਧਿਆਨ ਦਿਓ : ∠RPQ ਅਤੇ ∠LRP ਅੰਦਰਲੇ ਇਕਾਂਤਰ ਕੋਣ ਹਨ ।
ਅਤੇ ∠RPQ = ∠LRP
∴ RS || PQ
ਹੁਣ ਸਾਡੇ ਕੋਲ ਹੈ ।
PR || QS
[∵ m || l ਅਤੇ PR, m ਦਾ ਹਿੱਸਾ ਹੈ ਅਤੇ QS, ਰੇਖਾ l ਦਾ ਹਿੱਸਾ ਹੈ। ]
ਅਤੇ PQ ॥ RS
∴ PQSR ਇੱਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 4.
(i) ਕਿਸੇ ਰੇਖਾ ਦੇ ਬਾਹਰੀ ਬਿੰਦੂ ਤੋਂ ਉਸ ਰੇਖਾ ਦੇ ਸਮਾਂਤਰ ਕਿੰਨੀਆਂ ਰੇਖਾਵਾਂ ਖਿੱਚੀਆਂ ਜਾ ਸਕਦੀਆਂ ਹਨ ?
(a) 0
(b) 2
(c) 1
(d) 3
ਉੱਤਰ:
(c) 1
(ii) ਹੇਠ ਲਿਖਿਆਂ ਵਿਚੋਂ ਕਿਸ ਦੀ ਵਰਤੋਂ ਕਰ ਕੇ ਇੱਕ ਰੇਖਾ ਦੇ ਸਮਾਂਤਰ ਰੇਖਾ ਖਿੱਚੀ ਜਾ ਸਕਦੀ ਹੈ ।
(a) ਕੋਣ ਮਾਪਕ
(b) ਫੁੱਟਾ
(c) ਪ੍ਰਕਾਰ
(d) ਫੁੱਟਾ ਅਤੇ ਪ੍ਰਕਾਰ ।
ਉੱਤਰ:
(d) ਫੁੱਟਾ ਅਤੇ ਪ੍ਰਕਾਰ ।
