Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 11 Perimeter and Area Ex 11.1 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 7 Maths Chapter 11 Perimeter and Area Ex 11.1
1. Find the perimeter and the area of a rectangle having :
(i) Length = 28 cm, Breadth = 15 cm
(ii) Length = 9.4 cm Breadth = 2.5 cm
Solution:
(i) Given length of rectangle = 28 cm
Breadth of rectangle = 15 cm
Perimeter of rectangle = 2 [length + Breadth]
= 2 [28 + 15]
= 2 × 43
= 86 cm
Area of rectangle = length × Breadth
= 28 × 15
= 420 cm2
(ii) Perimeter of rectangle = 2 [9.4 + 2.5]
= 2 × 11.9
= 23.8 cm
Area of rectangle = 9.4 × 2.5
= 23.5 cm2
2. Find the perimeter and the area of a square whose side measures
(i) 29 cm
(ii) 8.3 cm
Solution:
(i) Given side of square = 29 cm
Perimeter of square = 4 × side
= 4 × 29
= 116 cm
Area of square = (side)2
= (29)2
= 841 cm2
(ii) Perimeter of square = 4 × 8.3
= 33.2 cm
Area of square = 8.3 × 8.3
= 68.89 cm2
![]()
3. The perimeter of a square park is 148 m. Find its area.
Solution:
Given the perimeter of square park = 148 m
Side of the square park = \(\frac{perimeter}{4}\)
= \(\frac {148}{4}\)
Area of the square park = (side)2
= (37)2
= 1369 m2
4. The area of a rectangle is 580 cm2. Its length is 29 cm. Find its breadth and also, the perimeter.
Solution:
Given area of rectangle = 580 cm2
Length of the rectangle = 29 cm
Let breadth of the rectangle = b cm
Area of the rectangle = length × breadth
580 = 29 × b
\(\frac {580}{29}\) = b
b = 20 cm
Perimeter of rectangle = 2 [length + breadth]
= 2 [29 + 20]
= 2 × 49
= 98 cm
5. A wire is in the shape of a rectangle. Its length is 48 cm and breadth is 32 cm. If the same wire is rebent into the shape of a square, what will be the measure of each side. Also, find which shape encloses more area and by how much ?
Solution:
Given length of the rectangle = 48 cm
Breadth of the rectangle = 32 cm
Perimeter of the rectangle = 2 [length + breadth]
= 2 [48 + 32]
= 2 × 80
= 160 cm
Let side of square = a cm
Perimeter of the square = 4 × a
Since wire is rebent into the shape of a square
Perimeter of square = Perimeter of rectangle
4 a = 160
Therefore, a = \(\frac {160}{4}\)
= 40 cm
Area of square = (side)2
= 40 × 40
= 1600 cm2
Area of rectangle = length × breadth
= 48 × 32
= 1536 cm2
∴ Square encloses more area by 64 cm2
![]()
6. The area of a square park is the same as that of a rectangular park. If the side of the square park is 75 m and the length of the rectangular park is 125 m, find the breadth of the rectangular park. Also, find the perimeter of rectangular park.
Solution:
Given side of square park = 75 m
Area of square park = (75)2
= 75 × 75
= 5625 m2
Length of rectangular park = 125 m
Let breadth of rectangular park = b m
Area of rectangular park = length × breadth
= 125 × b m2
Given that
Area of rectangular park = Area of square park
125 × b = 5625
= 45 m
Perimeter of rectangular park = 2 [length + breadth]
= 2 [125 + 45]
= 2 × 170
= 340 m
7. A door of length 2.5 m and breadth 1.5 m is fitted in a wall. The length of wall, is 9 m and breadth is 6 m. Find the cost of painting the wall, if the rate of painting the wall is ₹ 30 per m2.
Solution:
Length of door = 2.5 m
Breadth of door = 1.5 m
Area of door = length × breadth
= 2.5 × 1.5
= 3.75 m2
Area of wall = 9 × 6
= 54 m2
Area of wall painting = Area of wall including door – Area of door
= 54 – 3.75
= 50.25 m2
Cost of painting 1 m2 of wall = ₹ 30
Cost of painting 50.25 m2 of wall = ₹ 50.25 × 30
= ₹ 1507.50
![]()
8. A door of dimensions 3 m × 2 m and a window of dimensions 2.5 m × 1.5 m is fitted in a wall. The length of the wall is 7.8 m and breadth is 3.9 m. Find the cost of painting the wall, if the rate of painting the wall is ₹ 25 per m2.
Solution:
Area of door = 3 × 2 = 6 m2
Area of window = 2.5 m × 1.5 m
= 3.75 m2
Area of wall = 7.8 m × 3.9 m
= 30.42 m2
Area of painting the wall = Area of wall – Area of door – Area of window
= 30.42 – 6 – 3.75
= 20.67 m2
Cost of painting the wall = ₹ 25 × 20.67
= ₹ 516.75
9. Find the area and the perimeter of the following figures.
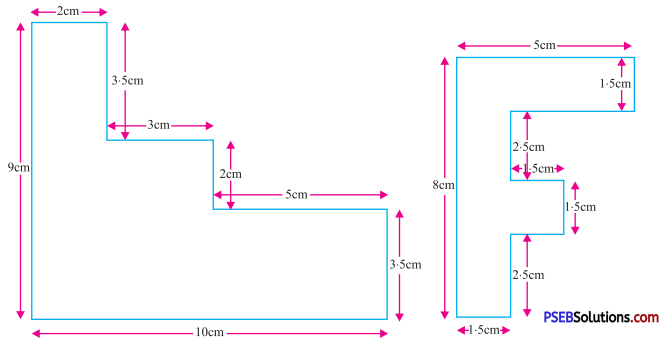
Solution:
(i) Perimeter of the given figure
= AB + BC + CD + DE + EF + FG + GH + HA
= 2 + 3.5 + 3 + 2 + 5 + 3.5 + 10 + 9
= 38 cm2
Area of the figure = Area of rectangle ABCJ + Area of rectangle JDEI + Area of rectangle IFGH
= 2 × 3.5 + 5 × 2 + 10 × 3.5
= 7 + 10 + 35
= 52 cm2
(ii) Perimeter of the given figure
= 8cm + 5 cm + 1.5 cm + 2.5 cm + 2.5 cm + 1.5 cm + 1.5 cm + 1.5 cm + 2.5 cm + 1.5 cm
= 29 cm
Area of the given figure = Area of rectangle I + Area of rectangle II + Area of rectangle III
= 8 cm × 1.5 cm + 3.5 cm × 1.5 cm + 1.5 cm × 1.5 cm
= 12 cm2 + 5.25 cm2 + 2.25 cm
= 19.5 cm2
![]()
10. Multiple Choice Questions :
Question (i).
What is the area of a rectangle of dimensions 12 cm × 10 cm ?
(a) 44 cm2
(b) 120 cm2
(c) 1200 cm2
(d) 1440 cm2
Answer:
(b) 120 cm2
Question (ii).
Find the breadth of a rectangle whose length is 12 cm and perimeter is 36 cm.
(a) 6 cm
(b) 3 cm
(c) 9 cm
(d) 12 cm
Answer:
(a) 6 cm
Question (iii).
If each side of a square is 1 m then its area is ?
(a) 10 cm2
(b) 100 cm2
(c) 1000 cm2
(d) 10000 cm2
Answer:
(d) 10000 cm2
Question (iv).
Find the area of a square whose perimeter is 96 cm.
(a) 576 cm2
(b) 626 cm2
(c) 726 cm2
(d) 748 cm2.
Answer:
(a) 576 cm2
Question (v).
The area of a rectangular sheet is 500 cm2. If the length of the sheet is 25 cm, what is its breadth ?
(a) 30 cm
(b) 40 cm
(c) 20 cm
(d) 25 cm.
Answer:
(c) 20 cm
Question (vi).
What happens to the area of a square, if its side is doubled ?
(a) The area becomes 4 times, the area of original square.
(b) The area becomes \(\frac {1}{4}\) times, the area of original square.
(c) The area becomes 16 times, the area of original square.
(d) The area becomes \(\frac {1}{6}\) times, 6 the area of original square.
Answer:
(a) The area becomes 4 times, the area of original square.
