PSEB 7th Class Maths Solutions Chapter 11 Perimeter and Area Ex 11.2

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 11 Perimeter and Area Ex 11.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 11 Perimeter and Area Ex 11.2

1. Estimate the area of the following figures by counting unit squares.

Question (i).

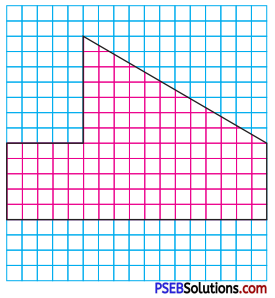
Solution:
In the given figure, number of squares covered completely = 135
Area of a square = 1 sq. unit
Area of (135 square) figure = 135 sq. units, (approx.)

Question (ii).

Solution:
In the given figure number of square covered completely = 114
Area of one square = 1 unit
∴ Area of 114 squares = 114 sq units approx
Thus area of given figure = 114 sq units approx.

2. In the following figures find the area of 

Question (i).
ΔABC

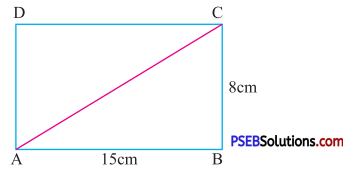
Solution:
Given length of rectangle = 15 cm
Breadth of rectangle = 8 cm
The diagonal AC divides the rectangle into two triangles ΔABC and ΔADC
So, area of ΔABC = \(\frac {1}{2}\) × Area of rectangle ABCD
= \(\frac {1}{2}\) × length × breadth
= \(\frac {1}{2}\) × 15 × 8
= 60 cm²

Question (ii).
ΔCOD

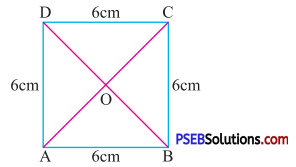
Solution:
Given side of square = 6 cm
The diagonals AC and BD divides the square into four equal posses (triangles)
So, area of ΔCOD = \(\frac {1}{4}\) × Area of square
= \(\frac {1}{4}\) × 6 × 6
= 9 cm²

3. Find the area of following parallelograms.

Question (i).

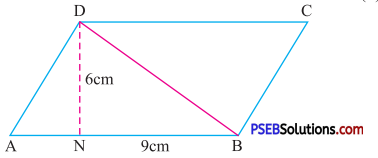
Solution:
Given base of parallelogram = 9 cm
Height of parallelogram = 6 cm
Area of parallelogram = Base × height
= 9 × 6
= 54 cm²

Question (ii).

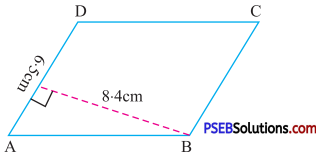
Solution:
Given base of parallelogram = 6.5 cm
Height of parallelogram= 8.4 cm
Area of parallelogram = Base × height
= 6.5 × 8.4
= 54.6 cm²

4. Find the value of x in the following parallelograms.

Question (i).

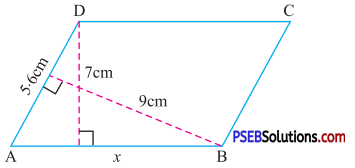
Solution:
Given base (AD) of parallelogram = 5.6 cm
Corresponding height of parallelogram = 9 cm
Area of parallelogram = 5.6 × 9 cm² ….(1)
Also in the paralleogram, base (AB) = x
Corresponding height of parallelogram = 7 cm
Area of parallelogram will be = x × 7 ….(2)
From (1) and (2), we get
x × 7 = 5.6 × 9
x = \(\frac{5.6 \times 9}{7}\)
= 7.2

Question (ii).

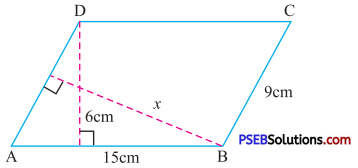
Solution:
Given base (AB) of parallelogram = 15 cm
Corresponding height = 6 cm
Area of parallelogram =15 × 6 cm² ….(1)
Also Base (AD || BC) of parallelogram = 9 cm
Corresponding height = x
So area of parallelogram = 9 × x ….(2)
From (1) and (2)
9 × x = 15 × 6
x = \(\frac{15 \times 6}{9}\)
= 10 cm.

5. The adjacent sides of a parallelogram are 28 cm and 45 cm and the altitude on longer side is 18 cm. Find the area of parallelogram.
Solution:
Given base of the parallelogram = 45 cm
Corresponding height = 18 cm
Area of parallelogram = Base × Height
= 45 × 18
= 810 cm2

6. ABCD is a parallelogram given in figure. DN and DM are the altitudes on side AB and CB respectively. If area of the parallelogram is 1225 cm², AB = 35 cm and CB = 25 cm, find DN and DM.

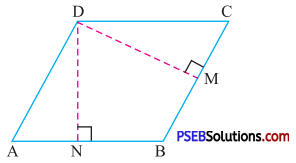
Solution:
In the given parallelogram ABCD
Base (AB) = 35 cm
Let height (DN) = x cm
So area of parallelogram = 35 × x cm²
But given area of parallelogram (ABCD) = 1225 cm²
Therefore 35x = 1225
x = \(\frac {1225}{35}\)
= 35 cm
Similarly, for base (BC) and height (DM)
1225 = BC × DM
\(\frac{1225}{\mathrm{BC}}\) = DM
or DM = \(\frac {1225}{25}\)
= 49 cm.

7. Find the area of the following triangles.

Question (i).

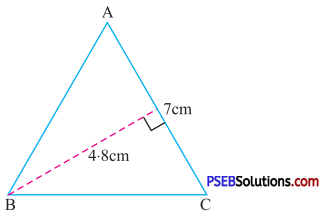
Solution:
Given base of triangle = 7 cm
Height of triangle = 4.8 cm
Area of triangle = \(\frac {1}{2}\) × Base × Height
= \(\frac {1}{2}\) × 7 × 4.8
= 16.8 cm².

Question (ii).

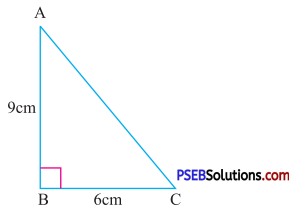
Solution:
Given base of triangle =6 cm
Height of triangle = 9 cm
Area of triangle = \(\frac {1}{2}\) × Base × Height
= \(\frac {1}{2}\) × 6 × 9
= 27 cm²

8. Find the value of x in the following triangles.

Question (i).

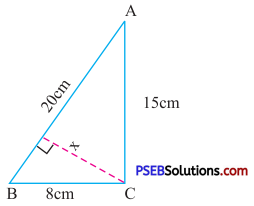
Solution:
In ΔABC, BC = 8 cm, AC = 15 cm
Area of triangle ABC = \(\frac {1}{2}\) × Base × height
= \(\frac {1}{2}\) × BC × AC
= \(\frac {1}{2}\) × 8 × 15
= 60 cm² …(1)
Also, in ΔABC, AB = 20 cm
height = x
Area of triangle ABC = \(\frac {1}{2}\) × Base × Height
= \(\frac {1}{2}\) × 20 × x ….(2)
From (1) and (2)
\(\frac {1}{2}\) × 20 × x = 60
x = \(\frac{60 \times 2}{20}\)
x = 6 cm.

Question (ii).

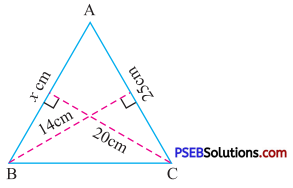
Solution:
In ΔABC, base (AC) = 25 cm
height = 14 cm
Area of triangle ABC = \(\frac {1}{2}\) × Base × height
\(\frac {1}{2}\) × 14 × 25 ….(1)
Also, in ΔABC, base AB = x cm
height = 20 cm
So, area of ΔABC = \(\frac {1}{2}\) × Base × Height
= \(\frac {1}{2}\) × x × 20 ….(2)
From (1) and (2) we get
\(\frac {1}{2}\) × x × 20 = \(\frac {1}{2}\) × 14 × 25
x = 17.5 cm

9. ABCD is a square, M is a point on AB such that AM = 9 cm and area of ΔDAM is 171 cm². What is the area of the square ?

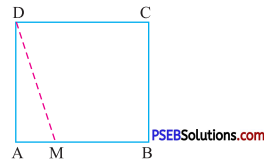
Solution:
Given area of ΔDAM = 171 cm²
Base of triangle = 9 cm
As, area of triangle ΔDAM = \(\frac {1}{2}\) × base × height
171 = \(\frac {1}{2}\) × 9 × (DA)
Hence height (DA) = \(\frac{171 \times 2}{9}\)
= 18 cm
Hence side of square (DA) = 18 cm
Therefore area of square = (side)²
= (18)²
= 324 cm²

10. ΔABC is right angled at A as shown in figure. AD is perpendicular to BC, if AB = 9 cm, BC = 15 cm and AC = 12 cm. Find the area of ΔABC, also find file length of AD.

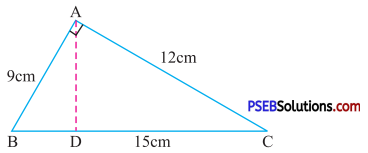
Solution:
Given AB = 9 cm
BC = 15 cm
AC = 12 cm
Let AD = x cm
Area of triangle = \(\frac {1}{2}\) × Base × height
= \(\frac {1}{2}\) × 12 × 9 cm².
= 54 cm² ….(1)
Since, AD is perpendicular to BC
So, area of triangle = \(\frac {1}{2}\) × BC × AD
= \(\frac {1}{2}\) × 15 × AD ….(2)
From (1) and (2) we get
\(\frac {1}{2}\) × 15 × AD = 54
AD = \(\frac{54 \times 2}{15}\)
AD = 7.2 cm

11. ΔABC is isosceles with AB = AC = 9 cm, BC = 12 cm and the height AD from A to BC is 4.5 cm. Find the area of ΔABC. What will be the height from B to AC i.e. BN ?

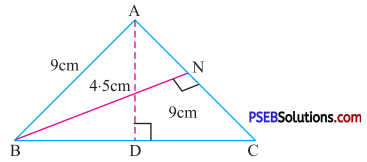
Solution:
In triangle ABC, Base (BC) = 12 cm
AD = 4.5 cm
AD is perpendicular to BC
So, Area of ΔABC = \(\frac {1}{2}\) × base × height
= \(\frac {1}{2}\) × 12 × 4.5 cm
= 27 cm ….(1)
Also, in ΔABC, Base (AC) = 9 cm
Let corresponding height (BN) = x
So area of ΔABC = \(\frac {1}{2}\) × base × height
= \(\frac {1}{2}\) × 9 × BN ….(2)
From (1) and (2)
\(\frac {1}{2}\) × 9 × BN = 27
BN = \(\frac{27 \times 2}{9}\)
= 6 cm.

12. Multiple choice questions :

Question (i).
Find the height of a parallelogram whose area is 246 cm² and base is 20 cm.
(a) 1.23 cm²
(b) 13.2 cm²
(c) 12.3 cm²
(d) 1.32 cm²
Answer:
(c) 12.3 cm²

Question (ii).
One of the side and the corresponding height of a parallelogram are 7 cm and 3.5 cm respectively. Find the area of the parallelogram.
(a) 21 cm²
(b) 24.5 cm²
(c) 21.5 cm²
(d) 24 cm²
Answer:
(b) 24.5 cm²

Question (iii).
The height of a triangle whose base is 13 cm and area is 65 cm² is :
(a) 12 cm
(b) 15 cm
(c) 10 cm
(d) 20 cm
Answer:
(c) 10 cm

Question (iv).
Find the area of an isosceles right angled triangle, whose equal sides are of length 40 cm each.
(a) 400 cm²
(b) 200 cm²
(c) 600 cm²
(d) 800 cm²
Answer:
(d) 800 cm²

Question (v).
If the sides of a parallelogram are increased to twice of its original length, how much will be the perimeter of the new parallelogram ?
(a) 1.5 times
(b) 2 times
(c) 3 times
(d) 4 times
Answer:
(b) 2 times

Question (vi).
In a right angled triangle one leg is double the other and area is 64 cm² find the smaller leg.
(a) 8 cm
(b) 16 cm
(c) 24 cm
(d) 32 cm.
Answer:
(a) 8 cm