Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 11 Perimeter and Area Ex 11.3 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 7 Maths Chapter 11 Perimeter and Area Ex 11.3
1. Find the circumference of circle whose
(i) Radius (r) = 21 cm
(ii) Radius (r) = 3.5 cm
(iii) Diameter = 84 cm
Solution:
(i) Given radius (r) = 21 cm
circumference of circle = 2πr
= 2 × \(\frac {22}{7}\) ×21
= 132 cm
(ii) Given radius (r) = 3.5 cm
Circumference = 2πl
= 2 × \(\frac {22}{7}\) × 3.5
= 22 cm
(iii) Given Diameter (d) = 84 cm
radius (r) = \(\frac{d}{2}=\frac{84}{2}\)
= 42 cm
Circumference = 2πr
= 2 × \(\frac {22}{7}\) × 42
= 264 cm
2. If the circumference of a circular sheet is 176 m, find its radius.
Solution:
Given circumference of circular sheet = 176 m
Let radius = r
So 2πr = 176
r = \(\frac{176}{2 \pi}\)
\(\frac{176}{2 \times \frac{22}{7}}\)
= 28 m
![]()
3. A circular disc of diameter 8.4 cm is divided into two parts what is the perimeter of each semicircular part ?
Solution:
Given diameter of a circular disc = 8.4 cm
radius (r) = \(\frac{8.4}{2}\) = 4.2 cm
Perimeter of semicircular part = πr + 2r
= \(\frac {22}{7}\) × 4.2 + 2 × 4.2
= 22 × 0.6 + 8.4
= 21.6 cm
4. Find the area of the circle having
(i) Radius r = 49 cm
(ii) Radius r = 2.8 cm
(iii) Diameter = 4.2 cm
Solution:
(i) Given radius (r) = 49 cm
Area of circle = πr2
= \(\frac {22}{7}\) × 49 × 49
= 7546 cm2
(ii) Given radius (r) = 2.8 cm
Area of circle = πr2
= \(\frac {22}{7}\) × 2.8 × 2.8
= 24.64 cm2
(iii) Given diameter (d) = 4.2 cm
radius (r) = \(\frac{d}{2}=\frac{4.2}{2}\)
Area of circle = πr2
= \(\frac {22}{7}\) × 2.1 × 2.1
= 13.86 cm2
5. A gardener wants to fence a circular garden of radius 15 m. Find the length of wire, if he makes three rounds offense. Also, find the cost of wire if it costs ₹ 5 per meter (Take π = 3.14).
Solution:
Given radius of circular garden (r) = 15 m
Circumference of the circular garden = 2πr
= 2 × 3.14 × 15
= 94.2 m
So, length of the wire to make three rounds offense
= 3 × 94.2
= 282.6 cm
Cost of wire= ₹ 5 × 282.6
= ₹ 1413
![]()
6. Which of the following has larger area and by how much ?
(a) Rectangle with length 15 cm and breadth 5.4 cm
(b) Circle of diameter 5.6 cm.
Solution:
(a) Given length of rectangle = 15 cm
breadth = 5.4 cm
Area of rectangle = length × breadth
= 15 × 5.4
= 81 cm2
(b) Given diameter of circle (d) = 5.6 cm
radius (r) = \(\frac{d}{2}=\frac{5.6}{2}\)
= 2.8 cm
Area of the circle = πr2
= \(\frac {22}{7}\) × (2.8)2
= 24.64 cm2
Hence, Rectangle has more area = 81 – 24.64
= 56.36 cm2
7. From a rectangular sheet of length 15 cm and breadth 12 cm a circle of radius 3.5 cm is removed. Find the area of remaining sheet.
Solution:
Given length of rectangular sheet = 15 cm
Breadth of rectangle sheet = 12 cm
Area of rectangular sheet = length × breadth
= 15 × 12
= 180 cm2
Given radius of circle (r) = 3.5 cm
Area of circle = πr2
= \(\frac {22}{7}\) × (3.5)2
= 38.5 cm2
Since circle is removed from rectangular sheet.
So, area of remaining sheet = Area of rectangular Sheet – Area of circle
= 180 – 38.5
= 141.5 cm2
8. From a circular sheet of radius 7 cm, a circle of radius 2.1 cm is removed, find the area of remaining sheet.
Solution:
Radius of the circular sheet = 7 cm
Area of the circular sheet = 1 cm
= πr2 = \(\frac {22}{7}\) × 7 × 7 cm2
=154 cm2
Radius of the circle = 2.1 cm
Area of the circle
\(\frac {22}{7}\) × 2.1 × 1.1 = \(\frac{22}{7} \times \frac{21}{10} \times \frac{21}{10}\)
= \(\frac {1386}{100}\)
= 13.86 cm2
Area of the remaining sheet = 154 cm2 – 13.86 cm2
= 140.14 cm2
![]()
9. Smeep took a wire of length 88 cm and bent it into the shape of a circle, find the radius and area of the circle. If the same wire is bent into a square, what will be the side of the square ? Which figure encloses more area ?
Solution:
Given length of wire = 88 cm
The wire is bent into the shape of circle.
Circumference of circle = length of the
2πr = 88
r = \(\frac{88}{2 \pi}=\frac{44}{\pi} \mathrm{cm}\)
= 14 cm
Area of the circle = πr2
= π × (14)2
= \(\frac {22}{7}\) × 14 × 14
= 616 cm2
If the same wire is bent into the square
Let side of the square = a
Perimeter of square = length of the wire
4 × a = 88
a = \(\frac {88}{4}\)
= 22 cm
Area of the square = (side)2
= (22)2
= 484 cm2
Hence circle enclosed more area.
10. A garden is 120 m long and 85 m broad. Inside the garden, there is a circular pit of diameter 14 m. Find the cost of planting the remaining part of the garden at the rate of ₹ 5.50 per square meter.
Solution:
Given length of garden = 120 m
Breadth of garden = 85 m
Area of garden = length × breadth
= 120 × 85
= 10200 m2
Given diameter of circular pit (d) = 14 m
radius (r) = \(\frac{d}{2}=\frac{14}{2}\)
= 7 m
Area of circular pit = πr2
= \(\frac {22}{7}\) × 7 × 7
= 154 m2
Remaining part of garden = Area of garden for planting – Area of circular pit
= 10200 – 154
= 10046 m2
Cost of planting the remaining part of the garden
= ₹ 5.50 × 10046
= ₹ 55243
![]()
11. In the figure PQ = QR and PR = 56 cm. The radius of inscribed circle is 7 cm. Q is centre of semicircle. What is the area of shaded region ?
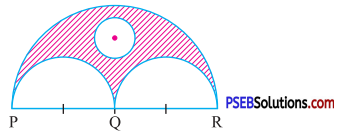
Solution:
Given PQ = QR
PR = 56 cm
Radius of inscribed circle = 7 cm
So PR = PQ + QR
= PQ + PQ = 2PQ
Hence, PQ = \(\frac{\mathrm{PR}}{2}=\frac{56}{2}\)
= 28 cm
So QR = PQ = 28 cm
Area of shaded region = Area of semicircle of diameter PR – Area of semicircle of diameter PQ – Area of semicircle of diameter QR – Area of inscribe circle
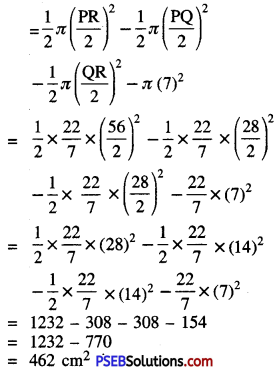
12. The minute hand of a circular clock is 18 cm long. How far does the tip of minute hand move in one hour ?
Solution:
Given minute hand of a circular clock = 18 cm
Distance covered by minute hand in 1 hour = 2πr
= 2 × 3.14 × 18
= 2 × \(\frac {314}{100}\) × 18
= \(\frac {11304}{100}\)
= 113.04 cm.
13. Multiple choice questions :
Question (i).
The circumference of a circle of diameter 10 cm is :
(a) 31.4 cm
(b) 3.14 cm
(c) 314 cm
(d) 35.4 cm
Answer:
(a) 31.4 cm
Question (ii).
The circumference of a circle with radius 14 cm is :
(a) 88 cm
(b) 44 cm
(c) 22 cm
(d) 85 cm
Answer:
(a) 88 cm
![]()
Question (iii).
What is the area of the circle of radius 7 cm ?
(a) 49 cm
(b) 22 cm2
(c) 154 cm2
(d) 308 cm2
Answer:
(c) 154 cm2
Question (iv).
Find the diameter of a circle whose area is 154 cm2 ?
(a) 4 cm
(b) 6 cm
(c) 14 cm
(d) 12 cm
Answer:
(c) 14 cm
Question (v).
A circle has area 100 times the area of another circle. What is the ratio of their circumferences ?
(a) 10 : 1
(b) 1 : 10
(c) 1 : 1
(d) 2 : 1
Answer:
(a) 10 : 1
Question (vi).
Diameter of a circular garden is 9.8 cm. Which of the following is its area ?
(a) 75.46 cm2
(b) 76.46 cm2
(c) 74.4 cm2
(d) 76.4 cm2
Answer:
(a) 75.46 cm2
