PSEB 7th Class Maths Solutions Chapter 11 ਪਰਿਮਾਪ ਅਤੇ ਖੇਤਰਫਲ Ex 11.3

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 11 ਪਰਿਮਾਪ ਅਤੇ ਖੇਤਰਫਲ Ex 11.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 11 ਪਰਿਮਾਪ ਅਤੇ ਖੇਤਰਫਲ Exercise 11.3

1. ਚੱਕਰ ਦਾ ਘੇਰਾ ਪਤਾ ਕਰੋ ਜਿਸਦਾ

ਪ੍ਰਸ਼ਨ (i).
ਅਰਧ ਵਿਆਸ (r) = 21 cm
ਉੱਤਰ:
ਅਰਧ ਵਿਆਸ (r) = 21 cm
ਚੱਕਰ ਦਾ ਘੇਰਾ = 2πr
=2 × \(\frac{22}{7}\) × 21
=132 cm

ਪ੍ਰਸ਼ਨ (ii).
ਅਰਧ ਵਿਆਸ (r) = 3.5 cm
ਉੱਤਰ:
ਅਰਧ ਵਿਆਸ (r) = 3.5 cm
ਚੱਕਰ ਦਾ ਘੇਰਾ = 2
= 2 × \(\frac{22}{7}\) × 3.5
= 22 cm

ਪ੍ਰਸ਼ਨ (iii).
ਵਿਆਸ (d) = 84 cm
ਉੱਤਰ:
ਵਿਆਸ (d) = 84 cm
ਅਰਧ ਵਿਆਸ (r) = \(\frac{d}{2}\) = \(\frac{84}{2}\) = 42 cm
ਚੱਕਰ ਦਾ ਘੇਰਾ = 2πr
= 2 × \(\frac{22}{7}\) × 42
= 264 cm

ਪ੍ਰਸ਼ਨ 2.
ਜੇਕਰ ਚੱਕਰਾਕਾਰ ਸ਼ੀਟ ਦਾ ਘੇਰਾ 176 m ਹੋਵੇ ਤਾਂ ਇਸਦਾ ਅਰਧ ਵਿਆਸ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਦਿੱਤਾ ਗਿਆ ਚੱਕਰਾਕਾਰ ਸ਼ੀਟ ਦਾ ਘੇਰਾ
= 176 m
ਅਰਧ ਵਿਆਸ = r
ਇਸ ਲਈ 2πr = 176
r = \(\frac{176}{2 \pi}\) = \(\frac{176}{2 \times \frac{22}{7}}\)
= 28 m

ਪ੍ਰਸ਼ਨ 3.
8 cm ਵਿਆਸ ਵਾਲੀ ਚੱਕਰਾਕਾਰ ਡਿਸਕ (disc) ਨੂੰ ਦੋ ਭਾਗਾਂ ਵਿੱਚ ਵੰਡਿਆ ਗਿਆ । ਹਰੇਕ ਅਰਧ | ਚੱਕਰਾਕਾਰ ਭਾਗ ਦਾ ਘੇਰਾ ਕੀ ਹੈ ?
ਹੱਲ:
ਇਕ ਚੱਕਰਾਕਾਰ ਡਿਸਕ ਦਾ ਵਿਆਸ
= 8 cm
ਅਰਧ ਵਿਆਸ (r) = \(\frac{8}{2}\) = 4 cm
ਅਰਧ ਚਕਰਾਚਾਰ ਭਾਗ ਦਾ ਘੇਰਾ
= πr + 2r
= \(\frac{22}{7}\) × 4 + 2 × 4
= 12.6 + 8
= 20.6 cm

4. ਚੱਕਰ ਦਾ ਖੇਤਰਫ਼ਲ ਪਤਾ ਕਰੋ ਜਿਸਦਾ

ਪ੍ਰਸ਼ਨ (i).
ਅਰਧ ਵਿਆਸ (r) = 49 cm
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਅਰਧ ਵਿਆਸ (r)
= 49 cm
ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ = πr²
= \(\frac{22}{7}\) × 49 × 49
= 7546 cm²

ਪ੍ਰਸ਼ਨ (ii).
ਅਰਧ ਵਿਆਸ (r) = 2.8 cm
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਅਰਧ ਵਿਆਸ (r)
= 2.8 cm
ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ = πr²
= \(\frac{22}{7}\) × 2.8 × 2.8
= 24.64 cm²

ਪ੍ਰਸ਼ਨ (iii).
ਵਿਆਸ (d) = 4.2 cm
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਵਿਆਸ (d) = 42 cm
ਅਰਧ ਵਿਆਸ (r) = \(\frac{d}{2}\) = \(\frac{4.2}{2}\) = 2.1 cm
ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ = πr²
= \(\frac{22}{7}\) × 2.1 × 2.1 cm²
= 13.86 cm²

ਪ੍ਰਸ਼ਨ 5.
ਇਕ ਮਾਲੀ 15 m ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਚੱਕਰਾਕਾਰ ਬਾਗ ਨੂੰ ਵਾੜ ਲਗਾਉਣਾ ਚਾਹੁੰਦਾ ਹੈ । ਤਾਰ ਦੀ ਲੰਬਾਈ ਪਤਾ ਕਰੋ । ਜੇਕਰ ਉਹ ਵਾੜ ਦੇ ਤਿੰਨ ਚੱਕਰ ਲਗਾਉਂਦਾ ਹੈ ਤਾਂ ₹ 5 ਪ੍ਰਤੀ m ਦੀ ਦਰ ਨਾਲ ਤਾਰ ਲਗਾਉਣ ਦਾ ਖਰਚ ਪਤਾ ਕਰੋ (π = 3.14 ਲਓ)
ਹੱਲ:
ਚੱਕਰਾਕਾਰ ਬਾਗ ਦਾ ਅਰਧ ਵਿਆਸ
(r) = 15 m
ਚੱਕਰਾਕਾਰ ਬਾਗ ਦਾ ਘੇਰਾ = 2πr
= 2 × 3.14 × 15 m
= 94.2 m.
ਵਾੜ ਦੇ ਤਿੰਨ ਚੱਕਰ ਲਗਾਉਣ ਲਈ ਤਾਰ ਦੀ ਲੰਬਾਈ
= 3 × 94.2 cm
= 282.6 cm
ਤਾਰ ਦੀ ਕੀਮਤ = ₹ 5 × 282.6
= ₹ 1413

6. ਹੇਠਾਂ ਦਿੱਤੇ ਵਿੱਚੋਂ ਕਿਸਦਾ ਖੇਤਰਫ਼ਲ ਜ਼ਿਆਦਾ ਹੈ ਤੇ ਕਿੰਨਾ ?

ਪ੍ਰਸ਼ਨ (a).
15 cm ਲੰਬਾਈ ਤੇ 5.4 cm ਚੌੜਾਈ ਵਾਲੀ ਆਇਤ ਦਾ ।
ਉੱਤਰ:
ਆਇਤ ਦੀ ਲੰਬਾਈ
= 15 cm
ਚੌੜਾਈ = 5.4 cm
= 15 × 5.4 cm²
= 81 cm²

ਪ੍ਰਸ਼ਨ (b).
5.6 cm ਵਿਆਸ ਵਾਲੇ ਚੱਕਰ ਦਾ ।
ਉੱਤਰ:
ਚੱਕਰ ਦੇ ਵਿਆਸ ਨੂੰ ਦੇਖਦੇ ਹੋਏ (d)
= 5.6 cm
ਅਰਧ ਵਿਆਸ (r) = \(\frac{d}{2}\) = \(\frac{5.6}{2}\) = 2.8 cm
ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ = πr²
= \(\frac{22}{7}\) × (2.8)² cm²
= 24.64 cm²
ਇਸ ਲਈ ਆਇਤ ਦਾ ਖੇਤਰਫਲ ਜ਼ਿਆਦਾ ਹੈ।
= (81 – 24.64) cm²
= 56.36 cm²

ਪ੍ਰਸ਼ਨ 7.
15 cm ਲੰਬਾਈ ਅਤੇ 12 cm ਚੌੜਾਈ ਵਾਲੀ ਆਇਤਾਕਾਰ ਸ਼ੀਟ ਵਿਚੋਂ 3.5 cm ਅਰਧ ਵਿਆਸ ਵਾਲੀ ਚੱਕਰਾਕਾਰ ਸ਼ੀਟ ਵੱਖ ਕੀਤੀ ਗਈ ਹੈ ਬਾਕੀ ਸ਼ੀਟ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਆਇਤਾਕਾਰ ਸ਼ੀਟ ਦੀ ਲੰਬਾਈ
= 15 cm
ਆਇਤਾਕਾਰ ਸ਼ੀਟ ਦੀ ਚੌੜਾਈ = 12 cm
ਆਇਤਾਕਾਰ ਸ਼ੀਟ ਦਾ ਖੇਤਰਫਲ
= ਲੰਬਾਈ × ਚੌੜਾਈ
= 15 × 12 cm²
= 180 cm²
ਚੱਕਰਾਕਾਰ ਸ਼ੀਟ ਦਾ ਅਰਧ ਵਿਆਸ (r)
= 3.5 cm
ਚੱਕਰਾਕਾਰ ਸ਼ੀਟ ਦਾ ਖੇਤਰਫਲ = πr²
= \(\frac{22}{7}\) × (3.5)²
= 38.5 cm²
ਇਸ ਲਈ ਆਇਤਾਕਾਰ ਸ਼ੀਟ ਤੋਂ ਚੱਕਰਾਕਾਰ ਸ਼ੀਟ ਨੂੰ ਹਟਾਉਣ ਤੇ ਸ਼ੀਟ ਦਾ ਬਚਿਆ ਹੋਇਆ ਖੇਤਰਫਲ = ਆਇਤਾਕਾਰ ਸ਼ੀਟ ਦਾ ਖੇਤਰਫਲ – ਚੱਕਰਾਕਾਰ ਸ਼ੀਟ ਦਾ ਖੇਤਰਫਲ
= (180 – 38.5) cm²
= 141.5 cm²

ਪ੍ਰਸ਼ਨ 8.
7 cm ਅਰਧ ਵਿਆਸ ਵਾਲੀ ਚੱਕਰਾਕਾਰ ਸ਼ੀਟ ਵਿੱਚੋਂ 2.1 cm ਅਰਧ ਵਿਆਸ ਵਾਲੀ ਚੱਕਰਾਕਾਰ ਸ਼ੀਟ ਵੱਖ ਕੀਤੀ ਗਈ ਹੈ । ਬਾਕੀ ਸ਼ੀਟ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਵੱਡੀ ਚੱਕਰਾਕਾਰ ਸ਼ੀਟ ਦਾ ਅਰਧ ਵਿਆਸ
= 7 cm
ਚੱਕਰਾਕਾਰ ਸ਼ੀਟ ਦਾ ਖੇਤਰਫਲ = 1 cm
= πr² = \(\frac{22}{7}\) × 7 × 7 cm²
= 154 cm
ਛੋਟੀ ਚਕਰਾਕਾਰ ਸ਼ੀਟ ਦਾ ਅਰਧ ਵਿਆਸ = 2.1 cm
ਛੋਟੀ ਚੱਕਰਾਕਾਰ ਸ਼ੀਟ ਦਾ ਖੇਤਰਫਲ
= \(\frac{22}{7}\) × 2.1 × 1.1 = \(\frac{22}{7}\) × \(\frac{21}{10}\) × \(\frac{21}{10}\)
= \(\frac{1386}{100}\) = 13.86 cm²
ਬਾਕੀ ਬਚੀ ਸ਼ੀਟ ਦਾ ਖੇਤਰਫ਼ਲ
= 154 cm² – 13.86 cm²
= 14014 cm²

ਪ੍ਰਸ਼ਨ 9.
ਸਮੀਪ ਨੇ 88 cm ਲੰਬਾਈ ਦੀ ਇੱਕ ਤਾਰ ਲਈ ਅਤੇ ਉਸਨੂੰ ਚੱਕਰ ਦੇ ਆਕਾਰ ਵਿੱਚ ਮੋੜਿਆ । ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ ਤੇ ਖੇਤਰਫ਼ਲ ਪਤਾ ਕਰੋ । ਜੇਕਰ ਉਹੀ ਤਾਰ ਨੂੰ ਵਰਗ ਦੇ ਆਕਾਰ ਵਿੱਚ ਮੋੜਿਆ ਜਾਵੇ ਤਾਂ ਵਰਗ ਦੀ ਭੁਜਾ ਦੀ ਲੰਬਾਈ ਕੀ ਹੋਵੇਗੀ ? ਕਿਹੜੀ ਆਕ੍ਰਿਤੀ ਜ਼ਿਆਦਾ ਖੇਤਰਫ਼ਲ ਘੇਰਦੀ ਹੈ ?
ਹੱਲ:
ਤਾਰ ਦੀ ਲੰਬਾਈ = 88 cm
ਤਾਰ ਚੱਕਰ ਦੇ ਆਕਾਰ ਵਿੱਚ ਮੁੜੀ ਹੋਈ ਹੈ ।
ਚੱਕਰ ਦਾ ਘੇਰਾ = ਤਾਰ ਦੀ ਲੰਬਾਈ
2πr = 88.
r = \(\frac{88}{2 \pi}\) = \(\frac{44}{\pi}\) cm
= 14 cm
ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ
= 2π²
= π × (14)²
= \(\frac{22}{7}\) × 14 × 14
= 616 cm²
ਜੇਕਰ ਉਹੀ ਤਾਰ ਵਰਗ ਤੋਂ ਮੁੜੀ ਹੋਈ ਹੈ ਤਾਂ ਵਰਗ ਦੀ ਭੁਜਾ = a
ਵਰਗ ਦਾ ਘੇਰਾ = ਤਾਰ ਦੀ ਲੰਬਾਈ
4 × a = 88
a = \(\frac{88}{4}\) = 22 cm²
ਵਰਗ ਦਾ ਖੇਤਰਫਲ = (ਭੁਜਾ)²
= (22)²
= 484 cm²
ਇਸ ਲਈ ਚੱਕਰ ਨੇ ਜ਼ਿਆਦਾ ਖੇਤਰ ਨੂੰ ਘੇਰਿਆ ਹੈ ।

ਪ੍ਰਸ਼ਨ 10.
ਇਕ ਬਾਗ ਦੀ ਲੰਬਾਈ 120 m ਅਤੇ ਚੌੜਾਈ 85 m ਹੈ । ਬਾਗ ਦੇ ਵਿੱਚ 14 m ਵਿਆਸ ਵਾਲਾ ਚੱਕਰਾਕਾਰ ਪਿਟ ਹੈ । ਬਾਕੀ ਬਚੇ ਬਾਗ ਵਿੱਚ ₹ 5.50 ਪ੍ਰਤੀ ਵਰਗਮੀਟਰ ਦੇ ਹਿਸਾਬ ਨਾਲ ਬੂਟੇ ਲਗਾਉਣ ਦਾ ਖਰਚ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਬਾਗ ਦੀ ਲੰਬਾਈ
= 120 m
ਬਾਗ ਦੀ ਚੌੜਾਈ = 85 m
ਬਾਗ ਦਾ ਖੇਤਰਫਲ = ਲੰਬਾਈ × ਚੌੜਾਈ
= 120 × 85
= 10200 m²
ਚੱਕਰਾਕਾਰ ਪਿਟ ਦਾ ਵਿਆਸ (d)
= 14 m
ਅਰਧ ਵਿਆਸ (r) = \(\frac{d}{2}\) = \(\frac{14}{2}\) = 7 m
ਚੱਕਰਾਕਾਰ ਪਿਟ ਦਾ ਖੇਤਰਫਲ
= πr²
= \(\frac{22}{7}\) × 7 × 7
= 154 m²
ਬਾਗ ਦਾ ਬਚਿਆ ਹੋਇਆ ਭਾਗ = ਬੂਟੇ ਲਗਾਉਣ ਲਈ ਬਾਗ ਦਾ ਖੇਤਰਫਲ = ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ – ਚੱਕਰਾਕਾਰ ਪਿਟ ਦਾ ਖੇਤਰਫਲ
= 10200 – 154
= 10046 m²
ਬਾਗ ਦੇ ਬਚੇ ਹੋਏ ਭਾਗ ’ਤੇ ਬੂਟੇ ਲਗਾਉਣ ਦੀ ਕੀਮਤ
= ₹ 5.50 × 10046
= ₹ 55243

ਪ੍ਰਸ਼ਨ 11.
ਚਿੱਤਰ ਵਿੱਚ PQ = QR ਵਿੱਚ ਅਤੇ PR = 56 cm ਕੱਟੇ ਗਏ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ 7 cm ਹੈ । Q ਅਰਧ ਚੱਕਰ ਦਾ ਕੇਂਦਰ ਹੈ । ਰੰਗੀਨ ਭਾਗ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ !

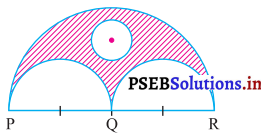
ਹੱਲ:
ਦਿੱਤਾ ਗਿਆ PQ = QR
PR = 56 cm
ਕੱਢੇ ਗਏ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ = 7 cm
ਇਸ ਲਈ PR = PQ + QR
= PQ + PQ = 2PQ
ਇਸ ਲਈ PQ = \(\frac{PR}{2}\) = \(\frac{56}{2}\)
= 28 cm
ਇਸ ਲਈ QR = PQ = 28 cm
ਰੰਗੀਨ ਭਾਗ ਦਾ ਖੇਤਰਫਲ = PR ਵਿਆਸ ਦੇ
ਅਰਧ ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ – PQ ਵਿਆਸ ਦੇ
ਅਰਧ ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ – QR ਚੱਕਰ ਦੇ
ਅਰਧ-ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ – ਕੱਟੇ ਗਏ ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ

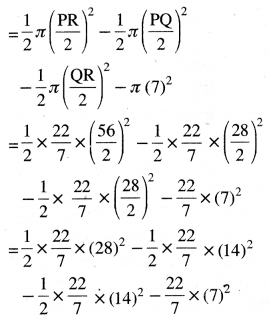
= 1232 – 308 – 308 – 154
= 1232 – 770
= 462 cm²

ਪ੍ਰਸ਼ਨ 12.
ਚੱਕਰਾਕਾਰ ਘੜੀ ਦੀ ਮਿੰਟਾਂ ਵਾਲੀ ਸੂਈ ਦੀ ਲੰਬਾਈ 18 cm ਹੈ । ਮਿੰਟਾਂ ਵਾਲੀ ਸੂਈ ਦੀ ਨੋਕ (Tip) 1 ਘੰਟੇ ਵਿੱਚ ਕਿੰਨੀ ਦੂਰੀ ਤੈਅ ਕਰਦੀ ਹੈ ?
ਹੱਲ:
ਮਿੰਟਾਂ ਵਾਲੀ ਸੂਈ ਦੀ ਲੰਬਾਈ = ਘੜੀ ਦਾ ਅਰਧ ਵਿਆਸ = 18 cm
ਮਿੰਟਾਂ ਵਾਲੀ ਸੂਈ ਦੀ ਨੋਕ ਦੁਆਰਾ 1 ਘੰਟੇ ਵਿਚ ਤੈਅ ਦੂਰੀ
= 2πr
= 2 × 3.14 × 18
= 2 × \(\frac{314}{100}\) × 18 = \(\frac{11304}{100}\)
= 113.04 cm

13. ਬਹੁਵਿਕਲਪੀ ਪ੍ਰਸ਼ਨ :

ਪ੍ਰਸ਼ਨ (i).
10 cm ਵਿਆਸ ਵਾਲੇ ਚੱਕਰ ਦਾ ਘੇਰਾ ਹੈ :
(a) 31.4 cm
(b) 3.14 cm
(c) 314 cm
(d) 354 cm
ਉੱਤਰ:
(a) 31.4 cm

ਪ੍ਰਸ਼ਨ (ii).
14 ਸਮ ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਚੱਕਰ ਦਾ ਘੇਰਾ ਹੈ :
(a) 88 cm
(b) 44 cm
(c) 22 cm
(d) 85 cm
ਉੱਤਰ:
(a) 88 cm

ਪ੍ਰਸ਼ਨ (iii).
7 cm ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ ਕੀ ਹੈ :
(a) 49 cm²
(b) 22 cm²
(c) 154 cm²
(d) 308 cm²
ਉੱਤਰ:
(c) 154 cm²

ਪ੍ਰਸ਼ਨ (iv).
ਚੱਕਰ ਦਾ ਵਿਆਸ ਪਤਾ ਕਰੋ ਜਿਸਦਾ ਖੇਤਰਫਲ 154 cm² ਹੈ :
(a) 4 cm
(b) 6 cm
(c) 14 cm
(d) 12 cm
ਉੱਤਰ:
(c) 14 cm

ਪ੍ਰਸ਼ਨ (v).
ਇਕ ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ ਦੁਸਰੇ ਚੱਕਰ ਦੇ ‘ ਖੇਤਰਫਲ ਦੇ 100 ਗੁਣਾ ਦੇ ਬਰਾਬਰ ਹੈ ਉਹਨਾਂ ਦੇ ਘੇਰੇ ਦਾ ਅਨੁਪਾਤ ਕੀ ਹੈ ?
(a) 10 : 1
(b) 1:10
(c) 1 : 1
(d) 2 : 1
ਉੱਤਰ:
(a) 10 : 1

ਪ੍ਰਸ਼ਨ (vi).
ਜੇਕਰ ਚੱਕਰਾਕਾਰ ਪਾਰਕ ਦਾ ਵਿਆਸ਼ 9.8 cm ਹੈ ਤਾਂ ਇਸਦਾ ਖੇਤਰਫਲ ਹੈ :
(a) 75.46 cm²
(b) 76.46 cm²
(c) 74.4 cm²
(d) 76.4 cm²
ਉੱਤਰ :
(a) 75.46 cm²