PSEB 7th Class Maths Solutions Chapter 11 Perimeter and Area Ex 11.4

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 11 Perimeter and Area Ex 11.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 11 Perimeter and Area Ex 11.4

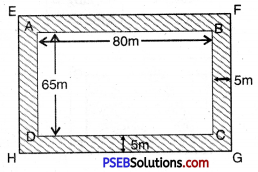
1. An rectangular park is 80 m long and 65 in wide. A path of 5 m width is constructed outside the park. Find the area of path.
Solution:
Let ABCD be a rectangular park.
Length of the park = 80 m
Breadth of the park = 65 m

Area of the rectangular park
ABCD = Length × Breadth
= 80 m × 65 m
= 5200 m²
Length of rectangular garden EFGH (including park)
= 80 + 5 + 5
= 90 m
Breadth = 65 + 5 + 5
= 75 m
Area of rectangular path EFGH = 90 × 75
= 6750 m²
Area of the path = Area of rectangular park EFGH – Area of rectangle ABCD
= 6750 – 5200
= 1550 m²

2. A rectangular garden is 110 m long and 72 m broad. A path of uniform width 8 m has to be constructed around it. Find the cost of gravelling the path at ₹ 11.50 per m².
Solution:
Let ABCD represents the rectangular garden and the shaded region represents the path of width 8 m around the garden.
Length of rectangular garden l = 110 m

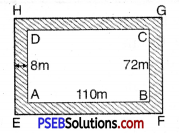
Breadth of rectangular garden b = 72 m
Area of rectangular garden ABCD = (110 × 72) m²
= 7920 m²
Length of rectangular garden including path = 110 m + (8m + 8m)
= 126 m
Breadth of rectangular garden including path = 72m + (8m + 8m) = 88 m
Area of garden including path = (126 × 88) m²
= 11088 m²
Area of path = Area of garden including path – Area of garden
Area of path = (11088 – 7920) m²
= 3168 m²
Cost of gravelling 1 m² of path = ₹ 11.50
Cost of gravelling 2928 m2 of path = ₹ 3168 × 11.50
= ₹ 36432

3. A room is 12 m long and 8 m broad. It is surrounded by a verandah, which is 3 m wide all around it. Find the cost of flooring the verandah with marble at ₹ 275 per m².
Solution:
Let ABCD. represents the rectangular floor of room and shaded region represents the verandah 3 m wide all along the outside of a room.

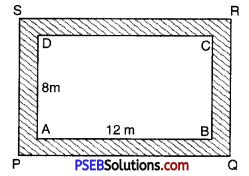
PQ = (3 + 12 + 3) m
= 18 m
PS = (3 + 8 + 3) m
= 14 m
Area of rectangle ABCD = 1 × b
= AB × AD
= 12 m × 8m
= 96 m²
Area of recangle PQRS = 1 × b
= PQ × PS
= 18 m × 14 m
= 252 m²
Area of verandah = [Area of rectangle PQRS] – [Area of rectangle ABCD]
= (252 – 96) m²
= 156 m²
(Rate of flooting the verandha with marble verandah = ₹ 275 per m²)
Cost of flooring verandah with moble.
= ₹ (156 × 275)
= ₹ 42900.

4. A sheet of paper measures 30 cm × 24 cm. A strip of 4 cm width is cut from it, all around. Find the area of remaining sheet and also the area of cut out strip.
Solution:
Let ABCD represent the sheet of 30 cm × 24 cm and shaded region represents the 4 cm width to be cut

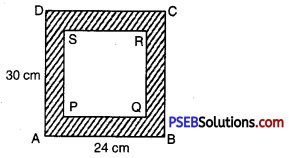
PQ = (30 – 4 – 4) cm
= 22 cm
PS = (24 – 4 – 4) cm
= 16 cm

(i) remaining sheet
[Area of rectangle ABCD] – [Area of rectangle PQRS]
= (30 × 24 – 22 × 16)
= (720 – 352 = 368) cm²
Area of the cut our strip i.e. area of rectangle PQRS = 22 × 16 cm²
= 352 cm²

5. A path of 2 m wide is built along the border inside a square garden of side 40 m. Find :

Question (i).
The Area of path.
Solution:
Let ABCD be the square park of side 40 m and the shaded region represents the path 2 m wide
EF = 40 m – (2 + 2) m
= 36 m

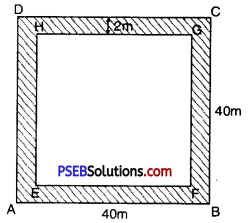
Area of square park ABCD = (Side)²
= 40 × 40
= 1600 m²
Area of EFGH = (Side)²
= 36 × 36
= 1296 m²
Area of path = Area of square park ABCD – Area of EFGH
= (1600 – 1296) m²
= 304 m²

Question (ii).
The cost of planting grass in the remaining portion of the garden at the rate of ₹ 50 per m².
Solution:
Cost of planting grass = 50 per m²
Cost of planting grass 1m² = ₹ 50
Cost of 1296 m² = 1296 × 50
= ₹ 64800

6. A nursery school play ground is 150 m long and 75 m wide. A portion of 75 m × 75 m is kept for see-saw slides and other park equipments. In the remaining portion 3 m wide path parallel to its width and parallel to remaining length (as shown in fig). The remaining area is covered by grass. Find the area covered by grass.

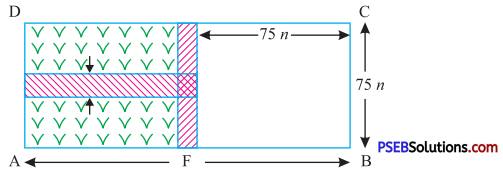
Solution:
Area of school ground
= 150 m × 75 m = 11250 m²
Area kept for see-saw slides and other equipments
= 75 × 75
= 5625 m²
Area of path parallel to width of ground = 75 × 3
= 225 m²
Area common to both paths = 3 × 3
= 9 m²
Total area covered by path
= (225 + 225 – 9)
= 441 m²
Area covered by grass = Area of ground – (Area kept for see-saw slides + area covered by paths)
= 11250 – (5625 + 441)
= (11250 – 6066) m²
= 5184 m²

7. Two cross roads each of width 8 m cut at right angle through the centre of a rectangular park of length 480 m and breadth 250 m and parallel to its sides. Find the area of roads. Also, find the area of park excluding cross roads.
Solution:

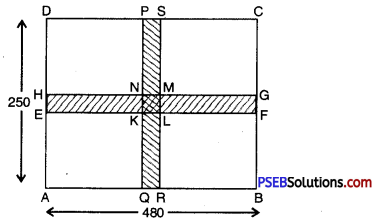
ABCD represent the rectangular park of length AB = 480 m and breadth BC = 250 m. Area of shaded portion i.e. area of rectangle EFGH and PQRS represent the area of cross roads, but the area of square KLMN is taken twice, So it will be subtracted.
Now EF = 480, FG = 8 m, PQ = 250 m, QR = 8 m, KL = 8 m.
Area covered by roads = Area of rectangle EFGH + area of rectangle PQRS – Area of square KLMN
= (EF × FG) + (PQ × QR) – (KL)²
= (480 × 8) + (250 × 8) – (8 × 8)
= 3840 + 2000 – 64
Area of the road = 5776 m²
Area of park excluding cross roads = 250 × 480 – (250 × 8 + 480 × 8 – 8 × 8)
= 114224 m²

8. In a rectangular field of length 92 m and breadth 70 m, two roads are constructed which are parallel to the sides and cut each other at right angles through the centre of field. If the width of each road is 4 m, find.
(i) The area covered by roads.
(ii) The cost of constructing the roads at the rate of ₹ 150 per m².
Solution:
Let ABCD represents the rectangular field of length ; AB = 92 m and breadth; AD = 70 m. Let the area of shaded portion
i. e. area of the rectangle PQRS and the area of rectangle EFGH represents the area of cross roads.

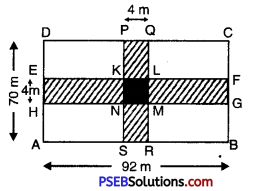
But in doing this, area of square KLMN is taken twice which is to be subtracted.
Now PQ = 4 m, PS = 70 m
and EH = 4 m, EF = 92 m
and KL = 4 m, KN = 4 m

= PQ × PS + EF × EH – KL × KN
= [(4 × 70) + (92 × 4) – (4 × 4)] m²
= (280 + 368 – 16) m²
= (648 – 16) m²
= 632 m²

(ii) Cost of constructing 1 m² of roads = ₹ 150
Therefore cost of constructing 632 m² of roads = ₹ (150 × 632)
= ₹ 94800.

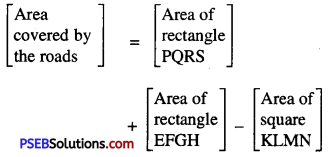
9. Find the area of shaded region in each of the following figures.

Question (i).

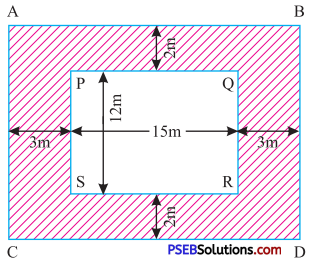
Solution:
Length of rectangle ABDC
= 3m + 15m + 3m
= 21 m
Breadth of rectangle ABDC
= 2m + 12m + 2m
= 16 m
Area of rectangle ABDC
= length × breadth
= 21 × 16 m²
= 336 m²
Length of rectangle PQRS = 15 m
Breadth of rectangle PQRS = 12 m
Area of rectangle PQRS = 15 × 12 m²
= 180 m²
Area of shaded region = Area of rectangle ABCD – Area of rectangle PQRS
= 336 m² – 180 m²
= 156 m²

Question (ii).

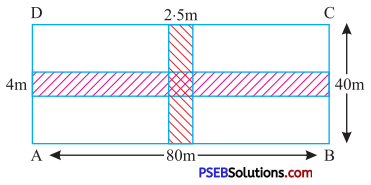
Solution:

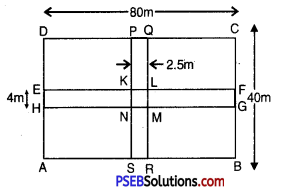
SR = PQ = 2.5 m
EH = FG = 4 m
KL = 2.5 m
LM = 4 m
Area of shaded region = [Area of rectangle PQRS] + [Area of rectangle EFGH] – Area of rectangle KLMN
= 40 × 2.5 + 80 × 4 – 2.5 × 4
= 100 + 320 – 10
= 420 – 10
= 410 m²