Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 6 ਤ੍ਰਿਭੁਜਾਂ Ex 6.2 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 7 Maths Chapter 6 ਤ੍ਰਿਭੁਜਾਂ Exercise 6.2
1. ਪਤਾ ਕਰੋ ਕਿ ਹੇਠ ਦਿੱਤੇ ਹੋਏ ਕੋਣਾਂ ਦੇ ਮਾਪਾਂ ਨਾਲ ਤਿਭੁਜ ਸੰਭਵ ਹੈ :
ਪ੍ਰਸ਼ਨ (a).
35°, 70°, 65°
ਉੱਤਰ:
ਨਹੀਂ ਕਾਰਨ : ਤਿੰਨ ਕੋਣਾਂ ਦਾ ਜੋੜ
= 35°+ 70° + 65° = 170°
ਪਰ ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ ਤਿਭੁਜ ਦੇ ਤਿੰਨਾਂ ਕੋਣਾਂ ਦਾ ਜੋੜ 180° ਹੁੰਦਾ ਹੈ ।
∴ ਇਸ ਲਈ ਤ੍ਰਿਭੁਜ ਦੇ ਕੋਣ 35°, 70° ਅਤੇ 65° ਨਹੀਂ ਹੋ ਸਕਦੇ
ਪ੍ਰਸ਼ਨ (b).
70°, 50°, 60°
ਉੱਤਰ:
ਹਾਂ ।
ਕਾਰਨ : ਤਿੰਨ ਕੋਣਾਂ ਦਾ ਜੋੜ
= 70° + 50° + 60° = 180°
ਕਿਉਂਕਿ ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ ਤ੍ਰਿਭੁਜ ਦੇ ਅੰਦਰਲੇ ਤਿੰਨਾਂ ਕੋਣਾਂ ਦਾ ਜੋੜ ਹਮੇਸ਼ਾ 180° ਹੁੰਦਾ ਹੈ ।
∴ ਇਕ ਤਿਭੁਜ ਦੇ ਕੋਣ 70°, 50° ਅਤੇ 60° ਹੋ ਸਕਦੇ ਹਾਂ
ਪ੍ਰਸ਼ਨ (c).
90°, 80°, 20°
ਉੱਤਰ:
ਨਹੀਂ
ਕਾਰਨ : ਤਿੰਨ ਕੋਣਾਂ ਦਾ ਜੋੜ
= 90° + 80° + 20° = 190°
ਕਿਉਂਕਿ ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ ਤਿਭੁਜ ਦੇ ਅੰਦਰਲੇ ਤਿੰਨਾਂ ਕੋਣਾਂ ਦਾ ਜੋੜ ਹਮੇਸ਼ਾ 180°ਹੁੰਦਾ ਹੈ ।
∴ ਇੱਕ ਤਿਭੁਜ ਦੇ ਕੋਣ 90°, 80° ਅਤੇ 20° ਨਹੀਂ ਹੋ ਸਕਦੇ
![]()
ਪ੍ਰਸ਼ਨ (d).
60°, 60°, 60°
ਉੱਤਰ:
ਹਾਂ ।
ਕਾਰਨ : ਤਿੰਨ ਕੋਣਾਂ ਦਾ ਜੋੜ
= 60° + 60° + 60° = 180°
ਕਿਉਂਕਿ ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ ਤਿਭੁਜ ਦੇ ਅੰਦਰਲੇ ਤਿੰਨਾਂ ਕੋਣਾਂ ਦਾ ਜੋੜ ਹਮੇਸ਼ਾ 180° ਹੁੰਦਾ ਹੈ ।
∴ ਇੱਕ ਤਿਭੁਜ ਦੇ ਕੋਣ 60°, 60° ਅਤੇ 60° ਹੋ ਸਕਦੇ ਹਨ ਉੱਤਰ
ਪ੍ਰਸ਼ਨ (e).
90°, 90°, 90°
ਉੱਤਰ:
ਨਹੀਂ ।
ਕਾਰਨ : ਤਿੰਨ ਕੋਣਾਂ ਦਾ ਜੋੜ
= 90° + 90° + 90° = 270°
ਕਿਉਂਕਿ ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ ਤਿਭੁਜ ਦੇ ਅੰਦਰਲੇ ਤਿੰਨਾਂ ਕੋਣਾਂ ਦਾ ਜੋੜ ਹਮੇਂਸ਼ਾ 180° ਹੁੰਦਾ ਹੈ ।
2. ਹੇਠ ਦਿੱਤੇ ਚਿੱਤਰਾਂ ਵਿੱਚ x ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ।
ਪ੍ਰਸ਼ਨ (i).
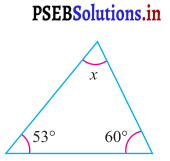
ਉੱਤਰ:
ਤਿਭੁਜ ਦੇ ਅੰਦਰਲੇ ਕੋਣਾਂ ਦੇ ਜੋੜ ਗੁਣ ਅਨੁਸਾਰ
x + 53° + 60° = 180°
x + 113° = 180°
x = 180° – 113°
x = 67°
![]()
ਪ੍ਰਸ਼ਨ (ii).
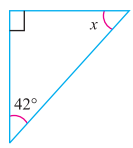
ਉੱਤਰ:
ਤ੍ਰਿਭੁਜ ਦੇ ਅੰਦਰਲੇ ਕੋਣਾਂ ਦੇ ਜੋੜ ਗੁਣ ਅਨੁਸਾਰ
90° + x + 42° = 180°
132° + x = 180°
x = 180° – 132°
x = 48°
ਪ੍ਰਸ਼ਨ (iii).
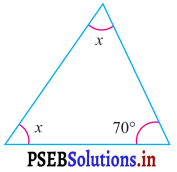
ਉੱਤਰ:
ਤਿਭੁਜ ਦੇ ਅੰਦਰਲੇ ਕੋਣਾਂ ਦੇ ਜੋੜ ਗੁਣ ਅਨੁਸਾਰ
x + x + 70° = 180°
2x + 70° = 180°
2 = 180° – 70°
x = 110°
x = \(\frac{110^{\circ}}{2}\)
x = 55°
ਪ੍ਰਸ਼ਨ (iv).
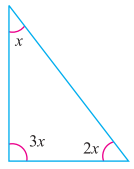
ਉੱਤਰ:
ਤ੍ਰਿਭੁਜ ਦੇ ਅੰਦਰਲੇ ਕੋਣਾਂ ਦੇ ਜੋੜ ਗੁਣ ਅਨੁਸਾਰ
x + 3x + 2x = 180°
∴ 6x = 180°
x = \(\frac{180^{\circ}}{6}\)
x= 30°
![]()
ਪ੍ਰਸ਼ਨ (v).
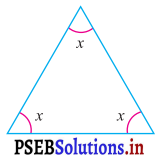
ਉੱਤਰ:
ਤਿਭੁਜ ਦੇ ਅੰਦਰਲੇ ਕੋਣਾਂ ਦੇ ਜੋੜ ਗੁਣ ਅਨੁਸਾਰ
x + x + x = 180°
3x = 180°
x = \(\frac{180^{\circ}}{3}\)
x = 60°
ਪ੍ਰਸ਼ਨ (vi).
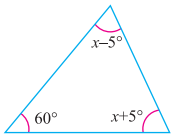
ਉੱਤਰ:
ਤਿਭੁਜ ਦੇ ਅੰਦਰਲੇ ਕੋਣਾਂ ਦੇ ਜੋੜ ਗੁਣ ਅਨੁਸਾਰ
x – 5° + 60° + x + 5° = 180°
2x + 60° = 180°
2x = 180° – 60°
2x = 120°
x = \(\frac{120^{\circ}}{2}\)
x = 60°
![]()
3. ਦਿੱਤੇ ਹੋਏ ਚਿੱਤਰਾਂ ਵਿੱਚ x ਅਤੇ y ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ।
ਪ੍ਰਸ਼ਨ (i).
ਉੱਤਰ:
ਤ੍ਰਿਭੁਜ △ABC ਵਿੱਚ BC ਨੂੰ ਬਿੰਦੂ D ਤੱਕ ਵਧਾਇਆ ਗਿਆ ਹੈ ।
∴ 60° + x = 110° (ਤਿਭੁਜ ਦੇ ਬਾਹਰਲੇ ਕੋਣ ਗੁਣ ਦੇ ਅਨੁਸਾਰ)
|x = 110° – 60°
x = 50° (1)
ਤਿਭੁਜ △ABC ਵਿੱਚ
60° + x + y = 180° (ਤ੍ਰਿਭੁਜ ਦੇ ਕੋਲ ਜੋੜ ਗੁਣ ਅਨੁਸਾਰ)
60° + 50° +y = 180° [(1) ਦੀ ਵਰਤੋਂ ਕਰਨ ਤੇ]
110° + y = 180°
y = 180° – 110°
y = 70°
ਇਸ ਲਈ x = 50°
y = 70°
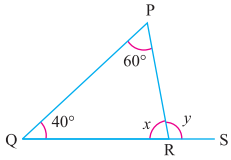
ਪ੍ਰਸ਼ਨ (ii).

ਉੱਤਰ:
ਤਿਭੁਜ △PQR ਵਿੱਚ ।
∠P + ∠Q + ∠R = 180° ਤਿਭੁਜ ਦੇ ਕੋਣ ਜੋੜ ਗੁਣ ਅਨੁਸਾਰ)
60° + 40° + x = 180°
100° + x = 180°
x = 180° – 100°
ਇਸ ਲਈ x = 80°
ਤ੍ਰਿਭੁਜ △PQR ਵਿੱਚ, QR ਨੂੰ ਵਧਾਇਆ ਗਿਆ ਹੈ ।
∴ y = 60° + 40° (ਤਿਭੁਜ ਦੇ ਬਾਹਰਲੇ ਕੋਣ ਗੁਣ ਅਨੁਸਾਰ)
y = 100°
x = 80°
![]()
ਪ੍ਰਸ਼ਨ (iii).
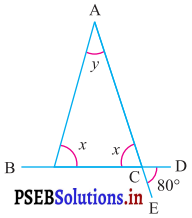
ਉੱਤਰ:
∠ACB = ∠ECD
∴ x = 80° ….(1) (ਸਿਖਰ ਸਨਮੁੱਖ ਕੋਣ)
∠ACD + ∠ECD = 180° (ਰੇਖੀ ਜੋੜਾ)
∴ ∠ACD + 80° = 180° [(1) ਦੀ ਵਰਤੋਂ ਕਰਨ ‘ਤੇ]
∠ACD = 180°- 80°
= 100° …(2)
ਤ੍ਰਿਭੁਜ △ABC ਵਿੱਚ BC ਨੂੰ ਬਿੰਦੂ D ਵਧਾਇਆ ਗਿਆ ਹੈ ।
x + y = ∠ACD (ਬਾਹਰਲੇ ਕੋਣ ਗੁਣ ਅਨੁਸਾਰ)
80° + y = 100° ((1) ਅਤੇ (2) ਦੀ ਵਰਤੋਂ ਕਰਨ ਤੇ)
y = 100° – 80°
y = 20°
ਇਸ ਲਈ x = 80° ਅਤੇ y = 20°
ਪ੍ਰਸ਼ਨ (iv).
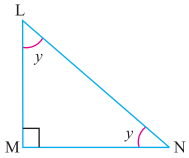
ਉੱਤਰ:
ਤਿਭੁਜ ਦੇ ਕੋਣ ਜੋੜ ਗੁਣ ਦੇ ਅਨੁਸਾਰ
∠L+ ∠M + ∠N = 180°
y + 90° + y = 180°
2y + 90° = 180°
2y = 180° – 90°
2y = 90°
y = \(\frac{90^{\circ}}{2}\)
y = 45°
![]()
ਪ੍ਰਸ਼ਨ (v).
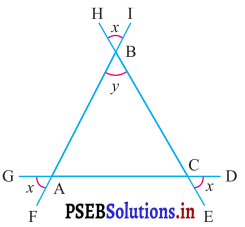
ਉੱਤਰ:
∠ABC = ∠HBI (ਸਿਖਰ ਸਨਮੁੱਖ ਕੋਣ)
∴ y = x …(1)
∠BAC = ∠GAF (ਸਿਖਰ ਸਨਮੁੱਖ ਕੋਣ)
∴ ∠BAC = x ..(2)
∠ACB = ∠ECD (ਸਿਖਰ ਸਨਮੁੱਖ ਕੋਣ)
∴ ∠ACB = x ….(3)
ਹੁਣ ਤਿਭੁਜ △ABC ਵਿੱਚ
∠BAC + ∠ABC + ∠ACB = 180° (ਤਿਭੁਜਾਂ ਦੇ ਕੋਣ ਜੋੜ ਗੁਣ)
x + x + x = 180° [(1), (2) ਅਤੇ (3) ਦੇ ਅਨੁਸਾਰ]
3x = 180°
x = \(\frac{180^{\circ}}{3}\)
x = 60° ….(4)
y = x
= 60°
((1) ਅਤੇ (4) ਦੀ ਵਰਤੋਂ ਕਰਨ ‘ਤੇ)
ਇਸ ਲਈ x = 60°, y = 60°
ਪ੍ਰਸ਼ਨ (vi).
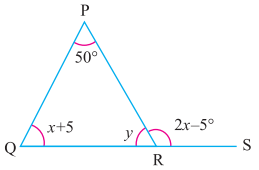
ਉੱਤਰ:
ਤਿਭੁਜ △PQR, ਵਿੱਚ QR ਨੂੰs ਬਿੰਦੂ ਤੱਕ ਵਧਾਇਆ ਗਿਆ ਹੈ ।
∴ 2x – 5° = 50° + x + 5° (ਬਾਹਰਲੇ ਕੋਣ ਦੇ ਜੋੜ ਗੁਣ ਅਨੁਸਾਰ)
2x – 5°= 55° + x
2x – x = 55° + 5°
x = 60° …(i)
ਤ੍ਰਿਭੁਜ △PQR ਵਿੱਚ ਕੋਣ ਜੋੜ ਗੁਣ ਦੇ ਅਨੁਸਾਰ
50° + x + 5° + y = 180°
55° + 60° + y = 180°
115° + y = 180°
y = 180° – 115°
y = 65°
ਇਸ ਲਈ x = 60° ਅਤੇ y = 65°
![]()
ਪ੍ਰਸ਼ਨ 4.
ਤ੍ਰਿਭੁਜ ਦੇ ਕੋਣਾਂ ਦਾ ਅਨੁਪਾਤ 5 : 6 : 7 ਹੈ | ਹਰੇਕ ਕੋਣ ਦਾ ਮਾਪ ਬੋਤੈ ਕਰੋ ।
ਹੱਲ :
ਮੰਨ ਲਓ ਕਿ ਦਿੱਤੇ ਗਏ ਕੋਣਾਂ ਦਾ ਮਾਪ (5x)°, (6x)°, (7x)° ਹੈ !
ਤਿਭੁਜ ਦੇ ਕੋਣਾਂ ਦੇ ਜੋੜ ਦੇ ਗੁਣ ਅਨੁਸਾਰ
(5x)° + (6x)° + (7x)° = 180°
(18x)° = 180°
x = \(\frac{180}{18}\)
x = 10
ਲੋੜੀਂਦੇ ਕੋਣ ਹਨ : (5x)°, (6x)°, (7x)°
= (5 × 10)°, (6 × 10)°, (7 × 10)°
= 50°, 60°, 70°
ਪ੍ਰਸ਼ਨ 5.
ਤ੍ਰਿਭੁਜ ਦੇ ਇੱਕ ਕੋਣ ਦਾ ਮਾਪ 60° ਹੈ । ਦੂਸਰੇ ਦੋ ਕੋਣਾਂ ਦਾ ਅਨੁਪਾਤ 4 : 8 ਹੈ | ਕੋਣ ਪਤਾ ਕਰੋ ।
ਹੱਲ :
ਤਿਭੁਜ ਦਾ ਇੱਕ ਕੋਣ = 60°
ਮੰਨ ਲਓ ਦੁਸਰੇ ਦੇ ਕੋਣ (4x)° ਅਤੇ (8x)° ਹਨ |
ਤਿਭੁਜ ਦੇ ਕੋਣ ਜੋੜ ਗੁਣ ਦੇ ਅਨੁਸਾਰ
60° + (4x)° + (8x)° = 180°
60° + (12x)° = 180°
(12x)° = 180° – 60°
(12x)° = 120°
x = \(\frac{120}{12}\)
x = 10
ਲੋੜੀਂਦੇ ਕੋਣ ਹਨ = (4x)°, (8x)°
(4 × 10)°, (8 × 10)°
= 40°, 80°
![]()
ਪ੍ਰਸ਼ਨ 6.
ਤ੍ਰਿਭੁਜ ABC ਵਿੱਚ, ∠B = 50°, ∠C= 62° ਤਾਂ ∠A ਪਤਾ ਕਰੋ ।
ਹੱਲ :
ਤਿਭੁਜ △ABC ਵਿੱਚ,
∠B = 50°, ∠C = 62°
ਤਿਭੁਜ ਦੇ ਕੋਣਾਂ ਦੇ ਜੋੜ ਗੁਣ ਅਨੁਸਾਰ
∠A + ∠B + ∠C = 1800
∠A + 50° + 62° = 180°
∠A + 112° = 180°
∠A = 180° – 12°
∠A = 68°
ਪ੍ਰਸ਼ਨ 7.
ਇੱਕ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਵਿੱਚ ਦੋ ਨਿਊਨ ਕੋਣਾਂ ਦਾ ਅਨੁਪਾਤ 2 : 3 ਹੈ । ਕੋਣ ਪਤਾ ਕਰੋ ।
ਹੱਲ :
ਸਮਕੋਣੀ ਤਿਭੁਜ ਦਾ ਇੱਕ ਕੋਣ ਹੁੰਦਾ ਹੈ = 90°
ਮੰਨ ਲਓ ਬਾਕੀ ਦੋ ਕੋਣ ਹਨ (2x)°, (3x)°
ਤ੍ਰਿਭੁਜ ਦੇ ਕੋਲ ਜੋੜ ਗੁਣ ਦੇ ਅਨੁਸਾਰ
90° + (2x)° + (3x)° = 180°
90° + (5x)° = 180°
(5x)° = 180° – 90°
(5x)° = 90°
x = \(\frac{90}{5}\)
x = 18
ਸਾਨੂੰ ਚਾਹੀਦੇ ਹਨ = (2x)°, (3x)°
= (2 × 18)°, (3 × 18)°
= 36°, 54°
![]()
ਪ੍ਰਸ਼ਨ 8.
ਤਿਭੁਜ ਦੇ ਤਿੰਨ ਕੋਣ (2x + 20)°, (x + 30)° ਅਤੇ (2x – 10)° ਹਨ । ਕੋਣ ਪਤਾ ਕਰੋ ।
ਹੱਲ :
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ ਤ੍ਰਿਭੁਜ ਦੇ ਤਿੰਨਾਂ ਕੋਣਾਂ ਦਾ ਜੋੜ 180° ਹੁੰਦਾ ਹੈ ।
∴ (2x + 20)° + (x + 30)° + (2x – 10)° = 180°
(5x + 40)° = 180°
(5x)° = 180° – 40°
(5x)° = 140°
x = \(\frac{140}{5}\)
x = 28
ਲੋੜੀਂਦੇ ਕੋਣ ਹਨ। = (2x + 20)°, (x + 30)° ਅਤੇ (2x – 10)°
= (2 × 28 + 20)°, (28 + 30)° ਅਤੇ (2 × 28 – 10)°
= (56 + 20)°, (58)° ਅਤੇ (56 – 10)°
= 76°, 58° ਅਤੇ 46°
9. ਬਹੁਵਿਕਲਪੀ ਪ੍ਰਸ਼ਨ :
ਪ੍ਰਸ਼ਨ (i).
ਇੱਕ ਭੁਜ ਦੇ ਦੋ ….. ਹੋ ਸਕਦੇ ਹਨ ।
(a) ਨਿਊਨ ਕੋਣ
(b) ਅਧਿਕ ਕੋਣ
(c) ਸਮਕੋਣ
(d) ਇਹਨਾਂ ਵਿੱਚੋਂ ਕੋਈ ਵੀ ਨਹੀਂ ।
ਉੱਤਰ:
(a) ਨਿਊਨ ਕੋਣ
ਪ੍ਰਸ਼ਨ (ii).
ਹੇਠਾਂ ਦਿੱਤਿਆਂ ਕੋਣਾਂ ਦੇ ਕਿਹੜੇ ਮਾਪਾਂ ਨਾਲ ਤਿਕੋਣ ਸੰਭਵ ਹੈ ।
(a) 30°, 40°, 100°
(b) 60°, 60°, 70°
(c) 60°, 50°, 70°
d) 90°, 89°, 92°
ਉੱਤਰ:
(c) 60°, 50°, 70°
![]()
ਪ੍ਰਸ਼ਨ (iii).
ਜੇਕਰ ਇੱਕ ਸਮਦੋਭੁਜੀ ਦੇ ਬਰਾਬਰ ਕੋਣਾਂ ਵਿੱਚੋਂ ਇੱਕ ਕੋਣ 45° ਹੈ ਤਾਂ ਇਸਦਾ ਤੀਸਰਾ ਕੋਣ ਪਤਾ ਕਰੋ ।
(a) 45°
(b) 60°
(c) 100°
(d) 90°
ਉੱਤਰ:
(d) 90°
ਪ੍ਰਸ਼ਨ (iv).
ਇੱਕ ਤ੍ਰਿਭੁਜ ਵਿੱਚ ਅਧਿਕ ਕੋਣਾਂ ਦੀ ਸੰ°ਖਿਆ ………… ਹੋ ਸਕਦੀ ਹੈ ।
(a) 2
(b) 1
(c) 3
(d) 4
ਉੱਤਰ:
(b) 1
