Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 6 Triangles Ex 6.4 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 7 Maths Chapter 6 Triangles Ex 6.4
1. Which of the following can be the sides of a triangle ?
(a) 8 cm, 10 cm, 18 cm
(b) 6 cm, 4 cm, 8 cm
(c) 35 cm, 38 cm, 40 cm
(d) 3 cm, 4 cm, 10 cm
Solutions:
Drawing of a triangle with given three sides is possible if sum of lengths of any two sides of a triangle is greater than the third side.
(a) Since 8 + 10 = 18
So, 8 cm, 10 cm, 18 cm cannot be the lengths of the sides of the triangle
(b) Since 6 + 4 > 8
4 + 8 >6
8 + 6 > 4
So, 6 cm, 4 cm, 8 cm can be lengths of the sides of a triangle.
(c) Since 35 + 38 > 40
38 + 40 > 35
40 + 35 > 38
So, 35 cm, 38 cm, 40 cm can be lengths of the sides of a triangle.
(d) Since 3 + 4 < 10
So, 3 cm, 4 cm, 10 cm cannot be the lengths of the sides of a triangle.
![]()
2. A point O is in interior of a ΔABC use symbols >, < or = to make the following statements true.
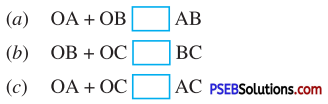
Answer:
(a) OA + OB > AB
(b) OB + OC > BC
(c) OA + OC > AC
3. ABCD is a quadrilateral
Is AB + BC + CD + DA > AC + BD ?

Solution:
Yes ; AB + BC + CD + DA > AC + BD
Proof : In ΔABC ; AB + BC > AC
[∵ sum of lengths of any two sides of a triangle is always greater than the third side] …. (i)
In ΔADC ; CD + DA > AC
[using same reason as above] …. (ii)
In ΔABD ; AB + DA > BD
[using same reason as above] …. (iii)
In ΔBCD ; BC + CD > BD
[using same reason as above] …. (iv)
Adding (i), (ii), (iii) and (iv), we get :
(AB + BC) + (CD + DA) + (AB + DA) + (BC + CD] > AC + AC + BD + BD (AB + AB) + (BC + BC) + (CD + CD) + (DA + DA) > 2AC + 2BD
2AB + 2BC + 2CD + 2DA > 2AC + 2BD
or 2 (AB + BC + CD + DA) > 2 (AC + BD)
or AB + BC + CD + DA > AC + BD
Proved.
![]()
4. AD is a median of < ABC
Is AB + BC + CA > 2AD ?
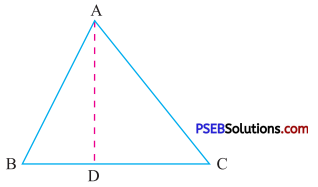
Solution:
In ΔABD
AB + BD > AD …(1)
{∵ Sum of the lengths of any two sides of a triangle is greater than the third side}
In ΔACD
CA + DC > AD …(2) (using same reason as above)
Adding (1) and (2), we get
AB + BD + CA + DC > AD + AD
AB + (BD + DC) + CA > 2AD
[D is mid point of BC BD + DC = BC]
Hence AB + BC + CA > 2AD.
5. The length of two sides of a triangle are 4 cm and 6 cm. Between what two measures should the length of the third side fall ?
Solution:
We know that the sum of two sides of a triangle is always greater than the third side.
Therefore, third side has to be less than the sum of the two sides.
The third is thus less than 4 cm + 6 cm = 10 cm
The third side cannot be less than the difference of the two sides.
Thus the third side has to be more than 6 cm – 4 cm = 2 cm the length of third side should be greater than 2 cm and less than 10 cm.
Hence the length of the third side should fall between 2 cm and 10 cm.
