Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 7 Congruence of Triangles Ex 7.2 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 7 Maths Chapter 7 Congruence of Triangles Ex 7.2
1. In the following pair of triangles examine whether the triangles are congruent or not. Write the rule of congruence if triangles are congruent.
Question (i).
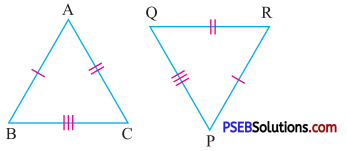
Answer:
ΔABC and ΔPQR
Side AB = Side PR ….(Given)
Side BC = Side PQ ….(Given)
Side AC = Side QR ….(Given)
So, By SSS congruence rule
ΔABC ≅ ΔPQR
Question (ii).
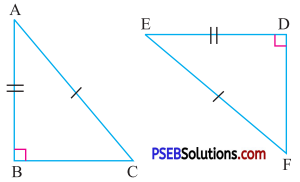
Answer:
In ΔABC and ΔEDF
∠B = ∠D ….(Each 90°)
Hypotenuse AC = Hypotenuse EF (given)
Side AB = Side DE ….(given)
So, by RHS congruence rule
ΔABC ≅ ΔEDF.
Question (iii).
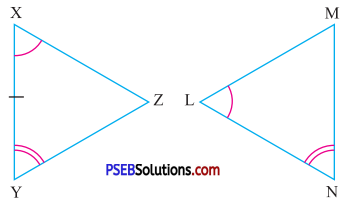
Answer:
In ΔXYZ and ΔLMN
∠X = ∠L
Side XY = Side LN ….(given)
∠Y = ∠N …..(given)
So by ASA congruence rule
ΔXYZ ≅ ΔLNM
![]()
Question (iv).
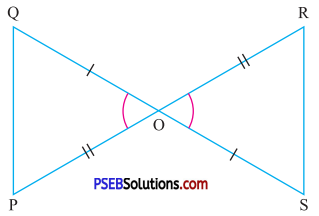
Answer:
In ΔOPQ and ΔOSR
Side OQ = Side QR ….(given)
∠POQ = ∠SOR ….(Vertically opp. ∠s)
Side OP = Side OR ….(given)
So, by SAS congruence rule
ΔOPQ ≅ ΔORS
Question (v).
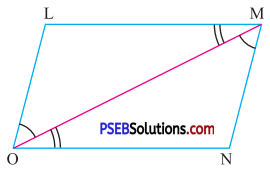
Answer:
In ΔOML and ΔMON
∠LOM = ∠OMN ….(given)
Side OM = Side MO ….(common)
∠OML = ∠MON ….(given)
So, by ASA congmence rule
ΔLOM ≅ ΔOMN
Question (vi).
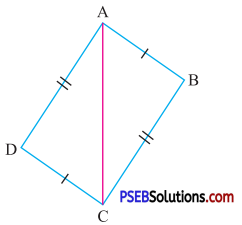
Answer:
In ΔACD and ΔACB
Side AC = Side AC ….(common)
Side CD = Side AB ….(given)
Side AD = Side BC ….(given)
So, by SSS congruence rule
ΔACD ≅ ΔACB.
![]()
2. In fig. ΔAMP ≅ ΔAMQ, Give reason for the following steps.
| Steps | Reasons |
| (i) PM = QM | ……………………….. |
| (ii) ∠PMA = ∠QMA | ……………………….. |
| (iii) AM = AM | ……………………….. |
| (iv) ΔAMP ≅ ΔAMQ | ……………………….. |
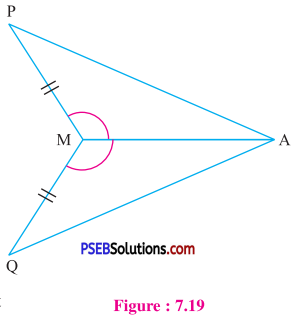
Solution:
| Steps | Reasons |
| (i) PM = QM | (i) given |
| (ii) ∠PMA = ∠QMA | (ii) given |
| (iii) AM = AM | (iii) common |
| (iv) ΔAMP ≅ ΔAMQ | (iv) By SAS congruence rule |
![]()
3. In given figure AB = AC and BD = DC. Prove that :
(i) ΔABD as ΔACD
(ii) ∠B ≅ ∠C
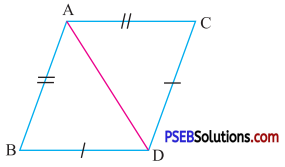
Solution:
In ΔABD and ΔACD
Side AB = Side AC ….(given)
Side BD = Side DC ….(given)
Side AD = Side AD ….(common)
So, by SSS congruence rale
(i) ΔABD ≅ ΔACD
(ii) ∠B = ∠C ….(By the corresponding parts of congruent triangles are equal)
4. In the given (figure 7.20), AC = CE and BC = CD. Prove that ΔACB ≅ ΔECD.
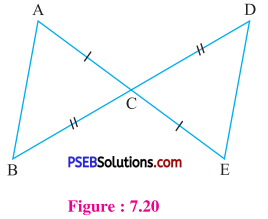
Solution:
In ΔACB and ΔECD
Side AC = Side CE …..(given)
∠ACB = ∠ECD (vertically opposite angles)
Side BC = Side CD
So, by SAS congruence rule.
5. In the given figure
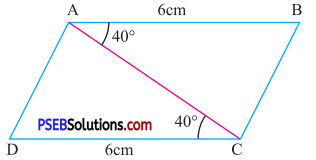
(i) Write three pairs of equal parts in ΔADC and ΔCBA
(ii) Is ΔADC ≅ ΔCBA ? Give reasons.
(iii) Is AD = CB ? Give reasons.
Solutions:
(i) In ΔADC and ΔCBA, three pairs of equal parts are
Side DC = Side AB (given)
∠ACD = ∠BAC (each 60°)
Side AC = Side CA (common).
(ii) Yes, from part (i) by using SAS congruence rules
We conclude that ΔADC ≅ ΔCBA with correspondence A → C, D → B, C → B.
(iii) Yes, from part (ii) ΔADC ≅ ΔCBA we know that, the corresponding parts of congruent triangle are equals.
Therefore AD = CB.
![]()
6. In the given figure PQ || RS and PQ = RS. Prove that
(i) ΔPOQ ≅ ΔSOR
(ii) ∠POQ = ∠SOR.
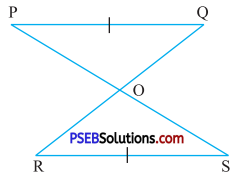
Solution:
In ΔPOQ and ΔSOR
∠OPQ = ∠OSR (Alternate interior angles)
Side PQ = Side RS (given)
∠OQP = ∠ORS (Alternate interior angles)
(i) By ASA congruence rule,
ΔPOQ ≅ ΔSOR
(ii) From part (i) ΔPOQ ≅ ΔSOR we know that, the corresponding parts of congruent triangles are equal
∴ ∠POQ = ∠SOR
7. In the given figure, M is midpoint of AD and ∠A = ∠D. Show that ΔAMB ≅ ΔDMC
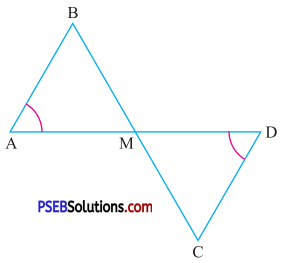
Solution:
In ΔAMB and ΔDMC
∠A = ∠D ….(given)
Side AM = Side MD (∵ M is mid point of AD ∴)
∠AMB = ∠DMC (vertically opposite angles)
So, by ASA congruence
ΔAMB ≅ ΔDMC
![]()
8. In flie given figure SP ⊥ PQ, RQ ⊥ PQ and PR = QS.
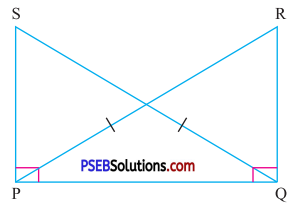
(i) Write three parts of equal parts in ΔPQR and ΔSPQ
(ii) Prove that ΔPQR ≅ ΔQPS
Solution:
(i) In ΔPQR and ΔSPQ, three equal parts are
∠PQR = ∠SPQ (each 90°)
Hypotenuse PR = Hypotenuse SQ ….(given)
Side PQ = Side PQ (common)
(ii) From part (i) by using RHS congruence rule.
We conclude that ΔPQR = ΔQPS with correspondence
P ↔ Q, Q ↔ P, R ↔ S
9. In given figure AB ⊥ QR, AC ⊥ QP and QC = QB. Prove that
(i) ΔQAB ≅ ΔQAC
(ii) ∠AQB ≅ ∠AQC
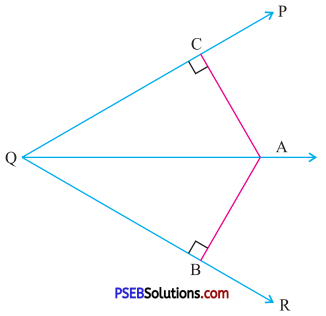
Solution:
(i) In ΔQAB and ΔQAC
∠ABQ = ∠ACQ (Each 90°)
Hyp. AQ = Hyp AQ (common side)
Side QB = Side QC …(given)
So, by RHS congruence rule
ΔQAB ≅ ΔQAC
(ii) From part (i) ΔQAB = ΔQAC.
We know that the corresponding parts of congruent triangles are equal.
Therefore
∠AQB = ∠AQC.
10. Multiple Choice Questions :
Question (i).
Which of the following is not a congruence rule
(a) ASA
(b) SAS
(c) SSS
(d) AAA
Answer:
(d) AAA
Question (ii).
If ΔABC as ΔPQR, then the correct statement is
(a) ∠A = ∠Q
(b) ∠A = ∠R
(c) ∠A = ∠P
(d) AB = QR
Answer:
(c) ∠A = ∠P
Question (iii).
If ∠A = ∠D, ∠B = ∠E and AB = DE, then ΔABC ≅ ΔDEF, by the congruence rule :
(a) SSS
(b) ASA
(c) SAS
(d) RHS
Answer:
(b) ASA
![]()
11. ASA congruence criterion is same as SAS congruence criterion. (True/False)
Answer:
False
12. Two right angled triangles are always congruent. (True/False)
Answer:
False
13. ‘=’ symbol used for congruence of triangles. (True/False)
Answer:
False
