Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 1 ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ Ex 1.2 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 8 Maths Chapter 1 ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ Exercise 1.2
ਪ੍ਰਸ਼ਨ 1.
ਹੇਠ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਨੂੰ ਸੰਖਿਆ ਰੇਖਾ ‘ਤੇ ਅੰਕਿਤ ਕਰੋ :
ਹੱਲ:
(i) ਅਸੀਂ ਸਿਫਰ ਤੋਂ ਸ਼ੁਰੂ ਕਰਕੇ ਸੱਜੇ ਪਾਸੇ 7 ਚਿੰਨ੍ਹ ਲਗਾਉਂਣੇ ਹਨ, ਜਿਹਨਾਂ ਦੀ ਹਰੇਕ ਤੋਂ ਦੂਰੀ ਤੇ ਹੈ ।
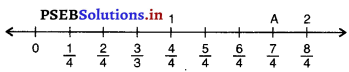
ਬਿੰਦੂ A ਪਰਿਮੇਯ ਸੰਖਿਆ \(\frac{7}{4}\) ਨੂੰ ਦਿਖਾਉਂਦਾ ਹੈ ।
(ii) ਅਸੀਂ ਸਿਫਰ ਤੋਂ ਸ਼ੁਰੂ ਕਰਦੇ ਹੋਏ ਖੱਬੇ ਪਾਸੇ 7 ਚਿੰਨ੍ਹ ‘ ਲਗਾਉਂਦੇ ਹਾਂ ਜਿਹਨਾਂ ਦੀ ਹਰੇਕ ਤੋਂ ਦੂਰੀ \(\frac{1}{6}\) ਹੈ ।
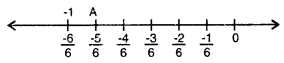
ਬਿੰਦੂ A ਪਰਿਮੇਯ ਸੰਖਿਆ \(\frac{-5}{6}\) ਦਰਸਾਉਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 2.
\(\frac{-2}{11}\), \(\frac{-5}{11}\), \(\frac{-9}{11}\) ਨੂੰ ਸੰਖਿਆ ਰੇਖਾ ‘ਤੇ ਅੰਮ੍ਰਿਤ ਕਰੋ ।
ਹੱਲ:

![]()
ਪ੍ਰਸ਼ਨ 3.
ਇਸ ਤਰ੍ਹਾਂ ਦੀਆਂ ਪੰਜ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਲਿਖੋ ਜੋ 2 ਨਾਲੋਂ ਛੋਟੀਆਂ ਹੋਣ।
ਹੱਲ:

∴ 2 ਨਾਲੋਂ ਛੋਟੀਆਂ ਪੰਜ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ, ਇਹਨਾਂ ਵਿਚੋਂ ਕੋਈ ਵੀ ਹੋ ਸਕਦੀ ਹੈ ।
\(\frac{9}{5}\), \(\frac{8}{5}\), \(\frac{7}{5}\), \(\frac{6}{5}\), \(\frac{5}{5}\), \(\frac{4}{5}\), \(\frac{3}{5}\), \(\frac{2}{5}\), \(\frac{1}{5}\) ਆਦਿ ।
ਪ੍ਰਸ਼ਨ 4.
\(-\frac{2}{5}\) ਅਤੇ \(\frac{1}{2}\) ਦੇ ਵਿਚਕਾਰ ਦਸ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਅਸੀਂ ਇਹਨਾਂ ਨੂੰ ਸਮਾਨ ਹਰ ਵਾਲੀਆਂ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਵਿਚ ਬਦਲਦੇ ਹਾਂ ।
ਅਰਥਾਤ \(\frac{-2}{5}\) x \(\frac{4}{4}\) = \(\frac{-8}{20}\)
ਅਤੇ \(\frac{1}{2}\) x \(\frac{10}{10}\) = \(\frac{10}{20}\)
∴ \(\frac{-4}{10}\) ਅਤੇ \(\frac{5}{10}\) ਵਿਚਕਾਰ ਦਸ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਇਨ੍ਹਾਂ ਵਿਚੋਂ ਕੋਈ ਵੀ ਹੋ ਸਕਦੀਆਂ ਹਨ ।
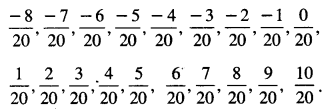
![]()
ਪ੍ਰਸ਼ਨ 5.
(1) \(\frac{2}{3}\) ਅਤੇ \(\frac{4}{5}\)
(ii) \(\frac{-3}{2}\) ਅਤੇ \(\frac{5}{3}\)
(iii) \(\frac{1}{4}\) ਅਤੇ \(\frac{1}{2}\) ਦੇ ਚਕਾਰ ਪੰਜ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
(i) ਅਸੀਂ \(\frac{2}{3}\) ਅਤੇ \(\frac{4}{5}\) ਦੇ ਵਿਚਕਾਰ ਪੰਜ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਪਤਾ ਕਰਨੀਆਂ ਹਨ ।
∴ ਇਥੇ ਅਸੀਂ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ \(\frac{2}{3}\) ਅਤੇ \(\frac{4}{5}\) ਦੇ ਵਿਚਕਾਰ ਸੰਖਿਆ ਪਤਾ ਕਰਨ ਦੇ ਲਈ ਮੱਧ ਪਤਾ ਕਰਾਂਗੇ ।

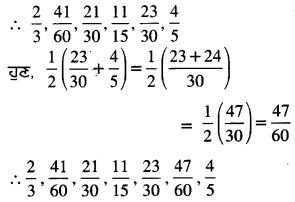
(ii) \(\frac{-3}{2}\) ਅਤੇ \(\frac{5}{3}\) ਦੇ ਵਿਚਕਾਰ ਦੀਆਂ ਪੰਜ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਪ੍ਰਾਪਤ ਕਰਨ ਦੇ ਲਈ ਅਸੀਂ ਉਨ੍ਹਾਂ ਦੇ ਸਮਾਨ ਹਰ ਵਾਲੀਆਂ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਵਿਚ ਬਦਲਾਂਗੇ ।
ਅਰਥਾਤ, \(\frac{-3}{2}\) × \(\frac{3}{3}\) = \(\frac{-9}{6}\)
ਅਤੇ \(\frac{5}{3}\) × \(\frac{2}{2}\) = \(\frac{10}{6}\)
∴ \(\frac{-9}{6}\) ਅਤੇ \(\frac{10}{6}\) ਦੇ ਵਿਚਕਾਰ ਦੀਆਂ ਪੰਜ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਇਨ੍ਹਾਂ ਵਿਚੋਂ ਕੋਈ ਵੀ ਹੋ ਸਕਦੀਆਂ ਹਨ ।
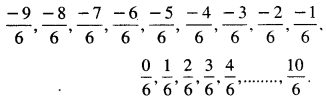
(iii) \(\frac{1}{4}\) ਅਤੇ \(\frac{1}{2}\) ਦੇ ਵਿਚਕਾਰ ਦੀਆਂ ਪੰਜ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਪ੍ਰਾਪਤ ਕਰਨ ਦੇ ਲਈ ਅਸੀਂ ਉਨ੍ਹਾਂ ਨੂੰ ਸਮਾਨ ਹਰ ਵਾਲੀਆਂ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਵਿਚ ਬਦਲਾਂਗੇ ।
ਅਰਥਾਤ, \(\frac{1}{4}\) × \(\frac{100}{100}\) = \(\frac{100}{400}\)
ਅਤੇ \(\frac{1}{2}\) × \(\frac{200}{200}\) = \(\frac{200}{400}\)
∴ \(\frac{100}{400}\) ਅਤੇ \(\frac{200}{400}\) ਦੇ ਵਿਚਕਾਰ ਪੰਜ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਇਹਨਾਂ ਵਿਚੋਂ ਕੋਈ ਵੀ ਹੋ ਸਕਦੀਆਂ ਹਨ ।
\(\frac{100}{400}\), \(\frac{101}{400}\), \(\frac{102}{400}\), \(\frac{103}{400}\), ……….. \(\frac{200}{400}\).
ਪ੍ਰਸ਼ਨ 6.
-2 ਨਾਲੋਂ ਵੱਡੀਆਂ ਪੰਜ ਪਰਿਯ ਸੰਖਿਆਵਾਂ ਲਿਖੋ।
ਹੱਲ:
-2 ਨਾਲੋਂ ਵੱਡੀਆਂ ਪੰਜ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਹਨ :
\(-\frac{3}{2}\), -1, \(-\frac{1}{2}\), 0, \(\frac{1}{2}\)
ਇਹੋ ਜਿਹੀਆਂ ਅਨੇਕ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਹੋ ਸਕਦੀਆਂ ਹਨ ।
![]()
ਪ੍ਰਸ਼ਨ 7.
\(\frac{3}{5}\) ਅਤੇ \(\frac{3}{4}\) ਦੇ ਵਿਚ ਦਸ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਅਸੀਂ ਇਨ੍ਹਾਂ ਸਮਾਨ ਹਰ ਵਾਲੀਆਂ ਪਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਵਿਚ ਬਦਲਾਂਗੇ ।
ਅਰਥਾਤ \(\frac{3}{5}\) × \(\frac{20}{20}\) = \(\frac{60}{100}\)
ਅਤੇ \(\frac{3}{4}\) × \(\frac{25}{25}\) = \(\frac{75}{100}\)
∴ \(\frac{60}{100}\) ਅਤੇ \(\frac{75}{100}\) ਦੇ ਵਿਚ ਦਸ ਰਿਮੇਯ ਸੰਖਿਆਵਾਂ ਇਹਨਾਂ ਵਿਚੋਂ ਕੋਈ ਵੀ ਹੋ ਸਕਦੀਆਂ ਹਨ ।

