Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 10 Visualising Solid Shapes Ex 10.3 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.3
1. Can a polyhedron have for its faces:
Question (i)
3 triangles?
Solution:
[Note: Polyhedron is a solid, which is made by polygonal regions and these polygonal regions are called its faces.]
No, a polyhedron cannot have 3 triangles for its faces because it have atleast 4 faces.
![]()
Question (ii)
4 triangles?
Solution:
Yes, a polyhedron can have 4 triangles for its faces as triangular pyramid.
Question (iii)
a square and four triangles?
Solution:
Yes, a polyhedron can have a square and four triangles for its faces as a pyramid with square base.
2 Is it possible to have a polyhedron with any given number of faces? (Hint: Think of a pyramid.)
Solution:
Yes, it can be possible only if the number of faces is greater than or equal to 4, because a polyhedron has atleast 4 faces.
![]()
3. Which are prisms among the following?
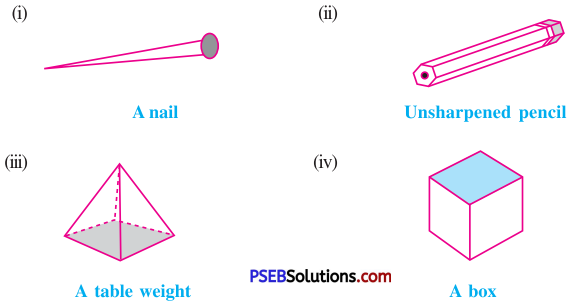
Solution:
Note: A prism is a polyhedron whose base and top are congruent polygons and lateral faces are rectangles.
(i) No, a nail is not a prism because its base and top are not congruent polygons.
(ii) Yes, an unsharpened pencil is a prism because its base and top are congruent polygons and faces are rectangles.
(iii) No, a table weight is not a prism because its top and base are not congruent polygons.
(iv) Yes, box is a prism because its base and top are congruent polygons and lateral faces are rectangles.
4.
Question (i)
How are prisms and cylinders alike?
Solution:
Top and base of a prism and of a cylinder are congruent and parallel to each other and a prism becomes a cylinder, if the number of sides of its base becomes larger and larger.
![]()
Question (ii)
How are pyramids and cones alike?
Solution:
The pyramids and cones are alike because their lateral faces meet at a vertex. Also, a pyramid becomes a cone if the number of sides of its base becomes larger and larger.
5. Is a square prism same as a cube? Explain.
Solution:
No, a square prism is not same as a cube. It can be a cuboid also.
6. Verify Euler’s formula for these solids:
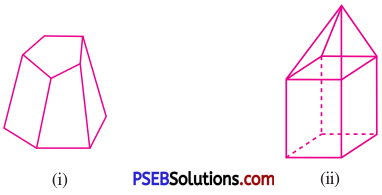
Solution:
(i) For figure (i)
F = 7, V= 10 and E = 15
∴ F + V = 7 + 10 = 17
Now, F + V – E = 17 – 15 = 2
Thus, F + V – E = 2
Hence, Euler’s formula is verified.
(ii) For figure (ii)
F = 9, V = 9 and E = 16
∴ F + V = 9 + 9 = 18
Now, F + V – E = 18 – 16 = 2
Thus, F + V – E = 2
Hence, Euler’s formula is verified.
![]()
7. Using Euler’s formula find the unknown:
| (i) | (ii) | (iii) | |
| Faces | ? | 5 | 20 |
| Vertices | 6 | ? | 12 |
| Edges | 12 | 9 | ? |
Solution:
(i) Here, F = ?, V = 6 and E = 12
Now, F + V – E = 2 (∵ Euler’s formula)
∴ F + 6 – 12 = 2
∴ F – 6 = 2
∴ F = 2 + 6
∴ F = 8
(ii) Here, F = 5, V = ? and E = 9
Now, F + V – E = 2 (∵ Euler’s formula)
∴ 5 + V – 9 = 2
∴ V – 4 = 2
∴ V = 2 + 4
∴ V = 6
(iii) Here, F = 20, V = 12 and E = ?
Now, F + V – E = 2 (∵ Euler’s formula)
∴ 20 + 12 – E = 2
∴ 32 – E = 2
∴ – E = 2 – 32
∴ – E = – 30
∴ E = 30
![]()
8. Can a polyhedron have 10 faces, 20 edges and 15 vertices?
Solution:
Here, F = 10, E = 20 and V = 15
By Euler’s formula, F + V – E = 2
LHS = F + V – E
= 10 + 15 – 20
= 25 – 20 = 5
Thus, F + V – E ≠ 2
Hence, such a polyhedron is not possible.
