PSEB 8th Class Maths Solutions Chapter 13 ਸਿੱਧਾ ਅਤੇ ਉਲਟ ਸਮਾਨ ਅਨੁਪਾਤ Ex 13.1

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 13 ਸਿੱਧਾ ਅਤੇ ਉਲਟ ਸਮਾਨ ਅਨੁਪਾਤ Ex 13.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 13 ਸਿੱਧਾ ਅਤੇ ਉਲਟ ਸਮਾਨ ਅਨੁਪਾਤ Exercise 13.1

ਪ੍ਰਸ਼ਨ 1.
ਇਕ ਰੇਲਵੇ ਸਟੇਸ਼ਨ ਦੇ ਨੇੜੇ ਕਾਰ ਪਾਰਕਿੰਗ ਫੀਸ ਇਸ ਤਰ੍ਹਾਂ ਹੈ :
4 ਘੰਟੇ ਤੱਕ — ₹ 60
8 ਘੰਟੇ ਤੱਕ — ₹ 100
12 ਘੰਟੇ ਤੱਕ — ₹ 140
24 ਘੰਟੇ ਤੱਕ — ₹80
ਪੜਤਾਲ ਕਰੋ ਕਿ ਕੀ ਕਾਰ ਪਾਰਕਿੰਗ ਫੀਸ, ਪਾਰਕਿੰਗ ਸਮੇਂ ਦੇ ਸਿੱਧੇ ਅਨੁਪਾਤ ਵਿਚ ਹੈ ।
ਹੱਲ:
4 ਘੰਟੇ ਦੇ ਲਈ ਪਾਰਕਿੰਗ ਫੀਸ ਤੋਂ 60 ਹੈ ।
∴ \(\frac{60}{4}\) = \(\frac{15}{1}\)
8 ਘੰਟੇ ਦੇ ਲਈ ਪਾਰਕਿੰਗ ਫੀਸ ਤੋਂ 100 ਹੈ !
∴ \(\frac{100}{8}\) = \(\frac{25}{2}\)
ਇਸ ਲਈ, ਪਾਰਕਿੰਗ ਫੀਸ ਪਾਰਕਿੰਗ ਸਮੇਂ ਦੇ ਸਿੱਧੇ ਅਨੁਪਾਤ ਵਿਚ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਇਕ ਪੇਂਟ ਦੇ ਮੂਲ ਮਿਸ਼ਰਨ (base) ਦੇ 8 ਭਾਗਾਂ ਵਿਚ ਲਾਲ ਰੰਗ ਦੇ ਪਦਾਰਥ ਦਾ 1 ਭਾਗ ਮਿਲਾ ਕੇ ਮਿਸ਼ਰਨ ਤਿਆਰ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਹੇਠਾਂ ਲਿਖੀ ਸਾਰਣੀ ਵਿਚ, ਮੂਲ ਮਿਸ਼ਰਨ ਦੇ ਉਹ ਭਾਗ ਪਤਾ ਕਰੋ ਜਿਨ੍ਹਾਂ ਨੂੰ ਮਿਲਾਏ ਜਾਣ ਦੀ ਜ਼ਰੂਰਤ ਹੈ :

ਹੱਲ:
ਦਿੱਤੀ ਗਈ ਸਾਰਣੀ ਹੈ :

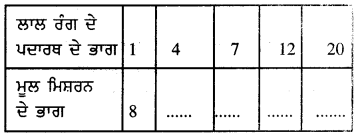
ਇੱਥੇ, ਲਾਲ ਰੰਗ ਦੇ ਪਦਾਰਥ ਦੇ ਭਾਗ ਦਾ ਮੂਲ ਮਿਸ਼ਨ ਦੇ ਭਾਗ ਦੇ ਅਨੁਪਾਤ = \(\frac{1}{8}\) ਹੈ ।
∴ ਹਰੇਕ ਭਾਗ ਦੇ ਲਈ ਅਨੁਪਾਤ ਬਰਾਬਰ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ ।
∴ \(\frac{4}{32}\) = \(\frac{1}{8}\), \(\frac{7}{56}\) = \(\frac{1}{8}\), \(\frac{12}{96}\) = \(\frac{1}{8}\), \(\frac{20}{160}\) = \(\frac{1}{8}\).
ਇਸ ਲਈ, ਸਾਰਣੀ ਇਸ ਤਰ੍ਹਾਂ ਹੋਵੇਗੀ :

ਪ੍ਰਸ਼ਨ 3.
ਪ੍ਰਸ਼ਨ 2 ਵਿਚ ਜੇ ਲਾਲ ਰੰਗ ਦੇ ਪਦਾਰਥ ਦੇ 1 ਭਾਗ ਦੇ ਲਈ 75 mLਮੂਲੇ ਮਿਸ਼ਰਨ ਦੀ ਜ਼ਰੂਰਤ ਹੈ, ਤਾਂ ਮੂਲ ਮਿਸ਼ਰਨ ਦੇ 1800mL ਵਿੱਚ ਸਾਨੂੰ ਕਿੰਨਾ ਲਾਲ ਰੰਗ ਦਾ ਪਦਾਰਥ ਮਿਲਾਉਣਾ ਚਾਹੀਦਾ ਹੈ ?
ਹੱਲ:
ਲਾਲ ਰੰਗ ਦੇ ਪਦਾਰਥ ਦੇ ਭਾਗ ਦਾ ਮੂਲ ਮਿਸ਼ਰਨ ਦੇ ਭਾਗ ਨਾਲ ਅਨੁਪਾਤ = \(\frac{1}{8}\)
∴ ਜੇਕਰ ਲਾਲ ਰੰਗ ਦੇ ਪਦਾਰਥ ਦੇ 1 ਭਾਗ ਦੇ ਲਈ 75 mL ਮੂਲ ਮਿਸ਼ਰਨ ਦੀ ਜ਼ਰੂਰਤ ਹੋਵੇ ।
ਅਰਥਾਤ ਮੂਲ ਮਿਸ਼ਰਨ ਦਾ 75 mL ਜ਼ਰੂਰਤ ਹੈ = 1
ਭਾਗ ਲਾਲ ਰੰਗ ਦੇ ਪਦਾਰਥ ਦੇ ਲਈ
1 ,, ,, ,, = \(\frac{1}{75}\) ਭਾਗ ਲਾਲ ਰੰਗ ਦੇ ਪਦਾਰਥ ਦੇ ਲਈ
∴ 1800 mL ,, ,, = \(\frac{1}{75}\) × 1800 ਭਾਗ ਲਾਲ ਰੰਗ ਦੇ ਪਦਾਰਥ ਦੇ ਲਈ
= 24 ਭਾਗ ।

ਪ੍ਰਸ਼ਨ 4.
ਕਿਸੇ ਸਾਫਟ ਡਰਿੰਕ ਫੈਕਟਰੀ ਵਿਚ ਇਕ ਮਸ਼ੀਨ 840 ਬੋਤਲਾਂ 6 ਘੰਟੇ ਵਿਚ ਭਰਦੀ ਹੈ । ਉਹ ਮਸ਼ੀਨ ਪੰਜ ਘੰਟੇ ਵਿਚ ਕਿੰਨੀਆਂ ਬੋਤਲਾਂ ਭਰੇਗੀ ?
ਹੱਲ:
6 ਘੰਟਿਆਂ ਵਿਚ ਭਰੀਆਂ ਜਾਣ ਵਾਲੀਆਂ ਬੋਤਲਾਂ ਦੀ ਸੰਖਿਆ = 840
1 ਘੰਟੇ ,, ,, ,, ,, = \(\frac{840}{6}\)
5 ਘੰਟੇ ,, , , ,, = \(\frac{840}{6}\) × 5
= 700 ਬੋਤਲਾਂ ।

ਪ੍ਰਸ਼ਨ 5.
ਇਕ ਬੈਕਟੀਰੀਆ (bacteria) ਜਾਂ ਜੀਵਾਣੂ ਦੇ ਫੋਟੋਗ੍ਰਾਫ (ਚਿੱਤਰ) ਨੂੰ 50,000 ਗੁਣਾ ਵੱਡਾ ਕਰਨ ‘ਤੇ ਉਸਦੀ ਲੰਬਾਈ 5 cm ਹੋ ਜਾਂਦੀ ਹੈ, ਜਿਵੇਂ ਕਿ ਪਾਠ ਪੁਸਤਕ ਵਿੱਚ ਦਿੱਤੇ ਚਿੱਤਰ ਵਿਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ । ਇਸ ਬੈਕਟੀਰੀਆ ਦੀ ਅਸਲ ਲੰਬਾਈ ਕੀ ਹੈ ? ਜੇਕਰ ਫੋਟੋਗ੍ਰਾਫ ਨੂੰ ਸਿਰਫ 20,000 ਗੁਣਾ ਵੱਡਾ ਕੀਤਾ ਜਾਵੇ, ਤਾਂ ਉਸਦੀ ਵਧਾਈ ਗਈ ਲੰਬਾਈ ਕੀ ਹੋਵੇਗੀ ?
ਹੱਲ:
ਬੈਕਟੀਰੀਆ ਦੀ ਲੰਬਾਈ, ਜਦੋਂ ਉਸਨੂੰ 50,000 ਗੁਣਾ ਵਧਾਇਆ ਜਾਂਦਾ ਹੈ = 5 cm
,, ,, ,, ,, 1 ਗੁਣਾ ,, ,, (ਅਰਥਾਤ ਅਸਲ ਲੰਬਾਈ)
= \(\frac{5}{50,000}\) cm
= \(\frac{1}{10,000}\) cm
= \(\frac{1}{10^{4}}\) cm
= 10^-4 cm
ਬੈਕਟੀਰੀਆ ਦੀ ਲੰਬਾਈ, ਜਦੋਂ ਉਸਨੂੰ 1 ਗੁਣਾ ਵਧਾਇਆ ਜਾਂਦਾ ਹੈ ।
= \(\frac{1}{10,000}\) cm
,, ,, ,, ,, ,, 20,000 ਗੁਣਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
= \(\frac{1}{10,000}\) × 20,000
= 2 cm.

ਪ੍ਰਸ਼ਨ 6.
ਇਕ ਜਹਾਜ਼ ਦੇ ਮਾਡਲ ਵਿਚ, ਉਸਦਾ ਮਸਤੂਲ (mast) 9 cm ਉੱਚਾ ਹੈ, ਜਦਕਿ ਅਸਲ ਵਿਚ ਜਹਾਜ਼ ਦਾ ਮਸਤੂਲ 12 m ਉੱਚਾ ਹੈ । ਜੇ ਜਹਾਜ਼ ਦੀ ਲੰਬਾਈ 28 m ਹੈ, ਤਾਂ ਉਸਦੇ ਮਾਡਲ ਦੀ ਲੰਬਾਈ ਕਿੰਨੀ ਹੈ ?
ਹੱਲ:
ਸਮਤੁਲ ਦੀ ਅਸਲ ਉੱਚਾਈ = 12 m.
= 1200 cm
ਮਾਡਲ ਵਿਚ ਸਮਤੂਲ ਦੀ ਉੱਚਾਈ = 9 cm
∴ ਅਨੁਪਾਤ = \(\frac{1200}{9}\)
= \(\frac{400}{3}\)
ਜਹਾਜ਼ ਦੀ ਅਸਲ ਲੰਬਾਈ = 28 m
= 2800 cm
ਮੰਨ ਲਉ ਮਾਡਲ ਵਿਚ ਜਹਾਜ਼ ਦੀ ਲੰਬਾਈ
= x cm
∴ ਲੰਬਾਈਆਂ ਵਿਚ ਅਨੁਪਾਤ ਹੋਵੇਗਾ = \(\frac{400}{3}\)
ਅਰਥਾਤ \(\frac{2800}{x}\) = \(\frac{400}{3}\)
⇒ x = \(\frac{2800×3}{400}\)
= 21 cm.

ਪ੍ਰਸ਼ਨ 7.
ਮੰਨ ਲਉ 2 kg ਖੰਡ ਵਿਚ 9 × 10⁶ ਕ੍ਰਿਸਟਲ ਹਨ । ਹੇਠਾਂ ਲਿਖੀ ਖੰਡ ਵਿਚ ਖੰਡ ਦੇ ਕਿੰਨੇ ਕ੍ਰਿਸਟਲ ਹੋਣਗੇ ?
(i) 5 kg
(ii) 1.2 kg.
ਹੱਲ:
2 kg ਖੰਡ ਵਿਚ ਕ੍ਰਿਸਟਲਾਂ ਦੀ ਸੰਖਿਆ
= 9 × 10⁶
1 kg ਖੰਡ ਵਿਚ ਕ੍ਰਿਸਟਲਾਂ ਦੀ ਸੰਖਿਆ
\(\frac{9}{2}\) × 10⁶
∴ 5 kg ਖੰਡ ਵਿਚ ਕ੍ਰਿਸਟਲਾਂ ਦੀ ਸੰਖਿਆ
= \(\frac{9}{2}\) × 5 × 10⁶
= \(\frac{45}{2}\) × 10⁶
= 22.5 × 10⁶
ਦੁਬਾਰਾ :
= 2.25 × 10⁷ ਕ੍ਰਿਸਟਲ
1 kg ਖੰਡ ਵਿਚ ਕ੍ਰਿਸਟਲਾਂ ਦੀ ਸੰਖਿਆ
= \(\frac{9}{2}\) × 10⁶
1.2 kg ਖੰਡ ਵਿਚ ਕ੍ਰਿਸਟਲਾਂ ਦੀ ਸੰਖਿਆ
= \(\frac{9}{2}\) × 1.2 × 10⁶
= \(\frac{10.8}{2}\) × 10⁶
= 5.4 × 10⁶ ਕ੍ਰਿਸਟਲ।

ਪ੍ਰਸ਼ਨ 8.
ਰਸ਼ਮੀ ਦੇ ਕੋਲ ਇੱਕ ਸੜਕ ਦਾ ਨਕਸ਼ਾ ਹੈ, ਜਿਸਦੇ ਪੈਮਾਨੇ ਵਿਚ 1 cm ਦੀ ਦੂਰੀ 18 km ਦਰਸਾਉਂਦੀ ਹੈ । ਉਹ ਉਸ ਸੜਕ ਤੇ ਆਪਣੀ ਗੱਡੀ ਤੋਂ 72 km ਦੀ ਦੂਰੀ ਤੈਅ ਕਰਦੀ ਹੈ । ਉਸਦੇ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ ਨਕਸ਼ੇ ਵਿਚ ਕੀ ਹੋਵੇਗੀ ?
ਹੱਲ:
18 km ਸੜਕ ਨਕਸ਼ੇ ਉੱਤੇ ਦਰਸਾਉਂਦੀ ਹੈ 1 cm ਵਿਚ
∴ 1 km ਸੜਕ ਨਕਸ਼ੇ ਉੱਤੇ ਦਰਸਾਉਂਦੀ ਹੈ \(\frac{1}{18}\) cm ਵਿਚ
∴ 72 km ਸੜਕ ਨਕਸ਼ੇ ਉੱਤੇ ਦਰਸਾਉਂਦੀ ਹੈ \(\frac{1}{18}\) × 72
= 4 cm ਵਿਤੋਂ
⇒ ਨਕਸ਼ੇ ਵਿਚ

ਪ੍ਰਸ਼ਨ 9.
ਇਕ 5 m 60 cm ਉੱਚੇ ਖਵੇਂ ਖੰਭੇ ਦੇ ਪਰਛਾਵੇ ਦੀ ਲੰਬਾਈ 3 m 20 cm ਹੈ । ਉਸ ਸਮੇਂ ਪਤਾ ਕਰੋ :
(i) 10 m 50 cm ਉੱਚੇ ਇਕ ਹੋਰ ਖੰਭੇ ਦੇ ਪਰਛਾਵੇਂ ਦੀ ਲੰਬਾਈ ।
(ii) ਉਸ ਖੰਭੇ ਦੀ ਉੱਚਾਈ ਜਿਸਦੇ ਪਰਛਾਵੇਂ ਦੀ ਲੰਬਾਈ 5 m ਹੈ ।
ਹੱਲ:
(i) ਜੇਕਰ 5 m 60 cm ਅਰਥਾਤ (560 cm) ਉੱਚੇ ਖੰਬੇ ਦੇ ਪਰਛਾਵੇਂ ਦੀ ਲੰਬਾਈ = 3 m 20 cm
= 320 cm
ਤਾਂ 1 cm ,, ,, ,, ,, ,, = \(\frac{320}{560}\) cm
∴ 10 m 50 cm (ਅਰਥਾਤ (1050 cm) ਉੱਚੇ ਖੰਬੇ ਦੇ ਪਰਛਾਵੇਂ ਦੀ ਲੰਬਾਈ
= \(\frac{320}{560}\) × 1050
= 600 cm
= 6 m.

(ii) ਜੇਕਰ ਪਰਛਾਵੇਂ ਦੀ ਲੰਬਾਈ 3 m 20 cm ਅਰਥਾਤ 320 cm ਹੋਵੇ ਤਾਂ ਖੰਬੇ ਦੀ ਉੱਚਾਈ = 560 cm
,, ,, ,, 1 cm ,, ,, ,, = \(\frac{560}{320}\) cm
,, ,, 5 m ਅਰਥਾਤ 500 cm ,, = \(\frac{560}{320}\) × 500
= 875 cm
= 8 m 75 cm.

ਪ੍ਰਸ਼ਨ 10.
ਮਾਲ ਦਾ ਲੱਦਿਆ ਹੋਇਆ ਇਕ ਟਰੱਕ 25 ਮਿੰਟ ਵਿਚ 14 km ਚਲਦਾ ਹੈ । ਜੇਕਰ ਚਾਲ ਉਹੀ ਰਹੇ, ਤਾਂ ਉਹ 5 ਘੰਟੇ ਵਿਚ ਕਿੰਨੀ ਦੂਰੀ ਤੈਅ ਕਰ ਲਵੇਗਾ ।
ਹੱਲ:
ਟਰੱਕ ਦੁਆਰਾ 25 ਮਿੰਟ ਵਿਚ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ =14 km
ਟਰੱਕ ਦੁਆਰਾ 1 ਮਿੰਟ ਵਿਚ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ = \(\frac{14}{25}\)
ਟਰੱਕ ਦੁਆਰਾ 5 ਘੰਟਿਆਂ ਵਿਚ = 5 × 60 = 300 ਮਿੰਟ ਵਿਚ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ
= \(\frac{14}{25}\) × 300 km.
= 168 km.