Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 13 ਸਿੱਧਾ ਅਤੇ ਉਲਟ ਸਮਾਨ ਅਨੁਪਾਤ Ex 13.2 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 8 Maths Chapter 13 ਸਿੱਧਾ ਅਤੇ ਉਲਟ ਸਮਾਨ ਅਨੁਪਾਤ Exercise 13.2
ਪ੍ਰਸ਼ਨ 1.
ਹੇਠਾਂ ਲਿਖੇ ਵਿੱਚ ਕਿਹੜੇ ਉਲਟ ਸਮਾਨ ਅਨੁਪਾਤ ਵਿਚ ਹਨ ?
(i) ਕਿਸੇ ਕੰਮ ‘ਤੇ ਲੱਗੇ ਵਿਅਕਤੀਆਂ ਦੀ ਸੰਖਿਆ ਅਤੇ | ਉਸ ਕੰਮ ਨੂੰ ਪੂਰਾ ਕਰਨ ਵਿਚ ਲੱਗਾ ਸਮਾਂ ।
(ii) ਇਕ ਸਮਾਨ ਚਾਲ ਨਾਲ ਕਿਸੇ ਯਾਤਰਾ ਵਿਚ ਲਿਆ ਗਿਆ ਸਮਾਂ ਅਤੇ ਤੈਅ ਕੀਤੀ ਦੂਰੀ ।
(iii) ਖੇਤੀ ਕੀਤੀ ਗਈ ਜ਼ਮੀਨ ਦਾ ਖੇਤਰਫਲ ਅਤੇ ਕੱਟੀ ਗਈ ਫ਼ਸਲ ।
(iv) ਇਕ ਨਿਸ਼ਚਿਤ ਯਾਤਰਾ ਵਿਚ ਲਿਆ ਗਿਆ ਸਮਾਂ ਅਤੇ ਵਾਹਨ ਦੀ ਚਾਲ ।
(v) ਕਿਸੇ ਦੇਸ਼ ਦੀ ਜਨਸੰਖਿਆ ਅਤੇ ਪ੍ਰਤੀ ਵਿਅਕਤੀ ਜ਼ਮੀਨ ਦਾ ਖੇਤਰਫਲ ।
ਹੱਲ:
(i), (iv) ਅਤੇ (v) ਕਥਨ ਉਲਟ ਸਮਾਨ ਅਨੁਪਾਤੀ ਹਨ ।
ਪ੍ਰਸ਼ਨ 2.
ਇਕ ਟੈਲੀਵਿਜ਼ਨ ਗੇਮ ਸ਼ੋ (game show) ਵਿਚ, ₹ 1,00,000 ਰੁਪਏ ਦੀ ਇਨਾਮੀ ਰਾਸ਼ੀ ਜੇਤੂਆਂ ਵਿਚ ਬਰਾਬਰ ਰੂਪ ਵਿਚ ਵੰਡੀ ਜਾਣੀ ਹੈ । ਹੇਠਾਂ ਲਿਖੀ ਸਾਰਣੀ ਨੂੰ ਪੂਰਾ ਕਰੋ ਅਤੇ ਪਤਾ ਕਰੋ ਕਿ ਕੀ ਇਕ ਵਿਅਕਤੀਗਤ ਜੇਡੁ ਨੂੰ ਦਿੱਤੇ ਜਾਣ ਵਾਲੇ ਇਨਾਮ ਦੀ ਧਨ ਰਾਸ਼ੀ ਜੇਤੂਆਂ ਦੀ ਸੰਖਿਆ ਦੇ ਸਿੱਧੇ ਸਮਾਨ ਅਨੁਪਾਤ ਹੈ ਜਾਂ ਉਲਟ ਸਮਾਨ ਅਨੁਪਾਤ ਵਿਚ ਹੈ !

ਹੱਲ:
ਕੁੱਲ ਇਨਾਮ ਦੀ ਰਾਸ਼ੀ = ₹ 100000
ਦਿੱਤੀ ਗਈ ਸਾਰਣੀ ਦੇ ਅਨੁਸਾਰ :
ਜੇਕਰ ਜੇਤੂਆਂ ਦੀ ਸੰਖਿਆ 1 ਹੋਵੇ,
ਤਾਂ, ਇਨਾਮ ਦੀ ਰਾਸ਼ੀ = ₹ 100000
ਜੇਕਰ ਜੇਤੂਆਂ ਦੀ ਸੰਖਿਆ 2 ਹੋਵੇ ।
ਤਾਂ ਇਨਾਮ ਦੀ ਰਾਸ਼ੀ = ₹ 50,000 ਹਰੇਕ ਜੇਤੂਆਂ ਦੇ ਲਈ
ਜੇਕਰ ਜੇਤੂਆਂ ਦੀ ਸੰਖਿਆ 4 ਹੋਵੇ,
ਤਾਂ ਇਨਾਮ ਰਾਸ਼ੀ = ₹ \(\frac{100,000}{4}\) = ₹ 25,000 ਹਰੇਕ ਜੇਤੂ ਦੇ ਲਈ
ਜੇਕਰ ਜੇਤੂਆਂ ਦੀ ਸੰਖਿਆ 5, ਹੋਵੇ
ਤਾਂ ਇਨਾਮ ਰਾਸ਼ੀ = ₹ \(\frac{100000}{5}\) = ₹ 20,000 ਹਰੇਕ ਜੇਤੂ ਦੇ ਲਈ
ਜੇਕਰ ਜੇਤੂਆਂ ਦੀ ਸੰਖਿਆ 8 ਹੋਵੇ
ਤਾਂ ਇਨਾਮ ਰਾਸ਼ੀ = ₹ \(\frac{100000}{10}\) = ₹ 10,000 ਹਰੇਕ ਜੇਤੂ ਦੇ ਲਈ
ਜੇਕਰ ਜੇਤੂਆਂ ਦੀ ਸੰਖਿਆ 20 ਹੋਵੇ,
ਤਾਂ ਇਨਾਮ ਰਾਸ਼ੀ = ₹ \(\frac{100000}{20}\) = ₹ 5,000 ਹਰੇਕ ਜੇਤੂ ਦੇ ਲਈ
ਇੱਥੇ, ਜੇਤੂ ਨੂੰ ਦਿੱਤੀ ਗਈ ਰਾਸ਼ੀ ਜੇਤੂਆਂ ਦੇ ਉਲਟ ਸਮਾਨਅਨੁਪਾਤੀ ਹੁੰਦੀ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 3.
ਰਹਿਮਾਨ ਤੀਲੀਆਂ ਜਾਂ ਡੰਡੀਆਂ ਦੀ ਵਰਤੋਂ ਕਰਦੇ ਹੋਏ, ਇਕ ਪਹੀਆ ਬਣਾ ਰਿਹਾ ਹੈ । ਉਹ ਬਰਾਬਰ ਤੀਲੀਆਂ ਇਸ ਤਰ੍ਹਾਂ ਲਗਾਉਣੀਆਂ ਚਾਹੁੰਦਾ ਹੈ ਕਿ ਕਿਸੇ ਵੀ ਲਗਾਤਾਰ ਤੀਲੀਆਂ ਦੇ ਜੋੜਿਆਂ ਦੇ ਵਿਚਕਾਰ ਦੇ ਕੋਣ ਬਰਾਬਰ ਹੋਣ ।
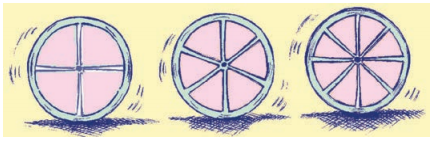
ਹੇਠ ਲਿਖੀ ਸਾਰਣੀ ਨੂੰ ਪੂਰਾ ਕਰਕੇ, ਉਸਦੀ ਸਹਾਇਤਾ ਕਰੋ :

ਹੱਲ:
ਜਦੋਂ 4 ਤੀਲੀਆਂ ਹੋਣ, ਤਾਂ ਉਸਦੇ ਵਿਚਲਾ ਕੋਣ = 90°
ਜਦੋਂ 6 ਤੀਲੀਆਂ ਹੋਣ, ਤਾਂ ਉਸਦੇ ਵਿਚਲਾ ਕੋਣ = 60°
ਗੁਣਨਫਲ xy = 90° × 4 = 360° ਅਤੇ 6 × 60°
= 360°
∴ x ਅਤੇ y ਉਲਟ ਸਮਾਨ ਅਨੁਪਾਤੀ ਹੈ ।
∴ ਜਦੋਂ 8 ਉਲਟ ਸਮਾਨ ਅਨੁਪਾਤੀ ਹਨ ।
= \(\frac{360^{\circ}}{8}\) = 45°
ਜਦੋਂ 10 ਤੀਲੀਆਂ ਹੋਣ, ਤਾਂ ਉਸਦੇ ਵਿਚਲਾ ਕੋਣ
= \(\frac{360^{\circ}}{10}\) = 36°
ਜਦੋਂ 12 ਤੀਲੀਆਂ ਹੋਣ, ਤਾਂ ਉਸਦੇ ਵਿਚਲਾ ਕੋਣ
= \(\frac{360^{\circ}}{12}\)
= 30°
ਪ੍ਰਸ਼ਨ 3. (i).
ਕੀ ਤੀਲੀਆਂ ਦੀ ਸੰਖਿਆ ਅਤੇ ਲਗਾਤਾਰ ਤੀਲੀਆਂ ਦੇ ਕਿਸੇ ਜੋੜੇ ਦੇ ਵਿਚਲਾ ਕੋਣ ਉਲਟ ਸਮਾਨ ਅਨੁਪਾਤ ਵਿਚ ਹੈ ?
ਹੱਲ:
ਹਾਂ ।
ਪ੍ਰਸ਼ਨ 3. (ii).
15 ਤੀਲੀਆਂ ਵਾਲੇ ਇਕ ਪਹੀਏ ਦੇ ਲਗਾਤਾਰ ਤੀਲੀਆਂ ਦੇ ਕਿਸੇ ਜੋੜੇ ਵਿਚਲਾ ਕੋਣ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਜਦੋਂ ਤੀਲੀਆਂ ਦੀ ਸੰਖਿਆ 15 ਹੋਵੇ, ਤਾਂ ਉਸਦੇ ਵਿਚਲਾ ਕੋਣ = \(\frac{360^{\circ}}{15}\) = 24°.
![]()
ਪ੍ਰਸ਼ਨ 3. (iii).
ਜੇ ਲਗਾਤਾਰ ਤੀਲੀਆਂ ਦੇ ਹਰੇਕ ਜੋੜੇ ਵਿਚਲਾ ਕੋਣ 40° ਹੈ, ਤਾਂ ਲੋੜੀਂਦੀਆਂ ਤੀਲੀਆਂ ਦੀ ਸੰਖਿਆ ਕਿੰਨੀ ਹੋਵੇਗੀ ?
ਹੱਲ:
ਜਦੋਂ ਤੀਲੀਆਂ ਦੇ ਵਿਚਲਾ ਕੋਣ = 40° ਹੋਵੇ
ਤਾਂ ਤੀਲੀਆਂ ਦੀ ਸੰਖਿਆ = \(\frac{360^{\circ}}{40}\) = 9 ਤੀਲੀਆਂ
ਪ੍ਰਸ਼ਨ 4.
ਜੇਕਰ ਕਿਸੇ ਡੱਬੇ ਦੀ ਮਿਠਾਈ ਨੂੰ 24 ਬੱਚਿਆਂ ਵਿਚ | ਵੰਡਿਆ ਜਾਵੇ ਤਾਂ, ਹਰੇਕ ਬੱਚੇ ਨੂੰ 5 ਮਿਠਾਈਆਂ ਮਿਲਦੀਆਂ ਹਨ । ਜੇ ਬੱਚਿਆਂ ਦੀ ਸੰਖਿਆ ਵਿਚ 4 ਦੀ ਕਮੀ ਹੋ ਜਾਵੇ ਤਾਂ, ਹਰੇਕ ਬੱਚੇ ਨੂੰ ਕਿੰਨੀਆਂ ਮਿਠਾਈਆਂ ਮਿਲਣਗੀਆਂ ?
ਹੱਲ:
ਬੱਚਿਆਂ ਦੀ ਸੰਖਿਆ = 24
ਹਰੇਕ ਬੱਚੇ ਨੂੰ ਮਿਲੀ ਮਿਠਾਈਆਂ ਦੀ ਸੰਖਿਆ = 5
∴ ਮਿਠਾਈਆਂ ਦੀ ਕੁੱਲ ਸੰਖਿਆ = 24 × 5
= 120
ਜਦੋਂ ਬੱਚਿਆਂ ਦੀ ਸੰਖਿਆ = 20 (ਅਰਥਾਤ 4 ਘੱਟ) ਹੋਵੇ ।
∴ ਹਰੇਕ ਬੱਚੇ ਨੂੰ ਮਿਲੀ ਮਿਠਾਈਆਂ ਦੀ ਸੰਖਿਆ
= \(\frac{120}{20}\) = 6
![]()
ਪ੍ਰਸ਼ਨ 5.
ਇਕ ਕਿਸਾਨ ਦੀ ਡੇਅਰੀ ਵਿਚ 20 ਪਸ਼ੂਆਂ ਦੇ ਲਈ 6 ਦਿਨ ਦਾ ਭੋਜਨ ਪਿਆ ਹੈ । ਜੇ ਇਸ ਡੇਅਰੀ ਵਿਚ 10 ਪਸ਼ੁ ਹੋਰ ਆ ਜਾਣ, ਤਾਂ ਇਹ ਭੋਜਨ ਕਿੰਨੇ ਦਿਨਾਂ ਤੱਕ ਕਾਫ਼ੀ ਹੋਵੇਗਾ ?
ਹੱਲ:
ਪਸ਼ੂਆਂ ਦੀ ਸੰਖਿਆ = 20
ਕਿਉਂਕਿ ਭੋਜਨ 6 ਦਿਨਾਂ ਦੇ ਲਈ ਪੁਰਾ ਹੈ ।
ਇਸ ਲਈ ਕੁੱਲ ਜਿੰਨੇ ਦਿਨਾਂ ਦੇ ਲਈ ਭੋਜਨ ਕਾਫ਼ੀ ਹੈ।
= 20 × 6 = 120 ਦਿਨ
ਜਦੋਂ 10 ਪਸ਼ੂ ਹੋਰ ਆ ਜਾਣ ਤਾਂ ਪਸ਼ੂਆਂ
ਅਰਥਾਤ (20 + 10) ਪਸ਼ੂਆਂ ਦੇ ਲਈ ਕਾਫ਼ੀ ਦਿਨ \(\frac{120}{30}\)
= 4 ਦਿਨ
ਪ੍ਰਸ਼ਨ 6.
ਇਕ ਠੇਕੇਦਾਰ ਇਹ ਗਣਨਾ ਕਰਦਾ ਹੈ ਕਿ ਜਸਮਿੰਦਰ ਦੇ ਘਰ ਵਿਚ ਦੁਬਾਰਾ ਤਾਰ ਲਗਾਉਣ ਦਾ ਕੰਮ 3 ਵਿਅਕਤੀ 4 ਦਿਨ ਵਿਚ ਕਰ ਸਕਦੇ ਹਨ । ਜੇ ਉਹ ਤਿੰਨ ਦੀ ਥਾਂ ਤੇ ਚਾਰ ਵਿਅਕਤੀਆਂ ਨੂੰ ਇਸ ਕੰਮ ਤੇ ਲਗਾਉਂਦਾ ਹੈ, ਤਾਂ ਇਹ ਕੰਮ ਕਿੰਨੇ ਦਿਨਾਂ ਵਿਚ ਪੂਰਾ ਹੋ ਜਾਵੇਗਾ ?
ਹੱਲ:
ਜੇਕਰ 3 ਵਿਅਕਤੀ ਘਰ ਵਿਚ ਦੁਬਾਰਾ ਤਾਰ ਲਗਾਉਣ ਦਾ ਕੰਮ 4 ਦਿਨ ਵਿਚ ਕਰਦੇ ਹਨ, ਤਾਂ 1 ਵਿਅਕਤੀ ਦੁਬਾਰਾ ਤਾਰ ਦਾ ਕੰਮ ਕਰਨ ਵਿਚ ਲਗਿਆ ਸਮਾਂ = 4 × 3 = 12 ਦਿਨ
∴ 4 ਵਿਅਕਤੀ ਤਾਰ ਲਗਾਉਣ ਦਾ ਕੰਮ ਕਰਦੇ ਹਨ
= \(\frac{12}{4}\) = 3 ਦਿਨ
![]()
ਪ੍ਰਸ਼ਨ 7.
ਬੋਤਲਾਂ ਦੇ ਇਕ ਬੈਚ (batch) ਨੂੰ 25 ਬਕਸਿਆਂ . ਵਿਚ ਰੱਖਿਆ ਜਾਂਦਾ ਹੈ, ਜੇ ਹਰੇਕ ਬਕਸੇ ਵਿਚ 12 ਬੋਤਲਾਂ ਹਨ । ਜੇ ਇਸ ਬੈਚ ਦੀਆਂ ਬੋਤਲਾਂ ਨੂੰ ਇਸ ਤਰ੍ਹਾਂ ਰੱਖਿਆ ਜਾਵੇ ਤਾਂ ਕਿ ਹਰੇਕ ਬੱਕਸੇ ਵਿਚ 20 ਬੋਤਲਾਂ ਹੋਣ, ਤਾਂ ਕਿੰਨੇ ਬਕਸੇ ਭਰ ਜਾਣਗੇ ?
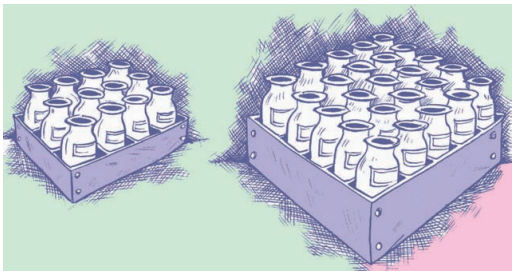
ਹੱਲ:
1 ਬਕਸੇ ਵਿਚ ਬੋਤਲਾਂ ਦੀ ਸੰਖਿਆ = 12
25 ਬਕਸਿਆਂ ਵਿਚ ਬੋਤਲਾਂ ਦੀ ਸੰਖਿਆ
= 12 × 25
= 300 ਬੋਤਲਾਂ
ਜਦੋਂ ਇਕ ਬਕਸੇ ਵਿਚ 20 ਬੋਤਲਾਂ ਹੋਵੇ ਤਾਂ ਬਕਸਿਆਂ ਦੀ ! ਸੰਖਿਆ
= \(\frac{300}{20}\) = 15 ਬਕਸੇ
ਪ੍ਰਸ਼ਨ 8.
ਇਕ ਫੈਕਟਰੀ ਨੂੰ ਕੁੱਝ ਵਸਤੂਆਂ 63 ਦਿਨਾਂ ਵਿਚ ਬਣਾਉਣ ਦੇ ਲਈ 42 ਮਸ਼ੀਨਾਂ ਦੀ ਜ਼ਰੂਰਤ ਹੁੰਦੀ ਹੈ । ਉਨ੍ਹੀਆਂ ਹੀ ਵਸਤੂਆਂ 54 ਦਿਨ ਵਿਚ ਬਣਾਉਣ ਦੇ ਲਈ, ਕਿੰਨੀਆਂ ਮਸ਼ੀਨਾਂ ਦੀ ਜ਼ਰੂਰਤ ਹੋਵੇਗੀ ?
ਹੱਲ:
42 ਮਸ਼ੀਨਾਂ ਦਿੱਤੀਆਂ ਗਈਆਂ ਵਸਤੂਆਂ ਨੂੰ 63 ਦਿਨ ਵਿਚ ਬਣਾ ਸਕਦੀਆਂ ਹਨ ।
1 ਮਸ਼ੀਨ ਦਿੱਤੀਆਂ ਗਈਆਂ ਵਸਤੂਆਂ ਨੂੰ ਜਿੰਨੇ ਦਿਨ ਵਿਚ | ਬਣਾ ਸਕਦੀ ਹੈ = 63 × 42 ਦਿਨ
ਹੁਣ ਉੱਨੀਆਂ ਹੀ ਵਸਤੂਆਂ ਬਣਾਉਣ ਦੇ ਲਈ 54 ਦਿਨਾਂ ਵਿਚ ਜਿੰਨੀਆਂ ਮਸ਼ੀਨਾਂ ਚਾਹੀਦੀਆਂ ਹਨ ।
= \(\frac{63×42}{54}\) = 49 ਮਸ਼ੀਨਾਂ
![]()
ਪ੍ਰਸ਼ਨ 9.
ਇਕ ਕਾਰ ਇਕ ਸਥਾਨ ਤੱਕ ਪਹੁੰਚਣ ਵਿਚ 60 km/h ਦੀ ਚਾਲ ਵਿੱਚ ਚੱਲ ਕੇ 2 ਘੰਟਿਆਂ ਦਾ ਸਮਾਂ ਲੈਂਦੀ ਹੈ । 80 km/h ਦੀ ਚਾਲ ਨਾਲ ਉਸ ਕਾਰ ਨੂੰ ਕਿੰਨਾ ਸਮਾਂ ਲੱਗੇਗਾ ?
ਹੱਲ:
ਕਾਰ ਦੀ ਚਾਲ = 60 km/h.
ਸਮਾਂ = 2 ਘੰਟੇ
∴ ਤੈਅ ਕੀਤੀ ਗਈ ਦੁਰੀ = ਚਾਲ × ਸਮਾਂ
= 60 × 2
= 120 km
∴ 80 km/h ਦੀ ਚਾਲ ਨਾਲ ਦਿੱਤਾ ਗਿਆ ਸਮਾਂ
= \(\frac{120}{80}\)
= \(\frac{3}{2}\) = 1\(\frac{1}{2}\) ਘੰਟੇ
ਪ੍ਰਸ਼ਨ 10.
ਦੋ ਵਿਅਕਤੀ ਇਕ ਘਰ ਵਿਚ ਨਵੀਂਆਂ ਖਿੜਕੀਆਂ 3 ਦਿਨ ਵਿਚ ਲਗਾ ਸਕਦੇ ਹਨ :
(i) ਕੰਮ ਸ਼ੁਰੂ ਹੋਣ ਤੋਂ ਪਹਿਲਾਂ, ਇੱਕ ਵਿਅਕਤੀ ਬੀਮਾਰ ਹੋ ਜਾਂਦਾ ਹੈ । ਹੁਣ ਇਹ ਕੰਮ ਕਿੰਨੇ ਦਿਨ ਵਿਚ ਪੂਰਾ ਹੋ ਪਾਵੇਗਾ ?
(ii) ਇਕ ਹੀ ਦਿਨ ਵਿਚ ਖਿੜਕੀਆਂ ਲਗਾਉਣ ਦੇ ਲਈ, ਕਿੰਨੇ ਵਿਅਕਤੀਆਂ ਦੀ ਜ਼ਰੂਰਤ ਹੋਵੇਗੀ ?
ਹੱਲ:
ਵਿਅਕਤੀਆਂ ਦੀ ਸੰਖਿਆ = 2
(i) ਖਿੜਕੀਆਂ ਨੂੰ ਲਗਾਉਣ ਵਿਚ ਲਗਾਏ ਗਏ ਦਿਨਾਂ ਦੀ ਸੰਖਿਆ = 3
∴ 1 ਵਿਅਕਤੀ ਖਿੜਕੀ ਲਗਾਉਣ ਵਿਚ ਜਿੰਨੇ ਦਿਨ ਲੈਂਦਾ ਹੈ ।
= 3 × 2
= 6 ਦਿਨ
(ii) 1 ਦਿਨ ਵਿਚ ਖਿੜਕੀਆਂ ਲਗਾਉਣ ਵਾਲੇ ਵਿਅਕਤੀਆਂ ਦੀ ਸੰਖਿਆ = 2 × 3 = 6 ਵਿਅਕਤੀ ।
![]()
ਪ੍ਰਸ਼ਨ 11.
ਕਿਸੇ ਸਕੂਲ ਵਿਚ, 45 ਮਿੰਟ ਦੀ ਅੰਤਰਾਲ ਦੇ 8 ਪੀਰੀਅਡ ਹੁੰਦੇ ਹਨ । ਇਹ ਕਲਪਨਾ ਕਰਦੇ ਹੋਏ ਕਿ ਸਕੂਲ ਦੇ ਕੰਮ ਦਾ ਸਮਾਂ ਉੱਨਾ ਹੀ ਹੁੰਦਾ ਹੈ, ਜੇਕਰ ਸਕੂਲ ਵਿਚ ਬਰਾਬਰ ਅੰਤਰਾਲ ਦੇ 9 ਪੀਰੀਅਡ ਹੋਣ, ਤਾਂ ਹਰੇਕ ਪੀਰੀਅਡ ਕਿੰਨੇ ਸਮੇਂ ਦਾ ਹੋਵੇਗਾ ?
ਹੱਲ:
ਪ੍ਰਤੀਦਿਨ ਪੀਰੀਅਡਾਂ ਦੀ ਸੰਖਿਆ = 8
ਹਰੇਕ ਪੀਰੀਅਡ ਦਾ ਸਮਾਂ = 45 ਮਿੰਟ
∴ ਕੁੱਲ ਸਮਾਂ = 45 × 8
= 360 ਮਿੰਟ
ਜੇਕਰ ਪੀਰੀਅਡਾਂ ਦੀ ਸੰਖਿਆ = 9 ਹੋਵੇ
ਤਾਂ ਹਰੇਕ ਪੀਰੀਅਡ ਦਾ ਸਮਾਂ = \(\frac{360}{9}\)
= 40 ਮਿੰਟ ।
