Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 5 Data Handling Ex 5.2 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 8 Maths Chapter 5 Data Handling Ex 5.2
1. A survey was made to find the type of music that a certain group of young people liked in a city. Given pie chart shows the findings of this survey.
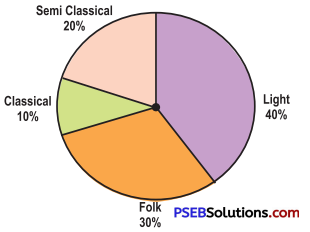
From this pie chart answer the following:
Question (i).
If 20 people liked classical music, how many young people were surveyed ?
Solution:
Let the required number of total young people surveyed = x
∴ 10% of x = 20
∴ \(\frac {10}{100}\) × x = 20
∴ x = \(\frac{20 \times 100}{10}\)
∴ x = 200
200 young people were surveyed.
Question (ii).
Which type of music is liked by the maximum number of people ?
Solution:
Maximum number of people like the light music.
Question (iii).
If a cassette company were to make 1000 CD’s, how many of each type would they make ?
Solution:
Total number of CD’s = 1000
(a) Number of CD’s for semi classical music = 20 % of 1000
= \(\frac {20}{100}\) × 1000 = 200
(b) Number of CD’s for classical music = 10 % of 1000
= \(\frac {10}{100}\) × 1000 = 100
(c) Number of CD’s for folk music = 30 % of 1000
= \(\frac {30}{100}\) × 1000 = 300
(d) Number of CD’s for light music = 40 % of 1000
= \(\frac {40}{100}\) × 1000 = 400
![]()
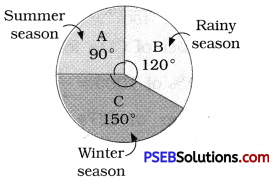
2. A group of 360 people were asked to vote for their favourite season from the ? three seasons rainy, winter and summer:

Question (i).
Which season got the most votes ?
Solution:
Winter season got the most votes (150).
Question (ii).
Find the central angle of each sector.
Solution:
Total Votes = 90 + 120 + 150 = 360
∴ Central angle of the sector corresponding to :
Summer season = \(\frac {90}{360}\) × 360° = 90°
Rainy season = \(\frac {120}{360}\) × 360° = 120°
Winter season = \(\frac {150}{360}\) × 360° = 150°
Question (iii).
Draw a pie chart to show this information.
Solution:
Draw three radi in such a way that it makes angles of 90°, 120° and 150° at the centre.
![]()
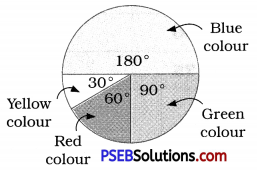
3. Draw a pie chart showing the following information. The table shows the colours preferred by a group of people.
| Colours | Number of people |
| Blue | 18 |
| Green | 9 |
| Red | 6 |
| Yellow | 3 |
| Total | 36 |

Solution:
Central angle of the sector corresponding to :
(i) The blue colour = \(\frac {18}{36}\) × 360°
= 18 × 10° = 180°
(ii) The green colour = \(\frac {9}{36}\) × 360° = 90°
(iii) The red colour = \(\frac {6}{36}\) × 360° = 60°
(iv) The yellow colour = \(\frac {3}{36}\) × 360° = 30°
Thus, the required pie chart is given below.
4. The given pie chart gives the marks scored in an examination by a student in Hindi, English, Mathematics, Social Science and Science. If the total marks obtained by the students were 540, answer the following questions.
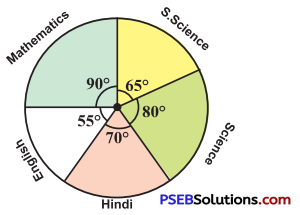
Question (i).
In which subject did the student score 105 marks ?
[Hint: For 540 marks, the central angle = 360°. So for 105 marks, what is the central angle ?]
Solution:
Toted marks = 540
∴ Central angle corresponding to 540 marks = 360°
∴ Central angle corresponding to 105 marks = \(\frac {360}{540}\) × 105° = 70°
The sector having central angle 70° is corresponding to Hindi.
Thus, the student scored 105 marks in Hindi.
![]()
Question (ii).
How many more marks were obtained by the student in Mathematics than in Hindi?
Solution:
The central angle corresponding to the sector of Mathematics = 90°
∴ Marks scored in Mathematics = \(\frac{90^{\circ}}{360^{\circ}}\) × 540 = 135
30 (135 – 105) more marks were obtained by the student in Mathematics than in Hindi.
Question (iii).
Examine whether the sum of the marks obtained in Social Science and Mathematics is more than that in Science and Hindi.
[Hint:Just study the central angles.]
Solution:
The sum of the central angles for Social Science and Mathematics = 65° + 90° = 155°
The sum of the central angles for Science and Hindi = 80° + 70° = 150°
∴ Marks obtained in Social Science and Mathematics is more than the marks scored in Science and Hindi.
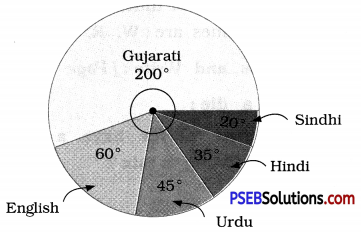
5. The number of students in a hostel, speaking different languages is given below. Display the data in a pie chart:

Solution:
Central angle of the sector representing:
(i) Gujarati language = \(\frac {40}{72}\) × 360°
= 40 × 5° = 200°
(ii) English language = \(\frac {12}{72}\) × 360°
= 12 × 5°= 80°
(iii) Urdu language = \(\frac {9}{72}\) × 360°
= 9 × 5° = 45°
(iv) Hindi language = \(\frac {7}{72}\) × 360°
= 7 × 5° = 35°
(v) Sindhi language = \(\frac {4}{72}\) × 360°
= 4 × 5° = 20°
The required pie chart is as follows.