PSEB 8th Class Maths Solutions Chapter 7 ਘਣ ਅਤੇ ਘਣਮੂਲ InText Questions

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 7 ਘਣ ਅਤੇ ਘਣਮੂਲ InText Questions and Answers.

PSEB 8th Class Maths Solutions Chapter 7 ਘਣ ਅਤੇ ਘਣਮੂਲ InText Questions

ਕੋਸ਼ਿਸ਼ ਕਰੋ :

ਪ੍ਰਸ਼ਨ 1
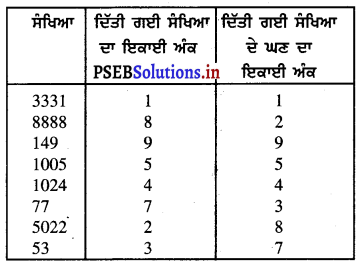
ਹੇਠਾਂ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਵਿਚੋਂ ਹਰੇਕ ਦੇ ਘਣ ਦੀ ਇਕਾਈ ਦਾ ਅੰਕ ਪਤਾ ਕਰੋ :
(i) 3331
(ii) 8888
(iii) 149
(iv) 1005
(v) 1024
(vi) 77
(vii) 5022
(viii) 53.
ਹੱਲ:
ਜਿਵੇਂ ਕਿ ਸਾਨੂੰ ਪਤਾ ਹੈ ਕਿ ਅੰਕਾਂ 0, 1, 4, 5, 6 ਅਤੇ 9 ਉੱਤੇ ਖ਼ਤਮ ਹੋਣ ਵਾਲੀਆਂ ਸੰਖਿਆਵਾਂ ਦੇ ਘਣ ਕ੍ਰਮਵਾਰ 0, 1, 4, 5, 6 ਅਤੇ 9 ਉੱਤੇ ਖ਼ਤਮ ਹੁੰਦੇ ਹਨ । ਜਦਕਿ 2 ਉੱਤੇ ਖ਼ਤਮ ਹੋਣ ਵਾਲੀ ਸੰਖਿਆ ਦਾ ਘਣ 8 ਉੱਤੇ ਅਤੇ 8 ਉੱਤੇ ਖ਼ਤਮ ਹੋਣ ਵਾਲੀ ਸੰਖਿਆ ਦਾ ਘਣ 2 ਉੱਤੇ ਖ਼ਤਮ ਹੁੰਦਾ ਹੈ । ਇਸੇ ਤਰ੍ਹਾਂ 3 ਅਤੇ 7 ਉੱਤੇ ਖ਼ਤਮ ਹੋਣ ਵਾਲੀਆਂ ਸਿਖਿਆਵਾਂ ਦੇ ਘਣ ਕ੍ਰਮਵਾਰ 7 ਅਤੇ 3 ਉੱਤੇ ਖ਼ਤਮ ਹੁੰਦੇ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਦਿੱਤੀ ਗਈ ਸੰਖਿਆ ਦੇ ਇਕਾਈ ਅੰਕ ਨੂੰ ਦੇਖਣ ਤੇ ਅਸੀਂ ਇਸਦੇ ਘਣ ਦੇ ਇਕਾਈ ਅੰਕ ਦਾ ਪਤਾ ਲਗਾ ਸਕਦੇ ਹਾਂ ਹੁਣ ਪੁਛੀ ਗਈ ਸੰਖਿਆ ਵਿਚ ਹਰੇਕ ਦੇ ਘਣ ਦਾ ਇਕਾਈ ਅੰਕ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹੈ :

ਕੁੱਝ ਰੋਚਕ ਪੈਟਰਨ
ਟਾਂਕ ਸੰਖਿਆਵਾਂ ਦੇ ਜੋੜਾਂ ਦੇ ਹੇਠਾਂ ਲਿਖੇ ਪੈਟਰਨ ਦੇਖੋ :
1 = 1 = 1³
3 + 5 = 8 = 2³
7 + 9 + 11 = 27 = 3³
13 + 15 + 17 + 19 = 64 = 4³
21 + 23 + 25 + 27 + 29 = 125 = 5³
31 + 33 + 35 + 37 + 39 + 41 = 216 = 6³
43 + 45 + 47 + 49 + 51 + 53 + 55 = 343 = 7³
57 + 59 + 61 + 63 + 65 + 67 + 69 + 71 = 512 = 8³
73 + 75 + 77 + 79 + 81 + 83 + 85 + 87 + 89 = 729 = 9³
91 + 93 + 95 + 97 + 99 + 101 + 103 + 105 + 107 + 109 = 1000 = 10³

ਕੋਸ਼ਿਸ਼ ਕਰੋ :

ਪ੍ਰਸ਼ਨ 1.
ਉਪਰੋਕਤ ਪੈਟਰਨ ਦਾ ਪ੍ਰਯੋਗ ਕਰਦੇ ਹੋਏ, ਹੇਠਾਂ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਨੂੰ ਕ੍ਰਮਵਾਰ ਟਾਂਕ ਸੰਖਿਆਵਾਂ ਦੇ ਜੋੜ ਦੇ ਰੂਪ ਵਿਚ ਦਰਸਾਓ :
(a) 6³
(b) 8³
(c) 7³.
ਹੱਲ:
(a) 6³ = 216 = 31 + 33 + 35 + 37 + 39 + 41
(b) 8³ = 512 = 57 + 59 + 61 + 63 + 65 + 67 + 69 + 7
(c) 7³ = 343 = 43 + 45 + 47 + 49 + 51 + 53 + 55
ਹੇਠਾਂ ਲਿਖੇ ਪੈਟਰਨ ਨੂੰ ਦੇਖੋ :
2³ – 1³ = 1 + 2 × 1 × 3
3³ – 2³ = 1 + 3 × 2 × 3
4³ – 3³ = 1 + 4 × 3 × 3

ਪ੍ਰਸ਼ਨ 2.
ਉਪਰੋਕਤ ਪੈਟਰਨ ਦਾ ਪ੍ਰਯੋਗ ਕਰਦੇ ਹੋਏ, ਹੇਠਾਂ ਲਿਖਿਆ ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ :
(i) 7³ – 6³
(ii) 12³ – 11³
(iii) 20³ – 19³
(iv) 51³ – 50³.
ਹੱਲ:
(i) ਦਿੱਤੇ ਗਏ ਪੈਟਰਨ ਦੇ ਅਨੁਸਾਰ :
7³ – 6³ = 1 + 7 × 6 × 3
= 1 + 126 = 127
(ii) 12³ – 11³ = 1 + 12 × 11 × 3
= 1 + 396 = 397
(iii) 20³ – 19³ = 1 + 20 × 19 × 3
= 1 + 1140 = 1141
(iv) 51³ – 50³ = 1 + 51 x 50 x 3
= 1 + 7650 = 7651

ਕੋਸ਼ਿਸ਼ ਕਰੋ :

ਹੇਠਾਂ ਲਿਖਿਆਂ ਵਿਚੋਂ ਕਿਹੜੀਆਂ ਸੰਖਿਆਵਾਂ ਪੂਰਨ ਘਣ ਹਨ ?

ਪ੍ਰਸ਼ਨ (i).
400
ਹੱਲ:
400

∴ 400 = \(\underline{2 \times 2 \times 2}\) × 2 × 5 × 5
ਇੱਥੇ, ਅਭਾਜ ਗੁਣਨਖੰਡ ਦਾ ਇਕ ਤ੍ਰਿਗੁੱਟ ਬਣਾਉਣ ਦੇ ਬਾਅਦ 2 × 5 × 5 ਬਾਕੀ ਰਹਿੰਦਾ ਹੈ ।
ਇਸ ਲਈ, 400 ਇਕ ਪੂਰਨ ਘਣ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii).
3375
ਹੱਲ:
3375

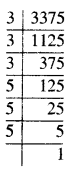
∴ 3375 = \(\underline{3 \times 3 \times 3}\) × 5 × 5 × 5
ਇੱਥੇ, ਅਭਾਜ ਗੁਣਨਖੰਡ 3 ਅਤੇ 5 ਹਰੇਕ ਤਿੰਨ ਦੇ ਸਮੂਹ ਵਿਚ ਆਉਂਦਾ ਹੈ ।
ਇਸ ਲਈ, 3375 ਇਕ ਪੂਰਨ ਘਣ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iii).
8000
ਹੱਲ:
8000

∴ 8000 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × \(\underline{5 \times 5 \times 5}\)
ਇੱਥੇ, ਅਭਾਜ ਗੁਣਨਖੰਡ 2, 2 ਅਤੇ 5 ਹਰੇਕ ਤਿੰਨ ਦੇ | ਸਮੂਹ ਵਿਚ ਆਉਂਦਾ ਹੈਂ ।
ਇਸ ਲਈ, 8000 ਇਕ ਪੂਰਨ ਘਣ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iv).
15625
ਹੱਲ:
15625

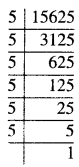
∴ 15625 = 5 × 5 × 5 × 5 × 5 × 5
ਇੱਥੇ, ਅਭਾਜ ਗੁਣਨਖੰਡ 5 ਤਿੰਨ ਦੇ ਸਮੂਹ ਵਿਚ ਆਉਂਦਾ ਹੈ ।
ਇਸ ਲਈ, 15625 ਇਕ ਪੂਰਨ ਘਣ ਹੈ ।

ਪ੍ਰਸ਼ਨ (v).
9000
ਹੱਲ:
9000

∴ 9000 = \(\underline{2 \times 2 \times 2}\) × 3 × 3 × \(\underline{5 \times 5 \times 5}\)
ਇੱਥੇ, 2 ਦਾ ਇਕ ਗੁੱਟ ਅਤੇ 5 ਦਾ ਇਕ ਗੁੱਟ ਬਣਾਉਣ ਤੋਂ ਬਾਅਦ 3 × 3 ਬਾਕੀ ਰਹਿੰਦਾ ਹੈ ।
ਇਸ ਲਈ, 000 ਇਕ ਪੂਰਨ ਘਣ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ (vi).
6859
ਹੱਲ:
6859

∴ 6859 = \(\underline{19 \times 19 \times 19}\)
ਇੱਥੇ, ਅਭਾਜ ਗੁਣਨਖੰਡ 19 ਤਿੰਨ ਦੇ ਸਮੂਹ ਵਿਚ ਆਉਂਦਾ ਹੈ ।
ਇਸ ਲਈ, 6859 ਇਕ ਪੂਰਨ ਘਣ ਹੈ ।

ਪ੍ਰਸ਼ਨ (vii).
2025
ਹੱਲ:
2025

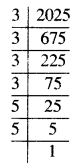
∴ 2025 = \(\underline{3 \times 3 \times 3}\) × 3 × 5 × 5
ਇੱਥੇ, 3 ਦਾ ਇਕ ਗੁੱਟ ਬਣਾਉਣ ਤੋਂ ਬਾਅਦ 3 × 5 × 5 ਬਾਕੀ ਰਹਿੰਦਾ ਹੈ ।
ਇਸ ਲਈ, 2025 ਇਕ ਪੂਰਨ ਘਣ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ (viii).
10648.
ਹੱਲ:
10648

∴ 10648 = \(\underline{2 \times 2 \times 2}\) x \(\underline{11 \times 11 \times 11}\)
ਇੱਥੇ, ਹਰੇਕ ਅਭਾਜ ਗੁਣਨਖੰਡ ਤਿੰਨ ਬਾਰ ਆਉਂਦਾ ਹੈ ।
ਇਸ ਲਈ, 10648 ਇਕ ਪੂਰਨ ਘਣ ਹੈ ।

ਸੋਚੋ, ਚਰਚਾ ਕਰੋ ਅਤੇ ਲਿਖੋ :

1. ਪੜਤਾਲ ਕਰੋ ਕਿ ਹੇਠਾਂ ਲਿਖੀਆਂ ਵਿਚ ਕਿਹੜੀਆਂ ਸੰਖਿਆਵਾਂ ਪੂਰਨ ਘਣ ਹਨ :

ਪ੍ਰਸ਼ਨ (i).
2700
ਹੱਲ:
2700

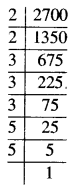
∴ 2700 = 2 × 2 × \(\underline{3 \times 3 \times 3}\) × 5 × 5
ਇੱਥੇ, ਅਭਾਜ ਗੁਣਨਖੰਡ 2 ਅਤੇ 5 ਤਿੰਨ-ਤਿੰਨ ਦੇ ਸਮੂਹਾਂ ਵਿਚ ਨਹੀਂ ਆ ਰਹੇ ਹਨ ।
ਇਸ ਲਈ, 2700 ਇਕ ਪੂਰਨ ਘਣ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii).
1600
ਹੱਲ:
16000

∴ 16000 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × 2 × 5 × 5 × 5
ਇੱਥੇ, ਅਭਾਜ ਗੁਣਨਖੰਡ 2, 2 ਅਤੇ 5 ਦੇ ਤ੍ਰਿਗੁੱਟ ਬਣਾਉਣ ਦੇ ਬਾਅਦ ਇਕ 2 ਬਾਕੀ ਰਹਿੰਦਾ ਹੈ ।
ਇਸ ਲਈ, 16000 ਇਕ ਪੁਰਨ ਘਣ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iii).
64000
ਹੱਲ:
64000

∴ 64000 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × 5 × 5 × 5
ਇੱਥੇ, ਅਭਾਜ ਗੁਣਨਖੰਡ 2, 2, 2 ਅਤੇ 5 ਹਰੇਕ ਤਿੰਨਤਿੰਨ ਦੇ ਸਮੂਹਾਂ ਵਿਚ ਆ ਰਹੇ ਹਨ ।
ਇਸ ਲਈ, 64000 ਇਕ ਪੂਰਨ ਘਣ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iv).
900
ਹੱਲ:
900

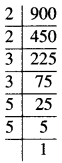
∴ 900 = 2 × 2 × 3 × 3 × 5 × 5
ਇੱਥੇ, ਅਭਾਜ ਗੁਣਨਖੰਡ 2, 3 ਅਤੇ 5 ਹਰੇਕ ਤਿੰਨ-ਤਿੰਨ ਦੇ ਸਮੂਹਾਂ ਵਿਚ ਨਹੀਂ ਆ ਰਹੇ ਹਨ ।
ਇਸ ਲਈ 900 ਇਕ ਪੂਰਨ ਘਣ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ (v).
125000
ਹੱਲ:
125000

∴ 125000 = \(\underline{2 \times 2 \times 2}\) × \(\underline{5 \times 5 \times 5}\) × \(\underline{5 \times 5 \times 5}\)
ਇੱਥੇ, ਅਭਾਜ ਗੁਣਨਖੰਡ 2, 5 ਅਤੇ 5 ਤਿੰਨ-ਤਿੰਨ ਦੇ ਸਮੂਹਾਂ ਵਿਚ ਆ ਰਹੇ ਹਨ ।
ਇਸ ਲਈ, 125000 ਇਕ ਪੂਰਨ ਘਣ ਹੈ ।

ਪ੍ਰਸ਼ਨ (vi).
36000
ਹੱਲ:
36000

∴ 36000 = \(\underline{2 \times 2 \times 2}\) × 2 × 2 × 3 × 3 × \(\underline{5 \times 5 \times 5}\)
ਇੱਥੇ, ਅਭਾਜ ਗੁਣਨਖੰਡ 2 ਅਤੇ 5 ਦਾ ਇਕ-ਇਕ ਤਿਗੁੱਟ ਬਣਾਉਣ ਦੇ ਬਾਅਦ 2 × 2 × 3 × 3 ਬਾਕੀ ਰਹਿੰਦਾ ਹੈ ।
ਇਸ ਲਈ, 36000 ਇਕ ਪੂਰਨ ਘਣ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ (vii).
21600
ਹੱਲ:
21600

∴ 21600 = \(\underline{2 \times 2 \times 2}\) × 2 × 2 × \(\underline{2 \times 2 \times 2}\) × 5 × 5
ਇੱਥੇ, ਅਭਾਜ ਗੁਣਨਖੰਡ 2 ਅਤੇ 3 ਦੇ ਗੁੱਟ ਬਣਾਉਣ ਦੇ ਬਾਅਦ 2 × 2 × 5 × 5 ਬਾਕੀ ਰਹਿੰਦਾ ਹੈ ।
ਇਸ ਲਈ, 21600 ਇਕ ਪੁਰਨ ਘੱਣ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ (viii).
10000
ਹੱਲ:
10000

∴ 10000 = \(\underline{2 \times 2 \times 2}\) × 2 × \(\underline{5 \times 5 \times 5}\) × 5
ਇੱਥੇ, ਅਭਾਜ ਗੁਣਨਖੰਡ 2 ਅਤੇ 5 ਦੇ ਗੁੱਟ ਬਣਾਉਣ ਦੇ ਬਾਅਦ 2 × 5 ਬਾਕੀ ਰਹਿੰਦਾ ਹੈ ।
ਇਸ ਲਈ, 10000 ਇਕ ਪੂਰਨ ਘਣ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ (ix).
2700000
ਹੱਲ:
27000000
∴ \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × \(\underline{3 \times 3 \times 3}\) × \(\underline{5 \times 5 \times 5}\) × \(\underline{5 \times 5 \times 5}\)

ਇੱਥੇ, ਅਭਾਜ ਗੁਣਨਖੰਡ 2, 2, 3, 5, 5 ਹਰੇਕ ਤਿੰਨ-ਤਿੰਨ ਦੇ ਸਮੂਹਾਂ ਵਿਚ ਆਉਂਦੇ ਹਨ। ‘
ਇਸ ਲਈ, 27000000 ਇਕ ਪੂਰਨ ਘਣ ਹੈ ।

ਪ੍ਰਸ਼ਨ (x).
1000.
ਇਹਨਾਂ ਪੂਰਨ ਘਣਾਂ ਵਿਚ ਤੁਸੀਂ ਕੀ ਪੈਟਰਨ ਦੇਖਦੇ ਹੋ ?
ਹੱਲ:
1000
∴ 1000 = \(\underline{2 \times 2 \times 2}\) × \(\underline{5 \times 5 \times 5}\)

ਇੱਥੇ, ਅਭਾਜ ਗੁਣਨਖੰਡ 2, 5 ਹਰੇਕ ਤਿੰਨ-ਤਿੰਨ ਦੇ ਸਮੂਹਾਂ ਵਿਚ ਆਉਂਦੇ ਹਨ ।
ਇਸ ਲਈ, 1000, ਇਕ ਪੂਰਨ ਘਣ ਹੈ ।
ਉਪਰੋਕਤ ਸਾਰੇ ਪੂਰਨ ਘਣਾਂ ਵਿੱਚ ਅਸੀਂ ਦੇਖਦੇ ਹਾਂ ਕਿ ਸਾਰਿਆਂ ਵਿਚ ਸਮਾਨ ਅਭਾਜ ਗੁਣਨਖੰਡਾਂ ਦੇ ਪੂਰਨ ਗੁੱਟ ਬਣਦੇ ਹਨ ।

ਸੋਚੋ, ਚਰਚਾ ਕਰੋ ਅਤੇ ਲਿਖੋ :

ਪ੍ਰਸ਼ਨ 1.
ਦੱਸੋ ਕਿ ਸੱਚ ਹੈ ਜਾਂ ਝੂਠ : ਕਿਸੀ ਸੰਪੂਰਨ ਸੰਖਿਆ ” ਦੇ ਲਈ, m² < m³ ਅਤੇ ਹੁੰਦਾ ਹੈ । ਕਿਉਂ ?
ਹੱਲ:
ਹਾਂ, ਇਹ ਸੱਚ ਹੈ ।
ਕਿਉਂਕਿ m² ਵਿਚ ਸੰਪੂਰਨ m ਦੋ ਬਾਰ ਆਉਂਦਾ ਹੈ ।
ਜਦਕਿ m³ ਵਿਚ ਸੰਪੂਰਨ m ਤਿੰਨ ਬਾਰ ਆਉਂਦਾ ਹੈ ।