Punjab State Board PSEB 9th Class Science Important Questions Chapter 10 गुरुत्वाकर्षण Important Questions and Answers.
PSEB 9th Class Science Important Questions Chapter 10 गुरुत्वाकर्षण
दीर्घ उत्तरात्मक प्रश्न (Long Answer Type Questions)
प्रश्न 1.
न्यूटन के सार्वत्रिक गुरुत्वाकर्षण नियम की परिभाषा लिखो तथा गणितीय दृष्टि से दो वस्तुओं के मध्य लग रहे आकर्षण बल का सूत्र स्थापित करो।
उत्तर-
न्यूटन के गुरुत्वाकर्षण का सार्वत्रिक नियम ((Newton’s Universal Law of Gravitation) – इस ब्रह्मांड में विद्यमान प्रत्येक कण को एक बल के साथ आकर्षित करता है जो
(i) दोनों के पुंजों के गुणनफल के समानुपाती होता है और
(ii) दोनों के केंद्र के बीच दूरी के वर्ग के व्युत्क्रमानुपाती होता है। यह बल सदैव ही उन वस्तुओं के केंद्रों को मिलाने वाली रेखा की दिशा में लगता है।

गणितीय दृष्टि से – ऊपर दर्शाए चित्र अनुसार मान लो हमारे पास दो गेंदें A तथा B हैं जिनके द्रव्यमान क्रमशः m1 तथा m2 हैं। इनके केंद्रों के मध्य की दूरी ‘r’ है।
न्यूटन के अनुसार गेंद A, गेंद B पर गुरुत्वाकर्षण बल FBA लगाएगी तथा FAB बल गेंद A पर गेंद B द्वारा लगेगा। इन दोनों बलों की मात्रा समान है परंतु एक-दूसरे के विपरीत दिशा में लग रहे हैं।
FAB = – FBA
मान लो FAB = – FBA = F
तो न्यूटन के गुरुत्वाकर्षण नियम अनुसार
F ∝ m1 m2 ……………. (i)
तथा F ∝ \(\frac{1}{r^{2}}\) …………..(ii)
समीकरण (i) तथा (ii) से
F ∝ \(\frac{m_{1} \times m_{2}}{r^{2}}\)
या F = G\(\frac{m_{1} \times m_{2}}{r^{2}}\)
यहां ‘G’ को सार्वत्रिक गुरुत्वीय स्थिरांक कहा जाता है। इसको यह नाम इसलिए दिया गया है क्योंकि समस्त ब्रह्मांड में इसका संख्यात्मक मान एक ही रहता है तथा यह सूत्र न्यूटन का सार्वत्रिक गुरुत्वाकर्षण का नियम है।
G का मान, G = 6.67 × 10-11 N – m2/Kg2 है।
![]()
प्रश्न 2.
ग्रहों की गति के संदर्भ में केप्लर के नियम लिखिए।
उत्तर-
ग्रहों की गति के संदर्भ में केप्लर के नियम – सोलहवीं शताब्दी तक अनेक खगोलशास्त्रियों ने ग्रहों की गति से संबंधित बहुत से आँकड़े एकत्रित कर लिए थे। जोहांस केप्लर ने इन आँकड़ों के आधार पर तीन नियम व्युत्पन्न किए। इन्हें केप्लर के नियम कहा जाता है। ये नियम इस प्रकार हैं :
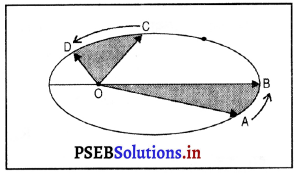
1. कक्षा का नियम (प्रथम नियम) – प्रत्येक ग्रह की कक्षा एक दीर्घवृत्त होती है और सूर्य इस दीर्घवृत्त के एक फोकस पर होता है जैसा कि निम्न चित्र में दिखाया गया है। इस चित्र में सूर्य की स्थिति को O से दर्शाया गया है।
2. क्षेत्रफल का नियम (दूसरा नियम) – सूर्य तथा ग्रह को मिलाने वाली रेखा समान समय में समान क्षेत्रफल तय करती है। इस प्रकार यदि A से B तक गति करने में लगा समय C से D तक गति करने में लगे समय के बराबर हो तो क्षेत्रफल OAB तथा क्षेत्रफल OCD बराबर होंगे।
3. परिक्रमण काल का नियम (तीसरा नियम) – सूर्य से किसी ग्रह की औसत दूरी (r) का धन उस ग्रह के सूर्य के परितः परिक्रमण काल T के वर्ग के अनुक्रमानुपाती होता है।
अथवा T2 ∝ r3
कैप्लर ने कोई सिद्धांत प्रस्तुत न कर सका जो ग्रहों की गति की व्याख्या कर सके।
न्यूटन ने यह दिखाया कि ग्रहों की गति के कारण गुरुत्वाकर्षण वह बल ही है जो सूर्य उन पर लगाता है।
अथवा r3/T2 = स्थिरांक।
प्रश्न 3.
राबर्ट बॉयल ने प्रयोग द्वारा कैसे सिद्ध किया कि निर्वात में सभी वस्तुएं एक ही दर से नीचे गिरती हैं ?
उत्तर-
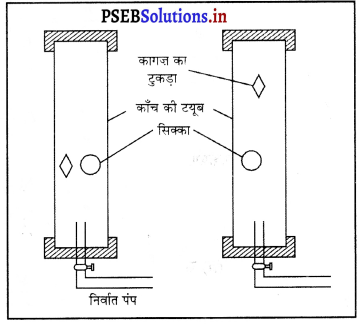
बॉयल प्रयोग – राबर्ट बॉयल ने एक लंबी काँच की ट्यूब ली जैसा कि चित्र में दिखाया गया है। एक सिक्का और कागज़ का टुकड़ा ट्यूब के भीतर रखा गया। ट्यूब के सिरों को बंद कर दिया गया। ट्यूब में से वायु को निर्वात पंप द्वारा निष्कासित कर दिया गया। जब ट्यूब को शीघ्रता से उल्टा किया गया तो यह देखने में आया कि सिक्का तथा कागज़ का टुकड़ा एक साथ ट्यूब की तली में पहुँचे । अब फिर इस प्रयोग को दोहराया गया जब ट्यूब के भीतर वायु थी। इस बार देखा गया कि कागज़ का टुकड़ा धीरे-धीरे नीचे गिरता है जबकि सिक्का शीघ्र ही ट्यूब की तली पर पहुँच गया। इस प्रयोग से यह स्पष्ट होता है कि निर्वात में सभी वस्तुएं हल्की तथा भारी एक ही त्वरण से पृथ्वी निर्वात पंप की ओर गति करती हैं।
प्रश्न 4.
एक वस्तु का भार पृथ्वी की सतह पर 90 कि०ग्रा० (Kg) है। चंद्रमा की सतह पर इसका भार कितना होगा, जिसका द्रव्यमान पृथ्वी के द्रव्यमान का \(\frac {1}{9}\) और त्रिज्या पृथ्वी की त्रिज्या का \(\frac {1}{2}\) है।
हल :
वस्तु का पृथ्वी की सतह पर भार = 90 Kg
मान लो पृथ्वी का द्रव्यमान (Me) = M
मान लो पृथ्वी का अर्धव्यास (Re) = R
अब चंद्रमा का द्रव्यमान (Mm) = \(\frac {1}{9}\) × पृथ्वी का द्रव्यमान
= \(\frac {1}{9}\) × M
या Mm = \(\frac{\mathrm{M}}{9}\)
चंद्रमा का अर्धव्यास (Rm) = \(\frac {1}{2}\) × पृथ्वी का अर्धव्यास
= \(\frac {1}{2}\) × R
Rm = \(\frac{\mathrm{R}}{2}\)
हम जानते हैं कि

= \(\frac {1}{9}\) × 4
= \(\frac {4}{9}\)
क्योंकि द्रव्यमान एक स्थिर राशि है
∴ = \(\frac {4}{9}\)
या वस्तु का चंद्रमा की सतह पर भार \(\frac {4}{9}\) × वस्तु का पृथ्वी की सतह पर भार

= 40 कि०ग्रा० उत्तर।
![]()
प्रश्न 5.
(क) सिद्ध करो कि गुरुत्वीय त्वरण का मान वस्तु के द्रव्यमान के मान से स्वतंत्र होता है।
(ख) ‘g’ का मान ज्ञात करो।
उत्तर-
(क) जैसा कि दिखाया गया है पृथ्वी तल पर m द्रव्यमान वाली एक वस्तु पर विचार करो। मान लो M और R क्रमशः पृथ्वी के द्रव्यमान और अर्धव्यास हैं।
मानो वस्तु पर क्रिया कर रहा गुरुत्व बल F है।

इस समीकरण में वस्तु का द्रव्यमान ‘m’ नहीं है। इससे पता चलता है कि गुरुत्व बल के कारण किसी वस्तु द्वारा प्राप्त त्वरण इसके द्रव्यमान से स्वतंत्र होता है। अतः हम कहते हैं कि सभी आकार और द्रव्यमान वाली वस्तुएं किसी स्थान पर समान त्वरण से गिरती हैं।
(ख) ‘g’ का मान ज्ञात करना-
G = 6.67 × 10-11 Nm2 Kg-2
पृथ्वी का अर्ध-व्यास, R = 6400 Km
= 6400 × 1000 m
= 6.4 × 106 m
पृथ्वी का द्रव्यमान, M = 6 × 1024 Kg
या g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)
g = \(\frac{6.67 \times 10^{-11} \times 6 \times 10^{24}}{\left(6.4 \times 10^{6}\right)^{2}}\)
g = 9.8 m s-2
प्रश्न 6.
(क) स्वतंत्र गिर रही वस्तुओं के समीकरण की परिभाषा दें।
(ख) स्वतंत्र गिर रही वस्तुओं के गति समीकरण में परिवर्तन कैसे होता है ?
(ग) जब वस्तु को बिल्कुल सीधे ऊपर फेंका जाता है तो उसके द्वारा प्राप्त अधिकतम ऊंचाई ज्ञात करने के लिए समीकरण लिखो।
(घ) सिद्ध करो कि गिरने का समय और ऊपर जाने का समय समान होता है।
उत्तर-
(क) गुरुत्व के अधीन क्रिया करने वाले गति समीकरण स्वतंत्र गिर रही वस्तुओं के समीकरण कहलाते है।
(ख) उन्हें एक समान गति वाली समीकरणों में a के स्थान पर g का विस्थापन करके प्राप्त किया जा सकता है। स्वतंत्र गिरावट के निम्नलिखित समीकरण होंगे-
(i) v = u + gt
(ii) h = ut + \(\frac {1}{2}\)gt2
(iii) v2 – u2 = 2gh
यहां पर से प्रारंभिक वेग, v अंतिम वेग, h प्राप्त ऊँचाई तथा t समय है।
जब वस्तु को छोड़ा जाता है तो वस्तु का प्रारंभिक वेग शून्य होता है अर्थात् u = 0
(ग) अधिकतम ऊंचाई के लिए व्यंजक – आओ आरंभिक वेग ५ वाली किसी वस्तु को ऊपर फेंके जाने पर प्राप्त अधिकतम ऊंचाई के लिए व्यंजक ज्ञात करें।
उच्चतम बिंदु पर अंतिम वेग शून्य होगा। गुरुत्व-वेग g ऋण होगा। यदि h अधिकतम ऊंचाई है तो,
v2 – u2 = 2gh
या 02 – u2 = 2(-g) h
∴ h = \(\frac{u^{2}}{2 g}\)
(घ) ऊपर जाने तथा नीचे आने का समय अर्थात् अवरोहण तथा आरोहण समय-
उच्चतम बिंदु तक पहुंचने में लगा समय अवरोहण समय है। अधिकतम ऊंचाई से नीचे वापिस आने में लगा समय आरोहण समय है।
अवरोहणयहां-
υ = 0, a = -g
υ = u + at
0 = u – gt
t = \(\frac{u}{g}\)
आरोहण समय-अब, उच्चतम बिंदु पर वेग u है।
∴ u = 0
और h = \(\frac{u^{2}}{2 g}\)
h = ut + \(\frac {1}{2}\)gt2 से = h = \(\frac {1}{2}\)gt2
∴ \(\frac{u^{2}}{2 \mathrm{~g}}\) = \(\frac {1}{2}\)gt2
∴ \(\frac{u^{2}}{2 \mathrm{~g}}\) = gt2
t = \(\frac{u}{g}\)
∴ आरोहण समय अवरोहण समय के बराबर है।
प्रश्न 7.
उन कारकों का वर्णन करो जिनके फलस्वरूप गुरुत्वीय त्वरण ‘g’ के मान में अंतर आता है।
उत्तर-
गुरुत्वीय त्वरण के मान में अंतर निम्नलिखित कारणों से होता है-
(i) पृथ्वी की ऊँचाई कारण ‘g’ में अंतर (Variation ing with altitude)-‘g’ का मान पृथ्वी की सतह पर अधिकतम होता है। जैसे-जैसे हम पृथ्वी की सतह से ऊपर की ओर जाते हैं तो ‘g’ का मान कम होता जाता है। पृथ्वी की सतह से ऊपर किसी भी ऊँचाई पर ‘g’ के मान की गणना हम एक निश्चित गणितीय सूत्र की सहायता से निकाल सकते हैं
यदि
ge = पृथ्वी की सतह पर गुरुत्वीय त्वरण
gh = पृथ्वी की ऊँचाई h पर गुरुत्वीय त्वरण
R = पृथ्वी का अर्ध-व्यास
हम जानते हैं कि
gh = ge[latex]\frac{\mathrm{R}^{2}}{(\mathrm{R}+h)^{2}}[/latex]
‘h’ का मान पता होने पर gh का मान निकाला जा सकता है।
विशेष अवस्था (Special Case) – पृथ्वी के अर्ध-व्यास से आधी ऊँचाई h पर अर्थात् है पर अर्थात् h = \(\frac{\mathrm{R}}{2}\) पर सूत्र से
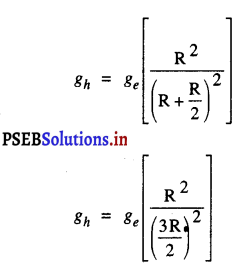

gh = 4.36 m/s2
एक और रोचक बात यह है कि पृथ्वी के केंद्र पर ‘g’ का मान शून्य होगा।
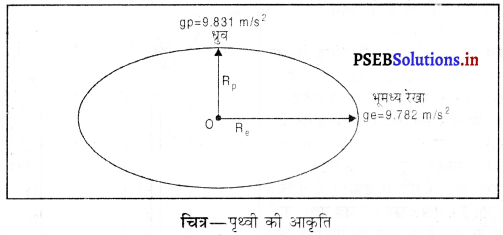
(ii) पृथ्वी की आकृति कारण ‘g’ में अंतर (Variation in g due to shape of earth) – पृथ्वी पूरी तरह से गोल नहीं है। इसकी आकृति अंडाकार है। यह ध्रुवों के पास थोड़ी-सी समतल तथा भूमध्य रेखा के पास थोड़ीसी बाहर की ओर उभरी हुई होती है। जैसा कि नीचे चित्र में दिखाया गया है।
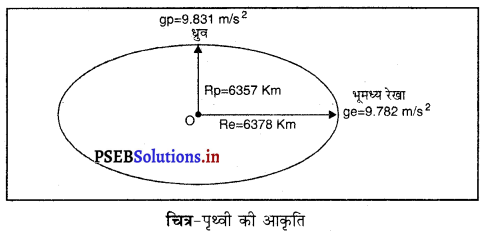
ऊपर दिखाए गए चित्र अनुसार पृथ्वी का भूमध्य रेखीय अर्ध-व्यास 6378 कि०मी० तथा ध्रुवीय अर्ध-व्यास 6357 कि०मी० है। इसलिए पृथ्वी (ध्रुवों पर) का अधिकतम ‘g’ का मान gp = 9.831 m/s2 तथा कम-से-कम (भूमध्य रेखा पर) मान ge = 9.782 m/s2 है। हम जो ‘g’ का मान लेते हैं वह gp तथा ge का मध्यमान होता है।
(iii) गहराई का प्रभाव (Effect of depth) – यदि हम नीचे गुफा में या खानों में चले जाएं तो ‘g’ का मान कम हो जाता है अर्थात् गहराई के साथ ‘g’ का मान कम होता जाता है। पृथ्वी के केंद्र पर इसका मान शून्य हो जाता है।
\(\frac{\mathrm{W}_{d}}{\mathrm{~W}_{e}}\) = \(\frac{g_{d}}{g_{e}}\) = [1 – \(\frac{d}{R}\)]
![]()
प्रश्न 8.
किसी वस्तु के चंद्रमा तथा पृथ्वी के भारों की तुलना करो।
उत्तर-
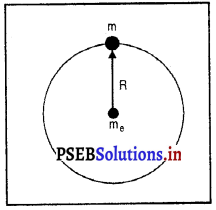
पृथ्वी तथा चंद्रमा पर वस्तु के भार की तुलना-
प्रत्येक ग्रह पर गुरुत्वीय त्वरण (g) का मान उसके द्रव्यमान तथा उसके अर्ध-व्यास पर निर्भर करता है। इसी कारण से चंद्रमा पर किसी वस्तु का भार, उसके पृथ्वी पर भार का \(\frac {1}{6}\) गुणा होता है।
माना वस्तु का द्रव्यमान ‘m’ है। यदि Me पृथ्वी का द्रव्यमान तथा Re पृथ्वी की त्रिज्या हो तो पृथ्वी पर वस्तु का भार (Fe)
Fe = \(\frac{\mathrm{GM}_{e} \times m}{\mathrm{R}_{e}^{2}}[latex] …………… (i)
इसी प्रकार यदि Mm चंद्रमा का द्रव्यमान तथा Rm चंद्रमा की त्रिज्या हो तो चंद्रमा पर वस्तु का भार (Fm)

∴ पृथ्वी का द्रव्यमान चंद्रमा के द्रव्यमान से लगभग 100 गुणा अधिक है तथा अर्ध-व्यास चार गुणा अधिक है।
∴ Me = 100 Mm तथा
Re = 4 Rm
Me तथा Re का मान लगाने पर

= 6 लगभग
अतः Fe = 6 × Fm
अत: यह स्पष्ट हो गया है कि चंद्रमा पर वस्तु का द्रव्यमान ‘m’ ही रहता है, परंतु उसका भार चंद्रमा की अपेक्षा पृथ्वी पर 6 गुणा अधिक होता है।
प्रश्न 9.
‘g’ तथा ‘G’ के मध्य संबंध स्थापित करो।
उत्तर-
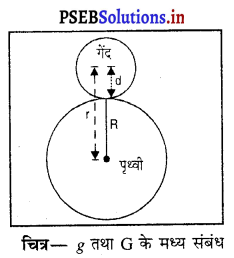
‘g’ तथा ‘G’ के मध्य संबंध (Relation betweeng and G) – मान लो ‘m’ द्रव्यमान तथा ‘d’ अर्ध-व्यास वाली एक गेंद पृथ्वी की सतह पर पड़ी है जिसका द्रव्यमान M तथा अर्ध-व्यास R है।
मान लो पृथ्वी तथा गेंद के केंद्रों की बीच की दूरी, r है भाव है,
r = d + R
पृथ्वी गेंद को अपने केंद्र की ओर F बल से आकर्षित करती है।
∴ F = G[latex]\frac{\mathrm{M} \times m}{\mathrm{R}^{2}}\) ……………. (i)
∴ F = m × गेंद में पृथ्वी द्वारा उत्पन्न त्वरण
F = m × g ……………… (ii)
यहां ‘g’ का पृथ्वी पर गुरुत्वीय त्वरण कहते हैं तथा पृथ्वी की सतह पर इसका अधिकतम मान 9.81 m/s2 है। समीकरण (i) तथा (ii) की तुलना करने पर
m × g = G\(\frac{\mathrm{M} \times m}{r^{2}}\)
या g = \(\frac{\mathrm{GM}}{r^{2}}\) ………..(iii)
अब क्योंकि गेंद का अर्ध-व्यास, पृथ्वी के अर्ध-व्यास की तुलना में बहुत कम है।
अर्थात् r = R
∴ g = G\(\frac{\mathrm{M}}{\mathrm{R}^{2}}\) …………… (iv)
समीकरण (iv) g तथा G में संबंध दर्शाती है।
प्रश्न 10.
एक व्यक्ति पृथ्वी तल की तुलना में चंद्रमा की सतह पर अधिक ऊँची छलांग लगा सकता है, क्यों ? व्याख्या करें।
उत्तर-
मान लो ‘m’ द्रव्यमान वाला व्यक्ति M द्रव्यमान वाली पृथ्वी जिसका अर्ध-व्यास ‘R’ है की सतह पर खड़ा है। पृथ्वी उस व्यक्ति को अपने केंद्र की ओर गुरुत्वाकर्षण बल लगाकर आकर्षित करती है।
F = व्यक्ति का द्रव्यमान × व्यक्ति में पृथ्वी द्वारा उत्पन्न त्वरण
F = m × g ………….. (i)
यहां ‘g’ को पृथ्वी का गुरुत्वीय त्वरण कहते हैं।
हम जानते हैं कि
F = G.\(\frac{m \times \mathrm{M}}{\mathrm{R}^{2}}\)
m × g = G.\(\frac{m \times \mathrm{M}}{\mathrm{R}^{2}}\)
या g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\) …………. (ii)
यदि समीकरण (ii) में चंद्रमा का द्रव्यमान तथा अर्ध-व्यास भरे जाएं तो चंद्रमा पर g का मान gm कहलाता है।


∴ चंद्रमा की सतह पर गुरुत्वीय त्वरण = \(\frac{1}{6}\) x पृथ्वी की सतह पर गुरुत्वीय त्वरण। अब क्योंकि चंद्रमा की सतह पर लग रहा गुरुत्वीय त्वरण पृथ्वी की सतह पर लग रहे गुरुत्वीय त्वरण का \(\frac{1}{6}\) वां भाग है, इसलिए व्यक्ति पृथ्वी की सतह से चंद्रमा की सतह पर 6 गुणा ऊँची छलांग लगा सकता है।
![]()
प्रश्न 11.
आर्किमीडीज़ का सिद्धांत क्या है ? प्रायोगिक क्रिया द्वारा इसको सत्यापित कीजिए।
उत्तर-
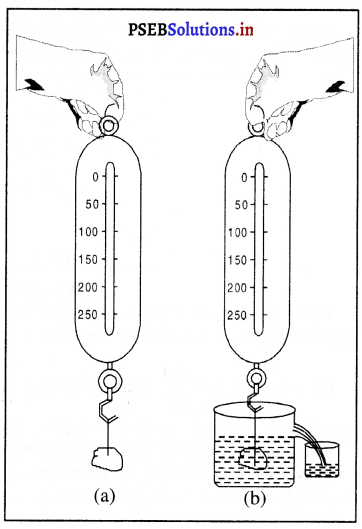
आर्किमीडीज़ का सिद्धांत – “जब किसी ठोस वस्तु को किसी तरल में पूर्ण या आंशिक रूप से डुबोया जाता है तो वह ऊपर की दिशा में एक बल को अनुभव करती है जो वस्तु द्वारा हटाए गए। तरल के भार के बराबर होता है।”
प्रायोगिक पड़ताल – एक पत्थर का टुकड़ा लीजिए और इसे कमानीदार तुला (Spring balance) के हुक्क से बाँधिए । तुला को स्टैंड से अथवा हाथ से पकड़ कर पत्थर को लटकाइए जैसा कि चित्र में दिखाया गया है। पत्थर का भार कमानीदार तुला का पाठ्याँक नोट कर ज्ञात कीजिए। अब बीकर को पूरा पानी से भरकर पत्थर को बीकर में रखे पानी में धीरे से डुबोइए जैसा चित्र (b) में दर्शाया गया है। आप देखेंगे कि जब पत्थर पानी में डूब जाता है तो कमानीदार तुला का पाठ्याँक कम हो जाता है अर्थात् पानी में डुबोने पर पत्थर के भार में कमी आ गई है। पहले पाठयाँक में से दूसरे पाठ्याँक को घटा कर पत्थर के भार में हुई कमी ज्ञात कर सकते हैं। जैसे ही पत्थर को डुबोया जाएगा, पत्थर के आयतन के बराबर पानी विस्थापित होगा। इस विस्थापित पानी को दूसरे बीकर में इकट्ठा कर भार कर लें। यह पानी का भार पत्थर के भार में हुई कमी के बराबर होगा। इस प्रकार आर्किमीडीज़ का नियम सत्यापित हो जाता है।
लघु उत्तरात्मक प्रश्न (Short Answer Type Questions)
प्रश्न 1.
इनमें से कौन-सा अधिक है-1 Kg लोहे पर पृथ्वी द्वारा लग रहा गुरुत्वाकर्षण बल या पृथ्वी पर 1 Kg लोहे द्वारा लग रहा गुरुत्वाकर्षण बल और क्यों ?
उत्तर-
न्यूटन के गुरुत्वाकर्षण-बल के नियम अनुसार दो वस्तुओं के बीच परस्पर आकर्षण बल होता है। इसलिए न तो लोहा पृथ्वी पर तथा न ही पृथ्वी लोहे पर अधिक बल लगाती है। परंतु क्योंकि लोहे का द्रव्यमान पृथ्वी के द्रव्यमान से कम है, इसलिए पृथ्वी, 1 Kg लोहे के टुकड़े को अपनी ओर आकर्षित कर लेती है जिसकी गति यह दर्शाती है कि पृथ्वी 1 Kg लोहे के टुकड़े पर अधिक बल लगाती है।
प्रश्न 2.
G को सार्वत्रिक गुरुत्वीय नियतांक क्यों कहते हैं ? .
उत्तर-
G को सार्वत्रिक स्थिरांक इसलिए कहा जाता है कि समस्त ब्राह्मांड में इसका संख्यात्मक मान एक ही रहता है जिसका मान है, G = 6.67 × 10-11 Nm2/Kg2
प्रश्न 3.
क्या ‘g’ का मान एक ज्ञात स्थान पर भिन्न-भिन्न वस्तुओं के लिए समान होता है या भिन्न ?
उत्तर-
पृथ्वी के गुरुत्वीय त्वरण (g) तथा सार्वत्रिक गुरुत्वीय G के मध्य सम्बन्ध से हम जानते हैं कि
g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)
इसी समीकरण से यह पता चलता है कि ‘g’ का मान वस्तु के द्रव्यमान पर निर्भर नहीं करता। इसलिए हम इस निष्कर्ष पर पहुंचते हैं कि किसी ज्ञात स्थिति पर भिन्न-भिन्न वस्तुओं के लिए ‘g’ का मान बराबर है।
प्रश्न 4.
एक वस्तु का भार भूमध्य रेखा पर ध्रुवों पर अधिक कहां होता है ?
उत्तर-
पृथ्वी की आकृति पूरी तरह से गोल नहीं होती, परंतु थोड़ी-सी अंडाकार है। यह ध्रुवों के पास समतल (चपटी) है जबकि भूमध्य रेखा के पास थोड़ी सी बाहर की ओर उभरी हुई होती है।
भूमध्य रेखीय अर्ध-व्यास लगभग 6378 Km है जबकि ध्रुवीय अर्ध-व्यास 6357 Km है। भूमध्य रेखीय अर्ध-व्यास, ध्रुवीय अर्ध-व्यास से 21 Km अधिक है।
हम जानते हैं कि g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}[latex] अर्थात् ‘g’ का मान R के व्युत्क्रमानुपाती। g α = ([latex]\frac{1}{R^{2}}\)) होता है इसलिए भूमध्य रेखा पर ‘g’ का मान कम होगा तथा ध्रुवों पर ‘g’ का मान अधिक होगा।
प्रश्न 5.
एक वस्तु पृथ्वी के केंद्र पर भारविहीन क्यों हो जाती है ?
उत्तर-
पृथ्वी के केंद्र पर वस्तु का भारहीन होना – हम जानते हैं कि पृथ्वी से नीचे जाते समय ‘g’ का मान कम होता है तथा पृथ्वी के केंद्र पर गुरुत्वीय त्वरण (g) = 0 होता है। इसलिए कोई वस्तु जिसका द्रव्यमान m है,
वस्तु का भार = m × o
= 0 शून्य है।
अर्थात् वस्तु भारहीन होती है।
![]()
प्रश्न 6.
टेनिस की गेंद मैदानों से पर्वतों पर अधिक उछलती है। व्याख्या करें।
उत्तर-
ज्यों-ज्यों ऊँचाई पर जाते हैं तो गुरुत्वीय त्वरण (g) का मान कम होता जाता है जिसके कारण गेंद का गुरुत्वाकर्षण बल पहाड़ों पर कम होता है जिसके फलस्वरूप गेंद पहाड़ों पर मैदानी इलाकों की अपेक्षा अधिक उछलती है।
प्रश्न 7.
पृथ्वी-तल पर एक वस्तु का भार लगभग 9.8 N है। इस कथन की पुष्टि करें।
उत्तर-
हम जानते हैं कि पृथ्वी की सतह पर गुरुत्वीय त्वरण (g) का मान 9.8 m/s2 है तथा वस्तु के भार के लिए संबंध है-
w = m × g
9.8 = m × 9.8
m = \(\frac{9.8}{9.8}\)
m = 1 किलोग्राम
दिए गए कथन का अर्थ है कि पृथ्वी की सतह पर वस्तु का द्रव्यमान 1 किलोग्राम है।
प्रश्न 8.
गुरुत्व अधीन स्वतंत्र रूप से गिर रही वस्तु की गति कैसी होगी ?
उत्तर-
गुरुत्व अधीन स्वतंत्र गिर रही वस्तु एक समान गति से नीचे गिरेगी। यदि भिन्न-भिन्न द्रव्यमान तथा आकार की वस्तुओं को निर्वात में से पृथ्वी की ओर नीचे गिरने दिया जाए तो उनमें एक समान गुरुत्वीय त्वरण होगा।
प्रश्न 9.
एक पदार्थ का आवश्यक विशेष गुण कौन-सा है, द्रव्यमान अथवा भार ?
उत्तर-
किसी पदार्थ का आवश्यक गुण द्रव्यमान होता है न कि उसका भार क्योंकि कोई ऐसा स्थान नहीं जहां पर पदार्थ का द्रव्यमान न हो। पृथ्वी के केंद्र पर वस्तु का भार शून्य हो सकता है परंतु द्रव्यमान नहीं। इसके अतिरिक्त कोई भी वस्तु जिसका द्रव्यमान होता है तथा जो स्थान घेरती है वह पदार्थ होता है जोकि पदार्थ की परिभाषा है। इसलिए पदार्थ का आवश्यक गुण उसका द्रव्यमान है न कि उसका भार।
प्रश्न 10.
एक विद्यार्थी विपिन, जो कहता है कि वह 52 Kg का है, के द्रव्यमान और भार के गुणों की तुलना करो।
उत्तर-
विपिन 52 कि० ग्रा० का है, से भाव है कि उसका द्रव्यमान 52 कि० ग्रा० है अर्थात् यह उसके शरीर का निर्माण करने वाले रुधिर, हड्डियाँ तथा त्वचा आदि की मात्रा को दर्शाता है। विपिन का भार वह आकर्षण बल है जिससे पृथ्वी उसको अपनी ओर आकर्षित करती है। यदि विपिन पृथ्वी से ऊपर किसी भी बिंदु पर चला जाएगा तो उसका द्रव्यमान 52 कि० ग्रा० ही रहेगा जबकि उसका भार प्रत्येक बिंदु पर भिन्न-भिन्न होगा। ऊँचाई पर जाने से विपिन का भार कम हो जाएगा। द्रव्यमान एक दिशाहीन राशि है जबकि भार एक बल है इसलिए सदिश राशि है। द्रव्यमान को किलोग्राम में मापते हैं तथा भार को न्यूटन (N) में मापा जाता है।
प्रश्न 11.
गुरुत्वाकर्षण बल के गुण लिखो जिनके कारण इसका दैनिक जीवन में महत्त्व है।
उत्तर-
गुरुत्वाकर्षण बल के गुण निम्नलिखित हैं जिनके कारण इनका दैनिक जीवन में महत्त्व है-
- यह एक परस्पर बल है अर्थात् दो वस्तुएं एक-दूसरे को आकर्षित करती हैं।
- यह बल वस्तुओं के द्रव्यमानों के सीधे तौर पर निर्भर करता है।
- यह बल तात्कालिक तथा समकालिक है अर्थात् दोनों ही वस्तुएं एक ही समय एक-दूसरे को आकर्षित करती
- यह बल सदैव आकर्षण करता है न कि प्रतिकर्षण
- यह बल वस्तुओं के आकार तथा आकृति पर निर्भर नहीं करता।
- यह उस माध्यम के स्वभाव पर भी निर्भर नहीं करता जहां पर एक जैसा आकर्षण-बल हो।
![]()
प्रश्न 12.
निम्नलिखित में अंतर बताओ
(i) गुरुत्वीय त्वरण (g) तथा (G) सार्वत्रिक स्थिरांक
(ii) भार तथा द्रव्यमान
(iii) द्रव्यमान केंद्र तथा गुरुत्व केंद्र।
उत्तर-
(i) g तथा (G) में अंतर-
| ‘g’ | ‘G’ |
| (1) यह गुरुत्वीय त्वरण को प्रदर्शित करता है। | (1) यह गुरुत्वाकर्षण स्थिरांक को प्रदर्शित करता है। |
| (2) इसका मान भिन्न-भिन्न स्थानों पर भिन्न-भिन्न होता है। | (2) इसका मान सभी स्थानों पर समान है। इसलिए इसे सार्वत्रिक स्थिरांक भी कहते हैं। |
| (3) इसका पृथ्वी पर मान 9.8 m/s2 है। | (3) इसका मान 9.67 × 10-11 N-m2 Kg-2 है। |
(ii) भार तथा द्रव्यमान में अंतर-
| भार (Weight) | द्रव्यमान (Mass) |
| (1) भार वह बल है जिससे वस्तु पृथ्वी के केंद्र की ओर आकर्षित होती है। | (1) द्रव्यमान वस्तु में विद्यमान पदार्थ की मात्रा है। |
| (2) भार एक सदिश राशि है। | (2) द्रव्यमान एक अदिश राशि है। |
| (3) यह अचर राशि नहीं, अपितु एक स्थान से दूसरे स्थान पर बदलती रहती है। | (3) यह एक अचर राशि है। |
| (4) भार को स्प्रिंग तुला से मापा जाता है। | (4) द्रव्यमान को दंड तुला से मापा जाता है। |
| (5) वस्तु का भार पृथ्वी के केंद्र पर शून्य हो सकता है। (अर्थात् = 0)। | (5) वस्तु का द्रव्यमान कभी भी शून्य नहीं हो सकता। |
| (6) इसे न्यूटन या किलोग्राम भार में मापा जाता है। | (6) इसे किलोग्राम में मापा जाता है। |
(iii) द्रव्यमान केंद्र तथा गुरुत्व केंद्र में अंतर – पृथ्वी की सतह पर या उसके पास का वह बिंदु जहां गुरुत्वीय बल स्थिर होता है, उसे द्रव्यमान कहते हैं। द्रव्यमान केंद्र ही वह बिंदु है जहां वास्तव में वस्तु पर गुरुत्वाकर्षण बल अनुभव किया जाता है। जबकि वस्तु का गुरुत्व केंद्र वह बिंदु है जहाँ गुरुत्व बल संपूर्ण वस्तु पर क्रिया करता हुआ माना जा सकता है।
प्रश्न 13.
आप विषुवत् रेखा ( भूमध्य ) पर स्थित किसी स्थान पर से W भार की चीनी खरीदते हैं और उसे अंटार्कटिका ले जाते हैं। क्या वहाँ उसका भार वही रहेगा ? यदि नहीं, तो यह कम होगा या अधिक ?
उत्तर-
अंटार्कटिका पर ‘g’ का मान वह नहीं होता जो भूमध्य रेखा पर होता है । अंटार्कटिका में ‘g’ का मूल्य बढ़ता है इसलिए जब चीनी का बैग भूमध्य रेखा पर स्थित किसी स्थान से खरीद कर वहाँ ले जाया जाएगा तो उस का भार बढ़ जाएगा परंतु द्रव्यमान में कोई अंतर नहीं आएगा क्योंकि द्रव्यमान एक स्थिर राशि है।
प्रश्न 14.
हम सभी सितारों को हिलाए-डुलाए बगैर अपनी अंगुली भी नहीं हिला सकते। टिप्पणी करो।
उत्तर-
जब हम अपनी अंगुली हिलाते हैं, तो अंगुली और इस ब्रह्मांड की सभी वस्तुओं की दूरी बदल जाने के कारण गुरुत्वाकर्षण बल बदल जाता है। अतः सभी वस्तुएं हिल-डुल जाती हैं, भले ही यह हिल-डुल बहुत नगण्य क्यों न हो।
प्रश्न 15.
जब कोई वस्तु भूमि पर गिरती है तो उसे मिलने के लिए पृथ्वी ऊपर की ओर गति करती है । पृथ्वी की गति दिखाई क्यों नहीं देती ?
उत्तर-
क्योंकि पृथ्वी का द्रव्यमान वस्तु के द्रव्यमान की अपेक्षा बहुत अधिक होता है। इसलिए इसमें उत्पन त्वरण नगण्य होता है। इसलिए इसकी गति दिखाई नहीं देती।
.
प्रश्न 16.
गुरुत्वाकर्षण और गुरुत्व की परिभाषा दो।
उत्तर-
गुरुत्वाकर्षण – यह इस ब्रह्मांड की किन्हीं दो वस्तुओं के मध्य आकर्षण बल है।
गुरुत्व – यह पृथ्वी (या ग्रह) द्वारा इसके तल या इसके निकट स्थित सभी वस्तुओं पर लगाया गया आकर्षण बल है। गुरुत्व गुरुत्वाकर्षण का एक विशेष उदाहरण है- जब दो वस्तुओं में से एक वस्तु पृथ्वी हो।
प्रश्न 17.
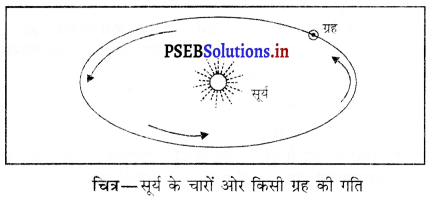
सूर्य के चारों ओर ग्रहों की गति का क्या कारण है ?
उत्तर-
सभी ग्रह अपने-अपने परिपथ में सूर्य के चारों ओर उसके गुरुत्वाकर्षण के कारण घूमते हैं। यह गति भी बिल्कुल उसी प्रकार है जिस प्रकार चंद्रमा गुरुत्वाकर्षण के कारण पृथ्वी की परिक्रमा करता है।
![]()
प्रश्न 18.
गुरुत्वाकर्षण बल प्रायः नगण्य क्यों होता है ?
उत्तर-
सामान्य द्रव्यमान के लिए गुरुत्वाकर्षण बल इतना कम होता है कि इसे अति संवेदनशील उपकरण के द्वारा ही ज्ञात किया जा सकता है।
यदि आप और आपका मित्र 1 मीटर दूर खड़े हों और आप दोनों का भार चालीस-चालीस कि० ग्रा० हो तो
F = G\(\frac{m_{1} m_{2}}{r^{2}}\)
= \(\frac{6.67 \times 10^{-11} \times 40 \times 40}{(1)^{2}}\)
F = 1.0672 × 10-7N
यह मान अत्यधिक कम है अर्थात् यह नगण्य है।
प्रश्न 19.
गुरुत्वाकर्षण बल का प्रयोग जिन व्यावहारिक क्रियाओं से होता है, उनके कुछ उदाहरण दो।
उत्तर-
गुरुत्वाकर्षण बल पर आधारित व्यावहारिक क्रियाएँ-
- सूर्य और पृथ्वी में क्रिया कर रहे गुरुत्वाकर्षण बल के कारण ही पृथ्वी, सूर्य के गिर्द अपनी वर्तुल गति को कायम रखती है।
- सौर मंडल का अस्तित्व गुरुत्वाकर्षण बल के कारण ही होता है।
- ग्रह के तल पर वायुमंडल भी गुरुत्वाकर्षण बल के कारण ही होता है।
- समुद्र में उठने वाला ज्वार-भाटा सूर्य और चांद के पानी पर क्रिया करने वाले गुरुत्वाकर्षण बल के कारण ही होता है।
- हम गुरुत्वाकर्षण बल के कारण ही पृथ्वी पर पक्की तरह खड़े रह सकते हैं।
- कृत्रिम उपग्रह के चक्कर लगाने का बल भी गुरुत्वाकर्षण बल ही है।
प्रश्न 20.
द्रव्यमान के अभिलक्षण लिखिए।
उत्तर-
द्रव्यमान – किसी वस्तु में उपस्थित द्रव्य की मात्रा को द्रव्यमान कहते हैं जिसके प्रमुख अभिलक्षण निम्नलिखित होते हैं-
- यह एक अदिश राशि है।
- यह प्रत्येक स्थान पर समान रहता है।
- इसे भौतिक तुला से मापा जाता है।
प्रश्न 21.
भार के अभिलक्षण लिखिए।
उत्तर-
भार – किसी वस्तु का भार वह बल है, जिससे पृथ्वी उसे अपनी ओर खींचती है। इसके प्रमुख अभिलक्षण निम्नलिखित होते हैं-
- यह एक सदिश राशि है।
- इसे कमानीदार तुला से मापा जाता है।
- यह स्थान-स्थान पर बदलता रहता है। ।
- यह द्रव्यमान के अनुक्रमानुपाती होता है।
प्रश्न 22.
जब हम पृथ्वी तल से ऊपर जाते हैं तो हमारे भार पर क्या प्रभाव पड़ता है ?
उत्तर-
किसी वस्तु का भार वस्तु के द्रव्यमान (m) तथा गुरुत्वीय त्वरण (g) का गुणनफल होता है। गुरुत्वीय त्वरण का मान वस्तु की केंद्र से दूरी पर निर्भर करता है।
क्योंकि g = \(\frac{\mathrm{GM}_{e}}{\mathrm{R}^{2}}\)
गुरुत्वीय त्वरण वस्तु की पृथ्वी के केंद्र से दूरी के वर्ग के व्युत्क्रमानुपाती होता है। अतः भार भी वस्तु की पृथ्वी के केंद्र से दूरी के वर्ग के व्युत्क्रमानुपाती होगा। अर्थात् ज्यों-ज्यों हम पृथ्वी तल से ऊपर जाते हैं तो हमारी पृथ्वी के केंद्र से दूरी बढ़ जाती है जिसके कारण हमारा भार भी कम होता जाता है। यदि हम पृथ्वी तल से पृथ्वी के अर्ध-व्यास के बराबर ऊपर चले जाएं तो वस्तु का भार पृथ्वी के भार की अपेक्षा \(\frac{1}{4}\) गुणा रह जाएगा।
प्रश्न 23.
जब किसी वस्तु को ऊपर की ओर फेंका जाता है तो वस्तु की गति पर क्या प्रभाव पड़ता है ? उसका त्वरण कितना होता है ?
उत्तर-
जब किसी वस्तु को ऊपर की ओर फेंका जाता है तो पृथ्वी उसे अपने गुरुत्व बल के कारण नीचे की और आकर्षित करती है। गुरुत्व बल वस्तु की गति के विपरीत दिशा में कार्य करता है अतः वस्तु का वेग कम होता जाता है। ऊपर की ओर फेंकी गई वस्तु का त्वरण नीचे की ओर गिरती हुई वस्तु के त्वरण के बराबर होता है परंतु ऋणात्मक होता है।
ऊपर फेंकी गई वस्तु का त्वरण = -9.8m/s2 है। इसलिए जब वस्तु ऊपर की ओर फेंकी जाती है उसका वेग 9.8m/s2 की दर से घटता जाता है। वेग तब तक घटता जाता है जब तक वह शून्य नहीं हो जाता। अधिकतम ऊँचाई पर पहुँच कर वेग शून्य हो जाता है।
![]()
प्रश्न 24.
चंद्रमा पृथ्वी की ओर गिरता रहता है, इसका तात्पर्य क्या है ? यह पृथ्वी तल पर गिर क्यों नहीं जाता ?
उत्तर-
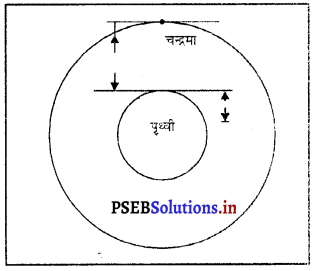
चंद्रमा अपने अक्ष के चारों ओर घूमता हुआ पृथ्वी की ओर गिरता है, पर अपकेंद्रण बल के कारण अपने ही कक्ष में रहता है। यह अपकेंद्रण बल पृथ्वी और चंद्रमा के बीच आकर्षण बल के कारण उत्पन्न होता है। इस बल के अभाव में चंद्रमा अपने पथ से दूर हट जाता है।
यदि चंद्रमा हमारी पृथ्वी से h ऊँचाई पर है तो गुरुत्वाकर्षण बल को इस प्रकार प्रकट किया जा सकता है-
\(\frac{\mathrm{G} m \mathrm{M}}{(\mathrm{R}+h)^{2}}\) = \(\frac{m v_{0}^{2}}{(\mathrm{R}+h)}\)
\(\frac{\mathrm{GM}}{(\mathrm{R}+h)}\) = \(v_{0}^{2}\)
∴ υ0 = \(\sqrt{\frac{\mathrm{GM}}{\mathrm{R}+h}}\)
α\(\frac{1}{d^{2}}\)
पृथ्वी
जहाँ υ0 कक्षीय वेग (orbital velocity) है।
अतः υ0 वेग से घूमता चंद्रमा अपने कक्ष में घूमता रहेगा। यह पृथ्वी की ओर गिरता रहेगा पर हर बार गिरने से चूकता भी रहेगा।
प्रश्न 25.
पृथ्वी सेब को आकर्षित करती है तो सेब भी पृथ्वी को आकर्षित करता है ? यदि हाँ, तो पृथ्वी सेब की ओर गति क्यों नहीं करती ?
उत्तर-
सेब निश्चित रूप से पृथ्वी को अपनी ओर आकर्षित करता है, पर सेब का द्रव्यमान बहुत कम है और उसकी तुलना से पृथ्वी का द्रव्यमान बहुत अधिक है। सेब और पृथ्वी के बीच का गुरुत्वाकर्षण बल पृथ्वी पर बहर कम पर सेब पर बहुत अधिक त्वरण उत्पन्न करता है जिस कारण वह पृथ्वी की ओर गिरता है। पृथ्वी में उत्पन्न त्वमा इतना कम होता है कि वह सेब की ओर गति नहीं करती। पृथ्वी का विस्थापन बल लगभग शून्य ही होता है।
प्रश्न 26.
यदि किसी कारणवश गुरुत्वीय बल लुप्त हो जाए तो हम पृथ्वी से अंतरिक्ष में क्यों फेंक दिए जाएंगे ?
उत्तर-
हाँ, हम वास्तव में ही अंतरिक्ष में उड़ने लगेंगे यदि गुरुत्व बल को समाप्त कर दिया जाए। हर अंतरिक्ष में अपकेंद्रण बल के कारण उड़ने लगेंगे।
प्रश्न 27.
मान लीजिए पृथ्वी का द्रव्यमान एकाएक 10% बढ जाए, किंतु उसके आकार में कोई परिवर्तन न हो, तब आपके भार में क्या परिवर्तन होगा ? यदि पृथ्वी की त्रिज्या उसकी वर्तमान त्रिज्या की दुगुनी हो जाए, किंतु उसका द्रव्यमान वही रहे तो आपके भार में क्या परिवर्तन होगा ?
उत्तर-
(i) पृथ्वी के आकार में बिना परिवर्तन किए हुए यदि इसका द्रव्यमान 10% बढ़ जाए तो (g) का मान भी बढ़ जाएगा जिसके परिणामस्वरूप हमारा भार भी 10% बढ़ जाएगा।
∵ g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\) तथा W = mg
‘g’ का मान ‘M’ के समानुपाती होता है और उसकी दूरी के वर्ग के व्युत्क्रमानुपाती होता है।
(ii) यदि पृथ्वी का अर्ध-व्यास वर्तमान व्यवस्था से दुगुना हो जाए और इसके द्रव्यमान में कोई अंतर न किया जाए तो (g) का मान कम हो जाएगा और हमारा भार \(\sqrt{2}\) गुणा कम हो जाएगा।
प्रश्न 28.
अंतरिक्ष में किसी स्थान पर 1Kg पुंज पर पृथ्वी का गुरुत्वाकर्षण बल 5 m/s2 का त्वरण उत्पन्न करता है। यदि उसकी जगह 3Kg का द्रव्यमान हो तो कितना त्वरण उत्पन्न होगा ?
उत्तर-
किसी स्थान पर गुरुत्वाकर्षण बल के कारण उत्पन्न त्वरण किसी वस्तु के द्रव्यमान से स्वतंत्र होता है, इसलिए 3Kg द्रव्यमान वाली वस्तु का उसी स्थान पर त्वरण उतना ही अर्थात् 5m/s2 होगा।
![]()
प्रश्न 29.
सिद्ध कीजिए यदि दो वस्तुओं पर पृथ्वी द्वारा आरोपित गुरुत्वीय बल बराबर हैं तो उन दोनों वस्तुओं के द्रव्यमान भी बराबर होंगे।
उत्तर-
मान लो दो वस्तुओं के द्रव्यमान क्रमशः m1 तथा m2 हैं तथा ये दोनों वस्तुएँ पृथ्वी के केंद्र से समान दूरी R पर रखी हैं । पृथ्वी के द्रव्यमान M तथा वस्तु के द्रव्यमान m1 के बीच आकर्षण बल F1 है।
∴ F1 = \(\frac{\mathrm{GM} \times m_{1}}{R^{2}}\)
इसी प्रकार, पृथ्वी के द्रव्यमान M तथा वस्तु के द्रव्यमान m2 के बीच आकर्षण बल F2 है।
F2 = \(\frac{\mathrm{GM} \times m_{2}}{R^{2}}\)
परंत दिया गया है : F1 = F2
\(\frac{\mathrm{GM} \times m_{1}}{R^{2}}\) = \(\frac{\mathrm{GM} \times m_{2}}{R^{2}}\)
अतः m1 = m2
अर्थात् दोनों वस्तुओं के द्रव्यमान बराबर हैं।
प्रश्न 30.
उत्प्लावन बल तथा उत्प्लावन केंद्र से क्या अभिप्राय है ?
उत्तर-
उत्प्लावन बल तथा उत्प्लावन केंद्र – प्रत्येक द्रव अपने अंदर पूर्ण अथवा आंशिक रूप से डुबोई गई वस्तु पर ऊपर की ओर एक बल लगाता है। इस बल को उत्प्लावन बल (उत्क्षेप) कहते हैं। यह बल वस्तु द्वारा हटाए गए द्रव के गुरुत्व-केंद्र पर कार्य करता है, जिसे उत्प्लावन केंद्र कहते हैं।
प्रश्न 31.
नदियों पर बनाए गए बाँधों की दीवारें नीचे मोटी व ऊपर पतली क्यों बनाई जाती हैं ?
उत्तर-
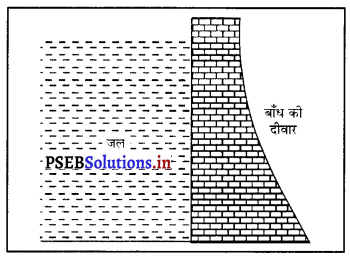
बाँध की दीवारों का नीचे मोटी व ऊपर पतली होना-बाँधों की गहराई बहुत अधिक होती है तथा द्रव के अंदर किसी बिंदु पर दाब, उस बिंदु की मुक्त तल से गहराई के अनुक्रमानुपाती होता है। इसलिए बांध की तली में जल का दाब अधिकतम होता है। अतः बाँध की दीवार पर सबसे अधिक दाब नीचे होता है ; जैसे-जैसे ऊपर आते हैं दाब भी कम होता जाता है। अत: बाँध की दीवार नीचे से मोटी बनाई जाती है, जिससे वह अधिक दाव-बल को सहन कर सके।
प्रश्न 32.
रेलगाड़ी की पटरियों के नीचे लकड़ी अथवा लोहे के चौड़े स्लीपर क्यों लगाए जाते हैं ?
उत्तर-
यदि रेलगाड़ी की पटरियों के नीचे चौड़े स्लीपर न लगाए जाएँ तो रेल की पटरियाँ अधिक दबाव के कारण पृथ्वी में फँस सकती हैं। पटरियों के नीचे स्लीपर लगाने से क्षेत्रफल अधिक हो जाता है, जिससे दाब कम पड़ता है और रेल की पटरियाँ पृथ्वी में नहीं धंस सकतीं।
प्रश्न 33.
एक तख्ते पर कुछ पुस्तकें फैलाकर रखने की अपेक्षा वही पुस्तकें एक जगह पर ऊपर-नीचे रखने पर तख्ता अधिक नीचे की ओर झुक जाता है, ऐसा क्यों ?
उत्तर-
हम जानते हैं कि दाब तथा क्षेत्रफल व्युत्क्रमानुपाती होते हैं अर्थात् P ∝ \(\frac{1}{\mathrm{~A}}\) इसलिए तो पर पुस्तकों को फैलाकर रखने से, उनके द्वारा घिरा क्षेत्रफल (A) अधिक होगा, जिसके कारण तख्ते पर दाव (P = F/A) कम लगेगा। इन्हीं पुस्तकों को ऊपर नीचे रखने से उनके द्वारा घिरा क्षेत्रफल (A) कम होगा जिससे तख्ते पर दाब बढ़ जाएगा और तख्ता नीचे की ओर झुक जाएगा।
![]()
प्रश्न 34.
भारी वाहनों के पहियों के टायर काफी चौड़ें क्यों बनाए जाते हैं।
उत्तर-
भारी वाहनों के टायर काफी चौड़े बनाना – भारी वाहनों के टायर चौड़े होने से क्षेत्रफल A अधिक हो जाता है तथा परिणामस्वरूप सड़क अथवा पृथ्वी पर लगने वाला दाब कम हो जाता है। इसीलिए वाहन के पहिये कम दाब के कारण सड़क में धंसने से बच जाते हैं।
प्रश्न 35.
नदी के जल की अपेक्षा समुद्र के जल में तैरना क्यों अधिक सुगम होता है ? ।
उत्तर-
नदी की अपेक्षा समुद्र में तैरना सुगम – नदी के जल का घनत्व, समुद्र (नमक घुला होने के कारण) के जल के घनत्व से कम होता है, इसलिए मनुष्य को समुद्र में तैरने के लिए जल का कम आयतन हटाना पड़ेगा (अर्थात् शरीर का कम भाग जल में डूबेगा) ; अत: मनुष्य का नदी के जल की अपेक्षा समुद्र के जल में तैरना अधिक सुगम होता है।
प्रश्न 36.
कएँ से जल खींचते समय जल से भरी बाल्टी जल की सतह से ऊपर आने पर धीरे-धीरे भारी क्यों प्रतीत होने लगती है ?
उत्तर-
जब बाल्टी जल में डूबी होती है, तब उस पर उसके द्वारा हटाए गए जल के भार के बराबर उत्प्लावन बल लगता है जिस कारण बाल्टी वास्तविक भार की अपेक्षा कम भारी प्रतीत होती है। जैसे-जैसे बाल्टी को जल से बाहर निकालते हैं, उस पर लगने वाले उत्प्लावन बल कम होने लगता है और बाल्टी भारी लगने लगती है।
प्रश्न 37.
समान बल लगाने से मोटी कील की अपेक्षा नुकीली कील, दीवार में शीघ्र क्यों घुस जाती है ?
उत्तर-
मोटी तथा नुकीली कीलों पर दाब – नुकीली कील के सिरे का क्षेत्रफल, मोटी कील के सिरे के क्षेत्रफल की अपेक्षा बहुत कम होता है। अतः दोनों कीलों पर एक-समान बल लगाने से नुकीली कील द्वारा दीवार पर मोटी कील की अपेक्षा अधिक दाब (P = F / A) लगाता है, जिससे नुकीली कील दीवार में आसानी से घुस जाती है।
महत्त्वपूर्ण सूत्र (Important Formulae)
1. F = G\(\frac{\mathrm{Mm}}{\mathrm{R}^{2}}\)
2. F = mg
3. g = G\(\frac{\mathrm{M}}{\mathrm{R}^{2}}\)
4. v = u + gt
5. v2 = u2 + 2gh
6. h = ut + \(\frac {1}{2}\)gt2
7. gm = \(\frac {1}{6}\)ge
(gm = चंद्रमा पर त्वरण, ge = पृथ्वी पर त्वरण)
आवश्यक आंकड़े-
पृथ्वी
द्रव्यमान = 6 × 1024 Kg
अर्ध-व्यास = 6.4 × 106 m (6400 Km)
सूर्य से दूरी = 1.5 × 1011 m
चंद्रमा
द्रव्यमान = 7.3 × 1022 Kg
![]()
संख्यात्मक प्रश्न (Numerical Problems)
प्रश्न 1.
1 Kg द्रव्यमान वाले दो गोलों में दूरी 3m है। उनमें गुरुत्वाकर्षण बल की गणना करो। ज्ञात है G = 6.67 × 10-11 Nm2/Kg2.
हल :

यहाँ m1 = m2 = 1 Kg
दोनों गोलों के बीच दूरी, (r) = 3m
सार्वत्रिक स्थिरांक, (G) = 6.67 × 10-11 Nm2/Kg2
हम जानते हैं कि F = G.\(\frac{m_{1} \times m_{2}}{r^{2}}\)
F = \(\frac{6.67 \times 10^{-11} \times 1 \times 1}{(3)^{2}}\)
= \(\frac{6.67 \times 10^{-11}}{9}\)N
F = 0.741 × 10-11 N
F = 7.41 × 10-12 N (लगभग)
प्रश्न 2.
बृहस्पति ग्रह का द्रव्यमान 1.9 × 1027 Kg और सूर्य का 1.99 × 1030 Kg है। दोनों के केंद्रों में 7.8 × 1011m दूरी है। सूर्य द्वारा बृहस्पति पर लगाया गया गुरुत्वाकर्षण बल कितना होगा?
हल :
बृहस्पति का द्रव्यमान, (m1) = 1.9 × 1027 Kg
सूर्य का द्रव्यमान, (m2) = 1.99 × 1030 Kg
बृहस्पति तथा सूर्य के बीच दूरी (r) = 7.8 × 1011 m
G = 6.67 × 10-11 N – m2/Kg2
हम जानते हैं कि F = G.\(\frac{m_{1} \cdot m_{2}}{r^{2}}\)

= 4.1446 × 1024 N
प्रश्न 3.
चंद्रमा की त्रिज्या 1.7 × 106 m और इसका द्रव्यमान 7.35 × 1022 Kg है। चंद्रमा की सतह पर गुरुत्वीय-स्वरण कितना है ? (ज्ञात है कि G = 6.67 × 10-11 N – m2/Kg2) .
हल :
चंद्रमा की त्रिज्या, (R) = 1.7 × 106 m
चंद्रमा का द्रव्यमान, (M) = 7.35 × 1022 Kg
G = 6.67 × 10-11 N-m2/Kg2
हम जानते हैं कि, चंद्रमा पर गुरुत्वीय-त्वरण
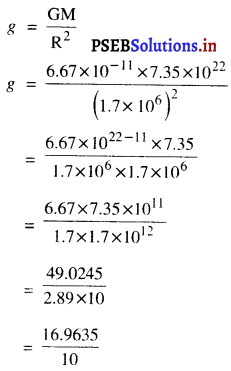
= 1.69m/s2 (लगभग)
= 1.70m/s2
प्रश्न 4.
वस्तु के भार में प्रतिशत परिवर्तन बताएं जब इसको भू-मध्य रेखा से ध्रुवों तक ले जाया जाता है। ध्रुव त्रिज्या 6357 कि०मी० है और भू-मध्य रेखीय त्रिज्या 6378 कि०मी० है।
हल :
ध्रुवीय अर्ध-व्यास , (r) = 6357 Km
भूमध्य रेखीय अर्ध-व्यास, (R) = 6378 Km
∴ h = R – r
⇒ h = 6378 – 6357
h = 21 Km
R = 6400 Km (लगभग)
हम जानते हैं कि

= \(\frac{2 h}{\mathrm{R}}\) x 100
= \(\frac{2 \times 21 \times 100}{6400}\)
= \(\frac{42}{64}\)
= 0.656
= 0.7% (लगभग)
प्रश्न 5.
पृथ्वी पर सूर्य और चंद्रमा द्वारा लग रहे गुरुत्वाकर्षण बलों की तुलना करो। कौन अधिक बल लगाता है और कितना ?
हल :
पृथ्वी का द्रव्यमान, (Me) = 6 × 1024 Kg
चंद्रमा का द्रव्यमान, (Mm) = 7.3 × 1022 Kg
सूर्य का द्रव्यमान, (Ms) = 2 × 1030 Kg
पृथ्वी और चंद्रमा के बीच की दूरी (Rem) = 3.84 × 108 m
पृथ्वी और सूर्य के बीच की दूरी (Res) = 1.5 × 1011 m
पृथ्वी और चंद्रमा के बीच गुरुत्वीय बल Fem = G\(\frac{\mathrm{M} e \times \mathrm{M}_{s}}{\mathrm{R}_{e m}^{2}}\)

= 179.97
= 180 (लगभग)
∴ सूर्य पर अधिक गुरुत्वीय बल लगता है जो लगभग 180 गुणा अधिक होता है।
![]()
प्रश्न 6.
पृथ्वी की सतह से कितनी ऊँचाई पर गुरुत्वीय त्वरण का मान सतह ऊपर इसके मान से आधा होगा ? पृथ्वी की त्रिज्या ‘R’ मान लीजिए।
हल :
मान लो ‘h’ ऊंचाई है जो पृथ्वी की सतह से ऊपर है जहाँ g’ = \(\frac{g}{2}\) है, तो

√2 R = R + h
h = √2 R – R
h = R (√2 – 1)
= R (1.414- 1)
= R (0.414)
= (0.414 R
प्रश्न 7.
एक गेंद 40 मी० ऊँचे मीनार के शीर्ष-बिंदु से फेंकी जाती है। 20 मी० की दूरी तय करने के पश्चात् इसका वेग कितना होगा ? पृथ्वी से टकराने पर इसका वेग कितना होगा ?
हल :
(i) यहां (h) = 40 m
आरंभिक वेग, (u) = 0
गुरुत्वीय त्वरण (a) = g = 10m/s2
तय की गई दूरी (S) = 20m
हम जानते हैं कि υ2 – u2 = 2aS
υ2 – 0 = 2 × 10 × 20
υ2 = 400
υ = 20 m/s
(ii) यहां u = 0
a = g = 10
तय की गई दूरी (S) = 40 km
हम जानते हैं कि υ2 – u2 = 2aS
υ2 – 0 = 2 × 10 × 40
υ2 = 800
υ = \(\sqrt{800}\)
= \(\sqrt{400 \times 2}\)
υ = 20√2
अर्थात् पृथ्वी पर टकराते समय वेग = 20√2 m/s
प्रश्न 8.
पृथ्वी की सतह से कितनी ऊंचाई पर ‘g’ का मान पृथ्वी की सतह पर मान का 4% रह जाएगा? पृथ्वी की त्रिज्या = 6400 कि० मी० (Km) दी गई है।
हल :
मान लो पृथ्वी की सतह से ‘h’ दूरी पर (ऊँचाई) ‘g’ का मान पृथ्वी की सतह के मान का 4% हो जाता है।
अर्थात्
g’ = g का 4%

h = 4 R
h = 4 × 6400 Km [यहां R = 6400 Km]
h = 25600 Km
प्रश्न 9.
पृथ्वी के तल से कितनी ऊँचाई पर ‘g’ मान पृथ्वी के तल पर इसके मान का 50% होगा ? पृथ्वी की त्रिज्या 6400 कि० मी० (Km) दी गई है।
हल :
मान लो पृथ्वी की सतह से ‘h’ ऊँचाई पर ‘g’ का मान पृथ्वी की सतह के मान का 50% रह जाता है।
∴ g’ = g का 50%
g’ = \(\frac{50}{100}\) × g
= \(\frac {1}{2}\)g

R × 0.414 = h
6400 × 0.414 = h
h = 2649.6 Km
प्रश्न 10.
10 कि० ग्रा० और 25 कि० ग्राम के दो गोलों के केंद्रों के बीच की दूरी 5 मी० है। दोनों गोलों के बीच लगा गुरुत्वाकर्षण बल ज्ञात करो जबकि G = 6.7 × 10-11 Nm2/Kg2.
हल :
M1 = 10 कि० ग्रा०, M2 = 25 कि० ग्रा०
r = 5 मी०, G = 6.7 × 10-11 Nm2/Kg2
न्यूटन के गुरुत्वाकर्षण नियम अनुसार
F = G\(\frac{\mathrm{M}_{1} \mathrm{M}_{2}}{r^{2}}\)
= \(\frac{6.7 \times 10^{-11} \times 10 \times 25}{(5)^{2}}\)N
F = 6.7 × 10-10N
![]()
प्रश्न 11.
कल्पना कीजिए कि आप और आपके मित्र, प्रत्येक का द्रव्यमान 50 Kg है। मान लीजिए कि आप इस प्रकार खड़े हैं कि आप दोनों के गुरुत्व केंद्रों के बीच की दूरी 1 m है। अपने और अपने मित्र के बीच लगने वाले गुरुत्वाकर्षण बल की गणना कीजिए।
हल :
(i) आप और आपके मित्र का अलग-अलग द्रव्यमान M1 = M2 = 50 कि० ग्रा०
गुरुत्व केंद्रों के मध्य दूरी (r) = 1 मी०
G = 6.67 × 10-11 N – m2/kg2
F = ?
हम जानते हैं कि,
F = G\(\frac{\mathrm{M}_{1} \mathrm{M}_{2}}{r^{2}}\)
= \(\frac{6.7 \times 10^{-11} \times 50 \times 50}{(1)^{2}}\)
= 16.625 × 10-9N
प्रश्न 12.
यदि किसी वस्तु का भार 49N है तो इसका द्रव्यमान क्या होगा ?
हल :
वस्तु का भार, W = 49 N
g = 9.8ms-2
भार = द्रव्यमान × गुरुत्वीय त्वरण
W = m × g
49 = m × 9.8
m = \(\frac{49}{9.8}\)
= 5 Kg
प्रश्न 13.
एक वस्तु 50 m/s के वेग से लंबात्मक दिशा में ऊपर की ओर फेंकी गई। वस्तु कितने समय बाद अधिकतम ऊँचाई प्राप्त कर लेगी।
हल :
आरंभिक वेग. (u) == 50 m/s
गुरुत्वीय त्वरण (g) = -10m/s2
अधिकतम ऊँचाई पर अंतिम वेग, (υ) = 0
समय, (t) = ?
हम जानते हैं कि,
υ = u + gt
0 = 50 – 10 × t
10t = 50
t = \(\frac{50}{10}\)
t = 5s
इस तरह 5 सैकेंड बाद वस्तु अधिकतम ऊँचाई प्राप्त कर लेगी।
प्रश्न 14.
किसी पत्थर को छत के किनारे से गिराया गया। यदि वह 2m ऊँची खिड़की को 0.1 सैकेंड में पार करे तो खिड़की के ऊपरी किनारे से छत कितनी ऊपर है ?
हल :
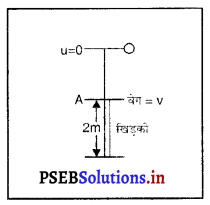
खिड़की पार करने में तय हुई दूरी (S) = 2m
g = 9.8ms-2; t = 0.1s
अब पत्थर खिड़की के ऊपरी किनारे A तक पहुंचता है तो उसका वेग υ है
अब, S = ut + \(\frac {1}{2}\)gt2
2 = v × 0.1 × \(\frac {1}{2}\) × 9.8 × (0.1)2
2 = 0.1υ + 0.049
0.1υ = 1.951
υ = 1.951 × 10
= 19.51ms-1
यहां प्रारंभिक वेग u = 0
यह वेग पथ OA के लिए अंतिम वेग है।
इसलिए υ2 – u2 = 2gs
(19.51)2 – 02 = 2 × 9.8 × S
S = \(\frac{19.51 \times 19.51}{2 \times 9.8}\)
= 19.42m
प्रश्न 15.
यदि पृथ्वी पर आपका भार 60 Kg हो तो आपको पृथ्वी के केंद्र से कितनी दूर जाना पड़ेगा ताकि आपका भार 30 Kg रह जाए ?
हल :
मान लो पृथ्वी तल से h दूरी पर भार 30 Kg होता है।

R + h = √2 R
h = √2 R – R
= ( √2 – 1) R
= (1.414- 1) R
= 0.414 × 6400 (∴ R = 6400 Km)
= 2649.9 Km
![]()
प्रश्न 16.
70 kg द्रव्यमान के किसी मनुष्य का चन्द्रमा पर भार क्या होगा ? उसका पृथ्वी तथा चन्द्रमा पर द्रव्यमान क्या होगा ?
हल :
द्रव्यमान एक अचर राशि है, इसलिए मनुष्य का पृथ्वी तथा चांद दोनों पर द्रव्यमान समान होगा।
पृथ्वी पर मनुष्य का द्रव्यमान = 70 kg
चंद्रमा पर मनुष्य का द्रव्यमान = 70 kg
पृथ्वी पर मनुष्य का भार (W1) = ?
पृथ्वी पर गुरुत्वीय त्वरण g = 9.8 m/s2
मनुष्य का चंद्रमा पर भार (W2) = ?
हम जानते हैं
= W1 = mg
= 70 × 9.8 = 686 N
अत: पृथ्वी पर मनुष्य का भार = 686 N
चंद्रमा पर मनुष्य का भार (W2) = \(\frac{1}{6}\) × पृथ्वी पर मनुष्य का भार
= \(\frac{W_{1}}{6}\)
= \(\frac{686 N}{6}\)
= 114.33 N
प्रश्न 17.
चंद्रमा के तल पर गुरुत्व प्रवेग का मान ज्ञात करो।
चंद्रमा का द्रव्यमान = 7.4 × 1022 kg
चंद्रमा का अर्ध-व्यास = 1740 km
और G = 6.673 × 10-11 Nm2 kg-2
हल : यहां G = 6.673 × 10-11 Nm2 kg-2
चंद्रमा का द्रव्यमान M = 7.4 × 1022 kg
चंद्रमा का अर्ध-व्यास, R = 1740000 m
g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)
= \(\frac{6.673 \times 10^{-11} \times 7.4 \times 10^{22}}{1740000 \times 1740000}\)
= 1.63 मी० सै०-2
प्रश्न 18.
एक व्यक्ति का पृथ्वी पर भार 600 न्यूटन है। चंद्रमा पर गुरुत्वीय त्वरण, पृथ्वी पर गुरुत्वीय त्वरण का 1/6 है। यदि पृथ्वी पर गुरुत्वीय त्वरण 10 m/s2 है, तो चंद्रमा पर व्यक्ति का द्रव्यमान और भार क्या होंगे ?
हल :
मान लो व्यक्ति का द्रव्यमान m कि०ग्रा० है।
w = mg = 600 न्यूटन
m = \(\frac{600}{g}\)
= \(\frac{600}{10}\) = 60 किग्रा०
∴ वस्तुओं के द्रव्यमान गुरुत्वीय त्वरण ‘g’ पर निर्भर नहीं करते। इसलिए पृथ्वी तथा चंद्रमा पर दोनों जगह व्यक्ति का द्रव्यमान 60 किग्रा होगा।
चंद्रमा पर व्यक्ति का भार w1 = \(\frac{1}{6}\) × mg
\(\frac{m g}{6}\)
\(\frac{1}{6}\) mg
= \(\frac{1}{6}\) × 60 × 10
= 100 न्यूटन उत्तर
प्रश्न 19.
पृथ्वी का द्रव्यमान 6 × 1024 kg है तथा चंद्रमा का द्रव्यमान 7.4 × 1022 kg है। यदि पृथ्वी तथा चंद्रमा के बीच की दूरी 3.84 × 105 km है तो पृथ्वी द्वारा चंद्रमा पर लगाए गए बल का परिकलन कीजिए।
G = 6.7 × 10-11 Nm2kg2
हल :
पृथ्वी का द्रव्यमान (M) = 6 × 1024 kg
चंद्रमा का द्रव्यमान (m) = 7.4 × 1022 kg
पृथ्वी तथा चंद्रमा के बीच की दूरी,
(d) = 3.84 × 105 km
= 3.84 × 105 × 1000 m
= 3.84 × 108 m
G = 6.7 × 10-11 N m2 kg-2
पर लगाया गया बल,
F = G\(\frac{\mathrm{M} \times m}{d^{2}}\)
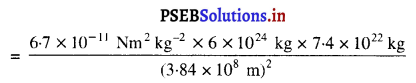
= 2.01 × 1020 N.
अतः पृथ्वी द्वारा चंद्रमा पर लगाया गया बल 2.01 × 1020 N है।
प्रश्न 20.
एक कार किसी कगार से गिर कर 0.5s में धरती पर आ गिरती है। परिकलन में सरलता के लिए g का मान 10 ms-2 लीजिए।
(i) धरती पर टकराते समय कार की चाल क्या होगी ?
(ii) 0.5s के दौरान इसकी औसत चाल क्या होगी ?
(ii) धरती से कगार कितनी ऊँचाई पर है ?
हल:
समय, t = 0.5 s
प्रारंभिक वेग, u = 0 m s-1
गुरुत्वीय त्वरण, g = 10 m s-2
कार का त्वरण, a = + 10 m s-2 (अधोमुखी दिशा)
(i) चाल υ = at
υ = 10 m s-2 × 0.5 s
= 5 m s-1
(ii) औसत चाल = \(\frac{u+v}{2}\)
= (0 ms-1 + 5ms-1)
= 2
= 2.5 ms-1
(iii) तय की गई दूरी S = 1/2 at2
= 1/2 × 10 ms-2 × (1/2 s)2
= 1/2 × 10 ms-2 × 1/4 s2
= 1.2 m
अतः
(i) धरती पर टकराते समय कार की चाल = 5 ms-1
(ii) 1/2 सेकंड के दौरान इसकी औसत चाल = 2.5 ms-1
(iii) धरती की सतह से कगार की ऊँचाई = 1.25 m
![]()
प्रश्न 21.
एक वस्तु को ऊर्ध्वाधर दिशा में ऊपर की ओर फेंका जाता है और यह 10 m की ऊँचाई तक पहुँचती है। परिकलन कीजिए
(i) वस्तु कितने वेग से ऊपर फेंकी गई तथा
(ii) वस्तु द्वारा उच्चतम बिंदु तक पहुंचने में लिया गया समय।
हल :
चली गई दूरी (S) = 10 m
अंतिम वेग (υ) = 0 ms-1
गुरुत्वीय त्वरण (g) = 9.8 ms-2
वस्तु का त्वरण (a) = – 9.8 ms-2 (ऊर्ध्वमुखी दिशा में फेंकने के कारण)
(i) υ2 = u2 + 2as
0 = u2 + 2 × (-9.8 ms-2) × 10 m
-u2 = – 2 × 9.8 × 10 m2s-2
u = \(\sqrt{196}\) ms-1
= 14 ms-1
(ii) υ = u + at
0 = 14 ms-1 – 9.8 ms-2 × t
t = 1.43 s.
प्रश्न 22.
पृथ्वी की सतह पर मापने पर एक वस्तु का भार 10 N आता है। चंद्रमा की सतह पर मापने पर इसका भार कितना होगा ?
उत्तर-
हमें ज्ञात है-
चंद्रमा पर वस्तु का भार=(1/6) × पृथ्वी पर इसका भार
अर्थात्,
Wm = \(\frac{\mathrm{W}_{e}}{6}\)
= \(\frac{10}{6}\)N
= 1.67 N.
अतएव चंद्रमा की सतह पर वस्तु का भार 1.67 N होगा।
प्रश्न 23.
एक लकड़ी का गुटका मेज़ पर रखा है। लकड़ी के गुटके का द्रव्यमान 5 kg है तथा इसकी विमाएँ 40 cm × 20 cm × 10 cm हैं। लकड़ी के टुकड़े द्वारा मेज पर लगने वाले दाब को ज्ञात कीजिए, यदि इसकी निम्न विमाओं की सतह मेज़ पर रखी जाती हैं। (a) 20 cm × 10 cm और (b) 40 cm × 20 cm।
हल:
(i) लकड़ी के गुटके का द्रव्यमान = 5 kg
विमाएं = 40 cm × 20 cm × 10 cm
यहाँ लकड़ी के गुटके का भार मेज़ की सतह पर प्रणोद लगाता है। चित्र (a)
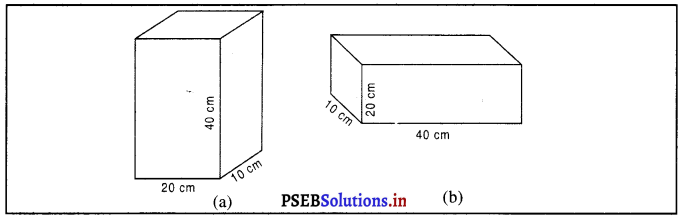
अर्थात्, प्रणोद (F’) = m × g
= 5 kg × 9.8 ms-2
= 49 N
सतह का क्षेत्रफल = लंबाई चौड़ाई
= 20 cm × 10 cm
= 200 cm2 = 0.02 cm2

= 2450 Nm-2
(ii) जब गुटके को 40 cm × 20 cm विमाओं की सतह चित्र (b) मेज़ पर रखी जाती है, यह मेज़ की सतह पर पहले जितना ही प्रणोद लगता है।
क्षेत्रफल = लंबाई × चौड़ाई
= 40 cm × 20 cm
= 800 cm2 = 0.08 m2
बल =  = \(\frac{49 \mathrm{~N}}{0.08 m^{2}}\) = 612.5 Nm-2
= \(\frac{49 \mathrm{~N}}{0.08 m^{2}}\) = 612.5 Nm-2
प्रश्न 24.
50 cm3 आयतन के लोहे के एक टुकड़े को कमानीदार तुला से लटकाकर जल में डुबोया जाता है। लोहे के टुकड़े द्वारा कमानी पर लगाए गए खिंचाव बल का मान न्यूटन में ज्ञात कीजिए।(लोहे का घनत्व = 7.6 × 103 kg/m3, जल का घनत्व = 1 × 103 kg/m3)
हल :
लोहे के टुकड़े का आयतन = 50 cm3
= 50 × 10-6 m3
लोहे के टुकड़े का द्रव्यमान = लोहे का घनत्व × आयतन
= (7.6 × 103 kg/m3) × (50 × 10-6 m3)
= 0.38 kg
अतः लोहे के टुकड़े का वायु में भार= 0.38 kg
मान लो जल में डुबोने पर लोहे के टुकड़े का भार = W Kg
∴ जल में डुबोने पर लोहे के टुकड़े के भार में कमी = (0.38 – W) kg

= 0.05
= 0.38 – W = 0.05
या W = 0.38 – 0.05 = 0.33 kg wt.
अतः लोहे के टुकड़े द्वारा कमानी पर लगाया गया खिंचाव बल
= 0.33 × g
= 0.33 × 10 = 3:3N
प्रश्न 25.
पानी में तैरते हुए किसी ठोस वस्तु का 4/5 भाग डूबा रहता है। वस्तु का घनत्व ज्ञात कीजिए। (पानी का घनत्व = 1000 kg/m3 है)
हल :
मान लो ठोस वस्तु का आयतन V तथा घनत्व d kg/m3 है।

∴ ठोस वस्तु का घनत्व (d) = \(\frac{4}{5}[latex] × 1000 = 800 kg/m3
![]()
प्रश्न 26.
जल में किसी वस्तु के आयतन का 4/5 भाग डूब जाता है। उसी वस्तु को यदि 1.6 आपेक्षिक घनत्व वाले द्रव में तैराया जाए तो वस्तु का कितना भाग डूबेगा ?
हल :
मान लो वस्तु का आयतन V तथा घनत्व d है।
जल में तैराने पर, वस्तु द्वारा हटाए गए जल का भार = वस्तु का भार
[latex]\frac{4}{5}\)V × 1 × g = V × d × g …………. (1)
मान लो द्रव में वस्तु के आयतन का x भाग डूबता है; अत:
वस्तु द्वारा हटाए गए द्रव का भार = वस्तु का भार
x V × 1.6 × g = V × d × g
समीकरण (1) तथा समीकरण (2) से,
\(\frac{4}{5}\)V × 1 × g = × V × 16 × g …………. (2)
अथवा x = \(\frac{4}{5 \times 1.6}=\frac{1}{2}\)
अतः द्रव में वस्तु के आयतन का आधा (\(\frac{1}{2}\)) भाग डूबेगा।
प्रश्न 27.
लकड़ी के एक टुकड़े का कुल भार 6 kg है। पानी में तैरते समय इसका 1/3 भाग पानी के भीतर रहता है। इस टुकड़े पर कितना भार रखने से वह पूरा डूबकर तैरेगा ?
हल :
मान लो लकड़ी के टुकड़े पर W भार रखने पर वह पानी में पूरा डूब जाता है। मान लो इसका आयतन V है। चूंकि तैरते समय टुकड़े के आयतन का 1/3 भाग पानी के भीतर रहता है, अत:
लकड़ी के टुकड़े का कुल भार = टुकड़े द्वारा हटाए गए जल का भार
अथवा
6 = \(\frac {1}{3}\)V × d × g …………… (1)
W kg भार और रख देने पर टुकड़ा पूरी तरह डूब जाता है, अत:
6 + W = V × d × g ……………… (2)
समीकरण (2) को समीकरण (1) से भाग देने पर,
\(\frac{6+W}{6}=\frac{3}{1}\)
अथवा 6 + W = 18
अतः लकड़ी के टुकड़े का भार W = 18 – 6 = 12 kg
प्रश्न 28.
कोई हैलीकॉप्टर किसी स्थिर नाव में फंसे हुए लोगों के लिए भोजन के पैकेट गिराने भेजा गया। यह 20 m की ऊँचाई पर 2 m/s के एक समान क्षैतिज वेग से चल रहा है। जब नाव का सबसे निकट वाला सिरा हैलीकॉप्टर के ठीक नीचे है तभी भोजन के पैकेट गिराए जाते हैं। यदि नाव 5 m लंबी है, तो क्या नाव में उपस्थित लोगों को पैकेट मिलेंगे ?
हल :
h = 20 मीटर, u = 2 मी०/से० g = 10 ms-2
ऊर्ध्वाधर रेंज R = 4\(\sqrt{2 h / g}\)
4\(\sqrt{\frac{2 \times 20}{10}}\) = 2√4
= 4 मीटर
नाव की लंबाई = 5 मी०
इसलिए नाव में बैठे आदमी भोजन के बंडल प्राप्त कर सकेंगे।
प्रश्न 29.
कोई गेंद एक 40 मी० ऊँची किसी मीनार की चोटी से गिराई गई। 20 मी० गिरने के पश्चात् इसका वेग कितना होगा ? पृथ्वी तल पर टकराते समय इसका वेग क्या होगा ?
हल :
h = 40 मी०, u = 0, a = 100 मी०/सैकंड2
तय की गयी दूरी (S) = 20 मी०, υ = ?
υ2 – u2 = 2gS
या u2 – (0)2 = 2 × 10 × 20
या υ2 = 400
या υ = 20 मी०/सेकंड
(ii) υ = ?, S = 40 मी
υ2 – u2 = 2aS
υ2 – (0)2 = 2 × 10 × 40
या υ2 = 800
या υ2 = \(\sqrt{800}=\sqrt{400 \times 2}\)
= 20√2 मी/सेकंड
∵ वस्तु नीचे गिराई गई
∴ v = – 20 ms-1
प्रश्न 30.
चांदी का आपेक्षिक घनत्व 10.8 है। पानी का घनत्व 103 kg m-3 है। S.I. मात्रक में चांदी का घनत्व क्या होगा ?
हल :
चांदी का आपेक्षिक घनत्व = 10.8
पानी का घनत्व = 103 kgm-3

∴ चांदी का घनत्व = चांदी का आपेक्षिक घनत्व × पानी का घनत्व
= 10.8 × 103 kg m-3
![]()
अति लघु उत्तरात्मक प्रश्न (Very Short Answer Type Questions)
प्रश्न 1.
सौर मण्डल में ग्रहों की सूर्य के इर्द-गिर्द घूर्णन गति किस कारण होती है ?
उत्तर-
उनके बीच परस्पर गुरुत्वाकर्षण बल के कारण।
प्रश्न 2.
चंद्रमा का पृथ्वी के इर्द-गिर्द गति के पथ का आकार कैसा होता है ?
उत्तर-
अंडाकार आकृति जैसा।
प्रश्न 3.
दो वस्तुओं के मध्य परस्पर लग रहे आकर्षण बल को गणितीय रूप में लिखो।
उत्तर-
F = G\(\frac{m_{1} \times m_{2}}{r^{2}}\)
प्रश्न 4.
G का मान कितना है ?
उत्तर-
G = 6.67 × 10-11 N-m2/kg2.
प्रश्न 5.
एक बैंच पर बैठे दो विद्यार्थियों के मध्य परस्पर गुरुत्वाकर्षण बल लगता है, परंतु दोनों विद्यार्थी इस बल को अनुभव नहीं करते। क्यों ?
उत्तर-
हम जानते हैं कि गुरुत्वाकर्षण बल F = G\(\frac{m_{1} \times m_{2}}{r^{2}}\) । यहां G का मान बहुत कम होता है जिस कारण यह बल बहुत कम होता है तथा अनुभव नहीं किया जाता।
प्रश्न 6.
पृथ्वी की सतह पर ‘g’ का मान कितना होता है ?
उत्तर-
पृथ्वी की सतह पर ‘g’ का मान अधिकतम होता है अर्थात् g = 9.81 m/s2।
![]()
प्रश्न 7.
क्या ‘g’ का मान ऋणात्मक हो सकता है ?
उत्तर-
जब वस्तु को ऊपर की ओर फेंका जाता है तो ‘g’ का मान कम होता है। इसलिए ‘g’ को ऋणात्मक लिया जाता है।
प्रश्न 8.
प्रक्षेप्य या प्रोजैक्टाइल का गति पथ कैसा होता है ?
उत्तर-
प्रक्षेप्य का गतिपथ पैराबोलिक पथ होता है।
प्रश्न 9.
किसी वस्तु में उपस्थित पदार्थ की मात्रा को क्या कहते हैं ?
उत्तर-
द्रव्यमान।
प्रश्न 10.
द्रव्यमान की SI इकाई क्या है ?
उत्तर-
किलोग्राम।
प्रश्न 11.
पृथ्वी के किस भाग में यह शून्य होता है?
उत्तर-
पृथ्वी के केंद्र पर।
प्रश्न 12.
द्रव्यमान तथा भार में से कौन-सी राशि अदिश या स्केलर है?
उत्तर-
द्रव्यमान।
![]()
प्रश्न 13.
भार की SI इकाई क्या है ?
उत्तर-
न्यूटन (N)।
प्रश्न 14.
भार कैसी राशि है-अदिश या सदिश ?
उत्तर-
भार एक बल है, इसलिए यह वैक्टर (सदिश राशि) है।
प्रश्न 15.
यदि किसी वस्तु का द्रव्यमान पृथ्वी पर 30 kg है तो बताओ चंद्रमा की सतह पर उसका द्रव्यमान कितना होगा ?
उत्तर-
द्रव्यमान एक स्थिर राशि है इसलिए चंद्रमा की सतह पर वस्तु का द्रव्यमान 30 kg होगा।
प्रश्न 16.
किसी वस्तु का गुरुत्वीय प्रवेग का मान पृथ्वी के अर्ध-व्यास की आधी ऊंचाई पर कितना होता है ?
उत्तर-
यहां h = \(\frac{\mathrm{R}}{2}\)
इसलिए
gh = ge × \(\frac{4}{9}\)
= 9.81 × \(\frac{4}{9}\)
= 4.36 m/s2
प्रश्न 17.
पृथ्वी के केंद्र पर ‘g’ का मान कितना होता है ?
उत्तर-
पृथ्वी के केंद्र पर g = 0।
प्रश्न 18.
बताओ किसी वस्तु का भार कहाँ अधिक होगा-ध्रुव या भूमध्य रेखा पर ?
उत्तर-
ध्रुव पर वस्तु का भार अधिक होगा।
प्रश्न 19.
दो वस्तुओं के मध्य दूरी तीन गुणा करने पर गुरुत्वीय बल पर क्या प्रभाव पड़ेगा ?
उत्तर-
पहले से \(\frac {1}{9}\) वाँ भाग रह जाएगा।
