PSEB 9th Class Science Important Questions Chapter 10 ਗੁਰੂਤਾ-ਆਕਰਸ਼ਣ

Punjab State Board PSEB 9th Class Science Important Questions Chapter 10 ਗੁਰੂਤਾ-ਆਕਰਸ਼ਣ Important Questions and Answers.

PSEB 9th Class Science Important Questions Chapter 10 ਗੁਰੂਤਾ-ਆਕਰਸ਼ਣ

ਵੱਡੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Long Answer Type Questions)

ਪ੍ਰਸ਼ਨ 1.
ਨਿਊਟਨ ਦੇ ਵਿਸ਼ਵ-ਵਿਆਪੀ ਗੁਰੂਤਾ-ਆਕਰਸ਼ਣ ਦੇ ਨਿਯਮ ਦੀ ਪਰਿਭਾਸ਼ਾ ਲਿਖੋ ਅਤੇ ਗਣਿਤਿਕ ਦ੍ਰਿਸ਼ਟੀ ਤੋਂ ਦੋ ਵਸਤੂਆਂ ਵਿਚਕਾਰ ਲੱਗ ਰਹੇ ਆਕਰਸ਼ਣ ਬਲ ਦੇ ਸੂਤਰ ਦਾ ਵਿਉਂਤਪੰਨ ਤਿਆਰ ਕਰੋ ।
ਉੱਤਰ-
ਨਿਊਟਨ ਦਾ ਗੁਰੂਤਾ-ਆਕਰਸ਼ਣ ਦਾ ਵਿਸ਼ਵ-ਵਿਆਪੀ ਨਿਯਮ (Newton’s Universal Law of Gravitation) – ਇਸ ਹਿਮੰਡ ਵਿੱਚ ਹਰੇਕ ਪਦਾਰਥਕ ਵਸਤੂ ਹਰ ਦੂਜੀ ਵਸਤੂ ਨੂੰ ਇੱਕ ਬਲ ਨਾਲ ਪਰਸਪਰ . ਆਕਰਸ਼ਿਤ ਕਰਦੀ ਹੈ, ਜਿਹੜਾ-
(i) ਉਨ੍ਹਾਂ ਦੇ ਪੁੰਜਾਂ ਦੇ ਗੁਣਨਫਲ ਦੇ ਸਿੱਧਾ ਅਨੁਪਾਤੀ ਹੁੰਦਾ ਹੈ ਅਤੇ
(ii) ਉਨ੍ਹਾਂ ਦੇ ਕੇਂਦਰਾਂ ਵਿਚਕਾਰ ਦੂਰੀ ਦੇ ਵਰਗ ਦੇ ਉਲਟ-ਅਨੁਪਾਤੀ ਹੁੰਦਾ ਹੈ । ਇਹ ਬਲ ਹਮੇਸ਼ਾ ਹੀ ਉਨ੍ਹਾਂ ਵਸਤੂਆਂ ਦੇ ਕੇਂਦਰਾਂ ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੀ ਰੇਖਾ ਦੀ ਦਿਸ਼ਾ ਵਿੱਚ ਲਗਦਾ ਹੈ |

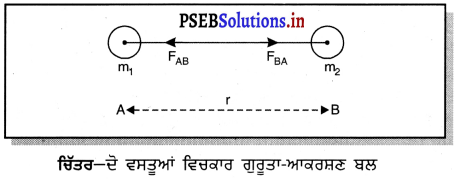
ਗਣਿਤਿਕ ਧਾਰਣਾਵਾਂ – ਉੱਪਰ ਦਰਸਾਏ ਗਏ ਚਿੱਤਰ ਦੇ ਹਵਾਲੇ ਵਿੱਚ ਮੰਨ ਲਉ ਸਾਡੇ ਕੋਲ ਦੋ ਗੇਂਦਾਂ A ਅਤੇ B ਹਨ ਜਿਨ੍ਹਾਂ ਦੇ ਪੁੰਜ ਕੁਮਵਾਰ m₁ ਅਤੇ m₂ ਹਨ ਜਿਨ੍ਹਾਂ ਦੇ ਕੇਂਦਰਾਂ ਦੇ ਵਿਚਾਲੇ ਦੀ ਦੂਰੀ r ਹੈ ।

ਨਿਊਟਨ ਅਨੁਸਾਰ ਗੇਂਦ A, ਗੇਂਦ B ਉੱਪਰ ਗੁਰੂਤਾ ਆਕਰਸ਼ਣ ਬਲ F_BA ਲਗਾਵੇਗੀ ਅਤੇ F_AB ਲ ਗੇਂਦ A ਉੱਪਰ ਗੇਂਦ B ਦੁਆਰਾ ਲਗਾਇਆ ਗਿਆ ਬਲ ਹੈ । ਇਨ੍ਹਾਂ ਦੋਨਾਂ ਬਲਾਂ ਦੀ ਮਾਤਰਾ ਬਰਾਬਰ ਹੈ, : ਪਰੰਤੁ ਉਹ ਇੱਕ-ਦੂਜੇ ਤੋਂ ਉਲਟ ਦਿਸ਼ਾ ਵਿੱਚ ਲੱਗ ਰਹੇ ਹਨ, ਜਿਵੇਂ ਕਿ ਉੱਪਰ ਦਿੱਤੇ ਗਏ ਚਿੱਤਰ ਵਿੱਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ ।
F_AB = F_BA
ਮੰਨ ਲਓ F_AB = F_BA = F
ਤਾਂ ਨਿਊਟਨ ਦੇ ਗੁਰੂਤਾ-ਆਕਰਸ਼ਣ ਨਿਯਮ ਅਨੁਸਾਰ, F ∝ m₁ × m₂ ………… (i)
ਅਤੇ F ∝ \(\frac{1}{r^{2}}\) ………. (ii)
ਸਮੀਕਰਨ (i) ਅਤੇ (ii) ਨੂੰ ਜੋੜਨ ਤੇ
F ∝ \(\frac{m_{1} \times m_{2}}{r^{2}}\)
F = ਸਥਿਰ-ਅੰਕ × \(\frac{m_{1} \times m_{2}}{r^{2}}\)
F = G\(\frac{m_{1} \times m_{2}}{r^{2}}\)
G ਨੂੰ ਵਿਸ਼ਵ-ਵਿਆਪੀ ਗੁਰੂਤਵੀ-ਸਥਿਰ-ਅੰਕ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਨੂੰ ਇਹ ਨਾਂ ਇਸ ਲਈ ਦਿੱਤਾ ਗਿਆ ਹੈ ਕਿਉਂਕਿ ਸਾਰੇ ਹੀ ਹਿਮੰਡ ਵਿੱਚ ਇਸ ਦਾ ਸੰਖਿਅਕ ਮੁੱਲ ਇਕੋ ਹੀ ਰਹਿੰਦਾ ਹੈ ।
G ਦਾ ਸੰਖਿਅਕ ਮੁੱਲ- G = 6.67 × 10^-11 N-m²/kg² ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਹਿਆਂ ਦੀ ਗਤੀ ਬਾਰੇ ਕੈਪਲਰ ਦੇ ਨਿਯਮ ਲਿਖੋ ।
ਉੱਤਰ-
ਲ੍ਹਿਆਂ ਦੀ ਗਤੀ ਬਾਰੇ ਕੈਪਲਰ ਦੇ ਨਿਯਮ – ਸੋਲ੍ਹਵੀਂ ਸਦੀ ਤੱਕ ਅਨੇਕ ਖਗੋਲ ਵਿਗਿਆਨੀਆਂ ਨੇ ਹਿਆਂ ਦੀ ਗਤੀ ਬਾਰੇ ਆਂਕੜੇ ਇਕੱਠੇ ਕੀਤੇ । ਜਹਾਂਸ ਕੈਪਲਰ ਨੇ ਇਹਨਾਂ ਆਂਕੜਿਆਂ ਦੇ ਆਧਾਰ ‘ਤੇ ਤਿੰਨ ਨਿਯਮ ਬਣਾਏ ਜਿਹੜੇ ਹਿਆਂ ਦੀ ਗਤੀ ਨੂੰ ਨਿਰਦੇਸ਼ਿਤ ਕਰਦੇ ਹਨ । ਇਹ ਨਿਯਮ ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਹਨ-
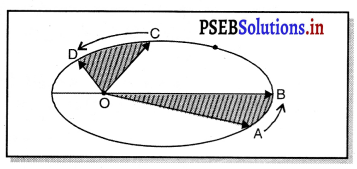
1. ਆਰਬਿਟ ਨਿਯਮ (ਪਹਿਲਾ ਨਿਯਮ) – ਹਰੇਕ ਹਿ ਦਾ ਹਿ ਪੱਥ ਅੰਡਾਕਾਰ ਹੁੰਦਾ ਹੈ ਅਤੇ ਸੂਰਜ ਇਸਦੇ ਕੇਂਦਰ ਤੇ ਹੁੰਦਾ ਹੈ ਜਿਸ ਤਰ੍ਹਾਂ ਚਿੱਤਰ ਵਿੱਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ । ਇਸ ਚਿੱਤਰ ਵਿੱਚ 0 ਦੁਆਰਾ ਸੂਰਜ ਦੀ ਸਥਿਤੀ ਨੂੰ ਵਿਖਾਇਆ ਗਿਆ ਹੈ ।

2. ਖੇਤਰਫਲ ਦਾ ਨਿਯਮ ਦੂਸਰਾ ਨਿਯਮ – ਸੂਰਜ ਅਤੇ ਗ੍ਰਹਿ ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੀ ਰੇਖਾ ਸਮਾਨ ਸਮੇਂ ਵਿੱਚ ਸਮਾਨ ਖੇਤਰਫਲ ਤੈਅ ਕਰਦੀ ਹੈ । ਜੇਕਰ ਤੋਂ 8 ਤੱਕ ਗਤੀ ਕਰਨ ਵਿੱਚ ਲੱਗਾ ਸਮਾਂ 0 ਤੋਂ 0 ਤੱਕ ਗਤੀ ਕਰਨ ਵਿੱਚ ਲੱਗੇ ਸਮੇਂ ਦੇ ਬਰਾਬਰ ਹੋਵੇ ਤਾਂ ਖੇਤਰਫਲ OAB ਅਤੇ OCD ਬਰਾਬਰ ਹੋਣਗੇ ।

3. ਪਰਿਕਰਮਾ ਕਾਲ (ਪੀਰੀਅਡ) ਨਿਯਮ (ਤੀਸਰਾ ਨਿਯਮ) – ਸੂਰਜ ਤੋਂ ਕਿਸੇ ਹਿ ਦੀ ਔਸਤ ਦੂਰੀ (r) ਦਾ ਘਣ ਉਸ ਹਿ ਦੇ ਹਿ ਪੱਥ ਪਰਿਕਰਮਾ ਅਰਥਾਤ ਕਾਲ 1 ਦੇ ਵਰਗ ਦੇ ਸਿੱਧਾ ਅਨੁਪਾਤੀ ਹੁੰਦਾ ਹੈ ।
ਅਰਥਾਤ \(\frac{r^{3}}{\mathrm{~T}^{2}}\) = ਸਥਿਰ ਅੰਕ
ਜਾਂ T² α r³
ਕੈਪਲਰ ਕੋਈ ਸਿਧਾਂਤ ਪੇਸ਼ ਨਾ ਕਰ ਸਕਿਆ ਜਿਹੜਾ ਗ੍ਰਹਿਆਂ ਦੀ ਵਿਆਖਿਆ ਕਰ ਸਕੇ । ਨਿਉਟਨ ਨੇ ਇਹ ਦਰਸਾਇਆ ਕਿ ਹਿਆਂ ਦੀ ਗਤੀ ਕਾਰਨ ਗੁਰੁਤਾਕਰਸ਼ਣ ਉਹ ਬਲ ਹੈ ਜਿਹੜਾ ਸੂਰਜ ਉਹਨਾਂ ‘ਤੇ ਲਗਾਉਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਰਾਬਰਟ ਬਾਇਲ ਨੇ ਪ੍ਰਯੋਗ ਦੁਆਰਾ ਕਿਵੇਂ ਸਿੱਧ ਕੀਤਾ ਕਿ ਨਿਰਵਾਤ (ਖਲਾਅ ਵਿੱਚ ਸਾਰੀਆਂ ਵਸਤੂਆਂ ਇੱਕ ਹੀ ਦਰ ਨਾਲ ਹੇਠਾਂ ਧਰਤੀ ਵੱਲ ਡਿੱਗਦੀਆਂ ਹਨ ?
ਉੱਤਰ-
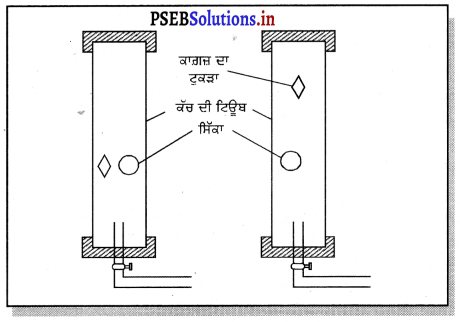
ਬਾਇਲ ਪ੍ਰਯੋਗ – ਰਾਬਰਟ ਬਾਇਲ ਨੇ ਇੱਕ ਲੰਮੀ ਕੱਚ ਦੀ ਟਿਊਬ ਲਈ, ਜਿਵੇਂ ਕਿ ਚਿੱਤਰ ਵਿੱਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ । ਇੱਕ ਭਾਰੀ ਸਿੱਕਾ ਅਤੇ ਇੱਕ ਕਾਗ਼ਜ਼ ਦਾ ਟੁਕੜਾ ਟਿਊਬ ਵਿੱਚ ਰੱਖਿਆ ਗਿਆ । ਟਿਊਬ ਦੇ ਸਿਰਿਆਂ ਨੂੰ ਬੰਦ ਕਰ ਦਿੱਤਾ । ਟਿਊਬ ਵਿੱਚੋਂ ਹਵਾ ਨੂੰ ਨਿਰਵਾਤ ਪੰਪ ਦੁਆਰਾ ਖ਼ਾਲੀ ਕਰ ਦਿੱਤਾ ਗਿਆ ।

ਜਦੋਂ ਟਿਉਬ ਨੂੰ ਛੇਤੀ ਨਾਲ ਉਲਟਾਇਆ ਗਿਆ, ਤਾਂ ਇਹ ਵੇਖਣ ਵਿੱਚ ਆਇਆ ਕਿ ਸਿੱਕਾ ਅਤੇ ਕਾਗਜ਼ ਦਾ ਟੁਕੜਾ ਇੱਕ ਸਮੇਂ ਹੀ ਟਿਉਬ ਦੇ ਹੇਠਾਂ ਤਲੀ ਵਿੱਚ ਪਹੁੰਚਦੇ ਹਨ । ਹੁਣ ਫਿਰ ਇਸ ਪ੍ਰਯੋਗ ਨੂੰ ਦੁਹਰਾਇਆ ਗਿਆ ਜਦੋਂ ਕੱਚ ਦੀ ਟਿਊਬ ਅੰਦਰ ਹਵਾ ਮੌਜੂਦ ਸੀ । ਇਸ ਵਾਰੀ ਦੇਖਣ ਵਿੱਚ ਆਇਆ ਕਿ ਕਾਗ਼ਜ਼ ਦਾ ਟੁਕੜਾ ਹੌਲੀ-ਹੌਲੀ ਹੇਠਾਂ ਵੱਲ ਡਿੱਗਦਾ ਹੈ ਜਦ ਕਿ ਸਿੱਕਾ ਛੇਤੀ ਹੀ ਟਿਊਬ ਦੀ ਤਲੀ ‘ਤੇ ਪਹੁੰਚ ਗਿਆ ਹੈ । ਇਸ ਪ੍ਰਯੋਗ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੋ ਜਾਂਦਾ ਹੈ ਕਿ ਨਿਰਵਾਤ ਵਿੱਚ ਸਾਰੀਆਂ ਵਸਤੂਆਂ ਹਲਕੀਆਂ ਅਤੇ ਭਾਰੀਆਂ ਇੱਕੋ ਵੇਗ ਨਾਲ ਧਰਤੀ ਵੱਲ ਗਤੀ ਕਰਦੀਆਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 4.
(ੳ) ਸਿੱਧ ਕਰੋ ਕਿ ਗੁਰੂਤਾ ਵੇਗ ਦਾ ਮੁੱਲ ਵਸਤੂ ਦੇ ਪੁੰਜ ਦੇ ਮੁੱਲ ਤੋਂ ਸੁਤੰਤਰ ਹੁੰਦਾ ਹੈ ।
(ਅ) g ਦਾ ਮਾਨ ਪਤਾ ਕਰੋ ।
ਉੱਤਰ-
(ਉ) ਜਿਵੇਂ ਵਿਖਾਇਆ ਗਿਆ ਹੈ ਕਿ ਧਰਤੀ ਸਤ੍ਹਾ ਤੇ ਸਥਿਤ m ਪੁੰਜ ਵਾਲੀ ਇੱਕ ਵਸਤੂ ਤੇ ਵਿਚਾਰ ਕਰੋ । ਮੰਨ ਲਉ M ਅਤੇ R ਕੁਮਵਾਰ ਧਰਤੀ ਦੇ ਪੁੰਜ ਅਤੇ ਅਰਧ-ਵਿਆਸ ਹਨ ।
ਮੰਨ ਲਉ F ਵਸਤੂ ਤੇ ਕਿਰਿਆ ਕਰ ਰਿਹਾ ਗੁਰੂਤਾ ਆਕਰਸ਼ਣ ਬਲ ਹੈ ।

ਇਸ ਵੇਗ ਨੂੰ ਗੁਰੂਤਾ ਵੇਗ ਆਖਦੇ ਹਨ ।

ਇਸ ਸਮੀਕਰਨ ਵਿੱਚ ਵਸਤੂ ਦਾ ਪੁੰਜ ਸ਼ਾਮਲ ਨਹੀਂ ਹੈ । ਇਸ ਤੋਂ ਪਤਾ ਚਲਦਾ ਹੈ ਕਿ ਗੁਰੂਤਾ-ਆਕਰਸ਼ਣ ਬਲ ਕਾਰਨ ਕਿਸੇ ਵਸਤੂ ਦੁਆਰਾ ਪ੍ਰਾਪਤ ਵੇਗ ਇਸ ਦੇ ਪੁੰਜ ਤੋਂ ਸੁਤੰਤਰ ਹੈ । ਇਸ ਲਈ ਅਸੀਂ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਸਾਰੇ ਆਕਾਰਾਂ ਅਤੇ ਪੰਜਾਂ ਵਾਲੀਆਂ ਵਸਤੂਆਂ ਕਿਸੇ ਵੀ ਥਾਂ ਤੇ ਸਮਾਨ ਵੇਗ ਨਾਲ ਡਿੱਗਦੀਆਂ ਹਨ ।

(ਅ) g ਦਾ ਮੁੱਲ ਪਤਾ ਕਰਨਾ G = 6.67 × 10^-11 Nm² / kg²
ਧਰਤੀ ਦਾ ਅਰਧ-ਵਿਆਸ, R = 6400 km
= 6400 × 1000 m
= 6.4 × 10⁶ m
ਧਰਤੀ ਦਾ ਪੁੰਜ M = 6 × 10²⁴ kg
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ, g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)
ਜਾਂ g = \(\frac{6.67 \times 10^{-11} \times 6 \times 10^{24}}{\left(6.4 \times 10^{6}\right)^{2}}\)
∴ g = 9.8 ms^-2

ਪ੍ਰਸ਼ਨ 5.
(ੳ) ਸੁਤੰਤਰ ਡਿੱਗ ਰਹੀਆਂ ਵਸਤੂਆਂ ਵਿੱਚ ਸਮੀਕਰਨ ਦੀ ਪਰਿਭਾਸ਼ਾ ਦਿਓ ।
(ਅ) ਸੁਤੰਤਰ ਡਿੱਗ ਰਹੀਆਂ ਵਸਤੂਆਂ ਦੀ ਗਤੀ ਸਮੀਕਰਨ ਵਿੱਚ ਪਰਿਵਰਤਨ ਕਿਵੇਂ ਹੁੰਦਾ ਹੈ ?
(ੲ) ਜਦੋਂ ਵਸਤੂਆਂ ਨੂੰ ਬਿਲਕੁਲ ਸਿੱਧੇ ਉੱਪਰ ਵੱਲ ਸੁੱਟਿਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਉਸ ਦੁਆਰਾ ਪ੍ਰਾਪਤ ਵੱਧ ਤੋਂ ਵੱਧ ਉੱਚਾਈ ਪਤਾ ਕਰਨ ਲਈ ਸਮੀਕਰਨ ਲਿਖੋ ।
(ਸ) ਸਿੱਧ ਕਰੋ ਕਿ ਹੇਠਾਂ ਆਉਣ ਅਤੇ ਉੱਪਰ ਜਾਣ ਦਾ ਸਮਾਂ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ ।
ਉੱਤਰ-
(ੳ) ਗੁਰੂਤਾ ਅਧੀਨ ਕਿਰਿਆ ਕਰਨ ਵਾਲੀ ਗਤੀ ਸਮੀਕਰਨ ਸੁਤੰਤਰ ਡਿੱਗਣ ਵਾਲੇ ਸਮੀਕਰਨ ਅਖਵਾਉਂਦੇ ਹਨ ।

(ਅ) ਇਕ ਸਮਾਨ ਗਤੀ ਵਾਲੇ ਸਮੀਕਰਨਾਂ ਵਿੱਚ a ਦੀ ਥਾਂ g ਲਿਖ ਕੇ ਪ੍ਰਾਪਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ । ਸੁਤੰਤਰ ਡਿੱਗ ਰਹੀਆਂ ਵਸਤੂਆਂ ਵਾਲੇ ਸਮੀਕਰਨ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹਨ-
(i) v = u + gt
(ii) n = ut + \(\frac {1}{2}\)gt²
(iii) v² – u² = 2gh
ਇੱਥੇ u ਮੁੱਢਲਾ ਵੇਗ, v ਅੰਤਿਮ ਵੇਗ, h ਪ੍ਰਾਪਤ ਉੱਚਾਈ ਅਤੇ t ਸਮਾਂ ਹੈ । ਜਦੋਂ ਵਸਤੂ ਨੂੰ ਛੱਡਿਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਵਸਤੂ ਦਾ ਮੁੱਢਲਾ ਵੇਗ ਜ਼ੀਰੋ ਹੁੰਦਾ ਹੈ, ਅਰਥਾਤ u = 0

(ੲ) ਵੱਧ ਤੋਂ ਵੱਧ ਉੱਚਾਈ ਲਈ ਵਿਅੰਜਕ – ਆਓ ਮੁੱਢਲੇ ਵੇਗ ਵਾਲੀ ਇੱਕ ਵਸਤੂ ਨੂੰ ਉੱਪਰ ਸੁੱਟੇ ਜਾਣ ਤੇ ਪ੍ਰਾਪਤ ਅਧਿਕਤਮ ਉੱਚਾਈ ਲਈ ਵਿਅੰਜਕ ਗਿਆਤ ਕਰੀਏ ।
ਉੱਚਤਮ ਬਿੰਦੂ ਤੇ ਪਹੁੰਚ ਕੇ ਅੰਤਿਮ ਵੇਗ ਜ਼ੀਰੋ ਹੋਵੇਗਾ । ਗੁਰੂਤਾ-ਪ੍ਰਵੇਗ ਰਿਣਾਤਮਕ ਹੋਵੇਗਾ । ਜੇਕਰ h ਅਧਿਕਤਮ ਉੱਚਾਈ ਹੈ, ਤਾਂ
v² – u² = 2ah
ਜਾਂ 0² – u² = 2 (-g) h [a = – g]
-u² = -2gh
u² = 2gh
∴ h = \(\frac{u^{2}}{2 g}\)

(ਸ) ਉੱਪਰ ਜਾਣ ਅਤੇ ਹੇਠਾਂ ਆਉਣ ਦਾ ਸਮਾਂ – ਉੱਚਤਮ ਬਿੰਦੂ ਤਕ ਪਹੁੰਚਣ ਲਈ ਲੱਗ ਰਿਹਾ ਸਮਾਂ ਅਵਰੋਹਣ ਸਮਾਂ ਹੈ | ਅਧਿਕਤਮ ਉੱਚਾਈ ਤੋਂ ਹੇਠਾਂ ਵਾਪਸ ਆਉਣ ਲਈ ਲੱਗਾ ਸਮਾਂ ਆਰੋਹਣ ਸਮਾਂ ਹੈ ।
ਅਵਰੋਹਣ (ਉੱਪਰ ਜਾਣ ਲਈ) ਸਮਾਂ
ਇੱਥੇ v = 0, a = – g
v = u + at
0 = u – gt
t = \(\)

ਆਰੋਹਣ (ਹੇਠਾਂ ਆਉਣ ਲਈ) ਸਮਾਂ-
ਹੁਣ, ਉੱਚਤਮ ਬਿੰਦੁ ਤੇ ਵੇਗ ਜ਼ੀਰੋ ਹੈ,
∴ u = 0

ਅਰਥਾਤ ਉੱਪਰ ਜਾਣ ਅਤੇ ਹੇਠਾਂ ਆਉਣ ਲਈ ਲੱਗਿਆ ਸਮਾਂ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਉਨ੍ਹਾਂ ਕਾਰਕਾਂ ਦਾ ਵਰਣਨ ਕਰੋ ਜਿਨ੍ਹਾਂ ਕਰਕੇ ਗੁਰੂਤਵੀ ਵੇਗ ‘g’ ਦੇ ਮੁੱਲ ਵਿੱਚ ਤਬਦੀਲੀ ਆਉਂਦੀ ਹੈ ?
ਉੱਤਰ-
ਗੁਰੂਤਵੀ ਵੇਗ ‘g’ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਨ ਵਾਲੇ ਕਾਰਕ-
1. ਧਰਤੀ ਦੀ ਉੱਚਾਈ ਕਾਰਨ g` ਵਿੱਚ ਤਬਦੀਲੀ (Variation in g with Altitude) – ‘g’ ਦਾ ਮੁੱਲ ਧਰਤੀ ਦੀ ਸਤ੍ਹਾ ਤੋਂ ਉੱਪਰ ਜਾਂ ਹੇਠਾਂ ਦੋਹਾਂ ਸਥਿਤੀਆਂ ਵਿੱਚ ਘਟਦਾ ਹੈ । ‘g’ ਦਾ ਮੁੱਲ ਸਿਰਫ਼ ਧਰਤੀ ਦੀ ਸਤ੍ਹਾ ਤੇ ਹੀ ਅਧਿਕਤਮ ਹੁੰਦਾ ਹੈ । ਜਿਵੇਂ ਹੀ ਅਸੀਂ ਧਰਤੀ ਦੀ ਸਤ੍ਹਾ ਤੋਂ ਉੱਪਰ ਵੱਲ ਨੂੰ ਜਾਂਦੇ ਹਾਂ, ਤਾਂ ‘g’ ਦਾ ਮੁੱਲ ਘੱਟਦਾ ਚਲਾ ਜਾਂਦਾ ਹੈ । ਧਰਤੀ ਦੀ ਸਤ੍ਹਾ ਤੋਂ ਉੱਪਰ ਕਿਸੇ ਵੀ ਉੱਚਾਈ ਤੇ ‘g’ ਦੇ ਮੁੱਲ ਦੀ ਗਣਨਾ ਅਸੀਂ ਇੱਕ ਨਿਸਚਿਤ ਗਣਿਤਕ ਸੂਤਰ ਨਾਲ ਕਰ ਸਕਦੇ ਹਾਂ ।
ਜੇਕਰ g_e = ਧਰਤੀ ਦੀ ਸਤ੍ਹਾ ਤੇ ਗੁਰੂਤਾ-ਪ੍ਰਵੇਗ
g_h = ਧਰਤੀ ਤੋਂ ਉੱਚਾਈ hਤੇ ਗੁਰੂਤਾ ਵੇਗ
ਅਤੇ R = ਧਰਤੀ ਦਾ ਅਰਧ-ਵਿਆਸ
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ, g_h = g_e[latex]\frac{\mathrm{R}^{2}}{(\mathrm{R}+h)^{2}}[/latex]
(R+h)”
‘h’ ਦਾ ਮੁੱਲ ਪਤਾ ਹੋਣ ਤੇ ‘g_h’ ਦਾ ਮੁੱਲ ਪਤਾ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ।

ਵਿਸ਼ੇਸ਼ ਸਥਿਤੀ (Special Case) – ਧਰਤੀ ਦੇ ਅਰਧ-ਵਿਆਸ ਨਾਲੋਂ ਅੱਧੀ ਉੱਚਾਈ hਤੇ ਅਰਥਾਤ ਜਦੋਂh = R/ 2 ਤਾਂ ਉੱਪਰ ਦਿੱਤੇ ਫ਼ਾਰਮੂਲੇ ਤੋਂ,

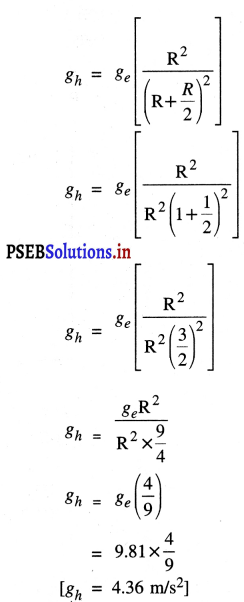
‘g’ ਦਾ ਮੁੱਲ ਧਰਤੀ ਤੇ ਕੇਂਦਰ ਤੇ ‘ਜ਼ੀਰੋ’ ਹੋਵੇਗਾ ।

2. ਧਰਤੀ ਦੀ ਆ ਕਾਰਨ ‘g’ ਵਿੱਚ ਤਬਦੀਲੀ (Variation in g` due to shape of Earth) – ਧਰਤੀ ਪੂਰੀ ਤਰ੍ਹਾਂ ਗੋਲਾਕਾਰ ਨਹੀਂ ਹੈ, ਪਰੰਤੂ ਥੋੜ੍ਹੀ ਜਿਹੀ ਇਲਿਪਸੀ (ਅੰਡਾਕਾਰ) ਆਤੀ ਦੀ ਹੈ । ਇਹ ਧਰਵਾਂ ਦੇ ਨੇੜੇ ਪੱਧਰੀ ਹੈ ਜਦੋਂ ਕਿ ਭੂ-ਮੱਧ ਰੇਖਾ ਦੇ ਨੇੜੇ ਥੋੜੀ ਜਿਹੀ ਬਾਹਰ ਵੱਲ ਨੂੰ ਉੱਠੀ ਹੋਈ ਹੈ ਜਿਵੇਂ ਕਿ ਚਿੱਤਰ ਵਿੱਚ ਵਿਖਾਇਆ ਹੈ ।

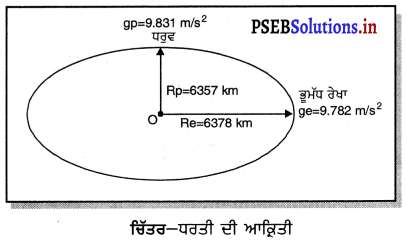
ਉੱਪਰ ਵਿਖਾਏ ਚਿੱਤਰ ਅਨੁਸਾਰ, ਭੂ-ਮੱਧ ਰੇਖੀ ਅਰਧ-ਵਿਆਸ ਲਗਪਗ 6378 ਕਿ. ਮੀ. ਅਤੇ ਧਰੁਵੀ ਅਰਧ-ਵਿਆਸ 6357 ਕਿ. ਮੀ. ਹੈ । ਹੁਣ ਕਿਉਂ ਜੋ ਭੂ-ਮੱਧ ਰੇਖੀ ਅਰਧ-ਵਿਆਸ, ਧਰੁਵੀ ਅਰਧ-ਵਿਆਸ ਨਾਲੋਂ ਲਗਪਗ 21 ਕਿ. ਮੀ. ਜ਼ਿਆਦਾ ਹੈ, ਇਸ ਲਈ ਧਰੁਵਾਂ ਤੇ g ਦਾ ਮੁੱਲ ਅਰਥਾਤ g_p ਜ਼ਿਆਦਾ ਅਰਥਾਤ 9.831 m/s² ਹੈ ਅਤੇ ਭੂ-ਮੱਧ ਰੇਖਾ ਤੇ ਘੱਟ ਅਰਥਾਤ g_e = 9.782 m/s² ਹੈ । ‘g’ ਦਾ ਮੁੱਲ ਜਿਹੜਾ ਅਸੀਂ ਆਮ ਤੌਰ ‘ਤੇ ਪ੍ਰਯੋਗ ਵਿੱਚ ਲਿਆਉਂਦੇ ਹਾਂ, ਇਨ੍ਹਾਂ ਦੋਹਾਂ ਮੁੱਲਾਂ ਦੀ ਔਸਤ ਹੁੰਦੀ ਹੈ । ਇਸ ਲਈ ‘g’ ਦੇ ਮੁੱਲ ਵਿੱਚ ਤਬਦੀਲੀ ਹੋਣ ਕਾਰਨ ਵਸਤੁ ਦਾ ਭਾਰ ਭੂ-ਮੱਧ ਰੇਖਾ ਤੇ ਨਿਊਨਤਮ ਅਤੇ ਧਰੁਵਾਂ ‘ਤੇ ਅਧਿਕਤਮ ਹੋਵੇਗਾ ।

3. ਡੂੰਘਾਈ ਦਾ ਪ੍ਰਭਾਵ (Effect of depth) – ਜੇ ਅਸੀਂ ਡੂੰਘਾਈ ਵਾਲੀ ਥਾਂ ਤੇ ਜਾਈਏ ਤਾਂ 8 ਦਾ ਮੁੱਲ ਘੱਟ ਜਾਂਦਾ ਹੈ । ਡੂੰਘਾਈ ਦੇ ਨਾਲ ਇਹ ਮੁੱਲ ਘੱਟ ਜਾਂਦਾ ਹੈ । ਧਰਤੀ ਦੇ ਕੇਂਦਰ ਤੇ ਇਸਦਾ ਮੁੱਲ ਜ਼ੀਰੋ ਹੋ ਜਾਂਦਾ ਹੈ ।
\(\frac{\mathbf{W}_{d}}{\mathbf{W}_{e}}\) = \(\frac{g_{d}}{g_{e}}\) = (1 – \(\frac{d}{\mathrm{R}}\))

ਪ੍ਰਸ਼ਨ 7.
‘g’ ਅਤੇ ‘G’ ਵਿਚਕਾਰ ਸੰਬੰਧ ਸਥਾਪਿਤ ਕਰੋ ।
ਉੱਤਰ-

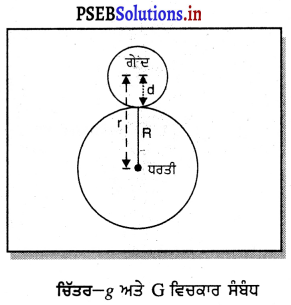
g ਅਤੇ G ਵਿਚਕਾਰ ਸੰਬੰਧ (Relation between g and G) – ਮੰਨ ਲਉ । ਪੁੰਜ ਅਤੇ d ਅਰਧ-ਵਿਆਸ ਵਾਲੀ ਇੱਕ ਗੇਂਦ ਧਰਤੀ ਦੀ ਸੜਾ ਜਿਸ ਦਾ ਪੁੰਜ M ਅਤੇ ਅਰਧ-ਵਿਆਸ R ਉੱਪਰ ਪਈ ਹੈ । ਮੰਨ ਲਉ ਕਿ ਧਰਤੀ ਅਤੇ ਗੇਂਦ ਦੇ ਕੇਂਦਰਾਂ ਵਿਚਕਾਰ ਦੂਰੀ r ਹੈ, ਅਰਥਾਤ r = d + R
ਧਰਤੀ ਗੇਂਦ ਨੂੰ ਆਪਣੇ ਕੇਂਦਰ ਵੱਲ ਬਲ F ਨਾਲ ਆਕਰਸ਼ਿਤ ਕਰੇਗੀ ।
∴ F = G\(\frac{\mathrm{Mm}}{r^{2}}\) ……….. (1)
ਹੁਣ F = m × ਗੇਂਦ ਵਿੱਚ ਧਰਤੀ ਦੁਆਰਾ ਉਤਪੰਨ ਕੀਤਾ ਗਿਆ ਪ੍ਰਵੇਰਾ
ਜਾਂ F = mg ………….(2)
ਇੱਥੇ g ਨੂੰ ਧਰਤੀ ਦਾ ਗੁਰੂਤਵੀ-ਦੇਗ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਧਰਤੀ ਦੀ ਸਤ੍ਹਾ ਉੱਤੇ ਇਸ ਦੀ ਮੁੱਲ ਅਧਿਕਤਮ ਅਰਥਾਤ 9.81 ms² ਹੁੰਦੀ ਹੈ । ਸਮੀਕਰਨ (1) ਦੇ ਬਲ ਦੀ ਸਮੀਕਰਨ (2) ਦੇ ਬਲ ਨਾਲ ਤੁਲਨਾ ਕਰਨ ਤੇ-
m × g = G \(\frac{m \mathbf{M}}{r^{2}}\)
g = G\(\frac{\mathrm{M}}{r^{2}}\) …………… (3)

ਕਿਉਂਕਿ ਗੇਂਦ ਦਾ ਅਰਧ-ਵਿਆਸ ਧਰਤੀ ਦੇ ਅਰਧ-ਵਿਆਸ ਦੀ ਤੁਲਨਾ ਵਿੱਚ ਬਹੁਤ ਘੱਟ ਹੈ ਅਰਥਾਤ r<< R ਤਾਂ
ਜੋ r = R
ਸਮੀਕਰਨ (3) ਤੋਂ g = G\(\frac{\mathrm{M}}{\mathrm{R}^{2}}\) ………….(4)
ਸਮੀਕਰਨ (4) ਧਰਤੀ ਦੇ ਗੁਰੂਤਾ ਵੇਗ ‘g’ ਅਤੇ ਵਿਸ਼ਵ-ਵਿਆਪੀ ਗੁਰੂਤਵੀ ਸਥਿਰ-ਅੰਕ ‘G’ ਵਿਚਕਾਰ ਸੰਬੰਧ ਦਰਸਾਉਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਵਿਆਖਿਆ ਕਰੋ ਕਿ ਇੱਕ ਵਿਅਕਤੀ ਚੰਨ ਦੀ ਸਤ੍ਹਾ ਉੱਤੇ ਧਰਤੀ ਨਾਲੋਂ ਜ਼ਿਆਦਾ ਉੱਚੀ ਛਲਾਂਗ ਕਿਉਂ ਲਗਾ ਸਕਦਾ ਹੈ ?
ਉੱਤਰ-
ਮੰਨ ਲਓ ਅ ਪੁੰਜ ਵਾਲਾ ਵਿਅਕਤੀ, M ਪੁੰਜ ਵਾਲੀ ਧਰਤੀ ਜਿਸਦਾ ਅਰਧ-ਵਿਆਸ Rਹੈ ਦੀ ਸੜਾ ਉੱਪਰ ਖੜ੍ਹਾ ਹੈ । ਧਰਤੀ ਉਸ ਵਿਅਕਤੀ ਨੂੰ ਆਪਣੇ ਕੇਂਦਰ ਵੱਲ ਗੁਰੂਤਾ-ਆਕਰਸ਼ਣ ਬਲ ਲਗਾ ਕੇ ਖਿੱਚਦੀ ਹੈ ।
∴ F = m × ਵਿਅਕਤੀ ਵਿੱਚ ਧਰਤੀ ਦੁਆਰਾ ਉਤਪੰਨ ਹੋਇਆ ਪ੍ਰਵੇਰਾ
F = m × G ………..(i)
ਇੱਥੇ g ਨੂੰ ਧਰਤੀ ਦਾ ਗੁਰੂਤਵੀ ਵੇਗ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
m × g = \(\frac{\mathrm{G} \times m \times \mathrm{M}}{\mathrm{R}^{2}}\)
ਜਾਂ g = G × \(\frac{\mathrm{M}}{\mathrm{R}^{2}}\) …………………(ii)

ਜੇਕਰ ਸਮੀਕਰਨ (ii) ਵਿੱਚ ਚੰਦਰਮਾ ਦੇ ਪੁੰਜ ਅਤੇ ਅਰਧ-ਵਿਆਸ ਦੇ ਮੁੱਲ ਭਰ ਦੇਈਏ, ਤਾਂ ਚੰਨ ਉੱਤੇ 8 ਦਾ ਮੁੱਲ 8w ਕਹਾਉਂਦਾ ਹੈ ।

∴ g_m = \(\frac{1}{6}\) × g
ਚੰਨ ਦੀ ਸਤ੍ਹਾ ਉੱਤੇ ਗੁਰੂਤਵੀ ਪ੍ਰਵੇਗ = \(\frac{1}{6}\) × ਧਰਤੀ ਦੀ ਸਤ੍ਹਾ ਉੱਤੇ ਗੁਰੂਤਵੀ ਵੇਗ ਹੁਣ ਕਿਉਂਕਿ ਚੰਨ ਦੀ ਸਤ੍ਹਾ ਉੱਤੇ ਲੱਗ ਰਿਹਾ ਗੁਰੂਤਵੀ ਵੇਗ ਧਰਤੀ ਦੀ ਸਤ੍ਹਾ ਉੱਤੇ ਲੱਗ ਰਹੇ ਗੁਰੂਤਵੀ ਵੇਗ
ਦਾ \(\frac{1}{6}\) ਵਾਂ ਭਾਗ ਹੈ ਇਸ ਲਈ ਵਿਅਕਤੀ ਧਰਤੀ ਦੀ ਸਤ੍ਹਾ ਨਾਲੋਂ ਚੰਨ ਦੀ ਸਤ੍ਹਾ ਤੇ 6 ਗੁਣਾ ਉੱਚੀ ਛਲਾਂਗ ਲਗਾ ਸਕਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਆਰਕੀਮਿਡੀਜ਼ ਦਾ ਸਿਧਾਂਤ ਕੀ ਹੈ ? ਪ੍ਰਯੋਗਿਕ ਕਿਰਿਆ ਦੁਆਰਾ ਇਸ ਨੂੰ ਸਿੱਧ ਕਰੋ ।
ਉੱਤਰ-
ਆਰਕੀਮਿਡੀਜ਼ ਦਾ ਸਿਧਾਂਤ- ਜਦੋਂ ਕਿਸੇ ਠੋਸ ਵਸਤੂ ਨੂੰ ਕਿਸੇ ਤਰਲ ਵਿੱਚ ਪੂਰਨ ਤੌਰ ਤੇ ਜਾਂ ਅੰਸ਼ਿਕ ਰੂਪ ਨਾਲ ਡੁਬੋਇਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਉਹ ਉੱਪਰ ਵੱਲ ਨੂੰ ਇੱਕ ਬਲ ਨੂੰ ਅਨੁਭਵ ਕਰਦੀ ਹੈ ਜੋ ਵਸਤੂ ਦੁਆਰਾ ਹਟਾਏ ਗਏ ਤਰਲ ਦੇ ਭਾਰ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ ।”

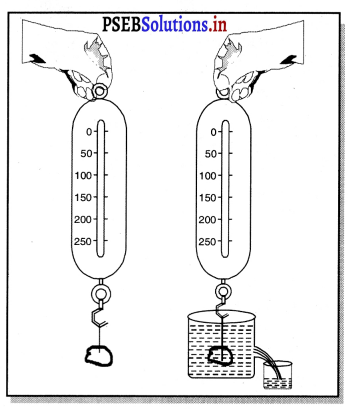
ਯੋਗਿਕ ਪੜਤਾਲ – ਇੱਕ ਪੱਥਰ ਦਾ ਟੁਕੜਾ ਲਓ ਅਤੇ ਇਸਨੂੰ ਕਮਾਨੀਦਾਰ ਤੁਲਾ (ਸਪਰਿੰਗ ਬੈਲੈਂਸ) ਦੇ ਹੁੱਕ ਨਾਲ ਬੰਨੋ । ਤੁਲਾ ਨੂੰ ਸਟੈਂਡ ‘ਤੇ ਲਟਕਾਓ ਜਾਂ ਫਿਰ ਹੱਥ ਵਿੱਚ ਪੱਕੜ ਕੇ ਪੱਥਰ ਨੂੰ ਲਟਕਾਓ । ਜਿਸ ਤਰ੍ਹਾਂ ਚਿੱਤਰ ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ । ਪੱਥਰ ਦਾ ਭਾਰ ਕਮਾਨੀਦਾਰ ਤੁਲਾ ਦੀ ਪੜ੍ਹਤ ਨੋਟ ਕਰਕੇ ਪਤਾ ਕਰੋ । ਹੁਣ ਬੀਕਰ ਨੂੰ ਪੂਰਾ ਪਾਣੀ ਨਾਲ ਭਰ ਕੇ ਪੱਥਰ ਨੂੰ ਬੀਕਰ ਵਿੱਚ ਪਏ ਪਾਣੀ ਵਿੱਚ ਡੁਬੋ ਦਿਉ ਜਿਵੇਂ ਚਿੱਤਰ (b) ਵਿੱਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ । ਤੁਸੀਂ ਵੇਖੋਗੇ ਕਿ ਜਦੋਂ ਪੱਥਰ ਪਾਣੀ ਵਿੱਚ ਡੁੱਬ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਕਮਾਨੀਦਾਰ ਤੁਲਾ ਦੀ ਪੜ੍ਹਤ ਘੱਟ ਹੋ ਜਾਂਦੀ ਹੈ ਅਰਥਾਤ ਪਾਣੀ ਵਿੱਚ ਡੁਬੋਣ ਨਾਲ ਪੱਥਰ ਦੇ ਭਾਰ ਵਿੱਚ ਘਾਟ ਆ ਗਈ ਹੈ । ਪਹਿਲੀ ਪੜ੍ਹਤ ਵਿੱਚੋਂ ਦੂਜੀ ਪੜ੍ਹਤ ਨੂੰ ਘਟਾ ਕੇ ਪੱਥਰ ਦੇ ਭਾਰ ਵਿੱਚ ਹੋਈ ਘਾਟ ਪਤਾ ਕਰ ਸਕਦੇ ਹਾਂ । ਜਿਉਂ ਹੀ ਪੱਥਰ ਨੂੰ ਡੁਬੋਇਆ ਜਾਵੇਗਾ, ਤਾਂ ਹੀ ਪੱਥਰ ਦੇ ਆਇਤਨ ਦੇ ਬਰਾਬਰ ਆਇਤਨ ਦਾ ਪਾਣੀ ਵਿਸਥਾਪਿਤ ਹੋਵੇਗਾ । ਇਸ ਵਿਸਥਾਪਿਤ ਪਾਣੀ ਨੂੰ ਇੱਕ ਹੋਰ ਬੀਕਰ ਵਿੱਚ ਇਕੱਠਾ ਕਰ ਲਉ । ਇਹ ਪਾਣੀ ਦਾ ਭਾਰ ਪੱਥਰ ਦੇ ਭਾਰ ਵਿੱਚ ਹੋਈ ਕਮੀ ਦੇ ਬਰਾਬਰ ਹੋਵੇਗਾ । ਇਸ ਤਰ੍ਹਾਂ ਆਰਕੀਮਿਡੀਜ਼ ਦਾ ਨਿਯਮ ਸਿੱਧ ਹੋ ਜਾਂਦਾ ਹੈ ।

ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Short Answer Type Questions)

ਪ੍ਰਸ਼ਨ 1.
ਕਿਹੜਾ ਜ਼ਿਆਦਾ ਹੈ, 1 kg ਲੋਹੇ ਉੱਪਰ ਲੱਗ ਰਿਹਾ ਧਰਤੀ ਵੱਲੋਂ ਆਕਰਸ਼ਣ-ਬਲ ਜਾਂ ਧਰਤੀ ਉੱਪਰ ਲੱਗ ਰਿਹਾ 1 kg ਲੋਹੇ ਵਲੋਂ ਆਕਰਸ਼ਣ-ਬਲ ਅਤੇ ਕਿਉਂ ?
ਉੱਤਰ-
ਨਿਊਟਨ ਦੇ ਗੁਰੂਤਾ-ਆਕਰਸ਼ਣ ਬਲ ਦੇ ਨਿਯਮ ਅਨੁਸਾਰ ਇਹ ਦੋ ਵਸਤੂਆਂ ਵਿਚਕਾਰ ਆਪਸੀ ਆਕਰਸ਼ਣ ਬਲ ਹੁੰਦਾ ਹੈ । ਇਸ ਲਈ ਨਾ ਤਾਂ ਧਰਤੀ ਲੋਹੇ ਉੱਪਰ ਅਤੇ ਨਾ ਹੀ ਲੋਹਾ ਧਰਤੀ ਉੱਪਰ ਜ਼ਿਆਦਾ ਬਲ ਲਗਾਉਂਦਾ ਹੈ । ਪਰ ਕਿਉਂਕਿ ਲੋਹੇ ਦਾ ਪੁੰਜ ਧਰਤੀ ਨਾਲੋਂ ਘੱਟ ਹੈ ਇਸ ਲਈ ਧਰਤੀ 1 kg ਲੋਹੇ ਦੇ ਟੁਕੜੇ ਨੂੰ ਆਪਣੇ ਵੱਲ ਖਿੱਚ ਲੈਂਦੀ ਹੈ ਜਿਸ ਦੀ ਗਤੀ ਇਹ ਦੱਸਦੀ ਹੈ ਕਿ ਧਰਤੀ 1 kg ਲੋਹੇ ਦੇ ਟੁਕੜੇ ਤੇ ਜ਼ਿਆਦਾ ਬਲ ਲਗਾ ਰਹੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
G ਨੂੰ ਵਿਸ਼ਵ-ਵਿਆਪੀ ਸਥਿਰ ਅੰਕ ਕਿਉਂ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
G ਨੂੰ ਵਿਸ਼ਵ-ਵਿਆਪੀ ਸਥਿਰ ਅੰਕ ਇਸ ਲਈ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਕਿ ਸਾਰੇ ਹੀ ਹਿਮੰਡ ਵਿੱਚ ਇਸਦਾ ਸੰਖਿਅਕ ਮੁੱਲ ਇੱਕੋ ਹੀ ਰਹਿੰਦਾ ਹੈ । ਇਸ G ਦਾ ਮੁੱਲ 6.67 ×10-^-11 N-m² /kg² ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਇੱਕ ਗਿਆਤ ਸਥਿਤੀ ਉੱਪਰ ਵੱਖ-ਵੱਖ ਵਸਤੂਆਂ ਲਈ ‘g’ ਦਾ ਮੁੱਲ ਸਮਾਨ ਹੁੰਦਾ ਹੈ ਜਾਂ ਵੱਖਰਾ ?
ਉੱਤਰ-
ਧਰਤੀ ਦੇ ਗੁਰੂਤਵੀ ਵੇਗ (g) ਅਤੇ ਵਿਸ਼ਵ-ਵਿਆਪੀ ਗੁਰੂਤਵੀ ਸਥਿਰ ਅੰਕ ਵਿਚਕਾਰ ਸੰਬੰਧ ਤੋਂ ਅਸੀਂ
ਜਾਣਦੇ ਹਾਂ ਕਿ g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\) ਹੁੰਦਾ ਹੈ ।

ਇਸ ਸੰਬੰਧ ਤੋਂ ਇਹ ਪਤਾ ਲਗਦਾ ਹੈ ਕਿ 8 ਦਾ ਮੁੱਲ ਵਸਤੂ ਦੇ ਪੁੰਜ ਤੇ ਨਿਰਭਰ ਨਹੀਂ ਕਰਦਾ । ਇਸ ਲਈ ਅਸੀਂ ਇਸ ਸਿੱਟੇ ‘ਤੇ ਪੁੱਜਦੇ ਹਾਂ ਕਿ ਕਿਸੇ ਗਿਆਤ ਸਥਿਤੀ ਉੱਪਰ ਵੱਖ-ਵੱਖ ਵਸਤੁਆਂ ਲਈ ‘g’ ਦਾ ਮੁੱਲ ਸਮਾਨ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਕੀ ਕਿਸੇ ਵਸਤੂ ਦਾ ਭਾਰ ਭੂ-ਮੱਧ ਰੇਖਾ ਤੇ ਜ਼ਿਆਦਾ ਹੁੰਦਾ ਹੈ ਜਾਂ ਧਰੁਵਾਂ ਉੱਤੇ ?
ਉੱਤਰ-

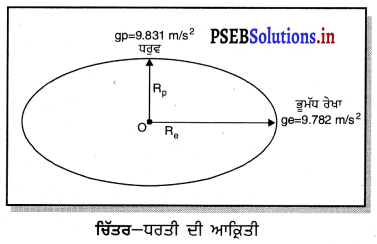
ਧਰਤੀ ਦੀ ਆਕ੍ਰਿਤੀ ਪੂਰੀ ਤਰ੍ਹਾਂ ਗੋਲ ਨਹੀਂ ਹੈ ਸਗੋਂ ਥੋੜੀ ਜਿਹੀ ਅੰਡਾਕਾਰ (ਇਲਿਪਸੀ) ਹੈ । ਇਹ ਧਰੁਵਾਂ ਦੇ ਨੇੜੇ ਪੱਧਰੀ ਹੈ ਜਦੋਂ ਕਿ ਭੂ-ਮੱਧ ਰੇਖਾ ਦੇ ਨੇੜੇ ਥੋੜੀ ਜਿਹੀ ਬਾਹਰ ਵੱਲ ਉੱਠੀ ਹੋਈ ਹੈ, ਜਿਵੇਂ ਕਿ ਚਿੱਤਰ ਵਿੱਚ ਵਿਖਾਇਆ ਗਿਆ ਹੈ ।

ਭੂ-ਮੱਧ ਰੇਖੀ ਅਰਧ-ਵਿਆਸ ਲਗਪਗ 6378 ਕਿ.ਮੀ. ਹੈ ਜਦੋਂ ਕਿ ਧਰੁਵੀ ਅਰਧ-ਵਿਆਸ 6357 ਕਿ. ਮੀ. ਹੈ । ਭੂ-ਮੱਧ ਰੇਖੀ ਅਰਧ-ਵਿਆਸ ਧਰੁਵੀ ਅਰਧ-ਵਿਆਸ ਨਾਲੋਂ 21 ਕਿ. ਮੀ. ਜ਼ਿਆਦਾ ਹੈ ।

ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\) ਅਰਥਾਤ g ਦਾ ਮੁੱਲ R ਦੇ ਉਲਟ ਅਨੁਪਾਤੀ (g ∝ \(\frac{1}{\mathrm{R}^{2}}\)) ਹੁੰਦਾ ਹੈ ਕਿਉਂਕਿ ਭੂ-ਮੱਧ ਰੇਖੀ ਅਰਧ-ਵਿਆਸ, ਧਰੁਵੀ ਅਰਧ-ਵਿਆਸ ਨਾਲੋਂ ਜ਼ਿਆਦਾ ਹੁੰਦਾ ਹੈ , ਇਸ ਲਈ ਭੂ-ਮੱਧ ਰੇਖਾ ਤੇ ‘g’ ਦਾ ਮੁੱਲ ਘੱਟ ਹੋਵੇਗਾ ਅਤੇ ਧਰੁਵ ਤੇ ‘g’ ਦਾ ਮੁੱਲ ਜ਼ਿਆਦਾ ਹੋਵੇਗਾ ।

ਪ੍ਰਸ਼ਨ 5.
ਕੋਈ ਵਸਤੂ ਧਰਤੀ ਦੇ ਕੇਂਦਰ ਤੇ ਭਾਰਹੀਨ ਕਿਉਂ ਹੋ ਜਾਂਦੀ ਹੈ ?
ਉੱਤਰ-
ਧਰਤੀ ਦੇ ਕੇਂਦਰ ਤੇ ਵਸਤੂ ਦਾ ਭਾਰਹੀਨ ਹੋਣਾ-ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ ਧਰਤੀ ਤੋਂ ਹੇਠਾਂ ਵੱਲ ਜਾਣ ਵੇਲੇ g ਦਾ ਮੁੱਲ ਘੱਟਦਾ ਹੈ ਅਤੇ ਧਰਤੀ ਦੇ ਕੇਂਦਰ ਤੇ ਗੁਰੂਤਾ ਵੇਗ (9) = 0 ਹੁੰਦਾ ਹੈ । ਇਸ ਲਈ ਕਿਸੇ ਵਸਤੂ ਜਿਸਦਾ ਪੁੰਜ ਅ ਹੈ ਦਾ ਧਰਤੀ ਦੇ ਕੇਂਦਰ ਤੇ ਭਾਰ = m × g
= m × 0
= 0 ਸਿਫ਼ਰ ਹੁੰਦਾ ਹੈ ਅਰਥਾਤ ਵਸਤੂ ਭਾਰਹੀਨ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਟੈਨਿਸ ਦੀ ਗੇਂਦ ਮੈਦਾਨਾਂ ਨਾਲੋਂ ਪਹਾੜਾਂ ਤੇ ਜ਼ਿਆਦਾ ਉਛਲਦੀ ਹੈ । ਵਿਆਖਿਆ ਕਰੋ ।
ਉੱਤਰ-
ਜਿਵੇਂ-ਜਿਵੇਂ ਅਸੀਂ ਉੱਚਾਈ ਤੇ ਜਾਂਦੇ ਹਾਂ, ਤਿਵੇਂ-ਤਿਵੇਂ ਗੁਰੁਤਵੀ ਵੇਗ (g) ਦਾ ਮੁੱਲ ਘੱਟਦਾ ਜਾਂਦਾ ਹੈ । ਪਹਾੜਾਂ ਦੀ ਮੈਦਾਨੀ ਇਲਾਕਿਆਂ ਨਾਲੋਂ ਉੱਚਾਈ ਵੱਧ ਹੁੰਦੀ ਹੈ ਜਿਸ਼ ਕਰਕੇ ਗੇਂਦ ‘ਤੇ ਲੱਗਣ ਵਾਲਾ ਗੁਰੂਤਾ-ਆਕਰਸ਼ਣ ਬਲ ਪਹਾੜਾਂ ਤੇ ਘੱਟ ਹੁੰਦਾ ਹੈ । ਇਸਦੇ ਸਿੱਟੇ ਵਜੋਂ ਪਹਾੜਾਂ ਤੇ ਗੇਂਦ ਮੈਦਾਨੀ ਇਲਾਕੇ ਦੀ ਤੁਲਨਾ ਵਿੱਚ ਵਧੇਰੇ ਉਛਲਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਧਰਤੀ ਦੀ ਸਤ੍ਹਾ ਤੇ ਕਿਸੇ ਵਸਤੂ ਦਾ ਭਾਰ ਲਗਪਗ 9.8 ਨਿਊਟਨ ਹੈ । ਇਸ ਕਥਨ ਦੀ ਪੁਸ਼ਟੀ ਕਰੋ ।
ਉੱਤਰ-
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ ਧਰਤੀ ਦੀ ਸਤ੍ਹਾ ਤੇ ਗੁਰੂਤਵੀ ਵੇਗ (g) ਦਾ ਮੁੱਲ 9.8 m² ਹੁੰਦਾ ਹੈ ਅਤੇ ਵਸਤੂ ਦੇ ਭਾਰ ਲਈ ਸੰਬੰਧ ਹੈ,
W = m × g
ਇੱਥੇ ਵੱਖ-ਵੱਖ ਰਾਸ਼ੀਆਂ ਦਾ ਮੁੱਲ ਭਰਨ ਮਗਰੋਂ,
9.8 = m × 9.8
ਜਾਂ m = \(\frac{9.8}{9.8}\)
m = 98
∴ m = 1 ਕਿਲੋਗ੍ਰਾਮ
ਦਿੱਤੇ ਗਏ ਕਥਨ ਦਾ ਅਰਥ ਹੈ ਕਿ ਧਰਤੀ ਦੀ ਸਤ੍ਹਾ ਤੇ ਵਸਤੂ ਦਾ ਪੁੰਜ 1 ਕਿਲੋਗ੍ਰਾਮ ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਗੁਰੂਤਾ ਅਧੀਨ ਸੁਤੰਤਰ ਡਿੱਗ ਰਹੀ ਵਸਤੂ ਦੀ ਗਤੀ ਕਿਸ ਤਰ੍ਹਾਂ ਦੀ ਹੋਵੇਗੀ ?
ਉੱਤਰ-
ਗੁਰੂਤਾ ਅਧੀਨ ਸੁਤੰਤਰ ਡਿੱਗ ਰਹੀ ਵਸਤੂ – ਗੁਰੂਤਾ ਅਧੀਨ ਸੁਤੰਤਰ ਡਿੱਗ ਰਹੀ ਵਸਤੂ ਇਕ ਸਮਾਨ ਗਤੀ ਨਾਲ ਹੇਠਾਂ ਡਿੱਗੇਗੀ । ਜੇਕਰ ਵੱਖ-ਵੱਖ ਪੁੰਜ ਅਤੇ ਆਕਾਰ ਦੀਆਂ ਵਸਤੂਆਂ ਨੂੰ ਨਿਰਵਾਯੂ ਵਿੱਚੋਂ ਧਰਤੀ ਵੱਲ ਹੇਠਾਂ ਡਿੱਗਣ ਦਿੱਤਾ ਜਾਵੇ, ਤਾਂ ਉਨ੍ਹਾਂ ਵਿੱਚ ਇਕ ਸਮਾਨ ਗੁਰੂਤਾ ਵੇਗ ਹੋਵੇਗਾ ਅਤੇ g ਦਾ ਮੁੱਲ ਵੱਧਦਾ ਰਹੇਗਾ ।

ਪ੍ਰਸ਼ਨ 9.
ਇੱਕ ਪਦਾਰਥ ਦਾ ਜ਼ਰੂਰੀ ਗੁਣ ਕਿਹੜਾ ਹੈ, ਪੁੰਜ ਜਾਂ ਭਾਰ ?
ਉੱਤਰ-
ਕਿਸੇ ਵਸਤੂ ਦਾ ਜ਼ਰੂਰੀ ਗੁਣ ਉਸ ਦਾ ਪੁੰਜ ਹੁੰਦਾ ਹੈ, ਨਾ ਕਿ ਉਸਦਾ ਭਾਰ, ਕਿਉਂਕਿ ਅਜਿਹੀ ਕੋਈ ਥਾਂ ਨਹੀਂ ਜਿੱਥੇ ਪਦਾਰਥ ਦਾ ਪੁੰਜ ਨਾ ਹੋਵੇ | ਧਰਤੀ ਦੇ ਕੇਂਦਰ ‘ਤੇ ਵਸਤੁ ਦਾ ਭਾਰ ਜ਼ੀਰੋ ਹੋ ਸਕਦਾ ਹੈ, ਪਰੰਤੁ ਪੁੰਜ ਜ਼ੀਰੋ ਨਹੀਂ ਹੋ ਸਕਦਾ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਕੋਈ ਵੀ ਵਸਤੂ ਜਿਸ ਦਾ ਪੁੰਜ ਹੁੰਦਾ ਹੈ ਅਤੇ ਜਿਹੜੀ ਥਾਂ ਘੇਰਦੀ ਹੈ ਉਹ ਪਦਾਰਥ ਹੁੰਦਾ ਹੈ। ਜੋ ਕਿ ਪਦਾਰਥ ਦੀ ਪਰਿਭਾਸ਼ਾ ਦੱਸਦੀ ਹੈ । ਇਸ ਲਈ ਪਦਾਰਥ ਦਾ ਜ਼ਰੂਰੀ ਗੁਣ ਉਸ ਦਾ ਪੁੰਜ ਹੈ ਨਾ ਕਿ ਉਸਦਾ ਭਾਰ ।

ਪ੍ਰਸ਼ਨ 10.
ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚ ਅੰਤਰ ਦੱਸੋ
(i) g (ਗੁਰੂਤਾ ਵੇਗ) ਅਤੇ (ਗੁਰੂਤਾ ਆਕਰਸ਼ਣ) ਸਥਿਰ ਅੰਕ G
(ii) ਭਾਰ ਅਤੇ ਪੁੰਜ
(iii) ਪੁੰਜ ਕੇਂਦਰ ਅਤੇ ਗੁਰੂਤਾ ਕੇਂਦਰ ।
ਉੱਤਰ-
(i) ਗੁਰੂਤਾ ਵੇਗ ਅਤੇ ਗੁਰੂਤਾ ਆਕਰਸ਼ਣ ਵਿੱਚ ਅੰਤਰ-

‘g’ (ਗਰਤਾ ਪਵੇਗ)	‘G’ (ਗੁਰੂਤਾ ਆਕਰਸ਼ਣ)
(1) ਇਹ ਗੁਰੂਤਾ ਵੇਗ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ ।	(1) ਇਹ ਗੁਰੂਤਾ ਆਕਰਸ਼ਣ ਸਥਿਰ ਅੰਕ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ ।
(2) ਇਸ ਦਾ ਮੁੱਲ ਭਿੰਨ-ਭਿੰਨ ਸਥਾਨਾਂ ਤੇ ਭਿੰਨ-ਭਿੰਨ ਹੁੰਦਾ ਹੈ ।	(2) ਇਸ ਦਾ ਮੁੱਲ ਸਭ ਸਥਾਨਾਂ ਤੇ ਬਰਾਬਰ ਹੈ ਇਸ ਲਈ ਇਸ ਨੂੰ ਸਰਵ-ਵਿਆਪਕ ਸਥਿਰ ਅੰਕ ਵੀ ਕਹਿੰਦੇ ਹਨ ।
(3) ਇਸ ਦਾ ਧਰਤੀ ਉੱਤੇ ਮੁੱਲ 9.8 m/s2 ਹੈ ।	(3) ਇਸ ਦਾ ਮੁੱਲ 6.67 × 10-11 N-m2/kg2 ਹੈ ।

(ii) ਭਾਰ ਅਤੇ ਪੁੰਜ ਵਿੱਚ ਅੰਤਰ-

ਭਾਰ (Weight)	ਪੁੰਜ (Mass)
(1) ਭਾਰ ਉਹ ਬਲ ਹੈ, ਜਿਸ ਨਾਲ ਵਸਤੂ ਧਰਤੀ ਦੇ ਕੇਂਦਰ ਵੱਲ ਖਿੱਚੀ ਜਾਂਦੀ ਹੈ ।	(1) ਪੁੰਜ ਵਸਤੂ ਵਿੱਚ ਉਪਸਥਿਤ ਪਦਾਰਥ ਦੀ ਮਾਤਰਾ ਹੈ ।
(2) ਭਾਰ ਇੱਕ ਸਦਿਸ਼ ਰਾਸ਼ੀ ਹੈ ।	(2) ਪੁੰਜ ਇੱਕ ਅਦਿਸ਼ ਰਾਸ਼ੀ ਹੈ ।
(3) ਇਹ ਰਾਸ਼ੀ ਸਥਿਰ ਨਹੀਂ ਹੈ । ਇਹ ਇੱਕ ਥਾਂ ਤੋਂ ਦੂਜੀ ਥਾਂ ਤੇ ਬਦਲਦੀ ਹੈ ।	(3) ਇਹ ਇੱਕ ਸਥਿਰ ਰਾਸ਼ੀ ਹੈ ।
(4) ਭਾਰ ਸਪਰਿੰਗ-ਬੈਲੇਂਸ ਨਾਲ ਮਾਪਿਆ ਜਾਂਦਾ ਹੈ ।	(4) ਪੁੰਜ ਡੰਡੀ-ਤੱਕੜੀ ਨਾਲ ਮਾਪਿਆ ਜਾਂਦਾ ਹੈ ।
(5) ਵਸਤੁ ਦਾ ਭਾਰ ਧਰਤੀ ਦੇ ਕੇਂਦਰ ਤੇ ਜ਼ੀਰੋ ਹੋ ਜਾਂਦਾ ਹੈ । (ਅਰਥਾਤ g = 0).	(5) ਪੁੰਜ ਕਿਸੇ ਥਾਂ ਤੇ ਵੀ ਜ਼ੀਰੋ ਨਹੀਂ ਹੁੰਦਾ ਹੈ ।
(6) ਇਸ ਨੂੰ ਨਿਊਟਨ ਜਾਂ ਕਿਲੋਗ੍ਰਾਮ ਭਾਰ ਵਿੱਚ ਮਾਪਿਆ ਜਾਂਦਾ ਹੈ ।	(6) ਇਸ ਨੂੰ ਕਿਲੋਗ੍ਰਾਮ ਵਿੱਚ ਮਾਪਿਆ ਜਾਂਦਾ ਹੈ ।

(iii) ਪੰਜ ਕੇਂਦਰ ਅਤੇ ਗੁਰੂਤਾ ਕੇਂਦਰ ਵਿੱਚ ਅੰਤਰ – ਧਰਤੀ ਦੀ ਸਤ੍ਹਾ ਉੱਤੇ ਜਾਂ ਇਸੇ ਦੇ ਨਜ਼ਦੀਕ ਉਹ ਬਿੰਦੂ ਜਿੱਥੇ ਗੁਰੂਤਵੀ ਬਲ ਸਥਿਰ ਹੁੰਦਾ ਹੈ, ਉਸ ਨੂੰ ਪੰਜ ਕੇਂਦਰ ਆਖਦੇ ਹਨ । ਪੁੰਜ ਕੇਂਦਰ ਉਹ ਬਿੰਦੂ ਹੈ ਜਿੱਥੇ ਅਸਲ ਵਿੱਚ ਵਸਤੁ ਉੱਤੇ ਗੁਰੂਤਾ-ਆਕਰਸ਼ਣ ਬਲ ਅਨੁਭਵ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਕਿਸੇ ਵਸਤੂ ਦਾ ਗੁਰੂਤਾ ਕੇਂਦਰ ਵਸਤੂ ਵਿੱਚ ਉਹ ਬਿੰਦੂ ਹੁੰਦਾ ਹੈ ਜਿੱਥੇ ਗੁਰੂਤਾ ਬਲ ਸੰਪੂਰਨ ਵਸਤੂ ਉੱਤੇ ਕਿਰਿਆ ਕਰਦਾ ਮੰਨਿਆ ਜਾ ਸਕਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 11.
ਅਸੀਂ ਸਾਰੇ ਤਾਰਿਆਂ ਨੂੰ ਹਿਲਾਏ-ਜੁਲਾਏ ਬਗੈਰ ਆਪਣੀ ਉਂਗਲੀ ਵੀ ਨਹੀਂ ਹਿਲਾ ਸਕਦੇ । ਟਿੱਪਣੀ ਕਰੋ ।
ਉੱਤਰ-
ਜਦੋਂ ਅਸੀਂ ਆਪਣੀ ਉਂਗਲੀ ਹਿਲਾਉਂਦੇ ਹਾਂ, ਤਾਂ ਉਂਗਲੀ ਅਤੇ ਬ੍ਰਹਿਮੰਡ ਦੀਆਂ ਸਾਰੀਆਂ ਵਸਤੂਆਂ ਵਿਚਕਾਰ ਦੁਰੀ ਬਦਲ ਜਾਣ ਕਾਰਨ ਗੁਰੂਤਾ ਆਕਰਸ਼ਣ ਬਲ ਬਦਲ ਜਾਂਦਾ ਹੈ । ਨਤੀਜੇ ਵਜੋਂ ਸਾਰੀਆਂ ਵਸਤੂਆਂ ਹਿਲ-ਜੁਲ ਜਾਂਦੀਆਂ ਹਨ, ਪਰ ਇਹ ਹਿਲ-ਜੁਲ ਬਹੁਤ ਹੀ ਘੱਟ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 12.
ਗੁਰੂਤਾ-ਆਕਰਸ਼ਣ ਅਤੇ ਗੁਰੁਤਾ ਦੀ ਪਰਿਭਾਸ਼ਾ ਦਿਓ ।
ਉੱਤਰ-
ਗੁਰੂਤਾ-ਆਕਰਸ਼ਣ – ਇਹ ਇਸ ਹਿਮੰਡ ਦੀਆਂ ਕਿਸੇ ਦੋ ਵਸਤੁਆਂ ਵਿਚਕਾਰ ਆਕਰਸ਼ਣ ਹੈ ।
ਗੁਰੂਤਾ – ਇਹ ਧਰਤੀ ਦੁਆਰਾ ਇਸ ਦੀ ਸਤਹ ਜਾਂ ਇਸ ਦੇ ਨੇੜੇ ਸਥਿਤ ਸਾਰੀਆਂ ਵਸਤਾਂ ‘ਤੇ ਲੱਗਣ ਵਾਲਾ ਆਕਰਸ਼ਣ ਬਲ ਹੈ ।

ਪ੍ਰਸ਼ਨ 13.
ਸੂਰਜ ਦੇ ਚਾਰੇ ਪਾਸੇ ਗ੍ਰਹਿਆਂ ਦੀ ਗਤੀ ਕਿਸ ਕਾਰਨ ਹੈ ?
ਉੱਤਰ-
ਸਾਰੇ ਹਿ ਆਪਣੇ-ਆਪਣੇ ਪੱਥ ਵਿੱਚ ਸੂਰਜ ਦੇ ਚਾਰੇ ਪਾਸੇ ਉਸਦੇ ਗੁਰੂਤਾ-ਆਕਰਸ਼ਣ ਦੇ ਕਾਰਨ ਘੁੰਮਦੇ ਹਨ । ਇਹ ਗਤੀ ਵੀ ਬਿਲਕੁਲ ਉਸੇ ਤਰ੍ਹਾਂ ਹੈ, ਜਿਸ ਤਰ੍ਹਾਂ ਚੰਨ ਧਰਤੀ ਦੇ ਗੁਰੂਤਾ-ਆਕਰਸ਼ਣ ਕਾਰਨ ਧਰਤੀ ਦੁਆਲੇ ਘੁੰਮਦਾ ਹੈ ।

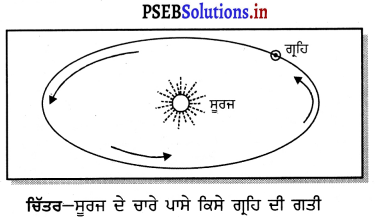
ਪ੍ਰਸ਼ਨ 14.
ਗੁਰੂਤਾ-ਆਕਰਸ਼ਣ ਬਲ ਦੀ ਵਰਤੋਂ ਜਿਨ੍ਹਾਂ ਵਿਵਹਾਰਿਕ ਕਿਰਿਆਵਾਂ ਵਿੱਚ ਹੁੰਦੀ ਹੈ, ਉਨ੍ਹਾਂ ਦੀਆਂ ਕੁੱਝ ਉਦਾਹਰਨਾਂ ਦਿਓ ।
ਉੱਤਰ-
ਗੁਰੂਤਾ-ਆਕਰਸ਼ਣ ਬਲ ਦੀਆਂ ਉਦਾਹਰਨਾਂ-

1. ਸੂਰਜ ਅਤੇ ਧਰਤੀ ਵਿੱਚ ਕਿਰਿਆ ਕਰ ਰਹੇ ਗੁਰੂਤਾ-ਆਕਰਸ਼ਣ ਕਾਰਨ ਹੀ ਧਰਤੀ, ਸੂਰਜ ਦੁਆਲੇ ਆਪਣੀ ਗਤੀ ਬਣਾਈ ਰੱਖਦੀ ਹੈ ।
2. ਸੂਰਜੀ ਪਰਿਵਾਰ ਦੀ ਹੋਂਦ ਗੁਰੂਤਾ-ਆਕਰਸ਼ਣ ਬਲ ਕਾਰਨ ਹੀ ਸੰਭਵ ਹੈ ।
3. ਹਿ ਦੇ ਤਲ ਤੇ ਵਾਯੂਮੰਡਲ ਵੀ ਗੁਰੂਤਾ-ਆਕਰਸ਼ਣ ਬਲ ਕਾਰਨ ਹੀ ਹੁੰਦੀ ਹੈ ।
4. ਸਮੁੰਦਰ ਵਿੱਚ ਆਉਣ ਵਾਲਾ ਉਪਸਥਿਤੀ ਜਵਾਰਭਾਟਾ ਸੁਰਜ, ਚੰਨ ਅਤੇ ਪਾਣੀ ਵਿਚਕਾਰ ਕਿਰਿਆ ਕਰ ਰਹੇ ਗੁਰੂਤਾ-ਆਕਰਸ਼ਣ ਬਲ ਕਾਰਨ ਹੀ ਹੁੰਦਾ ਹੈ ।
5. ਗੁਰੂਤਾ-ਆਕਰਸ਼ਣ ਬਲ ਕਾਰਨ ਹੀ ਅਸੀਂ ਧਰਤੀ ਤੇ ਮਜ਼ਬੂਤੀ ਨਾਲ ਖੜੇ ਹੋ ਸਕਦੇ ਹਾਂ।
6. ਬਣਾਉਟੀ ਉਪਗ੍ਰਹਿ ਨੂੰ ਚੱਕਰ ਲਗਾਉਣ ਲਈ ਲੋੜੀਂਦਾ ਬਲ ਵੀ ਗੁਰੂਤਾ-ਆਕਰਸ਼ਣ ਬਲ ਹੈ ।

ਪ੍ਰਸ਼ਨ 15.
ਪੁੰਜ ਦੇ ਗੁਣ ਦੱਸੋ ।
ਉੱਤਰ-
ਪੰਜ-ਕਿਸੇ ਵਸਤੂ ਵਿੱਚ ਮੌਜੂਦ ਪਦਾਰਥ ਦੀ ਮਾਤਰਾ ਨੂੰ ਪੰਜ ਕਹਿੰਦੇ ਹਨ ।
ਪੁੰਜ ਦੇ ਗੁਣ-ਇਸ ਦੇ ਮੁੱਖ ਗੁਣ ਹਨ-

1. ਇਹ ਇੱਕ ਸਕੇਲਰ ਰਾਸ਼ੀ ਹੈ ।
2. ਇਹ ਹਰ ਥਾਂ ਤੇ ਸਥਿਰ ਰਹਿੰਦਾ ਹੈ ।
3. ਇਸ ਨੂੰ ਭੌਤਿਕ ਤੁਲਾ ਦੁਆਰਾ ਮਾਪਿਆ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 16.
ਜਦੋਂ ਅਸੀਂ ਧਰਤੀ ਦੀ ਸਤ੍ਹਾ ਤੋਂ ਉੱਪਰ ਵੱਲ ਜਾਂਦੇ ਹਾਂ, ਤਾਂ ਭਾਰ ਤੇ ਕੀ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਕਿਸੇ ਵਸਤੂ ਦਾ ਭਾਰ ਉਸ ਦੇ ਪੁੰਜ ਅਤੇ ਗੁਰੂਤਵੀ ਵੇਗ ‘g’ ਦਾ ਗੁਣਨਫਲ ਹੁੰਦਾ ਹੈ । ਗੁਰੂਤਵੀ ਵੇਗ ਦਾ ਮੁੱਲ ਵਸਤੂ ਦੀ ਧਰਤੀ ਦੇ ਕੇਂਦਰ ਤੋਂ ਦੂਰੀ ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ ।
∴ g = \(\frac{\mathrm{GM}}{\mathrm{R}_{e}^{2}}\)

ਗੁਰੁਤਵੀ ਵੇਗ ਵਸਤੁ ਦੀ ਧਰਤੀ ਦੇ ਕੇਂਦਰ ਤੋਂ ਦੂਰੀ ਦੇ ਵਰਗ ਦੇ ਉਲਟ ਅਨੁਪਾਤੀ ਹੁੰਦਾ ਹੈ । ਇਸ ਲਈ ਭਾਰ ਵੀ ਵਸਤੂ ਦੀ ਧਰਤੀ ਦੇ ਕੇਂਦਰ ਤੋਂ ਦੂਰੀ ਦੇ ਵਰਗ ਦੇ ਉਲਟ ਅਨੁਪਾਤੀ ਹੋਵੇਗਾ । ਜਿਵੇਂ-ਜਿਵੇਂ ਧਰਤੀ ਦੇ ਤਲ ਤੋਂ ਉੱਪਰ ਜਾਂਦੇ ਹਾਂ, ਤਾਂ ਸਾਡੀ ਧਰਤੀ ਦੇ ਕੇਂਦਰ ਤੋਂ ਦੂਰੀ ਵੱਧਦੀ ਜਾਂਦੀ ਹੈ, ਜਿਸ ਕਰਕੇ ਸਾਡਾ ਭਾਰ ਘੱਟ ਹੁੰਦਾ ਜਾਂਦਾ ਹੈ । ਜੇਕਰ ਅਸੀਂ ਧਰਤੀ ਦੀ ਸਤਾ ਤੋਂ ਧਰਤੀ ਦੇ ਅਰਧ-ਵਿਆਸ ਦੇ ਬਰਾਬਰ ਉੱਪਰ ਵੱਲ ਨੂੰ ਜਾਈਏ, ਤਾਂ ਸਾਡਾ ਭਾਰ ਧਰਤੀ ਤੇ ਭਾਰ ਦੀ ਤੁਲਨਾ ਵਿੱਚ \(\frac {1}{4}\) ਹਿੱਸਾ ਰਹਿ ਜਾਵੇਗਾ ।

ਪ੍ਰਸ਼ਨ 17.
ਜਦੋਂ ਕਿਸੇ ਵਸਤੂ ਨੂੰ ਉੱਪਰ ਵੱਲ ਨੂੰ ਸੁੱਟਿਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਵਸਤੂ ਦੀ ਗਤੀ ‘ ਤੇ ਕੀ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ ? ਉਸਦਾ ਵੇਗ ਕਿੰਨਾ ਹੋਵੇਗਾ ?
ਉੱਤਰ-
ਜਦੋਂ ਕਿਸੇ ਵਸਤੂ ਨੂੰ ਉੱਪਰ ਵੱਲ ਨੂੰ ਸੁੱਟਿਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਧਰਤੀ ਉਸ ਨੂੰ ਆਪਣੀ ਗੁਰੁਤਾ ਬਲ ਕਾਰਨ ਹੇਠਾਂ ਵੱਲ ਨੂੰ ਖਿੱਚਦੀ ਹੈ । ਗੁਰੁਤਾ ਬਲ ਵਸਤੂ ਦੀ ਗਤੀ ਦੇ ਉਲਟ ਦਿਸ਼ਾ ਵਿੱਚ ਕਿਰਿਆ ਕਰਦਾ ਹੈ । ਇਸ ਲਈ ਵੇਗ ਘੱਟ ਹੋ ਜਾਂਦਾ ਹੈ । ਉੱਪਰ ਵੱਲ ਸੁੱਟੀ ਗਈ ਵਸਤੂ ਦਾ ਵੇਗ ਹੇਠਾਂ ਵੱਲ ਡਿੱਗਦੀ ਹੋਈ ਵਸਤੂ ਦੇ ਵੇਗ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ ਪਰ ਰਿਣਾਤਮਕ ਹੁੰਦਾ ਹੈ ।

ਉੱਪਰ ਵੱਲ ਸੁੱਟੀ ਗਈ ਵਸਤੂ ਦਾ ਵੇਗ = – 9.8 m/s² ਹੈ । ਇਸ ਲਈ ਜਦੋਂ ਵਸਤੁ ਉੱਪਰ ਵੱਲ ਨੂੰ ਸੁੱਟੀ ਜਾਂਦੀ ਹੈ, ਤਾਂ ਉਸਦਾ ਵੇਗ 9.8 m/s² ਦੀ ਦਰ ਨਾਲ ਘੱਟਦਾ ਹੈ । ਵੇਗ ਉਦੋਂ ਤਕ ਘੱਟਦਾ ਰਹਿੰਦਾ ਹੈ ਜਦੋਂ ਤਕ ਜ਼ੀਰੋ ਨਹੀਂ ਹੋ ਜਾਂਦਾ | ਅਧਿਕਤਮ ਉੱਚਾਈ ਤੇ ਵੇਗ ਜ਼ੀਰੋ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 18.
ਉਛਾਲ ਬਲ ਧਕੇਲ ਬਲ) ਅਤੇ ਉਛਾਲ ਕੇਂਦਰ ਦਾ ਕੀ ਅਰਥ ਹੈ ?
ਉੱਤਰ-
ਉਛਾਲ ਬਲ (ਧਕੇਲ ਬਲ)-ਹਰੇਕ ਤਰਲ ਆਪਣੇ ਅੰਦਰ ਪੂਰੀ ਤਰ੍ਹਾਂ ਜਾਂ ਅੰਸ਼ਿਕ ਰੂਪ ਨਾਲ ਡੁੱਬੀ ਹੋਈ ਵਸਤੂ ਦੇ ਉੱਪਰ ਵੱਲ ਨੂੰ ਇੱਕ ਬਲ ਲਗਾਉਂਦਾ ਹੈ ਜਿਸ ਨੂੰ ਉਛਾਲ ਬਲ (ਧਕੇਲ ਬਲ) ਕਹਿੰਦੇ ਹਨ । ਡੁੱਬੀ ਹੋਈ ਵਸਤੁ ਦੁਆਰਾ ਹਟਾਏ ਗਏ ਤਰਲ ਦੇ ਗੁਰੂਤਾ ਕੇਂਦਰ ’ਤੇ ਉਛਾਲ ਬਲ ਕਿਰਿਆ ਕਰਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਹਟਾਏ ਗਏ ਤਰਲ ਦੇ ਗੁਰੂਤਾ ਕੇਂਦਰ ਨੂੰ ਉਛਾਲ ਕੇਂਦਰ ਕਹਿੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 19.
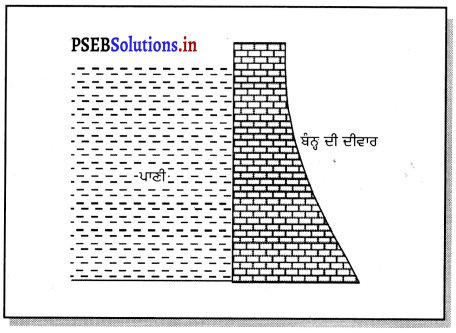
ਨਦੀਆਂ ਉੱਪਰ ਬਣਾਏ ਗਏ ਬੰਨ (ਡੈਮ ਦੀ ਦੀਵਾਰ ਹੇਠਾਂ ਮੋਟੀ ਅਤੇ ਉੱਪਰਲੇ ਹਿੱਸੇ ਵਿੱਚ ਪਤਲੀ ਕਿਉਂ ਬਣਾਈ ਜਾਂਦੀ ਹੈ ?
ਉੱਤਰ-
ਬੰਨ੍ਹ (ਡੈਮ ਦੀ ਦੀਵਾਰ ਦਾ ਹੇਠਲਾ ਹਿੱਸਾ ਮੋਟਾ ਅਤੇ ਉੱਪਰਲੇ ਭਾਗ ਵਿੱਚ ਪਤਲਾ ਬਣਾਉਣਾ-ਡੈਮ ਦੀ ਗਹਿਰਾਈ ਬਹੁਤ ਅਧਿਕ ਹੁੰਦੀ ਹੈ ਅਤੇ ਤਰਲ ਦੇ ਅੰਦਰ ਕਿਸੇ ਬਿੰਦੂ ਤੇ ਦਾਬ ਉਸ ਬਿੰਦੂ ਦੀ ਮੁਕਤ ਤਲ ਦੀ ਗਹਿਰਾਈ ਦੇ ਉਲਟ ਅਨੁਪਾਤੀ ਹੁੰਦਾ ਹੈ । ਡੈਮ ਦੀ ਤਲੀ ਤੇ ਪਾਣੀ ਦਾ ਦਾਬ ਵੱਧ ਤੋਂ ਵੱਧ ਹੁੰਦਾ ਹੈ । ਇਸ ਲਈ ਬੰਨ੍ਹ ਦੀ ਦੀਵਾਰ ਦੇ ਹੇਠਲੇ ਭਾਗ ਵਿੱਚ ਵੱਧ ਦਾਬ ਹੁੰਦਾ ਹੈ ਅਤੇ ਜਿਵੇਂ-ਜਿਵੇਂ ਉੱਪਰ ਵੱਲ ਨੂੰ ਜਾਈਏ ਦਾਬ ਘੱਟ ਜਾਂਦਾ ਹੈ । ਇਸ ਲਈ ਡੈਮ ਦੀ ਦੀਵਾਰ ਹੇਠਾਂ ਮੋਟੀ ਅਤੇ ਉੱਪਰਲੇ ਭਾਗ ਵਿਚ ਪਤਲੀ ਬਣਾਈ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 20.
ਭਾਰੀ ਵਾਹਨਾਂ ਦੇ ਪਹੀਆਂ ਦੇ ਟਾਇਰ ਜ਼ਿਆਦਾ ਚੌੜੇ ਕਿਉਂ ਬਣਾਏ ਜਾਂਦੇ ਹਨ ?
ਉੱਤਰ-
ਭਾਰੀ ਵਾਹਨਾਂ ਦੇ ਟਾਇਰ ਚੌੜੇ ਹੋਣ ਕਾਰਨ ਖੇਤਰਫਲ A ਵੱਧ ਜਾਂਦਾ ਹੈ ਅਤੇ ਫਲਸਰੂਪ ਸੜਕ ਜਾਂ ਜ਼ਮੀਨ ਤੇ ਲੱਗਣ ਵਾਲਾ ਦਾਬ ਘੱਟ ਹੋ ਜਾਂਦਾ ਹੈ ਕਿਉਂਕਿ ਦਾਬ ਅਤੇ ਖੇਤਰਫਲ ਉਲਟੇ ਅਨੁਪਾਤੀ ਹੁੰਦੇ ਹਨ । ਇਸੇ ਲਈ ਵਾਹਨਾਂ ਦੇ ਪਹੀਏ ਘੱਟ ਦਾਬ ਕਾਰਨ ਸੜਕ ਵਿੱਚ ਧੱਸਣ ਤੋਂ ਬੱਚ ਜਾਂਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 21.
ਨਹਿਰ ਦੇ ਪਾਣੀ ਵਿੱਚ ਸਮੁੰਦਰ ਦੇ ਪਾਣੀ ਵਿੱਚ ਤਰਨ ਨਾਲੋਂ ਜ਼ਿਆਦਾ ਸੁਖਾਲਾ ਕਿਉਂ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਨਹਿਰ ਦੀ ਤੁਲਨਾ ਵਿੱਚ ਸਮੁੰਦਰ ਦੇ ਪਾਣੀ ਵਿੱਚ ਤਰਨਾ ਸੁਖਾਲਾ-ਨਹਿਰ ਦੇ ਪਾਣੀ ਦੀ ਘਣਤਾ ਸਮੁੰਦਰ (ਲੂਣ ਘੁਲਿਆ ਹੋਣ ਕਾਰਨ) ਦੇ ਪਾਣੀ ਦੀ ਘਣਤਾ ਤੋਂ ਘੱਟ ਹੁੰਦਾ ਹੈ । ਇਸ ਲਈ ਮਨੁੱਖ ਨੂੰ ਸਮੁੰਦਰ ਵਿੱਚ ਤਰਨ ਲਈ ਘੱਟ ਪਾਣੀ ਦਾ ਆਇਤਨ ਹਟਾਉਣਾ ਪਵੇਗਾ (ਅਰਥਾਤ ਸਰੀਰ ਦਾ ਘੱਟ ਭਾਗ ਪਾਣੀ ਵਿੱਚ ਡੁੱਬੇਗਾ) । ਇਸ ਲਈ ਮਨੁੱਖ ਨੂੰ ਨਹਿਰ ਦੇ ਪਾਣੀ ਦੇ ਮੁਕਾਬਲੇ ਸਮੁੰਦਰ ਦੇ ਪਾਣੀ ਵਿੱਚ ਤਰਨਾ ਸੁਖਾਲਾ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 22.
ਖੂਹ ਵਿੱਚੋਂ ਪਾਣੀ ਖਿੱਚਦੇ ਸਮੇਂ ਪਾਣੀ ਨਾਲ ਭਰੀ ਹੋਈ ਬਾਲਟੀ ਪਾਣੀ ਦੀ ਸਤਾ ਤੋਂ ਉੱਪਰ ਆਉਣ ਤੇ ਹੌਲੀਹੌਲੀ ਭਾਰੀ ਕਿਉਂ ਮਾਲੂਮ ਹੋਣ ਲਗਦੀ ਹੈ ? . ਉੱਤਰ-
ਜਦੋਂ ਬਾਲਟੀ ਪਾਣੀ ਵਿੱਚ ਡੁੱਬੀ ਹੁੰਦੀ ਹੈ ਤਾਂ ਉਸ ਦੁਆਰਾ ਹਟਾਏ ਗਏ ਪਾਣੀ ਦੇ ਭਾਰ ਦੇ ਬਰਾਬਰ ਉਛਾਲ ਬਲ ਲਗਦਾ ਹੈ ਜਿਸ ਕਰਕੇ ਬਾਲਟੀ ਅਸਲੀ ਭਾਰ ਦੇ ਮੁਕਾਬਲੇ ਘੱਟ ਭਾਰੀ ਮਾਲੂਮ ਹੁੰਦੀ ਹੈ । ਜਿਵੇਂ-ਜਿਵੇਂ ਬਾਲਟੀ ਪਾਣੀ ਤੋਂ ਬਾਹਰ ਆਉਂਦੀ ਹੈ ਉਸ ਉੱਪਰ ਲੱਗਣ ਵਾਲਾ ਉਛਾਲ-ਬਲ ਦਾ ਮਾਨ ਘੱਟ ਹੋਣ ਲਗਦਾ ਹੈ ਅਤੇ ਬਾਲਟੀ ਭਾਰੀ ਜਾਪਣ ਲਗਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 23.
ਬਰਾਬਰ ਬਲ ਦੀ ਮਾਤਰਾ ਲਗਾਉਣ ਨਾਲ ਮੋਟੇ ਨੋਕ ਵਾਲੀ ਕਿੱਲ ਦੀ ਤੁਲਨਾ ਵਿੱਚ ਬਰੀਕ ਨੋਕ ਵਾਲੀ ਕਿੱਲ ਦੀਵਾਰ ਵਿੱਚ ਛੇਤੀ ਕਿਉਂ ਖੁੱਭ ਜਾਂਦੀ ਹੈ ? .
ਉੱਤਰ-
ਬਰੀਕ ਨੋਕ ਵਾਲੀ ਕਿੱਲ ਦੇ ਸਿਰੇ ਦਾ ਖੇਤਰਫਲ, ਮੋਟੀ ਕਿੱਲ ਦੇ ਸਿਰੇ ਦੇ ਖੇਤਰਫਲ ਦੀ ਤੁਲਨਾ ਵਿੱਚ ਘੱਟ ਹੈ । ਇਸ ਲਈ ਦੋਨੋਂ ਕਿੱਲਾਂ ਇੱਕ ਸਮਾਨ ਬਲ ਲਗਾਉਣ ਤੇ ਬਰੀਕ ਨੋਕ ਵਾਲੀ (ਨੁਕੀਲੀ) ਕਿੱਲ ਮੋਟੀ ਕਿੱਲ ਦੇ ਮੁਕਾਬਲੇ ਵੱਧ ਦਾਬ ਪਾਏਗੀ ਜਿਸ ਕਰਕੇ ਉਹ ਸੌਖ ਨਾਲ ਦੀਵਾਰ ਵਿੱਚ ਧੱਸ ਜਾਏਗੀ ।

ਮਹੱਤਵਪੂਰਨ ਸੂਤਰ (Important Formulae)

1. F = G\(\frac{\mathbf{M m}}{\mathbf{R}^{2}}\)
2. F = mg
3. g = G\(\frac{\mathrm{M}}{\mathrm{R}^{2}}\)
4. υ = u + gt
5. υ² = u² + 2gh
6. h = ut + \(\frac {1}{2}\)gt²
7. ਚੰਨ ਦੀ ਸਤ੍ਹਾ ‘ਤੇ ਗੁਰੂਤਵੀ ਵੇਗ (g_m ) = \(\frac {1}{6}\) × ਧਰਤੀ ਦੀ ਸਤ੍ਹਾ ‘ਤੇ ‘g’ ਦਾ ਮੁੱਲ
ਲੋੜੀਂਦੇ ਆਂਕੜੇ
ਧਰਤੀ
ਪੁੰਜ = 6 × 10²⁴kg
ਅਰਧ-ਵਿਆਸ = 6.4 × 10⁶ m (6400 km)
ਸੂਰਜ ਤੋਂ ਦੂਰੀ = 1.5 × 10¹¹ m
ਚੰਨ
ਪੁੰਜ = 7.3 × 10²² kg

ਸੰਖਿਆਤਮਕ ਪ੍ਰਸ਼ਨ (Numerical Problems)

ਪ੍ਰਸ਼ਨ 1.
1 kg ਵਾਲੇ ਦੋ ਗੋਲਿਆਂ ਵਿਚਕਾਰ ਗੁਰੂਤਾ-ਆਕਰਸ਼ਣ ਬਲ ਦੀ ਗਣਨਾ ਕਰੋ ਜਦੋਂ ਉਨ੍ਹਾਂ ਵਿਚਕਾਰ ਦੂਰੀ 3m ਹੋਵੇ । ਗਿਆਤ ਹੈ ਕਿ G = 6.67 x 10^-11 N-m²kg²
ਹੱਲ:

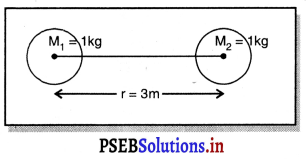
ਇੱਥੇ m₁ = m₂ = 1 kg
ਦੋਨਾਂ ਗੋਲਿਆਂ ਵਿਚਕਾਰ ਦੂਰੀ r = 3 m
ਵਿਸ਼ਵ-ਵਿਆਪੀ ਗੁਰੁਤਵੀ ਸਥਿਰ ਅੰਕ = G = 6.67 × 10^-11 N-m²/kg²
ਦੋਨਾਂ ਗੋਲਿਆਂ ਵਿਚਕਾਰ ਗੁਰੂਤਵੀ-ਆਕਰਸ਼ਣ ਬਲ, F = ?
ਨਿਊਟਨ ਦੇ ਗੁਰੂਤਾ-ਆਕਰਸ਼ਣ ਦੇ ਵਿਸ਼ਵ-ਵਿਆਪੀ ਨਿਯਮ ਅਨੁਸਾਰ,
F = \(\frac{\text { G. } m_{1} \cdot m_{2}}{r^{2}}\)
= \(\frac{6.67 \times 10^{-11} \times 1 \times 1}{3^{2}}\)
= \(\frac{6.67 \times 10^{-11}}{9}\)
= 0.741 × 10^-11 N
= 7.41 × 10^-12 ਨਿਊਟਨ

ਪ੍ਰਸ਼ਨ 2.
ਵਸਤੂ ਦੇ ਭਾਰ ਵਿੱਚ ਪ੍ਰਤਿਸ਼ਤ ਤਬਦੀਲੀ ਦੱਸੋ ਜਦੋਂ ਇਸ ਨੂੰ ਭੂ-ਮੱਧ ਰੇਖਾ ਤੋਂ ਧਰੁਵਾਂ ‘ਤੇ ਲਿਜਾਇਆ ਜਾਂਦਾ ਹੈ । ਧਰੁਵੀ ਅਰਧ-ਵਿਆਸ 6357 km ਹੈ ਅਤੇ ਭੂ-ਮੱਧ ਰੇਖੀ ਅਰਧ-ਵਿਆਸ 6378 km ਹੈ ।
ਹੱਲ:
ਧਰੁਵੀ ਅਰਧ-ਵਿਆਸ (r) = 6357 km
ਭੂ-ਮੱਧ ਰੇਖੀ ਅਰਧ-ਵਿਆਸ (R) = 6378 km
∴ h = R – r
= 6378 – 6357
h = 21 km
R = 6400 km (ਲਗਪਗ)

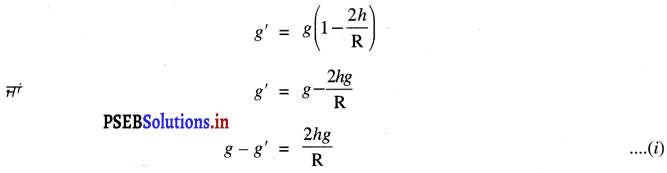
ਪ੍ਰਸ਼ਨ 3.
ਧਰਤੀ ਦੀ ਸਤ੍ਹਾ ਤੋਂ ਕਿੰਨੀ ਉੱਚਾਈ ਤੇ ਗੁਰੂਤਾ ਵੇਗ ਦਾ ਮੁੱਲ ਸਤ੍ਹਾ ਉੱਪਰਲੇ ਮੁੱਲ ਤੋਂ ਅੱਧਾ ਹੋਵੇਗਾ ? ਧਰਤੀ ਦਾ ਅਰਧ-ਵਿਆਸ ‘R’ ਮੰਨ ਲਓ ।
ਹੱਲ:
ਮੰਨ ਲਓ h ਉੱਚਾਈ ਹੈ ਜੋ ਧਰਤੀ ਦੀ ਸਤ੍ਹਾ ਤੋਂ ਉੱਪਰ ਹੈ ਜਿੱਥੇ g’ = \(\frac{g}{2}\) ਹੈ, ਤਾਂ

√2R = R + h
h = √2 R – R
∴ h = R(√2 – 1)
= R (1.414 – 1)
(∵ √2 = 1.414)
= R (0.414)
∴ h = 0.414 R

ਪ੍ਰਸ਼ਨ 4.
ਇੱਕ ਗੇਂਦ 40 ਮੀਟਰ ਉੱਚੇ ਮੀਨਾਰ ਦੇ ਸ਼ਿਖਰ ਤੋਂ ਸੁੱਟੀ ਜਾਂਦੀ ਹੈ । 20 ਮੀਟਰ ਦੂਰੀ ਤੈਅ ਕਰਨ ਉਪਰੰਤ ਇਸ ਦਾ ਵੇਗ ਕਿੰਨਾ ਹੋਵੇਗਾ ? ਧਰਤੀ ਤੇ ਟਕਰਾਉਣ ਵੇਲੇ ਇਸਦਾ ਵੇਗ ਕਿੰਨਾ ਹੋਵੇਗਾ ?
ਹੱਲ:
(i) ਇੱਥੇ, h = 40 m
u = 0
a = g = 10 m/s²
ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ S = 20 m
υ = ?
ਗਤੀ ਸਮੀਕਰਨ ਲਗਾਉਣ ਤੇ υ² – u² = 2aS
υ² – (0)² = 2 x 10 x 20
∴ υ² = 400
υ² = \(\sqrt{400}\)
= 20 m/s

(ii) υ = ?
a = g = 10 m/s²
u = 0
S = h = 40 m
υ² – u² = 2 aS
υ² – (0)² = 2 × 10 × 40
υ² = 800
υ = \(\sqrt{800}\)
= \(\sqrt{400 \times 2}\)
= \(\sqrt{400}\) × √2
= 20 × √2
∴ υ = 20√2 m/s

ਪ੍ਰਸ਼ਨ 5.
ਧਰਤੀ ਦੀ ਸਤ੍ਹਾ ਤੋਂ ਕਿੰਨੀ ਦੂਰੀ ਤੇ g ਦਾ ਮੁੱਲ ਧਰਤੀ ਦੀ ਸਤ੍ਹਾ ਦੇ ਮੁੱਲ ਦਾ 4% ਹੋ ਜਾਵੇਗਾ ? ਧਰਤੀ ਦਾ ਅਰਧ-ਵਿਆਸ = 6400 km ਦਿੱਤਾ ਹੈ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਧਰਤੀ ਦੀ ਸਤ੍ਹਾ ਤੋਂ h ਦੂਰੀ (ਉੱਚਾਈ) ਤੇ g ਦਾ ਮੁੱਲ ਧਰਤੀ ਦੀ ਸਤ੍ਹਾ ਦੇ ਮੁੱਲ ਦਾ 4% ਰਹਿ ਜਾਂਦਾ ਹੈ ।
ਤਾਂ, g’ = g ਦਾ 4%


ਜਾਂ h = 4 × R
= 4 × 6400 km
∴ h = 25600 km

ਪ੍ਰਸ਼ਨ 6.
ਜੇ ਕਿਸੇ ਵਸਤੂ ਦਾ ਭਾਰ 49 N ਹੋਵੇ, ਤਾਂ ਉਸਦਾ ਪੁੰਜ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਵਸਤੂ ਦਾ ਭਾਰ, W = 49 N
g = 9.8 ms^-2
ਭਾਰ = ਪੁੰਜ × ਗੁਰੂਤਵੀ ਵੇਗ
ਅਰਥਾਤ W = m × 8
ਜਾਂ 49 = m × 9.8
∴ m = \(\frac{49}{9.8}\) = 5 kg

ਪ੍ਰਸ਼ਨ 7.
ਕਿਸੇ ਪੱਥਰ ਨੂੰ ਛੱਤ ਦੇ ਕਿਨਾਰੇ ਤੋਂ ਹੇਠਾਂ ਸੁੱਟਿਆ ਗਿਆ ਹੈ । ਜੇ ਉਹ 2 m ਉੱਚੀ ਖਿੜਕੀ ਨੂੰ 0.1 s ਵਿੱਚ ਪਾਰ ਕਰੇ, ਤਾਂ ਖਿੜਕੀ ਦੇ ਉੱਪਰੀ ਕਿਨਾਰੇ ਤੋਂ ਛੱਤ ਕਿੰਨੀ ਉੱਪਰ ਹੈ ?
ਹੱਲ:

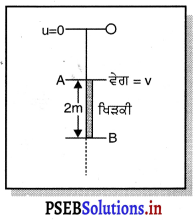
ਖਿੜਕੀ ਪਾਰ ਕਰਨ ਵਿੱਚ ਤੈਅ ਹੋਈ ਦੁਰੀ S = 2 m
g = 9.8 m/s² ; t = 0.1 s.
ਹੁਣ ਜਦੋਂ ਪੱਥਰ ਖਿੜਕੀ ਦੇ ਉੱਪਰੀ ਕਿਨਾਰੇ ਤਕ ਪੁੱਜਦਾ ਹੈ, ਤਾਂ ਉਸ ਦਾ ਵੇਗ υ ਹੈ ।
ਹੁਣ S = ut + \(\frac {1}{2}\)gt²
2 = υ × 0.1+ \(\frac {1}{2}\) × 9.8 × (0.1)²
2 = 0.1 υ + 0.049
0.1 υ = 1.951
υ = 1951 × 10
= 19.51 ms^-1
ਆਰੰਭਿਕ ਵੇਗ u = 0
ਇਹ ਵੇਗ ਪੱਥ OA ਦੇ ਲਈ ਅੰਤਿਮ ਵੇਗ ਹੈ ।
ਇਸ ਲਈ υ² – u² = 2gS
(19.51)² – (0)² = 2 × 9.8 × S
S = \(\frac{19.51 \times 19.51}{2 \times 9.8}\)
= 19.41 m

ਪ੍ਰਸ਼ਨ 8.
70kg ਪੁੰਜ ਦੇ ਕਿਸੇ ਮਨੁੱਖ ਦਾ ਚੰਦਰਮਾ ਤੇ ਭਾਰ ਕੀ ਹੋਵੇਗਾ ? ਉਸ ਦਾ ਧਰਤੀ ਅਤੇ ਚੰਦਰਮਾ ‘ਤੇ ਪੁੰਜ ਕੀ ਹੋਵੇਗਾ ?
ਹੱਲ:
ਪੁੰਜ ਇੱਕ ਸਥਿਰ ਰਾਸ਼ੀ ਹੈ, ਇਸ ਲਈ ਮਨੁੱਖ ਦਾ ਪੁੰਜ ਧਰਤੀ ਅਤੇ ਚੰਦਰਮਾ ‘ਤੇ ਬਰਾਬਰ ਹੋਵੇਗਾ
ਮਨੁੱਖ ਦਾ ਧਰਤੀ ‘ਤੇ ਪੁੱਜ = 70kg
∴ ਮਨੁੱਖ ਦਾ ਚੰਦਰਮਾ ‘ਤੇ ਪੰਜ = 70kg
ਮਨੁੱਖ ਦਾ ਧਰਤੀ ਤੇ ਭਾਰ (W₁) = ?
ਧਰਤੀ ਤੇ ਗੁਰੂਤਵੀ ਵੇਗ g = 9.8 m/s²
ਮਨੁੱਖ ਦਾ ਚੰਦਰਮਾ ’ਤੇ ਭਾਰ (W₂) = ?
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ (w) = mg
ਮਨੁੱਖ ਦਾ ਧਰਤੀ ਤੇ ਭਾਰ (W₁) = 70 × 9.8 = 686 N
ਹੁਣ ਮਨੁੱਖ ਦਾ ਚੰਦਰਮਾ ‘ਤੇ ਭਾਰ (W₂) = \(\frac {1}{6}\) × ਮਨੁੱਖ ਦਾ ਧਰਤੀ ‘ਤੇ ਭਾਰ
= \(\frac{\mathrm{W}_{1}}{6}\)
= \(\frac{686 \mathrm{~N}}{6}\)
= 114.33 N

ਪ੍ਰਸ਼ਨ 9.
ਇੱਕ ਵਿਅਕਤੀ ਦਾ ਧਰਤੀ ਤੇ ਭਾਰ 600 N ਹੈ । ਚੰਦਰਮਾ ਦੇ ਗੁਰੂਤਵੀ ਵੇਗ, ਧਰਤੀ ਦੇ ਗੁਰੂਤਵੀ ਵੇਗ ਦਾ \(\frac {1}{6}\) ਹੈ । ਜੇ ਧਰਤੀ ‘ਤੇ ਗੁਰੂਤਵੀ ਵੇਗ 10 m/s² ਹੈ ਤਾਂ ਚੰਦਰਮਾ ‘ ਤੇ ਵਿਅਕਤੀ ਦਾ ਪੁੰਜ ਤੇ ਭਾਰ ਪਤਾ ਕਰੋ ?
ਹੱਲ:
ਧਰਤੀ ‘ਤੇ ਵਿਅਕਤੀ ਦਾ ਪੁੰਜ = ਆ
g = 10 m/s²
w = mg = 600 N
m = \(\frac{600}{g}\)
= \(\frac{600}{10}\) = 60kg
ਚੰਦਰਮਾ ‘ਤੇ ਵੀ ਪੁੰਜ = 60 kg (∵ਪੁੰਜ ਸਥਿਰ ਹੈ)
ਚੰਦਰਮਾ ‘ਤੇ ਭਾਰ = \(\frac {1}{6}\) × mg
= \(\frac{m g}{6}\)
= \(\frac {1}{6}\)(600)
= 100 N

ਪ੍ਰਸ਼ਨ 10.
ਕਿਸੇ ਉੱਭਰੀ ਹੋਈ ਚੱਟਾਨ (ਕਿੰਗਰੇ) ਤੋਂ ਇਕ ਕਾਰ 0.5 sec ਵਿੱਚ ਧਰਤੀ ‘ਤੇ ਡਿੱਗਦੀ ਹੈ । ਮਨ ਲਓ g = 10 m/s² (ਗਣਨਾ ਨੂੰ ਸੌਖਾ ਕਰਨ ਲਈ) ।
(ਕ) ਧਰਤੀ ਨਾਲ ਟਕਰਾਉਂਦੇ ਹੋਏ ਕਾਰ ਦੀ ਚਾਲ ਕੀ ਹੋਵੇਗੀ ?
(ਖ) 0.5 s ਦੌਰਾਨ ਇਸਦੀ ਔਸਤ ਚਾਲ ਕੀ ਹੋਵੇਗੀ ?
(ਗ) ਧਰਤੀ ਤੋਂ ਕਿੰਗਰੇ ਕਿੰਨੀ ਉੱਚਾਈ ‘ਤੇ ਹੈ ?
ਹੱਲ:
ਸਮਾਂ t = 0.5 s.
ਮੁੱਢਲਾ ਵੇਗ u = 0 m/s
ਗੁਰੂਤਾ ਵੇਗ g = 10 m/s²
ਕਾਰ ਦਾ ਵੇਗ a = + 10 m/s² (ਥੱਲੇ ਵੱਲ)

(ਕ) ਚਾਲ V = u + at
= 0 + 10 m/s² × 0.5 s
= 5 m/s

(ਖ) ਔਸਤ ਚਾਲ = \(\frac{\mathrm{V}+u}{2}\)
= \(\frac{(0 \mathrm{~m} / \mathrm{s}+5 \mathrm{~m} / \mathrm{s})}{2}\)
= 2.5 m/s

(ਗ) ਤੈਅ ਕੀਤੀ ਦੂਰੀ
S = ut + \(\frac {1}{2}\)at²
= 0 × 0.5 s + \(\frac {1}{2}\) × 10 ms² × (0.5)²
= \(\frac {1}{2}\) × 10 m/s² × 0.25²
= 1.25 m
ਇਸ ਲਈ, S = 1.25 m

(i) ਧਰਤੀ ਨਾਲ ਟਕਰਾਉਂਦੇ ਸਮੇਂ ਕਾਰ ਦੀ ਚਾਲ = 5 m/s
(ii) 0.5 s ਦੌਰਾਨ ਇਸਦੀ ਔਸਤ ਚਾਲ = 2.5 m/s
(iii) ਧਰਤੀ ਤੋਂ ਕਿੰਗਰੇ (ਚੱਟਾਨ) ਦੀ ਉੱਚਾਈ = 1.25 m

ਪ੍ਰਸ਼ਨ 11.
ਇਕ ਵਸਤੂ ਨੂੰ ਸਿੱਧਾ ਉੱਪਰ ਵੱਲ ਸੁੱਟਿਆ ਜਾਂਦਾ ਹੈ ਅਤੇ ਉਹ 10 m ਦੀ ਉੱਚਾਈ ਤੱਕ ਜਾਂਦੀ ਹੈ । ਪਤਾ ਕਰੋ
(i) ਵੇਗ ਜਿਸ ਨਾਲ ਵਸਤੂ ਨੂੰ ਉੱਪਰ ਵੱਲ ਸੁੱਟਿਆ ਗਿਆ
(ii) ਵਸਤੂ ਦੁਆਰਾ ਉੱਚਤਮ ਬਿੰਦੂ ਤੱਕ ਪਹੁੰਚਣ ਵਿੱਚ ਲੱਗਿਆ ਸਮਾਂ ।
ਹੱਲ:
ਤੈਅ ਕੀਤੀ ਦੂਰੀ S = 10 m
ਅੰਤਿਮ ਵੇਗ V = 0 ms
ਗੁਰੂਤਾ ਵੇਗ g = 9.8 m/s²
ਵਸਤੂ ਦਾ ਪ੍ਰਵੇਗ a = – 9.8 m/s²(ਸਿੱਧਾ ਉੱਪਰ ਵੱਲ)

(i) v² = u² – 2aS
0 = u² – 2 × 9.8 m/s² × 10 m
– u = – 2 × 9.8 × 10 m/s.
u = \(\sqrt{196}\) ms^-1
u = 14 ms^-1

(ii) v = u + at
0 = 14 m/s – 9.8 m/s² × t
9.8 × t = 14
∴ t = \(\frac{14 \mathrm{~m} / \mathrm{s}}{9.8 \mathrm{~m} / \mathrm{s}^{2}}\)
= 1.43 s

ਪ੍ਰਸ਼ਨ 12.
ਧਰਤੀ ਦੀ ਸਤ੍ਹਾ ‘ਤੇ ਕਿਸੇ ਵਸਤੂ ਦਾ ਭਾਰ ਮਾਪਣ ਤੇ 10 N ਹੈ । ਚੰਨ ਦੀ ਸਤ੍ਹਾ ‘ਤੇ ਮਾਪਣ ਤੇ ਉਸਦਾ ਭਾਰ ਕਿੰਨਾ ਹੋਵੇਗਾ ?
ਹੱਲ:
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ
ਚੰਨ ‘ਤੇ ਵਸਤੂ ਦਾ ਭਾਰ (W_m) = 1/6 × ਧਰਤੀ ‘ਤੇ ਉਸਦਾ ਭਾਰ (W_e).
ਜਾਂ W_m = \(\frac {1}{6}\) × W_e
= \(\frac {1}{6}\) × 10
= 1.67 N
ਇਸ ਲਈ ਚੰਨ ਦੀ ਸਤ੍ਹਾ ਤੇ ਵਸਤੂ ਦਾ ਭਾਰ ਹੋਵੇਗਾ = 1.67 N

ਪ੍ਰਸ਼ਨ 13.
ਪਾਣੀ ਵਿੱਚ ਤੈਰਦੇ ਸਮੇਂ ਠੋਸ ਵਸਤੂ ਦਾ \(\frac {4}{5}\) ਭਾਗ ਡੁੱਬਿਆ ਰਹਿੰਦਾ ਹੈ | ਵਸਤੂ ਦੀ ਘਣਤਾ ਗਿਆਤ ਕਰੋ । ਪਾਣੀ ਦੀ ਘਣਤਾ = 1000 kg/m³)
ਹੱਲ:
ਮੰਨ ਲਓ ਠੋਸ ਵਸਤੂ ਦਾ ਆਇਤਨ V ਅਤੇ ਘਣਤਾ d kg/m ਹੈ ।

∴ ਠੋਸ ਵਸਤੂ ਦੀ ਘਣਤਾ (d) = \(\frac {4}{5}\) × 1000
= 800 kg/m³

ਪ੍ਰਸ਼ਨ 14.
ਪਾਣੀ ਵਿੱਚ ਕਿਸੇ ਵਸਤੂ ਦੇ ਕੁੱਲ ਆਇਤਨ ਦਾ \(\frac {4}{5}\) ਭਾਗ ਡੁੱਬ ਜਾਂਦਾ ਹੈ । ਜੇਕਰ ਉਸੇ ਵਸਤੂ ਨੂੰ 1.6 ਸਾਪੇਖ ਘਣਤਾ ਵਾਲੇ ਤਰਲ ਵਿੱਚ ਤਰਾਇਆ ਜਾਵੇ, ਤਾਂ ਵਸਤੂ ਦਾ ਕਿੰਨਾ ਭਾਗ ਡੁੱਬੇਗਾ ?
ਹੱਲ:
ਮੰਨ ਲਓ ਵਸਤੂ ਦਾ ਆਇਤਨ V ਅਤੇ ਉਸ ਦੀ ਘਣਤਾ d ਹੈ । ਪਾਣੀ ਵਿੱਚ ਤਰਾਉਣ ਸਮੇਂ ਵਸਤੂ ਦੁਆਰਾ ਹਟਾਏ ਵਿਸਥਾਪਿਤ ਕੀਤੇ) ਪਾਣੀ ਦਾ ਭਾਰ = ਵਸਤੂ ਦਾ ਹਵਾ ਵਿੱਚ ਭਾਰ
\(\frac {4}{5}\) V × 1 × g = V × d × g …………… (1)
ਮੰਨ ਲਓ ਤਰਲ ਵਿੱਚ ਵਸਤੂ ਦੇ ਕੁੱਲ ਆਇਤਨ ਦਾ 1 ਭਾਗ ਡੁੱਬ ਜਾਂਦਾ ਹੈ
∴ ਵਸਤੂ ਦੁਆਰਾ ਹਟਾਏ ਗਏ ਤਰਲ ਦਾ ਭਾਰ = ਵਸਤੂ ਦਾ ਹਵਾ ਵਿਚ ਭਾਰ
x V × 1.6 × g = V × d × 8 …………….. (2)
ਸਮੀਕਰਨ (1) ਅਤੇ (2) ਤੋਂ,
\(\frac {4}{5}\) V × 1 × g = x × V × 1.6 × g
ਜਾਂ x = \(\frac{4}{5 \times 1.6}\)
= \(\frac {1}{2}\)
ਇਸ ਲਈ ਵਸਤੂ ਦੇ ਆਇਤਨ ਦਾ ਅੱਧਾ (\(\frac {1}{2}\)) ਭਾਗ ਤਰਲ ਵਿੱਚ ਡੁੱਬੇਗਾ ।

ਪ੍ਰਸ਼ਨ 15.
ਲੱਕੜ ਦੇ ਟੁਕੜੇ ਦਾ ਕੁੱਲ ਭਾਰ 6 kg ਹੈ । ਪਾਣੀ ਵਿੱਚ ਤੈਰਦੇ ਸਮੇਂ ਇਭਾਗ \(\frac {1}{3}\) ਪਾਣੀ ਦੇ ਅੰਦਰ ਰਹਿੰਦਾ ਹੈ । ਇਸ ਟੁਕੜੇ ‘ਤੇ ਕਿੰਨਾ ਭਾਰ ਰੱਖੀਏ ਤਾਂ ਜੋ ਇਹ ਪੂਰਾ ਪਾਣੀ ਅੰਦਰ ਰਹਿ ਕੇ ਤੈਰਦਾ ਰਹੇ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਲੱਕੜ ਦੇ ਟੁਕੜੇ ਉੱਪਰ W ਭਾਰ ਰੱਖਣ ਨਾਲ ਇਹ ਪੂਰਾ ਪਾਣੀ ਦੇ ਅੰਦਰ ਡੁੱਬ ਕੇ ਤੈਰੇਗਾ ।
ਮੰਨ ਲਓ ਇਸ ਦਾ ਆਇਤਨ V ਹੈ ਕਿਉਂਕਿ ਤੈਰਦੇ ਸਮੇਂ ਟੁਕੜੇ ਦੇ ਆਇਤਨ \(\frac {1}{3}\) ਦਾ ਭਾਗ ਪਾਣੀ ਦੇ ਅੰਦਰ ਰਹਿੰਦਾ ਹੈ, ਇਸ ਲਈ,
ਟੁਕੜੇ ਦਾ ਭਾਰ ਵਿਸਥਾਪਿਤ ਪਾਣੀ ਦਾ ਭਾਰ,
6 = \(\frac {1}{3}\) V × d × g ………….. (1)
ਵਾਧੂ , ਭਾਰ W ਰੱਖ ਦੇਣ ਮਗਰੋਂ ਲੱਕੜੀ ਦਾ ਟੁਕੜਾ ਪੂਰੀ ਤਰ੍ਹਾਂ ਡੁੱਬ ਜਾਂਦਾ ਹੈ
∴ 6 + W = V × d × g …………….. (2)
ਸਮੀਕਰਨ (2) ਨੂੰ (2) ਨਾਲ ਭਾਗ ਦੇਣ ਤੇ ।
\(\frac{6+W}{6}=\frac{3}{1}\)
ਜਾਂ 6 + W = 18
∴ ਲੱਕੜ ਦੇ ਟੁਕੜੇ ਦਾ ਭਾਰ W = 18 – 6
= 12 kg

ਪ੍ਰਸ਼ਨ 16.
ਇੱਕ ਹੈਲੀਕਾਪਟਰ ਨੂੰ ਕਿਸੇ ਕਿਸ਼ਤੀ ਵਿੱਚ ਫਾਂਸੀਆਂ ਹੋਈਆਂ ਸਵਾਰੀਆਂ ਲਈ ਭੋਜਨ ਦੇ ਪੈਕਟ ਸੁੱਟਣ ਲਈ ਭੇਜਿਆ ਗਿਆ । ਇਹ 20 m ਦੀ ਉੱਚਾਈ ਤੇ 2 m/s ਦੇ ਇਕ ਸਮਾਨ ਖਿਤਿਜ ਵੇਗ ਨਾਲ ਉੱਡ ਰਿਹਾ ਹੈ ਜਦੋਂ ਕਿਸ਼ਤੀ ਦਾ ਨੇੜਲਾ ਸਿਰਾ ਹੈਲੀਕਾਪਟਰ ਦੇ ਠੀਕ ਹੇਠਾਂ ਹੈ, ਤਾਂ ਉਸ ਸਮੇਂ ਪੈਕਟ ਸੁੱਟੇ ਗਏ । ਜੇਕਰ ਕਿਸ਼ਤੀ 5 m ਲੰਮੀ ਹੈ, ਤਾਂ ਕੀ ਕਿਸ਼ਤੀ ਵਿੱਚ ਬੈਠੀਆਂ ਹੋਈਆਂ ਸਵਾਰੀਆਂ ਨੂੰ ਪੈਕਟ ਮਿਲ ਜਾਣਗੇ ।
ਹੱਲ:
ਇੱਥੇ h = 20 m, u = 2 m/s g = 10 ms^-2
ਉੱਚਾਈ ਵਾਲਾ ਰੇਂਜ, R = 2\(\sqrt{\frac{2 h}{g}}\)
= 2\(\sqrt{\frac{2 \times 20}{10}}\)
= 2√4
= 4 m
ਕਿਸ਼ਤੀ ਦੀ ਲੰਬਾਈ = 5 m
ਇਸ ਲਈ ਕਿਸ਼ਤੀ ਵਿੱਚ ਬੈਠੀਆਂ ਸਵਾਰੀਆਂ ਨੂੰ ਪੈਕਟ ਮਿਲ ਜਾਣਗੇ ।

ਬਹੁਤ ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Very Short Answer Type Questions)

ਪ੍ਰਸ਼ਨ 1.
ਸੂਰਜੀ ਮੰਡਲ ਵਿੱਚ ਗ੍ਰਹਿਆਂ ਦੀ ਸੂਰਜ ਦੁਆਲੇ ਬੇਰੋਕ ਘੁੰਮਣ ਗਤੀ ਕਿਸ ਕਾਰਨ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਉਨ੍ਹਾਂ ਵਿਚਕਾਰ ਪਰਸਪਰ ਗੁਰੂਤਵੀ ਆਕਰਸ਼ਣ ਬਲ ਕਾਰਨ ।

ਪ੍ਰਸ਼ਨ 2.
ਚੰਦਰਮਾ ਦਾ ਧਰਤੀ ਦੁਆਲੇ ਗਤੀ ਦੇ ਪੱਥ ਦਾ ਆਕਾਰ ਕਿਸ ਸ਼ਕਲ ਦਾ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਇਲਿਪਸੀ ਜਾਂ ਅੰਡਾਕਾਰ ਸ਼ਕਲ ਦਾ ।

ਪ੍ਰਸ਼ਨ 3.
ਦੋ ਵਸਤੂਆਂ ਵਿਚਾਲੇ ਲਗ ਰਹੇ ਆਪਸੀ ਆਕਰਸ਼ਣ ਬਲ ਨੂੰ ਗਣਿਤਿਕ ਰੂਪ ਵਿੱਚ ਲਿਖੋ । .
ਉੱਤਰ-
F = G.\(\frac{m_{1} \times m_{2}}{r^{2}}\)

ਪ੍ਰਸ਼ਨ 4.
G ਦਾ ਸੰਖਿਅਕ ਮੁੱਲ ਕਿੰਨਾ ਹੈ ?
ਉੱਤਰ-
G = 6.67 x 10^-11 N-m² kg²

ਪ੍ਰਸ਼ਨ 5.
ਇੱਕ ਬੈਂਚ ‘ਤੇ ਬੈਠੇ ਦੋ ਵਿਦਿਆਰਥੀਆਂ ਵਿਚਕਾਰ ਪਰਸਪਰ ਗੁਰੂਤਵੀ-ਆਕਰਸ਼ਣ ਬਲ ਲਗਦਾ ਹੈ ਪਰ ਦੋਨੋਂ ਵਿਦਿਆਰਥੀ ਇਸ ਬਲ ਨੂੰ ਅਨੁਭਵ ਨਹੀਂ ਕਰਦੇ, ਕਿਉਂ ?
ਉੱਤਰ-
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ ਗੁਰੂਤਾ-ਆਕਰਸ਼ਣ ਬਲ F = G. \(\frac{m_{1} \times m_{2}}{r^{2}}\) ਇੱਥੇ G ਦਾ ਮੁੱਲ ਬਹੁਤ ਘੱਟ ਹੁੰਦਾ ਹੈ। ਜਿਸ ਕਰਕੇ ਇਹ ਬਲ ਬਹੁਤ ਘੱਟ ਹੁੰਦਾ ਹੈ ਅਤੇ ਅਨੁਭਵ ਨਹੀਂ ਕੀਤਾ ਜਾਂਦਾ ।

ਪ੍ਰਸ਼ਨ 6.
ਧਰਤੀ ਦੀ ਸਤ੍ਹਾ ਤੇ ‘g’ ਦਾ ਮੁੱਲ ਕਿੰਨਾ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਧਰਤੀ ਦੀ ਸਤ੍ਹਾ ਤੇ g ਦਾ ਮੁੱਲ ਅਧਿਕਤਮ ਹੁੰਦਾ ਹੈ ਅਤੇ 8 = 9.81 m/s²

ਪ੍ਰਸ਼ਨ 7.
ਕੀ ‘g’ ਦਾ ਮੁੱਲ ਰਿਣਾਤਮਕ ਹੋ ਸਕਦਾ ਹੈ । ਕਦੋਂ ?
ਉੱਤਰ-
ਜਦੋਂ ਵਸਤੂ ਨੂੰ ਉੱਪਰ ਵੱਲ ਸੁੱਟਿਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ g ਦਾ ਮੁੱਲ ਘੱਟਦਾ ਹੈ । ਇਸ ਲਈ 8 ਨੂੰ ਰਿਣਾਤਮਕ ਲਿਆ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਪ੍ਰੋਜੈਕਟਾਈਲ ਦਾ ਗਤੀ ਪੱਥ ਕਿਹੋ ਜਿਹਾ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਪੈਰਾਬੋਲਿਕ ਪੱਥ ।

ਪ੍ਰਸ਼ਨ 9.
ਕਿਸੇ ਵਸਤੂ ਵਿੱਚ ਮੌਜੂਦ ਪਦਾਰਥ ਦੀ ਮਾਤਰਾ ਨੂੰ ਕੀ ਕਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਪੁੰਜ ।

ਪ੍ਰਸ਼ਨ 10.
ਪੁੰਜ ਨੂੰ ਮਾਪਣ ਵਾਲੀ SI ਇਕਾਈ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਕਿਲੋਗ੍ਰਾਮ ।

ਪ੍ਰਸ਼ਨ 11.
ਧਰਤੀ ਦੇ ਕਿਸ ਹਿੱਸੇ ਵਿੱਚ ਭਾਰ ਜ਼ੀਰੋ ਹੋ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਧਰਤੀ ਦੇ ਕੇਂਦਰ ‘ਤੇ ।

ਪ੍ਰਸ਼ਨ 12.
ਪੁੰਜ ਅਤੇ ਭਾਰ ਵਿਚੋਂ ਕਿਹੜੀ ਰਾਸ਼ੀ ਸਕੇਲਰ ਹੈ ?
ਉੱਤਰ-
ਪੰਜ ।

ਪ੍ਰਸ਼ਨ 13.
ਭਾਰ ਦੀ SI ਇਕਾਈ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਨਿਊਟਨ (N) ।

ਪ੍ਰਸ਼ਨ 14.
ਭਾਰ ਕਿਹੋ ਜਿਹੀ ਰਾਸ਼ੀ ਹੈ ? ਸਕੇਲਰ ਜਾਂ ਵੈਕਟਰ ?
ਉੱਤਰ-
ਭਾਰ ਇੱਕ ਕਿਸਮ ਦਾ ਬਲ ਹੈ, ਇਸ ਲਈ ਇਹ ਵੈਕਟਰ ਹੈ ।

ਪ੍ਰਸ਼ਨ 15.
ਜੇਕਰ ਕਿਸੇ ਵਸਤੂ ਦਾ ਧਰਤੀ ‘ਤੇ ਪੁੱਜ 30 ਕਿ. ਗ੍ਰਾਮ ਹੈ, ਤਾਂ ਦੱਸੋ ਚੰਦਰਮਾ ਦੀ ਸਤ੍ਹਾ ‘ਤੇ ਇਸ ਦਾ ਪੁੰਜ ਕਿੰਨਾ ਹੋਵੇਗਾ ?
ਉੱਤਰ-
ਪੰਜ ਇੱਕ ਸਥਿਰ ਰਾਸ਼ੀ ਹੈ । ਇਸ ਲਈ ਵਸਤੂ ਦਾ ਚੰਦਰਮਾ ਉੱਤੇ ਪੁੱਜ ਓਨਾ ਹੀ ਹੋਵੇਗਾ, ਜਿੰਨਾ ਉਸ ਦਾ ਪੁੰਜ ਧਰਤੀ ਉੱਪਰ ਹੈ ਅਰਥਾਤ 30 ਕਿ. ਗ੍ਰਾਮ ।

ਪ੍ਰਸ਼ਨ 16.
ਧਰਤੀ ਦੇ ਕੇਂਦਰ ’ ਤੇ ‘g’ ਦਾ ਮੁੱਲ ਕਿੰਨਾ ਹੋਵੇਗਾ ?
ਉੱਤਰ-
ਧਰਤੀ ਦੇ ਕੇਂਦਰ ‘ਤੇ G = 0

ਪ੍ਰਸ਼ਨ 17.
ਦੱਸੋ ਕਿਸੇ ਵਸਤੂ ਦਾ ਭਾਰ ਕਿੱਥੇ ਜ਼ਿਆਦਾ ਹੋਵੇਗਾ – ਧਰੁਵਾਂ ‘ਤੇ ਜਾਂ ਭੂ-ਮੱਧ ਰੇਖਾ ‘ਤੇ ?
ਉੱਤਰ-
ਧਰੁਵਾਂ ‘ਤੇ ।

ਪ੍ਰਸ਼ਨ 18.
ਦੋ ਵਸਤੂਆਂ ਵਿਚਕਾਰ ਦੂਰੀ ਤਿੰਨ ਗੁਣਾ ਕਰਨ ਤੇ ਗੁਰੂਤਵੀ ਆਕਰਸ਼ਣ ਬਲ ’ਤੇ ਕੀ ਪ੍ਰਭਾਵ ਪਵੇਗਾ ?
ਉੱਤਰ-
ਪਹਿਲਾਂ ਨਾਲੋਂ \(\frac {1}{9}\) ਵੀ ਭਾਗ ਰਹਿ ਜਾਵੇਗਾ ।