PSEB 9th Class Science Important Questions Chapter 11 कार्य तथा ऊर्जा

Punjab State Board PSEB 9th Class Science Important Questions Chapter 11 कार्य तथा ऊर्जा Important Questions and Answers.

PSEB 9th Class Science Important Questions Chapter 11 कार्य तथा ऊर्जा

दीर्घ उत्तरात्मक प्रश्न (Long Answer Type Questions)

प्रश्न 1.
स्थितिज ऊर्जा किसे कहते हैं ? स्थितिज ऊर्जा के लिए गणितीय सूत्र स्थापित करो तथा इस ऊर्जा की व्यावहारिक उदाहरणें भी दो।
उत्तर-
स्थितिज ऊर्जा (Potential Energy) – ” यह किसी वस्तु में उसके आकार या उसकी पृथ्वी की सतह से ऊपर या नीचे स्थिति के कारण धारण की हुई ऊर्जा होती है।”

गणितीय सूत्र – मान लो ‘m’ द्रव्यमान वाला पत्थर पृथ्वी की सतह से ऊँचाई ‘h’ तक ऊपर तक उठाया जाता है। ऐसा करने के लिए पृथ्वी के गुरुत्व के विरुद्ध पत्थर पर कार्य करना पड़ता है।
∴ किया गया कार्य = बल × ऊँचाई
W = F × h
परंतु F, = पत्थर का भार = mg
पत्थर पर किया गया यह कार्य उस पत्थर में स्थितिज ऊर्जा (P. E.) के रूप में स्टोर हो जाता है।
∴ स्थितिज ऊर्जा (P.E.) = mgh
इस समीकरण से स्पष्ट है कि जितनी अधिक ऊँचाई होगी उतनी ही अधिक पत्थर में स्थितिज ऊर्जा स्टोर होगी।

व्यावहारिक उदाहरणें-
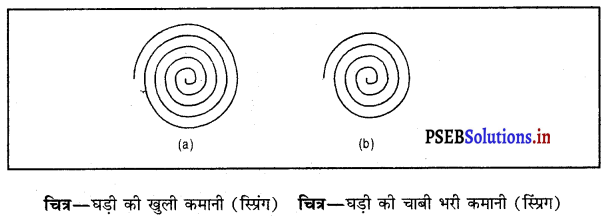
(i) पुराने जमाने की घड़ियां डिजिटल नहीं होती थीं और उन्हें चलाने के लिए चाबी भरनी पड़ती थी। जब इसकी कमानी पूरी तरह खुली होती है तो घड़ी नहीं चलती। परंतु जब हम इसकी कमानी की चाबी भरते हैं, तो हम कुछ कार्य करते हैं।

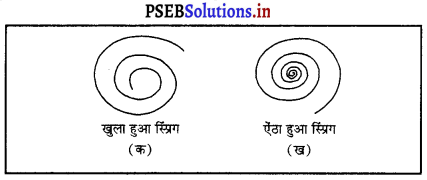
चित्र (ख) में दिखाए अनुसार चाबी घुमाने से कमानी सिकुड़ती जाती है जिस कारण इसमें स्थितिज ऊर्जा स्टोर होती जाती है। स्टोर की हुई यह स्थितिज ऊर्जा घड़ी की सुइयों को डायल पर चलाने में सहायता करती है।

(ii) अपने दोनों हाथों से एक कमानी को खोलने की कोशिश करो। आपके हाथों द्वारा कार्य हो रहा है। ऐसा करने से कसी हुई कमानी की लंबाई बढ़ती है तथा इस तरह इसमें स्थितिज ऊर्जा स्टोर हो जाती है।

प्रश्न 2.
गतिज ऊर्जा किसे कहते हैं ? गतिज ऊर्जा के लिए गणितीय सूत्र स्थापित करो तथा इस ऊर्जा की व्यावहारिक उदाहरणें भी दो।
उत्तर-
गतिज ऊर्जा (Kinetic Energy) – “किसी वस्तु में किसी भी प्रकार की गति के कारण उत्पन्न ऊर्जा गतिज ऊर्जा कहलाती है।” यदि वस्तु गतिशील नहीं है तो इसमें गतिज ऊर्जा नहीं है।

गणितीय सूत्र-मान लो ‘m’ द्रव्यमान वाली एक फुटबाल जो विराम अवस्था में है, पर बल F लगाया जाता है। इस बल के कारण फुटबाल ‘t’ समय में S दूरी तय करता हुआ वेग v प्राप्त कर लेता है। इसलिए इसमें प्रवेग ‘a’ उत्पन्न होता है।

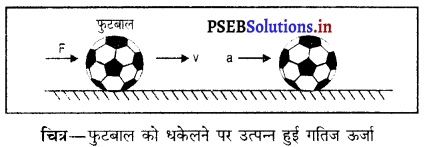
फुटबाल पर किया गया कार्य W = F × S …………… (1)
न्यूटन की गति के दूसरे नियम अनुसार, F = m × a ……………… (2)
हम जानते हैं गति का एक रेखीय समीकरण
S = ut + \(\frac {1}{2}\)at² …………….. (3)
तथा v = u + at ……………. (4)
फुटबाल विराम अवस्था से चली है;
u = 0
अब (3) तथा (4) समीकरणों में u = 0 भरने पर
S = \(\frac {1}{2}\)at² ………………. (5)
तथा v = at …………… (6)
सभीकरण (1) में समीकरण (2), (5) तथा (6) का मान रखने पर
W = (m . a)(\(\frac {1}{2}\)at²)
W = \(\frac {1}{2}\)ma²t²
W = \(\frac {1}{2}\) m at² ………….. (7)
समीकरण (6) को (7) में भरने से
W = \(\frac {1}{2}\)mv² ……………. (8)
समीकरण (8) सिद्ध करती है कि फुटबाल पर किया गया कार्य उसके अंदर गतिज रूप में स्टोर हो जाता है।
∴ किया गया कार्य = स्टोर की गई गतिज ऊर्जा = \(\frac {1}{2}\)mv²
गतिज ऊर्जा की इकाई जूल (J) है।
समीकरण (8) से यह सिद्ध हो गया है कि गतिशील वस्तु की गतिज ऊर्जा-
(i) वस्तु के पुंज के समानुपाती होती है अर्थात् भारी वस्तुओं में हल्की वस्तुओं की अपेक्षा अधिक गतिज ऊर्जा होती है।
(ii) वस्तु के वेग के वर्ग के समानुपाती होती है अर्थात् जितनी वस्तु की चाल अधिक होगी उतनी ही अधिक उस वस्तु की गतिज ऊर्जा होगी।

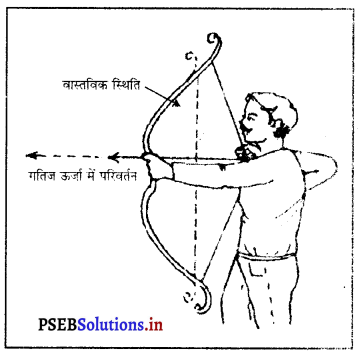
उदाहरण – आओ एक तीर तथा कमान के बारे में विचार करो। साधारण अवस्था में तीर तथा कमान में कोई भी ऊर्जा नहीं होती। जब हम तीर को कमान में रखते हैं तो हम उस पर कार्य करते हैं। यह कार्य तीर-कमान प्रणाली में स्थितिज ऊर्जा के रूप में स्टोर हो जाता है। अब जब तीर को कमान से छोड़ा जाता है तो स्टोर की गई स्थितिज ऊर्जा, गतिज ऊर्जा में बदल जाती है।

प्रश्न 3.
ऊर्जा संरक्षण नियम क्या है ? एक उदाहरण के साथ इस नियम की व्याख्या करो तथा इस वास्तविकता को सिद्ध करो।
उत्तर-
ऊर्जा संरक्षण नियम – इस नियम के अनुसार ऊर्जा की मात्रा सदैव ही अचर रहती है अर्थात् कुल ऊस सदैव उतनी ही रहती है। यद्यपि ऊर्जा के एक रूप को दूसरे रूप में परिवर्तित किया जा सकता है. इसकी मात्रा नहीं बदला जा सकता।

उदाहरण सहित व्याख्या – पृथ्वी की सतह से गेंद को ऊपर की ओर | अधिकतम गतिज ऊर्जा फेंको। आप गेंद पर कार्य करते हो। यह कार्य गेंद में स्थितिज ऊर्जा के रूप में स्टोर हो जाता है। इसे गुरुत्वीय स्थितिज ऊर्जा भी कहते हैं। गेंद ज्योंज्यों ऊपर की ओर जाती है, यह दूरी तय करती है, परंतु कम वेग के साथ। इस तरह स्थितिज ऊर्जा बढ़ती जाती है तथा गतिज ऊर्जा कम होती जाती है। गेंद द्वारा उच्चतम ऊँचाई तक पहुँच कर इसकी स्थितिज ऊर्जा अधिकतम तथा गतिज ऊर्जा न्यूनतम (शून्य) हो जाती है। हम गणितीय रूप से सिद्ध कर सकते हैं कि गेंद की गति के पथ पर किसी भी बिंदु पर इसकी स्थितिज तथा गतिज ऊर्जा का कुल जोड़ हमेशा स्थिर रहता है।

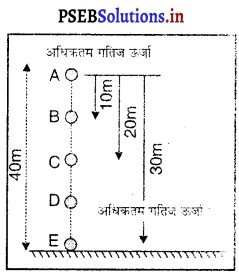
गणितीय रूप द्वारा ऊर्जा संरक्षण नियम की पुष्टि
मान लो 10 kg पुंज वाली एक गेंद फर्श से 30 मीटर की ऊँचाई पर स्थित एक बिंदु A से नीचे की ओर फेंकी जाती है जैसा कि चित्र में दिखाया गया है।

बिंदु A पर-
गेंद की स्थितिज ऊर्जा (P.E.) = m × g × h
= 10 × 10 × 30
= 3000J
गेंद क्योंकि आरंभ में विराम अवस्था में है इसलिए बिंदु A पर इसकी गतिज ऊर्जा (K.E.) = 0
∴ गेंद की कुल यांत्रिक ऊर्जा = P.E. + K.E.
= 3000 + 0 = 3000 J ……………. (i)

बिन्दु B पर-
गेंद अब 20 मीटर की ऊंचाई पर है।
स्थितिज ऊर्जा (P.E.) = m × g × h
= 10 × 10 × 20
= 2000J
समीकरण υ² – u² = 2gh की सहायता से
υ² = u² + 2gh
υ² = 0 + 2 × 10 × 10
∴ υ² = 200
∴ बिंदु B पर गेंद की गतिज ऊर्जा (K.E.) = \(\frac {1}{2}\)mv²
= \(\frac {1}{2}\) × 10 × (200)
= 1000 J
∴ बिंदु B पर गेंद की कुल यांत्रिक ऊर्जा = स्थितिज ऊर्जा + गतिज ऊर्जा
= 2000 + 1000
= 3000 J …………….. (ii)
इसी तरह C तथा D बिंदुओं पर भी कुल यांत्रिक ऊर्जा 3000 J ही होगी।
इन समीकरणों से सिद्ध होता है कि कुल ऊर्जा हमेशा संरक्षित रहती है।

प्रश्न 4.
यदि किसी वस्तु पर लग रहा बल गति की दिशा में न लगे तो किए गये कार्य की परिकल्पना कैसे करोगे ? उदाहरण देकर स्पष्ट करो तथा यह भी बताओ कि कार्य कब न्यूनतम तथा कब अधिकतम होता है ?
उत्तर-
जब वस्तु पर लग रहा बल गति की दिशा में नहीं होता-एक माली घास काटने वाली मशीन को लान में आगे की ओर चलाता है। वह मशीन की ओर अपना मुँह करके ग्राऊंड पर खड़े होकर मशीन के हैंडल HH₁ पर F बल लगाता है।

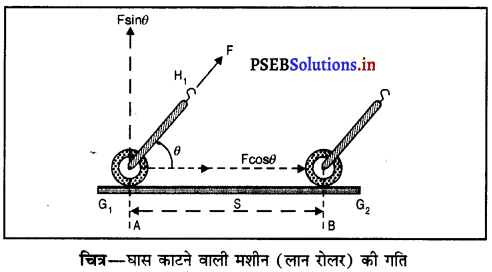
जैसा कि चित्र में स्पष्ट है; माली क्षैतिज दिशा में बल नहीं लगा रहा अपितु कोण बनाई दिशा की ओर बल लगाता है। ऐसी स्थिति में मशीन पर लगने वाला बल जो इसे स्थिति A से B की ओर क्षैतिज दिशा की ओर चलाता है F नहीं अपितु इसका क्षैतिज घटक = F cos θ होता है।

यहां विस्थापन घटक; F sin θ घास काटने वाली मशीन को संतुलित करता है।
∴ मशीन द्वारा किया गया कार्य, (W) = बल घटक × विस्थापन
= F cos θ × S

(i) जब बल वस्तु की दिशा में कार्य करता है तो θ = 0° तथा cos θ = 1
W = F cos θ × S
W = F × 1 × S
W = F × S
यह कार्य (W) का अधिकतम मान है।

(ii) जब बलं वस्तु की लंबात्मक दिशा पर लगता है तो θ = 90° तथा cos 90° = 0
∴ W = F cos 90° × S
W = F × 0 × S
W = 0
यह कार्य (W) का न्यूनतम मान है।

लघु उत्तरात्मक प्रश्न (Short Answer Type Questions)

प्रश्न 1.
कार्य किसे कहते हैं ? इसकी गणना कैसे की जाती है ? कार्य की इकाई भी लिखो।
उत्तर-
कार्य (Work) – “किसी बल द्वारा किया गया कार्य या किसी वस्तु द्वारा किया गया कार्य वस्तु पर लग रहे बल तथा बल की दिशा में उस द्वारा उत्पन्न विस्थापन के गुणनफल के बराबर होता है।”
यदि
F = वस्तु पर लग रहा बल है
S = वस्तु द्वारा बल की दिशा में हुआ विस्थापन है।
तो बल द्वारा किया गया कार्य, W = F × S ……….. (i)
हम जानते हैं कि वस्तु पर कोई बल लगता है, तो वस्तु में प्रवेग उत्पन्न होता है इसलिए यदि m = वस्तु का द्रव्यमान
a = वस्तु में उत्पन्न हुआ त्वरण हो
तो न्यूटन के दूसरे गति नियम अनुसार,
F = [m × a] …………….. (ii)
समीकरण (i) तथा (ii) से
W = m × a × S ………….. (iii)
कार्य की इकाई (Unit of Work) – जब बल न्यूटन (N) तथा दूरी मीटरों (m) हो, तो
कार्य = न्यूटन × मीटर
W = N × m
W = जूल (J)
∴ कार्य की S.I. इकाई जूल (J) तथा C.G.S. इकाई अर्ग (erg) है।
1 जूल = 10⁷ अर्ग।

प्रश्न 2.
एक उदाहरण देकर समझाओ कि यदि किसी वस्तु पर लग रहा बल वस्तु में विस्थापन उत्पन्न नहीं करता तो किया गया कार्य शून्य (0) होगा।
उत्तर-
इस कथन को निम्नलिखित उदाहरण देकर समझाया जा सकता है-
यदि एक बच्चा अधिक-से-अधिक बल लगा कर एक कार को धक्का लगाने की कोशिश करता है, परंतु यदि कार एक सैंटीमीटर तक नहीं हिलती तथा बच्चा पूरी तरह थक जाता है, तो हम भौतिक विज्ञान की भाषा में यह कहेंगे कि उसने कोई कार्य नहीं किया।

इस स्थिति में मान लो बच्चे ने F बल लगाया तथा विस्थापन S = 0 है तो
कार्य, W = F × S
W = F × 0
W = 0

प्रश्न 3.
एक पत्थर को धागे के साथ बाँधकर चक्कर में घुमाया गया है। बताओ इस वक्रीय गति में अभिकेंद्री जल कितना कार्य करता है ?
उत्तर-

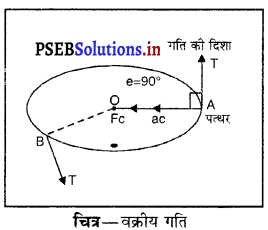
एक पत्थर को चित्र में दर्शाए अनुसार गोल चक्कर में घुमाया जाता है तो जिस उंगली से आपने धागे को पकड़ा हुआ है, उस पर आप कुछ बल लग रहा अनुभव करोगे! घूम रहे पत्थर पर लग रहे बल को अभिकेंद्री बल (Centripetal force) कहते हैं।

यह बल वक्रीय पथ के अर्धव्यास के साथ केंद्र की ओर लगता है। यदि ऐसी स्थिति में धागा पत्थर से खुल जाए तो पत्थर AT या BT स्पर्श रेखा के साथ बाहर की ओर गतिशील हो जाएगा जैसा कि चित्र में दिखाया गया है। अब क्योंकि अभिकेंद्री बस पत्थर की गति के लंबात्मक दिशा में लग रहा है। इसलिए अभिकेंद्री बल द्वारा कोई भी कार्य नहीं हो रहा है।

प्रश्न 4.
ऊर्जा की परिभाषा दो। आप उदाहरण देकर कैसे समझाओगे कि ऊर्जा तथा कार्य एक-दूसरे में एरिवर्तनशील हैं ?
उत्तर-
ऊर्जा (Energy) – “किसी वस्तु की किसी भी रूप में कार्य करने की क्षमता को, ऊर्जा कहते हैं।” ऊर्जा तथा कार्य दोनों ही दिशाहीन हैं।

ऊर्जा और कार्य की आपस में परिवर्तनशीलता – निम्नलिखित उदाहरण से यह स्पष्ट हो जाता है कि ऊर्जा तथा कार्य आपस में परिवर्तनशील हैं।

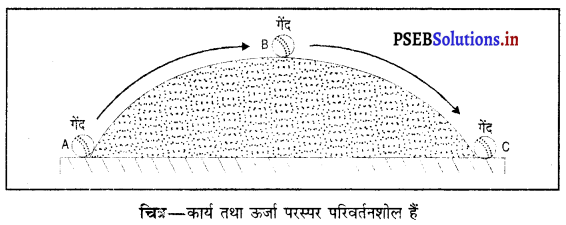
यदि आप गेंद को पृथ्वी से ऊपर की ओर फेंकते हो, तो आप ने पृथ्वी के गुरुत्वाकर्षण के विरुद्ध कोई कार्य किया है। ज्यों-ज्यों गेंद ऊपर की ओर जाती है तो गुरुत्वाकर्षण के विरुद्ध ऊर्जा प्राप्त करती है। यह गेंद द्वारा प्राप्त वह ऊर्जा है जो गेंद को अधिकतम ऊँचाई तक पहुँचने के बाद पृथ्वी की ओर नीचे फेंकने में सहायता करती है।

जब गेंद स्थिति A से उच्चतम बिंदु B तक पहुंचती है, तो गेंद पर किया गया कार्य गेंद के अंदर स्टोर हो जाता है। जब गेंद पथ BC द्वारा पृथ्वी पर वापिस गिरता है, तो गेंद में स्टोर हुआ कार्य अब गेंद द्वारा किया जाता है।
यही कारण है कि हम कहते हैं कि ऊर्जा तथा कार्य परस्पर परिवर्तनशील हैं।

प्रश्न 5.
शक्ति से आप क्या समझते हैं ? इसकी SI इकाई भी लिखो।
उत्तर-
शक्ति (Power ) – हरीश तथा करण 60-60 आम तोड़ने के लिए एक वृक्ष पर चढ़े। दोनों ने एक ही समय चढ़ना शुरू किया। हरीश ने 60 आम 30 मिनटों में तथा करण ने 60 आम 60 मिनटों में तोड़े। इसका अर्थ है कि करण ने एक जैसा कार्य करने के लिए अधिक समय लगाया। दोनों ने एक जैसा कार्य किया, दोनों में एक जितना सामर्थ्य अर्थात् ऊर्जा थी परंतु उनकी शक्ति बराबर नहीं है अर्थात् हरीश की शक्ति, करण से अधिक है।

शक्ति – “किसी वस्तु या मशीन की शक्ति उस द्वारा कार्य करने की दर होती है।” अर्थात् कार्य करने की दर को शक्ति कहते हैं।

यदि कार्य जूल तथा समय सैकेंड में मापा जाए तो शक्ति ‘वॉट’ में मापी जाती है।
∴ 1 वॉट =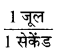
शक्ति की व्यापारिक इकाई ‘किलोवाट’ है।
1 किलोवाट = 1000 वाट = 1000 जूलासेकेंड

प्रश्न 6.
ऊर्जा रूपांतरण से आप क्या समझते हो ? स्थितिज ऊर्जा का गतिज ऊर्जा में रूपांतरण समझाने के लिए एक उदाहरण दो।
उत्तर-
ऊर्जा रूपांतरण (Energy Transformation) – ऊर्जा रूपांतरण नियमानुसार “ऊर्जा न तो उत्पन्न की जा सकती है और न ही नष्ट की जा सकती है। इसको केवल एक रूप से दूसरे रूप में बदला जा सकता है।” इसको ऊर्जा रूपांतरण कहते हैं।

उदाहरण – जब हम कमान में तीर खींचते हैं तो कमान की आकृति बदल जाती है। कमान पर किया गया कार्य तीरकमान प्रणाली में स्थितिज ऊर्जा के रूप में स्टोर हो जाता है। जब तीर छोड़ा जाता है तो इस स्थितिज ऊर्जा का कुछ भाग तीर की गतिज ऊर्जा में बदल जाता है। जब तीर निशाने पर धंस जाता है तो यह कुछ कार्य करता है। अर्थात् तीर की गतिज ऊर्जा, कार्य में बदल जाती है। इस कार्य का कुछ हिस्सा निशाने अंदर ऊष्मा उत्पन्न करता है अर्थात् ऊष्मीय ऊर्जा में बदल जाता है तथा शेष बचा कार्य आवाज़ पैदा करता है अर्थात् ध्वनि ऊर्जा में रूपांतरित हो जाता है।

प्रश्न 7.
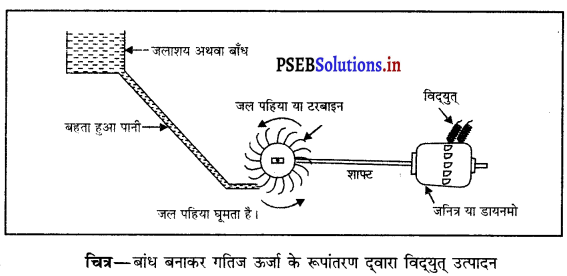
पानी द्वारा विद्युत् कैसे उत्पन्न होती है ?
अथवा
पन्न विद्युत् केंद्रों से विद्युत् कैसे उत्पन्न होती है ?
उत्तर-
बाँधों में पृथ्वी की सतह से काफ़ी ऊँचाई पर बहुत अधिक मात्रा में पानी एकत्रित करके रखा जाता है। बाँध कर यह रखा पानी जब नियंत्रित ढंग से छोड़ा जाता है तो स्टोर की गई यह स्थितिज ऊर्जा गतिज ऊर्जा में परिवर्तित हो जाती है। यह गतिज ऊर्जा जनरेटर की शॉफ्ट को चलाती है जिससे यह विद्युत् ऊर्जा में बदल जाती है।

प्रश्न 8.
एक प्रयोग द्वारा सिद्ध करो कि यांत्रिक ऊर्जा को ऊष्मीय ऊर्जा में बदला जा सकता है।
अथवा
जब हम लकड़ी के किसी तख्ते में हथौड़े से कील गाड़ते हैं तो कील गर्म हो जाती है। क्यों ?
उत्तर-
एक लकड़ी का तख्ता लेकर उस पर एक कील रखकर हथौड़े से मारो तो कील लकड़ी में कुछ अंश तक धंस जाती है परंतु जब कील पूरी तरह तख्ते में धंस जाती है तो फिर हथौड़े से मारने पर कील, हथौड़ा तथा तख्ता गर्म हो जाते हैं। इसका कारण इस प्रकार है। जब हथौड़ा ऊपर उठाया जाता है, तो उसमें उसकी स्थिति के कारण स्थितिज ऊर्जा होती है। जब यह कील पर गिरता है तो इसकी सारी ऊर्जा कील में स्थानांतरित हो जाती है जिससे कील को कुछ गतिज ऊर्जा मिलती है और वह लकड़ी के अंदर धंस जाता है। जब कील पूर्ण रूप से धंस जाता है तो हथौड़े की यांत्रिक ऊर्जा ऊष्मीय ऊर्जा में बदलकर कील, तख्ने तथा हथौडे को गर्म कर देती है अर्थात यांत्रिक ऊर्जा ऊष्मा में बदल जाती है।

प्रश्न 9.
कार्य, ऊर्जा और शक्ति में अंतर बताइए। इनमें प्रत्येक राशि का SI मात्रक लिखिए।
उत्तर-

क्रम	कार्य (Work)	ऊर्जा (Energy)	शक्ति (Power)
1.	बल लगाकर किसी वस्तु को बल की दिशा में विस्थापित करना, कार्य कहलाता है।	कार्य करने की क्षमता ऊर्जा कहलाती है।	जिस दर से ऊर्जा उपलब्ध कराई जाए या खर्च की जाए उसे शक्ति कहते हैं।
2	इसका मात्रक जूल है।	इसका मात्रक जूल है।	इसका मात्रक वाट या किलोवाट है।

प्रश्न 10.
स्थितिज ऊर्जा तथा गतिज ऊर्जा के बीच अंतर बताइए।
उत्तर-
गतिज ऊर्जा एवं स्थितिज ऊर्जा में अंतर-

गतिज ऊर्जा (P.E.)	स्थितिज ऊर्जा (K.E.)
(1) किसी पिंड की गतिज ऊर्जा उसकी गति के कारण होती है।	(1) किसी पिंड की स्थितिज ऊर्जा उस पिंड की स्थिति एवं आकार पर निर्भर करती है।
(2) गतिज ऊर्जा = \(\frac {1}{2}\) mυ2	(2) स्थितिज ऊर्जा = mgh
(3) किसी पिंड की गतिज ऊर्जा उस पिंड की चाल द्वारा मापी जाती है।	(3) स्थितिज ऊर्जा पिंड की ऊंचाई या गहराई जो कि पृथ्वी की सतह से मापी जाती है, पर निर्भर करती है।

प्रश्न 11.
एक घोड़ा तथा एक कुत्ता समान चाल से दौड़ रहे हैं। यदि घोड़े का भार कुत्ते के भार से दस गुणा हो तो उसकी गतिज ऊर्जा का क्या अनुपात होगा ?
उत्तर-
मान लो कुत्ते का द्रव्यमान m है।
∴ घोड़े का द्रव्यमान = 10 m
घोड़े का वेग = कुत्ते का वेग = υ (मान लो)
∴ घोड़े की गतिज ऊर्जा = \(\frac {1}{2}\) × (10 m) × υ²
∴ कुत्ते की गतिज ऊर्जा = \(\frac {1}{2}\) × m × υ²
घोड़े की गतिज ऊर्जा : कुत्ते की गतिज ऊर्जा = (\(\frac {1}{2}\) × 10m × υ²) : (\(\frac {1}{2}\) × m × υ²)
= \(\frac{\frac{1}{2} \times 10 m \times v^{2}}{\frac{1}{2} \times m \times v^{2}}\)
= \(\frac{10}{1}\)
= 10 : 1

प्रश्न 12.
(i) यदि किसी वस्तु का द्रव्यमान तीन गुणा कर दिया जाये तो उसकी गतिज ऊर्जा में क्या परिवर्तन होगा ?
(ii) यदि वस्तु की गति को तीन गुणा कर दिया जाये तो उसकी गतिज ऊर्जा में क्या परिवर्तन होगा ?
उत्तर-
(i) ∴ KE = \(\frac {1}{2}\)mυ²
यदि υ परिवर्तित न हो, तो KE ∝ m
इसलिए द्रव्यमान को तीन गुणा करने पर, गतिज ऊर्जा भी तीन गुणा हो जायेगी।

(ii) ∵
KE = \(\frac {1}{2}\)mυ² और द्रव्यमान अपरिवर्तित रहता है इसलिए K.E. ∝ υ² यदि वेग तीन गुणा कर दिया जाए तो वस्तु की गतिज ऊर्जा 9 गुणा हो जाएगी।

प्रश्न 13.
बराबर द्रव्यमान के दो पिंड को तथा 2h की ऊँचाइयों पर रखा गया है। बताओ उनकी स्थितिज ऊर्जा में क्या अनुपात है ?
उत्तर-
माना दोनों पिंड A तथा B का बराबर द्रव्यमान m है जोकि क्रमशः h और 2h ऊँचाइयों पर हैं।
पिंड A की स्थितिज ऊर्जा, (ΦA) = mgh ……………. (i)
पिंड B की स्थितिज ऊर्जा, (ΦB) = mg × 2h ……………. (ii)
समीकरण (i) को (ii) से भाग देने पर,
\(\frac{\phi \mathrm{A}}{\phi \mathrm{B}}\) = \(\frac{m g h}{m g \times 2 h}\) = \(\frac{1}{2}\)
अर्थात् स्थितिज ऊर्जाओं में अनुपात = 1 : 2

प्रश्न 14.
बराबर द्रव्यमान के दो पिंड v तथा 2v वेग से चल रहे हैं। उनकी गतिज ऊर्जा का अनुपात मालूम कीजिए।
उत्तर-
माना पिंड A एवं B का बराबर द्रव्यमान m है और वेग क्रमशः v एवं 2v हैं।
∴ A की गतिज ऊर्जा, K_A = \(\frac {1}{2}\)m(v)²
= \(\frac {1}{2}\)mv² ……………… (i)
B की गतिज ऊर्जा, K_B = \(\frac {1}{2}\)m (2v)²
= \(\frac {4}{2}\)mv² ……………. (ii)
= 2mv²
समीकरण (i) को (ii) से भाग देने पर,
\(\frac{\mathrm{K}_{\mathrm{A}}}{\mathrm{K}_{\mathrm{B}}}=\frac{\frac{1}{2} m \mathrm{v}^{2}}{2 m \mathrm{v}^{2}}\)
\(\frac {1}{4}\)
∴ गतिज ऊर्जाओं में अनुपात = 1 : 4

प्रश्न 15.
किन-किन परिस्थितियों में मानव की शारीरिक कार्य करने की क्षमता कम हो जाती है ?
उत्तर-
बीमारी तथा बुढ़ापे की परिस्थितियों में मानव की शारीरिक कार्य करने की क्षमता कम हो जाती है क्योंकि उसके शरीर की मांसपेशियों की ऊर्जा कम होती जाती है।

प्रश्न 16.
ऊपर से मुक्त रूप से गिरती हुई एक रबड़ की गेंद भूमि से टकरा कर ऊपर उछलती है। इस प्रक्रिया में क्या कुल ऊर्जा संरक्षित रहती है ? यदि हां तो वह किस-किस रूप में बदलती होगी, जब वह भूमि से टकराती है ?
उत्तर-
ऊर्जा संरक्षण सिद्धांत के अनुसार गेंद की कुल ऊर्जा संरक्षित रहती है। भूमि से टकराने के पश्चात् इसकी ऊर्जा निम्नलिखित रूपों में रूपांतरित हो जाती है-

1. ऊष्मीय ऊर्जा तथा ध्वनि ऊर्जा में
2. गतिज ऊर्जा में
3. स्थितिज ऊर्जा में।

प्रश्न 17.
किसी वस्तु को ऊर्ध्वाधर ऊपर फेंका गया है। इसके वेग में लगातार कमी होती जाती है। जब इसका वेग शून्य हो जाता है तब गतिज ऊर्जा का क्या होता है ?
उत्तर-
हम जानते हैं गतिज ऊर्जा = \(\frac {1}{2}\)mv²
जब वेग υ = 0 तो इसकी गतिज ऊर्जा = \(\frac {1}{2}\) × m × (0)²
अर्थात् वस्तु की गतिज ऊर्जा = 0

प्रश्न 18.
जब एक वस्तु को v वेग से ऊर्ध्वाधर रूप में ऊपर फेंका जाता है तो उसकी ऊर्जा किस प्रकार रूपांतरित होती है ?
उत्तर-
जब एक वस्तु को v वेग से ऊर्ध्वाधर ऊपर की ओर फेंका जाता है तब इसमें =mvगतिज ऊर्जा होती है। जैसे-जैसे पत्थर ऊपर जाता है वैसे-वैसे उसकी गतिज ऊर्जा स्थितिज ऊर्जा में बदल जाती है। अधिकतम ऊँचाई पर पहुंचकर उसका वेग शून्य हो जाता है। अतः गतिज ऊर्जा भी शून्य हो जाती है। स्पष्टतः इस स्थिति में समस्त गतिज ऊर्जा, स्थितिज ऊर्जा, mgh में परिवर्तित हो जाती है। इस ऊँचाई से जैसे ही पत्थर नीचे गिरने लगता है, उसकी स्थितिज ऊर्जा का परिवर्तन गतिज ऊर्जा में होने लगता है और जैसे ही यह पृथ्वी के धरातल पर पहुँचती है तो इसकी सारी स्थितिज ऊर्जा का गतिज ऊर्जा में परिवर्तन हो जाता है।

प्रश्न 19.
एक व्यक्ति एक सूटकेस उठाए खड़ा है, क्या वह कोई कार्य कर रहा है ?
उत्तर-
हम जानते हैं कि वस्तु द्वारा किया गया कार्य उस वस्तु पर लग रहे बल तथा बल की दिशा में उत्पन्न विस्थापन के गुणनफल के बराबर बल होता है। इस स्थिति में व्यक्ति द्वारा उठाए गए सूटकेस पर गुरुत्वीय बल के बराबर बल क्रिया कर रहा है परंतु इस बल द्वारा सूटकेस में विस्थापन उत्पन्न नहीं हुआ है। इसलिए व्यक्ति ने कोई कार्य नहीं किया है।
यहाँ F = mg
विस्थापन S = 0
हम जानते हैं कि, W = F × S
= m × g × S
= mg × 0
W = 0
अर्थात् सूटकेस उठाए हुआ खड़ा व्यक्ति कोई कार्य नहीं करता।

प्रश्न 20.
नाव चला रहा व्यक्ति नदी के किनारे के सापेक्ष विराम अवस्था में है। क्या वह कोई कार्य कर रहा
उत्तर-
क्योंकि किश्ती चला रहा व्यक्ति नदी के किनारे के सापेक्ष विराम अवस्था में है अर्थात् कोई विस्थापन नहीं हो रहा है। इसलिए वह कोई कार्य नहीं कर रहा है।

प्रश्न 21.
पानी की एक बाल्टी उठाए एक व्यक्ति एक समतल सड़क पर एकसमान वेग से चल रहा है। वह कितना कार्य कर रहा है ?
उत्तर-
जब पानी की बाल्टी उठाए व्यक्ति एक समतल सड़क पर एक समान वेग से चलता है तो उस समय उस व्यक्ति द्वारा लगाया गया बल बाल्टी के भार के बराबर ऊपर की तरफ होता है। इस अवस्था में बल तथा विस्थापन की दिशा के मध्य कोण 90° का होता है अर्थात् बल विस्थापन दिशा के लंबवत् होता है।
हम जानते हैं कि यदि बल तथा विस्थापन दिशा के मध्य कोण θ हो, तो
बल द्वारा किया गया कार्य W = F Cos θ × S
W = mg Cos θ × S
W = mg × o × S
W = 0
∴ किया गया कार्य शून्य है।

प्रश्न 22.
क्या एक वस्तु को गति देने के लिए किया गया कार्य इस बात पर निर्भर करता है कि वस्तु कितनी तेज़ चल रही है ?
उत्तर-
किसी वस्तु को गति प्रदान करने के लिए किया गया कार्य उसमें गतिज ऊर्जा उत्पन्न करता है जो वस्तु के वेग के समानुपाती होता है।

प्रश्न 23.
क्या पृथ्वी का गुरुत्वाकर्षण बल सुरक्षित है ?
उत्तर-
हाँ, पृथ्वी का गुरुत्वाकर्षण बल सुरक्षित रहता है क्योंकि बल द्वारा किया गया कार्य वस्तु में जमा रहता है। इसलिए गुरुत्वाकर्षण बल कंजरवेटिव (सुरक्षित) बल है।

प्रश्न 24.
कलाई की एक घड़ी के स्प्रिंग में ऊर्जा का कौन-सा रूप उपयोग में आता है ?
उत्तर-
जब घड़ी की कमानी पूरी तरह खुली होती है तो घड़ी नहीं चलती जैसा कि चित्र में दिखाया गया है। जब इसकी कमानी की चाबी को भरते हैं तो इसकी कमानी को बंद करने के लिए हम कुछ कार्य करते हैं। यह किया गया कार्य घड़ी की कमानी में स्थितिज ऊर्जा के रूप में स्टोर (जमा) हो जाता है। यह स्टोर की हुई स्थितिज ऊर्जा घड़ी की सूइयों को डायल पर चलाने में सहायता करती है। इस तरह स्थितिज ऊर्जा, गतिज ऊर्जा में परिवर्तित हो जाती है।

प्रश्न 25.
क्या किसी वस्तु की गतिज ऊर्जा ऋणात्मक हो सकती है ?
उत्तर-
नहीं, किसी वस्तु की गतिज ऊर्जा ऋणात्मक नहीं हो सकती क्योंकि गतिज ऊर्जा, द्रव्यमान तथा वेग के वर्ग के समानुपाती होती है।

प्रश्न 26.
वह स्थिति बतलाएं जब एक बल द्वारा कोई कार्य नहीं होता है ?
उत्तर-
स्थितियाँ जब बल द्वारा कोई कार्य नहीं होता
(i) यदि वस्तु पर लग रहा बल वस्तु को विस्थापन करने में असफल रहता है तो वस्तु पर उस बल द्वारा कोई कार्य किया हुआ नहीं माना जाता।

(ii) यदि वस्तु पर लग रहा बल वस्तु में हुए विस्थापन के लंब रूप में हो तो बल द्वारा कोई कार्य नहीं होता।
क्योंकि इस स्थिति में θ = 90°
बल द्वारा किया गया कार्य W = F Cos θ × S
= F Cos 90° × S
= F × o × S
W = 0

प्रश्न 27.
कार्य, स्थितिज ऊर्जा, गतिज ऊर्जा और शक्ति के S.I. मात्रक बतलाएं।
उत्तर-
कार्य की S.I. इकाई-कार्य की S.I. इकाई जूल (J) (न्यूटन मीटर) है।। स्थितिज तथा गतिज ऊर्जा की S.I. इकाई-जूल (J) शक्ति की S.I. इकाई-वाट।

प्रश्न 28.
जब कोई वस्तु क्षैतिज दिशा में चलती है तो गुरुत्वाकर्षण बल के विरुद्ध कोई भी कार्य नहीं हो रहा, क्यों ?
उत्तर-
जब कोई वस्तु क्षैतिज दिशा में चलती है, तो उस अवस्था में गुरुत्वाकर्षण बल जो नीचे पृथ्वी की ओर लगता है विस्थापन के दिशा में लंबात्मक रूप में होता है।
∴ θ = 90° तथा Cos θ = Cos 90° = 0
कार्य, W = F Cos θ × S
W = F × o × S
W = 0
अर्थात् कोई कार्य नहीं किया जाता है।

प्रश्न 29.
जब एक गेंद को ऊपर की ओर फेंका जाता है, किस बिंदु पर स्थितिज ऊर्जा तथा गतिज ऊर्जा अधिकतम होती है ?
उत्तर-
जब एक गेंद को ऊपर की ओर फेंका जाता है, तो आरंभ में इसका वेग अधिकतम होता है जिस कारण इसकी गतिज ऊर्जा अधिक होगी जबकि स्थितिज ऊर्जा कम। गेंद ज्यों-ज्यों ऊपर की ओर जाती है, वस्तु कम वेग से दूरी तय करती है। इसलिए समय के साथ स्थितिज ऊर्जा अधिक और गतिज ऊर्जा कम होती जाती है। गेंद द्वारा अधिकतम ऊँचाई पर पहुंच कर वेग शून्य हो जाता है इसलिए वहां गतिज ऊर्जा सबसे कम (शून्य) तथा स्थितिज ऊर्जा सबसे अधिक होती है।

प्रश्न 30.
वह स्थिति बताएं जब किसी वस्तु द्वारा किया गया कार्य शून्य हो परंतु उस पर बल लग रहा हो।
उत्तर-
ऐसा दो स्थितियों में संभव है कि वस्तु पर बल तो लग रहा है परंतु किया गया कार्य शून्य होता है।
(i) जब वस्तु पर लग रहा बल तथा बल द्वारा वस्तु में उत्पन्न हुआ विस्थापन एक-दूसरे के लंबात्मक हो।
ऐसी स्थिति में कोण θ = 90°
∴ cos 90° = 0
वस्तु द्वारा किया गया कार्य (W) = F cos θ × विस्थापन
= 0 × विस्थापन
अर्थात् W = 0

(ii) यदि वस्तु पर लग रहा बल वस्तु में थोड़ा-सा भी विस्थापन न करे।
बल = F
विस्थापन (S) = 0
कार्य (W) = F × S
= F × 0
अर्थात्, W = 0

प्रश्न 31.
बताएं कि समय, ऊर्जा में या शक्ति में शामिल होता है ?
उत्तर-
बल द्वारा किए गए कार्य (ऊर्जा) की गणना, W = F × S से की जाती है। इस समीकरण में समय शामिल नहीं है। अब, शक्ति की परिभाषा अनुसार, “शक्ति कार्य करने की दर है।”
अर्थात् शक्ति (P) =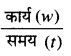

इस समीकरण में समय शामिल है अर्थात् शक्ति समय पर निर्भर करती है।
इससे यह निष्कर्ष निकलता है कि समय शक्ति में शामिल होता है न कि ऊर्जा में।

प्रश्न 32.
किसी वस्तु द्वारा किए गए कार्य तथा किसी वस्तु पर किए गए कार्य का अंतर उदाहरण देकर समझाओ।
उत्तर-
जब वस्तु का विस्थापन लगाए गए बाह्य बल की दिशा में होता है तो वस्तु पर कार्य किया जाता है। परंतु जब वस्तु का विस्थापन बल की विपरीत दिशा में होता है तो कार्य वस्तु द्वारा किया जाता है।

उदाहरण-यदि किसी बर्तन में भरी गैस को बल द्वारा दबाएँ तो कार्य गैस पर किया गया। अब यदि बर्तन की गैस फैलती है तो यह वायुमंडलीय दाब के विरुद्ध गैस द्वारा किया गया कार्य है।

प्रश्न 33.
एक पिंड पर बल लगाकर उसे विस्थापित किया जाता है, बताइए-
(i) पिंड पर किस दिशा में बल लगाने पर अधिकतर कार्य होगा ?
(ii) पिंड पर किस दिशा में बल लगाने पर कार्य शून्य होगा?
उत्तर-
पिंड पर किए गए कार्य W = F × S cos θ से,
(i) जब θ = 0° तो cos 0° = 1 जो कि cos θ का अधिकतम मान है।
W = F × S × cos o°
W = F × S × 1
अतः W (अधिकतम) = F × S
अतः यदि पिंड का विस्थापन लगाए गए बल की दिशा में है, (अर्थात् θ = 0°) तो किया गया कार्य अधिकतम होगा।

(ii) जब θ = 90° तो cos 90° = 0 जो कि cos θ का न्यूनतम मान है।
W = F × S × cos 90°
W = F × S × 0
अतः W (न्यूनतम) = 0
अत: यदि पिंड का विस्थापन लगाए गए बल के लंबवत् है, (अर्थात् e = 90°) तो किया गया कार्य शून्य (न्यूनतम) होगा।

प्रश्न 34.
इलेक्ट्रॉन को किसी वृत्तीय कक्षा में घूमते हुए एक चक्कर लगाने में कितना कार्य करना पड़ता
उत्तर-
वृत्तीय कक्षा में गति करते समय इलेक्ट्रॉन पर कार्य करने वाला अभिकेंद्र आकर्षण बल गति की दिशा के लंबवत् होता है अर्थात् बल और विस्थापन के बीच 90° का कोण होता है,
इसलिए कार्य (W) = F × S cos θ
= F × S cos 90°
= 0 (शून्य) होगा।

इस प्रकार, वृत्तीय गति में इलेक्ट्रॉन द्वारा एक या अधिक चक्कर लगाने में किया गया कार्य शून्य होता है।

प्रश्न 35.
ऊर्जा तथा सामर्थ्य में अंतर उदाहरण देकर स्पष्ट कीजिए।
उत्तर-
ऊर्जा तथा सामर्थ्य में अंतर – ऊर्जा द्वारा किए जा सकने वाले कार्य के कुल परिमाण है, इसका समय से कोई संबंध नहीं है।
सामर्थ्य-यह कार्य करने की दर है। इसका कार्य के कुल परिमाण से कोई संबंध नहीं है।

उदाहरण – एक मजदूर किसी कार्य को पूरा करने में 1 घंटा लगता है, जबकि दूसरा मज़दूर उसी काम को करने में 2 घंटे लगाता है। इस दशा में दोनों मजदूरों ने बराबर कार्य किया अर्थात् दोनों की बराबर ऊर्जा व्यय हुई, परंतु पहले मजदूर ने कार्य आधे समय में किया, इसलिए पहले मज़दूर का दूसरे मजदूर की अपेक्षा दोगुना सामर्थ्य है।

प्रश्न 36.
दो प्रोटॉनों को एक-दूसरे के समीप लाने पर स्थितिज ऊर्जा में वदधि होगी अथवा कमी ?
उत्तर-
प्रोटॉनों को एक-दूसरे के समीप लाने पर, प्रतिकर्षण बल बढ़ने से अधिक कार्य करना पड़ेगा। यह कार्य उनमें स्थितिज ऊर्जा के रूप में संचित होगा। इसलिए प्रोटॉनों को एक-दूसरे के समीप लाने में स्थितिज ऊर्जा में वृद्धि होगी।

प्रश्न 37.
एक घोड़ा, बल F लगाकर एक तांगे को सड़क पर नियत वेग υ से खींच रहा है। घोड़े की शक्ति के लिए व्यंजक प्राप्त कीजिए।
उत्तर-
मान लो घोड़ा t समय में ताँगे को S दूरी तक खींचता है।
क्योंकि घोड़े तथा ताँगे का वेग v नियत है, इसलिए t समय में ताँगे का विस्थापन S = υt ………..(1) [∵ त्वरण = 0]
∴ घोड़े द्वारा + समय में, ताँगे को खींचने में किया गया कार्य W = F × s
समीकरण (1) का प्रयोग करके,
या W = F × vt
घोड़े की शक्ति (P) = \(\frac{W}{t}=\frac{F \times v t}{t}\)
∴ P = F × v

प्रश्न 38.
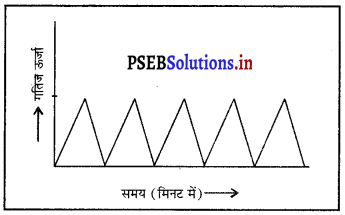
व्यायाम करते समय एक बालक 10 मिनट तक बार-बार उठता बैठता है। समय के साथ उसके शरीर की स्थितिज ऊर्जा में परिवर्तन को दर्शाने के लिए ग्राफ बनाइए।
उत्तर-
प्रत्येक बार उठने पर बालक की स्थितिज ऊर्जा बढ़ेगी तथा प्रत्येक बार बैठने पर स्थितिज ऊर्जा कम होगी। इसके ग्राफ प्रदर्शित चित्र के अनुरूप होगा।

महत्त्वपूर्ण सूत्र (Important Formulae)

1. गतिज ऊर्जा = \(\frac {1}{2}\)mυ²
2. स्थितिज ऊर्जा = mgh
यहाँ m = वस्तु का द्रव्यमान; g = गुरुत्वीय त्वरण तथा h = ऊँचाई
3. कार्य (W) = बल (F) × विस्थापन (S) शक्ति
4. शक्ति (P) =
या शक्ति (P) = \(\frac{\mathrm{F} \times \mathrm{S}}{t}\)
= F × υ
5. 1 जूल = 1 न्यूटन × 1 मीटर
6. 1 जूल =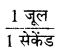
7. एक अश्व शक्ति (Horse Power) = 746 वॉट
8. 1 किलोवाट-घंटा = 36,00,000 जूल = 3.6 × 10⁶ जूल
9. 1 वाट घंटा = 3600 जूल

संख्यात्मक प्रश्न (Numerical Problems)

प्रश्न 1.
0.5 किलोग्राम द्रव्यमान वाले एक बक्से को उठाने के लिए 1 जूल ऊर्जा लगाई गई, तो यह कितना ऊँचा उठेगा ?
हल :
स्थितिज ऊर्जा, (P.E.) = 1 जूल
द्रव्यमान, (m) = 0.5 कि० ग्रा०
गुरुत्वीय प्रवेग, (g) = 10 m/s²
ऊँचाई, (h) = ?
हम जानते हैं कि, स्थितिज ऊर्जा P.E. = m × g × h
1 = 0.5 × 10 × h
1 = 5h
या h = \(\frac{1}{5}\) = 0.2
∴ बक्सा जितना ऊँचा उठेगा = 0.2 m

प्रश्न 2.
एक स्त्री 10 m गहरे कुएँ से 5 किलोग्राम भारी पानी की बाल्टी 10 सैकेंड में खींच लेती है। उसकी शक्ति कितनी है ?
हल :
पानी से भरी बाल्टी का द्रव्यमान, (m) = 5 कि० ग्रा०
कुएँ की गहराई, (h) = 10 मीटर
g = 10 मीटर / सै०²
महिला द्वारा किया गया कार्य = mgh
= 5 × 10 × 10
= 500 जूल
समय = 10 सैकेंड

= 50 जूल/सै० या वॉट उत्तर

प्रश्न 3.
200 न्यूटन बल से एक दीवार को दबा रहा एक व्यक्ति कितना कार्य कर रहा है ?
हल :
यहां, व्यक्ति द्वारा लगाया गया बल (f) = 200 N
बल की दिशा में उत्पन्न हुआ विस्थापन (S) = 0
[∵ व्यक्ति द्वारा लगाये गए बल से दीवार में कोई विस्थापन नहीं हुआ है।]
∴ व्यक्ति द्वारा किया गया कार्य (W) = F × S
= 200 N × 0
= 0
अर्थात् व्यक्ति ने 200N बल लगाने पर भी कोई कार्य नहीं किया है।

प्रश्न 4.
100 वॉट वाला बिजली का एक बल्ब कितनी विद्युत् ऊर्जा की खपत करेगा, यदि वह दो घंटों तक जलता रहे ?
हल:
बल्ब की शक्ति (P) = 100 वॉट
समय (t) = 2 घंटे
= 2 × 60 × 60 = 7200 सैकेंड
खपत की गई ऊर्जा की मात्रा (E) = ?
हम जानते हैं कि, p = \(\frac{\mathrm{W}}{t}\)
⇒ p = \(\frac{\mathrm{E}}{t}\)
या E = P × t
E = 100 वाट × 7200 सैकेंड
E = 7,20,000 जूल
E = 7.2 × 10⁵ जूल उत्तर

प्रश्न 5.
25 km की ऊँचाई से एक रॉकेट को 1 km/s के वेग से ऊपर की ओर दागा गया। यदि रॉकेट का द्रव्यमान 3 × 10⁶ हो, तो इसकी स्थितिज और गतिज ऊर्जा की गणना करो। (g = 10 m/s²)
हल :
रॉकेट का द्रव्यमान, (m) = 3 × 10⁶ कि० ग्रा०
वेग, (υ) = 1 km/s = 1000 मीटर / सै०
ऊँचाई, (h) = 25 km
= 25 × 1000 मीटर
= 25,000

(i) मीटर रॉकेट की स्थितिज ऊर्जा = m × g × h
= 3 × 10⁶ × 10 × 25000
= 75 × 10¹⁰ जूल

(ii) रॉकेट की गतिज ऊर्जा = \(\frac {1}{2}\)mυ²
= \(\frac {1}{2}\) × 3 × 10⁶ × (1000)²
= \(\frac {1}{2}\) × 3 × 10⁶ × 10⁶
= 1.5 × 10¹² जूल उत्तर

प्रश्न 6.
शिमला में विशेष प्रकार के रिक्शा होते हैं, जिनमें साइकिल वाली चैन नहीं होती और वह पेट्रोल के बिना ही चलते हैं, परंतु लोग ही उनको खींचते हैं। एक व्यक्ति ऐसे एक रिक्शे को 300 न्यूटन के बल से खींचकर सड़क पर उसमें 18 Km/h का वेग उत्पन्न कर रहा है। उस व्यक्ति की शक्ति की परिकलना करो।
हल :
व्यक्ति दवारा रिक्शा खींचने में लगाया गया बल, (F) = 300 N
रिक्शे में उत्पन्न हुआ वेग, (υ) = 18 Km/h
υ = \(\frac{18 \times 1000}{60 \times 60}\) m/s
υ = 5 m/s
व्यक्ति की शक्ति (P) = \(\frac{\mathrm{W}}{\mathrm{t}}\)
= \(\frac{\mathrm{F} \times \mathrm{S}}{\mathrm{t}}\) [∵ W = F × S]
= F × \(\frac{S}{t}\)
= F × υ (∵ υ = \(\frac{S}{t}\))
= 300 υ 5
= 1500 वॉट उत्तर

प्रश्न 7.
एक व्यक्ति 30 किलोग्राम भारी बक्सा सिर पर उठाकर-
(i) ऊपर की ओर
(ii) क्षैतिज दिशा में 10 मी० की दूरी चलता है। उसने कितना कार्य किया ?
हल :
बक्से का द्रव्यमान, (m) = 30 Kg
विस्थापन, (S) = 10 m
गुरुत्वीय प्रवेग (g) = 9.8 m/s²

(i) ऊपर की ओर व्यक्ति द्वारा किया गया कार्य, (W) = F × S
W = m × g × s
= 30 × 9.8 × 10
= 2940 जूल उत्तर

(ii) क्षैतिज दिशा में किया गया कार्य-

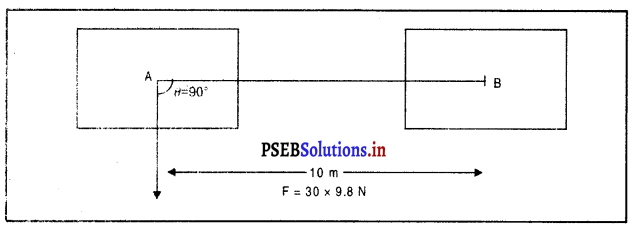
कार्य, W = F cos θ × S
= (30 × 9.8) × cos 90° × 10
= 30 × 9.8 × 0 × 10 [∵ cos 90° = 0]
= 0 (शून्य) उत्तर

प्रश्न 8.
1000 kg की 30 m/s की चाल से चल रही कार ब्रेक लगाने पर एक समान त्वरण से 50 मीटर की दूरी पर रुक जाती है। ब्रेक द्वारा कार पर लगे बल तथा कृत कार्य को ज्ञात कीजिए।
हल:
यहाँ, = 30 ms^-1
υ = 0
S = 50 m
अत्र υ² – u² = 2aS
(0)² – (30)² = 2 × a × 50
– (30 × 30) = 100 × a
a = \(\frac{-900}{100}\)
= -9m/s²
बल, F = m × a
= 1000 × 9 = 9000 न्यूटन
ब्रेक द्वारा किया कार्य = F × S
= 9000 × 50
= 45 × 10000
= 4.5 × 10⁵ J

प्रश्न 9.
एक मजदर 10 कि०ग्रा० भारी टोकरी अपने सिर पर रखकर समतल सड़क पर 100 मीटर क्षैतिज दिशा में चल रहा है। उसके द्वास गुरुत्वीय बल के विरुद्ध किया गया कार्य ज्ञात करो। (g = 9.8 मी०/सै०² )
हल :
टोकरी का भार = mg = 10 × 9.8
= 98 N
गुरुत्वीय बल की दिशा (नीचे) में विस्थापन = 0
∴ कार्य = बल × विस्थापन
= 98 × 0
= 0

प्रश्न 10.
एक बच्चा समतल क्षैतिज फर्श पर अपनी खिलौना गाड़ी को 10 मीटर की दूरी तक खींचता है। खिलौना गाड़ी से बंधी हुई डोरी क्षैतिज समतल के साथ 60° का कोण बनाती है। यदि बच्चे के द्वारा लगाया गया बल 5 N हो तो उसके द्वारा किए गए कार्य की गणना कीजिए।
हल :
यहाँ,
F = 5 N, θ = 60°, S = 10 मी०
बच्चे द्वारा किया गया कार्य (W) = F cos θ × S
= 5 cos 60° × 10
= 5 × \(\frac {1}{2}\) = × 10 [cos 60° = [∵ latex]\frac {1}{2}[/latex]
= 25 जूल उत्तर

प्रश्न 11.
पानी के पंप की विद्युत् शक्ति की गणना करो जो 100 kg पानी को 30 m ऊँची टैंकी में 30 सैकेंड में फेंकने का सामर्थ्य रखता है। (g = 10 m/s²)
हल :
यहाँ, m = 100 kg
S = 30 m
g = 10m/s²
t = 30s
गुरुत्व विरुद्ध पंप द्वारा किया गया कार्य, W = mgs
W = 100 × 10 × 30
W = 30000 J जूल
पंप की शक्ति (P) =
P = \(\frac{30000 \mathrm{~J}}{30 s}\)
30s P = 1000 J/s या वाट
P = 1 किलोवाट उत्तर

प्रश्न 12.
एक मशीन 240 सैकेंड में 1960 जूल कार्य करती है। मशीन की शक्ति क्या है ?
हल :

= 8.17 जूल/सैकेंड
= 8.17 वाट उत्तर

प्रश्न 13.
5 मीटर की ऊँचाई पर रखे 10 ग्राम वजन वाले पत्थर की ऊर्जा बताओ।( दिया है, g = 9.8 मी०/सै०²)
हल:
पत्थर का द्रव्यमान (m) = 10 ग्राम
\(\frac{10}{1000}\)
= .01 किलोग्राम
ऊँचाई (h) = 5 मीटर
गुरुत्वीय त्वरण (g) = 9.8 मी०/सै०²
पत्थर में उपस्थित ऊर्जा (P.E.) = mgh
= .01 × 5 × 9.8
= 0.49 जूल उत्तर

प्रश्न 14.
50 कि० ग्रा० द्रव्यमान का कोई व्यक्ति 30 सीढ़ियां 30 सैकेंड में चढ़ जाता है। यदि प्रत्येक सीढ़ी 20 सै० मी. ऊँची हो तो उस व्यक्ति द्वारा सीढ़ियां चढ़ने में प्रयुक्त शक्ति का परिकलन कीजिए।
हल :
m = 50 कि० ग्रा०, समय t = 30 सै०
सीढ़ियों की संख्या = 30
एक सीढ़ी की ऊँचाई = 20 सै०मी०
∴ 30 सीढ़ियों की कुल ऊँचाई = 30 × 20
= 600 सै०मी०
= 6 मीटर
किया गया कुल कार्य, (P.E.) = mgh
= 50 × 10 × 6
= 3000 जूल
शक्ति (P) = \(\frac{\text { P.E }}{t}\)
= \(\frac{3000}{30}\) = 100 वाट उत्तर

प्रश्न 15.
60 kg द्रव्यमान वाला व्यक्ति 30 सीढ़ियों वाली ऊँचाई को 40s में चढ़ जाता है। यदि प्रत्येक सीढ़ी 20 cm ऊँची हो तो किया गया कार्य ज्ञात करो।
हल:
तय कुल ऊँचाई = सीढ़ियों की संख्या × प्रत्येक सीढ़ी की ऊँचाई
= \(\frac{30 \times 20}{100}\)
= 6m
m = 60 kg, 8 = 10 ms^-2, h = 6m
किया गया कार्य = स्थितिज ऊर्जा, (P.E.) = mgh
= 60 × 10 × 6
= 3600 J

प्रश्न 16.
एक मनुष्य का भार 50 किलोग्राम है। यह 20 सैकेंड में एक पहाड़ी पर ऊर्ध्वारतः 10 मीटर चढ़ जाता है। उसकी शक्ति मालूम करें। (दिया है : g = 9.8 मी०/सै०²)
हल:
द्रव्यमान (m) = 50 kg
गुरुत्व त्वरण (g) = 9.8 मी०/सै०²
समय (t) = 20 सैकेंड
ऊँचाई (h) = 10 m
कार्य (W) = स्थितिज ऊर्जा
= mgh
= 50 × 9.8 × 10J
= 4900J

= \([\frac{4900 \mathrm{~J}}{20 \mathrm{~s}}/latex]
= 45 जूल/सैकेंड
= 45 वाट उत्तर

प्रश्न 17.
रोडवेज की एक बस 72 Km/h की चाल से पूर्व दिशा की ओर जा रही है। राकेश तथा मुकेश जिनका क्रमशः द्रव्यमान 50 kg तथा 55 kg है; बस में सफर कर रहे हैं। क्या उनकी गतिज ऊर्जा बराबर है ?
हल :
राकेश का वेग = बस का वेग = मुकेश का वेग
= 72 km/h
= [latex]\frac{72 \times 1000}{60 \times 60}\) m/s
v = 20 m/s
∴ राकेश की गतिज ऊर्जा = \(\frac {1}{2}\)m (राकेश का वेग)²
= \(\frac {1}{2}\) × 50 × (20)²
= \(\frac {1}{2}\) 50 × 20 × 20
10,000 J. …………….. (i)
मुकेश की गतिज ऊर्जा = \(\frac {1}{2}\)m (मुकेश का वेग)²
= \(\frac {1}{2}\) × 55 × 20 × 20
= 11,000 J. ……………. (ii)
:. मुकेश की गतिज ऊर्जा, राकेश की गतिज ऊर्जा से अधिक है।

प्रश्न 18.
मुक्त रूप से गिरता हुआ 1 kg द्रव्यमान का कोई हथौड़ा लकड़ी के टुकड़े पर लगी किसी कील पर गिरता है। यदि हथौड़ा 1 m ऊँचाई से गिरता है, तो कील से टकराने से ठीक पहले गतिज ऊर्जा कितनी होगी?
(g = 10 m/s²)
हल :
हथौड़े का द्रव्यमान, (m) = 1 kg
हथौड़े की ऊंचाई, (h) = 1 m
υ² – u² = 2gS
υ² – 0 = 2 × 10 × 1
υ² = 20
हथौड़े की गतिज ऊर्जा (K.E.) = \(\frac {1}{2}\) × m × υ²
= \(\frac {1}{2}\) × 1 × 20
= 10 जूल उत्तर

प्रश्न 19.
एक कार 54 कि०मी०/घंटा वेग से चल रही है। इसमें बैठे 40 कि० ग्रा० के लड़के की गतिज ऊर्जा क्या होगी ?
हल:
लड़के का वेग = कार का वेग
= 54 कि०मी०/ घंटा
= \(\frac{54 \times 1000}{60 \times 60}\)
= 15 m/s
लड़के का द्रव्यमान, (m) = 40 kg
लड़के की गतिज ऊर्जा (K.E.) = \(\frac {1}{2}\)mυ²
= \(\frac {1}{2}\) × 40 × (15)²
= 4500 जूल उत्तर

प्रश्न 20.
कोई वस्तु 5 सैकेंड में 50 जूल कार्य करती है। इसकी शक्ति क्या है ?
हल:
किया गया कार्य, (W) = 50 जूल
लगाया गया समय, (t) = 5 सैकेंड शक्ति

= 10 जूल/सैकेंड
= 10 वाट उत्तर

प्रश्न 21.
एक पंप का बल ज्ञात करो जो 19 मीटर ऊँची टंकी में 100 कि० ग्रा० पानी 25 सैकेंड में पहँचा सकता है। (g = 10 मी०/सै०² )
हल :
यहाँ, m = 100 कि०ग्रा०
h = 19 m
g = 10 मी०/सै०²
t = 25 सै०
कार्य, (W) = mgh
= 100 × 10 × 19
= 19000 जूल
शक्ति, (P) = \(\frac{\mathbf{W}}{t}\)
= \(\frac{19000}{25}\)
= 760 वॉट उत्तर

प्रश्न 22.
हृदय द्वारा एक धड़कन के लिए 1 जूल ऊर्जा व्यय होती है। हृदय की शक्ति का परिकलन कीजिए यदि यह एक मिनट में 72 बार धड़कता है।
हल :
हृदय की एक धड़कन द्वारा किया गया कार्य = 1 जूल
72 धड़कनों में किया गया कार्य = 72 × 1
= 72 जूल
समय = 1 मिनट
= 60 सैकेंड

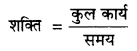
\(\frac{72}{60}\)
= 1.2 J/s
= 1.2 वॉट उत्तर

प्रश्न 23.
कोई व्यक्ति 100 W का बल्ब प्रतिदिन 10 घंटे जलाता है। 30 दिन में वह कितने यूनिट विदयुत् ऊर्जा की खपत करेगा ?
हल :
बल्ब की शक्ति (P) = 100 W
जितने समय तक बल्ब जला (t) = 10 × 30 घंटे
खपत हुई ऊर्जा (E) = P × t
= 100 × 10 × 30
= 30000 वाट घंटा
= \(\frac{30000}{1000}\) kWh
= 30 kWh
= 30 यूनिट उत्तर

प्रश्न 24.
एक घर में 500 वाट का विद्युत् चूल्हा 10 घंटे प्रतिदिन कार्य करता है। 30 दिन में उस घर की व्यय होने वाली ऊर्जा की यूनिट (kWh) में गणना करो।
हल :
चूल्हे की शक्ति = 500 वाट
जितने समय के लिए प्रयोग किया गया = 10 × 30 = 300 घंटे
30 दिनों में खर्च हुई ऊर्जा = 500 वाट × 300 घंटे
= 150000 वाट घंटा
= \(\frac{150000}{1000}\)
= 150 किलोवाट घंटा
= 150 यूनिट उत्तर

प्रश्न 25.
10 kg द्रव्यमान के पिंड को 5 m/s² के त्वरण के अधीन 2m की दूरी से विस्थापित किया जाता है। पिंड पर किए गए कार्य का परिकलन कीजिए।
हल :
यहां पिंड का द्रव्यमान (m) = 10 kg
पिंड का त्वरण (a) = 5 m/s²
पिंड में विस्थापन (S) = 2 m
हम जानते हैं, कार्य (W) = F × S
= m × a × S (परंतु F = m × a)
= 10 × 5 × 2
= 100 J

प्रश्न 26.
10 kg द्रव्यमान की एक वस्तु को कुछ ऊँचाई तक ऊपर उठाने में 490 J कार्य किया गया। जितनी ऊँचाई में से वस्तु को ऊपर उठाया गया मालूम कीजिए। गुरुत्वीय त्वरण g = 9.8m/²
हल :
यहाँ वस्तु का द्रव्यमान (m) = 10 kg
किया गया कार्य (W) = 490J
गुरुत्वीय त्वरण (g) = + 9.8 m/s²
मान लो वस्तु को h ऊँचाई में से ऊपर उठाया गया है, तो वस्तु पर किया गया कार्य
= वस्तु की स्थितिज ऊर्जा
W = mgh
490 = 10 × 9.8 × h
या h = \(\frac{490}{10 \times 9.8}\)
= \(\frac{490}{98}\)
ऊँचाई, h = 5m

प्रश्न 27.
एक वस्तु पर 20 N का बल लगाकर उसे 10 cm की दूरी में से विस्थापित करने में 1J का कार्य करना पड़ा। बल तथा विस्थापन के बीच का कोण ज्ञात कीजिए।
हल:
यहाँ बल (F) = 20 N
विस्थापन (S) = 10 cm = \(\frac{10}{100}\)m
= 0.1 m
वस्तु पर किया गया कार्य (W) = 1.0 J
बल की दिशा तथा विस्थापन के मध्य कोण = θ (मान लो)
अब W = FS cos θ
1 = 20 × 0.1 × cos θ
1 = 2 cos θ
cos θ = \(\frac {1}{2}\)
∴ θ = 60°

प्रश्न 28.
दो समान द्रव्यमान वाले पिंड क्रमशः एक समान वेग υ तथा 3υ से गति कर रहे हैं। इन पिंडों की गतिज ऊर्जाओं का अनुपात ज्ञात कीजिए।
हल :
मान लो प्रत्येक पिंड का द्रव्यमान m है।
पहले पिंड की गतिज ऊर्जा (E_K1) = \(\frac {1}{2}\)mυ² …………… (1)
दूसरे पिंड की गतिज ऊर्जा (E_K2) = \(\frac {1}{2}\)m(3υ)²
= \(\frac {1}{2}\)m(9υ)²
= 9 × \(\frac {1}{2}\)mυ² (2)
दोनों पिंडों का गतिज ऊर्जाओं का अनुपात = \(\frac{\mathrm{E}_{\mathrm{K}_{1}}}{\mathrm{E}_{\mathrm{K}_{2}}}\)
= \(\frac{\frac{1}{2} mv^{2}}{9 \times \frac{1}{2} m v^{2}}\)
= \(\frac {1}{9}\) = 1 : 9

प्रश्न 29.
एक 2 kg द्रव्यमान वाली वस्तु विरामावस्था से धरती पर गिरती है। गिरने के 2 बाद वस्तु की गतिज ऊर्जा कितनी होगी।g का मान 10 m/s² लें।
हल:
यहां द्रव्यमान (m) = 2 kg
प्रारंभिक वेग (u) = 0 (विरामावस्था)
समय (t) = 2s
अंतिम वेग (υ) = ?
गुरुत्वीय त्वरण (g) = 10 m/s²
υ = u + gt का प्रयोग करने पर
υ = 0 + 10 × 2
∴ υ = 20 m/s
अब 2 सेकंड के बाद वस्तु की गतिज ऊर्जा (EK)
= \(\frac {1}{2}\)mυ²
= \(\frac {1}{2}\) × 2 × (20)²
= \(\frac {1}{2}\) × 2 × 20 × 20J
= 400 J

प्रश्न 30.
एक समतल सड़क पर स्कूटर चालक ब्रेक लगा कर स्कूटर की चाल 36 km/h से कम करके 18 km/h कर देता है। बताओ ब्रेक द्वारा कितना कार्य किया गया यदि खाली स्कूटर का द्रव्यमान 86 kg और चालक तथा पेट्रोल का द्रव्यमान 64 kg हो।
हल:
कुल द्रव्यमान (m) = स्कूटर का द्रव्यमान + चालक तथा पेट्रोल का द्रव्यमान
= m₁ + m₂
= 86 kg + 64 kg
= 150 kg
प्रारम्भिक वेग (u) 36 km/h
= 36 × \(\frac {5}{18}\)m/s
= 10 m/s
अंतिम वेग (υ) = 18 km/h
= 18 × \(\frac {5}{18}\) m/s
= 5 m/s
ब्रेक द्वारा किया गया कार्य = स्कूटर द्वारा गतिज ऊर्जा की हानि
= प्रारंम्भिक गतिज ऊर्जा – अतिम गतिज ऊर्जा
= \(\frac {1}{2}\)mu² – \(\frac {1}{2}\)mυ²
= = \(\frac {1}{2}\)m (u² – υ²)
= \(\frac {1}{2}\)m (u + υ) (u – υ)
= \(\frac {1}{2}\) × 150 × (10 + 5) (10 – 5)
= \(\frac {1}{2}\) × 150 × 15 × 5
= 75 × 75
= 5625

प्रश्न 31.
एक कार एक समान वेग से गतिशील है। 18 km/h, 36 km/h, 54 km/h तथा 72 km/h कुछ अंतरालों पर कार में बैठे 40 kg द्रव्यमान वाले लड़के की इन वेगों पर गतिज ऊर्जा ज्ञात कीजिए तथा गतिज ऊर्जा और वेग के मध्य ग्राफ भी बनायें और बताइए कि ग्राफ की प्रकृति कैसी है?
उत्तर-
यहाँ, m = 40 Kg
υ₁ = 18 km/h = 18 × \(\frac{5}{18}\)m/s
= 5 m/s
υ₂ = 36 km/h – 10 m/s
υ₃ = 54 km/h = 15 m/s
υ₄ = 72 km/h = 20 m/s

K₁ = \(\frac{1}{2} \mathrm{~m} v_{1}^{2}\) = \(\frac {1}{2}\) × 40 × (5)²
= 500J

K₂ = \(\frac{1}{2} m v_{2}^{2}\)
\(\frac {1}{2}\) × 40 × (10)²
= 2000 J

K₃ = \(\frac{1}{2} m v_{3}^{2}\)
\(\frac {1}{2}\) × 40 × (15)²
= 4500 J

K₄ = \(\frac{1}{2} m v_{4}^{2}\)
\(\frac {1}{2}\) × 40 × (20)²
= 8000 J
चित्र में दर्शाए गए अनुसार गतिज ऊर्जा और वेग के मध्य ग्राफ परवलयाकार (पैराबोला) है क्योंकि गतिज ऊर्जा ∝ υ²

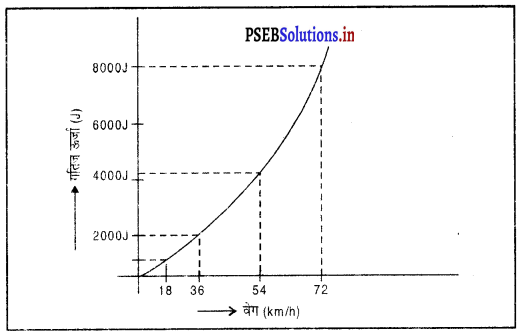
प्रश्न 32.
मान लो आपके हाथ में 1 kg द्रव्यमान की वस्तु है। आप इसे कितनी ऊँचाई तक ऊपर उठाएँगे ताकि गुरुत्वीय स्थितिज ऊर्जा 1J प्राप्त कर लें। (g = 10 ms^-2)
हल :
यहाँ स्थितिज ऊर्जा (p) = 1J
द्रव्यमान (n) = 1 kg
गुरुत्वीय त्वरण (g) = 10 ms^-2
हम जानते हैं, स्थितिज ऊर्जा (P) = mgh
1 = 1 × 10 × h
∴ h = \(\frac{1}{10}\)m
= 0.1 m = 10 cm

प्रश्न 33.
एक 1000 W विद्युत् हीटर प्रतिदिन 2 घंटे चलाया जाता है। 28 दिन के महीना भर चलाने में ऊर्जा का क्या खर्च आयेगा जबकि ऊर्जा की दर 3.00 ₹ प्रति यूनिट हो।
हल:
हीटर की शक्ति (P) = 1000 W = 1 kW
कुल समय (t) = 2 × 28 = 56h
ऊर्जा की खपत (E) = P × t
= 1 kW × 56h
= 56 kWh
= 56 यूनिट
ऊर्जा की दर = 3.00 ₹ प्रति यूनिट
∴ कुल खर्च = 56 × 3.00 ₹
= 168.00 ₹

प्रश्न 34.
मुक्त रूप से गिरता हुआ 1 किग्रा द्रव्यमान का एक हथौड़ा लकड़ी के टुकड़े पर लगी किसी कील पर गिरता है। यदि हथौड़ा 1 मीटर ऊँचाई से गिरता है तो कील से टकराने से पहले गतिज ऊर्जा कितनी होगी ? (g = 10 ms^-2)
हल :
दिया है : हथौड़े का द्रव्यमान (m) = 1 किग्रा.
हथौड़े की प्रारंभिक ऊँचाई (h) = 1 मीटर,
गुरुत्वीय त्वरण (g) = 10 ms^-2
कील से टकराने से पूर्व हथौड़े की गतिज ऊर्जा = ?
हथौड़े का प्रारंभिक वेग (u) = 0
मान लो हथौड़ा υ वेग से कोल से टकराता है, तो
समीकरण υ² = u² + 2gh से,
υ² = 0² + 2 × 10 × 1
= 20
υ = \(\sqrt{20}\) ms^-1
अतः कील से टकराने से पूर्व हथौड़े की गतिज ऊर्जा
E_K = \(\frac {1}{2}\)mυ²
= \(\frac {1}{2}\) × 1 × किग्रा × 20
= 10 जूल उसर

प्रश्न 35.
10kg का कोई पिण्ड 50 cm ऊँचाई से गिराया जाता है। पृथ्वी की सतह से टकराते समय ज्ञात कीजिए
(i) इसकी गतिज ऊर्जा,
(ii) इसका वेग,
(iii) स्पष्ट कीजिए कि वेग पिण्ड के द्रव्यमान पर निर्भर करता है?
हल :
दिया है, पिण्ड का द्रव्यमान (m) = 10 kg, प्रारंभिक ऊँचाई (h) = 50 cm = 0.5 m
प्रारंभिक वेग (u) = 0,
मान लो पृथ्वी की सतह से टकराते समय पिण्ड का वेग = υ है
समीकरण
υ² = u² + 2g h से,
υ² = 0² + 2 × (10) × (0.5)
= 10
∴ υ = \(\sqrt{10 \mathrm{~ms}^{-1}}\)
= 3.16 ms^-1

(i) सूत्र गतिज ऊर्जा E_K = \(\frac {1}{2}\)mυ²
पृथ्वी की सतह से टकराते समय पिण्ड की गतिज ऊर्जा = (E_K)
= \(\frac {1}{2}\) × 10 kg × 10 m²s^-2
= 50 जूल उत्तर

प्रश्न 36.
दो वस्तुओं के द्रव्यमानों में 5 : 6 का अनुपात है। यदि उनके वेग परस्पर बराबर हों तो उनकी गतिज ऊर्जाओं का अनुपात क्या होगा ?
हल :
मान लो पहली वस्तु का द्रव्यमान m₁ वेग, υ₁ तथा गतिज ऊर्जा (E_K1) और दूसरी वस्तु का द्रव्यमान m₂ वेग υ₂ तथा गतिज ऊर्जा (E_K2) है।


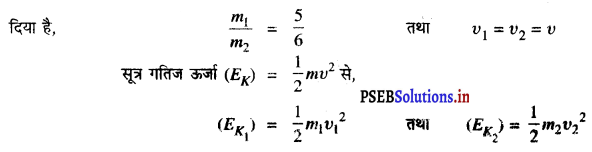
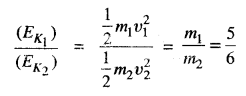
गतिज ऊर्जाओं का अनुपात 5 : 6 होगा।

प्रश्न 37.
1 किलोग्राम के पिण्ड की गतिज ऊर्जा 1 जूल है। इसकी चाल कितनी होगी ?
हल :
दिया है, पिण्ड का द्रव्यमान (m) = 1 किलोग्राम, पिण्ड की गतिज ऊर्जा (E_K) = 1 जूल, वेग (υ) = ?
गतिज ऊर्जा (E_K) = \(\frac {1}{2}\)mυ² से,
1 = \(\frac {1}{2}\) × 1 × υ²
υ² = 2
चाल (υ) = √2
= 1.414 ms^-1/sup>

प्रश्न 38.
एक गतिमान पिण्ड की गतिज ऊर्जा 400 जूल है। पिंड पर उसकी गति के विरुद्ध 25 N का औसत बल लगाने से पिण्ड कितनी दूर जाकर रुक जाएगा ?
हल :
दिया है, पिण्ड की गतिज ऊर्जा = 400 जूल, औसत बल = 25 न्यूटन
∴ पिण्ड की गतिज ऊर्जा = पिण्ड द्वारा रुकने तक किया गया कार्य
= बल × पिण्ड द्वारा चली गई दूरी
अथवा 400 जूल = 25 न्यूटन × पिण्ड द्वारा चली गई दूरी
अत: रुकने से पूर्व पिण्ड द्वारा चली गई दूरी = \(\frac{400}{25}\) = 16 मीटर

प्रश्न 39.
एक कार का इंजन 1000 N का बल लगाकर कार को 72 km/h की एक समान चाल से समतल सड़क पर खींच रहा है। इंजन की शक्ति का परिकलन किलोवाट में कीजिए।
हल :
दिया है, इंजन का बल (F) = 1000 N
कार का वेग (υ) = 72 Km/h
= 72 × \(\frac {5}{18}\) = 20 m/s
∴ इंजन की शक्ति (P) = F × υ
= 1000 N × 20 m/s
= 20000 W
= \(\frac{20000}{1000}\) KW
= 20 KW .

प्रश्न 40.
50 kg द्रव्यमान का एक लड़का दौड़कर 45 सीढ़ियां 9s में चढ़ता है। यदि प्रत्येक सीढ़ी की ऊंचाई 15 cm हो तो उसकी शक्ति का परिकलन कीजिए।g का मान 10 ms^-2 लीजिए।
हल :
लड़के का भार = mg = 50 kg × 10 m/s²
= 500 N
कुल ऊँचाई (h) = सीढ़ियों की संख्या × एक सीढ़ी की ऊँचाई
= 45 × 15 cm
= 675 cm
= 6.75 m
लगा समय t = 9s

= \(\frac{m g h}{t}\)
= \(\frac{500 \mathrm{~N} \times 6.75 \mathrm{~m}}{9 \mathrm{~s}}\)
= 375 W

प्रश्न 41.
0.05 किलोग्राम द्रव्यमान की एक वस्तु धरती से 1000 मीटर ऊँचाई से गुरुत्वीय त्वरण के अंतर्गत स्वतंत्रतापूर्वक नीचे गिरता है। इसका धरती पर पहुंचने पर वेग एवं कुल ऊर्जा ज्ञात कीजिए।
(g = 9.8 मीटर/सेकंड²)
हल :
दिया है, u = 0, h = 1000 मीटर, g = 9.8 मीटर/सेकंड², υ = ?
υ² = u² + 2gh से,
υ² = (0)² + 2 × 9.8 × 1000
= 19600 मीटर²/सैकेंडर²
∴ वस्तु का धरती पर पहुँचने का वेग (υ) = 140 मीटर/सेकंड।
धरती पर पहुंचने पर कुल ऊर्जा = स्थितिज ऊर्जा + गतिज ऊर्जा
= 0 + \(\frac {1}{2}\)mυ²
= \(\frac {1}{2}\)mυ²
\(\frac {1}{2}\) × 0.05 × (140)²
= 490 जूल

प्रश्न 42.
एक पंप प्रति सेकंड 100 kg जल 5 m की ऊँचाई तक उठाता है। पंप की सामर्थ्य की गणना कीजिए। (g = 10 ms^-2)
हल :
दिया है, समय (t) = 1 s, जल का द्रव्यमान (m) = 100 kg, ऊँचाई h = 5m

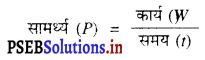
= 5000 W

प्रश्न 43.
40 वाट का एक बल्ब प्रतिदिन 10 घंटे जलाया जाता है। यदि 1 यूनिट की कीमत 2.50 ₹ है तो 30 दिन के महीने में उपभोग की गई विद्युत् ऊर्जा की कीमत ज्ञात कीजिए।
हल :
दिया है, बल्ब की शक्ति = 40 वाट,
समय = 10 घंटे, दिनों की संख्या = 30 दिन
1 यूनिट की कीमत = 2.50 ₹
एक माह में व्यय विद्युत् ऊर्जा = बल्ब को शक्ति × समय × दिनों की संख्या
= 40 वाट × 10 घंटे × 30 घंटे
= (\(\frac{40}{1000}\)) किलोवाट × 10 × 30 घंटे
= \(\frac{40 \times 10 \times 30}{1000}\) किलोवाट-घंटा
= 12 यूनिट
∴ विद्युत् ऊर्जा की कीमत = यूनिटों की संख्या × 1 यूनिट की कीमत
= 12 यूनिट × (2.50 ₹/प्रति यूनिट)
= 30₹

प्रश्न 44.
एक कुली 10 kg का बोझ धरती से 1.5 m ऊपर ऊठाकर अपने सिर पर रखता है। उसके द्वारा बोझे पर किए गए कार्य का परिकलन कीजिए।
हल :
बोझ का द्रव्यमान (m) = 10 kg तथा
विस्थापन (S) = 1.5 m
किया गया कार्य (V) = F × S
= mg × s
= 10 kg × 10 ms^-2 × 1.5 m
= 150 Nm = 225 J

प्रश्न 45.
यदि किसी कार का द्रव्यमान 1500 kg है तो उसके वेग को 30 km h^-1 से 60 km h^-1 तक बढ़ाने में कितना कार्य करना पड़ेगा ?
हल :
कार का द्रव्यमान (m) = 1500 kg
कार का प्रारंभिक वेग (u) = 30 km h^-1
= \(\frac{30 \times 1000 \mathrm{~m}}{100 \times 60 \mathrm{~s}}\)
= 8.33 m s^-1
कार का अंतिम वेग (υ) = 60 km h^-1 = 16.66 m s^-1

इसलिए कार की प्रारंभिक गतिज ऊर्जा (E_kf ) = \(\frac {1}{2}\)mu²
\(\frac {1}{2}\) × 1500 kg × (8.33 ms^-1)²
= 52041.68 J
कार की अंतिम गतिज ऊर्जा (E_ki = \(\frac {1}{2}\) × 1500 kg × (16.66 m s-‘)
= 208416.68J
अतः किया गया कार्य = गतिज ऊर्जा में परिवर्तन
= E_kf – E_ki
= 156375 J

प्रश्न 46.
15 kg द्रव्यमान की एक वस्तु 4 ms-1 के एक समान वेग से गतिशील है। वस्तु की गतिज ऊर्जा कितनी होगी ?
हल:
वस्तु का द्रव्यमान (m) = 15 kg
वस्तु का वेग (υ) = 4 ms^-1
वस्तु की गतिज ऊर्जा (E_k) = \(\frac {1}{2}\) mυ² से
= \(\frac {1}{2}\) × 15 kg × 4 m s^-1 × 4 ms^-1
= 120J

प्रश्न 47.
दो लड़कियाँ जिनमें से प्रत्येक का भार 200 N है एक रस्से पर 8 m की ऊँचाई तक चढ़ती हैं। हम एक लड़की का नाम A रखते हैं तथा दूसरी का BIइस कार्य को पूरा करने में लड़की A,20s का समय लेती है जबकि लकड़ी B, 50 s का समय लेती है। प्रत्येक लड़की द्वारा व्यय की गई शक्ति का परिकलन कीजिए।
हल :
(i) लड़की A द्वारा व्यय की गई शक्ति :
लड़की का भार (mg) = 200 N
विस्थापन (ऊँचाई) (h) = 8 m
लिया गया समय (t) = 20 s
किया गया कार्य शक्ति (P) =
= \(\frac{m g h}{t}\)
= \(\frac{m g h}{t}\)
= 80 W

(ii) लड़की B द्वारा व्यय की गई शक्ति :
लड़की का भार (mg) = 200 N
विस्थापन ऊँचाई (h) = 8 m
लिया गया समय (t) = 50s शक्ति (P) = \(\frac{m g h}{t}\)
= \(\frac{200 \mathrm{~N} \times 8 \mathrm{~m}}{50 \mathrm{~s}}\)
= 32 W

अति लघु उत्तरात्मक प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
कार्य का SI मात्रक लिखो।
उत्तर-
कार्य का SI मात्रक जूल (J) है।

प्रश्न 2.
एक किलोग्राम पत्थर के किसी टुकड़े को एक मीटर ऊँचाई तक उठाने में कितनी ऊर्जा की आवश्यकता होगी ?
उत्तर-
9.8 जूल। [∵ W = mgh = 1 × 9.8 × 1 = 9.8 जूल]

प्रश्न 3.
किसी पिंड के वेग में क्या परिवर्तन करना चाहिए जिससे कि पिंड का द्रव्यमान चार गुणा बढ़ाने पर भी उसकी गतिज ऊर्जा में कोई परिवर्तन न हो ?
उत्तर-
वेग आधा करना पड़ेगा।

प्रश्न 4.
यांत्रिक ऊर्जा के दो प्रकार बताओ।
उत्तर-

1. स्थितिज ऊर्जा
2. गतिज ऊर्जा।

प्रश्न 5.
ऊर्जा की SI इकाई क्या है ?
उत्तर-
जूल।

प्रश्न 6.
शक्ति की SI इकाई क्या है ?
उत्तर-
वाट।

प्रश्न 7.
यदि एक 5 किलोवाट शक्ति के किसी स्रोत को 3 घंटे तक उपयोग किया जाए तो ऊर्जा आपूर्ति कितनी होगी ?
उत्तर-
15 किलोवाट घंटा (kWh)।

प्रश्न 8.
व्यापारिक स्तर पर ऊर्जा के मात्रक का नाम लिखकर उसकी परिभाषा लिखिए।
उत्तर-
व्यापारिक स्तर पर ऊर्जा का मात्रक किलोवाट-घंटा है।
किलोवाट-घंटा – यदि एक किलोवाट शक्ति का 1 घंटा उपयोग किया जाये तो ऊर्जा की आपूर्ति एक किलोवाटघंटा (kWh) के बराबर होती है।

प्रश्न 9.
चाबी द्वारा खिलौना चलाने से कौन-सी ऊर्जा किस ऊर्जा में परिवर्तित होती है ?
उत्तर-
खिलौने की आकृति के कारण स्थितिज ऊर्जा गतिज ऊर्जा में परिवर्तित होती है।

प्रश्न 10.
हथेलियों के परस्पर रगड़ने से वे गर्म क्यों हो जाती हैं ?
उत्तर-
हथेलियों की गतिज ऊर्जा, ऊष्मीय ऊर्जा में रूपांतरित होती है।

प्रश्न 11.
पनचक्की द्वारा ऊर्जा का कौन-सा रूप कार्य में परिवर्तित होता है ?
उत्तर-
गतिज ऊर्जा।

प्रश्न 12.
शक्ति, ऊर्जा तथा समय का परस्पर संबंध बताओ।
उत्तर-

प्रश्न 13.
वे कौन-से दो कारक हैं जिन पर स्थितिज ऊर्जा निर्भर करती है ?
उत्तर-

1. द्रव्यमान और
2. वेग।

प्रश्न 14.
बाँध के एकत्रित पानी में कौन-सी ऊर्जा होती है ?
उत्तर-
स्थितिज ऊर्जा।

प्रश्न 15.
जब हम सीढ़ियां चढ़ते हैं तो कौन-सी ऊर्जा का प्रयोग करते हैं ?
उत्तर-
मांसपेशियों की ऊर्जा।

प्रश्न 16.
तेज़ आंधी वाले दिन कई मकानों की छतें क्यों उड़ जाती हैं ?
उत्तर-
तेज़ आंधी की गतिज ऊर्जा के कारण।

प्रश्न 17.
एक किलोवाट शक्ति का कोई इंजन एक घंटे में कितनी ऊर्जा की आपूर्ति करेगा ?
उत्तर-
ऊर्जा = 1 किलोवाट × 1 घंटा = 1 किलोवाट घंटा।

प्रश्न 18.
एक इंजन एक मिनट में 6000 जूल ऊर्जा पैदा करता है। उसकी शक्ति कितनी है ?
उत्तर-

= 100 जूल/सेकंड
= 100 वाट

प्रश्न 19.
एक किलोग्राम पानी को 5 मीटर ऊपर उठाने में कितना कार्य करना पड़ेगा ?
उत्तर-
पानी उठाने में किया गया कार्य = स्थितिज ऊर्जा
= m × g × h
= 1 × 10 × 5
= 50 जूल

प्रश्न 20.
अगर किसी वस्तु का वेग तीन गुना बढ़ा दिया जाए तो उसकी गतिज ऊर्जा पर क्या असर होगा ?
उत्तर-
∵ K.E. ∝ v²
∴ यह 9 गुना हो जायेगी।

प्रश्न 21.
5 किलोग्राम भार को 20 मीटर ऊँचाई तक उठाने के लिए लगभग कितनी ऊर्जा की आवश्यकता
होती है ?
उत्तर-
स्थितिज ऊर्जा = 5 × 10 × 20 = 1000 जूल।

प्रश्न 22.
यदि किसी वस्तु को गर्म किया जाये तो उसके कणों को गतिज ऊर्जा के साथ क्या होगा ?
उत्तर-
गतिज ऊर्जा में वृद्धि हो जाएगी।

प्रश्न 23.
गुलेल के खिंचे हुए रबड़ में ऊर्जा का कौन-सा रूप है ?
उत्तर-
स्थितिज ऊर्जा।

प्रश्न 24.
अधिकतम तथा न्यूनतम मात्रा में कार्य करने के लिए बल तथा विस्थापन के मध्य कितने अंश का कोण होना चाहिए ?
उत्तर-
अधिकतम कार्य के लिए θ = 0°
न्यूनतम कार्य के लिए θ = 90°

प्रश्न 25.
एक कुली सूटकेस को सिर पर उठाए हुए प्लेटफार्म पर आधे घंटे से खड़ा हुआ है। बताओ उसने कितना कार्य किया है ?
उत्तर-
शून्य, क्योंकि भार में कोई विस्थापन नहीं है।

प्रश्न 26.
एक व्यक्ति कठोर दीवार को 500 N बल से दबा रहा है। बताओ उसने कितना कार्य किया ?
उत्तर-
शून्य

प्रश्न 27.
एक कृत्रिम उपग्रह कितना कार्य करता है जब वह धरती के गिर्द घूमता है?
उत्तर-
शून्य क्योंकि धरती का गुरुत्व बल उपग्रह की गति की दिशा के लम्बवत् क्रिया करता है।

प्रश्न 28.
एक कार का वेग 4 गुना करने से उसकी गतिज ऊर्जा को कैसे प्रभावित करेगा ?
उत्तर-
कार की गतिज ऊर्जा पहले से 16 गुना बढ़ जाएगी क्योंकि गतिज ऊर्जा ∝ (वेग)²।

प्रश्न 29.
गतिज ऊर्जा पर किसका अधिक प्रभाव होगा-द्रव्यमान या वेग दो गुणा करने पर ?
उत्तर-
वेग का प्रभाव अधिक होगा।
गतिज ऊर्जा ∝ द्रव्यमान
तथा गतिज ऊर्जा ∝ (वेग)²।

प्रश्न 30.
स्थिति परिवर्तन के कारण उत्पन्न हुई स्थितिज ऊर्जा का एक उदाहरण दीजिए।
उत्तर-
बाँध के पीछे एकत्रित पानी में स्थितिज ऊर्जा होती है।

प्रश्न 31.
स्प्रिंग को दबाने से उसमें किस किस्म की ऊर्जा होती है।
उत्तर-
स्थितिज ऊर्जा।

प्रश्न 32.
एक ऐसा उदाहरण दें जब वस्तु में गतिज ऊर्जा तथा स्थितिज ऊर्जा उपस्थित हो।
उत्तर-
ऊँचाई पर उड़ रहे जहाज़ में दोनों स्थितिज ऊर्जा तथा गतिज ऊर्जा होती हैं।

प्रश्न 33.
एक ऐसा उदाहरण दें जब वस्तु की आकृति में हुए परिवर्तन के कारण स्थितिज ऊर्जा हो।
उत्तर-
खिंचे हुए कमान में आकृति परिवर्तन के फलस्वरूप स्थितिज ऊर्जा होती है।

प्रश्न 34.
क्या चलती हुई कार के ऊपर खड़े व्यक्ति में गतिज ऊर्जा होगी ?
उत्तर-
हाँ, उसमें गतिज ऊर्जा होगी क्योंकि वह कार के साथ कार की गति बाँट रहा है।

प्रश्न 35.
क्या गतिज ऊर्जा ऋणात्मक हो सकती है ?
उत्तर-
नहीं, क्योंकि दोनों m तथा 02 धनात्मक हैं।

प्रश्न 36.
क्या ऐसी परिस्थिति हो सकती है कि वस्तु में संवेग हो परंतु ऊर्जा न हो ?
उत्तर-
नहीं, यदि वस्तु में संवेग है तो वह वस्तु अवश्य गतिशील होगा और फिर उसमें गतिज ऊर्जा होगी।

प्रश्न 37.
ऊर्जा संरक्षण नियम क्या है ?
उत्तर-
ऊर्जा संरक्षण नियम – “ऊर्जा न तो उत्पन्न की जा सकती है और न ही नष्ट की जा सकती है। ऊर्जा केवल एक रूप से दूसरे रूप में रूपांतरित की जा सकती है।” अर्थात् ऊर्जा रूपांतरण के दौरान निकाय की कुल ऊर्जा नियत रहती है।

प्रश्न 38.
कौन-सी युक्ति विद्युत् ऊर्जा को यांत्रिक ऊर्जा में रूपांतरित करती है ?
उत्तर-
विद्युत् मोटर।

प्रश्न 39.
विद्युत् पंखे में कौन-सी ऊर्जा किस ऊर्जा में रूपांतरित होती है ?
उत्तर-
विद्युत् ऊर्जा यांत्रिक ऊर्जा में रूपांतरण होता है।

प्रश्न 40
हाइड्रो इलैक्ट्रिक पावर स्टेशन पर किस प्रकार की ऊर्जा का रूपांतरण होता है ?
उत्तर-
गिरते हुए पानी की स्थितिज ऊर्जा का रूपांतरण गतिज ऊर्जा में और फिर विद्युत् ऊर्जा में परिवर्तन।

प्रश्न 41.
वाट तथा किलोवाट में क्या संबंध है ?
उत्तर-
1 किलोवाट = 1000 वाट।

प्रश्न 42.
ऊर्जा के S.I. मात्रक तथा 1 kWh में संबंध बताओ।
उत्तर-
ऊर्जा का S.I. मात्रक जूल है-
1 kWh = 3.6 × 10⁶ जूल

प्रश्न 43.
जब हम किसी गेंद को फेंकते हैं तो किस प्रकार का ऊर्जा रूपांतरण होता है ?
उत्तर-
भोजन से रासायनिक क्रिया द्वारा हमारे शरीर को पेशीय ऊर्जा प्राप्त होती जिसका प्रयोग हम गेंद को फेंकने में करते हैं। यह पेशीय ऊर्जा गतिज ऊर्जा में परिवर्तित होती है।

प्रश्न 44.
बंदूक से निकली गोली लक्ष्य से टकरा कर रुक गई। बताइए गोली की गतिज ऊर्जा किन रूपों में रूपांतरित हुई।
उत्तर-
गोली की गतिज ऊर्जा लक्ष्य से टकराकर प्रकाश ऊर्जा, ध्वनि ऊर्जा तथा ऊष्मीय ऊर्जा में रूपांतरित हो गई।

प्रश्न 45.
ऊर्जा अदिश राशि है अथवा सदिश राशि ?
उत्तर-
ऊर्जा एक अदिश राशि है।

प्रश्न 46.
किन दशाओं में किसी पिंड पर बल लगाने से बल द्वारा किया गया कार्य शून्य होगा ?
उत्तर-
जब बल पिंड की गति के लंबवत् हो अथवा पिण्ड का विस्थापन शून्य हो।

प्रश्न 47.
कलाई घड़ी में ऊर्जा का स्रोत क्या होता है ?
उत्तर-
कमानी में संचित प्रत्यास्थ स्थितिज ऊर्जा।