Punjab State Board PSEB 9th Class Science Important Questions Chapter 8 ਗਤੀ Important Questions and Answers.
PSEB 9th Class Science Important Questions Chapter 8 ਗਤੀ
ਵੱਡੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Long Answer Type Questions)
ਪ੍ਰਸ਼ਨ 1.
ਗਣਿਤਿਕ ਵਿਧੀ ਦੁਆਰਾ ਗਤੀ ਦੀਆਂ ਸਮੀਕਰਣਾਂ ਨੂੰ ਸਥਾਪਿਤ ਕਰੋ ।
ਉੱਤਰ-
ਇੱਕ ਸਮਾਨ ਵੇਗ ਦੇ ਅਧੀਨ ਗਤੀ ਦੇ ਸਮੀਕਰਣ-ਇੱਕ ਸਮਾਨ ਵੇਗ ਨਾਲ ਸਰਲ ਰੇਖੀ ਗਤੀ ਕਰ ਰਹੀ ਵਸਤੂ ਦੇ ਲਈ ਅੱਗੇ ਲਿਖੇ ਸਮੀਕਰਨ ਹਨ-
(i) v = u + at
(ii) s = ut + \(\frac {1}{2}\)at2
(iii) v2 – u2 = 2aS
(i) ਗਤੀ ਦਾ ਪਹਿਲਾ ਸਮੀਕਰਨ-v= u + at
ਮੰਨ ਲਓ ਕਿਸੇ ਗਤੀਸ਼ੀਲ ਵਸਤੁ ਦਾ ਆਰੰਭਿਕ ਵੇਗ u ਅਤੇ ਇੱਕ ਸਮਾਨ ਵੇਗ ‘a’ ਹੈ । ਮੰਨ ਲਓ ‘t’ ਸੈਕਿੰਡ ਵਿੱਚ S ਦੁਰੀ ਤੈਅ ਕਰਨ ਬਾਅਦ ਵਸਤੁ ਦਾ ਅੰਤਿਮ ਵੇਗ v ਹੋ ਜਾਂਦਾ ਹੈ ।
1 ਸੈਕਿੰਡ ਵਿੱਚ ਵਸਤੂ ਦੇ ਵੇਗ ਵਿੱਚ ਵਾਧਾ = a
t ਸੈਕਿੰਡ ਵਿੱਚ ਵਸਤੂ ਦੇ ਵੇਗ ਵਿੱਚ ਵਾਧਾ = a × t
∴ t ਸੈਕਿੰਡ ਬਾਅਦ ਵਸਤੂ ਦਾ ਵੇਗ = ਵਸਤੂ ਦਾ ਆਰੰਭਿਕ ਵੇਗ +t ਸੈਕਿੰਡ ਵਿੱਚ ਵਸਤੂ ਦੇ ਵੇਗ ਵਿੱਚ ਹੋਇਆ ਵਾਧਾ
V = u + (a × t) ਅਰਥਾਤ
V = u + at
(ii) ਗਤੀ ਦੀ ਦੂਸਰਾ ਸਮੀਕਰਣ – S = ut + \(\frac {1}{2}\)at2
ਮੰਨ ਲਓ ਕਿਸੇ ਗਤੀਸ਼ੀਲ ਵਸਤੂ ਦਾ ਮੁੱਢਲਾ ਵੇਗ u ਅਤੇ ਇੱਕ ਸਮਾਨ ਵੇਗ a ਹੈ ਅਤੇ t ਸੈਕਿੰਡ ਤੋਂ ਬਾਅਦ ਵਸਤੂ ਦਾ ਅੰਤਿਮ ਵੇਗ v ਹੋ ਜਾਂਦਾ ਹੈ, ਤਾਂ
ਹਰ ਇੱਕ ਸੈਕਿੰਡ ਬਾਅਦ ਵਸਤੂ ਦੇ ਵੇਗ ਵਿੱਚ ਵਾਧਾ = a
∴ ਗਤੀ ਆਰੰਭ ਹੋਣ ਤੋਂ 1 ਸੈਕਿੰਡ ਬਾਅਦ ਵਸਤੁ ਦਾ ਵੇਗ = u + a
ਗਤੀ ਸਮਾਪਤ ਹੋਣ ਤੋਂ 1 ਸੈਕਿੰਡ ਪਹਿਲਾਂ ਵਸਤੂ ਦਾ ਵੇਗ = v – a
∴ ਇਹਨਾਂ ਦੋ ਸੈਕਿੰਡਾਂ ਵਿੱਚ ਵਸਤੂ ਦਾ ਔਸਤ ਵੇਗ = \(\frac{(u+a)+(v-a)}{2}\)
= \(\frac{u+v}{2}\)
ਇਸੇ ਤਰਾਂ ਗਤੀ ਆਰੰਭ ਹੋਣ ਤੋਂ 2 ਸੈਕਿੰਡ ਬਾਅਦ ਵਸਤੁ ਦਾ ਵੇਗ = (u + 2a)
ਗਤੀ ਸਮਾਪਤ ਹੋਣ ਤੋਂ ਬਾਅਦ 2 ਸੈਕਿੰਡ ਪਹਿਲਾਂ ਵਸਤੂ ਦਾ ਵੇਗ = (v – 2a)
∴ ਇਨ੍ਹਾਂ 2 ਸੈਕਿੰਡਾਂ ਵਿੱਚ ਵਸਤੁ ਦਾ ਔਸਤ ਵੇਗ = \(\frac{(u+2 a)+(v-2 a)}{2}\)
= \(\frac{u+v}{2}\)
ਇਸ ਲਈ ਗ ਰੇਡੀਅਨ ਹੋਣ ‘ਤੇ ਵਸਤੂ ਦਾ ਔਸਤ ਵੇਗ ਹਮੇਸ਼ਾ ਤੋਂ \(\frac{u+v}{2}\) ਰਹਿੰਦਾ ਹੈ ।
ਇਸ ਲਈ ਵਸਤੂ ਦੁਆਰਾ ‘t’ ਸੈਕਿੰਡ ਵਿੱਚ ਤੈਅ ਹੋਈ ਦੂਰੀ = ਵਸਤੂ ਦਾ ਔਸਤ ਵੇਗ × ਸਮਾਂ
S = (\(\frac{u+v}{2}\)) × t
ਪਰੰਤੂ ਗਤੀ ਦੀ ਪਹਿਲੀ ਸਮੀਕਰਨ ਅਨੁਸਾਰ v = u + at
∴ S = [latex]\frac{u+(u+a t)}{2}[/latex] × t
= (\(\frac{2 u+a t}{2}\)) × t
S = \(\frac{2 u t+a t^{2}}{2}\)
S = \(\frac{2 u t}{2}+\frac{a t^{2}}{2}\)
∴ S = ut + \(\frac {1}{2}\)at2
(iii) ਗਤੀ ਦਾ ਤੀਸਰਾ ਸਮੀਕਰਨ- v2 – u2 = 2as
ਗਤੀ ਦੇ ਪਹਿਲੇ ਸਮੀਕਰਨ ਤੋਂ, v = u + at
ਦੋਨਾਂ ਪਾਸੇ ਵਰਗ ਕਰਨ ਤੇ v2 = (u + at)2
= u2 + 2u at + a2 t2
v2 = u2 + 2a (ut + \(\frac {1}{2}\)at2)
ਪਰੰਤੂ ਗਤੀ ਦੀ ਦੂਜੀ ਸਮੀਕਰਨ ਤੋਂ, S = ut + \(\frac {1}{2}\)at2
∴ v2 = u2 + 2aS
ਜਾਂ v2 – u2 = 2aS
![]()
ਪ੍ਰਸ਼ਨ 2.
ਇੱਕ ਸਮਾਨ ਵੇਗ ਨਾਲ ਗਤੀਸ਼ੀਲ ਵਸਤੂ ਲਈ ਗਰਾਫ਼ ਵਿਧੀ (ਜਿਊਮੈਟਰੀਕਲ ਵਿਧੀ) ਦੁਆਰਾ ਹੇਠ ਲਿਖੇ ਸੰਬੰਧ ਸਥਾਪਿਤ ਕਰੋ ।
(i) v = u + at
(ii) S = ut + \(\frac {1}{2}\)at2
(iii) v2 = u2 + 2 aS
ਉੱਤਰ-
(i) ਗਰਾਫ਼ ਦੁਆਰਾ ਗਤੀ ਦੇ ਸਮੀਕਰਨਾਂ ਨੂੰ ਸਥਾਪਿਤ ਕਰਨਾ-
ਮੰਨ ਲਓ ਕੋਈ ਵਸਤੁ ਆਰੰਭਿਕ ਵੇਗ ਘ ਅਤੇ ਸਮਾਨ ਪਵੇਗa ਨਾਲ ਚਲਦੀ ਹੈ ਅਤੇ t ਸਮੇਂ ਬਾਅਦ ਵਸਤੂ ਦੇ
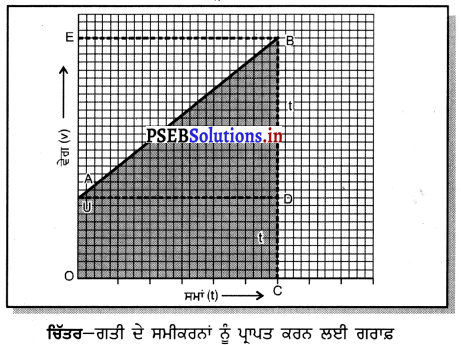
ਵੇਗ v ਹੋ ਜਾਂਦਾ ਹੈ । ਜੇਕਰ x-ਅਕਸ਼ ਤੇ ਸਮਾਂ ਅਤੇ y-ਅਕਸ਼ ਤੇ ਵੇਗ ਨੂੰ ਨਿਰੂਪਤ ਕਰੀਏ ਤਾਂ ਵਸਤੂ ਦਾ ਵੇਗ-ਸਮਾਂ ਗਰਾਫ਼ ਇੱਕ ਝੁਕੀ ਹੋਈ ਸਰਲ ਰੇਖਾ AB ਦੇ ਰੂਪ ਵਿੱਚ ਪ੍ਰਾਪਤ ਹੋਵੇਗਾ । ਇਸ ਗਰਾਫ਼ ਦੀ ਮੱਦਦ ਨਾਲ ਅਸੀਂ ਗਤੀ ਦੇ ਸਮੀਕਰਣਾਂ ਨੂੰ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਪ੍ਰਾਪਤ ਕਰ ਸਕਦੇ ਹਾਂ ।
BC = BD + DC
= BD + OA (∵ DC = OA)
ਇਸ ਵਿੱਚ BC = v ਅਤੇ OA = u ਰੱਖਣ ਮਗਰੋਂ,
v = BD + u
ਜਾਂ BD = v – u …………….. (1)
ਵੇਗਾ-ਸਮਾਂ ਗਰਾਫ਼ ਤੋਂ ਵਸਤੂ ਦੇ ਵੇਗ ਨੂੰ ਦਰਸਾਇਆ ਜਾ ਸਕਦਾ ਹੈ,

= \(\frac{\mathrm{BD}}{\mathrm{AD}}\)
a = \(\frac{B D}{O C}\) (∵ AD = OC)
ਪਰੰਤੂ OC = t
a = \(\frac{\mathrm{BD}}{t}\)
ਜਾਂ
BD = at …………(2)
ਸਮੀਕਰਨ (1) ਅਤੇ (2) ਤੋਂ
at = v – u
ਜਾਂ v = u + at
(ii) ਗਤੀ ਦਾ ਦੂਸਰਾ ਸਮੀਕਰਨ ਜਾਂ ਸਮਾਂ-ਸਥਿਤੀ ਸੰਬੰਧ) S = ut + \(\frac {1}{2}\)at2
ਮੰਨ ਲਓ ਇੱਕ ਵਸਤੂ ਦਾ ਇੱਕ ਸਮਾਨ ਵੇਗ a ਨਾਲ ( ਸਮੇਂ ਵਿੱਚ S ਦੂਰੀ ਤੈਅ ਕਰਦੀ ਹੈ । ਚਿੱਤਰ ਵਿੱਚ ਵਸਤੂ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ, ਵੇਗ ਸਮਾਂ ਗਰਾਫ਼ AB ਦੇ ਹੇਠਾਂ ਘਿਰੇ ਹੋਏ ਖੇਤਰ OABC ਦੇ ਖੇਤਰਫਲ ਦੁਆਰਾ ਪ੍ਰਾਪਤ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ ।
ਇਸ ਤਰ੍ਹਾਂ, ਵਸਤੂ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ = ਹੇਠ ਦਿੱਤੀ ਵਿਧੀ ਰਾਹੀਂ ਪਤਾ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ-
S = OABC ਦਾ ਖੇਤਰਫਲ ਜੋਕਿ ਸਮਲੰਬ ਚਤੁਰਭੁਜ ਹੈ
= ਆਇਤ OADC ਦਾ ਖੇਤਰਫਲ + ਤ੍ਰਿਭੁਜ ABD ਦਾ ਖੇਤਰਫਲ
= OA × OC + \(\frac {1}{2}\)(AD × BD)
ਇੱਥੇ OA = u
OC = AD = t
ਅਤੇ BD = at ਦਾ ਮਾਨ ਰੱਖਣ ਮਗਰੋਂ
S = u × t + \(\frac {1}{2}\) (t × at)
ਜਾਂ S = ut + \(\frac {1}{2}\)at2
(iii) ਤੀਸਰਾ ਗਤੀ ਸਮੀਕਰਣ- v2 – u2 = 2 as (ਵੇਗ ਸਥਿਤੀ ਸੰਬੰਧ ਸਥਾਪਿਤ ਕਰਨਾ)
ਚਿੱਤਰ ਵਿੱਚ ਦਰਸਾਇਆ ਗਿਆ ਵੇਗ-ਸਮਾਂ ਗਰਾਫ਼ ਤੋਂ ਵਸਤੁ ਦੁਆਰਾ ਇੱਕ ਸਮਾਨ ਪਵੇਗ a ਨਾਲ t ਸਮੇਂ ਵਿੱਚ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ ਨੂੰ ਸਮਲੰਬ ਚਤੁਰਭੁਜ OABC ਦੁਆਰਾ ਘੇਰੇ ਗਏ ਖੇਤਰਫਲ ਰਾਹੀਂ ਪ੍ਰਦਰਸ਼ਿਤ ਕੀਤਾ ਗਿਆ ਹੈ । ਅਰਥਾਤ-
S = ਸਮਲੰਬ ਚਤੁਰਭੁਜ OABC ਦਾ ਖੇਤਰਫਲ
= \(\frac{(\mathrm{OA}+\mathrm{BC}) \times \mathrm{OC}}{2}\)
ਇੱਥੇ OA = u, BC = v ਅਤੇ OC = t ਰੱਖਣ ਮਗਰੋਂ,
S = \(\frac{(u+v) \times t}{2}\) (3)
ਦੇਗ-ਸਮਾਂ ਸੰਬੰਧ v = u+ at ਤੋਂ ਪ੍ਰਾਪਤ ਹੈ t = \(\frac{v-u}{a}\) (4)
ਸਮੀਕਰਨ (3) ਅਤੇ (4) ਤੋਂ S = \(\frac{(v+u)(v-u)}{2 a}\)
ਜਾਂ 2 aS = v2 – u2
∴ v2 = u2 + 2as
ਪ੍ਰਸ਼ਨ 3
(ਉ) ਦੂਰੀ-ਸਮਾਂ ਗਰਾਫ਼ ਕੀ ਹੈ ?
(ਅ) ਦੂਰੀ-ਸਮਾਂ ਗਰਾਫ਼ ਦੀ ਢਾਲ ਕੀ ਦਰਸਾਉਂਦੀ ਹੈ ?
ਉੱਤਰ-
(ਉ) ਦੂਰੀ-ਸਮਾਂ ਗਰਾਫ਼ – ਇਹ ਕਿਸੇ ਵਸਤੂ ਦੁਆਰਾ ਤੈਅ ਹੋਈ ਦੂਰੀ ਅਤੇ ਇਸ ਦੂਰੀ ਨੂੰ ਤੈਅ ਕਰਨ ਲਈ ਲੱਗੇ ਸਮੇਂ ਵਿਚਕਾਰ ਰੇਖਾਂਕਿਤ ਪ੍ਰਦਰਸ਼ਣ ਹੈ ਅਰਥਾਤ ਸਮੇਂ ਦੇ ਸਾਪੇਖ ਦੂਰੀ ਨੂੰ ਚਿੱਤਰ ਦੁਆਰਾ ਨਿਰੂਪਣ ਕਰਨਾ ਹੈ । ਇਹ ਗਰਾਫ਼ ਸਰਲ ਰੇਖੀ ਹੋ ਸਕਦਾ ਹੈ ਅਤੇ ਨਹੀਂ ਵੀ ਹੋ ਸਕਦਾ ਹੈ ।
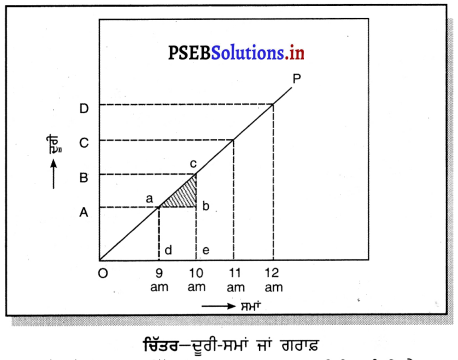
ਦੂਰੀ-ਸਮੇਂ ਦਾ ਅਰਥ – ਜਦੋਂ ਕੋਈ ਵਸਤੁ ਇੱਕ ਸਮਾਨ ਚਾਲ ਨਾਲ ਗਤੀਸ਼ੀਲ ਹੁੰਦੀ ਹੈ, ਤਾਂ ਇਹ ਸਮਾਨ ਸਮਾਂ ਅੰਤਰਾਲਾਂ ਵਿੱਚ ਸਮਾਨ ਦੁਰੀ ਤੈਅ ਕਰਦੀ ਹੈ । ਇੱਕ ਸਮਾਨ ਚਾਲ ਨਾਲ ਗਤੀਸ਼ੀਲ ਵਸਤੂ ਦਾ ਦੂਰੀ-ਸਮਾਂ ਗਰਾਫ਼ ਹਮੇਸ਼ਾ ਸਰਲ ਰੇਖੀ ਹੁੰਦਾ ਹੈ ।
ਉਦਾਹਰਨ – ਨਾਲ ਦਿੱਤੇ ਗਏ ਸਮਾਂ-ਦੁਰੀ ਗਰਾਫ਼ ਤੋਂ ਇਹ ਪਤਾ ਲਗਦਾ ਹੈ ਕਿ 9 AM ਤੋਂ 10 AM ਅਤੇ 11 AM ਤੋਂ 12 AM ਸਮਾਂ ਅੰਤਰਾਲਾਂ ਵਿੱਚ ਲੜੀਵਾਰ AB ਅਤੇ CD ਦੂਰੀ ਤੈਅ ਹੋਈ ਹੈ ।
ਅਤੇ AB = CD
ਇਸ ਲਈ ਸਮਾਨ ਦੂਰੀ ਸਮਾਨ ਸਮਾਂ ਅੰਤਰਾਲਾਂ ਵਿੱਚ ਤੈਅ ਹੁੰਦੀ ਹੈ ਜਿਸ ਕਰਕੇ ਚਾਲ ਇੱਕ ਸਮਾਨ ਹੈ ।
(ਅ) ਦੂਰੀ-ਸਮਾਂ ਗਰਾਫ਼ ਦੀ ਚਾਲ – ਮੰਨ ਲਓ a ਅਤੇ c ਸਮਾਂ-ਦੁਰੀ ਗਰਾਫ਼ ਤੇ ਇੱਕ-ਦੂਜੇ ਦੇ ਨੇੜੇ ਵਾਲੇ ਬਿੰਦੁ ਹਨ । ad ਅਤੇ ce ਦੋ ਲੰਬ ਕ੍ਰਮਵਾਰ 2 ਅਤੇ c ਤੋਂ ਸਮਾਂ-ਅਕਸ਼ (x-ਅਕਸ਼) ‘ਤੇ ਖਿੱਚੋ ।
ਹੁਣ ਤ੍ਰਿਭੁਜ ab-c ਵਿੱਚ ਅਨੁਪਾਤ \(\frac{b c}{a b}\) ਨੂੰ ਗਰਾਫ਼ ਦੀ ਢਾਲ ਕਹਿੰਦੇ ਹਨ ।
∴ ਰੇਖਾ ਦੀ ਢਾਲ = \(\frac{b c}{a b}\) ਜਿੱਥੇ bc ਵਸਤੂ ਦੁਆਰਾ ਤੈਅ ਹੋਈ ਦੂਰੀ ਹੈ ਅਤੇ ab ਇਸ ਦੂਰੀ ਨੂੰ ਤੈਅ ਕਰਨ ਲਈ ਲੱਗਿਆ ਸਮਾਂ ਹੈ ।

∴ ਰੇਖਾ OP ਦੀ ਢਾਲ ਵਸਤੁ ਦੀ ਚਾਲ ਨੂੰ ਦਰਸਾਉਂਦੀ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 4.
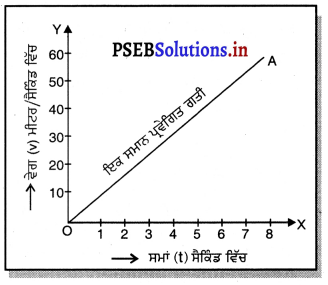
ਵੇਗ-ਸਮਾਂ ਗਰਾਫ਼ ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਇੱਕ ਸਮਾਨ ਵੇਗ ਨਾਲ ਗਤੀਸ਼ੀਲ ਕਿਸੇ ਵਸਤੂ ਦੀ ਦੂਰੀ ਕਿਵੇਂ ਪਤਾ ਕਰੋਗੇ ? ਉਦਾਹਰਨ ਸਹਿਤ ਸਮਝਾਓ ? · ਉੱਤਰ-
ਇੱਕ ਸਮਾਨ ਗਤੀ ਲਈ ਵੇਗ-ਸਮਾਂ ਗਰਾਫ਼-ਇੱਕ ਸਮਾਨ ਗਤੀ ਲਈ ਕਿਸੇ ਵਸਤੁ ਦਾ ਵੇਗ-ਸਮਾਂ ਗਰਾਫ਼ ਉਹ ਗਰਾਫ਼ ਹੁੰਦਾ ਹੈ ਜਦੋਂ ਕੋਈ ਵਸਤੂ ਸਥਿਰ ਵੇਗ ਨਾਲ ਚੱਲ ਰਹੀ ਹੋਵੇ । ਅਜਿਹੀ ਅਵਸਥਾ ਵਿੱਚ ਵੇਗ-ਸਮਾਂ ਗਰਾਫ਼ Xਧੁਰੇ ਦੇ ਸਮਾਨਾਂਤਰ ਹੁੰਦਾ ਹੈ । ਇਹ ਗਰਾਫ਼ ਚਿੱਤਰ ਵਿੱਚ ਸਰਲ ਰੇਖਾ RS ਦੁਆਰਾ ਦਰਸਾਇਆ ਗਿਆ ਹੈ ।
ਮੰਨ ਲਓ ਰਮੇਸ਼ ਆਪਣੇ ਮੋਟਰ ਸਾਈਕਲ ਤੇ 40 km/h ਦੇ ਸਥਿਰ ਵੇਗ ਨਾਲ ਜਾ ਰਿਹਾ ਹੈ । ਇਸਦਾ ਅਰਥ ਇਹ ਹੈ ਕਿ ਕਿਸੇ ਵੀ ਸਮਾਂ ਅੰਤਰਾਲ ‘ਤੇ ਉਸਦਾ ਵੇਗ 40 km/h ਤੇ ਸਥਿਰ ਰਹੇਗਾ । ਇਸ ਲਈ ਉਹ ਪਹਿਲੇ ਇੱਕ ਘੰਟੇ ਵਿੱਚ 40km, ਦੂਜੇ ਘੰਟੇ ਵਿੱਚ 80km ਅਤੇ ਤੀਜੇ ਘੰਟੇ ਵਿੱਚ 120km ਦੂਰੀ ਤੈਅ ਕਰੇਗਾ । ਅਗਲੇ ਹਰੇਕ ਘੰਟੇ ਵਿੱਚ ਵੀ ਉਸਦੀ ਦੁਰੀ ਇਸੇ ਤਰ੍ਹਾਂ ਵਧਦੀ ਜਾਵੇਗੀ ।
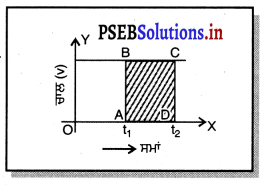
ਵੇਗ-ਸਮਾਂ ਗਰਾਫ਼ ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਅਸੀਂ ਕਿਸੇ ਵੀ ਦਿੱਤੇ ਸਮੇਂ ਵਿੱਚ ਰਮੇਸ਼ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਕੁੱਲ ਦੂਰੀ ਪਤਾ ਕਰ ਸਕਦੇ ਹਾਂ ।
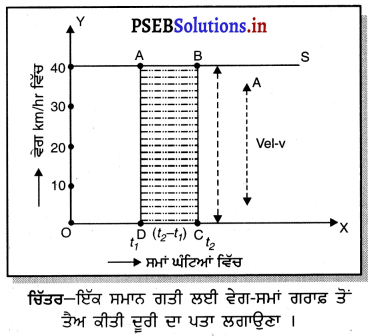
ਤੈਅ ਕੀਤੀ ਦੂਰੀ ਦਾ ਪਤਾ ਲਗਾਉਣਾ । ਸਰਲ ਰੇਖਾ ਗਰਾਫ਼ RS ਉੱਤੇ ਬਿੰਦੂ A ਅਤੇ B ਸਮਾਂ ਅੰਤਰਾਲਾਂ OD = t1 ਅਤੇ OC = t2) ਉੱਤੇ ਰਮੇਸ਼ ਦੀ ਸਥਿਤੀ ਵਿਖਾਉਂਦੇ ਹਨ | ਸਮਾਂ ਮੁਲ ਬਿੰਦੁ 0 ਤੋਂ ਮਾਪਿਆ ਗਿਆ ਹੈ । AD ਅਤੇ BC ਬਿੰਦੁ A ਅਤੇ B ਤੋਂ ਸਮਾਂ-ਧੁਰੇ ਉੱਤੇ ਲੰਬ ਖਿੱਚੇ ਗਏ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ABCD ਇੱਕ ਆਇਤ ਬਣ ਗਈ ਹੈ ।
ਸਮਾਂ ਅੰਤਰਾਲ (OC – OD) = (t2 – t1)
ਵਿੱਚ ਰਮੇਸ਼ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਦੂਰੀ = ਆਇਤ ABCD ਦਾ ਖੇਤਰਫਲ
ਜਾਂ = AD × DC
= ਵੇਗ × ਸਮਾਂ ਅੰਤਰਾਲ
= V × (t2 – t1)
S = V (t2 – t1)
ਜਾਂ S = 40 (t2 – t1) km
ਪ੍ਰਸ਼ਨ 5.
ਇੱਕ ਸਮਾਨ ਗਿਤ ਗਤੀ ਲਈ ਵੇਗ-ਸਮਾਂ ਗਰਾਫ਼ ਬਣਾਓ ਅਤੇ ਇਸ ਗਰਾਫ਼ ਤੋਂ ਤੁਸੀਂ ਵਸਤੂ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਦੂਰੀ ਦਾ ਕਿਵੇਂ ਪਤਾ ਕਰੋਗੇ ?
ਉੱਤਰ-
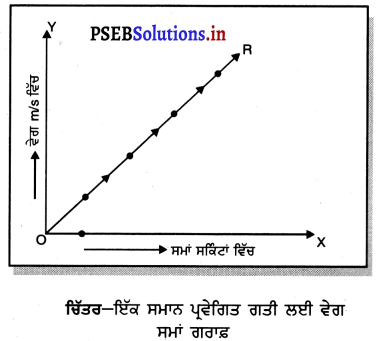
ਇੱਕ ਸਮਾਨ ਪ੍ਰਵੇਗਿਤ ਗਤੀ ਲਈ ਵੇਗਸਮਾਂ ਗਰਾਫ਼-ਜਦੋਂ ਕੋਈ ਵਸਤੂ ਸਥਿਰ ਵੇਗ ਨਾਲ ਨਹੀਂ ਪਰੰਤੂ ਲਗਾਤਾਰ ਵਧਦੇ ਵੇਗ ਨਾਲ ਚੱਲ ਰਹੀ ਹੋਵੇ, ਤਾਂ ਉਹ ਵਸਤੂ ਪ੍ਰਵੇਗਿਤ ਹੁੰਦੀ ਹੈ । ਉਸ ਅਵਸਥਾ ਵਿੱਚ ਵੇਗ-ਸਮਾਂ (v – t) ਗਰਾਫ਼ ਇੱਕ ਸਰਲ ਰੇਖਾ OR ਹੁੰਦੀ ਹੈ ਜੋ ਮੁਲ ਬਿੰਦੁ O ਤੋਂ ਸ਼ੁਰੂ ਹੁੰਦੀ ਹੈ ਅਤੇ ਇਹ ਦੋਵਾਂ ਧੁਰਿਆਂ ਤੇ ਬਰਾਬਰ ਝੁਕੀ ਹੋਈ ਪਰਾਂ ਜਾਂਦੀ ਹੈ ।
ਸਾਹਮਣੇ ਦਿੱਤੇ ਚਿੱਤਰ ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਅਸੀਂ ਇੱਕ ਸਮਾਨ ਵੇਗਤ ਗਤੀ ਨਾਲ ਚੱਲ ਰਹੀ ਵਸਤੂ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਦੁਰੀ ਪਤਾ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ ।
OR ਇੱਕ ਸਰਲ ਰੇਖੀ ਗਰਾਫ਼ ਹੈ । ਗਰਾਫ਼ ਉੱਤੇ ਦੋ ਬਿੰਦੁਆਂ A1 ਅਤੇ A2 ਤੋਂ ਸਮਾਂ ਧੁਰੇ ਉੱਤੇ A1A4 ਅਤੇ A2A3 ਲੰਬ ਖਿੱਚੋ | ਹੁਣ A2A3 ਉੱਤੇ ਇੱਕ ਲੰਬ AC ਵੀ ਖਿੱਚੋ | ਸਮਲੰਬ ਚਤੁਰਭੁਜ A1A2A3A4 ਦਾ ਖੇਤਰਫਲ ਵਸਤੂ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਦੂਰੀ ਹੋਵੇਗੀ ।
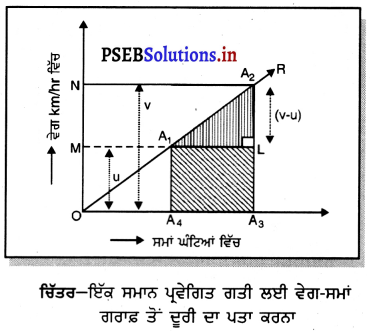
ਸਮਲੰਬ ਚਤੁਰਭੁਜ A1A2A3A4 ਦਾ ਖੇਤਰਫਲ = \(\frac { 1 }{ 2 }\)(A1A4 + A2A3) × A1L
S = \(\frac { 1 }{ 2 }\) (u + v) × ( t2 – t1)
S = (\(\frac{\mathrm{u}+v}{2}\)) × (t2 – t1)
ਅਰਥਾਤ ਤੈਅ ਕੀਤੀ ਦੂਰੀ = ਔਸਤ ਵੇਗ × ਸਮਾਂ
ਪ੍ਰਸ਼ਨ 6.
ਹੇਠ ਲਿਖਿਆਂ ਦੇ ਗਰਾਫ਼ ਖਿੱਚ ਕੇ ਉਦਾਹਰਨ ਦੁਆਰਾ ਸਮਝਾਓ ।
(i) ਇੱਕ ਸਮਾਨ ਵੇਗਿਤ ਗਤੀ
(ii) ਅਸਮਾਨ ਵੇਗਤ ਗਤੀ ।
ਉੱਤਰ-
(1) ਇੱਕ ਸਮਾਨ ਵੇਰਿਤ ਗਤੀ – ਜੇਕਰ ਕਿਸੇ ਵਸਤੂ ਦੇ ਵੇਗ ਵਿੱਚ ਸਮਾਨ ਸਮਾਂ ਅੰਤਰਾਲ ਵਿੱਚ ਸਮਾਨ ਪਰਿਵਰਤਨ (ਬਦਲਾਓ) ਹੁੰਦਾ ਹੈ, ਤਾਂ ਵਸਤੂ ਦੀ ਗਤੀ ਇੱਕ ਸਮਾਨ ਪ੍ਰਵੇਗਿਤ ਹੁੰਦੀ ਹੈ ।
ਚਿੱਤਰ ਵਿੱਚ ਸੁਤੰਤਰਤਾ ਨਾਲ ਡਿੱਗਦੇ ਹੋਏ ਇੱਕ ਪੱਥਰ ਦਾ ਵੇਗ-ਸਮਾਂ ਗਰਾਫ਼ ਪ੍ਰਦਰਸ਼ਿਤ ਹੈ । ਇਸ ਪੱਥਰ ਦਾ ਵੇਗ ਪ੍ਰਤੀ ਸੈਕਿੰਡ 9.8 ਮੀਟਰ/ਸੈਕਿੰਡ ਵੱਧ ਰਿਹਾ ਹੈ ਅਰਥਾਤ ਵਸਤੂ ਦੀ ਗਤੀ ਦਾ ਪਵੇਗ 9.8 ਮੀਟਰ/ਸੈਕਿੰਡ ਹੈ । ਇਹ ਗਰਾਫ਼ ਇੱਕ ਝੁਕੀ ਹੋਈ ਸਰਲ ਰੇਖਾ ਹੈ ਜੋ ਇਹ ਦਰਸਾਉਂਦਾ ਹੈ ਕਿ ਵਸਤ ਦੀ ਗਤੀ ਇੱਕ ਸਮਾਨ ਵੇਗਤ ਗਤੀ ਹੈ ।
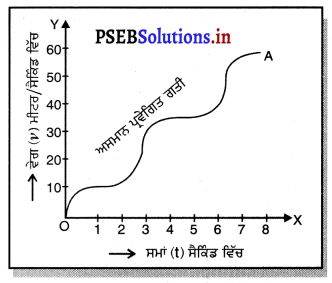
(ii) ਅਸਮਾਨ ਗਿਤ ਗਤੀ – ਜੇਕਰ ਕਿਸੇ ਵਸਤੂ ਦੇ ਵੇਗ ਵਿੱਚ ਸਮਾਨ ਸਮੇਂ ਅੰਤਰਾਲਾਂ ਵਿੱਚ ਪਰਿਵਰਤਨ ਹੁੰਦਾ ਹੈ, ਤਾਂ ਉਸ ਵਸਤੂ ਦੀ ਗਤੀ ਅਸਮਾਨ ਗਿਤ ਕਹਾਉਂਦੀ ਹੈ ।
ਚਿੱਤਰ ਵਿੱਚ ਇੱਕ ਕਾਰ ਦੀ ਗਤੀ ਦਾ ਵੇਗ-ਸਮਾਂ ਗਰਾਫ਼ ਦਿੱਤਾ ਗਿਆ ਹੈ । ਇਸ ਵਿੱਚ ਕਾਰ ਦਾ ਵੇਗ ਘੱਟਦਾ ਵੱਧਦਾ ਹੈ । ਇਹ ਗਰਾਫ਼ ਇੱਕ ਟੇਢੀ ਵਕਰ ਦੇ ਰੂਪ ਵਿੱਚ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ ਜੋ ਇਹ ਦਰਸਾਉਂਦੀ ਹੈ ਕਿ ਕਾਰ ਦੀ ਗਤੀ ਅਸਮਾਨ ਰੂਪ ਨਾਲ ਪ੍ਰਵੇਗਿਤ ਗਤੀ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 7.
(ਉ) ਚੱਕਰਾਕਾਰ ਵਿਤੀ ਗਤੀ ਕੀ ਹੁੰਦੀ ਹੈ ? ਸਮਾਨ ਚਾਲ ਦੀ ਤੀ ਗਤੀ ਪ੍ਰੇਰਿਤ ਕਿਉਂ ਹੁੰਦੀ ਹੈ ?
(ਅ) ਕੋਣੀ ਵੇਗ ਦੀ ਪਰਿਭਾਸ਼ਾ ਦਿਓ । ਇਸਦੀ ਇਕਾਈ ਕੀ ਹੈ ?
(ੲ) ਸਰਲ ਰੇਖੀ ਅਤੇ ਕੋਣੀ ਵੇਗ ਵਿੱਚ ਸੰਬੰਧ ਸਥਾਪਿਤ ਕਰੋ ।
ਉੱਤਰ-
(ਉ) ਚੱਕਰਾਕਾਰ ਵਿਤੀ ਗਤੀ – ਜੇਕਰ ਕਿਸੇ ਗਤੀਮਾਨ ਵਸਤੂ ਦਾ ਗਮਨ ਪੱਥ ਸਰਲ ਰੇਖੀ ਨਾ ਹੋ ਕੇ ਇੱਕ ਵਿਤੀ ਹੋਵੇ ਤਾਂ ਉਸ ਵਸਤੂ ਦੀ ਗਤੀ ਨੂੰ ਚੱਕਰਾਕਾਰ ਵਿਤੀ ਗਤੀ ਆਖਦੇ ਹਨ ।
ਵਿਤੀ ਗਤੀ ਵਿੱਚ ਚਾਲ ਨਾ ਬਦਲਣ ਤੇ ਵੀ ਹਰੇਕ ਬਿੰਦੂ ਤੇ ਦਿਸ਼ਾ ਵਿੱਚ ਹੋਣ ਵਾਲਾ ਪਰਿਵਰਤਨ ਵੇਗ ਵਿੱਚ ਪਰਿਵਰਤਨ ਪੈਦਾ ਕਰਦਾ ਹੈ, ਜਿਸ ਕਰਕੇ ਵਸਤੂ ਦੀ ਗਤੀ ਪਵੇਗਿਤ ਹੁੰਦੀ ਹੈ ।
(ਅ) ਕੋਣੀ ਵੇਗ – ਹਰੇਕ ਇਕਾਈ ਸਮੇਂ ਵਿੱਚ ਹੋਏ ਕੋਈ ਵਿਸਥਾਪਨ ਨੂੰ ਕੋਈ ਵੇਗ ਕਹਿੰਦੇ ਹਨ ।
ਜੇਕਰ t ਸਮੇਂ ਵਿੱਚ ਵਸਤੂ θ ਕੋਣ ਤੈਅ ਕਰਦੀ ਹੈ, ਤਾਂ ਕੋਣੀ ਵੇਗ ਇਸ ਤਰ੍ਹਾਂ ਪ੍ਰਗਟਾਇਆ ਜਾਂਦਾ ਹੈ :-


ਇਹ ω (ਐਮੇਗਾ) ਤੀ ਵੇਗ (ਵਰਤੁਲ ਵੇਗ) ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ ।
∴ ω = \(\frac{\theta}{t}\)
ਕੋਣੀ ਵੇਗ ਦੀ ਇਕਾਈ-ਕੋਣੀ ਵੇਗ ਨੂੰ ਰੇਡੀਅਨ ਪ੍ਰਤੀ ਸੈਕਿੰਡ ਵਿੱਚ ਮਾਪਿਆ ਜਾਂਦਾ ਹੈ ।
(ੲ) ਸਰਲ ਰੇਖੀ ਅਤੇ ਕੋਣੀ ਵੇਗ ਵਿੱਚ ਸੰਬੰਧ – ਮੰਨ ਲਓ ਇੱਕ ਵਸਤੂ ਇੱਕ ਸਮਾਨ ਸਰਲ ਰੇਖੀ ਵੇਗ v ਨਾਲ r = ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਵਿਤ ਵਿੱਚ ਗਤੀ ਕਰ ਰਹੀ ਹੈ ।
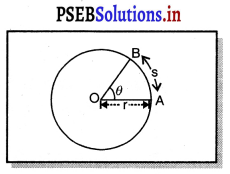
ਮੰਨ ਲਓ ਇਹ ਵਸਤੂ t ਸਮੇਂ ਵਿੱਚ ਸਰਲ ਰੇਖੀ ਦੂਰੀ S ਤੈਅ ਕਰਦੀ ਹੈ ਅਤੇ ਇਸ ਦੇ ਸਾਪੇਖ ਹੀ ਕੋਣ θ ਵਿਸਥਾਪਿਤ ਹੁੰਦਾ ਹੈ,
ਤਾਂ ਕੋਣ (ਰੇਡੀਅਨ ਵਿੱਚ) θ = \(\frac{\mathrm{S}}{r}\) ………….. (1)
= ਪਰੰਤੂ ਸਰਲ ਰੇਖੀ ਦੂਰੀ = ਚਾਲ × ਸਮਾਂ
S = v × t ……………. (2)
ਜਾਂ S = θ × r
ਸਮੀਕਰਨ (2) ਤੋਂ S ਦਾ ਮਾਨ (1) ਵਿੱਚ ਰੱਖਣ ਮਗਰੋਂ
θ × r = v × t
ਜਾਂ θ = \(\frac{v \times t}{\mathbf{r}}\)
ਜਾਂ \(\frac{\theta}{t}=\frac{v}{r}\)
ਪਰੰਤੂ ω = \(\frac{v}{r}\) [∵ \(\) = ω]
ਅਰਥਾਤ v = r × a
ਪ੍ਰਸ਼ਨ 8.
ਇੱਕ ਸਮਾਨ ਚੱਕਰਾਕਾਰ ਗਤੀ ਕੀ ਹੁੰਦੀ ਹੈ ? ਇੱਕ ਸਮਾਨ ਚਾਲ ਦੀ ਚੱਕਰਾਕਾਰ ਗਤੀ ਤ ਗਤੀ ਕਿਉਂ ਹੁੰਦੀ ਹੈ ? ਵਿਵਹਾਰਿਕ ਕਿਰਿਆ ਦੁਆਰਾ ਸਮਝਾਓ । ਇਸ ਤੋਂ ਕੀ ਸਿੱਟਾ ਨਿਕਲਦਾ ਹੈ ?
ਉੱਤਰ-
ਇੱਕ ਸਮਾਨ ਚੱਕਰਾਕਾਰ ਗਤੀ-ਇੱਕ ਸਮਾਨ ਚੱਕਰਾਕਾਰ ਗਤੀ ਉਹ ਗਤੀ ਹੁੰਦੀ ਹੈ ਜਿੱਥੇ ਕਿ ਇੱਕ ਸਮਾਨ ਵੇਗ ਦੀ ਮਾਤਰਾ ਵਿੱਚ ਤਬਦੀਲੀ ਕਾਰਨ ਨਹੀਂ ਪਰੰਤੁ ਵੇਗ ਦੀ ਦਿਸ਼ਾ ਵਿੱਚ ਤਬਦੀਲੀ ਕਾਰਨ ਹੁੰਦੀ ਹੈ | ਜਦੋਂ ਕੋਈ ਵਸਤੂ ਚੱਕਰਾਕਾਰ ਪੱਥ ਵਿੱਚ ਘੁੰਮਦੀ ਹੈ, ਤਾਂ ਉਸ ਚੱਕਰ ਦੇ ਘੇਰੇ ਦੇ ਹਰ ਇੱਕ ਬਿੰਦੁ ਤੇ ਗਤੀ ਦੀ ਦਿਸ਼ਾ ਬਦਲਦੀ ਹੈ । ਵਿਖਾਏ ਗਏ ਚਿੱਤਰ ਵਿੱਚ ਬਿੰਦੂ A, B, C, D ਵਸਤੂ ਦੀਆਂ ਚਾਰ ਸਥਿਤੀਆਂ ਦਰਸਾਉਂਦੇ ਹਨ । AT, BT, CT ਅਤੇ DT ਇਨ੍ਹਾਂ ਬਿੰਦੁਆਂ ਤੇ ਗਤੀ ਦੀਆਂ ਵੱਖ-ਵੱਖ ਦਿਸ਼ਾਵਾਂ ਹਨ । ਕਿਉਂ ਜੋ ਗਤੀ ਦੀ ਦਿਸ਼ਾ ਬਦਲ ਰਹੀ ਹੈ ਇਸ ਲਈ ਵਸਤੁ ਬਦਲੇ ਹੋਏ ਵੇਗ ਨਾਲ ਗਤੀ ਕਰਦੀ ਹੈ । ਇਸ ਲਈ ਇਹ ਗਤੀ ਇੱਕ ਸਮਾਨ ਵੇਗਤ ਹੈ ।
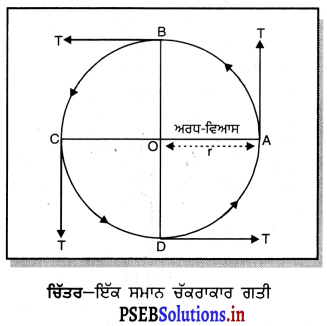
ਮਹੱਤਵਪੂਰਨ ਸਿੱਟਾ – ਮੰਨ ਲਓ ਇੱਕ ਦੌੜਾਕ ਅਰਧ ਵਿਆਸ = r ਵਾਲੇ ਚੱਕਰ ਦੇ ਘੇਰੇ ਦੁਆਲੇ ਇੱਕ ਪੂਰਾ ਚੱਕਰ t ਸੈਕਿੰਡ ਵਿੱਚ ਲਗਾਉਂਦਾ ਹੈ, ਤਾਂ ਉਸਦਾ ਵੇਗ
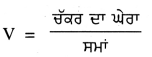
= \(\frac{2 \pi r}{t}\)
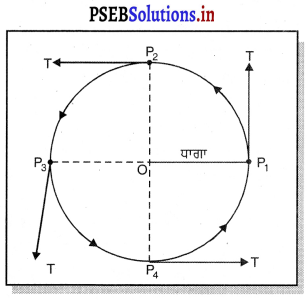
ਵਿਵਹਾਰਿਕ ਕਿਰਿਆ – ਤੁਸੀਂ 1 ਮੀਟਰ ਲੰਬਾ ਨਾਈਲੋਨ ਦਾ ਧਾਗਾ । ਲਓ । ਇਸਦੇ ਇੱਕ ਸਿਰੇ ਤੇ ਧਾਤ ਦਾ ਗੋਲਾ ਬੰਨੋ ਅਤੇ ਧਾਗੇ ਦਾ ਦੂਜਾ ਸਿਰਾ ਆਪਣੇ ਹੱਥ ਵਿੱਚ ਫੜ ਕੇ ਧਾਤ ਦੇ ਗੋਲੇ ਨੂੰ ਚੱਕਰਾਕਾਰ ਪੱਥ ਵਿੱਚ ਘਮਾਓ । ਜਦੋਂ ਗੋਲਾ ਘੁੰਮ ਰਿਹਾ ਹੈ ਤਾਂ ਇਸਦੀ ਚਾਲ ਉਸ ਸਮੇਂ ਇੱਕ ਸਮਾਨ ਰਹਿੰਦੀ ਹੈ, ਪਰ ਇਸਦਾ ਵੇਗ ਹਰੇਕ ਬਿੰਦ ਤੇ ਬਦਲਦਾ ਰਹਿੰਦਾ ਹੈ । ਵੇਗ ਵਿੱਚ ਤਬਦੀਲੀ ਦਾ ਕਾਰਨ ਗੋਲੇ ਦੀ . ਗਤੀ ਦੀ ਦਿਸ਼ਾ ਵਿੱਚ ਤਬਦੀਲੀ ਹੈ । ਗਤੀ ਦੀ ਦਿਸ਼ਾ ਹਮੇਸ਼ਾ ਚੱਕਰਾਕਾਰ ਪੱਥ ਦੀ ਸਪਰਸ਼ ਰੇਖਾ ਨਾਲ ਹੁੰਦੀ ਹੈ । ਸਪਰਸ਼ ਰੇਖਾ ਚੱਕਰ ਦੇ ਅਰਧ ਵਿਆਸ ਨੂੰ ਲੰਬ ਹੁੰਦੀ ਹੈ । P1 T ਅਤੇ P2T ਕੁਮਵਾਰ ਬਿੰਦੁ P1 ਅਤੇ P1 ਤੇ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਹਨ ਜੋ ਇਨ੍ਹਾਂ ਬਿੰਦੁਆਂ ਤੇ ਗੋਲੇ ਦੀ ਗਤੀ ਦੀਆਂ ਦਿਸ਼ਾਵਾਂ ਦਰਸਾਉਂਦੀਆਂ ਹਨ । ਜੇਕਰ ਕਿਸੇ ਵੀ ਸਮੇਂ ਗੋਲੇ ਨੂੰ ਛੱਡ ਦਿੱਤਾ ਜਾਏ ਤਾਂ ਇਹ ਸਪਰਸ਼ ਰੇਖਾ ‘ਤੇ ਤੀਰ ਦੀ ਦਿਸ਼ਾ ਵਿੱਚ ਜਾ ਡਿੱਗੇਗਾ ।
![]()
ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Short Answer Type Questions)
ਪ੍ਰਸ਼ਨ 1.
ਕਿਸੇ ਵਸਤੂ ਦੀ ਵਿਰਾਮ ਅਵਸਥਾ ਅਤੇ ਗਤੀ ਅਵਸਥਾ ਨੂੰ ਉਦਾਹਰਨ ਦੇ ਕੇ ਸਪੱਸ਼ਟ ਕਰੋ ।
ਉੱਤਰ-
ਵਿਰਾਮ ਅਵਸਥਾ – ਜੇਕਰ ਕਿਸੇ ਵਸਤੂ ਦੀ ਸਥਿਤੀ ਵਿੱਚ ਸਮੇਂ ਦੇ ਨਾਲ ਕੋਈ ਪਰਿਵਰਤਨ ਬਦਲਾਵ ਨਹੀਂ ਹੁੰਦਾ, ਤਾਂ ਉਹ ਵਸਤੁ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਅਖਵਾਉਂਦੀ ਹੈ ।
ਉਦਾਹਰਨ – ਮੇਜ਼ ਤੇ ਰੱਖੀ ਹੋਈ ਪੁਸਤਕ, ਧਰਤੀ ਤੇ ਖੜੇ ਹੋਏ ਦਰੱਖ਼ਤ ਅਤੇ ਬਿਜਲੀ ਦਾ ਖੰਭਾ ਆਦਿ ।
ਗਤੀ ਅਵਸਥਾ – ਜੇਕਰ ਕਿਸੇ ਵਸਤੂ ਦੀ ਸਥਿਤੀ ਵਿੱਚ ਸਮੇਂ ਦੇ ਨਾਲ ਪਰਿਵਰਤਨ ਹੁੰਦਾ ਹੈ ਅਰਥਾਤ ਵਸਤੁ ਲਗਾਤਾਰ ਆਪਣੇ ਆਲੇ-ਦੁਆਲੇ ਦੀਆਂ ਵਸਤੂਆਂ ਦੇ ਸਾਪੇਖ ਆਪਣੀ ਸਥਿਤੀ ਬਦਲਦੀ ਹੈ, ਤਾਂ ਉਹ ਗਤੀ ਅਵਸਥਾ ਵਿੱਚ ਹੁੰਦੀ ਹੈ ।
ਉਦਾਹਰਨ – ਸੜਕ ਤੋਂ ਚੱਲ ਰਹੀ ਕਾਰ, ਹਵਾ ਵਿੱਚ ਉੱਡਦਾ ਹੋਇਆ ਹਵਾਈ ਜਹਾਜ਼ ਆਦਿ ।
ਪ੍ਰਸ਼ਨ 2.
ਗਤੀ ਕਿੰਨੇ ਕਿਸਮ ਦੀ ਹੁੰਦੀ ਹੈ ? ਹਰੇਕ ਕਿਸਮ ਦੀ ਗਤੀ ਨੂੰ ਉਦਾਹਰਣ ਦੇ ਕੇ ਸਮਝਾਓ ।
ਉੱਤਰ-
ਗਤੀ ਦੀਆਂ ਕਿਸਮਾਂ – ਗਤੀ ਤਿੰਨ ਕਿਸਮ ਦੀ ਹੁੰਦੀ ਹੈ ।
(i) ਸਰੋਲ ਰੇਖੀ ਗਤੀ
(ii) ਚੱਕਰਾਕਾਰ ਵਿਤੀ ਗਤੀ
(iii) ਦੋਲਣ ਗਤੀ ।
ਵੱਖ-ਵੱਖ ਕਿਸਮ ਦੀ ਗਤੀ ਦੇ ਉਦਾਹਰਨ-
(i) ਮੰਨ ਲਓ ਇੱਕ ਪ੍ਰੇਖਕ O ਤੇ ਸਥਿਤ ਹੈ ਅਤੇ ਉਹ ਇੱਕ ਕਾਰ ਨੂੰ ਸੜਕ ਤੇ ਸਥਿਤੀ A ਖੜੀ ਹੋਈ ਵੇਖਦਾ ਹੈ । ਕੁੱਝ ਸਮੇਂ ਬਾਅਦ ਉਹ ਕਾਰ ਨੂੰ B ਸਥਿਤੀ ਤੇ ਦੇਖਦਾ ਹੈ । ਕਾਰ ਦੀ ਸਥਿਤੀ ਵਿੱਚ ਹੋਇਆ ਪਰਿਵਰਤਨ ਇਹ ਦਰਸਾਉਂਦਾ ਹੈ ਕਿ ਕਾਰ ਬਿੰਦੂ O ਦੇ ਸਾਪੇਖ ਗਤੀ ਅਵਸਥਾ ਵਿੱਚ ਹੈ ।
(ii) ਮੰਨ ਲਓ ਇੱਕ ਆਦਮੀ ਧਾਗੇ ਦੇ ਇੱਕ ਸਿਰੇ ਨਾਲ ਬੰਨ੍ਹੇ ਹੋਏ ਪੱਥਰ ਨੂੰ ਵਿਤ ਵਿੱਚ ਘੁਮਾ ਰਿਹਾ ਹੈ । ਇਹ ਕਿਸੇ ਸਮੇਂ ਤੇ A ਸਥਿਤੀ ਅਤੇ ਫਿਰ ਕੁੱਝ ਸਮੇਂ ਬਾਅਦ B ਸਥਿਤੀ ਤੇ ਵੇਖਦਾ ਹੈ । ਇਸ ਲਈ ਬਿੰਦੂ O ਦੇ ਸਾਪੇਖ ਪੱਥਰ ਦੀ ਸਥਿਤੀ ਬਦਲ ਗਈ ਹੈ । ਇਸ ਲਈ ਬਿੰਦੁ 0 ਕੇਂਦਰ ਦੇ ਸਾਪੇਖ ਗਤੀ ਵਿੱਚ ਹੈ ਪਰ 0 ਤੋਂ ਇਸ ਦੀ ਦੁਰੀ ਓਨੀ ਹੀ ਰਹਿੰਦੀ ਹੈ । ਇਸ ਲਈ ਵਸਤੂ ਦੀ ਗਤੀ ਚੱਕਰਾਕਾਰ ਵਿਤੀ ਗਤੀ ਹੈ ।
(iii) ਮੰਨ ਲਓ ਧਾਗੇ ਦੇ ਇੱਕ ਸਿਰੇ ਨਾਲ ਪੱਥਰ ਨੂੰ ਬੰਨ੍ਹ ਕੇ ਤੁਸੀਂ ਕਿਸੇ ਨਿਸਚਿਤ ਬਿੰਦੂ ਤੋਂ ਲਟਕਾ ਦਿੰਦੇ ਹੋ । ਪੱਥਰ ਨੂੰ ਫੜ ਕੇ ਇੱਕ ਦਿਸ਼ਾ ਵਿੱਚ ਲਿਜਾ ਕੇ ਛੱਡ ਦਿੰਦੇ ਹੋ ਤਾਂ ਇਹ ਮੱਧ ਸਥਿਤੀ A ਦੇ ਦੋਨੋਂ ਪਾਸੇ ਗਤੀ ਕਰਨ ਲੱਗੇਗਾ | ਇਸ ਤਰ੍ਹਾਂ ਦੀ ਗਤੀ ਨੂੰ ਦੋਲਣ ਗਤੀ ਆਖਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 3.
‘‘ਵਿਰਾਮ ਅਤੇ ਗਤੀ ਸਾਪੇਖ ਹਨ’’ ਇਸ ਕਥਨ ਦਾ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਵਿਰਾਮ ਅਤੇ ਗਤੀ ਸਾਪੇਖ ਹਨ-ਇਸ ਕਥਨ ਦਾ ਅਰਥ ਹੈ ਕਿ ਜੇਕਰ ਕੋਈ ਵਸਤੂ ਕਿਸੇ ਹੋਰ ਵਸਤੂ ਦੇ ਸਾਪੇਖ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਹੈ ਤਾਂ ਇਸ ਦਾ ਮਤਲਬ ਇਹ ਨਹੀਂ ਕਿ ਉਹ ਸੰਸਾਰ ਦੀਆਂ ਹੋਰ ਸਾਰੀਆਂ ਵਸਤੂਆਂ ਦੇ ਸਾਪੇਖ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਹੈ । ਇਹ ਵਸਤੂ ਹੋਰ ਵਸਤੂਆਂ ਦੇ ਸਾਪੇਖ ਗਤੀ ਵਿੱਚ ਹੋ ਸਕਦੀ ਹੈ । ਇਸ ਲਈ ਅਸੀਂ ਇਹ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਵਿਰਾਮ ਅਤੇ ਗਤੀ ਸਾਪੇਖ ਹਨ ।
ਉਦਾਹਰਨ – ਇੱਕ ਗਤੀਮਾਨ ਰੇਲ ਗੱਡੀ ਵਿੱਚ ਦੋ ਯਾਤਰੀ A ਅਤੇ B ਬਾਰੇ ਵਿਚਾਰ ਕਰੋ । ਦੋਨੋਂ ਯਾਤਰੀ ਇੱਕ-ਦੂਜੇ ਦੇ ਅਤੇ ਰੇਲ ਗੱਡੀ ਦੇ ਸਾਪੇਖ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਹਨ ਕਿਉਂਕਿ ਉਹਨਾਂ ਦੀ ਸਾਪੇਖ ਸਥਿਤੀ ਇੱਕ-ਦੂਜੇ ਦੇ ਅਤੇ ਰੇਲ ਗੱਡੀ ਦੇ ਮੁਕਾਬਲੇ ਨਹੀਂ ਬਦਲ ਰਹੀ ਹੈ । ਪਰੰਤੁ ਰੇਲ ਗੱਡੀ ਤੋਂ ਬਾਹਰ ਸਥਿਤ ਵੇਖਣ ਵਾਲੇ ਪ੍ਰੇਖਕਾਂ ਅਤੇ ਵਸਤੁਆਂ ਦੇ ਸਾਪੇਖ ਉਹਨਾਂ ਦੀ ਸਥਿਤੀ ਲਗਾਤਾਰ ਸਮੇਂ ਨਾਲ ਬਦਲ ਰਹੀ ਹੈ । ਇਸ ਲਈ ਉਹ ਰੇਲ ਗੱਡੀ ਤੋਂ ਬਾਹਰ ਸਥਿਤ ਪੇਖਕਾਂ ਅਤੇ ਵਸਤੁਆਂ ਦੇ ਸਾਪੇਖ ਗਤੀ ਵਿੱਚ ਹਨ । ਇਸ ਲਈ ਵਿਰਾਮ ਅਤੇ ਗਤੀ ਸਾਪੇਖ ਕਥਨ ਹੈ ।
ਪ੍ਰਸ਼ਨ 4.
ਅਦਿਸ਼ ਅਤੇ ਸਦਿਸ਼ ਰਾਸ਼ੀਆਂ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕਰੋ ।
ਉੱਤਰ-
ਅਦਿਸ਼ (ਸਕੇਲਰ) ਰਾਸ਼ੀਆਂ – ਜਿਹਨਾਂ ਭੌਤਿਕ ਰਾਸ਼ੀਆਂ ਨੂੰ ਦਰਸਾਉਣ ਲਈ ਸਿਰਫ਼ ਪਰਿਮਾਣ (ਮਾਪ) ਦੀ ਲੋੜ ਹੁੰਦੀ ਹੈ, ਉਹਨਾਂ ਨੂੰ ਅਦਿਸ਼ ਰਾਸ਼ੀਆਂ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
ਉਦਾਹਰਨ – ਲੰਬਾਈ, ਦੂਰੀ, ਪੁੰਜ, ਖੇਤਰਫਲ, ਸਮਾਂ, ਚਾਲ, ਕਾਰਜ, ਊਰਜਾ, ਤਾਪ, ਘਣਤਾ, ਆਇਤਨ, ਬਿਜਲਈ ਧਾਰਾ ਆਦਿ ।
ਕਿਸੇ ਵੀ ਆਦਿਸ਼ ਰਾਸ਼ੀ ਨੂੰ ਸਿਰਫ਼ ਸੰਖਿਆ ਦੁਆਰਾ ਹੀ ਵਿਅਕਤ (ਦਰਸਾਇਆ) ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ।
ਸਦਿਸ਼ ਰਾਸ਼ੀਆਂ ਨੂੰ ਗਣਿਤ ਦੇ ਸਧਾਰਨ ਨਿਯਮਾਂ ਦੇ ਅਨੁਸਾਰ ਹੀ ਜੋੜਿਆ, ਘਟਾਇਆ, ਗੁਣਾ ਅਤੇ ਭਾਗ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ।
ਸਦਿਸ਼ (ਵੈਕਟਰ) ਰਾਸ਼ੀਆਂ-ਜਿਨ੍ਹਾਂ ਭੌਤਿਕ ਰਾਸ਼ੀਆਂ ਨੂੰ ਦਰਸਾਉਣ ਲਈ ਪਰਿਮਾਣ (ਆਪ) ਅਤੇ ਦਿਸ਼ਾ ਦੋਨਾਂ ਦੀ ਲੋੜ ਹੁੰਦੀ ਹੈ, ਉਹ ਸਦਿਸ਼ ਰਾਸ਼ੀਆਂ ਕਹਾਉਂਦੀਆਂ ਹਨ ।
ਉਦਾਹਰਨ – ਵਿਸਥਾਪਨ, ਵੇਗ, ਸੰਵੇਗ, ਪਵੇਗ, ਬਲ, ਭਾਰ ਅਤੇ ਬਿਜਲਈ ਖੇਤਰ ਆਦਿ । ਕਿਸੇ ਵੀ ਸਦਿਸ਼ ਰਾਸ਼ੀ ਨੂੰ ਦਰਸਾਉਣ ਲਈ ਪਰਿਮਾਣ (ਆਪ) ਦੇ ਨਾਲ ਦਿਸ਼ਾ ਦਾ ਹੋਣਾ ਵੀ ਜ਼ਰੂਰੀ ਹੁੰਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 5.
ਸਦਿਸ਼ ਅਤੇ ਅਦਿਸ਼ ਰਾਸ਼ੀਆਂ ਵਿੱਚ ਅੰਤਰ ਦੱਸੋ ।
ਉੱਤਰ-
ਸਦਿਸ਼ ਅਤੇ ਅਦਿਸ਼ ਰਾਸ਼ੀਆਂ ਵਿੱਚ ਅੰਤਰ-
| ਸਦਿਸ਼ (ਸਕੇਲਰ) ਰਾਸ਼ੀਆਂ | ਅਦਿਸ਼ (ਵੈਕਟਰ) ਰਾਸ਼ੀਆਂ |
| (1) ਸਦਿਸ਼ ਰਾਸ਼ੀਆਂ ਉਹ ਭੌਤਿਕ ਰਾਸ਼ੀਆਂ ਹਨ, ਜਿਨ੍ਹਾਂ ਵਿੱਚ ਪਰਿਮਾਣ (ਮਾਘ) ਅਤੇ ਦਿਸ਼ਾ ਦੋਨੋਂ ਹੁੰਦੇ ਹਨ, ਜਿਵੇਂ ਬਲ, ਵੇਗ ਅਤੇ ਪ੍ਰਵੇਗ ਆਦਿ । | (1) ਅਦਿਸ਼ ਰਾਸ਼ੀਆਂ ਉਹ ਭੌਤਿਕ ਰਾਸ਼ੀਆਂ ਹਨ, ਜਿਨ੍ਹਾਂ ਵਿੱਚ ਸਿਰਫ਼ ਪਰਿਮਾਣ (ਮਾਪ) ਹੀ ਹੁੰਦਾ ਹੈ; ਜਿਵੇਂ, ਪੁੰਜ, ਆਇਤਨ, ਦੂਰੀ, ਸਮਾਂ ਆਦਿ । |
| (2) ਸਦਿਸ਼ ਰਾਸ਼ੀਆਂ ਨੂੰ ਇੱਕ ਤੀਰ ਦੇ ਸੰਕੇਤ ਨਾਲ ਦਰਸਾਇਆ ਜਾਂਦਾ ਹੈ, ਜਿੱਥੇ ਤੀਰ ਦੀ ਲੰਬਾਈ ਪਰਿਮਾਣ ਨੂੰ ਅਤੇ ਤੀਰ ਦਾ ਚਿੰਨ੍ਹ ਦਿਸ਼ਾ ਨੂੰ ਸੰਕੇਤ ਕਰਦਾ ਹੈ । | (2) ਅਦਿਸ਼ ਰਾਸ਼ੀਆਂ ਨੂੰ ਕਿਸੇ ਵਿਸ਼ੇਸ਼ ਵਿਧੀ ਜਾਂ ਸੰਕੇਤ ਦੁਆਰਾ ਨਿਰਪਤ ਨਹੀਂ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । |
| (3) ਇਹਨਾਂ ਦਾ ਸੰਕਲਣ ਤ੍ਰਿਭੁਜ ਅਤੇ ਸਮਾਨਾਂਤਰ ਚਤੁਰਭੁਜ ਦੇ ਨਿਯਮ ਦੁਆਰਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । | (3) ਅਦਿਸ਼ ਰਾਸ਼ੀਆਂ ਦਾ ਸੰਕਲਣ, ਬੀਜ ਗਣਿਤਿਕ ਢੰਗ ਜਾਂ ਨਿਯਮਾਂ ਅਨੁਸਾਰ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ । |
![]()
ਪ੍ਰਸ਼ਨ 6.
ਹੇਠ ਲਿਖੀਆਂ ਭੌਤਿਕ ਰਾਸ਼ੀਆਂ ਨੂੰ ਅਦਿਸ਼ ਅਤੇ ਸਦਿਸ਼ ਵਿੱਚ ਵਰਗੀਕ੍ਰਿਤ ਕਰੋ-
ਦੁਰੀ, ਵਿਸਥਾਪਨ, ਘਣਤਾ, ਬਲ, ਸੰਵੇਗ, ਵੇਗ, ਵੇਗ, ਚਾਲ, ਸਮਾਂ, ਆਇਤਨ, ਊਰਜਾ ।
ਉੱਤਰ-
ਅਦਿਸ਼ ਰਾਸ਼ੀਆਂ-ਦੁਰੀ, ਘਣਤਾ, ਚਾਲ, ਆਇਤਨ, ਊਰਜਾ ।
ਸਦਿਸ਼ ਰਾਸ਼ੀਆਂ-ਵਿਸਥਾਪਨ, ਬਲ, ਸੰਵੇਗ, ਵੇਗ, ਪ੍ਰਵੇਗ ।
ਪ੍ਰਸ਼ਨ 7.
ਦੁਰੀ ਅਤੇ ਵਿਸਥਾਪਨ ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ?
ਉੱਤਰ-
ਦੂਰੀ – ਕਿਸੇ ਗਤੀਮਾਨ ਵਸਤੂ ਦੁਆਰਾ ਕਿਸੇ ਨਿਸਚਿਤ ਸਮੇਂ ਵਿੱਚ ਤੈਅ ਕੀਤੇ ਗਏ ਮਾਰਗ (ਰਸਤਾ) ਦੀ ਲੰਬਾਈ ਵਸਤੂ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ ਹੁੰਦੀ ਹੈ । ਇਸ ਦਾ ਮਾਤ੍ਰਿਕ ਮੀਟਰ ਹੈ । ਦੂਰੀ ਇੱਕ ਅਦਿਸ਼ ਰਾਸ਼ੀ ਹੈ ।
ਵਿਸਥਾਪਨ – ਕਿਸੇ ਵਸਤੂ ਦਾ ਨਿਸਚਿਤ ਦਿਸ਼ਾ ਵਿੱਚ ਹੋਏ ਸਥਿਤੀ ਪਰਿਵਰਤਨ ਨੂੰ ਵਿਸਥਾਪਨ ਕਹਿੰਦੇ ਹਨ ।ਵਿਸਥਾਪਨ ਸਰਲ ਰੇਖੀ ਜਾਂ ਕੋਈ ਹੋ ਸਕਦਾ ਹੈ । ਇਹ ਅੰਤਿਮ ਅਤੇ ਆਰੰਭਿਕ ਸਥਿਤੀਆਂ ਦੇ ਵਿਚਕਾਰ ਨਿਊਨਤਮ ਦੁਰੀ ਹੁੰਦੀ ਹੈ । ਵਿਸਥਾਪਨ ਦਾ ਮਾਤ੍ਰਿਕ ਮੀਟਰ ਹੈ ਅਤੇ ਇਹ ਇੱਕ ਸਦਿਸ਼ ਰਾਸ਼ੀ ਹੈ ।
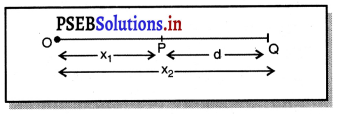
ਇੱਕ ਸਰਲ ਰੇਖਾ ਵਿੱਚ ਗਤੀਮਾਨ ਵਸਤੂ ਲਈ ਵਿਸਥਾਪਨ-ਮੰਨ ਲਓ ਇੱਕ ਵਸਤੁ ਆਪਣੀ P ਤੋਂ Q ਤੇ ਬਦਲਦੀ ਹੈ । ਜੇਕਰ ਨਿਸਚਿਤ ਮੁਲ ਬਿੰਦੁ ਤੋਂ ਇਸਦੀ
ਕੁਮਵਾਰ ਦੂਰੀ X1 ਅਤੇ X2 ਹੈ, ਤਾਂ ਵਿਸਥਾਪਨ d ਹੋਵੇਗਾ :-
d = (X2 – X1)
P ਤੋਂ Q ਵੱਲ ਰਾਤੀ ਲਈ ਵਿਸਥਾਪਨ ਨੂੰ ਧਨਾਤਮਕ ਅਤੇ ਉਲਟ ਦਿਸ਼ਾ ਵਿੱਚ ਗਤੀ ਹੋਣ ਦੀ ਅਵਸਥਾ ਵਿੱਚ ਰਿਣਾਤਮਕ ਚਿੰਨ ਰਾਹੀਂ ਦਰਸਾਇਆ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 8.
ਇੱਕ ਸਮਾਨ ਰੇਖੀ ਗਤੀ ਅਤੇ ਇੱਕ ਸਮਾਨ ਚੱਕਰਾਕਾਰ (ਵਿਤੀ ਗਤੀ ਵਿੱਚ ਕੀ ਅੰਤਰ ਹੈ ?
ਉੱਤਰ-
ਇੱਕ ਸਮਾਨ ਰੇਖੀ ਗਤੀ – ਜੇਕਰ ਕੋਈ ਗਤੀਮਾਨ ਵਸਤੂ ਕਿਸੇ ਸਰਲ ਰੇਖੀ ਪੱਥ ‘ਤੇ ਇਸ ਤਰ੍ਹਾਂ ਗਤੀ ਕਰੇ ਕਿ ਉਸਦੇ ਦੁਆਰਾ ਸਮਾਨ ਸਮੇਂ ਵਿੱਚ ਸਮਾਨ ਦੁਰੀ ਤੈਅ ਕੀਤੀ ਜਾਵੇ, ਤਾਂ ਵਸਤੂ ਦੀ ਗਤੀ ਇੱਕ ਸਮਾਨ ਰੇਖੀ ਗਤੀ ਅਖਵਾਉਂਦੀ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਦੀ ਗਤੀ ਵਿੱਚ ਚਾਲ ਦਾ ਪਰਿਮਾਣ (ਮਾਪ) ਸਮਾਨ ਰਹਿੰਦਾ ਹੈ ਅਤੇ ਪੱਥ ਦੇ ਵੱਖ-ਵੱਖ ਬਿੰਦੂਆਂ ਤੇ ਦਿਸ਼ਾ ਪਰਿਵਰਤਿਤ ਨਹੀਂ ਹੁੰਦੀ ਹੈ । ਇਸ ਲਈ ਇੱਕ ਸਮਾਨ ਰੇਖੀ ਗਤੀ ਵਿੱਚ ਵਸਤੁ ਦਾ ਵੇਗ ਨਹੀਂ ਹੁੰਦਾ ਹੈ ।
ਇੱਕ ਸਮਾਨ ਚੱਕਰਾਕਾਰ (ਵਿਤੀ) ਗਤੀ-ਜਦੋਂ ਕੋਈ ਵਸਤੂ ਇਸ ਤਰ੍ਹਾਂ ਗਤੀ ਕਰਦੀ ਹੈ ਕਿ ਉਸ ਦਾ ਪੱਥ ਚੱਕਰਾਕਾਰ ਹੋਵੇ ਅਤੇ ਚਾਲ ਇੱਕ ਸਮਾਨ ਹੋਵੇ, ਤਾਂ ਵਸਤੂ ਦੀ ਗਤੀ ਇੱਕ ਸਮਾਨ ਚੱਕਰਾਕਾਰ (ਵਿਤੀ) ਗਤੀ ਅਖਵਾਉਂਦੀ ਹੈ | ਭਾਵੇਂ ਵਸਤੂ ਦੀ ਚਾਲ ਦਾ ਪਰਿਮਾਣ ਸਮਾਨ ਰਹਿੰਦਾ ਹੈ ਪਰ ਗਤੀ ਦੀ ਦਿਸ਼ਾ ਹਰੇਕ ਬਿੰਦੂ ਤੇ ਬਦਲਦੀ ਰਹਿੰਦੀ ਹੈ । ਦਿਸ਼ਾ ਵਿੱਚ ਇਹ ਪਰਿਵਰਤਨ ਵਸਤੁ ਵਿੱਚ ਪ੍ਰਵੇਗ ਪੈਦਾ ਕਰਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 9.
ਦੂਰੀ ਅਤੇ ਵਿਸਥਾਪਨ ਵਿੱਚ ਅੰਤਰ ਦੱਸੋ ।
ਉੱਤਰ-
ਦੂਰੀ ਅਤੇ ਵਿਸਥਾਪਨ ਵਿੱਚ ਅੰਤਰ-
| ਦੂਰੀ | ਵਿਸਥਾਪਨ |
| (1) ਗਤੀਮਾਨ ਵਸਤੁ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਪੱਥ ਦੀ ਲੰਬਾਈ ਨੂੰ ਦੂਰੀ ਕਹਿੰਦੇ ਹਨ । | (1) ਕਿਸੇ ਨਿਸਚਿਤ ਦਿਸ਼ਾ ਵਿੱਚ ਅੰਤਿਮ ਅਤੇ ਆਰੰਭਿਕ ਸਥਿਤੀਆਂ ਦੇ ਵਿਚਕਾਰ ਦੀ ਦੂਰੀ ਨੂੰ ਵਿਸਥਾਪਨ ਕਹਿੰਦੇ ਹਨ । |
| (2) ਦੂਰੀ ਇੱਕ ਅਦਿਸ਼ ਰਾਸ਼ੀ ਹੈ । | (2) ਵਿਸਥਾਪਨ ਇੱਕ ਸਦਿਸ਼ ਰਾਸ਼ੀ ਹੈ । |
| (3) ਦੁਰੀ ਦੇ ਨਿਰੁਪਣ ਲਈ ਸਿਰਫ਼ ਪਰਿਮਾਣ ਦੀ ਲੋੜ ਹੁੰਦੀ ਹੈ । ਉਦਾਹਰਨ – ਇੱਕ ਪੱਥਰ ਉੱਪਰ ਵੱਲ h ਉੱਚਾਈ ਤੱਕ ਸੁੱਟਿਆ ਗਿਆ ਜੋ ਵਾਪਿਸ ਮੁੱਢਲੇ ਸਥਾਨ ‘ਤੇ ਆ ਗਿਆ ।∴ ਪੱਥਰ ਦੁਆਰਾ ਤੈਅ ਹੋਈ ਕੁੱਲ ਦੂਰੀ = h+h= 2h |
(3) ਵਿਸਥਾਪਨ ਦੇ ਨਿਰੁਪਣ ਲਈ ਪਰਿਮਾਣ ਅਤੇ ਦਿਸ਼ਾ ਦੋਨਾਂ ਦਾ ਹੋਣਾ ਜ਼ਰੂਰੀ ਹੈ । ਪੱਥਰ ਦਾ ਵਿਸਥਾਪਨ = h – h = 0 |
ਪ੍ਰਸ਼ਨ 10.
ਚਾਲ ਅਤੇ ਵੇਗ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ? ਇਹ ਕਿਹੋ ਜਿਹੀਆਂ ਰਾਸ਼ੀਆਂ ਹਨ ? ਇਹਨਾਂ ਦੇ ਮਾਤ੍ਰਿਕ ਲਿਖੋ ।
ਉੱਤਰ-
ਚਾਲ-ਕਿਸੇ ਵਸਤੂ ਦੁਆਰਾ ਇਕਾਈ ਸਮਾਂ ਅੰਤਰਾਲ ਵਿੱਚ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ ਉਸ ਵਸਤੂ ਦੀ ਚਾਲ ਹੁੰਦੀ ਹੈ ।

ਜਾਂ v = \(\frac{\mathrm{S}}{t}\)
ਮਾਤ੍ਰਿਕ – ਚਾਲ ਦਾ ਮਾਤ੍ਰਿਕ ਮੀਟਰ/ਸੈਕਿੰਡ ਹੁੰਦਾ ਹੈ । ਚਾਲ ਇੱਕ ਅਦਿਸ਼ ਰਾਸ਼ੀ ਹੈ ਕਿਉਂਕਿ ਇਸ ਵਿੱਚ ਦਿਸ਼ਾ ਨਹੀਂ ਹੁੰਦੀ ।
ਦੇਗ – ਕਿਸੇ ਵਸਤੂ ਦੁਆਰਾ ਇਕਾਈ ਸਮੇਂ ਵਿੱਚ ਨਿਸਚਿਤ ਦਿਸ਼ਾ ਵਿੱਚ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ ਹੈ । ਅਰਥਾਤ ਇਹ ਇਕਾਈ ਸਮੇਂ ਵਿੱਚ ਵਸਤੂ ਦਾ ਵਿਸਥਾਪਨ ਹੈ ।
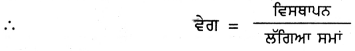
ਮਾਤ੍ਰਿਕ-ਵੇਗ ਦਾ ਮਾਤਿਕ ਮੀਟਰ/ਸੈਕਿੰਡ ਹੈ ।
ਵੇਗ ਇਕ ਸਦਿਸ਼ ਰਾਸ਼ੀ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 11.
ਚਾਲ ਅਤੇ ਵੇਗ ਵਿੱਚ ਅੰਤਰ ਦੱਸੋ ।
ਉੱਤਰ-
ਚਾਲ ਅਤੇ ਵੇਗ ਵਿੱਚ ਅੰਤਰ-
| ਚਾਲ | ਵੇਗ |
| (1) ਇਕਾਈ ਸਮੇਂ ਵਿੱਚ ਤੈਅ ਕੀਤੀ ਦੂਰੀ ਵਸਤੂ ਦੀ ਚਾਲ ਅਖਵਾਉਂਦੀ ਹੈ । | (1) ਇਕਾਈ ਸਮੇਂ ਵਿੱਚ ਕਿਸੇ ਨਿਸਚਿਤ ਦਿਸ਼ਾ ਵਿੱਚ ਤੈਅ ਹੋਈ ਦੂਰੀ ਨੂੰ ਵੇਗ ਆਖਦੇ ਹਨ ਜਾਂ ਇਕਾਈ ਸਮੇਂ ਵਿਚ ਹੋਏ ਵਿਸਥਾਪਨ ਨੂੰ ਵੇਗ ਕਹਿੰਦੇ ਹਨ । |
| (2) ਚਾਲ ਨੂੰ ਦਰਸਾਉਣ ਲਈ ਸਿਰਫ਼ ਪਰਿਮਾਣ ਦੀ ਲੋੜ ਹੁੰਦੀ ਹੈ । ਇਸ ਲਈ ਚਾਲ ਇੱਕ ਅਦਿਸ਼ ਰਾਸ਼ੀ ਹੈ । | (2) ਵੇਗ ਨੂੰ ਦਰਸਾਉਣ ਲਈ ਪਰਿਮਾਣ ਅਤੇ ਦਿਸ਼ਾ ਦੋਨਾਂ ਦੀ ਲੋੜ ਹੁੰਦੀ ਹੈ । ਇਸ ਲਈ ਇਹ ਇੱਕ ਸਦਿਸ਼ ਰਾਸ਼ੀ ਹੈ । |
| (3) ਚਾਲ ਨੂੰ ਤੀਰ ਨਾਲ ਪ੍ਰਦਰਸ਼ਿਤ ਨਹੀਂ ਕੀਤਾ ਜਾ ਸਕਦਾ । | (3) ਵੇਗ ਨੂੰ ਤੀਰ ਨਾਲ ਪ੍ਰਦਰਸ਼ਿਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ । ਤੀਰ ਦੀ ਲੰਬਾਈ ਵੇਗ ਦੇ ਪਰਿਮਾਣ ਅਤੇ ਤੀਰ ਦੀ ਦਿਸ਼ਾ ਵੇਗ ਦੀ ਦਿਸ਼ਾ ਪ੍ਰਦਰਸ਼ਿਤ ਕਰਦੀ ਹੈ । |
| (4) ਚਾਲ ਹਮੇਸ਼ਾ ਧਨਾਤਮਕ ਹੁੰਦੀ ਹੈ । | (4) ਵੇਗ ਧਨਾਤਮਕ ਅਤੇ ਰਿਣਾਤਮਕ ਦੋਨੋਂ ਤਰ੍ਹਾਂ ਦੀ ਹੁੰਦੀ ਹੈ । |
ਪ੍ਰਸ਼ਨ 12.
ਇੱਕ ਸਮਾਨ ਵੇਗ ਅਤੇ ਪਰਿਵਰਤਨਸ਼ੀਲ ਵੇਗ ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ?
ਉੱਤਰ-
ਇੱਕ ਸਮਾਨ ਵੇਗ – ਜੇਕਰ ਕੋਈ ਵਸਤੂ ਸਮਾਨ ਸਮਾਂ ਅੰਤਰਾਲਾਂ ਵਿੱਚ ਸਮਾਨ ਦੂਰੀ ਕਿਸੇ ਵਿਸ਼ੇਸ਼ ਦਿਸ਼ਾ ਵਿੱਚ ਤੈਅ ਕਰੇ ਤਾਂ ਵਸਤੂ ਨੂੰ ਸਮਾਨ ਵੇਗ ਨਾਲ ਗਤੀਸ਼ੀਲ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
ਪਰਿਵਰਤਨਸ਼ੀਲ ਵੇਗ – ਜੇਕਰ ਕੋਈ ਵਸਤੂ ਕਿਸੇ ਵਿਸ਼ੇਸ਼ ਦਿਸ਼ਾ ਵਿੱਚ ਸਮਾਨ ਸਮਾਂ ਅੰਤਰਾਲਾਂ ਵਿੱਚ ਅਸਮਾਨ ਦੂਰੀ ਤੈਅ ਕਰੇ ਜਾਂ ਫਿਰ ਸਮਾਨ ਸਮਾਂ ਅੰਤਰਾਲਾਂ ਵਿੱਚ ਸਮਾਨ ਦੂਰੀ ਤੈਅ ਕਰੇ, ਪਰੰਤੂ ਉਸਦੀ ਦਿਸ਼ਾ ਵਿੱਚ ਪਰਿਵਰਤਨ ਹੋ ਜਾਏ ਤਾਂ ਵਸਤੁ ਦੇ ਵੇਗ ਨੂੰ ਪਰਿਵਰਤਨਸ਼ੀਲ ਵੇਗ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 13.
ਔਸਤ ਚਾਲ ਅਤੇ ਔਸਤ ਵੇਗ ਕੀ ਹਨ ?
ਉੱਤਰ-
ਔਸਤ ਚਾਲ- ਕਿਸੇ ਗਤੀਮਾਨ ਵਸਤੂ ਦੁਆਰਾ ਇਕਾਈ ਸਮੇਂ ਵਿੱਚ ਤੈਅ ਹੋਈ ਔਸਤ ਦੂਰੀ ਨੂੰ ਉਸਦੀ ਔਸਤ ਚਾਲ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਔਸਤ ਚਾਲ ਪਤਾ ਕਰਨ ਲਈ ਵਸਤੂ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਕੁੱਲ ਦੂਰੀ ਨੂੰ ਤੈਅ ਕਰਨ ਲਈ ਲੱਗੇ ਸਮੇਂ ਨਾਲ ਭਾਗ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।

ਜੇਕਰ ਵਸਤੂ ਦੀ ਗਤੀ ਇੱਕ ਸਮਾਨ ਹੈ ਤਾਂ ਚਾਲ ਅਤੇ ਔਸਤ ਚਾਲ ਵਿੱਚ ਕੋਈ ਅੰਤਰ ਨਹੀਂ ਹੁੰਦਾ ਹੈ ।
ਔਸਤ ਵੇਗ – ਕਿਸੇ ਵਸਤੂ ਦੁਆਰਾ ਕਿਸੇ ਸਮੇਂ ਵਿੱਚ ਤੈਅ ਕੀਤੇ ਗਏ ਵਿਸਥਾਪਨ ਅਤੇ ਇਸ ਵਿਸਥਾਪਨ ਨੂੰ ਲੱਗੇ ਸਮੇਂ ਦੇ ਅਨੁਪਾਤ ਨੂੰ ਵਸਤੂ ਦਾ ਵੇਗ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।

ਜੇਕਰ ਵਸਤੂ ਦਾ ਵੇਗ ਨਿਸਚਿਤ ਦਿਸ਼ਾ ਵਿੱਚ ਇੱਕ ਸਮਾਨ ਦਰ ਨਾਲ ਪਰਿਵਰਤਿਤ ਹੋ ਰਿਹਾ ਹੈ, ਤਾਂ
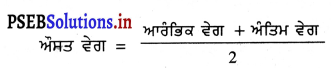
ਪ੍ਰਸ਼ਨ 14.
ਪ੍ਰਵੇਗ ਦੀ ਪਰਿਭਾਸ਼ਾ ਦਿਓ । ਇਹ ਕਿਹੋ ਜਿਹੀ ਰਾਸ਼ੀ ਹੈ ? ਇਸ ਦਾ ਮਾਤ੍ਰਿਕ ਵੀ ਲਿਖੋ ।
ਉੱਤਰ-
ਪ੍ਰਵੇਗ – ਕਿਸੇ ਗਤੀਮਾਨ ਵਸਤੂ ਦੇ ਵੇਗ ਪਰਿਵਰਤਨ ਦੀ ਦਰ ਨੂੰ ਉਸ ਵਸਤੂ ਦਾ ਵੇਗ ਕਹਿੰਦੇ ਹਨ । ਇਸ ਨੂੰ ‘a’ ਨਾਲ ਦਰਸਾਇਆ ਜਾਂਦਾ ਹੈ । ਇਹ ਇੱਕ ਸਦਿਸ਼ ਰਾਸ਼ੀ ਹੈ ।
ਮਾਤ੍ਰਿਕ-ਇਸ ਦਾ ਮਾ ਮੀਟਰ/ਸੈਕਿਡ ਹੈ ।

ਮੰਨ ਲਓ ਵਸਤੂ ਦਾ ਆਰੰਭਿਕ ਵੇਗ u ਅਤੇ t ਸਮੇਂ ਬਾਅਦ ਅੰਤਿਮ ਵੇਗ v ਹੋ ਜਾਂਦਾ ਹੈ, ਤਾਂ
ਪ੍ਰਵੇਗ \(\overrightarrow{(a)}=\frac{\vec{v}-\vec{u}}{t}\)
ਪ੍ਰਸ਼ਨ 15.
ਧਨਾਤਮਕ ਅਤੇ ਰਿਣਾਤਮਕ ਵੇਗ ਕੀ ਹਨ ?
ਉੱਤਰ-
ਧਨਾਤਮਕ ਵੇਗ – ਜੇਕਰ ਕਿਸੇ ਵਸਤੂ ਦੇ ਵੇਗ ਦਾ ਪਰਿਮਾਣ (ਅਰਥਾਤ ਵਸਤੂ ਦੀ ਚਾਲ) ਸਮੇਂ ਦੇ ਨਾਲ ਲਗਾਤਾਰ ਵੱਧ ਰਿਹਾ ਹੈ, ਤਾਂ ਉਸ ਵਸਤੂ ਦਾ ਵੇਗ ਧਨਾਤਮਕ ਹੁੰਦਾ ਹੈ ।
ਰਿਣਾਤਮਕ ਵੇਗ – ਜੇਕਰ ਕਿਸੇ ਵਸਤੂ ਦੇ ਵੇਗ ਦਾ ਪਰਿਮਾਣ ਸਮੇਂ ਦੇ ਨਾਲ ਲਗਾਤਾਰ ਘੱਟਦਾ ਹੈ ਤਾਂ ਵਸਤੂ ਦਾ ਵੇਗ ਰਿਣਾਤਮਕ ਹੁੰਦਾ ਹੈ । ਰਿਣਾਤਮਕ ਵੇਗ ਨੂੰ ਮੰਦਨ ਵੀ ਆਖਦੇ ਹਨ ।
![]()
ਪ੍ਰਸ਼ਨ 16.
ਇਕ ਸਮਾਨ ਵੇਗ ਅਤੇ ਅਸਮਾਨ ਵੇਗ ਦਾ ਕੀ ਅਰਥ ਹੈ ? ਉਦਾਹਰਨ ਦੇ ਕੇ ਸਮਝਾਓ ।
ਉੱਤਰ-
ਇੱਕ ਸਮਾਨ ਵੇਗ-ਜੇਕਰ ਕਿਸੇ ਵਸਤੂ ਦੇ ਵੇਗ ਵਿੱਚ ਸਮਾਨ ਸਮਾਂ ਅੰਤਰਾਲਾਂ ਵਿੱਚ ਸਮਾਨ ਰੂਪ ਨਾਲ ਪਰਿਵਰਤਨ ਹੋ ਰਿਹਾ ਹੈ, ਤਾਂ ਵਸਤੂ ਦਾ ਪ੍ਰਵੇਗ ਇੱਕ ਸਮਾਨ ਵੇਗ ਕਹਾਉਂਦਾ ਹੈ ।
ਉਦਾਹਰਨ – ਚੱਕਰਾਕਾਰ ਵਿਤੀ ਗਤੀ ਵਿੱਚ ।
ਅਸਮਾਨ ਵੇਗ-ਜੇਕਰ ਕਿਸੇ ਵਸਤੂ ਦੇ ਵੇਗ ਵਿੱਚ ਪਰਿਵਰਤਨ ਇੱਕ ਸਮਾਨ ਸਮੇਂ ਅੰਤਰਾਲਾਂ ਵਿੱਚ ਵੱਖ-ਵੱਖ ਹੋਵੇ, ਤਾਂ ਉਸ ਵਸਤੂ ਦਾ ਵੇਗ ਅਸਮਾਨ ਵੇਗ ਹੁੰਦਾ ਹੈ ।
ਉਦਾਹਰਨ-ਭੀੜ ਵਾਲੇ ਬਾਜ਼ਾਰ ਵਿੱਚ ਗੱਡੀ ਚਲਾਉਂਦੇ ਸਮੇਂ ਗੱਡੀ ਦਾ ਵੇਗ ਅਸਮਾਨ ਹੁੰਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 17.
ਗਰਾਫ਼ ਕੀ ਹੁੰਦਾ ਹੈ ? ਇਸ ਦੇ ਕੀ ਲਾਭ ਹਨ ?
ਉੱਤਰ-
ਗਰਾਫ਼ – ਦੋ ਭਿੰਨ ਅਕਸ਼ਾਂ ਤੇ ਕਿਸੇ ਇੱਕ ਰਾਸ਼ੀ ਨੂੰ ਕਿਸੇ ਦੂਜੀ ਰਾਸ਼ੀ ਦੇ ਸਾਪੇਖ ਚਿੱਤਰ ਰਾਹੀਂ ਦਰਸਾਉਣ ਨੂੰ ਗਰਾਫ਼ ਕਹਿੰਦੇ ਹਨ । ਅੱਜ-ਕਲ੍ਹ ਗਰਾਫ਼ ਦੀ ਉਪਯੋਗਿਤਾ ਬਹੁਤ ਜ਼ਿਆਦਾ ਹੈ । ਸਾਰੇ ਖੇਤਰਾਂ ਵਿੱਚ ਵਿਸ਼ਲੇਸ਼ਣ ਅਤੇ ਤੁਲਨਾਤਮਕ ਕੰਮਾਂ ਲਈ ਇਹ ਬਹੁਤ ਸਹਾਇਕ ਸਿੱਧ ਹੋਇਆ ਹੈ । ਇਸ ਦੇ ਹੇਠ ਲਿਖੇ ਪ੍ਰਮੁੱਖ ਲਾਭ ਹਨ:-
- ਦੋ ਜਾਂ ਦੋ ਤੋਂ ਵੱਧ ਰਾਸ਼ੀਆਂ ਦਾ ਤੁਲਨਾਤਮਕ ਅਧਿਐਨ ਬਹੁਤ ਸਰਲ ਅਤੇ ਸੌਖਾ ਹੋ ਜਾਂਦਾ ਹੈ ।
- ਵੱਖ-ਵੱਖ ਰਾਸ਼ੀਆਂ ਦਾ ਸੰਬੰਧ ਸੌਖਾ ਦਰਸਾਇਆ ਜਾ ਸਕਦਾ ਹੈ ।
- ਇੱਕ ਜਗ੍ਹਾ ਹੀ ਵਿਭਿੰਨ ਆਂਕੜੇ ਪੇਸ਼ ਕੀਤੇ ਜਾ ਸਕਦੇ ਹਨ ।
- ਗਰਾਫ਼ ਦੀ ਢਾਲ ਨਾਲ ਵੱਖ-ਵੱਖ ਰਾਸ਼ੀਆਂ ਅਤੇ ਸੂਚਨਾਵਾਂ ਨੂੰ ਪ੍ਰਗਟਾਇਆ ਜਾ ਸਕਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 18.
ਤੁਸੀਂ ਕਿਸੇ ਵਸਤੂ ਦੇ ਵੇਗ ਬਾਰੇ ਕੀ ਕਹੋਗੇ । ਜੇਕਰ
(i) ਸਮਾਂ-ਵਿਸਥਾਪਨ ਗਰਾਫ਼ ਸਰਲ ਰੇਖੀ ਹੈ ।
(ii) ਸਮਾਂ-ਵਿਗ ਗਰਾਫ਼ ਸਰਲ ਰੇਖੀ ਹੈ ।
ਉੱਤਰ-
(i) ਵਸਤੁ ਇੱਕ ਸਮਾਨ ਵੇਗ ਨਾਲ ਗਤੀਸ਼ੀਲ ਹੈ ।
(ii) ਜੇਕਰ ਗਰਾਫ਼ ਸਮਾਂ ਅਕਸ਼ ਦੇ ਸਮਾਨਾਂਤਰ ਹੋਵੇ ਤਾਂ ਇਸਦਾ ਅਰਥ ਹੈ ਕਿ ਵਸਤੂ ਇੱਕ ਸਮਾਨ ਵੇਗ ਨਾਲ ਗਤੀਸ਼ੀਲ ਹੈ । ਜੇਕਰ ਸਮਾਂ-ਵੇਗ ਗਰਾਫ਼ ਸਰਲ ਰੇਖੀ ਹੋਵੇ ਅਤੇ ਸਮਾਂ-ਅਕਸ਼ ਦੇ ਨਾਲ ਕੋਣ ਬਣਾਉਂਦੀ ਹੈ, ਤਾਂ ਇਸਦਾ ਅਰਥ ਹੈ ਕਿ ਵਸਤੂ ਅ ਅਸਮਾਨ ਵੇਗ ਨਾਲ ਗਤੀਸ਼ੀਲ ਹੈ ।
ਪ੍ਰਸ਼ਨ 19.
ਇੱਕ ਵਸਤੁ ਇੱਕ ਸਮਾਨ ਚਾਲ (v) ਨਾਲ ਗਤੀਸ਼ੀਲ ਹੈ । ਚਾਲ-ਸਮਾਂ ਗਰਾਫ਼t1 ਤੋਂ t sub<>2, ਸਮਾਂ ਦੇ ਵਿਚਾਲੇ ਉਸ ਦੁਆਰਾ ‘ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ ਦੀ ਤੁਸੀਂ ਕਿਵੇਂ ਗਣਨਾ ਕਰੋਗੇ ।
ਉੱਤਰ-
ਇੱਕ ਸਮਾਨ ਚਾਲ (v) ਨਾਲ-ਨਾਲ ਚੱਲਣ ਵਾਲੀ ਵਸਤੁ ਦਾ ਚਾਲ-ਸਮਾਂ ਗਰਾਫ਼ x-ਅਕਸ਼ ਦੇ ਸਮਾਨਾਂਤਰ ਸਰਲ ਰੇਖ ਹੋਵੇਗਾ ।
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ,
ਵਸਤੂ ਦੁਆਰਾ ਤੈਅ ਹੋਈ ਦੂਰੀ = ਵਸਤੂ ਦੀ ਚਾਲ × ਲੱਗਿਆ ਸਮਾਂ
= v × (t2 – t1)
= AB × (OD – OA)
= AB × AD
= ਆਇਤ ABCD ਦਾ ਖੇਤਰਫਲ
ਪ੍ਰਸ਼ਨ 20.
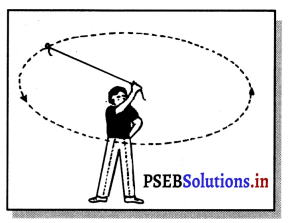
ਇੱਕ ਪੱਥਰ ਨੂੰ ਧਾਗੇ ਦੇ ਇੱਕ ਸਿਰੇ ਨਾਲ ਬੰਨ੍ਹ ਕੇ ਸਥਿਰ ਵੇਗ ਨਾਲ ਵਿਤੀ ਰੇਖਾ ਤੇ ਘੁਮਾਇਆ ਗਿਆ । ਧਾਗੇ ਨੂੰ ਛੱਡਣ ਤੇ ਪੱਥਰ ਦੀ ਦਿਸ਼ਾ ਕਿਹੜੀ ਹੋਵੇਗੀ ? ਇਸ ਆਧਾਰ ‘ਤੇ ਵਸਤੂਆਂ ਦੀ ਇੱਕ ਸਮਾਨ ਵਿਤੀ ਚੱਕਰਾਕਾਰ ਗਤੀ ਦਾ ਉਦਾਹਰਨ ਦਿਓ ।
ਉੱਤਰ-
ਧਾਗੇ ਨੂੰ ਛੱਡ ਦੇਣ ਨਾਲ ਪੱਥਰ ਦੀ ਦਿਸ਼ਾ ਵਿਤੀ ਪੱਥ ਦੀ ਸਪਰਸ਼ ਰੇਖਾ ਹੋਵੇਗੀ । ਧਾਗੇ ਨੂੰ ਛੱਡਣ ਸਮੇਂ ਪੱਥਰ ਉਸੇ ਦਿਸ਼ਾ ਵਿੱਚ ਗਤੀ ਕਰੇਗਾ ਜਿਸ ਦਿਸ਼ਾ ਵਿੱਚ ਉਹ ਗਤੀ ਕਰ ਰਿਹਾ ਸੀ ।
ਉਦਾਹਰਨ – ਚੰਨ ਅਤੇ ਧਰਤੀ ਦੀ ਗਤੀ, ਧਰਤੀ ਦੇ ਦੁਆਲੇ ਵਿਤੀ ਆਰਬਿਟ ਵਿੱਚ ਚੱਕਰ ਲਾਉਂਦਾ ਹੋਇਆ ਉਪਹਿ ।
![]()
ਪ੍ਰਸ਼ਨ 21.
ਦੋ ਰੇਲ-ਗੱਡੀਆਂ O ਬਿੰਦੂ ਤੋਂ ਉੱਤਰ ਵੱਲ ਅਤੇ ਦੱਖਣ ਵੱਲ ਜਾ ਰਹੀਆਂ ਹਨ । ਉੱਤਰ ਦਿਸ਼ਾ ਵਿੱਚ ਜਾਣ ਵਾਲੀ ਗੱਡੀ 60 ਕਿ. ਮੀ./ਘੰਟਾ ਅਤੇ ਦੱਖਣ ਦਿਸ਼ਾ ਵਿੱਚ ਜਾਣ ਵਾਲੀ ਗੱਡੀ ਦੀ ਚਾਲ 80 ਕਿ:ਮੀ:/ਘੰਟਾ ਹੈ । ਇੱਕ ਘੰਟੇ ਬਾਅਦ ਇਹਨਾਂ ਦਾ ਸਾਪੇਖ ਵਿਸਥਾਪਨ ਕਿੰਨਾ ਹੋਵੇਗਾ ?
ਉੱਤਰ-
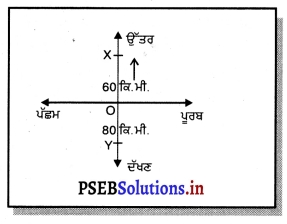
1 ਘੰਟੇ ਬਾਅਦ ਦੋਨਾਂ ਦਾ ਸਾਪੇਖ ਵਿਸਥਾਪਨ
= OX + OY
= 60 + 80
= 140 ਕਿ:ਮੀ:
ਪ੍ਰਸ਼ਨ 22.
ਚਲਦੀ ਰੇਲ ਗੱਡੀ ਵਿੱਚ ਬੈਠਾ ਇੱਕ ਵਿਅਕਤੀ ਗੇਂਦ ਨੂੰ ਲੰਬਾਤਮਕ ਉੱਪਰ ਵੱਲ ਨੂੰ ਸੁੱਟਦਾ ਹੈ । ਗੇਂਦ ਕਿਸ ਤਰ੍ਹਾਂ ਗਤੀ ਕਰਦੀ ਵਿਖਾਈ ਦੇਵੇਗੀ-
(i) ਰੇਲ ਗੱਡੀ ਵਿੱਚ ਬੈਠੇ ਵਿਅਕਤੀ ਨੂੰ ।
(ii) ਰੇਲ ਗੱਡੀ ਦੇ ਬਾਹਰ ਬੈਠੇ ਵਿਅਕਤੀ ਨੂੰ ।
ਉੱਤਰ-
(i) ਰੇਲ ਗੱਡੀ ਵਿੱਚ ਬੈਠੇ ਵਿਅਕਤੀ ਨੂੰ ਗੇਂਦ ਇੱਕ ਸਮਾਨ ਗਤੀ ਵਿੱਚ ਵਿਖਾਈ ਦੇਵੇਗੀ । ਇਹ ਗਤੀ ਬਿਲਕੁਲ ਉਸ ਵਰਗੀ ਹੈ, ਜਿਵੇਂ ਗੇਂਦ ਧਰਤੀ ਦੀ ਸਤ੍ਹਾ ‘ਤੇ ਸੁੱਟੀ ਗਈ ਹੋਵੇ ।
(ii) ਰੇਲ ਗੱਡੀ ਦੇ ਬਾਹਰ ਬੈਠੇ ਵਿਅਕਤੀ ਨੂੰ ਗੇਂਦ ਅਸਮਾਨ ਗਤੀ ਵਿੱਚ ਜਾਪੇਗੀ ਅਤੇ ਇਸ ਗਤੀ ਦਾ ਪੱਥ ਪੈਰਾਬੋਲਿਕ ਹੋਵੇਗਾ ਕਿਉਂਕਿ ਇਸ ਅਵਸਥਾ ਵਿੱਚ ਗੇਂਦ ਉੱਪਰ ਖਿਤਿਜੀ ਅਤੇ ਗੁਰੂਤਵੀ ਵੇਗ ਦੋਨੋਂ ਹੀ ਕਿਰਿਆ ਕਰਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 23.
ਇੱਕ ਫੁੱਟਬਾਲ ਸਿੱਧੀ ਉੱਪਰ ਵੱਲ ਨੂੰ ਸੁੱਟੀ ਗਈ ਹੈ । ਸਿਖਰ ਉੱਤੇ ਪਹੁੰਚ ਕੇ ਇਸ ਦਾ ਵੇਗ ਅਤੇ ਵੇਗ ਕੀ ਹੋਵੇਗਾ ?
ਉੱਤਰ-
ਉੱਪਰ ਵੱਲ ਸਿੱਧੀ ਛੁੱਟੀ ਫੁੱਟਬਾਲ ਦਾ ਵੇਗ ਹੌਲੀ-ਹੌਲੀ ਘਟੇਗਾ । ਸਿਖਰ ਉੱਤੇ ਪੁੱਜ ਕੇ ਇਸ ਦਾ ਵੇਗ ਸਿਫ਼ਰ ਹੋ ਜਾਵੇਗਾ ਅਤੇ ਵੇਗ ਗੁਰੂਤਵੀ ਵੇਗ g = – 9.81 m/s2 ਦੇ ਬਰਾਬਰ ਹੋਵੇਗਾ ।
ਪ੍ਰਸ਼ਨ 24.
ਕੀ ਇਹ ਸੰਭਵ ਹੋ ਸਕਦਾ ਹੈ ਕਿ ਕੋਈ ਵਿਅਕਤੀ ਸਥਿਰ (ਕਸਮਾਨ ਚਾਲ ਨਾਲ ਚੱਲੇ ਪਰ ਉਸਦਾ ਵੇਗ ਅਸਥਿਰ (ਅਸਮਾਨ) ਹੋਵੇ ? ਜੇ ਹਾਂ, ਤਾਂ ਇੱਕ ਉਦਾਹਰਨ ਦਿਓ ।
ਉੱਤਰ-
ਹਾਂ, ਇਹ ਸੰਭਵ ਹੋ ਸਕਦਾ ਹੈ । ਜਦੋਂ ਕੋਈ ਵਸਤੁ (ਵਿਅਕਤੀ) ਚੱਕਰਾਕਾਰ ਪੱਥ ਉੱਪਰ ਸਥਿਰ ਇੱਕ ਸਮਾਨ ਚਾਲ ਨਾਲ ਚਲਦੀ ਹੈ ਤਾਂ ਉਸ ਦੀ ਚੱਕਰਾਕਾਰ ਪੱਥ ਦੇ ਹਰੇਕ ਬਿੰਦੁ ਤੇ ਦਿਸ਼ਾ ਬਦਲਦੀ ਰਹਿੰਦੀ ਹੈ । ਗਤੀ ਦੀ ਇਹ ਦਿਸ਼ਾ ਉਸ ਬਿੰਦੂ ‘ਤੇ ਚੱਕਰ ਨੂੰ ਟੈਂਜੇਂਟ (ਸਪਰਸ਼ ਰੇਖਾ) ਦੀ ਦਿਸ਼ਾ ਵਿੱਚ ਹੁੰਦੀ ਹੈ । ਇਸ ਲਈ ਦਿਸ਼ਾ ਬਦਲਣ ਕਾਰਨ ਉਸਦਾ . ਵੇਗ ਅਸਥਿਰ (ਅਸਮਾਨ ਹੁੰਦਾ ਹੈ ।
ਭੌਤਿਕ ਰਾਸ਼ੀਆਂ ਦੇ ਚਿੰਨ੍ਹ ਅਤੇ ਜ਼ਰੂਰੀ ਸੂਤਰ (Symbols of Physical Quantities and Important Formulae)
(ੳ) ਭੌਤਿਕ ਰਾਸ਼ੀਆਂ ਦੇ ਚਿੰਨ੍ਹ
ਸਮਾਂ = t
ਚਾਲ = v
ਦੂਰੀ = S
(ਮੁੱਢਲਾ) ਆਰੰਭਿਕ ਵੇਗ = u
ਅੰਤਿਮ ਵੇਗ = υ
ਪ੍ਰਵੇਗ = a
ਔਸਤ ਵੇਗ = Vav
(ਅ ਜ਼ਰੂਰੀ ਸੂਤਰ
ਜੇਕਰ ਆਰੰਭਿਕ ਵੇਗ v ਸਮਾਂ t ਤੇ ਵੇਗ v ਅਤੇ ਸਮਾਨ ਵੇਗ a ਹੋਣ ਤਾਂ ਹੇਠ ਲਿਖੇ ਸੰਬੰਧ ਗਤੀ ਸਮੀਕਰਣ ਕਹਾਉਂਦੇ ਹਨ-
v = u + at (ਸਮਾਂ t ਤੇ ਵੇਗ)
S = ut + \(\frac {1}{2}\)at2 (ਸਮਾਂ ਅੰਤਰਾਲ ਵਿੱਚ ਵਿਸਥਾਪਨ)
v2 = u2 + 2as (ਵੇਗ ਵਰਗ ਸੰਬੰਧ)
Snn = u + \(\frac{a}{2}\)(2n -1) (n ਵੇਂ ਇਕਾਈ ਸਮਾਂ ਅੰਤਰਾਲ ਵਿੱਚ ਵਿਸਥਾਪਨ)
![]()
ਸੰਖਿਆਤਮਕ ਪ੍ਰਸ਼ਨ (Numerical Problems)
ਪ੍ਰਸ਼ਨ 1.
ਇੱਕ ਕਾਰ ਸਮਾਨ ਵੇਗ ਨਾਲ 18 ਕਿ. ਮੀ. /ਘੰਟਾ ਤੋਂ 36 ਕਿ. ਮੀ./ਘੰਟਾ ਦੀ ਗਤੀ 5 ਸੈਕਿੰਡ ਵਿੱਚ ਪ੍ਰਾਪਤ ਕਰ ਲੈਂਦੀ ਹੈ । ਇਸ ਦਾ ਪ੍ਰਵੇਗ ਅਤੇ ਇਸ ਸਮੇਂ ਵਿੱਚ ਤੈਅ ਹੋਈ ਦੂਰੀ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਇੱਥੇ u = 18 ਕਿ.ਮੀ. /ਘੰਟਾ
= \(\frac{18 \times 1000}{60 \times 60}\)
= 5 ਮੀ. /ਸੈਂ,
υ = 36 ਕਿ.ਮੀ. /ਘੰਟਾ |
= \(\frac{36 \times 1000}{60 \times 60}\)
= 10 ਮੀ./ਸੈਂ,.
t = 5 ਸੈਕਿੰਡ
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ, υ = u + at
10 = 5 + a x 5
∴ a = 1 ਮੀ./ਸੈਂ,2.
ਹੁਣ S = ut + = \(\frac {1}{2}\)at2
5 x 5 + \(\frac {1}{2}\) x (1) (5)2
= 25 + \(\frac {25}{2}\)
= 25 + 12.5
∴ S = 37.5 ਮੀਟਰ
ਪ੍ਰਸ਼ਨ 2.
ਇੱਕ ਪੁਲਿਸ ਦੀ ਗੱਡੀ ਹਾਈਵੇ ‘ਤੇ 30 km/h ਦੀ ਚਾਲ ਨਾਲ ਦੌੜਦੀ ਹੈ, ਉਸੇ ਹੀ ਪਾਸੇ ਚੋਰਾਂ ਦੀ ਗੱਡੀ ਜਿਸ ਦੀ ਚਾਲ 192 km/h ਹੈ ਦੌੜ ਰਹੀ ਹੈ, ਪੁਲਿਸ ਚੋਰਾਂ ਉੱਪਰ ਗੋਲੀ ਚਲਾਉਂਦੀ ਹੈ । ਜੇਕਰ ਗੋਲੀ ਦੀ ਚਾਲ 150 m/s ਹੋਵੇ, ਤਾਂ ਕਿਹੜੀ ਚਾਲ ਨਾਲ ਗੋਲੀ ਚੋਰਾਂ ਦੀ ਗੱਡੀ ਨਾਲ ਲੱਗੇਗੀ ?
ਹੱਲ:
ਗੋਲੀ ਨੂੰ ਛੱਡਣ ਦੀ ਚਾਲ = 150 m/s.
= \(\frac{150 \times 3600}{1000}\)
= 540 km/h
ਕੁੱਲ ਚਾਲ = 30 + 540 = 570 km/h
ਗੋਲੀ ਦੀ ਚਾਲ ਚੋਰਾਂ ਦੀ ਗੱਡੀ ਦੇ ਸਾਪੇਖ ਵਿੱਚ, ਜਿਹੜੀ ਉਸੇ ਹੀ ਪਾਸੇ ਜਾ ਰਹੀ ਹੈ-
= 570 – 192 = 378 km/h
= \(\frac{378 \times 1000}{60 \times 60}\)m/s
= \(\frac{378000}{3600}\) = 105 m/s
ਪ੍ਰਸ਼ਨ 3.
ਇੱਕ ਰੇਲ ਗੱਡੀ ਜਿਹੜੀ 50m ਚਲਦੀ ਹੈ, ਇੱਕ ਸਿੱਧੇ ਅਤੇ ਸਮਤਲ ਟ੍ਰੈਕ ਉੱਤੇ ਖੰਭੇ ਦੇ ਕੋਲ 5 ਸੈਕਿੰਡ ਵਿੱਚ ਪਹੁੰਚਦੀ ਹੈ ।
(i) ਗੱਡੀ ਦੀ ਚਾਲ ਦੱਸੋ
(ii) 450m ਲੰਬੇ ਪੁਲ ਨੂੰ ਪਾਰ ਕਰਨ ਵਿੱਚ ਗੱਡੀ ਕਿੰਨਾ ਸਮਾਂ ਲਵੇਗੀ ?
ਹੱਲ:
ਜਿਵੇਂ ਗੱਡੀ ਖੰਭੇ ਨੂੰ 5 ਸੈਕਿੰਡ ਵਿੱਚ ਪਾਰ ਕਰਦੀ ਹੈ, ਤਾਂ ਇਹ ਆਪਣੀ ਲੰਬਾਈ ਦੇ ਬਰਾਬਰ ਦੂਰੀ ਤੈਅ ਕਰਦੀ ਹੈ ।
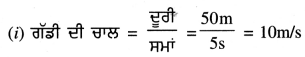
(ii) ਪੁਲ ਨੂੰ ਪਾਰ ਕਰਨ ‘ਤੇ ਜਿੰਨੀ ਲੰਬਾਈ ਗੱਡੀ ਤੈਅ ਕਰਦੀ ਹੈ = ਪੁਲ ਦੀ ਲੰਬਾਈ + ਗੱਡੀ ਦੀ ਲੰਬਾਈ
= 450m + 50m = 500 m
∴ ਪੁਲ ਨੂੰ ਪਾਰ ਕਰਨ ਵਿੱਚ ਲੱਗਿਆ ਸਮਾਂ-

= \(\frac{500}{10 \mathrm{~m} / \mathrm{s}}\) = 50 ਸੈਕਿੰਡ
ਪ੍ਰਸ਼ਨ 4.
ਇੱਕ ਵਸਤੂ ਵਿਰਾਮ ਅਵਸਥਾ ਤੋਂ 0.6 ਮੀਟਰ/ਸੈਕਿੰਡ2 ਦੇ ਵੇਗ ਨਾਲ ਗਤੀ ਕਰ ਰਿਹਾ ਹੈ । 300 ਮੀਟਰ ਚੱਲਣ ਤੋਂ ਬਾਅਦ ਇਸ ਦਾ ਵੇਗ ਕੀ ਹੋਵੇਗਾ ? ਇਸ ਦੂਰੀ ਨੂੰ ਤੈਅ ਕਰਨ ਲਈ ਕਿੰਨਾ ਸਮਾਂ ਲੱਗੇਗਾ ?
ਹੱਲ:
ਇੱਥੇ u = 0
a = 0.6 ਮੀਟਰ/ਸੈਕਿੰਡ2
S = 300 ਮੀਟਰ
υ = ?
t = ?
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ,
υ2 = u2 + 2as
υ2 = (0)2 + 2 x 0.6 x 300
= 360
∴ υ = \(\sqrt{360}\)
= 6 x \(\sqrt{10}\) ਮੀਟਰ/ਸੈਕਿੰਡ
= 19 ਮੀਟਰ/ਸੈਕਿੰਡ (ਲਗਪਗ)
ਹੁਣ S = ut + \(\frac {1}{2}\)at2
300 = 0 x t + \(\frac {1}{2}\) x 0.6 x t2
300 = 0 + 0.3t2
∴ t2 = \(\frac{300}{0.3}\)
= \(\frac{3000}{3}\) = 1000
t = \(\sqrt{1000}\)
= \(\sqrt{100 \times 10}\)
= 31.5 ਸੈਕਿੰਡ (ਲਗਪਗ)
![]()
ਪ੍ਰਸ਼ਨ 5.
15 ਮੀ. ਸੈਂ. ਦੀ ਗਣਨਾ ਕਿ. ਮੀ. /ਘੰਟਾ ਵਿੱਚ ਕਰੋ ।
ਹੱਲ:

= 54 ਕਿ.ਮੀ./ਘੰਟਾ
ਪ੍ਰਸ਼ਨ 6.
ਇੱਕ ਪੱਥਰ ਲੰਬਾਤਮਕ ਉੱਪਰ ਵੱਲ ਨੂੰ 5 m/s ਦੇ ਵੇਗ ਨਾਲ ਸੁੱਟਿਆ ਗਿਆ । ਇਸਦਾ ਵੇਗ ਲੰਬਾਤਮਕ ਦਿਸ਼ਾ ਵਿੱਚ ਹੇਠਾਂ ਵੱਲ 10/ms2 ਹੋ ਗਿਆ, ਤਾਂ ਪੱਥਰ ਦੁਆਰਾ ਪ੍ਰਾਪਤ ਵੱਧ ਤੋਂ ਵੱਧ ਉੱਚਾਈ ਗਿਆਤ ਕਰੋ ਅਤੇ ਇਸ ਵੱਧ ਤੋਂ ਵੱਧ ਉੱਚਾਈ ਨੂੰ ਪਹੁੰਚਣ ਲਈ ਪੱਥਰ ਨੂੰ ਕਿੰਨਾ ਸਮਾਂ ਲੱਗੇਗਾ ?
ਹੱਲ:
u = 5 ਮੀ: ਸੈਂ:
v = 0 (ਵੱਧ ਤੋਂ ਵੱਧ ਉੱਚਾਈ ‘ਤੇ)
ਪ੍ਰਵੇਗ (a) = g = – 10 ਮੀ: ਸੈਂ:2
v2 = u2 + 2gs
(0)2 = (5)2 + 2 × (-10) × h
0 = 25 -20 h
-25 = -20 h
∴ h = \(\frac{-25}{-20}\)
h = \(\frac{5}{4}\) = 1.25 ਮੀਟਰ
ਹੁਣ v = u + gt
0 = 5 +(-10) × t
-10 t = -5
∴ t = \(\frac{-5}{-10}=\frac{1}{2}\) = 0.5 ਸੈਕਿੰਡ
ਪ੍ਰਸ਼ਨ 7.
ਯਾਤਰਾ ਸ਼ੁਰੂ ਹੋਣ ਸਮੇਂ ਕਾਰ ਦਾ ਉਡੋਮੀਟਰ 2000 km ਦਰਸਾਉਂਦਾ ਹੈ ਅਤੇ ਯਾਤਰਾ ਦੀ ਸਮਾਪਤੀ ਤੇ 240 km ਦਰਸਾਉਂਦਾ ਹੈ । ਜੇਕਰ ਇਸ ਯਾਤਰਾ ਨੂੰ 8 h ਲੱਗੇ ਹੋਣ ਤਾਂ ਕਾਰ ਦੀ ਔਸਤ ਚਾਲ km/h ਅਤੇ ms ਵਿੱਚ ਪਤਾ ਕਰੋ ।
ਹੱਲ :
ਕਾਰ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ = = 2400 km-2000 km
= 400 km
ਦੂਰੀ ਤੈਅ ਕਰਨ ਨੂੰ ਲੱਗਿਆ ਸਮਾਂ t = 8 h
∴ ਕਾਰ ਦੀ ਔਸਤ ਚਾਲ Vav = \(\frac{\mathrm{S}}{t}\)
= \(\frac{400 \mathrm{~km}}{8 \mathrm{~h}}\)
= 50 km/h
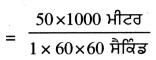
= 13.9 ਮੀਟਰ/ਸੈਕਿੰਡ (ms-1)
ਪ੍ਰਸ਼ਨ 8.
ਉਸ਼ਾ 90 m ਲੰਬੇ ਤਾਲਾਬ ਵਿੱਚ ਤੈਰਦੀ ਹੈ ।ਉਹ ਇੱਕ ਸਿਰੇ ਤਕ ਸਰਲ ਰੇਖੀ ਪੱਥ ‘ਤੇ ਜਾਂਦੀ ਹੈ ਅਤੇ ਵਾਪਸ ਆਉਂਦੀ ਹੈ । ਇਸ ਦੌਰਾਨ ਉਹ ਕੁੱਲ 180 m ਦੀ ਦੂਰੀ 1 ਮਿੰਟ ਵਿੱਚ ਤੈਅ ਕਰਦੀ ਹੈ । ਊਸ਼ਾ ਦੀ ਔਸਤ ਚਾਲ ਅਤੇ ਔਸਤ ਵੇਗ ਗਿਆਤ ਕਰੋ ।
ਹੱਲ:
ਤਾਲਾਬ ਦੀ ਲੰਬਾਈ = 90 km
ਉਸ਼ਾ ਦੁਆਰਾ 1 ਮਿੰਟ ਵਿੱਚ ਤੈਅ ਕੀਤੀ ਗਈ ਦੁਰੀ = 180 m
1 ਮਿੰਟ ਵਿੱਚ ਊਸ਼ਾ ਦਾ ਵਿਸਥਾਪਨ = 90 +(-90)
= 90 – 90
= 0 ਮੀਟਰ

![]()
ਪ੍ਰਸ਼ਨ 9.
ਬਰੇਕ ਲਗਾਉਣ ‘ਤੇ ਕਾਰ ਦਾ ਮੰਦਨ (Retardation) 6 m/s2 ਹੋ ਗਿਆ । ਜੇਕਰ ਕਾਰ ਦੀ ਬਰੇਕ ਲਗਾਉਣ ‘ਤੇ ਰੁਕਣ ਵਾਸਤੇ 2 ਸਕਿੰਟ ਲੱਗਣ, ਤਾਂ ਦੱਸੋ ਕਿ ਇਸ ਸਮੇਂ ਦੇ ਦੌਰਾਨ ਕਾਰ ਕਿੰਨੀ ਦੂਰੀ ਤੈਅ ਕਰੇਗੀ ?
ਹੱਲ:
ਇੱਥੇ a = 6 ms/2, t = 2s, υ = 0
υ = u + at
0 = u + (-6) × 2
∴ u = 12 m/s
ਹੁਣ
S = ut + \(\frac {1}{2}\)at2
S = 12 × 2 + \(\frac {1}{2}\) (-6) (2)2
= 24 + (-3 × 4)
= 24 – 12
= 12m
ਪ੍ਰਸ਼ਨ 10.
(i) ਘੜੀ ਦੀ ਸੈਕਿੰਡਾਂ ਵਾਲੀ ਸੂਈ
(ii) ਘੜੀ ਦੀ ਮਿੰਟਾਂ ਵਾਲੀ ਸੂਈ
(iii) ਘੜੀ ਦੀ ਘੰਟਿਆਂ ਵਾਲੀ ਸੂਈ ਦਾ ਕੋਈ ਵੇਗ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
(i) ਘੜੀ ਦੀ ਸੈਕਿੰਡਾਂ ਵਾਲੀ ਸੂਈ 60 ਸੈਕਿੰਡ ਵਿੱਚ ਇੱਕ ਚੱਕਰ ਪੂਰਾ ਕਰਦੀ ਹੈ । ਇਸ ਨੂੰ ਸਮਾਂ ਅੰਤਰਾਲ ਕਹਿੰਦੇ ਹਨ ।
θ = 2π ਰੇਡੀਅਨ
t = 1 ਮਿੰਟ = 60 ਸੈਕਿੰਡ
ਪਰੰਤੂ ਕੋਣੀ ਵੇਗ ω = \(\frac{\theta}{t}\)

= \(\frac{\pi}{30}\) ਰੇਡੀਅਨ/ਸੈਕਿੰਡ
(ii) ਮਿੰਟਾਂ ਵਾਲੀ ਸੂਈ ਲਈ θ = 2π ਰੇਡੀਅਨ
t = 1h
= 60 × 60 ਸੈਕਿੰਡ
∴ ਕੋਣੀ ਵੇਗ ω = \(\frac{\theta}{t}\)

= \(\frac{\pi}{1800}\) ਰੇਡੀਅਨ/ਸੈਕਿੰਡ
(iii) ਘੰਟਿਆਂ ਵਾਲੀ ਸੂਈ ਲਈ θ = 2π ਰੇਡੀਅਨ
t = 12 ਘੰਟੇ
= 12 × 60 × 60 ਸੈਕਿੰਡ

= \(\frac{\pi}{21600}\) ਰੇਡੀਅਨ/ਸੈਕਿੰਡ
ਪ੍ਰਸ਼ਨ 11.
ਇੱਕ ਰੇਡੀਅਨ ਕਿੰਨੇ ਡਿਗਰੀ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ ?
ਹੱਲ:
ਰੇਡੀਅਨ ਅਤੇ ਡਿਗਰੀ ਵਿੱਚ ਸੰਬੰਧ-
ਪੂਰੇ ਵਿਤ ਦੁਆਰਾ ਕੇਂਦਰ ‘ਤੇ ਬਣਾਇਆ ਕੋਣ = \(\frac{2 \pi r}{r}\)
= 2π ਰੇਡੀਅਨ
ਅਤੇ ਕੇਂਦਰ ਤੇ ਸਥਾਪਿਤ ਕੋਣ ਡਿਗਰੀਆਂ ਵਿੱਚ = 360°
∴ 2π ਰੇਡੀਅਨ = 360°
π ਰੇਡੀਅਨ = \(\frac{360}{2}\) = 180°
1 ਰੇਡੀਅਨ = \(\frac{180^{\circ}}{\pi}\)
= \(\frac{180^{\circ}}{\frac{22}{7}}\)
= \(\frac{180^{\circ} \times 7}{22}\)
∴ 1 ਰੇਡੀਅਨ = 57.3°
ਪ੍ਰਸ਼ਨ 12.
ਇੱਕ ਚੱਕਰਾਕਾਰ ਸਾਈਕਲ ਟਰੈਕ ਦਾ ਘੇਰਾ 314 ਮੀਟਰ ਹੈ । AB ਇਸ ਦਾ ਇੱਕ ਵਿਆਸ ਹੈ । ਇੱਕ ਸਾਈਕਲ ਸਵਾਰ ਇੱਕ ਸਮਾਨ ਵੇਗ 15.7 m/s ਨਾਲ A ਤੋਂ ਚੱਕਰ ਲਗਾਉਂਦਾ ਹੋਇਆ B ਤਕ ਪਹੁੰਚਦਾ ਹੈ ।
(ਉ) ਸਾਈਕਲ ਸਵਾਰ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਦੂਰੀ ਪਤਾ ਕਰੋ ।
(ਅ) ਜੇ AB ਉੱਤਰ-ਦੱਖਣ ਦਿਸ਼ਾ ਦਰਸਾਉਂਦਾ ਹੈ, ਤਾਂ ਸਾਈਕਲ ਸਵਾਰ ਦਾ ਵਿਸਥਾਪਨ ਪਤਾ ਕਰੋ ।
(ੲ) ਸਾਈਕਲ ਸਵਾਰ ਦਾ ਔਸਤ ਵੇਗ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
(ੳ)
ਵਿਆਸ = AB
= 314 m.
ਚਾਲ = 15.7 m/s.
15.7 m ਦੂਰੀ ਤੈਅ ਕਰਨ ਵਿੱਚ ਲੱਗਿਆ ਸਮਾਂ = 1 ਸੈਕਿੰਡ ,
1m ਦੂਰੀ ਤੈਅ ਕਰਨ ਵਿੱਚ ਲੱਗਿਆ ਸਮਾਂ = \(\frac{1}{15.7}\)
314 m ਦੂਰੀ ਤੈਅ ਕਰਨ ਵਿੱਚ ਲੱਗਿਆ ਸਮਾਂ = \(\frac{1 \times 314}{15.7}\)
= 20 ਸੈਕਿੰਡ
(ਅ) ਸਾਈਕਲ ਸਵਾਰ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਦੂਰੀ = 2πr = 314 ਮੀਟਰ
2πr = 314
r = \(\frac{314}{2 \times 3.14}\)
= 50 ਮੀਟਰ
ਵਿਆਸ = 2r
= 2 × 50 ਮੀਟਰ
= 100 ਮੀਟਰ (ਵਿਸਥਾਪਨ)
(ੲ)
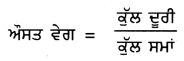
ਔਸਤ ਵੇਗ = \(\frac{314}{20}\)
= 15.7 ਮੀਟਰ/ਸੈਕਿੰਡ
![]()
ਬਹੁਤ ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Very Short Answer Type Questions)
ਪ੍ਰਸ਼ਨ 1.
ਗਤੀ ਕੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਗਤੀ – ਜਦੋਂ ਕੋਈ ਵਸਤੂ ਸਮੇਂ ਦੇ ਨਾਲ ਆਪਣੀ ਸਥਿਤੀ ਵਿੱਚ ਪਰਿਵਰਤਨ ਕਰਦੀ ਹੈ, ਤਾਂ ਉਸ ਵਸਤੂ ਨੂੰ ਗਤੀ ਵਿੱਚ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 2.
ਵਸਤੂ ਦਾ ਵਿਸਥਾਪਨ ਕੀ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਵਿਸਥਾਪਨ – ਵਸਤੂ ਦੀ ਅੰਤਿਮ ਸਥਿਤੀ ਅਤੇ ਆਰੰਭਿਕ ਸਥਿਤੀ ਦੇ ਵਿਚਾਲੇ ਦੀ ਨਿਊਨਤਮ ਦੂਰੀ ਨੂੰ ਵਿਸਥਾਪਨ ਕਹਿੰਦੇ ਹਨ |
ਪ੍ਰਸ਼ਨ 3.
ਦੋ ਵਿਭਿੰਨ ਭੌਤਿਕ ਰਾਸ਼ੀਆਂ ਕਿਹੜੀਆਂ ਹਨ ?
ਉੱਤਰ-
ਦੂਰੀ ਅਤੇ ਵਿਸਥਾਪਨ ।
ਪ੍ਰਸ਼ਨ 4.
ਵਾਹਨਾਂ ਦੀ ਗਤੀ ਮਾਪਣ ਲਈ ਕਿਸ ਯੰਤਰ ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ?
ਉੱਤਰ-
ਉਡੋਮੀਟਰ ਦੀ ।
ਪ੍ਰਸ਼ਨ 5.
ਇੱਕ ਸਮਾਨ ਗਤੀ ਕੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਇੱਕ ਸਮਾਨ ਗਤੀ – ਜਦੋਂ ਕੋਈ ਵਸਤੂ ਸਮਾਨ ਸਮੇਂ ਅੰਤਰਾਲਾਂ ਵਿੱਚ ਇੱਕ ਸਮਾਨ ਦੂਰੀ ਤੈਅ ਕਰਦੀ ਹੈ, ਤਾਂ ਉਸਦੀ ਗਤੀ ਇਕ ਸਮਾਨ ਗਤੀ ਹੁੰਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 6.
ਅਸਮਾਨ ਗਤੀ ਦੇ ਦੋ ਉਦਾਹਰਨ ਦਿਓ ।
ਉੱਤਰ-
ਸੜਕ ਤੇ ਜਾ ਰਹੀ ਕਾਰ, ਪਾਰਕ ਵਿੱਚ ਕਸਰਤ ਕਰ ਰਿਹਾ ਵਿਅਕਤੀ ।
![]()
ਪ੍ਰਸ਼ਨ 7.
ਚਾਲ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਚਾਲ – ਵਸਤੂ ਦੁਆਰਾ ਇਕਾਈ ਸਮੇਂ ਵਿੱਚ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ ਨੂੰ ਉਸ ਵਸਤੂ ਦੀ ਚਾਲ ਆਖਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 8. ਚਾਲ ਦਾ ਮਾਤ੍ਰਿਕ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਚਾਲ ਦਾ ਮਾਤ੍ਰਿਕ ਮੀਟਰ/ਸੈਕਿੰਡ ਹੈ । ਇਹ ਮਾਤ੍ਰਿਕ ਕਿਲੋਮੀਟਰ/ਘੰਟਾ ਅਤੇ ਸੈਂਟੀਮੀਟਰ/ਸੈਕਿੰਡ ਵੀ ਹੋ ਸਕਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 9.
ਔਸਤ ਚਾਲ ਕਿਵੇਂ ਪਤਾ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ?
ਉੱਤਰ-
ਔਸਤ ਚਾਲ – ਵਸਤੂ ਦੀ ਔਸਤ ਚਾਲ ਉਸ ਵਸਤੂ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ ਨੂੰ ਤੈਅ ਕਰਨ ਲਈ ਲੱਗੇ ਕੁੱਲ ਸਮੇਂ ਨਾਲ ਭਾਗ ਕਰਕੇ ਪ੍ਰਾਪਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ।
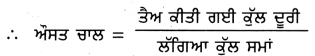
ਪ੍ਰਸ਼ਨ 10.
ਵੇਗ ਕੀ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਵੇਗ-ਇਕ ਨਿਸਚਿਤ ਦਿਸ਼ਾ ਵਿੱਚ ਚਾਲ ਨੂੰ ਵੇਗ ਕਹਿੰਦੇ ਹਨ ਜਾਂ ਇਕ ਨਿਸਚਿਤ ਦਿਸ਼ਾ ਵਿੱਚ ਇਕਾਈ ਸਮੇਂ ਵਿੱਚ ਵਸਤੁ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਦੁਰੀ ਨੂੰ ਵੇਗ ਕਹਿੰਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 11.
ਵੇਗ ਕੀ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਪ੍ਰਵੇਗ – ਕਿਸੇ ਵਸਤੂ ਦੇ ਇਕਾਈ ਸਮੇਂ ਵਿੱਚ ਵੇਗ ਪਰਿਵਰਤਨ ਨੂੰ ਪ੍ਰਵੇਗ ਕਹਿੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 12.
ਵੇਗ ਦਾ ਮਾਤ੍ਰਿਕ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਪ੍ਰਵੇਗ ਦਾ ਮਾਤਿਕ ਮੀਟਰ/ਸੈਕਿੰਡ2 (ms-2) ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 13.
ਇੱਕ ਸਮਾਨ ਗਿਤ ਗਤੀਆਂ ਲਈ ਵੇਗ-ਸਮਾਂ ਗਰਾਫ਼ ਕਿਸ ਤਰ੍ਹਾਂ ਦਾ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਇੱਕ ਸਿੱਧੀ ਰੇਖਾ ।
ਪ੍ਰਸ਼ਨ 14.
ਗਿਤ ਗਤੀ ਦਾ ਇਕ ਉਦਾਹਰਣ ਦਿਓ ।
ਉੱਤਰ-
ਇੱਕ ਵਿਤੀ (ਚੱਕਰਾਕਾਰ) ਪੱਥ ‘ਤੇ ਦੌੜਦਾ ਹੋਇਆ ਐਥਲੀਟ ।
ਪ੍ਰਸ਼ਨ 15.
ਇੱਕ ਐਥਲੀਟ ਨੂੰ ਛੇ-ਭੁਜੀ ਪੱਥ ‘ਤੇ ਇੱਕੋ ਦਿਸ਼ਾ ਵਿੱਚ ਦੌੜਦੇ ਹੋਏ ਇੱਕ ਚੱਕਰ ਪੂਰਾ ਕਰਨ ਲਈ ਕਿੰਨੀ ਵਾਰੀ ਦਿਸ਼ਾ ਬਦਲਣੀ ਪਵੇਗੀ ?
ਉੱਤਰ-
ਛੇ ਵਾਰੀ ।
ਪ੍ਰਸ਼ਨ 16.
ਜੇਕਰ ਇੱਕ ਐਥਲੀਟ r ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਵਿਤੀ ਪੱਥ ਦਾ 1 ਚੱਕਰ ਲਗਾਉਣ ਲਈ ‘t’ ਸੈਕਿੰਡ ਲੈਂਦਾ ਹੈ, ਤਾਂ ਉਸ ਐਥਲੀਟ ਦਾ ਵੇਗ ਕੀ ਹੋਵੇਗਾ ?
ਉੱਤਰ-
v = \(\frac{2 \pi r}{t}\)
ਪ੍ਰਸ਼ਨ 17.
ਜੇਕਰ ਕੋਈ ਵਸਤੂ ਚੱਕਰਾਕਾਰ ਪੱਥ ਤੇ ਇੱਕ ਸਮਾਨ ਚਾਲ ਨਾਲ ਚਲ ਰਹੀ ਹੈ, ਤਾਂ ਉਸ ਦੀ ਗਤੀ ਕਿਸ ਕਿਸਮ ਦੀ ਹੋਵੇਗੀ ? |
ਉੱਤਰ-
ਅਸਮਾਨ ਅਤੇ ਵੇਗਤ ਗਤੀ ।
ਪ੍ਰਸ਼ਨ 18.
ਇੱਕ ਵਸਤੁ r ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਵਿਤੀ ਪੱਥ ‘ਤੇ ਗਤੀ ਕਰ ਰਹੀ ਹੈ । ਇੱਕ ਪੂਰਾ ਚੱਕਰ ਲਗਾਉਣ ਵਿੱਚ ਇਸ ਦੀ ਕੁੱਲ ਤੈਅ ਹੋਈ ਦੂਰੀ ਅਤੇ ਵਿਸਥਾਪਨ ਪਤਾ ਕਰੋ ।
ਉੱਤਰ-
ਵਿਸਥਾਪਨ = 0 (ਜ਼ੀਰੋ)
ਕੁੱਲ ਤੈਅ ਹੋਈ ਦੁਰੀ = 2πr
![]()
ਪ੍ਰਸ਼ਨ 19.
ਇੱਕ ਕ੍ਰਿਕੇਟ ਖਿਡਾਰੀ ਗੇਂਦ ਨੂੰ ਉੱਪਰ ਸੁੱਟ ਕੇ ਫਿਰ ਪਕੜ ਲੈਂਦਾ ਹੈ । ਦੱਸੋ ਗੇਂਦ ਦਾ ਵਿਸਥਾਪਨ ਕਿੰਨਾ ਹੋਇਆ ਹੈ ?
ਉੱਤਰ-
ਕੁੱਲ ਵਿਸਥਾਪਨ = ਜ਼ੀਰੋ, ਕਿਉਂਕਿ ਇਸ ਪ੍ਰਕਿਰਿਆ ਦੌਰਾਨ ਗੇਂਦ ਆਪਣੀ ਮੁੱਢਲੀ ਸਥਿਤੀ ‘ਤੇ ਆ ਜਾਂਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 20.
ਦੂਰੀ-ਸਮਾਂ ਗਰਾਫ਼ ਦੀ ਢਾਲ ਕੀ ਦੱਸਦੀ ਹੈ ?
ਉੱਤਰ-
ਵਸਤੂ ਦੀ ਚਾਲ ।
ਪ੍ਰਸ਼ਨ 21.
ਪ੍ਰਕਾਸ਼ ਦੀ ਚਾਲ 3 × 108 m/s ਹੈ । ਇਹ km/h ਵਿੱਚ ਕਿੰਨੀ ਹੋਵੇਗੀ ?
ਉੱਤਰ-
ਪ੍ਰਕਾਸ਼ ਦੀ ਚਾਲ = 3 × 108 m/s
= \(\frac{3 \times 10^{8} \times 3600}{1000}\)km/h
= 1.8 × 109 km/h
ਪ੍ਰਸ਼ਨ 22.
ਦੂਰੀ ਕਿਸ ਤਰ੍ਹਾਂ ਦੀ ਰਾਸ਼ੀ ਹੈ-ਸਕੇਲਰ ਜਾਂ ਵੈਕਟਰ ?
ਉੱਤਰ-
ਸਕੇਲਰ (ਸਦਿਸ਼) ਰਾਸ਼ੀ ।
ਪ੍ਰਸ਼ਨ 23.
ਹਵਾ ਵਿੱਚ ਧੁਨੀ ਦੀ ਚਾਲ ਕਿੰਨੀ ਹੈ ?
ਉੱਤਰ-
346 ms-1
ਪ੍ਰਸ਼ਨ 24.
ਅਸਮਾਨ ਚਾਲ ਨਾਲ ਚੱਲਣ ਵਾਲੇ ਵਾਹਨ ਦਾ ਦੁਰੀ-ਸਮਾਂ ਗਰਾਫ਼ ਦਾ ਆਕਾਰ ਕਿਹੋ ਜਿਹਾ ਹੋਵੇਗਾ ?
ਉੱਤਰ-
ਵਕਰ ਰੇਖਾ ਆਕਾਰ ।
![]()
ਪ੍ਰਸ਼ਨ 25.
ਚੱਕਰਾਕਾਰ (ਵਿਤੀ) ਗਤੀ ਕਿਸਨੂੰ ਕਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਚੱਕਰਾਕਾਰ (ਤੀ ਗਤੀ)-ਜਦੋਂ ਕੋਈ ਵਸਤੂ ਚੱਕਰਾਕਾਰ ਪੱਥ ‘ਤੇ ਗਤੀ ਕਰਦੀ ਹੈ, ਤਾਂ ਵਸਤੂ ਦੀ ਗਤੀ ਚੱਕਰਾਕਾਰ ਵਿਤੀ ਗਤੀ ਕਹਾਉਂਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 26.
ਕੋਣੀ ਵੇਗ ਕਿਸਨੂੰ ਕਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਕੋਣੀ ਵੇਗ-ਚੱਕਰਾਕਾਰ (ਤੀ ਪੱਥ ‘ਤੇ ਗਤੀ ਕਰਦੀ ਹੋਈ ਵਸਤੂ ਦਾ ਕੋਈ ਵਿਸਥਾਪਨ ਤੈਅ ਕਰਨ ਦੀ ਦਰ ਨੂੰ ਉਸ ਵਸਤੂ ਦਾ ਕੋਣੀ ਵੇਗ ਕਹਿੰਦੇ ਹਨ । ਇਸਨੂੰ (ω) ਐਮੈਗਾ ਨਾਲ ਪ੍ਰਦਰਸ਼ਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
