PSEB 9th Class Science Important Questions Chapter 9 बल तथा गति के नियम

Punjab State Board PSEB 9th Class Science Important Questions Chapter 9 बल तथा गति के नियम Important Questions and Answers.

PSEB 9th Class Science Important Questions Chapter 9 बल तथा गति के नियम

दीर्घ उत्तरात्मक प्रश्न (Long Answer Type Questions)

प्रश्न 1.
बल कितने प्रकार के होते हैं ? प्रत्येक को उदाहरण देकर स्पष्ट कीजिए।
उत्तर-
बल के प्रकार-बल दो प्रकार के होते हैं-
(i) संतुलित बल,
(ii) असंतुलित बल।

(i) संतुलित बल – जब किसी वस्तु पर एक-साथ कई बल क्रिया कर रहे हों और उनका परिणामी बल शून्य हो तो उन बलों को संतुलित बल कहते हैं। संतुलित बलों की अवस्था में यदि कोई वस्तु स्थिर है तो स्थिर रहेगी तथा यदि एक समान गति कर रही है तो वह उसी एक समान गति से गतिशील रहेगी, जैसे कि वस्तु पर कोई बल कार्य ही न कर रहा हो। इस प्रकार संतुलित बलों के प्रभाव से वस्तु की स्थिति में परिवर्तन नहीं होता है।

संतुलित बलों से वस्तु की आकृति बदल जाती है; जैसे- यदि रबड़ की एक गेंद को हथेलियों के बीच रखकर बराबर व विपरीत बल लगाएं तो गेंद की आकृति बदल जाती है। यह गेंद गोल न रहकर चपटी-सी हो जाती है।

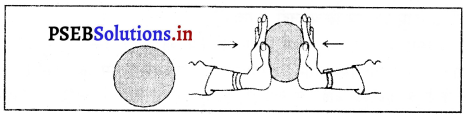
उदाहरण – रस्साकशी के खेल में जब दोनों टीमें रस्से को बराबर बल से खींचती हैं, तब परिणामी बल शून्य होता है। अतः दोनों टीमें अपने स्थान पर स्थिर बनी रहती हैं। इस दशा में दोनों टीमों द्वारा रस्से पर लगाया गया बल संतुलित है।

दो बलों के संतुलित होने की शर्त – दो समान तथा विपरीत दिशा में क्रिया कर रहे बल तभी संतुलित होते हैं, यदि वे एक रेखा में क्रिया करते हैं तथा उनका परिमाण समान होता है।

संतुलित बलों का प्रभाव – किसी वस्तु पर क्रिया कर रहे बल यदि इसकी विराम या गतिशील अवस्था में परिवर्तन नहीं कर सकते तो ये अवश्य ही वस्तु की आकृति में परिवर्तन करेंगे।

(ii) असंतुलित बल – जब किसी वस्तु पर लगे अनेक बलों का परिणामी बल शून्य न हो अर्थात् उनका कुछ नेट बल हो तो उन बलों को असंतुलित बल कहते हैं। यह बल वस्तु की गति की दिशा तथा अवस्था में परिवर्तन करता है।

उदाहरण (1) रस्साकशी का उदाहरण असंतुलित बल को दर्शाता है। यदि इनमें से एक टीम रस्से को अधिक बल लगा कर खींचती है तो उन दोनों टीमों द्वारा लगाये गए बल असंतुलित हो जाते हैं जिससे परिणामी बल उत्पन्न होता
है।

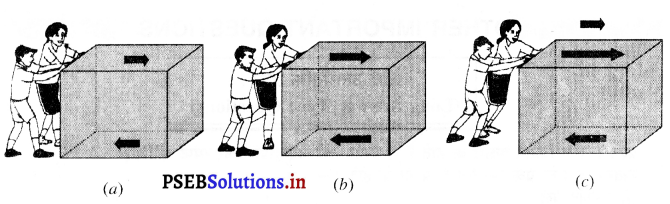
उदाहरण (2) मान लो दो बच्चे एक बक्से को खुरदरे फर्श पर धकेलने का यत्न कर रहे हैं जैसा कि चित्र (a) में दर्शाया गया है। वे कम बल के साथ बक्से को धकेलते हैं, तो बक्सा नहीं खिसकता है, क्योंकि घर्षण बल धकेलने की विपरीत दिशा में काम कर रहा है [चित्र (a)] । यह घर्षण बल बक्से के नीचे की सतह तथा फ़र्श की खुरदरी सतह के बीच उत्पन्न होता है। यह घर्षण बल, धकेलने में लगे बल को संतुलित करता है और यही कारण है कि बक्सा नहीं खिसकता है। अब बच्चे बक्से को ज़ोर से धकेलते हैं लेकिन बक्सा फिर भी नहीं खिसकता जैसा चित्र (b) में दिखाया है। ऐसा इसलिए है क्योंकि घर्षण बल अभी भी धकेलने वाले बल को संतुलित कर रहा है। अब बच्चे बक्से को अधिक ज़ोर से धकेलते हैं ताकि धकेलने वाला बल घर्षण बल से अधिक हो जाता है [चित्र (c)] । यहाँ असंतुलित बल के कारण बक्सा खिसकने लगता है।

असंतुलित बल वस्तु की गति को नष्ट कर सकते हैं। जब एक गेंद फ़र्श पर लुढ़कती है तो फ़र्श पर विपरीत दिशा में घर्षण बल क्रिया करने लगती है, जिससे बल असंतुलित हो जाते हैं। परिणामस्वरूप गेंद कुछ समय बाद रुक जाती है।

प्रश्न 2.
न्यूटन के पहले गति नियम की परिभाषा लिखो तथा इसकी व्याख्या करो।
उत्तर-
न्यूटन का पहला गति नियम- यह बताता है, “इस ब्रह्मांड में सभी वस्तुएँ तब तक विराम अवस्था में बनी रहेंगी अथवा सरल रेखीय एक समान गति में चलती रहेंगी, जब तक कोई बाहरी बल लगाकर उनकी अवस्था परिवर्तन के लिए उस पर क्रिया नहीं करता।”
इस नियम के अनुसार गति को दो भागों में विभाजित किया जा सकता है-

(i) पहले भाग के अनुसार जो वस्तु विराम अवस्था में है वह तब तक विराम अवस्था में ही रहेगी, जब तक इसकी अवस्था परिवर्तन के लिए बाहर से कोई बल नहीं लगाया जाता। यह स्वयं ही स्पष्ट है। हम देखते हैं कि मेज़ पर पड़ी पुस्तक तब तक वहीं पड़ी रहेगी, जब तक कोई उसे उठाता नहीं।

(ii) इस नियम के दूसरे भाग के अनुसार कोई वस्तु सरल रेखीय में एक समान गति से गतिशील तब तक रहेगी, जब तक उसे रोकने के लिए कोई बाहरी बल नहीं लगाया जाता। किंतु ऐसा हमारे दैनिक जीवन से कुछ भिन्न दिखाई देता है। उदाहरण के लिए जैसे ही हम बल लगाना बंद करते हैं तो चलती हुई साइकिल रुक जाती है। ध्यानपूर्वक अध्ययन से पता चला कि साइकिल के टायरों और भूमि के बीच घर्षण बल क्रिया करता है जो बाहरी बल है और विपरीत बल के रूप में क्रिया करता है। वायु के कारण भी गति अवरुद्ध होती है। इसलिए बाह्य बल के कारण चल रही साइकिल रुक जाती है।

प्रश्न 3.
जड़त्व किसे कहते हैं ? जड़त्व की विभिन्न किस्में बताओ। प्रत्येक के लिए उदाहरण भी दो।
उत्तर-
जड़त्व – जड़त्व वस्तु का वह गुण है जिसके फलस्वरूप वस्तु अपनी विराम अवस्था या सरल रेखीय गति की अवस्था को बदलने में अक्षम होती है।
इसी गुण के कारण न्यूटन के पहले गति नियम को जड़त्व का नियम भी कहा जाता है।

जड़त्व की किस्में-जड़त्व तीन प्रकार का होता है-
1. विराम-जड़त्व – इसका अर्थ है कि जो वस्तु विराम अवस्था में है वह विराम अवस्था में ही रहने का यत्न करती है। इसको निम्नलिखित उदाहरण द्वारा स्पष्ट किया जा सकता है रुकी हुई बस या रेलगाड़ी में आराम से खड़ा व्यक्ति बस या रेलगाड़ी के अचानक चलने पर पीछे की ओर गिरता है। इसका कारण यह है कि व्यक्ति का निचला धड़ तो गति में आ जाता है, किंतु उसका ऊपरी धड़ विराम-जड़त्व के कारण विराम अवस्था में ही रहने का यत्न करता है।

2. गति-जड़त्व – इसका अर्थ यह है कि जो वस्तु गतिशील है वह उसी दर से गति में रहने का यत्न करती है।
उदाहरण-
(i) चल रही बस या गाड़ी में आराम से बैठा व्यक्ति बस या गाड़ी के एकदम रुकने पर आगे की ओर गिरता है। ऐसी अवस्था में यात्री के शरीर का निचला भाग तो गाड़ी के रुकते ही विराम अवस्था में आ जाता है, किंतु उसके शरीर का ऊपरी भाग गति की दिशा में गतिशील रहने की कोशिश करता है।

(ii) लंबी छलांग लगाने से पहले एक एथलीट कुछ दूरी तक दौड़ लगाता है, ताकि उसके शरीर का गति-जड़त्व छलांग लगाते समय उसके पेशीय बल की सहायता करता है।

3. दिशायी-जड़त्व – वस्तु का यह गुण वस्तु को अपनी दिशा स्थिर रखने में सहायता करता है।
व्याख्या के लिए उदाहरण- पहिए पर मडगार्ड दिशायी-जड़त्व के कारण स्पर्श रेखीय दिशा में आ रहे कीचड़ से बचाव के लिए पत्थर की गति की दिशा लगाए जाते हैं।

एक धागे के साथ बंधे एक पत्थर पर विचार करें, जोकि क्षैतिज वृत्त में चक्र काट रहा है। यदि ऐसा करते हुए यह धागा टूट जाए तो दिशायी-जड़त्व के कारण पत्थर वृत्त की स्पर्श रेखीय दिशा में उड़ कर सरल रेखीय दिशा में गतिशील हो जाता है।

प्रश्न 4.
न्यूटन के दूसरे गति नियम की परिभाषा दो तथा इसकी व्याख्या करो। इस नियम की सहायता से बल का माप निकालो।
उत्तर-
न्यूटन का दूसरा गति नियम – न्यूटन का दूसरा गति नियम किसी वस्तु को गति में लाने के लिए आवश्यक बल की गणना करने में सहायक है। इस नियम के दो भाग हैं
(i) किसी वस्तु की संवेग परिवर्तन की दर उस पर क्रिया कर रहे बल के समानुपाती होती है। और
(ii) बाहरी बल के कारण हो रहा संवेग परिवर्तन लगाये गए बल की दिशा में क्रिया करता है।

अर्थात् इस नियम के अनुसार, “किसी वस्तु पर बाहर से लगाया गया बल, उस वस्तु के द्रव्यमान तथा उस वस्तु में बल की दिशा में उत्पन्न त्वरण के गुणनफल के अनुक्रमानुपाती होता है।”

व्याख्या – जब कोई बल किसी वस्तु पर क्रिया करता है, तो यह वस्तु का संवेग परिवर्तन करता है। यदि बल दुगुना होता है तो संवेग में भी दुगुना परिवर्तन होता है। अतः जितना अधिक बल लगाया जाता है, संवेग परिवर्तन की दर भी उतनी ही अधिक होती है। संवेग पुंज और वेग का गुणनफल है। प्रायः पुंज परिवर्तन नहीं होता। अतः संवेग परिवर्तन की दर वास्तव में वेग परिवर्तन की दर है। अत: लगाया गया बल त्वरण के समानुपाती है।

जब विराम अवस्था में पड़ी वस्तु पर कोई बाहरी बल क्रिया करता है तो वस्तु बल की दिशा में गतिशील हो जाती है। जब बल गतिशील वस्तु की गति की दिशा में क्रिया करता है तो वस्तु का संवेग बढ़ जाता है। जब बल गतिशील वस्तु पर गति की विपरीत दिशा में क्रिया करता है तो संवेग कम हो जाता है।

बल (F) ∝ संहति (m) × त्वरण (a)
अथवा बल (F) = K × m × a (जहाँ, K एक नियतांक है।) ……………… (1)
यदि हम बल F के मात्रक इस प्रकार चुनें कि एकांक बल, एकांक द्रव्यमान की वस्तु में एकांक त्वरण उत्पन्न कर सके, तब
समीकरण (1) में F = 1, m = 1 तथा a = 1 रखने पर,
1 = K × 1 × 1
अथवा K = 1
अतः समीकरण (1) से, F = 1 × m × a
F = m × a
अर्थात् बल = द्रव्यमान × त्वरण
इसे ही न्यूटन का गति का दूसरा नियम कहते हैं।

प्रश्न 5.
गति के दूसरे नियम की सहायता से बल के गणितिक परिमाण के लिए सूत्र को व्युत्पन्न करें।
उत्तर-
न्यूटन के दूसरे गति नियम से बल का गणितिक परिमाण-मान लो द्रव्यमान ‘m’ की एक वस्तु का आरंभिक वेग ‘u’ है। इस पर बल F, t समय के लिए लगता है जिस कारण इसका वेग ‘v’ हो जाता है।
आरंभिक संवेग p₁ = mu
अंतिम संवेग p₂ = mv
अब क्योंकि अंतिम वेग आरंभिक वेग से अधिक है, इसलिए अंतिम संवेग p₂ आरंभिक संवेग p₁ से अधिक होता है।
∴ संवेग में परिवर्तन = P₂ – P₁
= mv – mu
= m (v – u)
इस नियम के अनुसार
बाहरी बल F α संवेग में परिवर्तन की दर
Fα \(\frac{\left(p_{2}-p_{1}\right)}{t}\)
Fα \(\frac{m(v-u)}{t}\)
F= K\(\frac{m(v-u)}{t}\) जहां K एक स्थिरांक है ………………. (1)

हम जानते हैं कि वेग में परिवर्तन की दर को त्वरण कहते हैं।
∴ \(\frac{v-u}{t}\) = a ………………… (2)
समीकरणों (1) तथा (2) से
F = Kma.
F ; m तथा a के इकाई मूल्य के लिए K = 1
∴ F = ma ………………… (3)
समीकरण (3) न्यूटन के दूसरे गति नियम का गणितिक रूप है।
बल = द्रव्यमान × त्वरण

प्रश्न 6.
न्यूटन के तीसरे गति नियम की परिभाषा दो तथा इसकी व्याख्या करो।
उत्तर-
न्यूटन का तीसरा गति नियम- यह नियम बताता है कि, “प्रत्येक क्रिया के लिए बराबर और विपरीत प्रतिक्रिया होती है।” इस नियम अनुसार, एक बल की मौजूदगी नहीं होती। बल हमेशा जोड़ों (युग्म) में रहता है। अर्थात् क्रिया और प्रतिक्रिया के बल हमेशा दो विभिन्न वस्तुओं पर काम करते हैं।

व्याख्या-(1) दो एक समान स्प्रिंग तुलाओं पर विचार करो, जो एक-दूसरे के साथ हुक में हुक डाल कर जुड़े हुए हैं। स्प्रिंग तुला A का एक सिरा स्थिर सहारे में बंधा हुआ है। तुला B के स्वतंत्र सिरे को दाईं ओर खींचो। हन दोनों तुलाओं में एक समान पठन देखते हैं। तुला A तुला B को उसी बल के साथ विपरीत दिशा में खींचती है। यह चित्र में दिखाया गया है।

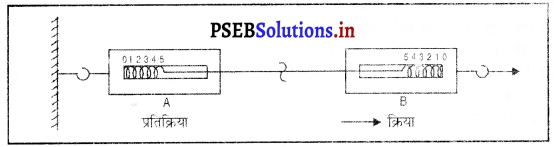
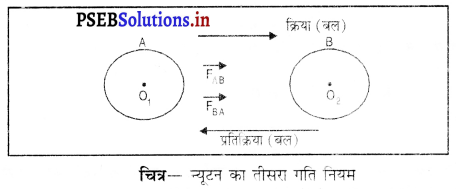
(2) रबड़ की दो गेंदें A तथा B मेज़ पर एक-दूसरे से कुछ दूरी पर रखो। जब आप गेंद A को गेंद B की ओर धकेलते हो तो गेंद A, गेंद B पर क्रिया (बल) करता है। इस क्रिया-बल को F द्वारा दर्शाया जाता है। न्यूटन के अनुसार गेंद B भी गेंद A पर प्रतिक्रिया (बल) करती है। यह प्रतिक्रिया बल FB द्वारा दर्शाया जाता है। यदि गेंदें दोनों एक जैसी हों तो क्रिया (बल) का परिमाण प्रतिक्रिया (बल) के परिमाण के बराबर होगा।
∴ F_A→B= – F_B→A
क्रिया तथा प्रतिक्रिया बल हमेशा एक-दूसरे की विपरीत दिशा में कार्य करते हैं। जैसे कि नीचे चित्र में दिखाया गया है कि क्रिया (बल) दाईं तरफ तथा प्रतिक्रिया (बल) बाईं तरफ कार्य करते हैं।

व्यावहारिक उदाहरण-
(i) जब लान सर्पिकलर की वक्र नोजलों से पानी बाहर निकलता है तो यह सर्पिकलर के पीछे की ओर बराबर बल लगाता है। इस तरह सर्पिकलर घूमना शुरू कर देता है तथा पानी सभी दिशाओं की ओर छिड़कना शुरू हो जाता है।
(ii) जब हम चलते हैं तो हमारे पाँव धरती को पीछे की ओर धकेलते हैं। प्रतिक्रिया स्वरूप धरती हमारे पैरों को आगे की ओर धकेलती है। धरती द्वारा हमारे पाँव पर हुई प्रतिक्रिया के फलस्वरूप ही हम चल पाते हैं।

प्रश्न 7.
इस कथन की व्याख्या करो, “न्यूटन के तृतीय गति नियम में क्रिया और प्रतिक्रिया एक ही वस्तु पर क्रिया नहीं कर सकते।”
उत्तर-
न्यूटन के तीसरे गति नियम अनुसार, “प्रत्येक क्रिया (बल) के लिए, उसके बराबर तथा उल्ट दिशा में एक प्रतिक्रिया (बल) होती है।”

इस नियम अनुसार, एक बल का अस्तित्व कभी भी नहीं होता। बल हमेशा युग्म में होते हैं। यदि किया तथा प्रतिक्रिया दोनों बल, जो कि एक-दूसरे के बराबर परंतु विपरीत दिशा में होते हैं। यदि एक ही वस्तु पर क्रिया करेंगे तो उनका परिणामी बल शून्य हो जाएगा तथा वस्तु विराम अवस्था में रहेगी। इस बात को अग्रलिखित उदाहरण द्वारा स्पष्ट किया जा सकता है.-

जब हम रबड़ की गेंद को दीवार पर मारते हैं तो गेंद दीवार से टकराती है तो उतने बल से उछल कर वापिस आ जाती है तथा आप इसे वापिस आते समय पकड़ सकते हैं। इससे सिद्ध होता है कि गेंद का दीवार पर क्रिया बल, दीवार द्वारा गेंद पर लगाए गए प्रतिक्रिया बल के बराबर तथा उल्ट दिशा में होता है। जब आप उसी रबड़ की गेंद को लटक रहे पतले कपड़े पर मारते हो तो गेंद आपकी तरफ वापिस नहीं आती क्योंकि कपड़े पर गेंद की क्रिया कपड़े को पीछे की ओर धकेलती है। अब क्योंकि कपड़े ने क्रिया समाप्त कर दी इसलिए यह गेंद पर प्रतिक्रिया करके इसको वापिस नहीं फेंक सकता तथा इस तरह गेंद कपड़े के ऊपर से ही सीधी धरती पर गिर जाती है।

प्रश्न 8.
संवेग संरक्षण नियम से क्या भाव है ? संवेग संरक्षण नियम को न्यूटन की गति के दूसरे तथा तीसरे नियम की सहायता से इसको गणितिक तौर पर सिद्ध करो।
उत्तर-
संवेग संरक्षण का नियम (Law of Conservation of Momentum) – इस नियम के अनुसार, “यदि कणों के किसी संकाय (system) पर कोई बाहरी बल क्रिया नहीं करता तो उस संकाय का कुल संवेग संरक्षित रहता है।”
न्यूटन की गति के दूसरे नियमानुसार
F = K\(\frac{m(v-u)}{t}\)
F = K\(\frac{(m v-m u)}{t}\)
F = K\(\frac{\left(p_{2}-p_{1}\right)}{t}\)
जहां आरंभिक संवेग P₁ = mu
अंतिम संवेग P₂ = mv
यदि वस्तु पर कोई बल न लग रहा हो तो F = 0
∴ K\(\frac{\left(p_{2}-P_{1}\right)}{t}\) = 0
या P₂ – P₁ = 0
अर्थात् P₂ = P₁ ……………. (i)

संवेग संरक्षण नियम – जब दो या दो से अधिक वस्तुएँ किसी बाहरी बल की सहायता से आपस में टकराती हैं तो टकराने से पहले और बाद में उनका संवेग बराबर होता है।

गणितिक प्रमाण – मान लो द्रव्यमान m₁ तथा m₂ की रबड़ गेंदें A तथा B आरंभिक वेग u₁ तथा u₂ के साथ गति कर रही हैं। उनका आपस में टकराने के पश्चात् ‘t’ समय में उनके अंतिम वेग v₁ तथा v₂ हो जाते हैं।

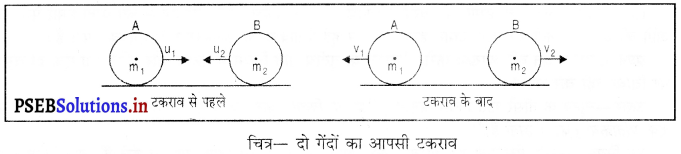
न्यूटन के दूसरे गति नियम से
गेंद A द्वारा गेंद B पर लगाया गया बल F_AB = गेंद A के संवेग में परिवर्तन की दर
F_AB = \(\frac{m_{1} v_{1}-m_{1} u_{1}}{t}\)
F_AB = \(\frac{m_{1}\left(v_{1}-u_{1}\right)}{t}\) …………….. (ii)

न्यूटन के तीसरे गति नियम से
गेंद B द्वारा गेंद A पर प्रतिक्रिया बल, F_BA = गेंद B के संवेग में परिवर्तन की दर
F_BA = \(\frac{m_{2} v_{2}-m_{2} u_{2}}{t}[latex]
F_BA = [latex]\frac{m_{2}\left(v_{2}-u_{2}\right)}{t}[latex] ………………. (iii)

न्यूटन के तीसरे गति नियम अनुसार,
F_AB = -F_BA
[latex]\frac{m_{1}\left(v_{1}-u_{1}\right)}{t}\) = \(\frac{m_{2}\left(v_{2}-u_{2}\right)}{t}\) [समीकरण (ii) तथा (iii) से]
m₁v₁ – m₁u₁ = – m₂v₂ + m₂u₂
– m₁u₁ – m₂u₂ – m₂v₂ – m₂v₂
या m₁u₁ + m₂u₂ = m₂v₂ + m₁v₂
अर्थात् टक्कर से पहले गेंदों A तथा B का कुल संवेग = टक्कर के बाद गेंदों A तथा B का कुल संवेग इससे यह सिद्ध होता है कि गेंदों का कुल संवेग संरक्षित रहता है।

लघु उत्तरात्मक प्रश्न (Short Answer Type Questions)

प्रश्न 1.
बल किसे कहते हैं ? बल की इकाइयां बताओ।
उत्तर-
बल – बल ऐसा कारक है जो-

1. वस्तु को गतिशील करता है या करने का प्रयत्न करता है।
2. गतिशील वस्तु को रोकता है या रोकने का प्रयत्न करता है तथा
3. वस्तु की गति को बढ़ाता या कम करता है। इस तरह, बल वह भौतिक कारण है जो वस्तु की गति अवस्था में परिवर्तन करता है या करने का प्रयत्न करता है।

बल एक सदिश राशि है।
बल का मात्रक (इकाई) – बल का मात्रक द्रव्यमान तथा त्वरण के मात्रक पर निर्भर करता है। बल का मानक मात्रक (S.I.) न्यूटन (N) तथा C.G.S. मात्रक डाइन (Dyne) है।
IN = 10⁵ डाइन

प्रश्न 2.
यदि कोई दौड़ता हुआ घोड़ा अचानक रुक जाता है, तो घुड़सवार आगे की ओर क्यों गिरता है ?
उत्तर-
जब घोड़ा दौड़ रहा होता है तो घोड़ा तथा घुड़सवार दोनों गति की अवस्था में होते हैं। जब घोड़ा अचानक रुक जाता है तो घोड़ा तथा घुड़सवार का निचला धड़ विराम अवस्था में आ जाता है जबकि घुड़सवार का ऊपरी धड़ गति की अवस्था में रहता है। इस कारण वह आगे की ओर गिरता है।

प्रश्न 3.
जब घोड़ा अचानक दौड़ना शुरू कर देता है, तो घुड़सवार पीछे की ओर क्यों गिरता है ?
उत्तर-
घोड़ा और घुड़सवार एक संकाय (System) बनाते हैं। प्रारंभ में दोनों विराम अवस्था में होते हैं। जब अचानक घोड़ा दौड़ने लगता है, तो घोड़े के साथ घुड़सवार के शरीर का निचला भाग भी आगे की ओर गतिशील हो जाता है, किन्तु शरीर का ऊपरी भाग स्थिर जड़ता के कारण विराम अवस्था में रहने का यत्न करता है। इसी कारण घोड़े के अचानक दौड़ने पर घुड़सवार पीछे की ओर गिरता है।

प्रश्न 4.
गतिशील बस में से नीचे उतरते समय सवारी आगे की तरफ गिर जाती है, क्यों ?
उत्तर-
गतिशील बस में से नीचे उतरते समय सवारी आगे की तरफ गिर पड़ती है क्योंकि जब सवारी पैर नीचे रखती है तो धरती को छूने से उसका निचला भाग (पैर) विराम अवस्था में आ जाता है परंतु ऊपर वाला भाग गति में ही रहता है। इस तरह सवारी आगे की तरफ गिर पड़ती है।

प्रश्न 5.
संवेग की परिभाषा दो। इसकी इकाई भी लिखो।
उत्तर-
संवेग (Momentum) – वस्तु के द्रव्यमान और वेग के गुणनफल को संवेग कहते हैं।
यदि m = वस्तु का द्रव्यमान और \(\vec{v}\) = वस्तु का वेग हो तो
वस्तु की सरल रेखीय संवेग \(\vec{p}\) = m × \(\vec{v}\)
संवेग एक सदिश राशि है। इसकी दिशा वही होती है जो वेग की होती है।
संवेग की इकाइयां-CGS प्रणाली में संवेग g cms^-1 और मानक इकाइयों (SI) में kg ms^-1 में मापा जाता

प्रश्न 6.
यदि गतिशील साइकिल की आगे वाली ब्रेक लगाएं तो हम आगे की ओर गिर जाते हैं। क्यों ?
उत्तर-
यदि गतिशील साइकिल की आगे वाली ब्रेक लगाते हैं तो साइकिल सवार को आगे की ओर झटका लगता है। आगे वाली ब्रेक लगाने पर साइकिल एकदम रुक जाता है तो आपके शरीर का निचला भाग विराम अवस्था में आ जाता है, परंतु आपका ऊपरी भाग गति जड़त्व के कारण गति अवस्था में ही रहने की कोशिश करता है तथा आप आगे की ओर झटका महसूस करते हैं। इसलिए यह सलाह दी जाती है कि गतिशील साइकिल की आगे पहिए वाली ब्रेक नहीं लगानी चाहिए।

प्रश्न 7.
बल का किसी वस्तु पर क्या प्रभाव पड़ता है ?
उत्तर-
बल के प्रभाव-

1. यह वस्तु की गति को कम या अधिक करके इसकी चाल में परिवर्तन लाता है।
2. यह वस्तु की गति की दिशा को बदल देता है।
3. यह वस्तु की आकृति में परिवर्तन कर सकता है।

प्रश्न 8.
क्रिकेट के खिलाड़ी तेज़ी से आती हुई बॉल को पकड़ते समय अपने हाथ पीछे की ओर क्यों खींचते हैं ?
उत्तर-
तेज गति से आती हुई बॉल को रोकने के लिए बहुत अधिक बल लगाना पड़ता है। बॉल को पकड़ते समय हाथों को पीछे खींचने से गेंद का त्वरण पहले से कुछ कम होता है और उसे रोकने के लिए कम बल लगाने की आवश्यकता होती है।

प्रश्न 9.
नाव को आगे बढ़ाने के लिए पतवारों को विपरीत दिशा में क्यों चलाना पड़ता है ?
उत्तर-
क्रिया और प्रतिक्रिया समान और विपरीत दिशा में होती है। नाव को आगे बढ़ाने के लिए पतवार से पानी को पीछे की ओर धकेलना पड़ता है। इस बल की प्रतिक्रिया से नाव आगे की ओर बढ़ती है।

प्रश्न 10.
एक कार तथा एक ट्रक दोनों बराबर वेग से चल रहे हैं। इनमें से किसका संवेग अधिक होगा और रोकने के लिए किस में अधिक बल की आवश्यकता पड़ेगी ?
उत्तर-

• कार और ट्रक दोनों समान वेग से चल रहे हैं। इनमें से कार का द्रव्यमान कम होता है। अतः कार का संवेग कम होगा तथा ट्रक का संवेग अधिक होगा।
• यदि दोनों को समान समयांतराल में रोका जाए, तो दोनों का अंतिम संवेग शून्य तो है ही जाएगा परंतु ट्रक का संवेग अधिक होने के कारण ट्रक के संवेग में परिवर्तन कार की अपेक्षा अधिक होगा। अत: ट्रक को रोकने के लिए कार की अपेक्षा अधिक बल लगाना पड़ेगा।

प्रश्न 11.
तीव्र गति से आ रही गोली खिड़की के शीशे में गोल छिद्र बना देती है, जबकि पत्थर मारने पर शीशा चटक जाता है। क्यों ?
उत्तर-
यदि खिड़की के शीशे पर पत्थर मारा जाए, तो वह टुकड़े-टुकड़े हो जाता है, जबकि तीव्र गति से आ रहो गोली इसमें गोल छिद्र बना देती है। इसका कारण यह है कि छिद्र के पास वाले काँच के कण तीव्र गति से आ रही गोली के साथ जड़ता के कारण गति नहीं कर पाते और बिखरते नहीं।

प्रश्न 12.
तीव्र वेग से गतिशील किसी पत्थर लगने से खिड़की का कांच टूट जाता है, क्यों ?
उत्तर-
जब कोई पत्थर का टुकड़ा खिड़की के शीशे से टकराता है तो वह स्थान अधिक गति में आ जाता है जबकि शीशे का शेष भाग जड़त्व के कारण विराम अवस्था में ही रहता है। पत्थर के टुकड़े का वेग कम होने के कारण, पत्थर के आर-पार जाने से पहले ही शीशे का शेष भाग वह वेग ले लेता है और वह टूट जाता है।

प्रश्न 13.
बोझ से लदा कोई ट्रक तथा कार बराबर परिणाम v के वेग से एक-दूसरे के विपरीत गतिशील हैं जबकि उनमें आमने-सामने की टक्कर होती है और फलस्वरूप दोनों ही विराम अवस्था में आ जाते हैं। यदि टक्कर 10 s तक रही तो,
(अ) दोनों में से किस पर प्रतिघात का अधिक बल लगेगा ?
(ब) किस वाहन के संवेग में अधिक परिवर्तन हुआ ?
(स) किस वाहन में अधिक त्वरण उत्पन्न हुआ ?
(द) कार को ट्रक की अपेक्षा अधिक क्षति होने की संभावना क्यों है ?
उत्तर-
(अ) कार पर बल का प्रभाव अधिक होगा क्योंकि उसका द्रव्यमान कम था।
(ब) ट्रक की गति में अधिक परिवर्तन होगा। (स) कार का त्वरण अधिक होगा।
(द) कार की हानि ट्रक की अपेक्षा अधिक होगी क्योंकि उस पर अधिक बल लगेगा।

प्रश्न 14.
संवेग संरक्षण का नियम लिखें।
उत्तर-
संवेग संरक्षण का नियम (Law of Conservation of Momentum) – जब दो (या दो से अधिक) वस्तुएँ एक-दूसरे पर क्रिया करती हैं, तो उनका कुल संवेग सदैव समान रहता है, जब तक कि कोई बाहरी बल उन पर क्रिया नहीं करता अर्थात् बाह्य बल शून्य होने पर संकाय (System) का कुल संवेग (Totul fomenta71) अचर (Constant) रहता है।

प्रश्न 15.
यदि क्रिया-प्रतिक्रिया के बराबर होती है तो स्पष्ट कीजिए कि घोड़े के द्वारा खींची गाड़ी आगे की ओर कैसे चलती है ?
उत्तर-
न्यूटन के गति के तीसरे नियम के आधार पर क्रिया-प्रतिक्रिया सदा समान होते हैं। जब गाडी को घोड़े के द्वारा खींचा जाता है तो वह अपने पैरों से धरती को पीछे की ओर दबाता है। धरती की प्रतिक्रिया ऊपर की ओर कार्य करती है। प्रतिक्रियात्मक बल दो भागों में बंट जाता है। बल का उर्ध्वाधर घटक घोड़े को संतुलन देता है और क्षैतिज घटक गाड़ी को आगे की दिशा में गति देता है। गाड़ी के पहियों और सड़क के बीच घर्षण बल पीछे की ओर कार्य करता है। जब बल सड़क और पहियों के घर्षण बल से अधिक हो जाता है तब गाड़ी चलने लगती है।

प्रश्न 16.
सड़क पर चलने वाले वाहनों के टायरों को खुरदरा लहरदार क्यों बनाया जाता है ?
उत्तर-
सड़कों पर वाहनों का चलना वाहनों के टायरों तथा सड़कों के बीच घर्षण के कारण ही होता है। यदि टायर चिकने होंगे, तो सड़क और टायरों के बीच घर्षण कम होगा जिससे वाहनों की गति पर नियंत्रण करना कठिन होगा और दुर्घटना हो सकती है। इन दुर्घटनाओं से बचने के लिए वाहनों के टायरों को खुरदरा तथा लहरदार बनाया जाता है ताकि सड़क और टायरों के बीच घर्षण बढ़ सके जिससे टायरों की सड़क के साथ पकड़ अच्छी हो और उन्हें फिसलने से रोका जा सके।

प्रश्न 17.
रेत की दलदल या बालुपंक बहुत चिकने और छोटे रेत के कणों से बनता है। यदि कोई व्यक्ति या भारी जंतु रेगिस्तान में ऐसे स्थान पर चलता है तो क्या हो सकता है ?
उत्तर-
रेत के कण बहुत छोटे और चिकने होते हैं इसलिए किसी व्यक्ति या भारी जानवर के द्वारा उस पर चलने के लिए जब बल लगाया जाता है तो ये अपेक्षाकृत कम प्रभावी परिणाम दे पाते हैं क्योंकि घर्षण कम उत्पन्न होता है। जब हम चलते हैं तो पैरों से पृथ्वी को पीछे की ओर धकेलते हैं और वह हमें आगे बढ़ने के लिए प्रतिक्रिया प्रदान करती है पर यह कार्य घर्षण से ही संभव हो सकता है। पर रेगिस्तान में रेत के कणों के कारण पर्याप्त घर्षण की प्राप्ति नहीं हो पाती। इसलिए रेत में चलना मुश्किल है।

प्रश्न 18.
जब कभी अचानक हमारा पैर केले के छिलके पर पड़ जाता है तो हमारे लिए अपने शरीर का पंतुलन बनाए रखना कठिन क्यों हो जाता है ?
उत्तर-
जब हमारा पैर अचानक केले के छिलके पर पड़ जाता है तो उसके चिकनेपन के कारण घर्षण कम होता है जिससे हमारे शरीर का संतुलन बिगड़ जाता है।

प्रश्न 19.
व्याख्या करो कि धूल भरा कंबल एक या दो बार ज़ोर से झटकने पर धूल रहित कैसे हो जाता है ?
उत्तर-
जब एक धूल भरे कंबल को ज़ोर से झटका जाता है अथवा छड़ी से पीटा जाता है तो उससे धूल-कण नीचे गिर जाते हैं क्योंकि धूल-कण विराम जड़त्व के कारण विराम की अवस्था में ही रहना चाहते हैं पर छड़ी से पीटे जाने के कारण कंबल आगे-पीछे गति करने लगता है। इसके परिणामस्वरूप धूल-कण नीचे गिर जाते हैं।

प्रश्न 20.
क्या किसी वस्तु को एक समान वेग से चलते रहने के लिए बल की आवश्यकता होती है ?
उत्तर-
वेग की दर को त्वरण कहते हैं। जब कोई वस्तु एक समान वेग से चलती है तो उसमें कोई त्वरण उत्पन्न नहीं होता। वस्तु का त्वरण उस पर लग रहे बल के समानुपाती है अर्थात् वस्तु में उत्पन्न त्वरण उस पर लग रहे बल पर निर्भर करता है। इसलिए किसी वस्तु को एक समान वेग में चलते रहने के लिए बल की आवश्यकता होती है।

प्रश्न 21.
किसी वस्तु के जड़त्व और द्रव्यमान में क्या संबंध है ?
उत्तर-
किसी वस्तु में उपस्थित पदार्थ की मात्रा को उसका द्रव्यमान कहते हैं। इस तरह द्रव्यमान वस्तु के जड़त्व का मापक है अर्थात् वस्तु का जड़त्व उसके द्रव्यमान पर निर्भर करता है। वस्तु का द्रव्यमान जितना अधिक होगा, उतना ही जड़त्व बढ़ेगा तथा कम द्रव्यमान वाली वस्तु का जड़त्व भी कम होता है।

उदाहरण 1. यदि हम फुटबाल को किक करते हैं तो यह बहुत दूर चली जाती है परंतु यदि उसी आकार के ही एक पत्थर के टुकड़े को किक करते हैं तो वह अपनी जगह से नहीं हिलता तथा पाँव को चोट लगती है। इसका कारण यह है कि पत्थर में गति के परिवर्तन को रोकने की सामर्थ्य अधिक होती है अर्थात् पत्थर का जड़त्व अधिक होता है।

उदाहरण 2. एक ही आकार की रबड़ तथा स्टील की दो गेंदें मेज़ पर रखो। गति में लाने के लिए स्टील की गेंद की अपेक्षा रबड़ की गेंद पर कम बल लगाना पड़ता है। इसका कारण है कि रबड़ की गेंद का पुंज, स्टील की गेंद के पुंज से कम होता है।
इससे सिद्ध होता है कि कम पुंज वाली वस्तु का घनत्व और जड़त्व भी कम होता है।

प्रश्न 22.
पंखे का स्विच बंद करने के बाद भी पंखा कछ समय तक घूमता क्यों रहता है ?
उत्तर-
जब पंखा गति में होता है तो गतिज जड़त्व के कारण स्विच बंद करने के बाद भी पंखा गति की अवस्था में रहने की कोशिश करता है । वायु के घर्षण बल के विरोध कारण ही यह केवल कुछ ही समय के लिए गति में रहता है।

प्रश्न 23.
बंदूक से निकली गोली और वायु का अणु यद्यपि एक ही गति से चलते हैं, परंतु किसी व्यक्ति से टकराने पर गोली अधिक खतरनाक होती है। व्याख्या करो।
उत्तर-
किसी वस्तु का संवेग उसके द्रव्यमान तथा वेग के गुणनफल के बराबर होता है। इसलिए बंदूक से निकली गोली का संवेग वायु के अणु के संवेग से अधिक होता है क्योंकि गोली का द्रव्यमान अधिक है। अधिक संवेग होने के कारण, इसके संवेग को समाप्त करने के लिए अधिक बल की आवश्यकता पड़ती है जिसके कारण व्यक्ति को अधिक चोट लगती है।

प्रश्न 24.
एक ऊबड़-खाबड़ सड़क पर 30 km/h के समान वेग से गति कर रही कार पर क्रिया कर रहे बल की मात्रा ज्ञात करो।
उत्तर-
क्योंकि वस्तु समान वेग से चल रही है, इसलिए वस्तु का त्वरण शून्य होगा तथा इस पर क्रिया कर रहा बल भी शून्य होगा।
क्योंकि F = m × a
F = m × 0
F = 0

प्रश्न 25.
एक क्रिकेट की गेंद की अपेक्षा रबड़ की गेंद को पकड़ना आसान होता है यद्यपि दोनों एक ही वेग से गति कर रही हों ? क्यों ?
उत्तर-
यद्यपि क्रिकेट तथा रबड़ की गेंदों का वेग एक समान है पर क्रिकेट की गेंद का द्रव्यमान अधिक होने के कारण इसका संवेग भी अधिक होता है जिसके फलस्वरूप वह हाथ पर अधिक चोट लगाता है। इसलिए क्रिकेट की गेंद की अपेक्षा रबड़ की गेंद को पकड़ना आसान है।

प्रश्न 26.
अधिक द्रव्यमान वाली वस्तुओं को गतिशील करने के लिए अधिक प्रारंभिक बल की आवश्यकता होती है। क्यों ?
उत्तर-
हम जानते हैं कि वस्तु का जड़त्व उसके द्रव्यमान पर निर्भर करता है। इसलिए अधिक द्रव्यमान वाली वस्तु का जडत्व अधिक होगा। इसलिए उसको गतिशील करने के लिए अधिक प्रारंभिक बल की आवश्यकता होगी।

प्रश्न 27.
जब बंदूक में से गोली निकलती है तब बंदूक पीछे की ओर धक्का मारती है, क्यों ? व्याख्या करो।
उत्तर-
जब बंदूक में से गोली नहीं चलाई गई, तो बंदूक तथा गोली दोनों विराम अवस्था में होती हैं जिसके कारण दोनों का भिन्न-भिन्न तथा कुल संवेग शून्य होता है। बंदूक चलाने के बाद गोली बहुत तेज़ वेग से बंदूक में से आगे की ओर निकलती है अर्थात् इसका बहुत अधिक संवेग होता है। अब संवेग संरक्षण नियम के अनुसार अब भी कुल संवेग शून्य होना चाहिए जैसा कि गोली चलाने से पहले था। इसलिए गोली के आगे की ओर संवेग को संतुलित करने के लिए बंदूक का संवेग बराबर तथा उल्ट दिशा में होता है। इसलिए बंदूक गोली की अपेक्षा अधिक भारी होने के कारण कम वेग से पीछे की ओर गति करती है जिससे वह पीछे की ओर धक्का मारती है।

प्रश्न 28.
जब कोई व्यक्ति नाव से किनारे की ओर छलांग लगाता है तो नाव विपरीत दिशा में गति करती है, क्यों ? व्याख्या करो।
उत्तर-
नाव से छलांग लगाते समय व्यक्ति आवश्यक गति प्राप्त करने के लिए आगे की ओर बल लगाता है। उसकी प्रतिक्रिया नाव पर होती है जो न्यूटन के गति के तीसरे नियम के आधार पर विपरीत दिशा में होती है। इसके परिणामस्वरूप नाव विपरीत दिशा में गति करती हुई किनारे से दूर हटती है।

प्रश्न 29.
जब कोई चलती हुई बस अचानक रुक जाती है तो हम आगे की ओर क्यों गिरते हैं ?
उत्तर-
जब कोई गतिशील बस अचानक ब्रेक लगाने पर रुक जाती है, तो हम आगे की ओर गिरते हैं। ऐसा इसलिए होता है कि हमारे पांव तथा शरीर का निचला भाग बस के रुकने के साथ ही विराम अवस्था में आ जाते हैं, परंतु शरीर का ऊपरी भाग गतिज जड़त्व के कारण गतिशील रहने की कोशिश करता है। इसलिए हम आगे की ओर गिरते हैं।

प्रश्न 30.
न्यूटन के द्वितीय गति नियम का क्या महत्त्व है ? ।
उत्तर-
न्यूटन की गति के दूसरे नियम की महत्ता-

1. न्यूटन की गति का दूसरा नियम किसी वस्तु को गति में लाने के लिए आवश्यक बल की मात्रा निकालने में सहायता करता है।
2. न्यूटन की गति के दूसरे नियम का कथन, “किसी वस्तु में संवेग में परिवर्तन की दर, उस पर लगाये गए बाहरी बल के समानुपाती होती है तथा संवेग में परिवर्तन की दिशा लगाए गए बल की दिशा में होती है।”

न्यूटन का दूसरा गति नियम संवेग के संकल्प की व्याख्या करता है तथा बताता है कि वस्तु पर लग रहा बल, उसमें उत्पन्न हुए त्वरण के समानुपाती होता है।

प्रश्न 31.
जब आप किसी पुस्तक के नीचे पड़े कागज़ को तेज़ी से झटका मारकर उठाते हो तो पुस्तक बिल्कुल नहीं हिलती। क्यों ?
उत्तर-
जब हम पुस्तक के नीचे पड़े कागज़ को शीघ्रता से झटका लगाकर उठाते हैं तो पुस्तक बिल्कुल नहीं हिलती। इसका कारण यह है कि बाहरी बल (झटका मारते समय लगा बल) केवल पुस्तक के नीचे पड़े कागज़ पर ही लगता है जिस कारण कागज़ बाहर निकल जाता है तथा पुस्तक विराम जड़त्व के कारण उसी ही स्थिति अर्थात् विराम अवस्था में रहती है।

प्रश्न 32.
जड़त्व क्या है ? जड़त्व का माप क्या है ?
उत्तर-
जड़त्व (Inertia) – जड़त्व वस्तु का वह गुण है जिसके फलस्वरूप वस्तु अपनी विराम या सरल रेखीय गति अवस्था या गति की दिशा में परिवर्तन की अवस्था को बदलने में अयोग्य या अक्षम है।

स्वाभाविक तौर पर एक वस्तु अपनी उसी अवस्था में रहती है जब तक कि उस पर कोई बाहरी बल न लगे। जड़त्व तीन प्रकार का होता है-

1. विराम जड़त्व (Inertia of Rest)
2. गतिज जड़त्व (Inertia of Motion)
3. दिशा जड़त्व (Inertia of Direction)

जड़त्व का माप – जड़त्व वस्तु के द्रव्यमान पर निर्भर करता है अर्थात् जड़त्व की इकाई किलोग्राम (kg) है जो कि द्रव्यमान की इकाई है।

प्रश्न 33.
स्पष्ट कीजिए कि गति के द्वितीय नियम \(\overrightarrow{\mathrm{F}}\) = m\(\vec{a}\) में न्यूटन का गति-विषयक पहला नियम निहित है।
उत्तर-
न्यूटन के गति के द्वितीय नियम से,
\(\overrightarrow{\mathrm{F}}\) = m\(\vec{a}\)
यदि F = 0 हो तो a = 0 अर्थात् यदि वस्तु पर बाह्य बल न लगाया जाए तो वस्तु में त्वरण भी उत्पन्न नहीं होगा। त्वरण के शून्य होने पर या तो वस्तु विरामावस्था में ही रहेगी या एकसमान वेग से गतिमान रहेगी। यही न्यूटन का गति का पहला नियम है। अत: न्यूटन के गति के द्वितीय नियम में प्रथम नियम निहित है।

प्रश्न 34.
संतुलित बल तथा असंतुलित बल में अंतर लिखिए।
उत्तर-

संतुलित बल	असंतुलित बल
(1) संतुलित बल जब किसी वस्तु पर एक साथ कार्य करते हैं तो उनका परिणाम शून्य नहीं होता।	(1) असंतुलित बल जब वस्तु पर एक साथ कार्य करते हैं तो उनका परिणाम शन्य होता है।
(2) यदि वस्तु विरामावस्था में हो तो संतुलित बल उसे गति प्रदान नहीं कर सकता।	(2) यदि कोई वस्तु विरामावस्था में हो तो असंतुलित बल उसे गति प्रदान कर सकता है।
(3) यह बल गतिमान वस्तु की चाल तथा दिशा में परिवर्तन नहीं कर सकता।	(3) यह बल गतिमान वस्तु की चाल तथा दिशा में परिवर्तन कर सकता है।
(4) यह बल वस्तु के आकार में परिवर्तन ला सकता है।	(4) यह बल वस्तु के आकार में परिवर्तन नहीं ला सकता है।

प्रश्न 35.
यदि एक ही आकार के फुटबाल तथा पत्थर के टुकड़े को पांव से ठोकर मारें तो कौन-सा पदार्थ अधिक दूर जाएगा और क्यों ?
उत्तर-
यादि एक ही आकार के फुटबाल और पत्थर को ठोकर मारें तो फुटबाल दूर लुढक जाएगी, परंतु पत्थर अपनी जगह से नहीं हटेगा और हमारे पाँव में भी चोट लग सकती है। फुटबाल की अपेक्षा पत्थर में अपनी गति के परिवर्तन को रोकने की क्षमता अधिक है। इसका कारण उसकी द्रव्यमान का अधिक होना है, परंतु किसी वस्तु का द्रव्यमान हो उसके जड़त्व का माप होती है। पत्थर का जड़त्व अधिक है।

प्रश्न 36.
नाव को आगे बढ़ाने के लिए पतवारों को विपरीत दिशा में क्यों चलाना पड़ता है ?
उत्तर-

वह बल, जो किसी दिशा में गति प्रदान करता है, हमारे द्वारा लगाए बल की प्रतिक्रिया होती है। नाव को आगे | बढ़ाने के लिए पतवार से पानी को पीछे की ओर धकेलना पड़ता है। इस बल की प्रतिक्रिया से नाव आगे की ओर बढ़ती है क्योंकि क्रिया और प्रतिक्रिया समान और विपरीत दिशा में होती है।

प्रश्न 37.
घर्षण बल का कारण क्या है ?
उत्तर-
ठोस वस्तुओं के तल समतल नहीं होते। इनमें कुछ अनियमितताएँ होती हैं. जब एक तल A दूसरे तल B पर सरकता है, तो बल की अनियमितताएँ दूसरे की अनियमतताओं की जकड़ में आ जाती हैं। इस जकड़न को तोड़ने के लिए बहुत बल की आवश्यकता होती है। इसी विरोधी बल को ही घर्षण बल कहते हैं। घर्षण बल सदा गति से विपरीत दिशा में किया करते हैं।

प्रश्न 38.
यदि हथौडा हत्थे में ढीला हो तो हत्थे को ऊर्ध्वाधर पथ्वी पर पटकने से हथौडा हत्थे में क्यों कस
उत्तर-
हथौड़ा ऊपर से कुछ पतला और नीच से मोटा होता है। नीचे पटकने की अवस्था में हथौड़ा और हत्था दोनों नीचे की ओर गतिमान हो जाती है। पृथ्वी पर लगते ही हत्थे का वेग शून्य हो जाता है पर हथौड़ा गति के जड़त्व के कारण गतिमान रहता है और वह हत्थे में कस जाता है।

प्रश्न 39.
तेल टैंकरों को भरते समय उनके ऊपर कुछ खाली स्थान क्यों छोड़ दिया जाता है ?
उत्तर-
तेल टैंकरों में भरा तेल अति वाष्पशील प्रकृति का पदार्थ होता है। जब तेल वाष्पित होता है तो इसके वाष्प स्थान घेरते हैं और वे दाब डालते हैं। तेल के वाष्पण के लिए पर्याप्त स्थान देने के लिए टैंकर भरते समय उसके ऊपर खाली स्थान छोड़ा जाता है। यदि टैंकर में पर्याप्त खाली स्थान न छोड़ा जाए तो अधिक वाष्प-दाब के कारण टैंकर के फटने का भय उत्पन्न हो जाता है।

प्रश्न 40.
क्रिकेट के खिलाड़ी तेज़ी से आती हुई बॉल को पकड़ते समय अपने हाथ पीछे की ओर क्यों खींचते हैं ?
उत्तर-

क्रिकेट की गेंद पकड़ते समय खिलाड़ी अपने हाथ पीछे की ओर खींच लेता है – इसका कारण यह है कि यदि खिलाड़ी हाथ को स्थिर रखकर गेंद पकड़ता है तो गेंद को रुकने में बहुत कम समय लगता है जिससे वेग-परिवर्तन की दर (अर्थात् मंदन) अधिक रहती है। अत: खिलाड़ी की हथेली को गेंद रोकने में अधिक बल (F = m × a) लगाना होता है जिससे खिलाड़ी की हथेली में चोट लग सकती है।। इसलिए खिलाड़ी गेंद को अधिक समय में रोकने के लिए हाथ को गेंद की गति की दिशा में पीछे खींचता है जिससे कि वेग- परिवर्तन की दर (अर्थात् मंदन) कम हो तथा उसे कम बल लगाना पड़े। इससे खिलाड़ी के हाथ में चोट लगने की संभावना कम हो जाती है।

प्रश्न 41.
घर्षण बल के उपयोग लिखिए।
उत्तर-

1. घर्षण बल के कारण हम मनुष्य सीधे खड़े रह पाते हैं।
2. घर्षण बल वाहनों को सड़कों पर फिसलने से रोकता है।
3. घर्षण बल न होने के कारण अनेक मशीनें नहीं चल पाएंगी।

प्रश्न 42.
कुएँ से जल खींचते समय यकायक रस्सी टूट जाने पर पानी खींचने वाला व्यक्ति पीछे की ओर क्यों गिर पड़ता है ?
उत्तर-
कुएँ से जल खींचते समय यकायक रस्सी टूट जाने पर पानी खींचने वाला व्यक्ति पीछे की ओर गिर पड़ता है–इसका कारण यह है कि जब कोई व्यक्ति रस्सी द्वारा जल से भरी बाल्टी को खींचता है तो बाल्टी भी उसी बल से व्यक्ति को अपनी ओर खींचती है। यदि रस्सी यकायक (अचानक) टूट जाए तो बाल्टी द्वारा व्यक्ति पर लगाया गया बल समाप्त हो जाता है तथा व्यक्ति अपने द्वारा लगाए गए बल के कारण पीछे की ओर गिर पड़ता है।

प्रश्न 43.
जैवलिन थ्रो में यदि खिलाड़ी किसी निश्चित रेखा को पार लेता है तो यह फाउल माना जाता है, किंतु खिलाड़ी इस रेखा पर रुकने में प्रायः असफल रहते हैं। स्पष्ट कीजिए, क्यों ?
उत्तर-
जैवलिन थ्री में तीव्र गति से भाला फेंकने के लिए खिलाड़ी तीव्र गति से आगे की ओर भागता है, इसलिए निश्चित रेखा तक पहुँचते समय खिलाड़ी गति की अवस्था में होता है। अतः शरीर गति जड़त्व के कारण प्रायः वह निश्चित रेखा तक अपने को रोकने में असफल रहता है।

महत्त्वपूर्ण सूत्र (Important Formulae)

1. बल (F) = m × a
2. त्वरण (a) = \(\frac{\mathrm{F}}{m}\)
3. त्वरण (a) = \(\frac{v-u}{t}\)
4. संवेग (p) = m × v
5. दाब (P) =

संख्यात्मक प्रश्न (Numerical Problems)

प्रश्न 1.
किसी 10 ग्राम के द्रव्यमान में 5 मीटर/सेकंड² का त्वरण उत्पन्न करने में अधिक बल की आवश्यकता होगी अथवा 20 ग्राम के द्रव्यमान में 2 मीटर/सेकंड² का त्वरण उत्पन्न करने में ?
हल :
पहली अवस्था में,
दिया है, द्रव्यमान (m₁) = 10 ग्राम, = 10 × 10^-3 किग्रा, त्वरण (a₁) = 5 मीटर/सेकंड
∴ बल (F₁) = m₁ × a₁
= (10 × 10^-3 किग्रा) × (5 मीटर/सेकंड²)
= 5 × 10^-2 किग्रा-मीटर/सेकंड
= 5 × 10^-2 न्यूटन
= 0.05 न्यूटन।

दूसरी अवस्था में,
दिया है : द्रव्यमान (m₂) = 20 ग्राम = 20 × 10^-3 किग्रा, त्वरण (a₂) = 5 मीटर/सेकंड²
∴ बल (F₂) = m₂ × a₂
= (20 × 10^-3 किग्रा) × (2 मीटर/सेकंड²)
= 40 × 10^-2 किग्रा-मीटर/सेकंड
= 40 × 10^-2 न्यूटन
= 0.4 न्यूटन।

क्योंकि F₂ का परिमाण F₁ से अधिक है, अतः पहली अवस्था में अर्थात् 10 ग्राम द्रव्यमान में 5 मीटर/सेकंड² का त्वरण उत्पन्न करने के लिए अधिक बल की आवश्यकता होगी।

प्रश्न 2.
किसी 3 kg द्रव्यमान की किसी वस्तु पर 12 न्यूटन बल लगाने से उत्पन्न त्वरण क्या होगा ?
हल:
बल (F) = 12 N (न्यूटन)
द्रव्यमान (m) = 3 kg
त्वरण (a) = ?
F = m × a,
12 = 3 × a
a = \(\frac{12}{3}\) = 4 ms^-2

प्रश्न 3.
किसी 6 kg द्रव्यमान की एक गेंद में 4 m/s² का त्वरण उत्पन्न करने के लिए कितने बल की आवश्यकता होगी ?
हल:
द्रव्यमान, (m) = 6 kg
त्वरण, (a) = 4 ms^-2
बल, (F) = ?
F = m × a
= 6 × 4 = 24 (न्यूटन)

प्रश्न 4.
70g द्रव्यमान की क्रिकेट की कोई गेंद 0.5 m/s के वेग से गतिमान है। क्रिकेट का कोई खिलाड़ी इसे 0.5 सै० में रोक लेता है। खिलाड़ी द्वारा बॉल को रोकने के लिए लगाए गए बल की गणना कीजिए।
हल :
गेंद का द्रव्यमान (m) = 70 ग्राम
= \(\frac{70}{1000}\) = 0.07 कि०ग्रा०
u = 0.5 मी०/सै०
t = 0.5 सेकंड
υ = 0
∴ υ = u + at
∴ 0 = 0.5 + a × 0.5
a = \(\frac{0.5}{0.5}\) = -1 मी०सै०²
F = ma
F = 0.07 × 1 = 0.07 N.

प्रश्न 5.
दो पिंडों पर समान बल लगाने पर उनमें त्वरणों का अनुपात 1 : 2 है। पहले पिंड का द्रव्यमान 2 किग्रा है। दूसरे पिंड का द्रव्यमान क्या होगा?
हल :
दिया है, (\(\frac{a_{1}}{a_{2}}\)) = \(\frac{1}{2}\) m₁ = 2 किग्रा. m₂ = ?
सूत्र F = m × a से,
m₁ × a₂ = m₂ × a₂
अतः दूसरे पिंड का द्रव्यमान (m₂) = \(\frac{m_{1} \times a_{1}}{a_{2}}\) = \(\frac{2 \times 1}{2}\) = 1 किग्रा।

प्रश्न 6.
किसी वस्तु पर 1.2 s समय के लिये कोई बल लगाने पर उसकी चाल 1.8 m/s से 4.2 m/s हो जाती है। बाद में उसी बल को 2s के लिये लगाया गया। 2 सेकंड में चाल में परिवर्तन कितना होगा ?
हल :
प्रारंभिक वेग, (u) = 1.8 ms^-1
अंतिम वेग, (υ) = 4.2 ms^-1
समय, (t) = 1.2s
बल, (F) = ?
मान लिया कि वस्तु का द्रव्यमान m है।
हम जानते हैं कि F × t = m (υ – u)
F × 1.2 = m (4.2 – 18)
F × 1.2 = m × 2.4
F = \(\frac{m \times 2.4}{1.2}\)
F = 2m
अब बल F = 2 m वस्तु पर 2 s के लिए लगाकर चाल में परिवर्तन (υ – u) करता है।
[F × t = m (υ – u)]
2m × 2 = m (υ – u)
\(\frac{2 m \times 2}{m}\) = υ – u
∴ चाल में परिवर्तन (υ – u) = 4 ms^-1 है।

प्रश्न 7.
10g द्रव्यमान की कोई गोली 0.003 सेकंड में किसी राइफल की नाल से होकर 300 मी०/सै० के वेग से बाहर निकलती है। राइफल द्वारा गोली पर कितना बल लगाया गया ?
हल :
m = 10 ग्राम
= \(\frac{10}{1000}\) = .01 कि०ग्रा०
t = 0.003 सै०
u = 0
υ = 300 मी०सै०
υ = u + at
a = \(\frac{v-u}{t}\)
= \(\frac{300-0}{.003}\) = 10⁵ मी०सै०²
F = m × a
F = 0.01 × 10⁵ = 10³ N
= 1000 न्यूटन।

प्रश्न 8.
एक 5 किग्रा द्रव्यमान की वस्तु पर 2 सेकंड के लिए एक नियत बल कार्यरत होता है। यह वस्तु के वेग को 3 मीटर/सेकंड से बढ़ाकर 7 मीटर/सेकंड कर देता है। लगाए गए बल की मात्रा ज्ञात कीजिए। यदि इस बल को 5 सेकंड के लिए आरोपित किया जाए तो वस्तु का अंतिम वेग क्या होगा?
हल :
दिया है : m = 5 किग्रा, u = 3 मीटर/सेकंड, υ = 7 मीटर/सेकंड, t = 2 सेकंड,
F = ? यदि बल t = 5 सेकंड तक लगे तो υ = ?
सूत्र a = \(\frac{v-u}{t}\) से.
वस्तु का त्वरण (a) = \(\frac{7-3}{2}\)
= \(\frac{4}{2}\) = 2 मीटर/सेकंड²
सूत्र F = m × a से,
F = 5 किग्रा × 2 मीटर/सेकंड
= 10 किग्रा-मीटर/सेकंड²
= 10 न्यूटन।

प्रश्न 9.
10 kg द्रव्यमान वाली किसी वस्तु पर 10 s के लिए कोई बल क्रिया करता है इसके बाद बल हटा दिया जाता है। वस्तु अगले 5 s में 50 m दूरी तय करती है। बल ज्ञात करो।
हल :
यहां पर वस्तु का आरंभिक वेग, (u) = 0
वस्तु का द्रव्यमान, (m) = 10 kg
समय, (t) = 10s
मान लो F बल लग रहा है।
बल हटाने पर तय की गई दूरी (S) = 50 m
दूरी तय करने में लगा समय (t) = 5s
वेग का अंतिम वेग (υ) = \(\frac{S}{t}=\frac{50 \mathrm{~m}}{5 \mathrm{~s}}\)
υ = 10 m/s
हम जानते हैं कि υ = u + at
10 = 0 + a × 10
10 = 10a
∴ a = 1 m/s²
F = m × a
अब F = 10 × 1
F = 10 N

प्रश्न 10.
12 m/s के वेग से चल रही 0.25 kg द्रव्यमान वाली एक वस्तु को 0.6 N का बल लगाकर रोक लिया जाता है। वस्तु को रोकने के लिए लगाया गया समय पता करो।
हल:
वस्तु का प्रारंभिक वेग, (u) = 12 m/s
वस्तु का अंतिम वेग, (υ) = 0 [∵ वस्तु अंत में विराम अवस्था में आ जाती है।
वस्तु का द्रव्यमान, (m) = 0.25 kg
वस्तु पर लग रहा बल (F) = 0.6 N
मान लो वस्तु को रोकने पर लगा समय = t s
मान लो वस्तु के अंदर उत्पन्न हुआ त्वरण ‘a’ है।
हम जानते हैं, F = m × (- a)

t = 5
∴ वस्तु को रोकने में लगा समय = 5 s

प्रश्न 11.
एक कार 108 kg/h की गति से चल रही है और ब्रेक लगाने के बाद यह रुकने में 4s का समय लेती है। कार पर ब्रेक लगाए जाने के बाद लगने वाले बल की गणना करें। कार का कुल द्रव्यमान (यात्रियों सहित) 1000 kg है।
हल :
कार का प्रारंभिक वेग (u) = 108 km/h
= 108 × 1000 m
60 × 60 s
= 30 m s^-1
तथा कार का अंतिम वेग (υ) = 0 m s^-1
कार का कुल द्रव्यमान (m) = 1000 kg तथा गाड़ी को रोकने में लगा समय (t) = 4 s तथा
ब्रेक लगाने वाले बल F का परिणाम = m\(\frac{(v-u)}{t}\)
मान रखने पर,
F = 1000 kg × \(\frac{(0-30)}{4 s}\) m s^-1
= – 750 kg m s^-2
= -750N
ऋणात्मक चिह्न दर्शाता है कि ब्रेक के द्वारा लगाया गया बल गाड़ी की गति के विपरीत दिशा में आरोपित है।

प्रश्न 12.
1000 kg द्रव्यमान की किसी कार को तथा 10000 kg से लदे हुए किसी ट्रक को 2 सेकंड में रोकने के लिए क्रमशः कितने बल की आवश्यकता होगी, यदि दोनों 5 m/s के वेग से गतिशील हों ?
हल :
u = 5 m/s, υ = 0, t = 2 सेकंड
υ = u + at
υ = 5 + a × 2
a = \(\frac{5}{2}\) मी०/से०²
कार को रोकने के लिए F₁ = m × a
= 100 × (\(\frac{-5}{2}\)) = – 250 N
ट्रक को रोकने के लिए F₂ = ma₂
= 10000 × (\(\frac{-5}{2}\))
= – 2500 N

प्रश्न 13.
किस में अधिक बल की आवश्यकता होगी, 2 किग्रा द्रव्यमान वाली किसी वस्तु को 5 मीटर/सेकंड² की दर से त्वरित करने में या 4 किग्रा द्रव्यमान वाली वस्तु को 2 मीटर/सेकंड² की दर से त्वरित करने में ?
हल :
दिया है, m₁ = 2 किग्रा, a₁ = 5 मीटर/सेकंड²
m₂ = 1 किग्रा, a₂ = 2 मीटर/सेकंड²
प्रथम वस्तु के लिए आवश्यक बल
F₁ = m₁a₁
= 2 किग्रा × 5 मीटर/सेकंड²
= 10 न्यूटन
द्वितीय वस्तु के लिए आवश्यक बल
F₂ = m₂ a₂
= 4 किग्रा × 2 मीटर/सेकंड
= 8 न्यूटन।
F₁ > F₂
उपर्युक्त से स्पष्ट है कि प्रथम वस्तु को त्वरित करने के लिए अधिक बल की आवश्यकता होगी।

प्रश्न 14.
5 न्यूटन का बल किसी द्रव्यमान m₁ को 10 मीटर/सेकंड² का त्वरण देता है तथा द्रव्यमान m₂ को 20 मीटर/सेकंड² का त्वरण देता है। यदि दोनों द्रव्यमानों को एक साथ दिया जाए तो इस बल के द्वारा कितना त्वरण उत्पन्न होगा ?
हल :
दिया है, F = 5 न्यूटन, m₁ का त्वरण a₁ = 10 मीटर/सेकंड²
m₂ का त्वरण a₂ = 20 मीटर/सेकंड, दोनों को एक साथ जोड़ने पर त्वरण a = ?
सूत्र F = m a से, m = \(\frac{F}{a}\)
∴ m₁ = \(\frac{F}{a_{1}}=\frac{5}{10}\) = 0.5 किग्रा
तथा m₂ = \(\frac{F}{a_{2}}=\frac{5}{20}\) = 0.25
∴ दोनों को जोड़ने पर कुल द्रव्यमान = m₁ + m₂ = 0.5 + 0.25 = 0.75 किग्रा
∴ सूत्र F = m a से,
दोनों पिंडों का त्वरण = \(\frac{F}{m_{1}+m_{2}}\) = \(\frac{5}{0.75}\) = 0.67 मीटर/सेकंडर²

प्रश्न 15.
45 Km/n के वेग से चलती हुई 1000 kg द्रव्यमान की कोई कार एक पेड़ से टकरा कर 5 सै में रुक जाती है। कार द्वारा पेड़ पर कितना बल लगाया गया ?
हल :
m = 1000 कि० ग्रा०
u = 45 कि० मी०/घंटा
= \(\frac{45 \times 1000}{60 \times 60}\)
= \(\frac{25}{2}\) मी०/सै०
= 12.5 मी०/सै०
t = 5 सै०
υ = 0
υ = u + at
υ – u = at
a = \(\frac{v-u}{t}\)
= \(\frac{0-12.5}{5}\)
a = 2.5 मी०सै०
F = m × a
= 1000 × 2.5
= 2500 N

प्रश्न 16.
एक 100 kg द्रव्यमान वाली बंदूक द्वारा 0.02 kg द्रव्यमान की गोली दागी जाती है। यदि गोली की चाल 80 m/s हो तो बंदूक की पीछे की ओर धक्का लगाने की चालत मालूम करो।
हल :
गोली का द्रव्यमान (m) = 0.02 kg
गोली की चाल (υ) = 80 m/s
बंदूक का द्रव्यमान (M) = 100 kg
मान लो बंदूक का वेग V है। संवेग संरक्षण नियमानुसार,
गोली चलने के पश्चात् पूरे संकाय का संवेग = गोली चलने से पहले संवेग + गोली चलने के बाद संवेग
0 = mv + MV
V = \(\frac{-m v}{\mathbf{M}}\)
= \(\frac{-0.02 \times 80}{100}\)
= \(\frac{-2 \times 80}{100 \times 100}\)
= \(\frac{-16}{1000}\)
∴ बंदूक का वेग (V) = – (0.016 m/s
ऋण चिन्ह बन्दूक का पीछे की ओर धक्के की ओर संकेत करता है परंतु उसका वेग – 0.016 m/s है।

प्रश्न 17.
एक 30 kg भारी विस्फोटक गोला 48 m/s की गति से उड़ रहा है। विस्फोट के बाद इसका 18 kg का भार वाला एक भाग रुक जाता है जबकि शेष भाग उड़ जाता है। उड़ने वाले भाग का वेग ज्ञात करो।
हल :
यहां विस्फोटक गोले का द्रव्यमान (M) = 30 kg
विस्फोटक गोले का वेग (V) = 48 m/s
विस्फोटक गोले के एक भाग का द्रव्यमान (m₁) = 18 kg
विस्फोटक गोले के एक भाग का वेग = 0
विस्फोटक गोले का शेष भाग जो गतिशील नहीं है का द्रव्यमान (m₂) = (30 – 18) kg
= 12 kg
शेष भाग का वेग = υ₂ (मान लो)
अब संवेग संरक्षण नियमानुसार
MV = m₁υ₁ + m₂υ₂
30 × 48 = 18 × 0 + 12υ₂
30 × 48 = 12υ₂
υ₂ = \(\frac{30 \times 48}{12}\)
υ₂ = 30 × 4
υ₂ = 120 m/s

प्रश्न 18.
3 कि. ग्रा० की एक राइफल से 0.03 कि. ग्रा० की एक गोली चलाई गई जो 100 मी०/सै० वेग से नली से बाहर निकली। यदि गोली को 0:003 सै० नली से बाहर निकलने में लगे हों तो राइफल पर लगे बल की गणना करो।
हल :
m₁ = 3 कि० ग्रा०, m₂ = 0.03 कि० ग्रा०
u₁ = u₂ = 0, v₁ = ?, v₂ = 100 मी०/सै०
संवेग संरक्षण के नियम के अनुसार
m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂
0+ 0 = 3 × v₁ + 100 (0.03)
v₁ = \(-\frac{10(0 \times 0.0)}{3}\)
= -1 मी०सै०
(ऋणात्मक चिन्ह राइफल के विपरीत दिशा में धक्का लगाने को दर्शाता है।)

= -1000 कि० ग्रा०/सै०²
= -1000 N

प्रश्न 19.
5000 g द्रव्यमान की बंदूक से 20 g की गोली पृथ्वी की अपेक्षा 500 ms^-1 के वेग से छूटती है, बंदूक का प्रतिक्षेप वेग (Recoil velocity) बताएँ।
हल :
संवेग संरक्षण सिद्धांत के अनुसार
MV + mv = 0
V = \(-\frac{m v}{\mathrm{M}}\)
अब m = 0.020 kg, υ = 500 ms^-1 तथा M = 5.00 kg रखने पर
V = \(-\frac{20 \times 500}{5000}\)
या V = -2 ms^-1
ऋण चिहन बंदक के प्रक्षेपित होने की ओर संकेत करता है।

प्रश्न 20.
किसी द्रव्यमान m₁ पर 5 न्यूटन का बल लगाने पर 8 m/s² का त्वरण उत्पन्न होता है, जबकि इसी परिमाण का बल किसी द्रव्यमान m₂ में 24 m/s² का त्वरण उत्पन्न करता है। यदि दोनों द्रव्यमानों को परस्पर बांधकर एक कर दिया जाये, तो इस बल द्वारा संयुक्त द्रव्यमान में कितना त्वरण उत्पन्न होगा ?
हल :
पहला द्रव्यमान (m₁) = \(\frac{\mathrm{F}}{a_{1}}=\frac{5}{8}\) kg
दूसरा द्रव्यमान m₂ = \(\frac{\mathrm{F}}{a_{2}}=\frac{5}{24}\) kg
संयुक्त द्रव्यमान (m) = m₁ + m₂
\(\frac{5}{8}+\frac{5}{24}=\frac{20}{24}\) = \(\frac{5}{6}\) kg
5 न्यूटन द्वारा \(\frac{5}{6}\)kg द्रव्यमान से उत्पन्न त्वरण
a = \(\frac{\mathrm{F}}{m}=\frac{5}{5 / 6}\) = 6 ms^-2

प्रश्न 21.
दो ब्लॉक आकार तथा साइज में बराबर हैं परंतु भिन्न-भिन्न धातुओं के बने हैं। बराबर परिमाण के बल लगाने पर वह क्षैतिज तल में गतिशील हो जाते हैं। यदि एक ब्लॉक में उत्पन्न त्वरण दूसरे में उत्पन्न त्वरण के पाँच गुना हो, तो दोनों के द्रव्यमान का अनुपात क्या होगा ?
हल :
हम जानते हैं, F = ma
अत: पहले ब्लॉक के लिए F₁ = m₁a₁
तथा दूसरे ब्लॉक के लिए F₂ = m₂a
∵ F₁ = F₂ (दिया गया है।)
∴ m₁a₁ = m₂ a₂
= \(\frac{m_{1}}{m_{2}}=\frac{a_{2}}{a_{1}}\)
= \(\frac{m_{1}}{m_{2}}=\frac{5 a_{1}}{a_{2}}\) [∵ a₂ = 5a₁]
या \(\frac{m_{1}}{m_{2}}\) = 5
अतः पहले ब्लॉक का द्रव्यमान दूसरे से पाँच गुना है।

प्रश्न 22.
2 kg के एक पिस्टल से 20 g द्रव्यमान की एक गोली 150 ms^-1 के क्षैतिज वेग से छोड़ी जाती है। पिस्टल के पीछे हटने के वेग का परिकलन करें।
हल :

गोली का द्रव्यमान, m₁ = 20 g (= 0.02 kg)
पिस्टल का द्रव्यमान m₂ = 2 kg
प्रशिक्षण से पहले गोली का प्रारंभिक वेग (u₁) तथा पिस्टल का प्रारंभिक वेग (u₂) क्रमशः शून्य है।
अर्थात् u₁ = u₂ = 0
गोली का अंतिम वेग υ₁ = + 150 m s^-1
गोली की दिशा बाएँ से दाएँ परिपाटी के अनुसार धनात्मक ली गई है। माना कि पिस्टल का प्रतिक्षेपित वेग υ है।
गोली छूटने के पहले, गोली तथा पिस्टल का कुल संवेग,
= (2 + 0.02) kg × 0 m s^-1
= 0 kg m s^-1
गोली छूटने के बाद कुल संवेग,
= 0.02 kg × (+ 150 m s-1) + 2 kg × υ m s^-1
= (3 + 2υ) kg × m s^-1
संवेग संरक्षण के नियम के अनुसार,
गोली छूटने के बाद का कुल संवेग = गोली छूटने के पहले का कुल संवेग
3 + 2υ = 0
υ = 0 – 3
⇒ υ = – 1.5 m s^-1
ऋणात्मक चिह्न यह दर्शाता है कि पिस्टल गोली के विपरीत दिशा में अर्थात् दाईं से बाईं ओर प्रतिक्षेपित होगी।

प्रश्न 23.
40 kg द्रव्यमान वाली एक लड़की, 5 ms^-1 के क्षैतिज वेग से एक 3 kg द्रव्यमान वाली स्थिर गाड़ी पर कूदती है। गाड़ी के पहिए घर्षण रहित हैं। गाड़ी की गति प्रारंभ करने की अवस्था में लड़की का वेग क्या होगा ? मान लें कि क्षैतिज दिशा में कोई असंतुलित बल कार्य नहीं कर रहा है।
हल :
मान लो कि गाड़ी की प्रारंभिक गति के समय गाड़ी तथा लड़की का वेग υ है।
= 40 kg × 5 m s^-1 + 3 kg × 0 m s^-1
= 200 kg m s
लड़की तथा गाड़ी का लड़की के कूदने से पहले कुल संवेग
= (40 + 3) kg × υ m s^-1
= 43 υ kg m s^-1

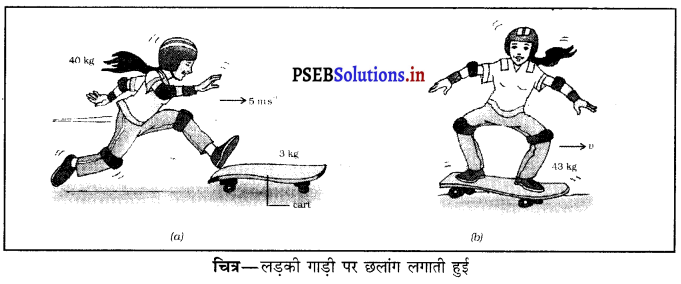
= 43 υ kg m s^-1
संवेग संरक्षण के नियम के अनुसार
43υ = 200
⇒ υ = 200/43
= + 4.65 m s^-1
गाड़ी पर सवार लड़की 4.65 m s^-1 के वेग से छलांग लगाने की दिशा में चलेगी।

प्रश्न 24.
हॉकी की प्रतिद्वंदी टीमों के दो खिलाड़ी गेंद को हिट करने के प्रयास में परस्पर टकरा जाते हैं तथा आपस में उलझ जाते हैं। एक का द्रव्यमान 60 kg है और वह 5.0 ms^-1 के वेग से गति में था, जबकि दूसरा खिलाड़ी, जिसका द्रव्यमान 55 kg है 6.0 m s^-1 के वेग से पहले खिलाड़ी की ओर गति कर रहा था। टकराकर उलझने के बाद वे दोनों किस दिशा में किस वेग से गति करेंगे। मान लें कि दोनों खिलाड़ियों के पैर तथा पृथ्वी के बीच कार्यरत घर्षण बल नगण्य है।
हल :
मान लो कि पहला खिलाड़ी बाएँ से दाएँ दौड़ रहा है तथा परिपाटी के अनुसार, बाएँ से दाएँ गति की दिशा धनात्मक तथा दाएँ से बाएँ गति की दिशा को ऋणात्मक लेते हैं।
दिया है,
m₁ = 60 kg ; u₁ = + 5 m s^-1 ; तथा
m₂ = 55 kg ; u₂ = – 6 m s^-1
टक्कर से पहले दोनों खिलाड़ियों का कुल संवेग
= 60 kg × (+ 5 m s^-1) + 55 kg × (- 6 m s^-1)
= – 30 kg m s^-1

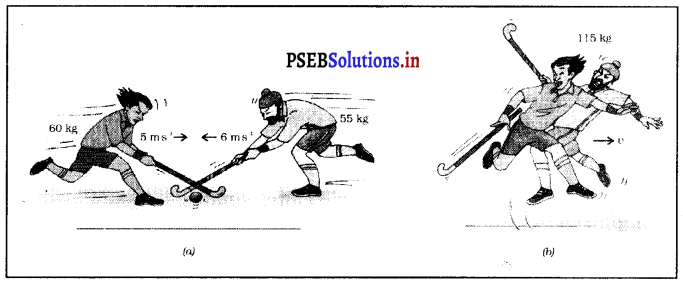
माना कि दोनों खिलाड़ियों के टकराने के पश्चात् उलझने पर वेग υ है,
टक्कर के पश्चात् कुल संवेग = (m₁ + m₂) × υ
= (60 + 55) kg × υ m s^-1
= 115 × υ kg m s^-1
संवेग संरक्षण के नियम के अनुसार,
υ = – 30/115
= – 0.26 m s^-1
अतः उलझने के पश्चात् दोनों खिलाड़ी दाएँ से बाएँ 0.26 m s^-1 के वेग से गतिशील हैं।

प्रश्न 25.
एक लंबी मेज पर सीधी रेखा में जा रही 20 ग्राम द्रव्यमान की गेंद का वेग-समय ग्राफ संलग्न चित्र में प्रदर्शित है। गेंद को विरामावस्था में लाने के लिए मेज द्वारा कितना बल लगाया जाएगा?

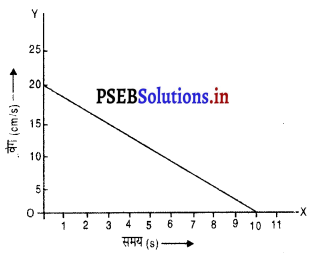
हल :
ग्राफ से स्पष्ट है कि t = 0 पर गेंद का प्रारंभिक वेग u = 20 सेमी/सेकंड तथा t = 10 सेकंड बाद गेंद का वेग υ = 20 गेंद का द्रव्यमान m = 20 ग्राम
∴ ग्राफ एक सरल रेखा है, इससे स्पष्ट है कि गेंद एक नियत त्वरण के अधीन गति करती है।
सूत्र a = \(\frac{v-u}{t}\) से,

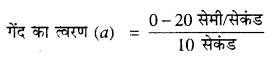
= -2 सेमी/सेकंडर²
= -0.02 मीटर/सेकंड²
∴ सूत्र F = m a से,
मेज द्वारा गेंद पर लगाया गया बल
F = 20 ग्राम × (- 0.02 मीटर/सेकंड²)
= \(\frac{20}{1000}\) किग्रा × (-0.02 मीटर/सेकंडर²)
= – 0.0004 न्यूटन
ऋणात्मक चिह्न यह प्रदर्शित करता है कि मेज द्वारा गेंद पर बल गति के विपरीत दिशा में लगाया जाता है।

अति लघु उत्तरात्मक प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
वस्तुओं की गति के बारे में पूर्णत: भिन्न संकल्पना किन वैज्ञानिकों ने दी थी ?
उत्तर-
गैलीलियो और आइजैक न्यूटन ने।

प्रश्न 2.
किसी वस्तु को गति की अवस्था में लाने के लिए क्या करना पड़ता है ?
उत्तर-
उसे खींचना, धकेलना या ठोकर लगाना पड़ता है।

प्रश्न 3.
वस्तु ऊपर से नीचे क्यों गिरती है ?
उत्तर-
असंतुलित गुरुत्वीय बल के कारण।

प्रश्न 4.
किसी वस्तु की दिशा बदलने के लिए कैसे बल की आवश्यकता होती है ? संतुलित बल या असंतुलित बल।
उत्तर-
असंतुलित बल की आवश्यकता।

प्रश्न 5.
कोई वस्तु कुछ दूर लुढ़कने के बाद क्यों रुक जाती है ?
उत्तर-
घर्षण बल के कारण।

प्रश्न 6.
घर्षण बल किस प्रकार घटाया जा सकता है ?
उत्तर-
समतल सतह पर लुब्रीकेंट के लेप से।

प्रश्न 7.
गति के तीन नियम किस वैज्ञानिक ने प्रस्तुत किए थे ?
उत्तर-
न्यूटन ने।

प्रश्न 8.
न्यूटन की गति का पहला नियम क्या है ?
उत्तर-
प्रत्येक वस्तु अपनी स्थिर अवस्था या सरल रेखा में एक समान गति की अवस्था में बनी रहती है जा तक कि उस पर कोई बाहरी बल कार्यरत न हो।

प्रश्न 9.
जड़त्व किसे कहते हैं ?
उत्तर-
जड़त्व – किसी वस्तु के विरामावस्था में रहने या समान वेग से गतिशील रहने की प्रवृत्ति को जड़ता कहते हैं।

प्रश्न 10.
गति का पहला नियम किस अन्य नाम से जाना जाता है ?
उत्तर-
जड़त्व का नियम ।

प्रश्न 11.
एकदम ब्रेक लगाने से गाड़ी में बैठे यात्रियों को झटका क्यों लगता है ?
उत्तर-
यात्रियों का शरीर गतिज जड़त्व के कारण गति अवस्था में ही बने रहने की प्रवृत्ति रखता है।

प्रश्न 12.
गाड़ियों में सुरक्षा बेल्ट का उपयोग क्यों किया जाता है ?
उत्तर-
इनसे हमारे आगे बढ़ने की गति धीमी हो जाती है।

प्रश्न 13.
बल की परिभाषा दीजिए।
उत्तर-
बल – बल वह बाहरी कारक है जो किसी वस्तु की विराम की अवस्था या गतिमान वस्तु की चाल तथा दिशा को बदलने या बदलने की प्रवृत्ति रखता है।

प्रश्न 14.
संतुलित बल किसे कहते हैं ?
उत्तर-
संतुलित बल – यदि वस्तु पर लगने वाले सभी बलों का परिणामी बल शून्य हो तो वस्तु पर लगने वाले सभी बल, संतुलित बल कहलाते हैं।

प्रश्न 15.
असंतुलित बल किसे कहते हैं ?
उत्तर-
असंतुलित बल – यदि किसी वस्तु पर लगने वाले सभी बलों का परिणामी बल शून्य न हो, तो वे बल असंतुलित बल कहलाते हैं।

प्रश्न 16.
रबड़ की गेंद को हथेलियों के बीच में रखकर दबाते समय किस प्रकार का बल लगता है ?
उत्तर-
संतुलित बल।

प्रश्न 17.
घर्षण की परिभाषा लिखें।
उत्तर-
घर्षण – जब एक वस्तु किसी अन्य वस्तु के संपर्क में रहते हुए गति करती है तो उस गति की दिशा के विपरीत एक बल कार्य करता है जिसे घर्षण कहते हैं।

प्रश्न 18.
जब हम साइकिल के पैडल को चलाना बंद कर देते हैं तो साइकिल रुक जाती है, क्यों ?
उत्तर-
साइकिल के टायर और सड़क के बीच लगने वाला घर्षण बल उसकी गति को कम करके साइकिल को रोक देता है।

प्रश्न 19.
संवेग क्या होता है ?
उत्तर-
संवेग-किसी वस्तु का संवेग उसके वेग तथा द्रव्यमान का गुणनफल है।
∴ संवेग = द्रव्यमान × वेग।

प्रश्न 20.
न्यूटन का दूसरा गति-नियम क्या है ?
उत्तर-
किसी वस्तु पर क्रिया कर रहा बल उस वस्तु के पुंज और त्वरण के गुणनफल के बराबर होता है।

प्रश्न 21.
न्यूटन का तीसरा नियम क्या है ?
उत्तर-
क्रिया और प्रतिक्रिया समान किंतु विपरीत दिशा में क्रिया करती है।

प्रश्न 22.
संवेग सदिश राशि है या अदिश राशि ?
उत्तर-
संवेग एक सदिश राशि है।

प्रश्न 23.
एक एथलीट तब छलांग लंबी लगा सकता है, जब वह भागता हुआ आता है। जब वह अचानक ही छलांग लगा देता है तो छलांग छोटी रह जाती है। ऐसा क्यों ?
उत्तर-
जब एथलीट दूरी से दौड़ता हुआ आता है तो उसके गति-जड़त्व में वृद्धि हो जाती है। इसी कारण वह लंबी छलांग लगा पाता है। दूसरा स्थिति में छलांग छोटी होगी।

प्रश्न 24.
गोली चल चुकने के बाद बंदूक और गोली का कुल संवेग कितना होता है ?
उत्तर-
शून्य।

प्रश्न 25.
बल की मानक इकाई क्या है ?
उत्तर-
न्यूटन।

प्रश्न 26.
यदि वस्तु पर क्रिया कर रहा परिणामी बल शून्य हो तो बल संतुलित होंगे या असंतुलित ?
उत्तर-
बल संतुलित होंगे।

प्रश्न 27.
यदि 1 kg द्रव्यमान पर 1 न्यूटन बल लगाया जाए तो परिणामी त्वरण क्या होगा ?
उत्तर-
F = m × a
1 = 1 × a
a = 1 ms^-2

प्रश्न 28.
वस्तु पर क्रिया कर रहे अनेक बल उसकी स्थिति में कोई परिवर्तन नहीं करते। बल संतुलित हैं या असन्तुलित ?
उत्तर-
बल संतुलित है।

प्रश्न 29.
चार ऐसे उदाहरण दो जहां बल लगाने से स्थिर वस्तु गतिशील हो जाती है।
उत्तर-

1. झाड़ से कूड़ा-कर्कट हटाना,
2. ठोकर मार कर गेंद को लुढ़काना,
3. घोड़े के द्वारा तांगा खींचना,
4. हॉकी से बाल को हिट मारना।

प्रश्न 30.
जब बॉल को बैट के द्वारा हिट मारी जाती है तो क्या परिवर्तन दिखाई देता है ?
उत्तर-
बॉल की चाल शून्य से कुछ मान तक बढ़ जाती है।

प्रश्न 31.
किसका जड़त्व अधिक होगा ?
(i) एक पुस्तक या स्कूल बैग
(ii) पानी से भरा घड़ा या रेफ्रिजिरेटर।
उत्तर-
(i) स्कूल बैग
(ii) रेफ्रिजिरेटर।

प्रश्न 32.
हल्की और भारी वस्तुओं में से जड़त्व किसका अधिक होता है ?
उत्तर-
भारी वस्तुओं का जड़त्व अधिक होता है।

प्रश्न 33.
संवेग का S.I. मात्रक लिखिए।
उत्तर-
संवेग का S.I. मात्रक किलोग्राम मीटर/सै० होता है।

प्रश्न 34.
न्यूटन बल की परिभाषा दीजिए।
उत्तर-
न्यूटन बल – वह बल जो एक किलोग्राम द्रव्यमान की वस्तु में 1 मी/सै2 का त्वरण उत्पन्न कर देता है। न्यूटन बल कहलाता है।

प्रश्न 35.
किसी बाहरी बल की अनुपस्थिति में जब दो वस्तुएं परस्पर टकराती हैं तो निकाय (System) के संवेग में संपूर्ण परिवर्तन क्या होगा ?
उत्तर-
कोई परिवर्तन नहीं होगा क्योंकि कुल संवेग संरक्षित रहता है।

प्रश्न 36.
बंदूक से गोली चलाने पर बंदूक पीछे क्यों हटती है ?
उत्तर-
बंदूक संवेग संरक्षण के नियम के कारण पीछे हटती है।

प्रश्न 37.
तैरने के दौरान कोई व्यक्ति पानी को अपने हाथों से पीछे क्यों दबाता है ?
उत्तर-
पानी को हाथों से पीछे दबाने पर प्रतिक्रिया का बल उसे आगे की ओर धकेलता है।

प्रश्न 38.
कैरम बोर्ड पर खेलते समय प्रायः पाऊडर का प्रयोग क्यों करना पड़ता है ?
उत्तर-
घर्षण को कम करने के लिए।

प्रश्न 39.
क्रिया और प्रतिक्रिया एक ही पिंड पर कार्य करती हैं या अलग-अलग पिंडों पर ?
उत्तर-
अलग-अलग पिंडों पर।

प्रश्न 40.
दरी को छड़ी से पीटने पर धूल क्यों झड़ जाती है ?
उत्तर-
स्थिर जड़त्व के कारण।

प्रश्न 41.
खिलाड़ी कूदने से पहले क्यों दौड़ता है ?
उत्तर-
संवेग बढ़ाने के लिए ताकि अधिक ऊँची कूद लगाई जा सके।

प्रश्न 42.
संवेग संरक्षण का नियम क्या है ?
उत्तर-
संवेग संरक्षण नियम – दो वस्तुओं के संवेग का योग टकराने से पहले और टकराने के बाद बराबर रहता है जबकि उन पर कोई असंतुलित बल कार्य न कर रहा हो।

प्रश्न 43.
बल का मात्रक लिखिए।
उत्तर-
बल का मात्रक न्यूटन है।

प्रश्न 44.
बल कैसी राशि है?
उत्तर-
बल एक सदिश राशि है।

प्रश्न 45.
एक बस और एक गेंद समान चाल से चल रहे हैं। दोनों में से किसे रोकने के लिए अधिक बल लगाना पड़ेगा ?
उत्तर-
अधिक संवेग के कारण बस को रोकने के लिए अधिक बल लगाना पड़ेगा।

प्रश्न 46.
कोई लड़की 20 kg द्रव्यमान के डिब्बे को 60 N बल लगाकर धकेलती है। डिब्बे का त्वरण क्या होगा?
उत्तर-
a = \(\frac{\mathrm{F}}{m}=\frac{60 \mathrm{~N}}{20 \mathrm{~kg}}\) = 3 m/s²

प्रश्न 47.
ब्रेक लगाने पर एक चलती गाड़ी रुक जाती है, इस प्रक्रिया में गाड़ी के संवेग का क्या होता है ?
उत्तर-
इस प्रक्रिया में गाड़ी के संवेग का अधिकांश भाग पृथ्वी को तथा शेष भाग वायु के अणुओं को चला जाता है।

प्रश्न 48.
यदि किसी वस्तु पर असंतुलित बल न लगा हो तो क्या वस्तु समान वेग से चलती रहेगी ?
उत्तर-
हां, वस्तु एक समान वेग से चलती रहेगी।

प्रश्न 49.
यदि किसी वस्तु पर नेट बाह्य बल शून्य है तो क्या वह वस्तु अवश्य ही विरामावस्था में होगी ?
उत्तर-
आवश्यक नहीं है कि वस्तु विरामावस्था में हों कि वस्तु एकसमान चाल से एक निश्चित दिशा में चल रही हो सकती है।

प्रश्न 50.
1 किग्रा-भार कितने न्यूटन के बराबर होता है ?
उत्तर-
1 किग्रा-भार = 9.8 न्यूटन।

प्रश्न 51.
1 न्यूटन में कितने किग्रा-भार होता है ?
उत्तर-
1 न्यूटन = 0.102 किग्रा-भार।

प्रश्न 52.
जड़त्व किस भौतिक पर निर्भर करता है ?
उत्तर-
द्रव्यमान पर।

प्रश्न 53.
दो समान वेग वाले पिंडों के द्रव्यमान 1 : 2 के अनुपात में हैं। उनके जड़त्वों में क्या अनुपात होगा ?
उत्तर-
1 : 2 का अनुपात होगा।

प्रश्न 54.
किसी पिंड पर लगे बल (F), द्रव्यमान (m) तथा त्वरण (a) में परस्पर संबंध बताइए।
उत्तर-
बल (F) = द्रव्यमान (m) × त्वरण (a)।

प्रश्न 55.
एक कार को 300 न्यूटन के बल से सड़क पर खींचने से वह एक नियत वेग से चलती है। कार व पृथ्वी के बीच कितना घर्षण बल कार्य कर रहा है?
उत्तर-
300 न्यूटन।

प्रश्न 56.
पदार्थ का वह कौन-सा गुण है, जो पदार्थ की अवस्था परिवर्तन का विरोध करता है?
उत्तर-
जड़त्व का गुण।

प्रश्न 57.
रॉकेट का क्रिया-सिद्धांत, न्यूटन के गति के किस नियम पर आधारित है?
उत्तर-
न्यूटन के गति के तीसरे नियम पर।

प्रश्न 58.
किसी वस्तु के द्रव्यमान तथा त्वरण के गुणनफल को क्या नाम दिया गया है ?
उत्तर-
संवेग।

प्रश्न 59.
‘m’ द्रव्यमान वाली एक वस्तु पर ‘F’ बल कार्य कर रहा है और त्वरण ‘a’ उत्पन्न होता है ? यदि बल की मात्रा आधी कर दी जाये तो त्वरण पर क्या प्रभाव पड़ेगा ?
उत्तर-
क्योंकि a ∝ F, इसलिए बल की मात्रा \(\frac{F}{2}\) कर त्वरण \(\frac{a}{2}\) हो जाएगा।

प्रश्न 60.
एक ट्रक और एक कार v वेग से गतिशील हैं, दोनों एक-दूसरे से आमने-सामने संघट्ट करते हैं तथा कुछ समय बाद दोनों रुक जाते हैं। अगर संघट्ट का समयांतराल 1s है, तो
(a) कौन-सी गाड़ी पर बल का सबसे अधिक प्रभाव पड़ेगा ?
(b) किस गाड़ी से संवेग में सबसे अधिक परिवर्तन होगा ?
(c) किस गाड़ी का त्वरण सबसे अधिक होगा ?
(d) ट्रक की अपेक्षा कार को अधिक नुकसान क्यों होगा ?
उत्तर-
(a) दोनों गाड़ियों पर बराबर बल लगेगा क्योंकि क्रिया तथा प्रतिक्रिया समान होते हैं। अब क्योंकि चार का द्रव्यमान कम है इसलिए कार पर प्रभाव अधिक होगा।
(b) क्योंकि क्रिया तथा प्रतिक्रिया समान होते हैं तथा यह संवेग का परिवर्तन होता है, इसलिए कार तथा ट्रक का संवेग परिवर्तन भी समान होगा।
(c) कार का त्वरण अधिक होगा क्योंकि इसका द्रव्यमान ट्रक के द्रव्यमान की अपेक्षा कम है।
(d) कार का कम जड़त्व होने के कारण इसे अधिक नुकसान होगा।