PSEB 9th Class Maths Solutions Chapter 1 Number Systems Ex 1.2

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 1 Number Systems Ex 1.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.2

Question 1.
State whether the following statements are true or false. Justify your answers:
(i) Every irrational number is a real number.
Answer:
This statement is true. The collection of real numbers contain all the rational numbers and all the irrational numbers.

(ii) Every point on the number line is of the form √m, where m is a natural number.
Answer:
This statement is false. The negative numbers represented on the number line are never of the form √m, where m is a natural number. For natural number m, √m is always a positive number.

(iii) Every real number is an irrational number.
Answer:
This statement is false. The collection of real numbers is made-up of rational numbers and irrational numbers. So, every real number is either a rational number or an irrational number.

Question 2.
Are the square roots of all positive integers irrational? if not, give an example of the square root of a number that is a rational number.
Answer:
No, The square roots of all positive integers are not irrational. The square root of any perfect square number is always a rational number.
e.g., √4 = 2, √9 = 3, √16 = 4, ……

Question 3.
Show how √5 can be represented on the number line.
Answer:

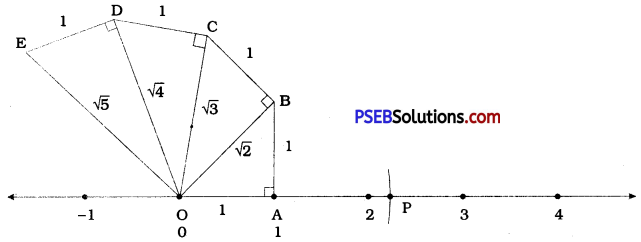
Start by taking point O on the number line which represents O. Choosing proper unit, locate point A on the number line to represent
1. Draw seg AB of unit length perpendicular to seg OA. Construct seg OB. Then, by Pythagoras’ theorem, OB = √2. Draw seg BC of unit length perpendicular to seg OB. Construct seg OC.
Then, OC = √3. Draw seg CD of unit length perpendicular to seg OC. Construct seg OD.
Then, OD = √4. Draw seg DE of unit length perpendicular to seg OD. Construct seg 0E.
Then, 0E = √5. Draw an arc with centre O and radius OE to Intersect the number line at P Then, point P on the number line represents √5.

Alternate Method:
This can be solved In fewer steps as shown in the following manner:
On the number line l, take a point O corresponding to 0. Choosing the proper unit, take a point A on l such that OA = 2 units. Construct right angled Δ OAP such that ΔOAP = 90° and AP = 1 unit.

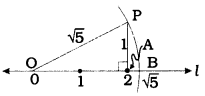
Then, by Pythagoras theorem,
OP² = OA² + AP²
= (2)² + (1)² = 4 + 1 = 5
∴ OP = √5
Draw an arc with centre O and radius OP to intersect l at B. B is the point corresponding to Draw an arc with centre O and radius OP to intersect I at B. B is the point corresponding to √5.

Question 4.
Classroom activity (Constructing the ‘square root spiral’): Take a large sheet of paper and construct the ‘square root spiral’ in the following fashion. Start with a point O and draw a line segment OP₁ of unit length. Draw a line segment P₁P₂ perpendicular to OP₁ of unit length (see Fig. 1.9). Now draw a line segment P₂P₃ perpendicular to OP₂. Then draw a line segment P₃P₄ perpendicular to OP₃. Continuing in this manner, you can get the line segment P_n-1P_n by drawing a line segment of unit length perpendicular to OP_n-1. In this manner, you will have created the points P₂, P₃, …………, P_n, ………, and joined them to create a beautiful spiral depicting √2, √3, √4, ………..

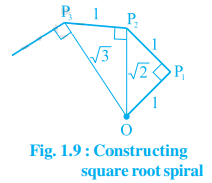
Answer:
Take a large sheet of paper and construct the ‘square root spiral’ in the following fashion:

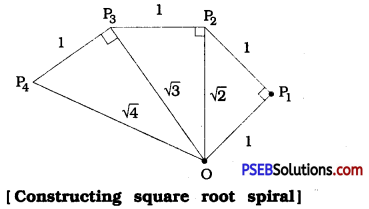
Start with a point O and draw a line segment OP₁ of unit length. Draw a line segment P₁P₂ perpendicular to OP₁ of unit length (see Fig. 1.9). Now draw a line segment P₂P₃ perpendicular to OP₂. Then draw a line segment P₃P₄ perpendicular to OP₃. Continuing in this manner, you can get the line segment P_n-1P_n by drawing a line segment of unit length perpendicular to OP_n-1. In this manner, you will have created the points P₂, P₃, …………, P_n, ………, and joined them to create a beautiful spiral depicting √2, √3, √4, ………..