Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 6 Lines and Angles Ex 6.2 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 6 Lines and Angles Ex 6.2
Question 1.
In the given figure, find the values of x and y and then show that AB || C
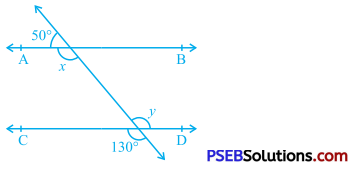
Answer:
Ray QA stands on line PS.
∴ ∠ PQA and ∠ AQR form a linear pair.
∴ ∠ PQA + ∠ AQR = 180° [Linear pair axiom]
∴ 50° + x = 180°
∴ x = 130° ……………. (1)
Lines PS and CD intersect at R.
∴ ∠ CRS and ∠ QRD are vertically opposite angles.
∴ ∠ QRD = ∠ CRS
∴ y = 130° ……………. (2)
From (1) and (2),
x = y.
But, these angles are alternate interior angles formed by transversal PS for lines AB and CD and they are equal.
Hence, AB || CD.
![]()
Question 2.
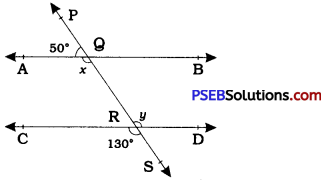
In the given figure, if AB || CD, CD || EF and y : z = 3 : 7, find x.
Answer:
AB || CD and CD || EF.
∴ AB || EF (Lines parallel to the same line)
∴ x = z (Alternate interior angles)
Now, AB || CD.
∴ x + y = 180° (Interior angles on the same side of transversal)
Now, x = z and x + y = 180°
∴ z + y = 180°
Moreover, y : z = 3 : 7
Sum of the ratios 3 + 7 = 10
Then, z = \(\frac{7}{10}\) × 180° = 126°
Now, x = z = 126°
![]()
Question 3.
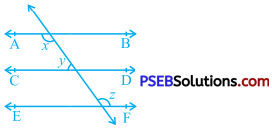
In the given figure, if AB || CD, EF ⊥ CD and ∠ GED = 126°, find ∠ AGE, ∠ GEF and ∠ FGE.
Answer:
Here, AB || CD and GE is transversal for them.
∴ ∠ AGE and ∠ GED are equal alternate interior angles.
∴ ∠ GED = ∠ AGE
∴ ∠ AGE = 126° (Given : ∠ GED= 126°)
EF ⊥ CD
∴ ∠ FED = 90°
∠ GEF + ∠ FED = ∠ GED (Adjacent angles)
∴ ∠ GEF + 90° = 126°
∴ ∠ GEF = 126° – 90°
∴ ∠ GEF = 36°
Ray GE stands on line AF.
∴ ∠ AGE + ∠ FGE = 180° (Angles of linear pair)
∴ 126° + ∠ FGE = 180°
∴ ∠ FGE =180°- 126°
∴ ∠ FGE = 54°
![]()
Question 4.
In the given figure, if PQ || ST, ∠ PQR = 110° and ∠ RST = 130°, find ∠ QRS.
[Hint: Draw a line parallel to ST through point R.]
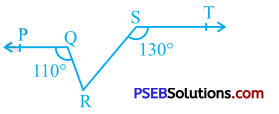
Answer:
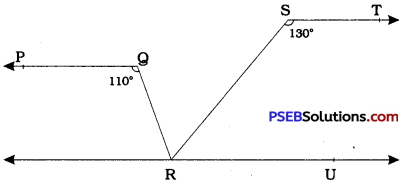
Draw line RU parallel to line ST.
PQ || ST and ST || RU
∴ PQ || RU
ST || RU and SR is a transversal for them.
∴ ∠ TSR + ∠ SRU = 180° (Interior angles on the same . side of the transversal)
∴ 130° + ∠ SRU = 180°
∴ ∠ SRU = 50° ………………. (1)
PQ || RU and QR is a transversal for them.
∴ ∠ PQR = ∠ QRU (Alternate interior angles)
∴ 110° = ∠ QRU
∴ ∠ QRU =110° ……………… (2)
Now, ∠ QRS and ∠ SRU are adjacent angles.
∴ ∠ QRS + ∠ SRU = ∠ QRU
∴ ∠ QRS + 50° = 110° [by (1) and (2)]
∴ ∠ QRS = 60°
![]()
Question 5.
In the given figure, if AB || CD, ∠ APQ = 50° and ∠ P RD = 127°, find x and y.
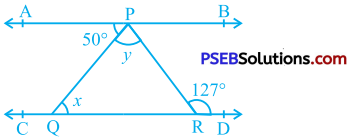
Answer:
Here, AB || CD and PQ is transversal for them.
∴ ∠ APQ = ∠ PQR (Alternate interior angles)
∴ 50° = x (Given: ∠ APQ = 50°)
∴ x = 50°
Again, AB || CD and PR is transversal for them.
∴ ∠ APR = ∠ PRD (Alternate interior angles) )
∴ ∠ APR = 127° (Given: ∠ PRD = 127°)
∴ ∠ APQ + ∠ QPR = 127°
(∵ ∠ APQ and ∠ QPR are adjacent angles and their non-common arms form ∠ APR)
∴ 50° + y = 127°
∴ y = 127°- 50°
∴ y = 77°
![]()
Question 6.
In the given figure, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB || CD.
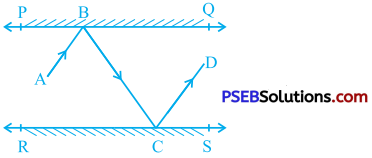
Answer:
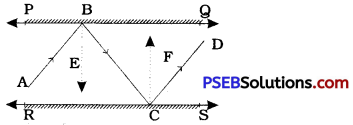
Construction: Draw ray BE perpendicular to line PQ and ray CF perpendicular to line RS.
We know that for plane mirrors, angle of incidence = angle of reflection.
Hence, at point B,
∠ ABE = ∠ EBC …………. (1)
and ’ at point C,
∠ BCF = ∠ FCD ………….. (2)
Now, PQ || RS, BE ⊥ PQ and CF ⊥ RS.
Hence, BE || CE
∴ ∠ EBC = ∠ BCF (Alternate interior angles) …………… (3)
From (1), (2) and (3), we get
∠ ABE = ∠ EBC = ∠ BCF = ∠ FCD
∴ ∠ ABE + ∠ EBC = ∠ BCF + ∠ FCD
∴ ∠ ABC = ∠ BCD [Adjacent angles: ∠ ABE and ∠ EBC, ∠ BCF and ∠ FCD]
But ∠ ABC and ∠ BCD are alternate interior angles formed by transversal BC for lines AB and CD and they are equal.
∴ AB || CD
