Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 4 ਭਿੰਨਾਤਮਕ ਸੰਖਿਆਵਾਂ Ex 4.4 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 5 Maths Chapter 4 ਭਿੰਨਾਤਮਕ ਸੰਖਿਆਵਾਂ Ex 4.4
ਪ੍ਰਸ਼ਨ 1.
ਪਤਾ ਕਰੋ ਕਿ ਹੇਠਾਂ ਦਿੱਤੀਆਂ ਭਿੰਨਾਂ ਨਿਊਨਤਮ ਰੂਪ ਵਿਚ ਹਨ ਜਾਂ ਨਹੀਂ :
(a) \(\frac{12}{14}\)
ਹੱਲ:
ਭਿੰਨ \(\frac{12}{14}\) ਨਿਊਨਤਮ ਰੂਪ ਵਿਚ ਹੈ ਜਾਂ ਨਹੀਂ, ਇਹ ਪਤਾ ਕਰਨ ਲਈ ਅਸੀਂ ਭਿੰਨ ਦੇ ਅੰਸ਼ 12 ਅਤੇ ਹਰ 14 ਦਾ ਮ.ਸ.ਵ. ਪਤਾ ਕਰਾਂਗੇ ।
12 ਅਤੇ 14 ਦਾ ਮ.ਸ.ਵ. = 2
ਇਹ ਭਿੰਨ ਨਿਊਨਤਮ ਰੂਪ ਵਿਚ ਨਹੀਂ ਹੈ ਕਿਉਂਕਿ ਅੰਸ਼ ਅਤੇ ਹਰ ਦਾ ਮ.ਸ.ਵ. 1 ਨਹੀਂ ਹੈ ।
ਭਿੰਨ \(\frac{12}{14}\) ਨੂੰ ਨਿਊਨਤਮ ਰੂਪ ਵਿਚ ਕਰਨ ਲਈ ਅਸੀਂ ਅੰਸ਼ 12 ਅਤੇ ਹਰ 14 ਨੂੰ ਮ.ਸ.ਵ. 2 ਨਾਲ ਭਾਗ ਕਰਾਂਗੇ ।
ਭਿੰਨ \(\frac{12}{14}\) = \(\frac{12 \div 2}{14 \div 2}\) = \(\frac{6}{7}\)
ਇਸ ਲਈ ਭਿੰਨ \(\frac{12}{14}\) ਦਾ ਨਿਊਨਤਮ ਰੂਪ \(\frac{6}{7}\) ਹੈ ।
(b) \(\frac{21}{35}\)
ਹੱਲ:
ਭਿੰਨ \(\frac{21}{35}\) ਨਿਊਨਤਮ ਰੂਪ ਵਿਚ ਹੈ ਜਾਂ ਨਹੀਂ ਇਹ ਪਤਾ ਕਰਨ ਲਈ ਅਸੀਂ ਭਿੰਨ ਦੇ ਅੰਸ਼ 21 ਅਤੇ ਹਰ 35 ਦਾ ਮ.ਬ.ਵ. ਪਤਾ ਕਰਾਂਗੇ । 21 ਅਤੇ 35 ਦਾ ਮ.ਸ.ਵ. = 7

ਇਹ ਭਿੰਨ ਨਿਊਨਤਮ ਰੂਪ ਵਿੱਚ ਨਹੀਂ ਹੈ ਕਿਉਂਕਿ ਅੰਸ਼ ਅਤੇ ਹਰ ਦਾ ਮ.ਸ.ਵ. 1 ਨਹੀਂ ਹੈ ।
ਭਿੰਨ \(\frac{21}{35}\) ਨੂੰ ਨਿਊਨਤਮ ਰੂਪ ਵਿਚ ਕਰਨ ਲਈ ਅਸੀਂ ਅੰਸ਼ 21 ਅਤੇ ਹਰ 35 ਨੂੰ ਮ.ਸ.ਵ. ਭਾਵ 7 ਨਾਲ ਭਾਗ ਕਰਾਂਗੇ ।
\(\frac{21}{35}\) = \(\frac{21 \div 7}{35 \div 7}\) = \(\frac{3}{5}\)
ਇਸ ਲਈ ਭਿੰਨ \(\frac{21}{35}\) ਦਾ ਨਿਊਨਤਮ ਰੂਪ \(\frac{3}{5}\) ਹੈ।
![]()
(c) \(\frac{13}{17}\)
ਹੱਲ:
ਭਿੰਨ \(\frac{13}{17}\) ਵਿੱਚ ਅੰਸ਼ 13 ਅਤੇ ਹਰ 17 ਦਾ ਮ.ਬ.ਵ. ਪਤਾ ਕਰਾਂਗੇ ।
13 ਅਤੇ 17 ਦਾ ਮ.ਸ.ਵ. = 1
ਇਸ ਲਈ ਭਿੰਨ \(\frac{13}{17}\) ਨਿਊਨਤਮ ਰੂਪ ਵਿੱਚ ਹੈ ।
(d) \(\frac{25}{50}\)
ਹੱਲ:
ਭਿੰਨ \(\frac{25}{50}\) ਵਿਚ ਅੰਸ਼ 25 ਅਤੇ ਹਰ 50 ਦਾ ਮ.ਸ., ਪਤਾ ਕਰਦੇ ਹਾਂ ।
25 ਅਤੇ 50 ਦਾ ਮ.ਸ.ਵ. = 25.
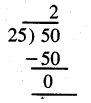
ਇਹ ਭਿੰਨ ਨਿਊਨਤਮ ਰੂਪ ਵਿਚ ਨਹੀਂ ਹੈ ਕਿਉਂਕਿ ਅੰਸ਼ ਅਤੇ ਹਰ ਦਾ ਮ.ਸ.ਵ. 1 ਨਹੀਂ ਹੈ ।
ਭਿੰਨ \(\frac{25}{50}\) ਨੂੰ ਨਿਊਨਤਮ ਰੂਪ ਵਿਚ ਕਰਨ ਲਈ ਅਸੀਂ ਅੰਸ਼ 25 ਅਤੇ ਹਰ 50 ਨੂੰ ਮ.ਸ.ਵ. 25 ਨਾਲ ਭਾਗ ਕਰਾਂਗੇ ।
\(\frac{25}{50}\) = \(\frac{25 \div 25}{50 \div 25}\) = \(\frac{1}{2}\)
ਇਸ ਲਈ ਭਿੰਨ \(\frac{25}{50}\) ਦਾ ਨਿਊਨਤਮ ਰੂਪ \(\frac{1}{2}\) ਹੈ।
(e) \(\frac{14}{21}\)
ਹੱਲ:
ਭਿੰਨ \(\frac{14}{21}\) ਵਿੱਚ ਅੰਸ਼ 14 ਅਤੇ ਹਰ 21 ਦਾ
ਮ.ਸਵ. ਪਤਾ ਕਰਦੇ ਹਾਂ ।
14 ਅਤੇ 21 ਦਾ ਮ..ਵ. = 7
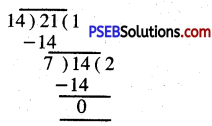
ਇਹ ਭਿੰਨ ਨਿਊਨਤਮ ਰੂਪ ਵਿਚ ਨਹੀਂ ਹੈ ਕਿਉਂਕਿ ਅੰਸ਼ ਅਤੇ ਹਰ ਦਾ ਮ.ਸ.ਵ. 1 ਨਹੀਂ ਹੈ ।
ਭਿੰਨ \(\frac{14}{21}\) ਨੂੰ ਨਿਊਨਤਮ ਰੂਪ ਵਿਚ ਕਰਨ ਲਈ ਅੰਸ਼ 14 ਅਤੇ ਹਰ 21 ਨੂੰ ਮ… 7 ਨਾਲ ਭਾਗ ਕਰਦੇ ਹਾਂ ।
\(\frac{14}{21}\) = \(\frac{14 \div 7}{21 \div 7}\) = \(\frac{2}{3}\)
ਇਸ ਲਈ ਭਿੰਨ \(\frac{14}{21}\) ਦਾ ਨਿਊਨਤਮ ਰੂਪ \(\frac{2}{3}\) ਹੈ ।
(f) \(\frac{8}{13}\)
ਹੱਲ:
ਭਿੰਨ \(\frac{8}{13}\) ਨਿਊਨਤਮ ਰੂਪ ਵਿੱਚ ਹੈ ਜਾਂ ਨਹੀਂ, ਇਹ ਪਤਾ ਕਰਨ ਲਈ ਅਸੀਂ ਭਿੰਨ ਦੇ ਅੰਸ਼ 8 ਅਤੇ ਹਰ 13 ਦਾ ਮ.ਸ. ਵ. ਪਤਾ ਕਰਾਂਗੇ ।

8 ਅਤੇ 13 ਦਾ ਮ.ਸ.ਵ. = 1
ਇਸ ਲਈ \(\frac{8}{13}\) ਨਿਊਨਤਮ ਰੂਪ ਵਿੱਚ ਹੈ ।
(g) \(\frac{7}{15}\)
ਹੱਲ:
ਭਿੰਨ \(\frac{7}{15}\) ਨਿਊਨਤਮ ਰੂਪ ਵਿਚ ਹੈ ਜਾਂ ਨਹੀਂ, ਇਹ ਪਤਾ ਕਰਨ ਲਈ ਅਸੀਂ ਭਿੰਨ ਦੇ ਅੰਸ਼ 7 ਅਤੇ ਹਰ 15 ਦਾ ਮ.ਏ.ਵ. ਪਤਾ ਕਰਾਂਗੇ । 7 ਅਤੇ 15 ਦਾ ਮ.ਸ.ਵ. = 1
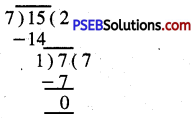
ਇਸ ਲਈ ਭਿੰਨ ਨਿਊਨਤਮ ਰੂਪ ਵਿਚ ਹੈ ।
![]()
(h) \(\frac{14}{27}\)
ਹੱਲ:
ਭਿੰਨ \(\frac{14}{27}\) ਨਿਊਨਤਮ ਰੂਪ ਵਿਚ ਹੈ ਜਾਂ ਨਹੀਂ, ਇਹ ਪਤਾ ਕਰਨ ਲਈ ਅਸੀਂ ਭਿੰਨ ਦੇ ਅੰਸ਼
14 ਅਤੇ ਹਰ 27 ਦਾ ਮ.ਸ.ਵ. ਪਤਾ ਕਰਾਂਗੇ । . 14 ਅਤੇ 27 ਦਾ ਮ.ਸਵ. = 1
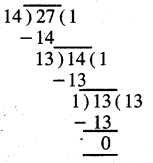
ਇਸ ਲਈ ਭਿੰਨ \(\frac{14}{27}\) ਨਿਊਨਤਮ ਰੂਪ ਵਿਚ ਹੈ ।
(i) \(\frac{25}{35}\)
ਹੱਲ:
ਭਿੰਨ \(\frac{25}{35}\) ਨਿਊਨਤਮ ਰੂਪ ਵਿਚ ਹੈ ਜਾਂ ਨਹੀਂ, ਇਹ ਪਤਾ ਕਰਨ ਲਈ ਅਸੀਂ ਭਿੰਨ ਦੇ ਅੰਸ਼ 25 ਅਤੇ ਹਰ 35 ਦਾ ਮ. ਸ.ਵ. ਪਤਾ ਕਰਾਂਗੇ । 25 ਅਤੇ 35 ਦਾ ਮ.ਸ.ਵ. = 5

ਕਿਉਂਕਿ ਮਸਵ. 1 ਨਹੀਂ ਹੈ । ਇਸ ਲਈ ਇਹ ਭਿੰਨ ਨਿਊਨਤਮ ਰੂਪ ਵਿੱਚ ਨਹੀਂ ਹੈ ।
\(\frac{25}{35}\) = \(\frac{25 \div 5}{35 \div 5}\) = \(\frac{5}{7}\)
\(\frac{25}{35}\) ਦਾ ਨਿਊਨਤਮ ਰੂਪ \(\frac{5}{7}\) ਹੈ ।
(j) \(\frac{18}{23}\)
ਹੱਲ:
ਭਿੰਨ \(\frac{18}{23}\) ਨਿਊਨਤਮ ਰੂਪ ਵਿਚ ਹੈ ਜਾਂ ਨਹੀਂ, ਇਹ ਪਤਾ ਕਰਨ ਲਈ ਅਸੀਂ ਭਿੰਨ ਦੇ ਅੰਸ਼ 18 ਅਤੇ ਹਰ 23 ਦਾ ਮ.ਸ.ਵ. ਪਤਾ ਕਰਾਂਗੇ । 18 ਅਤੇ 23 ਦਾ ਮ.ਸ.ਵ. = 1
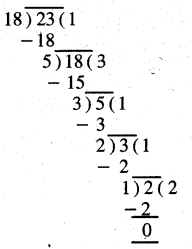
ਇਸ ਲਈ ਭਿੰਨ \(\frac{18}{23}\) ਨਿਊਨਤਮ ਰੂਪ ਵਿਚ ਹੈ ।
ਪ੍ਰਸ਼ਨ 2.
ਹੇਠਾਂ ਦਿੱਤੀਆਂ ਭਿੰਨਾਂ ਦਾ ਨਿਊਨਤਮ ਰੂਪ ਲਿਖੋ:
(a) \(\frac{4}{8}\)
ਹੱਲ:
4 ਅਤੇ 8 ਦਾ ਮ.ਸ.ਵ. 4 ਹੈ ।
ਇਸ ਲਈ \(\frac{4}{8}\) ਦਾ ਨਿਊਨਤਮ ਰੂਪ = \(\frac{4 \div 4}{8 \div 4}\)
= \(\frac{1}{3}\)
(b) \(\frac{12}{18}\)
ਹੱਲ:
12 ਅਤੇ 18 ਦਾ ਮ.ਸ.ਵ. 6 ਹੈ ।
ਇਸ ਲਈ \(\frac{12}{18}\) ਦਾ ਨਿਊਨਤਮ ਰੂਪ =
\(\frac{12 \div 6}{18 \div 6}\) = \(\frac{2}{3}\)
(c) \(\frac{15}{20}\)
ਹੱਲ:
15 ਅਤੇ 20 ਦਾ ਮ.ਸ.ਵ. = 5
ਇਸ ਲਈ \(\frac{15}{20}\) ਦਾ ਨਿਊਨਤਮ ਰੂਪ = \(\frac{15 \div 5}{20 \div 5}\) = \(\frac{3}{4}\)
(d) \(\frac{35}{45}\)
ਹੱਲ:
35 ਅਤੇ 45 ਦਾ ਮ.ਸ.ਵ. = 5
ਇਸ ਲਈ \(\frac{35}{45}\) ਦਾ ਨਿਊਨਤਮ ਰੂਪ = \(\frac{35 \div 5}{45 \div 5}\) = \(\frac{7}{9}\)
(e) \(\frac{24}{36}\)
ਹੱਲ:
24 ਅਤੇ 36 ਦਾ ਮ.ਸ.ਵ. = 12
ਇਸ ਲਈ \(\frac{24}{36}\) ਦਾ ਨਿਊਨਤਮ ਰੂਪ = \(\frac{24 \div 12}{36 \div 12}\) = \(\frac{2}{3}\)
(f) \(\frac{8}{12}\)
ਹੱਲ:
8 ਅਤੇ 12 ਦਾ ਮ.ਸ.ਵ. = 4 .
ਇਸ ਲਈ \(\frac{8}{12}\) ਦਾ ਨਿਊਨਤਮ ਰੂਪ = \(\frac{8 \div 4}{12 \div 4}\) = \(\frac{2}{3}\)
(g) \(\frac{18}{21}\)
ਹੱਲ:
18 ਅਤੇ 21 ਦਾ ਮ.ਸ.ਵ. = 3
ਇਸ ਲਈ \(\frac{18}{21}\) ਹੈ ਦਾ ਨਿਊਨਤਮ ਰੂਪ = \(\frac{18 \div 3}{21 \div 3}\) = \(\frac{6}{7}\)
(h) \(\frac{25}{45}\)
ਹੱਲ:
25 ਅਤੇ 45 ਦਾ ਮ.ਸ.ਵ. = 5
ਇਸ ਲਈ \(\frac{25}{45}\) ਦਾ ਨਿਊਨਤਮ ਰੂਪ = \(\frac{25 \div 5}{45 \div 5}\) = \(\frac{5}{9}\)
![]()
(i) \(\frac{6}{12}\)
ਹੱਲ:
6 ਅਤੇ 12 ਦਾ ਮ.ਸ.ਵ. = 6
ਇਸ ਲਈ \(\frac{6}{12}\) ਦਾ ਨਿਊਨਤਮ ਰੂਪ = \(\frac{6 \div 6}{12 \div 6}\) = \(\frac{1}{2}\)
(j) \(\frac{9}{27}\)
ਹੱਲ :
9 ਅਤੇ 27 ਦਾ ਮ.ਸ.ਵ. = 9
ਇਸ ਲਈ \(\frac{9}{27}\) ਦਾ ਨਿਊਨਤਮ ਰੂਪ = \(\frac{9 \div 9}{27 \div 9}\) = \(\frac{1}{3}\)
ਯਾਦ ਰੱਖੋ:-
- ਜਿਸ ਭਿੰਨ ਦਾ ਅੰਸ਼, ਹਰ ਨਾਲੋਂ ਛੋਟਾ ਹੁੰਦਾ ਹੈ, ਉਹ ਉੱਚਿਤ ਭਿੰਨ ਅਖਵਾਉਂਦੀ ਹੈ । ਜਿਵੇਂ \(\frac{3}{5}\), \(\frac{7}{9}\), \(\frac{14}{17}\) ਕਿਤ ਤਿੰਨਾਂ ਹਨ ।
- ਜਿਸ ਭਿੰਨ ਦਾ ਅੰਸ਼, ਹਰ ਨਾਲੋਂ ਵੱਡਾ ਹੁੰਦਾ ਹੈ, ਉਹ ਅਣਉੱਚਿਤ ਭਿੰਨ ਅਖਵਾਉਂਦੀ ਹੈ ।
ਜਿਵੇਂ \(\frac{8}{5}\), \(\frac{13}{8}\), \(\frac{24}{13}\) ਅਣਉੱਚਿਤ ਤਿੰਨਾਂ ਹਨ ।
