PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.4

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 3 Matrices Ex 3.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 3 Matrices Ex 3.4

Direction (1 – 17) Using elementary transformations, find the inverse of each of the matrices.

Question 1.
$\left[\begin{array}{cc} 1 & -1 \\ 2 & 3 \end{array}\right]$
Solution.
Let A = $\left[\begin{array}{cc} 1 & -1 \\ 2 & 3 \end{array}\right]$
We know that A = IA

Question 2.
$\left[\begin{array}{ll} 2 & 1 \\ 1 & 1 \end{array}\right]$
Solution.
Let A = $\left[\begin{array}{ll} 2 & 1 \\ 1 & 1 \end{array}\right]$

We know that A = IA

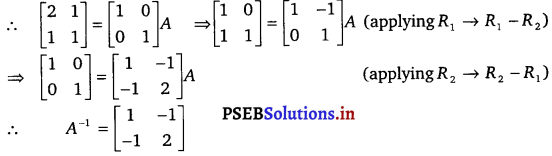
Question 3.
$\left[\begin{array}{ll} 1 & 3 \\ 2 & 7 \end{array}\right]$
Solution.
Let A = $\left[\begin{array}{ll} 1 & 3 \\ 2 & 7 \end{array}\right]$
We know that A = IA

Question 4.
$\left[\begin{array}{ll} 2 & 3 \\ 5 & 7 \end{array}\right]$
Solution.
Let A = $\left[\begin{array}{ll} 2 & 3 \\ 5 & 7 \end{array}\right]$
We know that A = IA

Question 5.
$\left[\begin{array}{ll} 2 & 1 \\ 7 & 4 \end{array}\right]$
Solution.
$\left[\begin{array}{ll} 2 & 1 \\ 7 & 4 \end{array}\right]$
We know that A = IA

Question 6.
$\left[\begin{array}{ll} 2 & 5 \\ 1 & 3 \end{array}\right]$
Solution.
Let A = \left[ $$\begin{array}{ll} 2 & 5 \\ 1 & 3 \end{array}$$ \right]
We know that A = IA

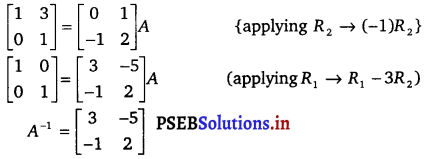
Question 7.
$\left[\begin{array}{ll} \mathbf{3} & 1 \\ 5 & 2 \end{array}\right]$
Solution.
Let A = $\left[\begin{array}{ll} \mathbf{3} & 1 \\ 5 & 2 \end{array}\right]$

We know that A = IA

Question 8.
$\left[\begin{array}{ll} 4 & 5 \\ 3 & 4 \end{array}\right]$
Solution.
Let A = $\left[\begin{array}{ll} 4 & 5 \\ 3 & 4 \end{array}\right]$
We know that A = IA

Question 9.
$\left[\begin{array}{cc} 3 & 10 \\ 2 & 7 \end{array}\right]$
Solution.
Let A = $\left[\begin{array}{cc} 3 & 10 \\ 2 & 7 \end{array}\right]$
We know that A = IA

Question 10.
$\left[\begin{array}{cc} 3 & -1 \\ -4 & 2 \end{array}\right]$
Solution.
$\left[\begin{array}{cc} 3 & -1 \\ -4 & 2 \end{array}\right]$
We know that A = IA.

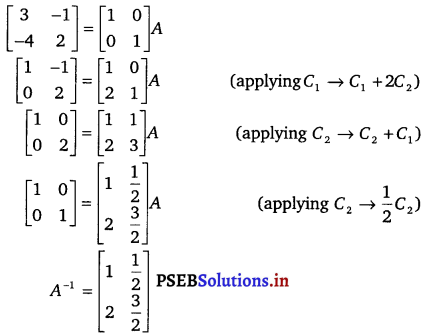
Question 11.
$\left[\begin{array}{rr} 2 & -6 \\ 1 & -2 \end{array}\right]$
Solution.
Let A = $\left[\begin{array}{rr} 2 & -6 \\ 1 & -2 \end{array}\right]$
We know that A = IA.

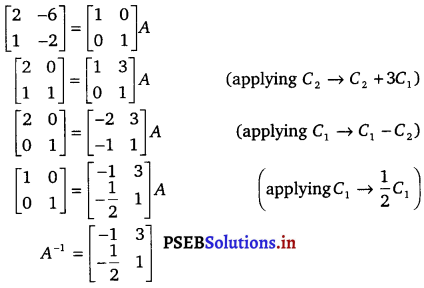
Question 12.
$\left[\begin{array}{cc} 6 & -3 \\ -2 & 1 \end{array}\right]$
Solution.
Let A = $\left[\begin{array}{cc} 6 & -3 \\ -2 & 1 \end{array}\right]$
We know that A = IA.

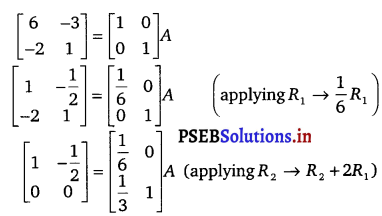
Now, in the above equation, we can see all the zeroes in the second law of the matrix on the L.H.S.
Threrefore, A^-1 does not exist.

Question 13.
$\left[\begin{array}{cc} \mathbf{2} & -\mathbf{3} \\ -1 & 2 \end{array}\right]$
Solution.
Let A = $\left[\begin{array}{cc} \mathbf{2} & -\mathbf{3} \\ -1 & 2 \end{array}\right]$

We know that A = IA.

⇒ $\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right]=\left[\begin{array}{ll} 2 & 3 \\ 1 & 2 \end{array}\right] A$ (applying R₁ → R₁ + R₂)

∴ A^-1 = $\left[\begin{array}{ll} 2 & 3 \\ 1 & 2 \end{array}\right]$

Question 14.
$\left[\begin{array}{ll} 2 & 1 \\ 4 & 2 \end{array}\right]$
Solution.
Let A = $\left[\begin{array}{ll} 2 & 1 \\ 4 & 2 \end{array}\right]$
We know that A = IA
∴ $\left[\begin{array}{ll} 2 & 1 \\ 4 & 2 \end{array}\right]=\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right] A$

Applying R₁ → R₁ – $\frac{1}{2}$ R₂, we have
$\left[\begin{array}{ll} 0 & 0 \\ 4 & 2 \end{array}\right]=\left[\begin{array}{rr} 1 & -\frac{1}{2} \\ 0 & 1 \end{array}\right] A$

Now, in the above equation, we can see all the zeroes in the first row of the matrix on the L.H.S.
Therefore, A^-1 does not exist.

Question 15.
$\left[\begin{array}{rrr} 2 & -3 & 3 \\ 2 & 2 & 3 \\ 3 & -2 & 2 \end{array}\right]$
Solution.
let A = $\left[\begin{array}{rrr} 2 & -3 & 3 \\ 2 & 2 & 3 \\ 3 & -2 & 2 \end{array}\right]$
We know that A = IA

Question 16.
$\left[\begin{array}{ccc} 1 & 3 & -2 \\ -3 & 0 & -5 \\ 2 & 5 & 0 \end{array}\right]$
Solution.
Let A = $\left[\begin{array}{ccc} 1 & 3 & -2 \\ -3 & 0 & -5 \\ 2 & 5 & 0 \end{array}\right]$
We know that A = IA

Question 17.
$\left[\begin{array}{ccc} 2 & 0 & -1 \\ 5 & 1 & 0 \\ 0 & 1 & 3 \end{array}\right]$
Solution.
Let A = $\left[\begin{array}{ccc} 2 & 0 & -1 \\ 5 & 1 & 0 \\ 0 & 1 & 3 \end{array}\right]$
We know that A = IA

Question 18.
Matrices A and B will be inverse of each other only if
(A) AB = BA
(B) AB = BA = 0
(C) AB = 0,BA = I
(D) AB = BA = I
Solution.
We know that if A is a square matrix of order m, and if there exists another square matrix B of the same order m, such that AB = BA = I, then B is said to be the inverse of A.
In this case, it is clear that A is the inverse of B.
Thus, matrices A and B will be inverse of each other only if AB = BA = I. Hence, the correct answer is (D).