Punjab State Board PSEB 12th Class Maths Book Solutions Chapter Differential Equations Ex 9.3 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 12 Maths Chapter 9 Differential Equations Ex 9.3
Direction (1 – 5): In each question form a differential equation representing the given family of curves by eliminating arbitrary constants a and b.
Question 1.
\(\frac{x}{a}+\frac{y}{b}\) = 1
Solution.
Given, family is \(\frac{x}{a}+\frac{y}{b}\) = 1
Differentiating both sides w.r.t. x, we get
\(\frac{1}{a}+\frac{1}{b} \frac{d y}{d x}\) = 0
⇒ \(\frac{1}{a}+\frac{1}{b} y\) = 0
Again, differentiating both sides w.r.t. x, we get
0 + \(\frac{1}{4}\) y” = 0
⇒ \(\frac{4}{4}\) y” = 0
⇒ y” = 0
Hence, the required differential equation of the given curve is y” = 0.
Question 2.
y2 = a(b2 – x2)
Sol.
Given, family is y2 = a(b2 —x2)
Differentiating both sides w.r.t. x, we get
2y \(\frac{d y}{d x}\) = a(- 2x)
2yy’ = – 2ax
yy’= – ax ……………(i)
Again, differentiating both sides w.r.t. x, we get
y’ . y’ + yy” = – a
= (y’)2 + yy” = – a ……………(ii)
Dividing equation (ii) by equation (i), we get
\(\frac{\left(y^{\prime}\right)^{2}+y y^{\prime \prime}}{y y^{\prime}}=\frac{-a}{-a x}\)
⇒ xyy” + x (y’)2 – yy” = 0
This is the required differential equation of the given curve.
![]()
Question 3.
y = ae3x + be– 2x
Solution.
Given, family is y = ae3x + be– 2x ………………(i)
Differentiating both sides w.r.t. x, we get
y’ = 3ae3x – 2 be– 2x ………….(ii)
Again, differentiating both sides w.r.t. x, we get
⇒ y” = 9ae3x + 4 be– 2x …………….(iii)
Multiplying equation (i) with equation (ii) and then adding it from equation (ii), we get
(2ae3x + 2be– 2x) + (3ae3x – 2 be– 2x) = 2y + y’
⇒ 5ae3x = 2y + y’
⇒ ae3x = \(\frac{2 y+y^{\prime}}{5}\)
Now, multiplying equation (i) with equation (iii) and subtracting equation (ii) for, it, we get
(3ae3x + 3be– 2x) – (3ae3x – 2be– 2x) = 3y – y’
⇒ 5be– 2x = 3y – y’
⇒ be– 2x = \(\frac{3 y-y^{\prime}}{5}\)
Substituting the values of ae3x and be– 2x in equation (iii), we get
y” = \(9 \cdot \frac{\left(2 y+y^{\prime}\right)}{5}+4 \frac{\left(3 y-y^{\prime}\right)}{5}\)
⇒ y” = \(\frac{18 y+9 y^{\prime}}{5}+\frac{12 y-4 y^{\prime}}{5}\)
⇒ y” = \(\frac{30 y+5 y^{\prime}}{5}\)
⇒ y” = 6y + y’
⇒ y” – y’ – 6y = 0
This is the required differential equation of the given curve.
![]()
Question 4.
y = e2x (a + bx)
Solution.
Given, y = e2x (a + bx) ………….(i)
Differentiating both sides w.r.t. x, we get
y’ = 2e2x (a + bx) + e2x . b
⇒ y’ = e2x (2a + 2 bx + b) ……………(ii)
Multiplying equation (i) with equation (ii) and then subtracting it from equation (ii), we get
y’ – 2y = e2x (2a + 2bx + b) – e2xx (2a + 2bx)
⇒ y’ – 2 = be2x ……………..(iii)
Differentiating both sides w.r.t. x, we get
y”k – 2y’ = 2be2x …………..(iv)
Dividing equation (iv) by equation (iii), we get
\(\frac{y^{\prime \prime}-2 y^{\prime}}{y^{\prime}-2 y}\) = 2
⇒ y” – 2y’ = 2y’ – 4y
⇒ y” – 4y’ + 4y = 0
This is the required differential equation of the given curve.
Question 5.
y = ex (a cos x + b sin x)
Solution.
Given, y = ex (a cos x + b sin x) …………..(i)
Differentiating both sides w.r.t. x, we get
y’ = ex (a cos x + b sin x) + ex (- a sin x + b cos x)
=> y’ = ex [(a + b) cos x – (a – b) sin x] ……………(ii)
Again, differentiating both sides w.r.t. x, We get
y” = ex [(a + b) cos x) – (a – b) sin x] + ex [- (a + b) sin x – (a – b) cos x]
y” = ex (2 b cos x – 2a sin x)
⇒ y” = 2 ex (b cos x – a sin x)
Adding equations (i) and (iii), we get
y + \(\frac{y^{\prime \prime}}{2}\) = ex [(a + b) cos x – (a – b) sin x]
⇒ y + \(\frac{y^{\prime \prime}}{2}\) = y’
⇒ 2y + y” = 2y
⇒ y” – 2y’ + 2y = 0
This is the required differential equation of the given curve.
![]()
Question 6.
Form the differential equation of the family of circles touching the y-axis at the origin.
Solution.
The equation of the circle with centre (a, 0) and radius a, which touches y-axis at origin
(x – a)2 + y2 = a2
x2 + y2 = 2ax ………….(i)
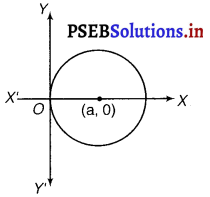
Differentiating equation w.r.t x
2x + 2y y’ = 2a
or x + y y’ = a
Put value of a in (i)
x2 + y2 = 2x (x + y y’)
= 2x2 + 2xy y’
∴ Required differential equation is
2xy \(\frac{d y}{d x}\) + x2 – y2 = 0
Question 7.
Form the differential equation of the family of parabolas having vertex at origin and axis along positive y-axis.
Solution.
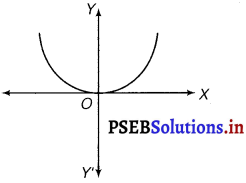
The equation of the parabola having the vertex at origin and the axis along the positive y-axis is
x2 = 4ay ………..(i)
Differentiating equation (i) w.r.t. x, we get 2x = 4ay’ ………….(ii)
Dividing equation (ii) by equation (i), wex
\(\frac{2 x}{x^{2}}=\frac{4 a y^{\prime}}{4 a y}\)
⇒ \(\frac{2}{x}=\frac{y^{\prime}}{y}\)
⇒ xy’ = 2y
⇒ xy’ – 2y = 0
This is the required differential equation.
![]()
Question 8.
Form the differential equation of the family of ellipse having foci on y-is and centre at origin.
Solution.
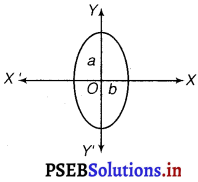
The equation of the family of ellipse having foci on they-axis and the centre at origin is as follows:
\(\frac{x^{2}}{b^{2}}+\frac{y^{2}}{a^{2}}\) = 1 …………….(i)
Differentiating equation (i) w.r.t. x, we get
\(\frac{2 x}{b^{2}}+\frac{2 y y^{\prime}}{a^{2}}\) = 0
⇒ \(\frac{x}{b^{2}}+\frac{y y^{\prime}}{a^{2}}\) = 0 …………..(ii)
Again, differentiating w.r.t. x, we get
\(\frac{1}{b^{2}}+\frac{y^{\prime} \cdot y^{\prime}+y \cdot y^{\prime \prime}}{a^{2}}\) = 0
⇒ \(\frac{1}{b^{2}}+\frac{1}{a^{2}}\left(y^{\prime 2}+y y^{\prime \prime}\right)\) = 0
⇒ \(\frac{1}{b^{2}}=-\frac{1}{a^{2}}\left(y^{2}+y y^{\prime \prime}\right)\)
x \(\left[-\frac{1}{a^{2}}\left(\left(y^{\prime}\right)^{2}+y y^{\prime \prime}\right)\right]+\frac{y y^{\prime}}{a^{2}}\) = 0
⇒ – x (y’)2 – xyy” + yy’ = 0
⇒ xyy’ + x(y’)2 – yy’ = 0
This is the required differential equation.
![]()
Question 9.
Form the differential equation of the family of hyperbolas having foci on x-axis and centre at origin.
Solution.
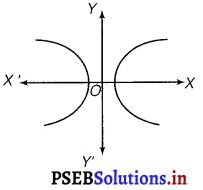
The equation of the family of hyperbolas with the centre at origin and foci along the x-axis is
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 ………………(i)
Differentiating both sides of equation (j) w.r.t. x, we get
\(\frac{2 x}{a^{2}}-\frac{2 y y^{\prime}}{b^{2}}\) = 0
\(\frac{x}{a^{2}}-\frac{y y^{\prime}}{b^{2}}\) = 0 …………….(ii)
Again, differentiating w.r.t. x, we get
\(\frac{1}{a^{2}}-\frac{y^{\prime} \cdot y^{\prime}+y y^{\prime \prime}}{b^{2}}\) = 0
\(\frac{1}{a^{2}}=\frac{1}{b^{2}}\left(\left(y^{\prime}\right)^{2}+y y^{\prime \prime}\right)\)
Substituting the value of in equation (ii), we get
\(\left.\frac{x}{b^{2}}\left(y^{\prime}\right)^{2}+y y^{\prime \prime}\right)-\frac{y y^{\prime}}{b^{2}}\) = 0
⇒ x (y’)2 + xyy” – yy’ = 0
⇒ xyy” + x(y’)2 – yy’ = 0
This is the required differential equation.
Question 10.
Form the differential equation of the family of circles having centre on y-axis and radius 3 units.
Solution.
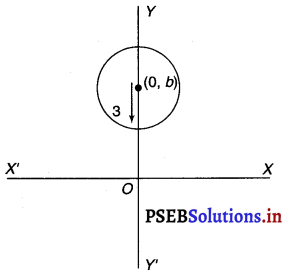
Let the centre of the circle on y-axis be (0, b).
The differential equation of the family of Circles with centre at (0, b) and radius 3 is as follows
x2 + (y – b)2 = 32
⇒ x2 + (y – b)2 = 9 ……………(i)
Differentiating equation (i) w.r.t. x,
2x + 2(y – b) . y’ = 0
⇒ (y – b) . y’ = – x
⇒ y – b = \(\)
Substituting the value of (y – b) in equation (i), we get
x2 + \(\left(\frac{-x}{y^{\prime}}\right)^{2}\) = 9
⇒ x2 \(\left[1+\frac{1}{\left(y^{\prime}\right)^{2}}\right]\) = 9
⇒ x2 ((y’)2 + 1) = 9 (y’)x2
⇒ (x2 – 9) (y’)2 + x2 = 0
This is the required differential equation.
![]()
Question 11.
Which of the following differential equations has y = c1 ex + c2 ex as the general solution?
(A) \(\frac{d^{2} y}{d x^{2}}\) + y = 0
(B) \(\frac{d^{2} y}{d x^{2}}\) – y = 0
(C) \(\frac{d^{2} y}{d x^{2}}\) + 1 = 0
(D) \(\frac{d^{2} y}{d x^{2}}\) – 1 = 0
Solution.
Given general solution is y = c1 ex + c2 e-x
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = c1 ex – c2 e-x
Again, differentiating w.r.t. x, we get
\(\frac{d^{2} y}{d x^{2}}\) = c1 ex + c2 e-x
⇒ \(\frac{d^{2} y}{d x^{2}}\) = y
⇒ \(\frac{d^{2} y}{d x^{2}}\) – y = 0
This is the required differential equation of the given equation of curve.
Hence, the correct answer is (B).
![]()
Question 12.
Which of the following differential equations has y = z as one of its particular solution?
(A) \(\frac{d^{2} y}{d x^{2}}-x^{2} \frac{d y}{d x}\) + xy = x
(B) \(\frac{d^{2} y}{d x^{2}}+x \frac{d y}{d x}\) + xy = x
(C) \(\frac{d^{2} y}{d x^{2}}-x^{2} \frac{d y}{d x}\) + xy = 0
(D) \(\frac{d^{2} y}{d x^{2}}+x \frac{d y}{d x}\) + xy = 0
Solution.
Given solution is y = x
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = 1 ……………….(i)
Again, differentiating w.r.t x, we get
\(\frac{d^{2} y}{d x^{2}\) = 0 ………………..(ii)
Now, on substituting the value of y, \(\frac{d^{2} y}{d x^{2}}\) and \(\frac{d y}{d x}\) from equation (i) and (ii) in each of the given alternatives, we find that only the differential
equation given in alternative C is correct.
\(\frac{d^{2} y}{d x^{2}}\) – x2 \(\frac{d y}{d x}\) + xy = 0 – x2 . 1 + x . x
= – x2 + x2 = 0
Hence, the correct answer is (C).
