Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 12 ਬੀਜਗਣਿਤਕ ਵਿਅੰਜਕ Ex 12.2 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 7 Maths Chapter 12 ਬੀਜਗਣਿਤਕ ਵਿਅੰਜਕ Exercise 12.2
ਪ੍ਰਸ਼ਨ 1.
ਖਾਲੀ ਥਾਂਵਾਂ ਭਰੋ :
(i) 5y + 7y = …………
(ii) 3xy + 2xy = ……….
(iii) 12a2 – 7a2 = ……
(iv) 8mn2 – 3mn2 = …………
ਹੱਲ:
(i) 12y
(ii) 5xy
(iii) 5a2
(iv) 5mn2
2. ਹੇਠ ਲਿਖੇ ਬੀਜਗਣਿਤਕ ਵਿਅੰਜਕਾਂ ਨੂੰ ਜੋੜੋ :
ਪ੍ਰਸ਼ਨ (a).
3xy2, 7xy2
ਉੱਤਰ:
ਦਿੱਤੇ ਹੋਏ ਪਦ ਸਮਾਨ ਪਦ ਹਨ । ਇਨ੍ਹਾਂ ਦੇ ਸੰਖਿਆਤਮਕ ਗੁਣਾਂਕ 3 ਅਤੇ 7 ਹਨ ।
ਲੋੜੀਂਦਾ ਜੋੜ ਹੇਠਾਂ ਦਿੱਤੇ ਅਨੁਸਾਰ ਹੈ :
3xy2 + 7xy2 = (3 + 7) xy2
= 10xy2
ਪ੍ਰਸ਼ਨ (b).
7x, – 3x, 2x
ਉੱਤਰ:
7x + (- 3x) + 2x = (7 – 3 + 2)x
= 6x
![]()
ਪ੍ਰਸ਼ਨ (c).
12p2q, 3p2q, -5p2q
ਉੱਤਰ:
(12p2q) + (3p2q) +(-5p2q)
= (12 + 3 – 5) pq
= 10p2q
ਪ੍ਰਸ਼ਨ (d).
3x2, -8x2, -5x2, 13x2
ਉੱਤਰ:
3x2 +(-8x2 + (-5x)2 + 13x2
= (3 – 8 – 5 + 13) x2
= 3x2
3. ਹੇਠ ਲਿਖੇ ਬੀਜਗਣਿਤਕ ਵਿਅੰਜਕਾਂ ਨੂੰ ਜੋੜੋ :
ਪ੍ਰਸ਼ਨ (a).
x + y ਅਤੇ 2x – 3y
ਉੱਤਰ:
ਖਤਿਜੀ ਵਿਧੀ
(x + y) + (2x – 3y)
= x + 2x + y – 3y
= 3x – 2y
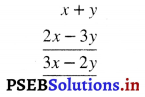
![]()
ਪ੍ਰਸ਼ਨ (b).
5a + 7b ਅਤੇ 3a – 2b
ਉੱਤਰ:
ਖਤਿਜੀ ਵਿਧੀ (5a + 7b) + (3a – 2b)
= 5a + 3a + 7a – 2b
= 8a + 5b
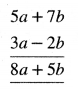
ਪ੍ਰਸ਼ਨ (c).
3m + 2n, 7m – 8n, 2m – n ॥
ਉੱਤਰ:
ਖਤਿਜੀ ਵਿਧੀ
(3m + 2n) + (7m – 8n) + (2m – n)
= 3m + 7m + 2m + 2n – 8n – n
= 12m – 7n
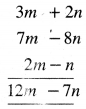
ਪ੍ਰਸ਼ਨ (d).
3x2 + 2x – 7 ਅਤੇ 5x2 – 7x + 8
ਉੱਤਰ:
ਖਤਿਜੀ ਵਿਧੀ
(3x2 + 2x – 7) + (5x2 – 7x + 8)
= 3x2 + 5x2 + 2x – 7x – 7 + 8
= 8x2 – 3x + 1

![]()
ਪ੍ਰਸ਼ਨ (e).
m2 + 2n2 – 2, -3m2 + 2 + 2p2 ਅਤੇ 4m2 – 3n2 + 5p2
ਉੱਤਰ:
ਖਤਿਜੀ ਵਿਧੀ
(m2 + 2n2 – p2) + (-3m2 + n2 + 2p2) + (4m2 – 3n2 + 5p2)
= m2 – 3m2 + 4m2 + 2n2 + n2 – 3n2 – p2 + 2p2 + 5p2
= 2m2 + on2 + 6p2
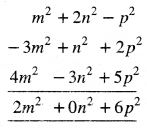
ਪ੍ਰਸ਼ਨ (f).
3xy + 7x2 – 2y2, 2xy + y2 ਅਤੇ 2x2 + y2
ਉੱਤਰ:
ਕਾਲਮ ਵਿਧੀ
(3xy + 7x2 – 2y2) + (2xy + y2) + (2x2 + y2)
= 3xy + 2xy + 7x2 + 2x2 – 2y2 + y2 + y2
= 5xy + 9x2 + 0y2
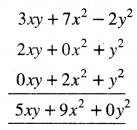
4. ਸਮਾਨ ਪਦਾਂ ਨੂੰ ਇਕੱਠੇ ਕਰ ਕੇ ਹੇਠ ਲਿਖੇ ਬੀਜਗਣਿਤਕ ਵਿਅੰਜਕਾਂ ਨੂੰ ਹੱਲ ਕਰੋ :
ਪ੍ਰਸ਼ਨ (a).
– 5ax + 3xy + 2xy – 8ax
ਉੱਤਰ:
-5ax + 3xy + 2xy – 8ax
= – 5a – 8ax + 3x + 2xy
= – 13ax + 5xy
![]()
ਪ੍ਰਸ਼ਨ (b).
3m – 2n + 5m – 3m + 8n
ਉੱਤਰ:
3m – 2n + 5m – 3m + 8n
= 3m + 5m – 3m – 2n + 8n
= 5m + 6n
ਪ੍ਰਸ਼ਨ (c).
3pq – 15r2 – 3l2m2 + 2r2 + 2l2m2 – 5pq
ਉੱਤਰ:
3pq – 15r2 – 3l2m2 + 2r2 + 2l2m2 – 5pq
= 3pq – 5pq – 15r2 + 2r2 – 3l2m2 + 2l2m2
= -2pq – 13r2 – 2l2m2
ਪ੍ਰਸ਼ਨ (d).
4x3 + 7x2 – 3x + 2 – 2x3 – 2x2 + 7x – 3
ਉੱਤਰ:
4x3 + 7x2 – 3x + 2 – 2x3 – 2x2 + 7x – 3 = 4x3 – 2x3 + 7x2 – 2x2 – 3x + 7x + 2 – 3
= 2x3 + 5x2 + 4x – 1
![]()
5. ਬੀਜਗਣਿਤਕ ਵਿਅੰਜਕਾਂ ਨੂੰ ਘਟਾਓ :
ਪ੍ਰਸ਼ਨ (a).
3x2 ਨੂੰ 7x2 ਵਿੱਚੋਂ ।
ਉੱਤਰ:
7x2 – 3x2 = 4x2
ਪ੍ਰਸ਼ਨ (b).
– 3ab ਨੂੰ 10ab ਵਿੱਚੋਂ ।
ਉੱਤਰ:
10ab – (-3ab) = 10ab + 3ab = 13ab
ਪ੍ਰਸ਼ਨ (c).
a + b ਨੂੰ a – b ਵਿੱਚੋਂ ।
ਉੱਤਰ:
(a – b) – (a + b) = a – b – d – b = -2b
![]()
ਪ੍ਰਸ਼ਨ (d).
15m + 10n ਨੂੰ 2m – 16n ਵਿੱਚੋਂ ।
ਉੱਤਰ:
2m – 16n – (15m + 10n) = 2m – 15m – 16n – 10n
= – 13m – 26n
ਪ੍ਰਸ਼ਨ (e).
2x + 8y – 3z ਨੂੰ – 3x + 2y + 1 ਵਿੱਚੋਂ ।
ਉੱਤਰ:
-3x + 2y + z – (2x + 8y – 3z)
= -3x + 2y + z – 2x – 8y + 3z
= – 5x – 6y + 4z
ਪ੍ਰਸ਼ਨ (f).
18m2 + 3n2 – 2mn – 7 ਨੂੰ 3m2 – 2n2 + 8mn – 8m + 4 ਵਿੱਚੋਂ ।
ਉੱਤਰ:
(3m2 – 2n2 + 8mn – 8m + 4) – (18m2 + 3n2 – 2mm – 7)
= 3m2 – 2n2 + 8mn – 8m + 4 – 18m2 – 3n2 + 2mm + 7
= 3m2 – 18m2 – 2n22 – 3n2 + 8mn + 2mn – 8m + 4 + 7.
= -15m2 – 5n2 + 10mn – 8m + 11
![]()
ਪ੍ਰਸ਼ਨ 6.
l – 2m + 5n ਵਿੱਚੋਂ ਕੀ ਘਟਾਈਏ ਕਿ 2l – 3m + 4n ਪ੍ਰਾਪਤ ਹੋਵੇ ?
ਹੱਲ:
ਲੋੜੀਂਦਾ ਵਿਅੰਜਕ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਅਸੀਂ 2l – 3m + 4n ਨੂੰ l – 2m + 5n ਵਿੱਚੋਂ ਘਟਾਉਂਦੇ ਹਾਂ, ਲੋੜੀਦੀ ਵਿਅੰਜਕ
= (l – 2m + 5n) – (2l – 3m + 4n)
= l – 2l – 2m + 3m + 5n – 4n
= -l + m + n.
ਲੋੜੀਂਦੀ ਵਿਅੰਜਕ -l + m + n ਹੈ ।
ਪ੍ਰਸ਼ਨ 7.
3x2 + 2xy – y2 ਵਿੱਚ ਕੀ ਜੋੜੀਏ ਕਿ x22 – 7xy + 3y2 ਪ੍ਰਾਪਤ ਹੋਵੇ ?
ਹੱਲ:
ਲੋੜੀਂਦਾ ਵਿਅੰਜਕ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਅਸੀਂ 3x2 + 2xy – y2 ਨੂੰ x2 – 7xy + 3y2 ਵਿਚੋਂ ਘਟਾਉਂਦੇ
ਹਾਂ ਲੋੜੀਂਦੀ ਵਿਅੰਜਕ = (x2 – 7xy + 3y2) – (3x2 + 2xy – y2)
= x2 – 3x2 – 7xy – 2xy + 3y2 + y2
= -2x2 – 9xy + 4y2
![]()
ਪ੍ਰਸ਼ਨ 8.
3a2 + 2b2 – 8ab + 8 ਨੂੰ a2 – b2 + 7ab + 3 ਅਤੇ 2a2 + 4b2 – 18ab + 7 ਦੇ ਜੋੜਫਲ ਵਿੱਚੋਂ ਘਟਾਓ ।
ਹੱਲ:
ਪਹਿਲਾ ਜੋੜ : a2 – b2 + 7ab + 3 ਅਤੇ 2a2 + 4b2 – 18ab + 7 ਨੂੰ ਜੋੜੋ ।
(a2 – b2 + 7ab + 3) + (2a2 + 4b2 – 18ab + 7)
= a2 + 2a2 – b2 + 4b2 + 7ab – 18ab + 3 + 7
= 3a2 + 3b2 – 11ab + 10 . ….(1)
ਹੁਣ ਅਸੀਂ 3a2 + 2b2 – 8ab + 8 ਨੂੰ (1) ਵਿਚੋਂ ਘਟਾਉਂਦੇ ਹਾਂ।
3a2 + 3b2 – 11ab + 10 – (3a2 + 2b2 – 8ab + 8)
= 3a2 – 3a2 + 3b2 – 2b2 – 11ab + 8ab + 10 – 8
= 0a2 + b2 – 3ab + 2
= b2 – 3ab + 2
ਪ੍ਰਸ਼ਨ 9.
x2 + 3xy + y2, 2x2 + 5xy – y2 ਨਾਲੋਂ ਕਿੰਨਾ ਘੱਟ ਹੈ ?
ਹੱਲ:
(2x2 + 5xy – y2) – (x2 + 3xy + y2)
= 2x2 – x2 + 5xy – 3xy – y2 – y2
= x2 + 2xy – 0y2
ਇਸ ਲਈ x2 + 3xy + y2, 2x2 + 5xy – y2
ਨਾਲੋਂ x2 + 2xy – 2y2 ਘੱਟ ਹੈ ।
![]()
10. ਬਹੁਵਿਕਲਪੀ ਪ੍ਰਸ਼ਨ :
ਪ੍ਰਸ਼ਨ (i).
‘‘ਸੰਖਿਆ 5 ਨੂੰ m ਅਤੇ n ਦੇ ਗੁਣਨਫਲ ਦੇ ਤਿੰਨ ਗੁਣਾ ਵਿੱਚ ਜੋੜਿਆ’’ ਦੇ ਲਈ ਬੀਜਗਣਿਤਕ ਵਿਅੰਜਕ ਹੈ :
(a) 5 + 3mn
(b) 3 + 5mn
(c) (5 + 3) mn
ਉੱਤਰ:
(a) 5 + 3mn
ਪ੍ਰਸ਼ਨ (ii).
ਬੀਜਗਣਿਤਕ ਵਿਅੰਜਕਾਂ 3x + 11 ਅਤੇ 2x – 7 ਦਾ ਜੋੜ ਹੈ :
(a) 5x + 4
(b) x + 4
(c) 5 – 18
ਉੱਤਰ:
(a) 5x + 4
![]()
ਪ੍ਰਸ਼ਨ (iii).
2a + 3b ਵਿੱਚੋਂ a + b ਘਟਾਉਣ ਤੇ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ-
(a) a + 2b
(b) -a – 2b
(c) 3a + 4b
(d) a + b
ਉੱਤਰ:
(a) a + 2b
