PSEB 8th Class Maths Solutions Chapter 11 ਖੇਤਰਮਿਤੀ Ex 11.1

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 11 ਖੇਤਰਮਿਤੀ Ex 11.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 11 ਖੇਤਰਮਿਤੀ Exercise 11.1

ਪ੍ਰਸ਼ਨ 1.
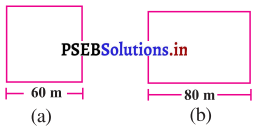
ਜਿਸ ਤਰ੍ਹਾਂ ਕਿ ਨਾਲ ਦਿੱਤੇ ਚਿੱਤਰ ਵਿਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ, ਕਿ ਇਕ ਆਇਤਾਕਾਰ ਅਤੇ ਇਕ ਵਰਗਾਕਾਰ ਖੇਤ ਦੇ ਮਾਪ ਦਿੱਤੇ ਗਏ ਹਨ । ਜੇ ਇਹਨਾਂ ਦੇ ਪਰਿਮਾਪ ਸਮਾਨ ਹੋਣ, ਤਾਂ ਕਿਸ ਖੇਤ ਦਾ ਖੇਤਰਫਲ ਜ਼ਿਆਦਾ ਹੋਵੇਗਾ ?

ਹੱਲ:
ਵਰਗ ਦੀ ਭੁਜਾ = 60 m
ਵਰਗ ਦਾ ਪਰਿਮਾਪ = 4 × ਭੁਜਾ ।
= 4 × 60 = 240 m
ਆਇਤ ਦੀ ਲੰਬਾਈ = 80 m
ਆਇਤ ਦਾ ਪਰਿਮਾ = ਵਰਗ ਦਾ ਪਰਿਮਾਪ
2 (a + b) = 240
2 (80 + b) = 240
160 + 2b = 240
2b = 240 – 160 = 80
⇒ b = 40
∴ ਆਇਤ ਦੀ ਚੌੜਾਈ = 40 m
ਹੁਣ, ਵਰਗ ਦਾ ਖੇਤਰਫਲ = (ਭੁਜਾ)² = (60)²
= 3600 m²
ਆਇਤ ਦਾ ਖੇਤਰਫਲ = a × b.
= 80 × 40 = 3200 m²
∴ ਵਰਗ ਦਾ ਖੇਤਰਫਲ ਜ਼ਿਆਦਾ ਹੋਵੇਗਾ ।

ਪ੍ਰਸ਼ਨ 2.
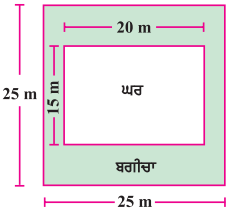
ਸ੍ਰੀਮਤੀ ਕੌਸ਼ਿਕ ਦੇ ਕੋਲ ਚਿੱਤਰ ਵਿਚ ਦਰਸਾਏ ਗਏ ਮਾਪ ਵਾਲਾ ਇੱਕ ਵਰਗਾਕਾਰ ਪਲਾਟ ਹੈ ।ਉਹ ਪਲਾਟ ਦੇ ਵਿਚ ਇਕ ਘਰ ਬਣਾਉਣਾ ਚਾਹੁੰਦੀ ਹੈ । ਘਰ ਦੇ ਚਾਰੇ ਪਾਸੇ ਇਕ ਬਗੀਚੇ ਨੂੰ ਤਿਆਰ ਕੀਤਾ ਗਿਆ ਹੈ । ₹ 55 ਪ੍ਰਤੀ ਵਰਗ ਮੀਟਰ ਦੀ ਦਰ ਨਾਲ ਇਸ ਬਗੀਚੇ ਨੂੰ ਤਿਆਰ ਕਰਨ ਦਾ ਖ਼ਰਚ ਪਤਾ ਕਰੋ ।

ਹੱਲ:
ਵਰਗਾਕਾਰ ਪਲਾਟ ਦੀ ਭੁਜਾ = 25 m
ਵਰਗਾਕਾਰ ਪਲਾਟ ਦਾ ਖੇਤਰਫਲ = (ਭੁਜਾ)²
= (25)² = 25 × 25
= 625 m²
ਘਰ ਦੀ ਲੰਬਾਈ = 20 m
ਘਰ ਦੀ ਚੌੜਾਈ = 15 m
ਘਰ ਦਾ ਖੇਤਰਫਲ = 20 × 15 = 300 m²
∴ ਬਗੀਚੇ ਦਾ ਖੇਤਰਫਲ = ਪਲਾਟ ਦਾ ਖੇਤਰਫਲ – ਘਰ ਦਾ ਖੇਤਰਫਲ
= (625 – 300)m²
= 325 m²
₹ 55 ਪ੍ਰਤੀ ਵਰਗ ਮੀਟਰ ਦੀ ਦਰ ਨਾਲ ਬਗੀਚੇ ਨੂੰ ਤਿਆਰ ਕਰਨ ਦਾ ਖ਼ਰਚ
= ₹ 325 × 55
= ₹ 17875.

ਪ੍ਰਸ਼ਨ 3.
ਜਿਸ ਤਰ੍ਹਾਂ ਕਿ ਚਿੱਤਰ ਵਿੱਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ, ਇਕ ਬਗੀਚੇ ਦਾ ਆਕਾਰ ਮੱਧ ਵਿਚ ਆਇਤਾਕਾਰ ਹੈ ਅਤੇ ਕਿਨਾਰਿਆਂ ਤੋਂ ਅਰਧ ਚੱਕਰ ਦੇ ਰੂਪ ਵਿਚ ਹੈ । ਇਸ ਬਗੀਚੇ ਦਾ ਪਰਿਮਾਪ ਅਤੇ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
[ਆਇਤ ਦੀ ਲੰਬਾਈ = 20 – 3.5 + 3.5) ਮੀਟਰ = 13 ਹੈ I]

ਹੱਲ:
ਅਰਧ ਚੱਕਰਾਕਾਰ ਕਿਨਾਰਿਆਂ ਦਾ ਅਰਧ ਵਿਆਸ = \(\frac{7}{2}\)m
∴ ਆਇਤਾਕਾਰ ਭਾਗ ਦੀ ਲੰਬਾਈ = 20 – (\(\frac{7}{2}\) + \(\frac{7}{2}\))
= (20 – 7) = 13 m
ਆਇਤਾਕਾਰ ਭਾਗ ਦੀ ਚੌੜਾਈ = 7 m
∴ ਬਗੀਚੇ ਦਾ ਖੇਤਰਫਲ = ਆਇਤਾਕਾਰ ਭਾਗ ਦਾ ਖੇਤਰਫਲ + 2 × (ਅਰਧਚੱਕਰ ਦਾ ਖੇਤਰਫਲ)
= (l × b) + 2(\(\frac{1}{2}\)πr²)
= (13 × 7) + πr²
= 91 + \(\frac{22}{7}\) × \(\frac{7}{2}\) × \(\frac{7}{2}\)
= 91 + \(\frac{77}{2}\)
= 91 + 38.5
= 129.5 m²
ਬਗੀਚੇ ਦਾ ਪਰਿਮਾਪ = ਆਇਤਾਕਾਰ ਭਾਗ ਦਾ ਪਰਿਮਾਪ + 2 (ਅਰਧਚੱਕਰ ਦਾ ਪਰਿਮਾਪ)
= 2 (l + b) + 2[\(\frac{1}{2}\)(2πr)]
= 2 (l + b) + 2πr
= 2[13 + 7] + 2 × \(\frac{22}{7}\) × 7
= 40 + 22 = 62 m.

ਪ੍ਰਸ਼ਨ 4.
ਫਰਸ਼ ਬਣਾਉਣ ਦੇ ਲਈ ਉਪਯੋਗ ਕੀਤੀ ਜਾਣ ਵਾਲੀ ਇਕ ਟਾਈਲ ਦਾ ਆਕਾਰ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਦਾ ਹੈ ਜਿਸਦਾ ਅਧਾਰ 24 cm ਅਤੇ ਇਸ ਦੀ ਸੰਗਤ ਉਚਾਈ 10 cm ਹੈ । 1080 ਵਰਗ ਮੀਟਰ ਖੇਤਰਫਲ ਦੇ ਇਕ ਫਰਸ਼ ਨੂੰ ਢੱਕਣ ਦੇ ਲਈ ਇਸ ਤਰ੍ਹਾਂ ਦੀਆਂ ਕਿੰਨੀਆਂ ਟਾਈਲਾਂ ਦੀ ਜ਼ਰੂਰਤ ਹੈ ? ਫਰਸ਼ ਦੀਆਂ ਨੁੱਕਰਾਂ ਨੂੰ ਢੱਕਣ ਦੇ ਲਈ ਤੁਸੀਂ ਟਾਈਲਾਂ ਨੂੰ ਲੋੜ ਅਨੁਸਾਰ ਕਿਸੇ ਵੀ ਰੂਪ ਵਿਚ ਤੋੜ ਸਕਦੇ ਹੋ ?
ਹੱਲ:
ਟਾਈਲ ਦੀ ਲੰਬਾਈ = 24 cm
ਟਾਈਲ ਦੀ ਉੱਚਾਈ = 10 cm
ਇਕ ਟਾਈਲ ਦਾ ਖੇਤਰਫਲ = 24 × 10
= 240 cm²
[∵ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਦਾ ਖੇਤਰਫਲ = ਆਧਾਰ × ਉੱਚਾਈ]
ਫਰਸ਼ ਦਾ ਖੇਤਰਫਲ = 1080 m²
= 1080 × 100 × 100cm²
[∵ 1 m = 100 cm]
∴ ਜ਼ਰੂਰੀ ਟਾਈਲਾਂ ਦੀ ਸੰਖਿਆ ।

= 45000 ਟਾਈਲਾਂ

ਪ੍ਰਸ਼ਨ 5.
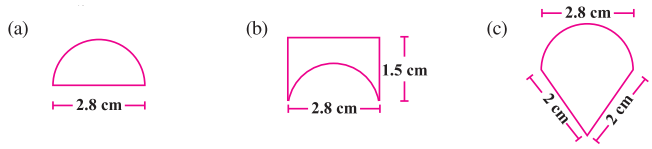
ਇਕ ਕੀੜੀ ਕਿਸੇ ਫਰਸ਼ ‘ਤੇ ਖਿਲਰੇ ਹੋਏ ਵੱਖ-ਵੱਖ ਅਕਾਰਾਂ ਦੇ ਭੋਜਨ ਪਦਾਰਥ ਦੇ ਟੁਕੜਿਆਂ ਦੇ ਚਾਰੇ ਪਾਸੇ ਘੁੰਮ ਰਹੀ ਹੈ । ਭੋਜਨ ਪਦਾਰਥ ਦੇ ਕਿਸੇ ਟੁਕੜੇ ਦੇ ਲਈ ਕੀੜੀ ਨੂੰ ਲੰਬਾ ਚੱਕਰ ਲਗਾਉਣਾ ਪਵੇਗਾ ? ਯਾਦ ਰੱਖੋ, ਚੱਕਰ ਦਾ ਘੇਰਾ, ਸੂਤਰ.C = 2πr ; ਇੱਥੇ 7 ਚੱਕਰ ਦਾ ਅਰਧਵਿਆਸ ਹੈ, ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਪ੍ਰਾਪਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ।

ਹੱਲ:
(a) ਇਸ ਸਥਿਤੀ ਵਿਚ, ਅਕਾਰ 2.8 cm ਵਿਆਸ ਵਾਲਾ ਅਰਧਚੱਕਰ ਹੈ :

ਅਰਧਚੱਕਰ ਦਾ ਵਿਆਸ = 2.8 cm
ਅਰਧਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ = \(\frac{2.8}{2}\) = 1.4 cm
∴ ਕੀੜੀ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ = \(\frac{1}{2}\)(2πr)
= πr
= \(\frac{22}{7}\) × 1.4 = 4.4 cm

(b) ਇਸ ਸਥਿਤੀ ਵਿਚ, ਅਕਾਰ ਚਿੱਤਰ ਵਿਚ ਦਿਖਾਏ ਅਨੁਸਾਰ ਹੈ :

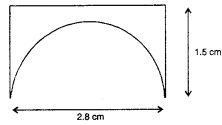
ਆਇਤ ਦੀ ਲੰਬਾਈ l = 2.8 cm
ਆਇਤ ਦੀ ਚੌੜਾਈ b = 1.5 cm
ਆਇਤ ਦਾ ਪਰਿਮਾਪ = 2 (l + b)
= 2 (2.8 + 1.5)
= 2 (4.3) = 8.6 cm.
ਅਰਧਚੱਕਰ ਦਾ ਵਿਆਸ = 2.8 cm
ਅਰਧਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ = \(\frac{2.8}{2}\) = 1.4 cm
∴ ਅਰਧਚੱਕਰ ਦਾ ਪਰਿਮਾਪ = πr
= \(\frac{22}{7}\) × 1.4 = 4.4 cm
∴ ਕੀੜੀ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ = [ਆਇਤ ਦਾ ਪਰਿਮਾਪ – ਅਰਧਚੱਕਰ ਦਾ ਪਰਿਮਾਪ]
= 8.6 – 4.4
= 4.2 cm

(c) ਇਸ ਸਥਿਤੀ ਵਿਚ ਆਕਾਰ ਚਿੱਤਰ ਵਿਚ ਦਿਖਾਏ ਅਨੁਸਾਰ ਹੈ :

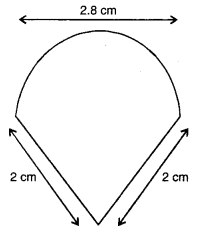
ਅਰਧਚੱਕਰ ਦਾ ਪਰਿਮਾਪੁ = 4.4 cm
∴ ਕੀੜੀ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ = 4.4 + 2 + 2
= 8.4 cm
∴ ਕੀੜੀ ਤੀਜੀ ਸਥਿਤੀ ਵਿਚ ਸਭ ਤੋਂ ਲੰਬਾ ਚੱਕਰ ਲਗਾਉਂਦੀ ਹੈ ।