PSEB 8th Class Maths Solutions Chapter 11 ਖੇਤਰਮਿਤੀ InText Questions

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 11 ਖੇਤਰਮਿਤੀ InText Questions and Answers.

PSEB 8th Class Maths Solutions Chapter 11 ਖੇਤਰਮਿਤੀ InText Questions

ਕੋਸ਼ਿਸ਼ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (a).
ਹੇਠਾਂ ਦਿੱਤੇ ਚਿੱਤਰਾਂ ਨੂੰ ਉਹਨਾਂ ਦੇ ਖੇਤਰਫਲਾਂ ਨਾਲ ਮਿਲਾਉ :

ਖੇਤਰਫਲ A = b × h
= 14 × 7
= 98 cm²

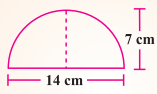
A = \(\frac{1}{2}\)(πr²)
= \(\frac{1}{2}\) × \(\frac{22}{7}\) × 7 × 7 = 77 cm²

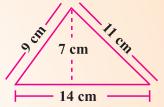
A = \(\frac{1}{2}\) × b × h
= \(\frac{1}{2}\) × 14 × 7 = 49 cm²

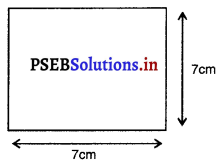
A = a² = (7)² = 7 × 7 = 49 cm²

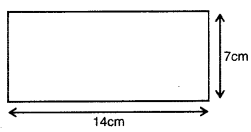
A = a × b = 14 × 7 = 98 cm²

ਪ੍ਰਸ਼ਨ (b).
ਹਰੇਕ ਅਕਾਰ ਦਾ ਪਰਿਮਾਪ ਲਿਖੋ ।
ਹੱਲ:
ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ :

ਖੇਤਰਫਲ = 98 cm²
ਪਰਿਮਾਪ = 2(14 + 7)
= 2(21) = 42 cm
ਅਰਧ ਚੱਕਰ

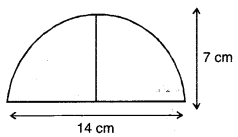
ਖੇਤਰਫਲ = A = 77 cm²
ਪਰਿਮਾਪ (P) = \(\frac{1}{2}\)(2πr)
= πr = \(\frac{22}{7}\) × 7 = 22 cm
ਤ੍ਰਿਭੁਜ :

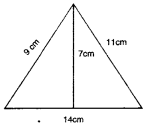
ਖੇਤਰਫਲ = 49 cm²
ਪਰਿਮਾਪ = (a + b + c)
= (11 + 9 + 14) = 34 cm.
ਵਰਗ :

ਖੇਤਰਫਲ = 49 cm²
ਪਰਿਮਾਪ = 4a = 4 (7) = 28 cm.
ਆਇਤ :

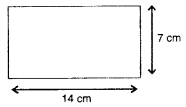
ਖੇਤਰਫਲ = 98 cm²
ਪਰਿਮਾਪ = 2 (a + b)
= 2 (14 + 7)
= 2 × 21
= 42 cm.

ਕੋਸ਼ਿਸ਼ ਕਰੋ :

ਪ੍ਰਸ਼ਨ 1.
ਨਜ਼ਮਾ ਦੀ ਭੈਣ ਦੇ ਕੋਲ ਵੀ ਇਕ ਸਮਲੰਬ ਦੇ ਆਕਾਰ ਦਾ ਪਲਾਟ ਹੈ ਜਿਸ ਤਰ੍ਹਾਂ ਕਿ ਚਿੱਤਰ ਵਿਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ । ਇਸਨੂੰ ਤਿੰਨ ਭਾਗਾਂ ਵਿਚ ਵੰਡੋ । ਦਰਸਾਉ ਕਿ ਸਮਲੰਬ WXYZ ਦਾ ਖੇਤਰਫਲ = \(\frac{h(a+b)}{2}\).

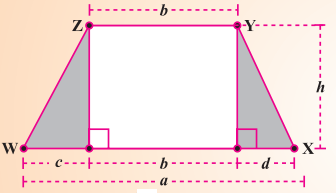
ਹੱਲ:
ਸਮਲੰਬ WXYZ ਵਿਚ,
Z ਅਤੇ Y ਤੋਂ WX ਉੱਤੇ ਲੰਬ ਖਿੱਚੋ ।
ਹੁਣ, ਸਮਲੰਬ ਵਿਚ ਤਿੰਨ ਭਾਗ ਸਮਕੋਣ ਭੁਜ PWZ, ਆਇਤ PQYZ, ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ XYQ.
∴ ਸਮਲੰਬ WXYZ ਦਾ ਖੇਤਰਫਲ
= △PWZ ਦਾ ਖੇਤਰਫਲ + ਆਇਤ PQYZ ਦਾ ਖੇਤਰਫਲ + △XYQ ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\) × c × h + b × h + \(\frac{1}{2}\) × h[a – (b + c)]
= \(\frac{1}{2}\)ch + bh + \(\frac{1}{1}\)h(a – b – c)
= \(\frac{1}{2}\)h[c + 2b + a – b – c]
= \(\frac{1}{2}\)h[a + b]
= \(\frac{h(a+b)}{2}\).

ਪ੍ਰਸ਼ਨ 2.
ਜੇਕਰ h = 10 cm, c = 6 cm, b = 12 cm, d = 4 cm, ਤਾਂ ਇਸਦੇ ਹਰੇਕ ਭਾਗ ਦਾ ਮਾਨ ਪਤਾ ਕਰੋ ਅਤੇ WXYZ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰਨ ਦੇ ਲਈ ਇਹਨਾਂ ਦਾ ਜੋੜ ਕਰੋ h, a ਅਤੇ b ਦੇ ਮੁੱਲ ਵਿਅੰਜਕ \(\frac{h(a+b)}{2}\) ਵਿਚ ਰੱਖਦੇ | ਹੋਏ ਇਸਦੀ ਪੜਤਾਲ ਕਰੋ ।

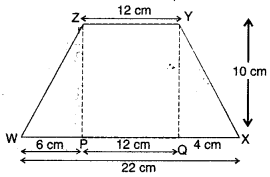
ਹੱਲ:
ਇਹ ਦਿੱਤਾ ਗਿਆ ਹੈ ਕਿ :
WP = c = 6 cm, XW = a = c + b + d
= (6 + 12 + 4) cm = 22 cm
YZ = b = 12 cm, PZ = h = 10 cm.
ਸਮਲੰਬ ਦਾ ਖੇਤਰਫਲ = △PWZ ਦਾ ਖੇਤਰਫਲ + ਆਇਤ PQYZ ਦਾ ਖੇਤਰਫਲ + △XYQ ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\) × 6 × 10 + 12 × 10 + \(\frac{1}{2}\) × 4 × 10
= (30 + 120 + 20) cm²
=170 cm²
ਪੜਤਾਲ :
ਸਮਲੰਬ ਦਾ ਖੇਤਰਫਲ = \(\frac{1}{2}\)(a + b)
= \(\frac{1}{2}\) × 10(22 + 12)cm²
= 5 (34) = 170 ²

ਕੋਸ਼ਿਸ਼ ਕਰੋ :

ਪ੍ਰਸ਼ਨ 1.
ਹੇਠਾਂ ਲਿਖੇ ਸਮਲੰਬਾਂ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ :

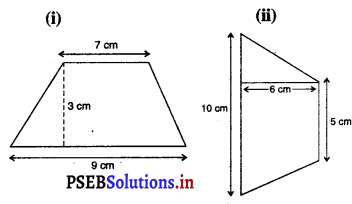
ਹੱਲ:
(i) ਸਮਲੰਬ ਦਾ ਖੇਤਰਫਲ = \(\frac{1}{2}\)h(a + b)
= \(\frac{1}{2}\)(3) [9 + 7] cm²
= \(\frac{1}{2}\) × 3 × 16 cm²
= 24 cm2.

(ii) ਸਮਲੰਬ ਦਾ ਖੇਤਰਫਲ = \(\frac{1}{2}\) × h(a + b)
= \(\frac{1}{2}\) × 6 × (10 + 5) cm²
= 3 (15)
= 45 cm²
ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਦਾ ਖੇਤਰਫਲ

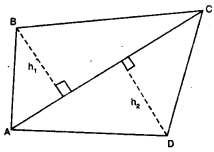
ਨਾਲ ਦੇ ਚਿੱਤਰ ਵਿਚ,
ਚਤੁਰਭੁਜ △BCD ਦਾ ਖੇਤਰਫਲ = △ABC ਦਾ ਖੇਤਰਫਲ + △ADC ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\) × AC × h₁ + \(\frac{1}{2}\)AC × h₂
= \(\frac{1}{2}\)AC (h₁ + h₂)

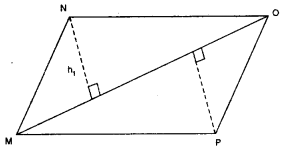
ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ MNOP ਦਾ ਖੇਤਰਫਲ = △MNO ਦਾ ਖੇਤਰਫਲ + △MPO ਦਾ ਖੇਤਰਫਲ
[ਕਿਉਂਕਿ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਦਾ ਵਿਕਰਨ ਇਹਨਾਂ ਨੂੰ ਦੋ ਸਰਬੰਗਸਮ ਤਿਭੁਜਾਂ ਵਿਚ ਵਿਭਾਜਿਤ ਕਰਦਾ ਹੈ ]
∴ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ MNOP ਦਾ ਖੇਤਰਫਲ
= 2 × △MNO ਦਾ ਖੇਤਰਫਲ
= 2 [\(\frac{1}{2}\) × MO × h₁]
= MO × h₁

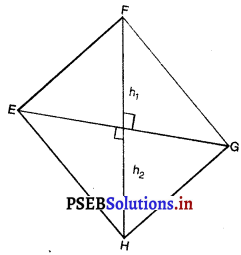
ਸਮਚਤੁਰਭੁਜ EFGH ਦਾ ਖੇਤਰਫਲ = △EFG ਦਾ ਖੇਤਰਫਲ + △EHG ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\) × EG × h₁ + \(\frac{1}{2}\) × EG × h₂
= \(\frac{1}{2}\)EG(h₁ + h₂)
[ਕਿਉਂਕਿ ਸਮਚਤੁਰਭੁਜ ਦੇ ਵਿਕਰਨ ਇਕ-ਦੂਸਰੇ ਦੇ ਲੰਬ ਸਮਦੁਭਾਜਕ ਹੁੰਦੇ ਹਨ h₁ + h₂ = FH]
∴ EFGH ਦਾ ਖੇਤਰਫਲ = \(\frac{1}{2}\) × EG × FH.
[ਸਮਚਤੁਰਭੁਜ ਦਾ ਖੇਤਰਫਲ ਵਿਕਰਨਾਂ ਦੇ ਗੁਣਨਫਲ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ ।]

ਕੋਸ਼ਿਸ਼ ਕਰੋ :

ਪ੍ਰਸ਼ਨ 1.
ਹੇਠਾਂ ਦਿੱਤੇ ਚਤੁਰਭੁਜਾਂ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ :

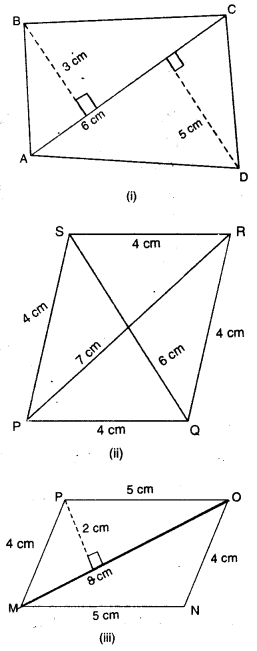
ਹੱਲ:
(i) ਚਤੁਰਭੁਜ ABCD ਦਾ ਖੇਤਰਫਲ :
ਚਤੁਰਭੁਜ ABCD ਦਾ ਖੇਤਰਫਲ
= △ABC ਦਾ ਖੇਤਰਫਲ + △ADC ਦਾ ਖੇਤਰਫਲ

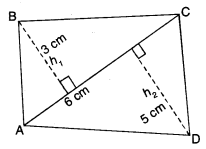
= \(\frac{1}{2}\) × AC × h₁ + \(\frac{1}{2}\) × AC × h₂
= \(\frac{1}{2}\) × 6 × 3 + \(\frac{1}{2}\) × 6 × 5
= 9 + 15 = 24 cm²

(ii) ਸਮਚਤੁਰਭੁਜ PQRS ਦਾ ਖੇਤਰਫਲ :

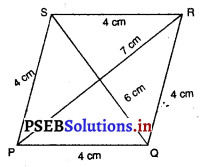
ਸਮਚਤੁਰਭੁਜ PQRS ਦਾ ਖੇਤਰਫਲ = \(\frac{1}{2}\) × PR × QS
= \(\frac{1}{2}\) × 7 × 6
= 21 cm²

(iii) ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ MNOP ਦਾ ਖੇਤਰਫਲ :

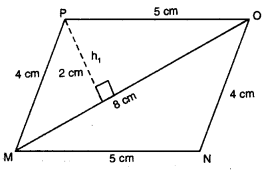
ਸਮਾਂਤਰ ਚਤੁਰਭੁਜੀ MNOP ਦਾ ਖੇਤਰਫਲ
= 2 × △MOP ਦਾ ਖੇਤਰਫਲ
= 2(\(\frac{1}{2}\) × MO × h₁)
= 2(\(\frac{1}{2}\) × 8 × 2)
= 16 cm².

ਕੋਸ਼ਿਸ਼ ਕਰੋ :

ਪ੍ਰਸ਼ਨ 1.
(i) ਹੇਠਾਂ ਦਿੱਤੇ ਬਹੁਭੁਜਾਂ (ਚਿੱਤਰ) ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰਨ ਦੇ ਲਈ ਇਸ ਨੂੰ ਵੱਖ-ਵੱਖ ਭਾਗਾਂ (ਤ੍ਰਿਭੁਜਾਂ ਅਤੇ ਸਮਲੰਬਾਂ) ਵਿਚ ਵੰਡੋ ।

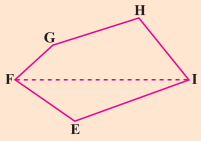
ਬਹੁਭੁਜ EFGHI ਦਾ ਇਕ ਵਿਕਰਨ FI ਹੈ ।

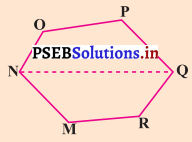
ਬਹੁਭੁਜ MNOPQR ਵਿਚ ਇਕ ਵਿਕਰਨ NQ ਹੈ ।
ਹੱਲ:
ਦਿੱਤੀ ਗਈ ਬਹੁਭੁਜ ਨੂੰ ਵੱਖ-ਵੱਖ ਭਾਗਾਂ ਵਿਚ ਵੰਡਣ ਦੇ ਲਈ ਸਾਨੂੰ ਕੁਮਵਾਰ H, E ਅਤੇ G ਵਿਚ F1 ਉੱਤੇ ਲੰਬ HI, EK ਅਤੇ GL ਖਿੱਚਦੇ ਹਾਂ ।

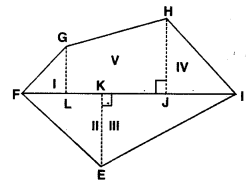
ਇਹ ਬਹੁਭੁਜ EFGHI ਨੂੰ ਚਿੱਤਰ ਵਿਚ ਦਰਸ਼ਾਏ ਅਨੁਸਾਰ ਪੰਜ ਭਾਗਾਂ ਵਿਚ ਵੰਡਦੀ ਹੈ ।
∴ ਬਹੁਭੁਜ EFGHI ਦਾ ਖੇਤਰਫਲੇ = △FLG ਦਾ ਖੇਤਰਫਲ + △EKF ਦਾ ਖੇਤਰਫਲ + △EIK ਦਾ ਖੇਤਰਫਲ + △IJH ਦਾ ਖੇਤਰਫਲ + ਸਮਲੰਬ △HGL ਦਾ ਖੇਤਰਫਲ ।

(ii) ਦਿੱਤੀ ਗਈ ਬਹੁਭੁਜ MNOPQR ਵਿਚ NQ ਵਿਕਰਨ ਹੈ ।

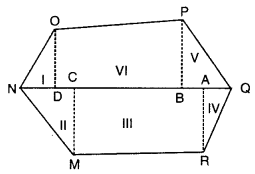
ਦਿੱਤੀ ਗਈ ਬਹੁਭੁਜ ਨੂੰ ਵੱਖ-ਵੱਖ ਭਾਗਾਂ ਵਿਚ ਵੰਡਣ ਦੇ ਲਈ ਅਸੀਂ M, R, P, ਅਤੇ O ਵਿਚ NQ ਉੱਤੇ ਕ੍ਰਮਵਾਰ ਲੰਬ CM, RA, PB ਅਤੇ OD ਖਿੱਚਦੇ ਹਾਂ ।
ਇਸ ਨਾਲ ਬਹੁਭੁਜ MNOPQR ਚਿੱਤਰ ਵਿਚ ਦਿਖਾਏ ਗਏ ਅਨੁਸਾਰ ਛੇ ਭਾਗਾਂ ਵਿਚ ਵੰਡੀ ਜਾਂਦੀ ਹੈ ।
∴ ਬਹੁਭੁਜ MNOPQR ਦਾ ਖੇਤਰਫਲ = △DON ਦਾ ਖੇਤਰਫਲ + △NCM ਦਾ ਖੇਤਰਫਲ + ਸਮਲੰਬ MCAR ਦਾ ਖੇਤਰਫਲ + △ARQ ਦਾ ਖੇਤਰਫਲ + △BQP ਦਾ ਖੇਤਰਫਲ + ਸਮਲੰਬ BPOD ਦਾ ਖੇਤਰਫਲ ।

ਪ੍ਰਸ਼ਨ (ii).
ਬਹੁਭੁਜ ABCDE ਨੂੰ ਵੱਖ-ਵੱਖ ਭਾਗਾਂ ਵਿਚ ਵੰਡਿਆ ਗਿਆ ਹੈ ਜਿਸ ਤਰ੍ਹਾਂ ਕਿ ਚਿੱਤਰ ਵਿਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ । ਜੇਕਰ AD = 8 cm, AH = 6 cm, AG = 4 cm, AF = 3 cm ਅਤੇ ਲੰਬ BF = 2 cm, CH = 3 cm, EG = 2.5 cm ਹੋਵੇ ਤਾਂ ਇਸਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।

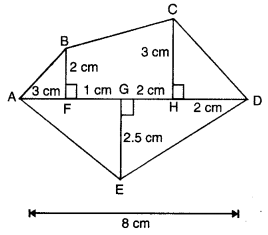
ਹੱਲ:
ਬਹੁਭੁਜ ABCDE ਦਾ ਖੇਤਰਫਲ = △AFB ਦਾ ਖੇਤਰਫਲ + ਸਮਲੰਬ FBCH ਦਾ ਖੇਤਰਫਲ + △CHD ਦਾ ਖੇਤਰਫਲ + △ADE ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\) × AF × BF + \(\frac{1}{2}\) × FH (BF + CH) + \(\frac{1}{2}\)HD × CH + \(\frac{1}{2}\) × AD × GE.
= (\(\frac{1}{2}\) × 3 × 2) + [\(\frac{1}{2}\) × 3 × (2 + 3)] + (\(\frac{1}{2}\) × 2 × 3) + (\(\frac{1}{2}\) × 8 × 2.5)
= 3 + \(\frac{15}{2}\) + 3 + 10
= 3 + 7.5 + 3 + 10 = 23.5 cm2
∴ ਬਹੁਭੁਜ ABCDE ਦਾ ਖੇਤਰਫਲ = 23.5 cm²

ਪ੍ਰਸ਼ਨ (iii).
ਜੇਕਰ MP = 9 cm, MD = 7 cm, MC = 6 cm, MB = 4 cm, MA = 2 cm ਤਾਂ ਬਹੁਭੁਜ MNOPQR ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ । NA, OC, QD ਅਤੇ RB ਵਿਕਰਨ MP ’ਤੇ ਖਿੱਚੇ ਗਏ ਲੰਬ ਹਨ ।

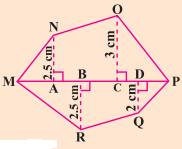
ਹੱਲ:
ਬਹੁਭੁਜ MNOPQR ਦਾ ਖੇਤਰਫਲ
= △MAN ਦਾ ਖੇਤਰਫਲ + ਸਮਲੰਬ ANOC ਦਾ ਖੇਤਰਫਲ + △OPC ਦਾ ਖੇਤਰਫਲ + △PQD ਦਾ ਖੇਤਰਫਲ + ਸਮਲੰਬ QRBD ਦਾ ਖੇਤਰਫਲ + △RBM ਦਾ ਖੇਤਰਫਲ ॥
= \(\frac{1}{2}\) × MA × AN + \(\frac{1}{2}\) × AC (AN + CO) + \(\frac{1}{2}\) × OC × CP + \(\frac{1}{2}\) × DP × DQ + \(\frac{1}{2}\) × BD(DQ + BR) + \(\frac{1}{2}\) × MB × BR
= \(\frac{1}{2}\) × 2 × 2.5 + \(\frac{1}{2}\) × 2.4(2.5 + 3) + \(\frac{1}{2}\) × 3 × 3 + \(\frac{1}{2}\) × 2 × 2 + \(\frac{1}{2}\) × 3(2 + 2.5) + \(\frac{1}{2}\) × 4 × 2.5
= 2.5 + 11 + 4.5 + 2 + \(\frac{13.5}{2}\) + 5
= 31.75 cm²

ਕੋਸ਼ਿਸ਼ ਕਰੋ :

ਪ੍ਰਸ਼ਨ 1.
ਹੇਠਾਂ ਦਿੱਤੇ ਘਣਾਵ ਦੀ ਕੁੱਲ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫ਼ਲ ਪਤਾ ਕਰੋ ।


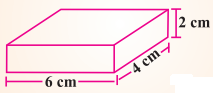
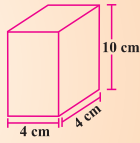
ਹੋਲ:
(i) ਘਣਾਵ ਦੀ ਲੰਬਾਈ (l) = 6 cm
ਘਣਾਵ ਦੀ ਚੌੜਾਈ (b) = 4 cm
ਘਣਾਵ ਦੀ ਉੱਚਾਈ (h) = 2 cm
∴ ਘਣਾਵ ਦੀ ਕੁੱਲ ਸਤਾ ਦਾ ਖੇਤਰਫਲ
= 2 (lb + bh + hl)
= 2 (6 × 4 + 4 × 2 + 2 × 6)
= 2 (24 + 8 + 12)
= 2 × 44 = 88 cm²

(ii) ਘਣਾਵ ਦੀ ਲੰਬਾਈ (l) = 4 cm
ਘਣਾਵ ਦੀ ਚੌੜਾਈ (b) = 4 cm
ਘਣਾਵ ਦੀ ਉੱਚਾਈ (h) = 10 cm
∴ ਘਣਾਵ ਦੀ ਕੁੱਲ ਸਤਾ ਦਾ ਖੇਤਰਫਲ
= 2 (lb + bh + hl)
= 2 (4 × 4 + 4 × 10 + 10 × 4)
= 2 (16 + 40 + 40)
= 2 × 96 = 192 cm²

ਕੋਸ਼ਿਸ਼ ਕਰੋ :

ਪ੍ਰਸ਼ਨ 1.
ਘਣ A ਦਾ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ ਅਤੇ ਘਣ B ਦਾ ਪਾਸਵੀਂ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।

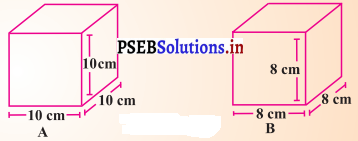
ਹੱਲ:
ਚਿੱਤਰ ਵਿਚ, ਘਣ ਦੇ ਕਿਨਾਰੇ ਦੀ ਲੰਬਾਈ = 10 cm
ਘਣ ਦਾ ਇਕ ਪਾਸੇ ਦੀ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ = 4x²
= 4 (10)² = 4 × 100
= 400 cm²
ਘਣ ਦਾ ਕੁੱਲ ਸੜਾ ਦਾ ਖੇਤਰਫਲ = 6x²
= 6 (10)² = 6 × 100
= 600 cm²
ਆਕ੍ਰਿਤੀ B ਵਿਚ,
ਘਣ ਦੇ ਕਿਨਾਰੇ ਦੀ ਲੰਬਾਈ = 8 cm
ਘਣ ਦਾ ਇਕ ਪਾਸੇ ਦੀ ਸੜਾ ਦਾ ਖੇਤਰਫਲ = 4x²
= 4 (8)²
=4 × 64
= 256 cm²
ਘਣ ਦਾ ਕੁੱਲ ਸੜਾ ਦਾ ਖੇਤਰਫਲ = 6x²
= 6 (8)²
= 6 × 64
= 384 cm²

ਕੋਸ਼ਿਸ਼ ਕਰੋ :

ਪ੍ਰਸ਼ਨ 1.
ਹੇਠਾਂ ਦਿੱਤੇ ਵੇਲਣਾਂ ਦੀ ਕੁੱਲ ਸਤਾ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ :

ਹੱਲ:
(i) ਵੇਲਣ ਦਾ ਅਰਧਵਿਆਸ (r) = 14 cm
ਵੇਲਣ ਦੀ ਉੱਚਾਈ (h) = 8 cm
∴ ਵੇਲਣ ਦਾ ਕੁੱਲ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ
= 2πr (h + r)
= 2 × \(\frac{22}{7}\) × 14 (8 +14)
= 2 × 22 × 2 (22) cm²
= 88 × 22 = 1936 cm²

(ii) ਵੇਲਣ ਦਾ ਵਿਆਸ = 2 m
∴ ਵੇਲਣ ਦਾ ਅਰਧਵਿਆਸ (r) = \(\frac{2}{2}\) = 1 m
ਵੇਲਣ ਦੀ ਲੰਬਾਈ (ਉੱਚਾਈ) (h) = 2 m
∴ ਵੇਲਣ ਦਾ ਕੁੱਲ ਸੜਾ ਦਾ ਖੇਤਰਫਲ
= 2πr (h + r)
= 2 × \(\frac{22}{7}\) × 1(2 + 1)
= 2 × \(\frac{22}{7}\) × 3
= \(\frac{132}{7}\) m²

ਕੋਸ਼ਿਸ਼ ਕਰੋ :

ਪ੍ਰਸ਼ਨ 1.
ਹੇਠਾਂ ਲਿਖੇ ਘਣਾਵਾਂ ਦਾ ਆਇਤਨ ਪਤਾ ਕਰੋ :

ਹੱਲ:
(i) ਘਣਾਵ ਦਾ ਆਇਤਨ = l × b × h
= (8 × 3 × 2)
= 48 cm³

(ii) ਘਣਾਵ ਦਾ ਆਇਤਨ = (l × b) × h
= (ਖੇਤਰਫਲ × ਉੱਚਾਈ)
= 24 × \(\frac{3}{100}\)m³
= \(\frac{72}{100}\) m³ = 0.72m³

ਕੋਸ਼ਿਸ਼ ਕਰੋ :

ਪ੍ਰਸ਼ਨ 1.
ਹੇਠਾਂ ਲਿਖੇ ਘਣਾਂ ਦਾ ਆਇਤਨ ਪਤਾ ਕਰੋ :
(a) 4 cm ਭੁਜਾ ਵਾਲਾ
(b) 1.5 m ਭੁਜਾ ਵਾਲਾ ।
ਹੱਲ:
(a) ਘਣ ਦੀ ਭੁਜਾ (x) = 4 cm
ਘਣ ਦਾ ਆਇਤਨ = x × x × x = x³
= (4)³ = 64 cm³

(b) ਘਣ ਦੀ ਭੁਜਾ (x) = 1.5 m
ਘਣ ਦਾ ਆਇਤਨ = x × x × x = x³
= (1.5)³ = 3,375 m³

ਕੋਸ਼ਿਸ਼ ਕਰੋ :

ਪ੍ਰਸ਼ਨ 1.
ਨਾਲ ਦਿੱਤੇ ਵੇਲਣਾਂ ਦਾ ਆਇਤਨ ਪੰਤਾ ਕਰੋ :

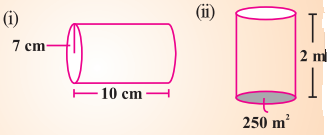
ਹੱਲ:
(i) ਵੇਲਣ ਦਾ ਅਰਥਵਿਆਸ r = 7 cm
ਵੇਲਣ ਦੀ ਉੱਚਾਈ h = 10 cm
ਵੇਲਣ ਦਾ ਆਇਤਨ = πr²h
= \(\frac{22}{7}\) × (7)² × 10
= \(\frac{22}{7}\) × 7 × 7 × 10
= 1540 cm³

(ii) ਵੇਲਣ ਦੀ ਉੱਚਾਈ (h) = 2 m
ਗੋਲਾਕਾਰ ਆਧਾਰ ਦਾ ਖੇਤਰਫਲ (πr²) = 250 m²
∴ ਵੇਲਣ ਦਾ ਆਇਤਨ : πr²h
= 250 × 2
= 500 m³