Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 14 सांख्यिकी Ex 14.2 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 14 सांख्यिकी Ex 14.2
प्रश्न 1.
आठवीं कक्षा के 30 विद्यार्थियों के रक्त समूह ये हैं :
A, B, O, AB, O, A, O, B, A, O, B, A, O, O,
A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O.
इन आँकड़ों को एक बारबारता बंटन सारणी के रूप में प्रस्तुत कीजिए। विद्यार्थियों में कौन-सा रक्त समूह अधिक सामान्य है और कौन-सा रक्त समूह विरलतम रक्त समूह है।
हल :
दिए गए आँकड़ों के लिए वर्गीकृत बारबारता बँटन सारणी इस प्रकार है :
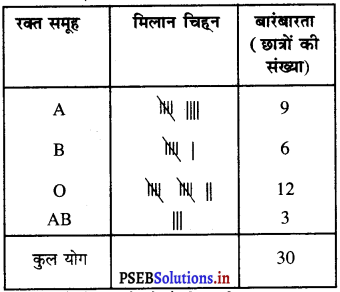
सारंणी से हम देखते हैं कि अधिक सामान्य रक्त समूह O है तथा सबसे विरल रक्त समूह AB है।
![]()
प्रश्न 2.
40 इंजीनियरों की उनके आवास से कार्यस्थल की (किलोमीटर में) दूरियाँ ये हैं :

0-5 को (जिसमें 5 सम्मिलित नहीं है)। पहला अंतराल लेकर ऊपर दिए हुए आँकड़ों से वर्गमाप 5 वाली एक वर्गीकृत बांरबारता बंटन सारणी बनाइए। इस सारणीबद्ध निरूपण में आपको कौन-से मुख्य लक्षण देखने को मिलते हैं ?
हल :
दिए गए आँकड़ों के लिए वर्गीकृत बांरबारता बंटन निम्न अनुसार है :
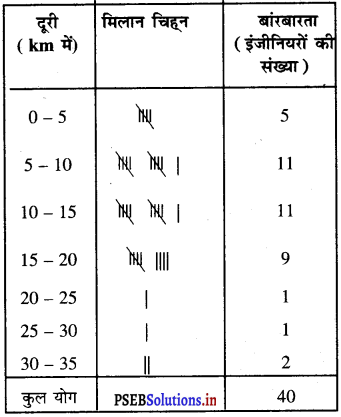
सारणी से हम देखते हैं कि 40 इंजीनियरों में से 36 (5 + 11 + 11 + 9) इंजीनियर अर्थात् कुल इंजीनियरों का 90% अपने कार्यस्थल से 20 किलीमीटर से कम दूरी पर रहते हैं।
प्रश्न 3.
30 दिन वाले महीने में एक बार की सापेक्ष आर्द्रता (%में) यह रही है :
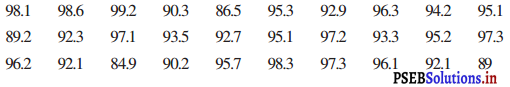
(i) वर्ग 84-86, 86-88 आदि लेकर एक वर्गीकृत बारबारता बंटन सारणी बनाइए।
(ii) क्या आप बता सकते हैं कि ये आँकड़े किस महीने या ऋतु से संबंधित हैं ?
(ii) इन आँकड़ों का परिसर क्या है ?
हल :
(i) दिए गए आँकड़ों के लिए वर्गीकृत बारबारता बंटन सारणी निम्न दिए अनुसार है :
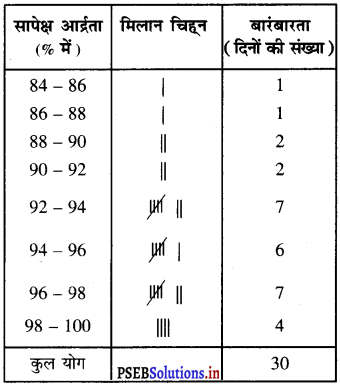
(ii) आँकड़ों से हम देखते हैं कि सापेक्ष आर्द्रता अधिक है, अत: ऐसा प्रतीत होता है कि आँकड़े वर्षा के मौसम में लिए गए हैं।
(iii) आँकड़ों से हम देखते हैं कि उच्चतम सापेक्ष आद्रता = 99.2% निम्नतम सापेक्ष आर्द्रता = 84.9%
परिसर = (99.2 – 84.9) %
= 14.3%
![]()
प्रश्न 4.
निकटतम सैंटीमीटरों में मापी गई 50 विद्यार्थियों की लंबाइयाँ ये हैं :

(i) 160 – 165, 165 – 170 आदि वर्ग अंतराल लेकर ऊपर दिए गए आँकड़ों को एक वर्गीकृत बारंबारता बंटन सारणी के रूप में निरूपित कीजिए।
(ii) इस सारणी की सहायता से आप विद्यार्थियों की लंबाइयों के संबंध में क्या निष्कर्ष निकाल सकते हैं ?
हल :
(i) दिए गए आँकड़ों के लिए वर्गीकृत बारंबारता बंटन सारणी निम्न अनुपात है :
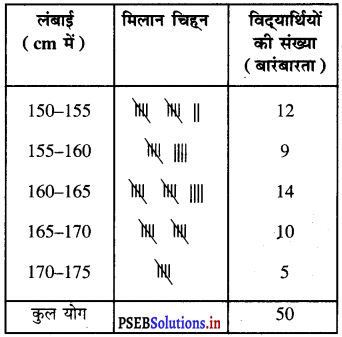
(ii) ऊपर की सारणी से एक निष्कर्ष हम यह निकाल सकते हैं कि 50% से अधिक विद्यार्थियों की लंबाई 165 cm से कम है।
प्रश्न 5.
एक नगर में वायु में सल्फर डाई-ऑक्साइड का सांद्रण भाग प्रति मिलियन [Parts per million (ppm)] में ज्ञात करने के लिए एक अध्ययन किया गया। 30 दिनों के प्राप्त किए गए ऑकड़े आगे दिए है :
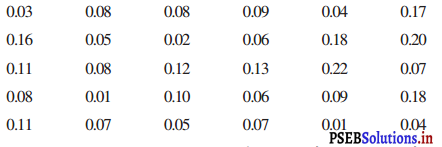
(i) 0.00 – 0.04, 0.04 – 0.08 आदि का वर्ग अंतरालं लेकर इन आँकड़ों की एक वर्गीकृत बारंबारता सारणी बनाइए।
(ii) सल्फर डाई-आक्साइड की सांद्रता कितने दिन 0.11 भाग प्रति मिलियन से अधिक रही ?
हल :
(i) दिए गए आँकड़ों के लिए बारंबारता सारणी निम्न अनुसार है :
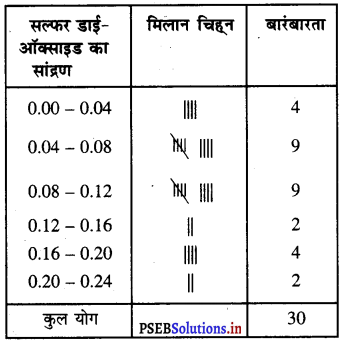
(ii) बारंबारता बंटन सारणी से हम देखते हैं कि 8 दिनों तक सल्फर डाइ-ऑक्साइड का सांद्रण 0.11 ppm से अधिक था।
![]()
प्रश्न 6.
तीन सिक्कों को एक साथ 30 बार उछाला गया। प्रत्येक बार चित (Head) आने की संख्या निम्न है :

ऊपर दिए गए आँकड़ों के लिए बारंबारता बंटन सारणी बनाइए।
हल :
दिए गए आंकड़ों के लिए बारंबारता बंटन सारणी निम्न अनुसार है :
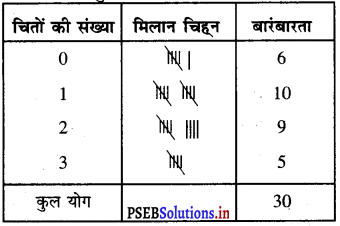
प्रश्न 7.
50 दशमलव स्थान तक शुद्ध ग का मान नीचे दिया गया है :
3.14159265358979323846264338327950288419716939937510
(i) दशमलव बिंदु के बाद आने वाले 0 से 9 तक के अंकों का एक बारंबारता बंटन बनाइए।
(ii) सबसे अधिक बार और सबसे कम बार आने वाले अंक कौन-कौन से हैं ?
हल :
(i) 50 दशमलव स्थानों तक का मान निम्न है :
π = 3.1415926535 8979323846
2643383279 5028841971 6939937510
π के मान के दशमलव बिंदु के बाद आने वाले अंकों की बारंबारता बंटन सारणी निम्न अनुसार है :
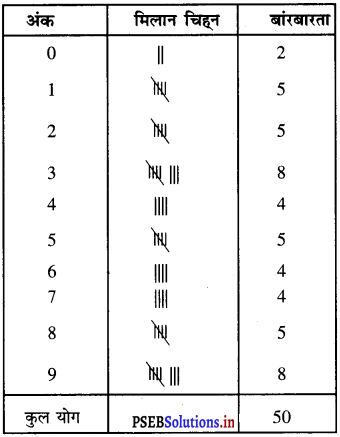
(ii) अधिक बारंबारता 8 है।
अतः, 3 सबसे अधिक बार आने वाला अंक है। सबसे कम बारंबारता 2 है।
अतः, 0 सबसे कम बार आने वाला अंक है।
![]()
प्रश्न 8.
तीस बच्चों से यह पूछा गया कि पिछले सप्ताह उन्होंने कितने घंटों तक टी० वी० के प्रोग्राम देखे। प्राप्त परिणाम ये रहे हैं :

(i) वर्ग चौड़ाई 5 लेकर और एक वर्ग अंतराल को 5-10 लेकर इन आँकड़ों की एक वर्गीकृत बारंबारता बंटन सारणी बनाइए।
(ii) कितने बच्चों ने सप्ताह में 15 या अधिक घंटों तक टेलीविजन देखा ?
हल :
(i) दिए गए आँकड़ों के लिए बारंबारता सारी निम्न अनुसार है :
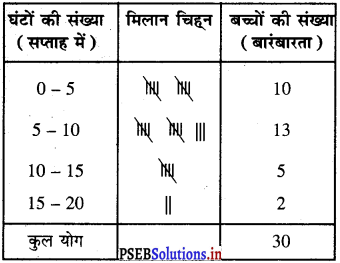
(ii) बारंबारता सारणी में हम देखते हैं कि वर्ग अंतराल 15-20 में बच्चों की संख्या 2 है।
अतः, 2 बच्चों ने सप्ताह में 15 या अधिक घंटों तक टेलीविज़न देखा।
प्रश्न 9.
एक कंपनी एक विशेष प्रकार की कार बैटरी बनाती है। इस प्रकार की 40 बैटरियों के जीवन-काल (वर्षों में) ये रहे हैं :

0.5 माप के वर्ग अंतराल लेकर तथा 2-2.5 से प्रारंभ करके इन आँकड़ों की एक वर्गीकृत बारंबारता बंटन सारणी बनाइए।
हल :
दिए गए आंकड़ों के लिए वर्गीकृत बारंबारता बंटन सारणी निम्न अनुसार है :