Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 14 सांख्यिकी MCQ Questions with Answers.
PSEB 9th Class Maths Chapter 14 सांख्यिकी MCQ Questions
बहुविकल्पीय प्रश्न:
दिये गए चार विकल्पों में से सही उत्तर का चयन करें।
प्रश्न 1.
वर्ग 150 – 160 का वर्ग चिन्ह है :
(A) 145
(B) 310
(C) 10
(D) 155
उत्तर:
(D) 155
प्रश्न 2.
अंकों 10, 8, 9, 7, 8 का माध्य है :
(A) 8.4
(B) 7.4
(C) 4.8
(D) 8.2
उत्तर:
(A) 8.4
प्रश्न 3.
पहली 10 प्राकृत संख्याओं की औसत है :
(A) 6.5
(B) 5.5
(C) 7.5
(D) 8.5
उत्तर:
(B) 5.5
प्रश्न 4.
किसी कक्षा में 9 विद्यार्थियों की ऊँचाई (सेमी० में) दी गई है :
155, 160, 145, 149, 150, 147, 152, 144, 148.
इन आंकड़ों का माध्य है :
(A) 150
(B) 147
(C) 149
(D) 148
उत्तर:
(C) 149
![]()
प्रश्न 5.
किसी कक्षा के 20 विद्यार्थियों के अंक (10 में से) निम्नलिखित है :
9, 6, 5, 9, 3, 2, 7, 7, 6, 5, 4, 9, 10, 10, 3, 4, 7, 6, 9, 9.
बहुलक अंक क्या है :
(A) 7
(B) 9
(C) 3
(D) 10.
उत्तर:
(B) 9
प्रश्न 6.
किसी बारंबारता बंटन में पाँच सतत वर्गों में से प्रत्येक की चौड़ाई 5 है तथा सबसे छोटे वर्ग की निम्न सीमा 10 है। सबसे बड़े वर्ग की उपरि सीमा है-
(A) 15
(B) 25
(C) 35
(D) 40
उत्तर:
(C) 35
प्रश्न 7.
मान लीजिए कि एक सतत बारंबारता बंटन में एक वर्ग का मध्य-बिंदु m है और उपरि वर्ग सीमा 1 है। इस वर्ग की निम्न वर्ग सीमा है-
(A) 2m + l
(B) 2m – l
(C) m – l
(D) m – 2l.
उत्तर:
(B) 2m – l
प्रश्न 8.
एक बारंबारता बंटन के वर्ग चिन्ह 15, 20, 25, ………….. हैं। वर्ग चिन्ह 20 के संगत वर्ग हैं-
(A) 12.5 – 17.5
(B) 17.5 – 22.5
(C) 18.5 – 21.5
(D) 19.5 – 20.5.
उत्तर:
(B) 17.5 – 22.5
प्रश्न 9.
वर्ग अंतराल 10-20, 20-30, में संख्या 20 निम्नलिखित में सम्मिलित है-
(A) 10-20
(B) 20-30
(C) दोनों अंतरालों में
(D) इनमें से किसी में भी नहीं।
उत्तर:
(B) 20-30
![]()
प्रश्न 10.
निम्नलिखित आँकड़ों के लिए, एक अंतराल 250-270 (270 सम्मिलित नहीं) लेते हुए बराबर मापों के वर्ग अंतरालों वाली एक वर्गीकृत बारंबारता सारणी की रचना की जाती है-
268, 220, 368, 258, 242, 310, 272, 342, 310, 290, 300, 320, 319, 304, 402, 318, 406, 292, 354, 278, 210, 240, 330, 316, 406, 215, 258, 236.
वर्ग अंतराल 310-330 की बारंबारता है :
(A) 4
(B) 5
(C) 6
(D) 7
उत्तर:
(C) 6
प्रश्न 11.
निम्नलिखित आँकड़ों के लिए एक वर्ग 63-72 (72 सम्मिलित है) लेते हुए बराबर मापों के वर्ग वाली एक वर्गीकृत बारंबारता सारणी की रचना की जाती है-
30, 32, 45, 54, 74, 78, 108, 112, 66, 76, 88, 40, 14, 20, 15, 35, 44, 66, 75, 84, 95, 96, 102, 110, 88, 74, 112, 14, 34, 44.
(A) 9
(B) 10
(C) 11
(D) 12.
उत्तर:
(B) 10
प्रश्न 12.
बारंबारता बंटन
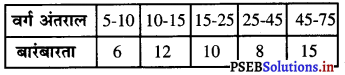
का एक आयतचित्र खींचने के लिए, वर्ग 25-45 की समायोजित बारंबारता है :
(A) 6
(B) 5
(C) 3
(D) 2
उत्तर:
(D) 2
प्रश्न 13.
पाँच संख्याओं का माध्य 30 है। यदि इनमें से एक संख्या को हटा दिया जाए, तो उनका माध्य 28 हो जाता है। हटाई गई संख्या है-
(A) 28
(B) 30
(C) 35
(D) 38.
उत्तर:
(D) 38.
प्रश्न 14.
यदि x, x + 3, x + 5, x + 7 प्रेक्षणों और x + 10 के माध्य 9 है, तो अंतिम तीन प्रेक्षणों का माध्य है-
(A) 10\(\frac{1}{3}\)
(B) 10\(\frac{2}{3}\)
(C) 11\(\frac{1}{3}\)
(D) 11\(\frac{2}{3}\)
उत्तर:
(C) 11\(\frac{1}{3}\)
![]()
प्रश्न 15.
यदि n प्रेक्षण x1, x2, ……. xn के माध्य को \(\bar{x}\) से निरूपित किया जाता है, तो \({ }_{i=1}^n\left(x_1-\bar{x}\right)\) का मान है-
(A) -1
(B) 0
(C) 1
(D) n – 1.
उत्तर:
(B) 0
प्रश्न 16.
यदि आँकड़ों के प्रत्येक प्रेक्षण में 5 की वृद्धि की जाती है तो उनका माध्य
(A) वही रहता है
(B) प्रारंभिक माध्य का पांच गुना हो जाता है
(C) 5 कम हो जाता है
(D) 5 बढ़ जाता है।
उत्तर:
(D) 5 बढ़ जाता है।
प्रश्न 17.
यदि x1, x2, ….., xn का माध्य \(\bar{x}\) है, y1, y2, ……. yn का माध्य \(\bar{y}\) है तथा x1, x2, ….., xn, y1, y2, ….. yn का माध्य \(\bar{z}\) बराबर है-
(A) \(\bar{x}\) + \(\bar{x}\)
(B) \(\frac{\bar{x}+\bar{y}}{2}\)
(C) \(\frac{\bar{x}+\bar{y}}{n}\)
(D) \(\frac{\bar{x}+\bar{y}}{2 n}\)
उत्तर:
(B) \(\frac{\bar{x}+\bar{y}}{2}\)
प्रश्न 18.
यदि x1, x2, …… xn का माध्य \(\bar{x}\) है, a ≠ 0, के लिए ax1, ax2, …… axn, \(\frac{x_1}{a}, \frac{x_2}{a}, \ldots \ldots, \frac{x_n}{a}\) का माध्य ज्ञात कीजिए।
(A) \(\left(a+\frac{1}{a}\right) \bar{x}\)
(B) \(\left(a+\frac{1}{a}\right) \frac{\bar{x}}{2}\)
(C) \(\left(a+\frac{1}{a}\right) \frac{\bar{x}}{n}\)
(D) \(\frac{\left(a+\frac{1}{a}\right) \bar{x}}{2 n}\)
उत्तर:
(B) \(\left(a+\frac{1}{a}\right) \frac{\bar{x}}{2}\)
प्रश्न 19.
यदि \(\bar{x}_1, \bar{x}_2, \bar{x}_3, \ldots, \bar{x}_n\) क्रमशः प्रेक्षणों की संख्या n1, n2, ….., nn, वाले n समूहों के माध्य हैं, तो सभी समूहों को मिलाकर लेने पर उनका माध्य \(\bar{x}\) निम्नलिखित से प्राप्त होता है-
(A) \(\sum_{i=1}^n n_i \bar{x}_i\)
(B) \(\frac{\sum_{i=1}^n n_i \bar{x}_i}{n^2}\)
(C) \(\frac{\sum_{i=1}^n n_i \bar{x}_i}{\sum_{i=1}^n n_1}\)
(D) \(\frac{\sum_{i=1}^n n_i x_i}{2 n}\)
उत्तर:
(C) \(\frac{\sum_{i=1}^n n_i \bar{x}_i}{\sum_{i=1}^n n_1}\)
![]()
प्रश्न 20.
100 प्रेक्षणों का माध्य 50 है। यदि इनमें से एक प्रेक्षण 50 को 150 से प्रतिस्थापित कर दिया जाए तो परिणामी माध्य हो जाएगा-
(A) 50.5
(B) 51
(C) 51.5
(D) 52
उत्तर:
(B) 51
प्रश्न 21.
50 संख्याएँ दी हुई हैं। इनमें से प्रत्येक संख्या को 53 में से घटाया जाता है तथा इस प्रकार प्राप्त संख्याओं का माध्य -3.5 ज्ञात किया जाता है। दी हुई संख्याओं का माध्य है-
(A) 46.5
(B) 49.5
(C) 53.5
(D) 56.5.
उत्तर:
(D) 56.5.
प्रश्न 22.
25 प्रेक्षणों का माध्य 36 है। इन प्रेक्षणों में से यदि प्रथम 13 प्रेक्षणों का माध्य 32 है तथा अंतिम 13 का माध्य 40 है तो 13वाँ प्रेक्षण है-
(A) 23
(B) 36
(C) 38
(D) 40
उत्तर:
(B) 36
प्रश्न 23.
78, 56, 22, 34, 45, 54, 39, 68, 54, 84 आँकड़ों का माध्यक है-
(A) 45
(B) 49.5
(C) 54
(D) 56.
उत्तर:
(C) 54
प्रश्न 24.
एक सतत् बारंबारता बंटन का बारंबारता बहुभुज खींचने के लिए, हम उन बिंदुओं को आलेखित करते हैं जिनकी कोटियाँ क्रमश: वर्गों की बारंबारताएँ होती हैं तथा भुज क्रमशः होते हैं-
(A) वर्गों की उपरि सीमाएँ
(B) वर्गों की निम्न सीमाएँ
(C) वर्गों के वर्ग चिन्ह
(D) पिछले वर्गों की उपरि सीमाएँ।
उत्तर:
(C) वर्गों के वर्ग चिन्ह
![]()
प्रश्न 25.
4, 4, 5, 7, 6, 7, 7, 12, 3 संख्याओं का माध्यक है-
(A) 4
(B) 5
(C) 6
(D) 7
उत्तर:
(C) 6
प्रश्न 26.
15, 14, 19, 20, 14, 15, 16, 14, 15, 18, 14, 19, 15, 17, 15 आँकड़ों का बहुलक है-
(A) 14
(B) 15
(C) 16
(D) 17.
उत्तर:
(B) 15
