Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 7 त्रिभुज Ex 7.2 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 7 त्रिभुज Ex 7.2
प्रश्न 1.
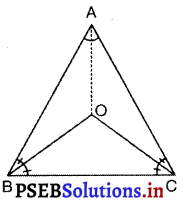
एक समद्विबाहु त्रिभुज ABC में जिसमें AB = AC है, ∠B और ∠C के समद्विभाजक परस्पर बिंदु O पर प्रतिच्छेद करते हैं। A और O को जोड़िए। दर्शाइए कि :
(i) OB = OC
(ii) AO कोण A को समद्विभाजित करता है।
हल :
ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC
∴ ∠C = ∠B (त्रिभुज में समान भुजाओं के सम्मुख कोण समान होते हैं।)
⇒ ∠OCA + ∠OCB = ∠OBA + ∠OBC
⇒ ∠OCB + ∠OCB = ∠OBC + ∠OBC
∵ OB, ∠B को समद्विभाजित करता है।
∴ ∠OBA = ∠OBC
और OC, ∠C को समद्विभाजित करता है।
∴ ∠OCA = ∠OCB
⇒ 2∠OCB = 2∠OBC
⇒ ∠OCB = ∠OBC
अब, ΔOBC में,
∠OCB = ∠OBC(ऊपर सिद्ध किया है)
∴ OB = OC
(समान कोणों की सम्मुख भुजाएँ)
(ii) अब ΔAOB और ΔAOC में,
AB = AC. (दिया है)
∠OBA = ∠OCA
∵ ∠B = ∠C
BO, ∠B और CO, ∠C को समद्विभाजित करता है
∴ \(\frac {1}{2}\)∠B = \(\frac {1}{2}\)∠C
⇒ ∠OBA = ∠OCA
OB = OC [(i) में सिद्ध किया है]
∴ ΔAOB = ΔAOC
(SAS सर्वांगसमता नियम से)
⇒ ∠OAB = ∠OAC
(सर्वामसम त्रिभुजों के संगत भाग)
अतः, AO; ∠A को समद्विभाजित करता है।
![]()
प्रश्न 2.
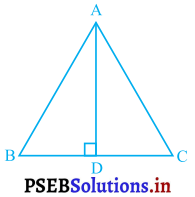
ΔABC में AD भुजा BC का लंब समद्विभाजक है (देखिए आकृति) दर्शाइए ΔABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है।
हल:
ΔABD और ΔACD में,
BD = CD [∵ AD, BC को समद्विभाजित करते हैं
(दिया है)] ∠ADB = ∠ADC = प्रत्येक 90°
[∵ AD ⊥ BC (दिया है)]
AD = AD (उभयनिष्ठ)
∴ ΔABD ≅ ΔACD
(SAS सर्वांगसम नियम से)
⇒ AB = AC
(सर्वांगसम त्रिभुजों के संगत भाग)
इसलिए, ABC एक समद्विबाहु त्रिभुज है।
प्रश्न 3.
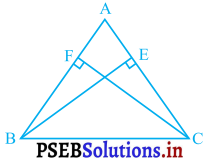
ABC एक समद्विबाहु त्रिभुज है, जिसमें बराबर भुजाओं AC और AB पर क्रमशः शीर्षलंब BE और CF खींचे गए हैं। (देखिए आकृति)। दर्शाइए कि ये शीर्षलंब बराबर हैं।
हल :
ΔABE और ΔACF में,
∠A = ∠A (उभयनिष्ठ)
∠AEB = ∠AFC
(प्रत्येक = 90°) [दिया है]
AB = AC (दिया है)
∴ ΔABE ≅ ΔACF
(AAS सर्वांगसमता नियम से)
इसलिए BE = CF
(सर्वांगसम त्रिभुजों के संगत भाग)
दूसरे शब्दों में समान भुजाओं पर खींचे गए शीर्षलंब समान होते हैं।
![]()
प्रश्न 4.
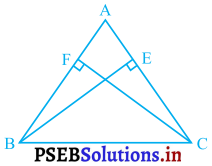
ABC एक त्रिभुज है जिसमें AC और AB पर खींचे गए शीर्ष लंब BE और CF बराबर हैं ( देखिए आकृति)। दर्शाइए कि
(i) ΔABE ≅ ΔACF
(ii) AB = AC, अर्थात् ΔABC एक समद्विबाहु त्रिभुज है।
हल :
ΔABE और ΔACF में,
∠A = ∠A (उभयनिष्ठ)
∠AEB = ∠AEC (प्रत्येक = 90°) [∵ BE ⊥ AC और CF ⊥ AB (दिया है)]
BE = CF (दिया है)
(i) ∴ ΔABE ≅ ΔACF
[AAS सर्वांगसमता नियम से]
(ii) इसलिए, AB = AC
सर्वांगसम त्रिभुजों के संगत भाग]
अर्थात्, ΔABC एक समद्विबाहु त्रिभुज है।
प्रश्न 5.
ARC और DBC समान आधार BC पर स्थित दो समद्विबाहु त्रिभुज हैं (देखिए आकृति)। दर्शाइए कि ∠ABD = ∠ACD है।
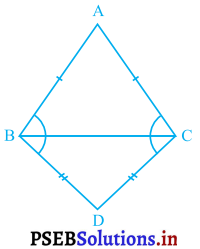
हल :
समद्विबाहु ΔABC में,
AB = AC (दिया है)
∴ ∠ACB = ∠ABC ………… (i)
(समान भुजाओं के सम्मुख कोण)
साथ ही, समद्विबाहु ΔBCD में,
BD = DC
∴ ∠BCD = ∠CBD ………… (ii)
(समान भुजाओं के सम्मुख कोण)
(i) और (ii) के संगत पक्षों को जोड़ने पर
∠ACB + ∠BCD = ∠ABC + ∠CBD
⇒ ∠ACD = ∠ABD
या ∠ABD = ∠ACD (इति सिद्धम)
![]()
प्रश्न 6.
ABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है। भुजा BA बिंदु D तक इस प्रकार बढ़ाई गई है कि AD = AB है ( देखिए आकृति)। दर्शाइए कि ∠BCD एक समकोण है।
हल :
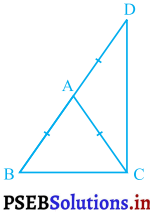
समद्विबाहु त्रिभुज ABC में,
AB = AC
∴ ∠ACB = ∠ABC …. (i)
(समान भुजाओं के सम्मुख कोण)
अब
AD = AB (रचना से)
AB = AC (दिया है)
∴ AD = AB = AC
⇒ AD = AC
अब ΔADC में,
AD = AC
⇒ ∠ADC = ∠ACD …………..(ii)
[ΔADC में समान भुजाओं के सम्मुख कोण] आकृति से हमें प्राप्त होता है :
∠BAC + ∠CAD = 180° … (iii)
(रैखिक युग्म)
जैसा कि हम जानते हैं कि त्रिभुज का बहिष्कोण अंतः सम्मुख कोणों के योगफल के बराबर होता है।
∴ ΔABC
∠CAD = ∠ABC + ∠ACB
= ∠ACB + ∠ACB
[(i) के प्रयोग से]
⇒ ∠CAD = 2∠ACB … (iv)
इसी प्रकार, ΔADC के लिए
∠BAC =∠ACD + ∠ADC [जैसा कि हम जानते हैं कि त्रिभुज का बहिष्कोण अंतः सम्मुख कोणों के योगफल के बराबर होता है।]
= ∠ACD + ∠ACD
[(ii) के प्रयोग से]
⇒ ∠BAC = 2 ∠ACD … (v)
(iii), (iv) और (v), से हमें प्राप्त होता है।
2∠ACB + 2∠ACD = 180°
या, 2(∠ACB + ∠ACD) = 180°
या, ∠ACB + ∠ACD = \(\frac {180°}{2}\)
⇒ ∠BCD =90°
अतः ∠BCD एक समकोण है।
प्रश्न 7.
ABC एक समकोण त्रिभुज है, जिसमें ∠A = 90° और AB = AC है। ∠B और ∠C ज्ञात कीजिए।
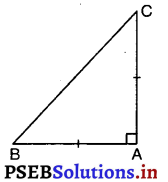
हल:
ABC एक समकोण त्रिभुज है, जिसमें
∠A = 90°
और AB = AC
ΔABC में,
AB = AC
∠C = ∠B ………..(i)
(समान भुजाओं के सम्मुख कोण)
अब, ΔABC में,
∠A + ∠B + ∠C = 180°
(कोण योगफल गुण)
⇒ 90° + ∠B + ∠B = 180° [∵ ∠A = 90° (दिया है) और ∠B = ∠C (i) से]
⇒ 2∠B = 180° – 90°
⇒ 2∠B = 90°
⇒ ∠B = \(\frac {90°}{2}\)
⇒ ∠B = 45°
साथ ही, ∠C = ∠B
⇒ ∠C= 45°
![]()
प्रश्न 8.
दर्शाइए कि किसी समबाहु त्रिभुज का प्रत्येक कोण 60° होता है।
हल :
माल लीजिए ABC एक समबाहु त्रिभुज है
∴ AB = BC = AC
AB = BC
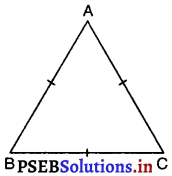
⇒ ∠C = ∠A …………(i)
(समान भुजाओं के सम्मुख कोण)
इसलिए,
AB = AC
⇒ ∠C = ∠B …… (ii)
(समान भुजाओं के सम्मुख कोण)
(i) और (ii) से हमें प्राप्त होता है
∠A = ∠B = ∠C …… (iii)
अब ΔABC में;
∠A + ∠B + ∠C = 180° ……. (iv)
[कोण योगफल गुण]
⇒ ∠A + ∠A + ∠A = 180°
⇒ 3∠A = 180
⇒ ∠A = \(\frac {180°}{3}\)
⇒ ∠A = 60°
(iii) से ; ∠A = ∠B = ∠C
⇒ ∠A = ∠B = ∠C = 60°
अतः, समबाहु त्रिभुज का प्रत्येक कोण 60° होता है।
