PSEB 9th Class Maths Solutions Chapter 12 हीरोन का सूत्र Ex 12.1

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 12 हीरोन का सूत्र Ex 12.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 12 हीरोन का सूत्र Ex 12.1

प्रश्न 1.
एक यातायात संकेत बोर्ड पर ‘आगे स्कूल है’ लिखा है और यह भुजा ‘a’ वाले एक समबाहु त्रिभुज के आकार का है। हीरोन के सूत्र का प्रयोग करके इस बोर्ड का क्षेत्रफल ज्ञात कीजिए। यदि संकेत बोर्ड का परिमाप 180 cm है, तो इसका क्षेत्रफल क्या होगा ?
हल :

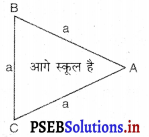
यातायात संकेत बोर्ड समबाहु त्रिभुज के आकार का है। आइए इसे ΔABC का नाम दें।
∴ समबाहु त्रिभुज ABC की प्रत्येक भुजा = a मात्रक (दिया है। )
समबाहु त्रिभुज का परिमाप अर्थात्
2s = a + a + a = 3a
अर्ध-परिमाप; s = \(\frac{3 a}{2}\)
इसलिए हीरोन के क्षेत्रफल के प्रयोग करने से त्रिभुज का क्षेत्रफल = \(\sqrt{s(s-a)(s-a)(s-a)}\)

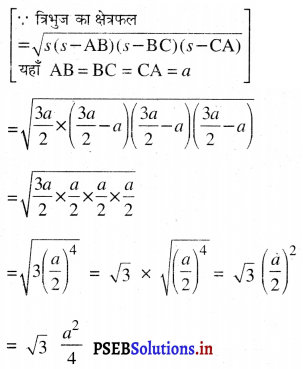
(ii) समबाहु त्रिभुज का परिमाप = 180 cm
⇒ a + a + a = 180 cm
⇒ 3a = 180 cm
⇒ a = \(\frac{180}{3}\) cm
⇒ a = 60 cm
⇒ 2S = 180 cm
⇒ S = \(\frac{180}{2}\)
⇒ S = 90 cm
∴ हीरोन के सूत्र का प्रयोग करने पर;
समबाहु त्रिभुज का क्षेत्रफल

= 90 (90 – 60) (90 – 60) (90 – 60)
वैकल्पिक विधि
a भुजा वाली समबाहु त्रिभुज का क्षेत्रफल
= \(\frac{\sqrt{3} a^2}{4}\) (ऊपर प्राप्त किया)
अतः, समबाहु त्रिभुज का क्षेत्रफल
= \(\frac{\sqrt{3}}{4}\) (60)²
[a = 60 cm का प्रयोग करने पर]
= \(\frac{\sqrt{3}}{4}\) × 3600 cm²
= \(\sqrt{3}\) × 900 cm²
= 900 \(\sqrt{3}\) cm²

प्रश्न 2.
किसी फलाईओवर (Flyover) की त्रिभुजाकार दीवार को विज्ञापनों के लिए प्रयोग किया जाता है। दीवार की भुजाओं की लंबाइयाँ 122 m, 22 m और 120 m हैं। ( देखिए आकृति)। इस विज्ञापन से प्रति वर्ष 5000 रु० प्रति m² की प्राप्ति होती है। एक कंपनी ने एक दीवार को विज्ञापन देने के लिए 3 महीने के लिए किराए पर लिया। उसने कुल कितना किराया दिया ?

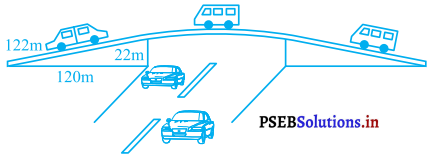
हल :
मान लीजिए कि फलाईओवर की त्रिभुजाकार दीवार की भुजाएँ a, b और c हैं :
:: a = 122 m, b = 22 m और c = 120 m
त्रिभुज का परिमाप,
2s = (122 + 22 + 120) m
अर्ध-परिमाप = \(\frac{264}{2}\) m
= 132 m
अब, s – a = (132 – 122) m = 10 m
s – b = (132 – 22) m = 110 m
s – c = (132 – 120) m = 12 m
इसलिए हीरोन के सूत्र से त्रिभुजाकार दीवार का क्षेत्रफल

दीवार पर विज्ञापन का 1 वर्ष (अर्थात् 12 महीने) का किराया = 5000 रु० प्रति m²
1 महीने का किराया = \(\frac{5000}{12}\) रु० प्रति m²
3 महीने का किराया = (\(\frac{5000}{12}\) × 3) रु० प्रति m²
= \(\frac{5000}{4}\) रु० प्रति m²
अब प्रति m² विज्ञापन के लिए दिया गया किराया = \(\frac{5000}{4}\) रु०
1320 m² विज्ञापन के लिए दिया गया किराया = (\(\frac{5000}{4}\) × 1320) रु०
= (5000 × 330) रु०
= 1650000 रु०
अतः, कंपनी द्वारा दिया गया किराया = 16,50,000 रु०

प्रश्न 3.
किसी पार्क में एक फिसल पट्टी (slide) बनी हुई है। इसकी पार्वीय दीवारों (side walls) में से एक दीवार पर किसी रंग से पेंट किया गया है और उस पर “पार्क को हरा-भरा और साफ़ रखिए” लिखा हुआ है ( देखिए आकृति)। यदि इस दीवार की विमाएँ 15 m, 11 m और 6 m हैं, तो रंग से पेंट हुए भाग का क्षेत्रफल ज्ञात कीजिए।

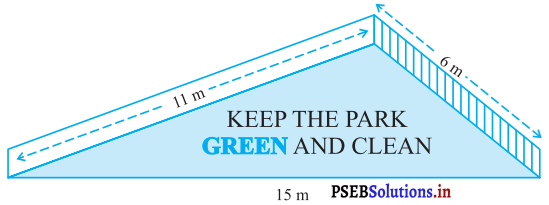
हल :
रंग से पेंट की हुई त्रिभुजाकार दीवार की भुजाएँ 15 m, 11 m और 6 m हैं।
∴ इस त्रिभुजाकार दीवारा का परिमाप
2s = (15 + 11 + 6) m
⇒ s = \(\frac{32}{2}\) m
⇒ s = 16 m
हीरोन सूत्र के प्रयोग से त्रिभुजाकार दीवार का क्षेत्रफल

= 4 × 5\(\sqrt{2}\) m²
= 20\(\sqrt{2}\) m²
अतः रंग से पेंट हुए भाग का क्षेत्रफल = 20\(\sqrt{2}\) m²

प्रश्न 4.
उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसकी दो भुजाएँ 18 cm और 10 cm हैं तथा उसका परिमाप 42 cm है।
हल :
त्रिभुज का परिमाप = 42 cm
⇒ 18 cm + 10 cm + तीसरी भुजा = 42 cm

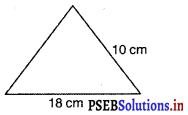
⇒ तीसरी भुजा = (42 – 18 – 10) cm
⇒ तीसरी भुजा = 14 cm
अब त्रिभुज का अर्ध-परिमाप;
s = 2 cm
⇒ s = \(\frac{42}{2}\) cm
अब त्रिभुज की तीन भुजाएँ 18 cm, 10 cm और 14 cm हैं।
त्रिभुज का क्षेत्रफल

अतः, त्रिभुज का क्षेत्रफल 21\(\sqrt{11}\) cm².

प्रश्न 5.
एक त्रिभुज की भुजाओं का अनुपात 12 : 17 : 25 है और उसका परिमाप 540 cm है। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
हल :
दिया है कि त्रिभुज की भुजाओं में अनुपात 12 : 17 : 25
∴ मान लीजिए cm में त्रिभुज की भुजाएँ 12x, 17x और 25x हैं।
त्रिभुज का परिमाप = 540 cm (दिया है)
⇒ 12x + 17x + 25x = 540 cm
⇒ 54x = 540 cm
⇒ x = \(\frac{540}{54}\) cm
⇒ x = 10 cm
अब त्रिभुज की भुजाएं हैं-
12x = 12 × 10 = 120 cm
17x = 17 × 10 = 170 cm
और 25x = 25 × 10 = 250 cm
परिमाप त्रिभुज का अर्ध-परिमाप;

= \(\frac{540}{2}\) cm
= 270 cm
हीरोन के सूत्र के प्रयोग से;
त्रिभुज का क्षेत्रफल

अतः, त्रिभुज का अभीष्ट क्षेत्रफल 9000 cm² है।

प्रश्न 6.
एक समदविबाहु त्रिभुज का परिमाप 30 cm है और उसकी बराबर भुजाएँ 12 cm लंबाई की हैं। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
हल :
समद्विबाहु त्रिभुज का परिमाप = 30 cm
⇒ 12 cm + 12 cm + तीसरी भुजा = 30 cm

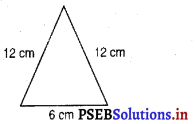
[∵ समद्विबाहु त्रिभुज में दो भुजाएँ बराबर होती हैं और यहां प्रत्येक बराबर भुजा 12 cm है।]
⇒ तीसरी भुजा = (30 – 12 – 12) cm
⇒ तीसरी भुजा = 6 cm
अब समद्विबाहु त्रिभुज s का अर्धपरिमाप

परिमाप
s = \(\frac{30}{2}\) cm
⇒ s = 15 cm
हीरोन के सूत्र के प्रयोग से; त्रिभुज का क्षेत्रफल

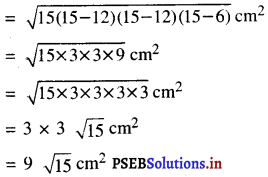
अतः, समद्विबाहु त्रिभुज का अभीष्ट क्षेत्रफल = 9\(\sqrt{15}\) cm²