Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Ex 9.3 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Ex 9.3
प्रश्न 1.
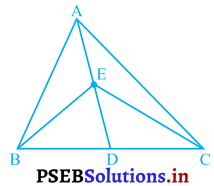
आकृति में, ΔABC की एक माध्यिका AD पर स्थित E कोई बिंदु है। दर्शाइए कि
ar (ΔABE) = ar (ACE) है।
हल :
ΔABC में, AD माध्यिका है।
ar (ΔABD) = ar (ΔACD) ……..(i)
[∵ माध्यिका त्रिभुज को बराबर क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करती है।]
पुनः, ΔEBC में, ED एक माध्यिका है। ,
ar (ΔEBD) = ar (ΔECD) …(ii)
(ii) को (i), में से घटाने पर हमें प्राप्त होता है
ar (ΔABD) = ar (ΔEBD)
= ar (ΔACD) – ar (ΔECD)
⇒ ar (ΔABE) = ar (ΔACE).
![]()
प्रश्न 2.
ΔABC में E, माध्यिका AD का मध्य-बिंदु है। दर्शाइए कि ar (BED) = \(\frac {1}{4}\)ar (ABC) है।
हल :
दिया है : ΔABC में, AD एक माध्यिका है और E माध्यिका AD का मध्य-बिंदु है।
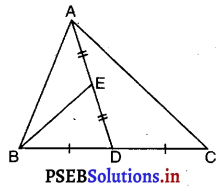
सिद्ध करना है : ar (ΔBED) = \(\frac {1}{4}\)r (ΔABC).
उपपत्ति : ΔABC में AD माध्यिका है।
∴ ar (ΔABD) = ar (ΔADC) [∵ माध्यिका त्रिभुज को बराबर क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करती है।]
∴ ar (ΔABD) = \(\frac {1}{2}\)ar (ΔABC) …(i)
ΔABD में, BC एक माध्यिका है।
∴ ar (ΔBED) = ar (ΔBAE)
∴ ar (ΔBED) = \(\frac {1}{2}\)ar (ΔABD) …(ii)
⇒ ar (ΔBED) = \(\frac {1}{2}\) × \(\frac {1}{2}\)ar (ΔABC)
[(i) और (ii) से]
= \(\frac {1}{4}\)ar (ΔABC)
इति सिद्धम्
प्रश्न 3.
दर्शाइए कि समांतर चतुर्भुजों के दोनों विकर्ण उसे बराबर क्षेत्रफलों वाले चार त्रिभुजों में बाँटते हैं।
हल :
मान लीजिए समांतर चतुर्भुज ABCD है और इसके विकर्ण AC और BD परस्पर बिंदु O पर प्रतिच्छेद करते हैं।
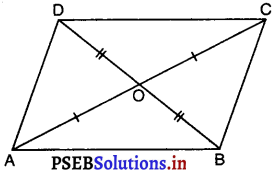
ΔABC और ΔADC में,
AB = DC (समांतर चतुर्भुज की सम्मुख भुजाएँ)
BC = AD
(समांतर चतुर्भुज सम्मुख भुजाएँ)
AC = AC (उभयनिष्ठ)
∴ ΔABC ≡ ΔCDA
(SSS सर्वांगसमता नियम)
जैसा कि हम जानते हैं कि समांतर चतुर्भुज के विकर्ण परस्पर समद्विभाजित होते हैं।
∴ आकृति में ; O समद्विभाजक बिंदु है।
अब ΔADC में;
DO एक माध्यिका है।
∴ ar (ΔAOD) = ar (ΔCOD) …………..(i)
(∵ माध्यिका त्रिभुज को बराबर क्षेत्र फलों वाले दो त्रिभुजों में विभाजित करती है।]
इसी प्रकार, ΔABC में, OB माध्यिका है
∴ ar (ΔAOB) = ar (ΔBOC) …(ii)
[उपरोक्त कारण ही]
ΔAOB और ΔAOD में; AO माध्यिका है।
∴ ar (ΔAOB) = ar (ΔAOD)
(उपरोक्त कारण ही) …(iii)
(i), (ii) और (iii) से हमें प्राप्त होता है :
ar (ΔAOB) = ar (ΔAOD) = ar (ΔBOC)
= ar (ΔCOD)
अतः समांतर चतुर्भुज के विकर्ण इसे बराबर क्षेत्रफलों वाले चार त्रिभुजों में बाँटते हैं।
![]()
प्रश्न 4.
आकृति में, ABC और ABD एक ही आधार AB पर बने दो त्रिभुज हैं। यदि रेखाखंड CD रेखाखंड AB से बिंदु पर समद्विभाजित होता है, तो दर्शाइए कि ar (ABC) = ar (ABD) है।
हल :
CM ⊥ AB और DN ⊥ AB खींचिए।
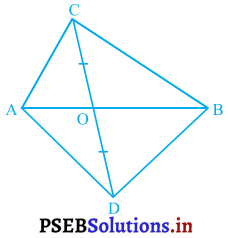
ΔCMO और ΔCNO में,
∠CMO = ∠DNO
[(प्रत्येक = 90°) रचना]
∠COM = ∠DON
(शीर्षाभिमुख कोण)
OC = OD
(O, CD का मध्य-बिंदु है)
∴ ΔCOM ≡ ΔDON
[AAS सर्वांगसमता का नियम]
इसलिए, CM = DN
(सर्वांगसम त्रिभुजों के संगत भाग) …….(i)
अब ar (ΔABC) = \(\frac {1}{2}\) × AB × CM …(ii)
ar (ΔADB) = \(\frac {1}{2}\) × AB × DN …(iii)
(i) को (iii) में प्रयोग करने पर हमें प्राप्त होता है
ar (ΔADB) = \(\frac {1}{2}\) × AB × CM ….(iv)
(ii) और (iv) से हमें प्राप्त होता है
ar (ΔABC) = ar (ΔADB)
प्रश्न 5.
D, E और F क्रमशः त्रिभुज ABC की भुजाओं BC, CA और AB के मध्य-बिंदु हैं। दर्शाइए कि :
(i) BDEF एक समांतर चतुर्भुज है
(ii) ar (DEF) = \(\frac {1}{4}\) ar (ABC)
(iii) ar (BDEF) = \(\frac {1}{2}\)ar (ABC)
हल :
(i) F, AB का मध्य-बिंदु और E, AC का मध्य-बिंदु है।
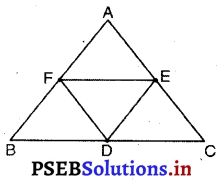
∴ FE || BC और FE = \(\frac {1}{2}\)BC
[∵ त्रिभुज की दो भुजाओं के मध्य-बिंदुओं को मिलाने वाली रेखा तीसरी भुजा के समांतर और इसका आधा होती है।]
या FE || BD
∵ BD, BC का ही भाग है] और FE = BD [∵ दिया है कि D, EC का मध्य-बिंदु है।
∴ BD = \(\frac {1}{2}\)BC
इसलिए, FE = \(\frac {1}{2}\) BC (ऊपर सिद्ध किया है) |
⇒ FE = BD
अब E, AC का मध्य-बिंदु और D, EC का मध्यबिंदु है।
∴ DE || AB और DE = \(\frac {1}{2}\) AB
[ऊपर वाले कारण का उपयोग करने पर
या DE || BF [∵ BE, AB का ही भाग है।]
और DE = BF
[∵ F, AB का मध्य-बिंदु है ∴ BF = \(\frac {1}{2}\) AB
परंतु DE = \(\frac {1}{2}\) AB (ऊपर सिद्ध किया है)
इसलिए, DE = BF]
अब,
FE || BD और DE || BF
या FE = BD और DE = BF
अतः, BDEF एक समांतर चतुर्भुज है।
(ii) BDEF एक समांतर चतुर्भुज है
∴ ar (ΔBDF) = ar (ΔDEF) ….(1) [∵ समांतर चतुर्भुज का विकर्ण इसे बराबर क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करता है।]
DCEF भी समांतर चतुर्भुज है[भाग (i) के चरणों का प्रयोग करने पर]
∴ ar (ΔDEF) = ar (ΔDEC) …(2)
साथ ही, AEDF एक समांतर चतुर्भुज है। [भाग (i) के चरणों का प्रयोग करने पर]
∴ ar (ΔAFE) = ar (ΔDEF) …(3)
(1), (2) और (3)से
ar (ΔDEF) = ar (ΔBDF) = ar(ΔDEC)
= ar (ΔAFE) …(4)
अब, ar (ΔABC) = ar (ΔAFE) + ar (ΔBDF) + ar (ΔDEC) + ar (ΔDEF)…(5)
⇒ ar (ΔABC) = ar (ΔDEF) + ar (ΔDEF) + ar (ΔDEF)) + ar (ΔDEF)
[(4) को (5) में प्रयोग करने पर]
⇒ ar (ΔABC) = 4 ar (DEF)
या, 4 ar (ΔDEF) = ar (ΔABC)
⇒ ar (ΔDEF) = \(\frac {1}{4}\)ar (ΔABC) …….(6)
(iii) ar (||gm BDEF) = ar (ΔBDF) + ar (ΔDEF)
= ar (ΔDEF) + ar (ΔDEF)
[(4) प्रयोग करने पर]
= 2 ar (ΔDEF)
= 2 × \(\frac {1}{4}\) ar (ΔABC)
[(6) का प्रयोग करने पर]
⇒ ar (||gm BDEF) = \(\frac {1}{2}\)ar (ΔABC)
![]()
प्रश्न 6.
आकृति में, चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि OB = OD है।
यदि AB = CD है, तो दर्शाइए कि
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB या ABCD एक समांतर चतुर्भुज है।
हल :
(i) BM ⊥ AC और DN ⊥ AC खींचिए।
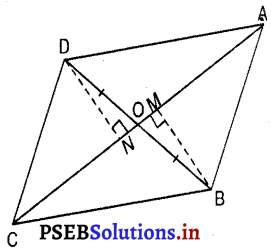
ΔDON और ΔBOM में,
OD = OB (दिया है)
∠DNO = ∠BMO
[प्रत्येक = 90° (रचना से)]
∠DON = ∠BOM
(शीर्षाभिमुख कोण)
∴ ΔDON ≡ ΔBOM
[AAS सर्वांगसमता नियम]
इसलिए, DN = BM
(सर्वांगसम त्रिभुजों के संगत भाग)
साथ ही, ar (ΔDON) = ar (ΔBOM) …(1)
अब, ΔDCN और ΔABM में,
∠DNC = ∠BMA
[प्रत्येक = 90° (रचना से)]
CD = AB (दिया है)
DN = BM (ऊपर सिद्ध किया)
∴ ΔDCN ≡ ΔBAM
[RHS सर्वांगसमता नियम]
∴ ar (ΔDCN) = ar (ΔBAM) …(2)
(1) और (2) को जोड़ने पर हमें प्राप्त होता है।
ar (ΔDON) + ar (ΔDCN) = ar (ΔBOM) + ar (ΔBAM)
⇒ ar (ΔDOC) = ar (ΔAOB)
(ii) भाग (ii) में हमने सिद्ध किया है कि
ar (ΔDOC) = ar (ΔAOB)
दोनों ओर ar (ΔBOC) को जोड़ने पर हमें प्राप्त होता है
ar (ΔDOC) + ar (ΔBOC) = ar (ΔAOB) + ar (ΔBOC)
⇒ ar (ΔDCB) = ar (ΔACB)
(iii) भाग (ii) में हमने सिद्ध किया है कि ar (ΔDCB) = ar (ΔACB)
इसलिए इन दोनों त्रिभुजों का एक ही आधार CB है
और दोनों एक ही समांतर रेखाओं CB और DA के बीस्थित है।
इसलिए, DA || CB
अब AB = CD
और, DA || CB
अत: ABCD एक समांतर चतुर्भुज है।
प्रश्न 7.
बिंदु D और E क्रमश: ΔABC की भुजाओं AB और AC पर इस प्रकार स्थित हैं कि ar (DBC) = ar (EBC) है। दर्शाइए कि DE || BC है।
हल :
दिया है कि
ar (ΔDBC) = ar (ΔEBC)
दो बराबर क्षेत्रफल वाली त्रिभुजों का एक ही आधार BC है।
इसलिए DE || BC
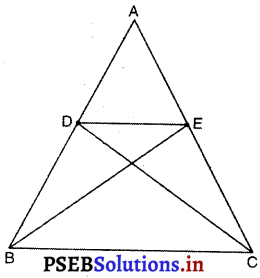
[∵ दो त्रिभुज जिनका एक ही आधार (या बराबर आधार) है और बराबर क्षेत्रफल है, एक ही समांतर रेखाओं के बीच स्थित होते हैं।]
![]()
प्रश्न 8.
XY त्रिभुज ABC की भुजा BC के समांतर एक रेखा है। यदि BE || AC और CF || AB रेखा XY से क्रमश: E और F पर मिलती है, तो दर्शाइए कि
ar (ABE) = ar (ACF)
हल :
ΔABE और ||gm BCYE एक ही आधार BE तथा एक ही समांतर रेखाओं BE और AC के बीच स्थित है।
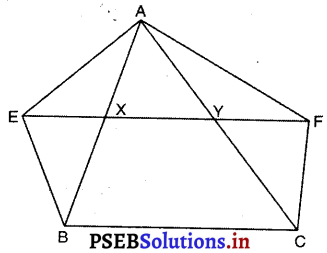
∴ ar (ΔABE) = \(\frac {1}{2}\) ar (||gm BCYE) …….(1)
साथ ही, ΔACF और || gm BCFX एक ही आधार CF तथा एक ही समांतर रेखाओं BX और CF के बीच स्थित है।
∴ ar (ΔACF) = \(\frac {1}{2}\)ar (||gm BCFX)…(2)
परंतु ||gm BCYE और ||gm BCFX एक ही आधार BC और एक ही समांतर रेखाओं BC और EF के बीच स्थित है।
ar (||gm BCYE) = ar (||gm BCEX) …(3)
(1), (2) और (3) से हमें प्राप्त होता है-
ar (ΔABE) = ar (ΔACF)
प्रश्न 9.
समांतर चतुर्भुज ABCD की एक भुजा AB को एक बिंदु P तक बढ़ाया गया है। A से होकर CP के समांतर खींची गई रेखा बढ़ाई गई CB को Q पर मिलती है और फिर समांतर चतुर्भुज PBQR को पूरा किया गया है (देखिए आकृति)। दर्शाइए कि ar (ABCD) = ar (PBQR) है।
हल :
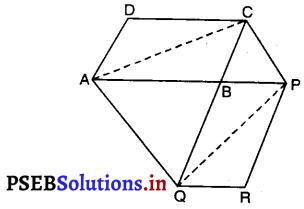
दिया है कि ABCD और PBQR समांतर चतुर्भुज है। साथ ही, CP || AQ.
हम देखते हैं कि
ΔACQ और ΔAPQ एक ही आधार AQ तथा एक ही समांतर रेखाओं AQ और CP के बीच स्थित हैं।
∴ ar (ΔACQ) = ar (ΔAPQ)
दोनों पक्षों में से ar (ΔABQ) घटाने पर हमें प्राप्त होता है:
ar (ΔACQ) – ar (ΔABQ)
= ar (ΔAPQ) – ar (ΔABQ)
⇒ ar (ΔACB) = ar (ΔPBQ)
या, \(\frac {1}{2}\) ar (|| gm ABCD) = \(\frac {1}{2}\)ar || gm PBQR) [∵ विकर्ण चतुर्भुज को बराबर क्षेत्रफल वाले त्रिभुजों में विभाजित करता है।
∴ त्रिभुज का क्षेत्रफल = \(\frac {1}{2}\)समांतर चतुर्भुज का क्षेत्रफल]
⇒ ar (|| gm ABCD) = ar (|| gm PBQR)
![]()
प्रश्न 10.
एक समलंब ABCD, जिसमें AB || DC है, के विर्कण AC और BD परस्पर O पर प्रतिच्छेद करते हैं। दर्शाइए कि ar (AOD) = ar (BOC) है।
हल :
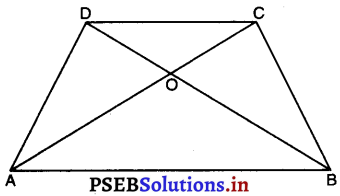
ΔABD और ΔABC एक ही आधार AB और एक समांतर रेखाओं AB और DC के बीच स्थित है।
∴ ar (ΔABD) = ar (ΔABC)
ar (ΔAOB) को दोनों पक्षों में से घटाने पर हमें प्राप्त होता है
ar (ΔABD) – ar (ΔAOB) = ar (ΔABC) – ar (ΔAOB)
⇒ ar Δ(AOD) = ar (ΔBOC) इति सिद्धम्
प्रश्न 11.
आकृति में, ABCDE एक पंचभुज है। B से होकर AC के समांतर खींची गई रेखा बढ़ाई गई DC को F पर मिलती है। दर्शाइए कि:
(i) ar (ACB) = ar (ACF)
(ii) ar (AEDF) = ar (ABCDE)
हल :
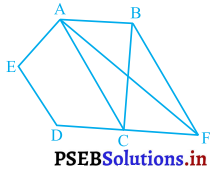
(i) दिया है BF || AC.
ΔACB और ΔACF एक ही आधार AC तथा एक ही समांतर रेखाओं AC और BF के बीच स्थित है।
∴ ar (ΔACB) = ar (ΔACF) …(1)
(ii) अब, ar (ΔABCDE) = ar (समलंब AEDC) + ar (ΔABC) …..(2)
= ar (समलंब AEDC) + ar (ΔACF)
[(1) को (2) में प्रयोग करने पर]
ar (समलंब AEDC) + ar (ΔACF)
=ar (चतुर्भुज AEDF)
या, ar (AEDF) = ar (ABCDE)
इति सिद्धम्
प्रश्न 12.
गाँव के एक निवासी इतवारी के पास एक चर्तुभुजाकार भूखंड था। उस गाँव की ग्राम पंचायत ने उसके भूखंड के एक कोने से उसका कुछ भाग लेने का निर्णय लिया ताकि वहाँ एक स्वास्थ्य केंद्र का निर्माण कराया जा सके। इतवारी उस प्रस्ताव को इस प्रतिबंध के साथ स्वीकार कर लेता है कि उसे इस भाग के बदले उसी भूखंड के संलग्न एक भाग ऐसा दे दिया जाए कि उसका भूखंड त्रिभुजाकार हो जाए। स्पष्ट कीजिए कि इस प्रस्ताव को किस प्रकार कार्यान्वित किया जा सकता है।
हल :
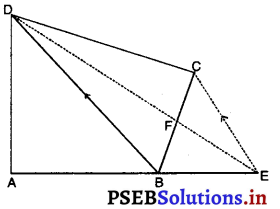
मान लीजिए इतवारी के पास एक चतुर्भुजाकार भूखंड ABCD है।
रचना : AB को E तक बढ़ाइए। BD को मिलाइए और CE || BD खींचिए।
उत्पत्ति : क्योंकि ΔBDC और ΔBDE एक ही आधार BD और एक ही समांतर रेखाओं BD और CE के बीच स्थित है।
∴ ar (ΔBDC) = ar (ΔBDE)
दोनों ओर ar (ΔABD) जोड़ने पर, ar (ΔABD) + ar (ΔBDC) = ar (ΔABD) + ar (ΔBDE)
ar (ABCD) = ar (AED)
अतः, स्वास्थ्य केंद्र के लिए दिया गया भूखंड = ar (CDF)
उक्त भूखंड के बदले इतवारी को मिला भूखंड = ar (BEF)
प्रश्न 13.
ABCD एक समलंब है, जिसमें AB || DC है। AC के समांतर एक रेखा AB को x पर और BC को Y पर प्रतिच्छेद करती है। सिद्ध कीजिए कि ar (ADX) = ar (ACY) है।
हल :
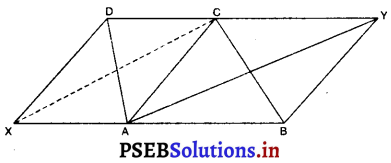
CX को मिलाइए। ΔADX और ΔACX एक ही आधार XA पर तथा एक ही समांतर रेखाओं XA और DC के बीच स्थित हैं।
∴ ar (ΔADX) = ar (ΔACX) ………(i)
साथ ही, ΔACX और ΔACY एक ही आधार CY तथा एक ही समांतर रेखाओं CY और XA के बीच स्थित हैं।
∴ ar (ΔACX) = ar (ΔACY) …(ii)
(i) और (ii) से हमें प्राप्त होता है
ar (ΔADX) = ar (ΔACY).
इति सिद्धम्
![]()
प्रश्न 14.
आकृति में, AP || BQ || CR है। सिद्ध कीजिए कि ar (AQC) = ar (PBR) है।
हल :
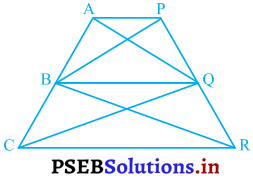
ΔABQ और ΔBPQ एक ही आधार BQ तथा एक ही समांतर रेखाओं AP और BQ के बीच स्थित है।
∴ ar (ΔABQ) = ar (ΔBPQ) …(1)
ΔBQC और ΔBQR एक ही आधार BQ तथा एक ही समांतर रेखाओं BQ और CR के बीच स्थित है।
∴ ar (ΔBQC) = ar (ΔBQR) …(2)
(1) और (2) को जोड़ने पर हमें प्राप्त होता है।
ar (ΔABQ) + ar (ΔBQC) = ar (ΔBPQ) + ar (ΔBQR)
⇒ ar (ΔAQC) = ar (ΔPBR) इति सिद्धम्
प्रश्न 15.
चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि ar (AOD) = ar (BOC) है। सिद्ध कीजिए कि ABCD एक समलंब है।
हल:
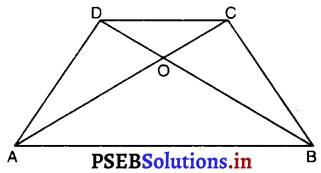
दिया है कि
ar (ΔAOD) = ar (ΔBOC)
दोनों ओर ar (ΔAOB) जोड़ने पर हमें प्राप्त होता है
ar (ΔAOD) + ar (ΔAOB) = ar (ΔBOC) + ar (ΔAOB)
⇒ ar (ΔABD) = ar (ΔABC)
जैसा कि हम जानते हैं कि यदि दो त्रिभुज बराबर क्षेत्रफल एक ही आधार पर स्थित हों, तो वे एक ही समांतर रेखाओं के बीच स्थित होती है। ΔABD और ΔABC एक ही आधार AB पर स्थित हैं और क्षेत्रफल के बराबर हैं।
∴ वे एक ही समांतर रेखाओं AB और DC के बीच स्थित हैं।
या, AB || DC.
अब, चतुर्भुज ABCD में AB || DC
इसलिए, ABCD एक समलंब है। [∵ समलंब में सम्मुख भुजाओं का एक युग्म समांतर होता है।]
![]()
प्रश्न 16.
आकृति में, ar (DRC) = ar (DPC) है और ar (BDP) = ar (ARC) है। दर्शाइए कि दोनों चतुर्भुज ABCD और DCPR समलंब हैं।
हल :
दिया है कि ΔDRC और ΔDPC एक ही आधार DC पर स्थित हैं।
साथ ही, ar (ΔDRC) = ar (ΔDPC) ….(1)
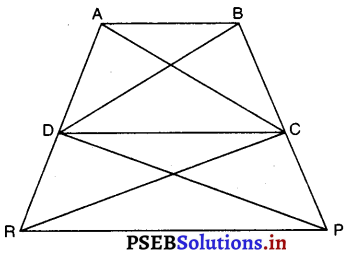
∴ DC || RP [∵ यदि बराबर क्षेत्रफल वाली दो त्रिभुज एक ही आधार पर स्थित हों तो वे सदैव एक ही समांतर रेखाओं के बीच स्थित होती है।]
चतुर्भुज DCPR में,
DC || RP
इसलिए, DCPR एक समलंब है।
साथ ही, दिया है कि
ar (ΔBDP) = ar (ΔARC) ………..(2)
(1) को इस प्रकार भी लिखा जा सकता है।
ar (ΔDPC) = ar (ΔDRC) ……… (3)
(3) को (2) में से घटाने पर हमें प्राप्त होता है।
ar (ΔBDP) – ar (ΔDPC)
= ar (ΔARC) – ar (ΔDRC)
⇒ ar (ΔBDC) = ar (ΔADC)
ΔBDC और ΔADC का बराबर क्षेत्रफल है और एक ही आधार पर स्थित है DC
AB || DC
[∵ यदि बराबर क्षेत्रफल वाली दो त्रिभुज एक ही आधार पर स्थित हों तो वे सदैव एक ही समांतर रेखाओं के बीच स्थित होती है।]
अब चतुर्भुज ABCD में
AB || DC
इसलिए ABCD, एक समलंब है।
