Punjab State Board PSEB 10th Class Social Science Book Solutions Geography Chapter 7 ਜਨਸੰਖਿਆ Textbook Exercise Questions and Answers.
PSEB Solutions for Class 10 Social Science Geography Chapter 7 ਜਨਸੰਖਿਆ
SST Guide for Class 10 PSEB ਜਨਸੰਖਿਆ Textbook Questions and Answers
ਅਭਿਆਸ ਦੇ ਪ੍ਰਸ਼ਨ
I. ਹੇਠ ਲਿਖੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ ਇਕ ਸ਼ਬਦ ਜਾਂ ਇਕ ਲਾਈਨ ਵਿਚ ਲਿਖੋ-
ਪ੍ਰਸ਼ਨ 1.
ਕਿਸੇ ਦੇਸ਼ ਦਾ ਸਭ ਤੋਂ ਵੱਡਮੁੱਲਾ ਸਾਧਨ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਦਿਮਾਗੀ ਤੇ ਸਰੀਰਕ ਤੌਰ ‘ਤੇ ਤੰਦਰੁਸਤ ਨਾਗਰਿਕ ।
ਪ੍ਰਸ਼ਨ 2.
ਆਜ਼ਾਦੀ ਤੋਂ ਪਹਿਲਾਂ ਦੇਸ਼ ਦੀ ਜਨਸੰਖਿਆ ਦੇ ਹੌਲੀ-ਹੌਲੀ ਵਧਣ ਦੇ ਕੀ ਕਾਰਨ ਸਨ ?
ਉੱਤਰ-
ਆਜ਼ਾਦੀ ਤੋਂ ਪਹਿਲਾਂ ਭਾਰਤ ਦੀ ਸਾਧਾਰਨ ਵਾਧਾ-ਦਰ (1%) ਸੀ । ਇਸ ਸਾਧਾਰਨ ਵਾਧੇ ਦਾ ਮੁੱਖ ਕਾਰਨ ਮਹਾਂਮਾਰੀਆਂ, ਲੜਾਈਆਂ ਅਤੇ ਕਾਲ ਦੇ ਕਾਰਨ ਮੌਤ-ਦਰ ਵੱਧ ਹੋਣਾ ਸੀ ।
ਪ੍ਰਸ਼ਨ 3.
ਸਾਲ 1901 ਵਿਚ ਭਾਰਤ ਦੀ ਆਬਾਦੀ ਕਿੰਨੀ ਸੀ ?
ਉੱਤਰ-
ਸਾਲ 1901 ਵਿਚ ਭਾਰਤ ਦੀ ਆਬਾਦੀ 23,83,96,327 (23.8 ਕਰੋੜ) ਸੀ ।
![]()
ਪ੍ਰਸ਼ਨ 4.
ਸਾਲ 1921 ਤੇ 1951 ਨੂੰ ਜਨਸੰਖਿਅਕ ਵੰਡ ਸਾਲ ਕਿਉਂ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
1921 ਅਤੇ 1951 ਦੀ ਜਨਗਣਨਾ ਸਾਲਾਂ ਦੇ ਪਿੱਛੋਂ ਜਨਸੰਖਿਆ ਵਿਚ ਤੇਜ਼ੀ ਨਾਲ ਵਾਧਾ ਹੋਇਆ | ਇਸ ਲਈ ਇਨ੍ਹਾਂ ਸਾਲਾਂ ਨੂੰ ਜਨਸੰਖਿਅਕ ਵੰਡ ਸਾਲ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 5.
ਸਾਲ 2001 ਵਿਚ ਭਾਰਤ ਦੀ ਜਨਸੰਖਿਆ ਕਿੰਨੀ ਸੀ ?
ਉੱਤਰ-
ਸਾਲ 2001 ਵਿਚ ਭਾਰਤ ਦੀ ਜਨਸੰਖਿਆ 1,02,70,15,421 (102.7 ਕਰੋੜ ਸੀ ।
ਪ੍ਰਸ਼ਨ 6.
ਭਾਰਤ ਦੀ ਜਨਸੰਖਿਆ ਦੀ ਨਜ਼ਰ ਤੋਂ ਸੰਸਾਰ ਵਿਚ ਕੀ ਸਥਾਨ ਹੈ ?
ਉੱਤਰ-
ਭਾਰਤ ਦਾ ਜਨਸੰਖਿਆਂ ਦੀ ਨਜ਼ਰ ਤੋਂ ਸੰਸਾਰ ਵਿਚ ਚੀਨ ਦੇ ਪਿੱਛੋਂ ਦੂਸਰਾ ਸਥਾਨ ਹੈ ।
ਪ੍ਰਸ਼ਨ 7.
ਭਾਰਤ ਦੇ ਕਿੰਨੇ ਰਾਜਾਂ ਦੀ ਸੰਖਿਆ 5 ਕਰੋੜ ਤੋਂ ਵੱਧ ਹੈ ?
ਉੱਤਰ-
2011 ਦੀ ਜਨਗਣਨਾ ਅਨੁਸਾਰ ਭਾਰਤ ਵਿਚ 10 ਰਾਜਾਂ ਦੀ ਜਨਸੰਖਿਆ 5 ਕਰੋੜ ਤੋਂ ਵੱਧ ਹੈ ।
ਇਹ ਰਾਜ ਹਨ-ਆਂਧਰਾ ਪ੍ਰਦੇਸ਼, ਬਿਹਾਰ, ਮੱਧ ਪ੍ਰਦੇਸ਼, ਮਹਾਂਰਾਸ਼ਟਰ, ਤਾਮਿਲਨਾਡੂ, ਉੱਤਰ ਪ੍ਰਦੇਸ਼ ਅਤੇ ਪੱਛਮੀ ਬੰਗਲੇ ।
ਪ੍ਰਸ਼ਨ 8.
ਦੇਸ਼ ਦੇ ਸਭ ਤੋਂ ਵੱਧ ਅਤੇ ਸਭ ਤੋਂ ਘੱਟ ਜਨਸੰਖਿਆ ਵਾਲੇ ਰਾਜਾਂ ਦੇ ਨਾਂ ਲਿਖੋ !
ਉੱਤਰ-
ਦੇਸ਼ ਵਿਚ ਸਭ ਤੋਂ ਵੱਧ ਜਨਸੰਖਿਆ ਵਾਲਾ ਰਾਜ ਉੱਤਰ ਪ੍ਰਦੇਸ਼ ਅਤੇ ਸਭ ਤੋਂ ਘੱਟ ਜਨਸੰਖਿਆ ਵਾਲਾ ਰਾਜ ਸਿੱਕਿਮ ਹੈ ।
ਪ੍ਰਸ਼ਨ 9.
ਪੰਜਾਬ ਵਿਚ 2001 ਵਿਚ ਕਿੰਨੀ ਜਨਸੰਖਿਆਂ ਸੀ ਅਤੇ ਜਨਸੰਖਿਆ ਈ ਨਜ਼ਰੇ ਤੋਂ ਪੰਜਾਬ ਦਾ ਦੇਸ਼ ਵਿਚ ਕਿਹੜਾ ਸਥਾਨ ਸੀ ?
ਉੱਤਰ-
ਸਾਲ 2001 ਵਿਚ ਪੰਜਾਬ ਦੀ ਜਨਸੰਖਿਆ ਲਗਪਗ 2 ਕਰੋੜ 40 ਲੱਖ ਸੀ । ਜਨਸੰਖਿਆ ਦੀ ਨਜ਼ਰ ਤੋਂ ਪੰਜਾਬ ਦਾ ਦੇਸ਼ ਵਿਚ ਪੰਦਰਵਾਂ ਸਥਾਨ ਸੀ ।
![]()
ਪ੍ਰਸ਼ਨ 10.
ਪੰਜਾਬ ਵਿਚ ਸਾਰੇ ਦੇਸ਼ ਦੀ ਕਿੰਨੇ ਪ੍ਰਤੀਸ਼ਤ ਵਜੋਂ ਰਹਿੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਪੰਜਾਬ ਵਿਚ ਸਾਰੇ ਦੇਸ਼ ਦੀ ਲਗਪਗ 2.3 ਪ੍ਰਤੀਸ਼ਤ ਜਨਸੰਖਿਆ ਰਹਿੰਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 11.
ਮੈਦਾਨੀ ਭਾਗਾਂ ਵਿਚ ਦੇਸ਼ ਦੇ ਕਿੰਨੇ ਪ੍ਰਤੀਸ਼ਤ ਲੋਕ ਰਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਮੈਦਾਨੀ ਭਾਗਾਂ ਵਿਚ ਦੇਸ਼ ਦੀ 40 ਪ੍ਰਤੀਸ਼ਤ ਜਨਸੰਖਿਆ ਰਹਿੰਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 12.
ਦੇਸ਼ ਦੇ ਪਿੰਡਾਂ ਵਿਚ ਕਿੰਨੇ ਪ੍ਰਤੀਸ਼ਤ ਲੋਕ ਰਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਦੇਸ਼ ਦੀ ਕੁੱਲ ਜਨਸੰਖਿਆ ਦਾ ਲਗਪਗ 71% ਜਨਸੰਖਿਆ ਪੇਂਡੂ ਖੇਤਰਾਂ ਵਿਚ ਰਹਿੰਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 13.
ਦੇਸ਼ ਵਿਚ ਜਨਸੰਖਿਆ ਦੀ ਔਸਤ ਘਣਤਾ ਕਿੰਨੀ ਹੈ ?
ਉੱਤਰ-
ਦੇਸ਼ ਵਿਚ ਜਨਸੰਖਿਆ ਦੀ ਔਸਤ ਘਣਤਾ ਲਗਪਗ 382 ਵਿਅਕਤੀ ਪ੍ਰਤੀ ਵਰਗ ਕਿਲੋਮੀਟਰ (2011 ਵਿਚ) ਹੈ ।
ਪ੍ਰਸ਼ਨ 14.
ਦੋਸ਼ ਵਿਚ ਸਭ ਤੋਂ ਵੱਧ ਅਤੇ ਸਭ ਤੋਂ ਘੱਟ ਜਨਸੰਖਿਆ ਘਣਤਾ ਵਾਲੇ ਰਾਜਾਂ ਦੇ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
2011 ਦੀ ਜਨਗਣਨਾ ਅਨੁਸਾਰ ਦੇਸ਼ ਦਾ ਸਭ ਤੋਂ ਵੱਧ ਘਣਤਾ ਵਾਲਾ ਰਾਜ ਬਿਹਾਰ ਅਤੇ ਸਭ ਤੋਂ ਘੱਟ ਘਣਤਾ ਵਾਲਾ ਰਾਜ ਅਰੁਣਾਚਲ ਪ੍ਰਦੇਸ਼ ਹੈ ।
ਪ੍ਰਸ਼ਨ 15.
ਪੰਜਾਬ ਵਿਚ ਵਸੋਂ ਦੀ ਘਣਤਾ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਪੰਜਾਬ ਵਿਚ ਵਸੋਂ ਦੀ ਘਣਤਾ 550 ਵਿਅਕਤੀ ਪ੍ਰਤੀ ਵਰਗ ਕਿਲੋਮੀਟਰ (2011 ਵਿੱਚ) ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 16.
ਕਿਹੜੇ ਕੇਂਦਰ ਸ਼ਾਸਿਤ ਪ੍ਰਦੇਸ਼ ਦੀ ਜਨਸੰਖਿਅਕ ਘਣਤਾ ਸਭ ਤੋਂ ਵੱਧ ਹੈ ?
ਉੱਤਰ-
ਰਾਸ਼ਟਰੀ ਰਾਜਧਾਨੀ ਖੇਤਰ ਦਿੱਲੀ ਦੀ ਜਨਸੰਖਿਅਕ ਘਣਤਾ ਸਭ ਤੋਂ ਵੱਧ ਹੈ ।
ਪ੍ਰਸ਼ਨ 17.
ਉਮਰ ਬਣਤਰ ਨੂੰ ਨਿਰਧਾਰਿਤ ਕਰਨ ਵਾਲੇ ਤੱਤਾਂ ਦਾ ਨਾਂ ਦੱਸੋ।
ਉੱਤਰ-
ਉਮਰ ਬਣਤਰ ਨੂੰ ਨਿਰਧਾਰਿਤ ਕਰਨ ਵਾਲੇ ਤੱਤਾਂ ਦੇ ਨਾਂ ਹਨ-
- ਪੈਦਾਇਸ਼ (fertility)
- ਮਿਤਤਾ (mortality)
- ਪ੍ਰਵਾਸ (migration) ।
ਪ੍ਰਸ਼ਨ 18.
ਦੇਸ਼ ਵਿਚ 0-14 ਸਾਲ ਤਕ ਦੇ ਉਮਰ ਵਰਗ ਵਿਚ ਕਿੰਨੇ ਪ੍ਰਤੀਸ਼ਤ ਜਨਸੰਖਿਆ ਮਿਲਦੀ ਹੈ ?
ਉੱਤਰ-
ਦੇਸ਼ ਵਿਚ 0-14 ਉਮਰ ਵਰਗ ਵਿਚ 37.2 ਪ੍ਰਤੀਸ਼ਤ ਜਨਸੰਖਿਆ ਹੈ ।
ਪ੍ਰਸ਼ਨ 19.
ਦੇਸ਼ ਵਿਚ 15 ਤੋਂ 65 ਸਾਲ ਤਕ ਦੇ ਉਮਰ ਵਰਗ ਵਿਚ ਕਿੰਨੇ ਪ੍ਰਤੀਸ਼ਤ ਲੋਕ ਰਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਦੇਸ਼ ਵਿਚ 15 ਤੋਂ 65 ਸਾਲ ਉਮਰ ਵਰਗ ਵਿਚ 58.4 ਪ੍ਰਤੀਸ਼ਤ ਜਨਸੰਖਿਆ ਹੈ ।
ਪ੍ਰਸ਼ਨ 20.
ਦੇਸ਼ ਦੀ ਜਨਸੰਖਿਆ ਵਿਚ ਕਿੰਨੇ ਪ੍ਰਤੀਸ਼ਤ ਵੋਟਰ ਹਨ ?
ਉੱਤਰ-
ਦੇਸ਼ ਦੀ ਜਨਸੰਖਿਆ ਵਿਚ 60 ਪ੍ਰਤੀਸ਼ਤ ਵੋਟਰ ਹਨ ।
![]()
ਪ੍ਰਸ਼ਨ 21.
ਲਿੰਗ-ਅਨੁਪਾਤ ਤੋਂ ਤੁਹਾਡਾ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਲਿੰਗ-ਅਨੁਪਾਤ ਤੋਂ ਭਾਵ ਪਤੀ ਇਕ ਹਜ਼ਾਰ ਮਰਦਾਂ ਤੇ ਔਰਤਾਂ ਦੀ ਸੰਖਿਆ ਤੋਂ ਹੈ ।
ਪ੍ਰਸ਼ਨ 22.
ਸਾਲ 2001 ਵਿਚ ਦੇਸ਼ ਦੀ ਵਸੋਂ ਦਾ ਲਿੰਗ-ਅਨੁਪਾਤ ਕੀ ਸੀ ?
ਉੱਤਰ-
2001 ਵਿਚ ਦੇਸ਼ ਦੀ ਵਸੋਂ ਦਾ ਲਿੰਗ-ਅਨੁਪਾਤ 1000 : 933 ਸੀ । (2011 ਵਿਚ 1000 : 944)
ਪ੍ਰਸ਼ਨ 23.
ਦੇਸ਼ ਦੇ ਪੇਂਡੂ ਅਤੇ ਸ਼ਹਿਰੀ ਖੇਤਰਾਂ ਵਿਚ ਲਿੰਗ-ਅਨੁਪਾਤ ਦੇ ਤੇਜ਼ੀ ਨਾਲ ਘਟਣ ਦੇ ਕੀ ਕਾਰਨ ਹਨ ?
ਉੱਤਰ-
ਲਿੰਗ-ਅਨੁਪਾਤ ਦੇ ਤੇਜ਼ੀ ਨਾਲ ਘਟਣ ਦੇ ਕਾਰਨ ਹਨ-
- ਔਰਤਾਂ ਦਾ ਦਰਜਾ ਹੇਠਾਂ ਹੋਣਾ ।
- ਜਨਗਣਨਾ ਦੇ ਸਮੇਂ ਔਰਤਾਂ ਦੀ ਬਜਾਏ ਘੱਟ ਗਣਨਾ ਕਰਨਾ ਜਾਂ ਮਰਦਾਂ ਦੀ ਗਣਨਾ ਵੱਧ ਕਰਨਾ ।
- ਲੜਕੀਆਂ ਦੀ ਜਨਮ-ਦਰ ਘੱਟ ਹੋਣਾ ।
- ਔਰਤ ਗਰਭ ਹੱਤਿਆ (female foeticide)
ਪ੍ਰਸ਼ਨ 24.
ਦੇਸ਼ ਦੇ ਸਿੱਖ ਫਿਰਕੇ ਦੇ ਲੋਕਾਂ ਦਾ ਲਿੰਗ-ਅਨੁਪਾਤ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਦੋਸ਼ ਦੋ ਸਿੱਖ ਫਿਰਕੇ ਵਿਚ ਲਿੰਗ-ਅਨੁਪਾਤ 1000 : 888 ਹੈ ।
ਪ੍ਰਸ਼ਨ 25.
ਆਰਥਿਕ ਆਧਾਰ ‘ਤੇ ਭਾਰਤ ਦੀ ਜਨਸੰਖਿਆ ਨੂੰ ਕਿਹੜੇ ਦੋ ਭਾਗਾਂ ਵਿਚ ਵੰਡਿਆ ਜਾ ਸਕਦਾ ਹੈ ?
ਉੱਤਰ-
ਆਰਥਿਕ ਆਧਾਰ ‘ਤੇ ਜਨਸੰਖਿਆ ਨੂੰ ਦੋ ਭਾਗਾਂ ਵਿਚ ਵੰਡਿਆ ਜਾ ਸਕਦਾ ਹੈ-
- ਕਾਮਿਆਂ ਦੀ ਜਨਸੰਖਿਆ
- ਅਕਾਮਿਆਂ ਦੀ ਜਨਸੰਖਿਆ
![]()
ਪ੍ਰਸ਼ਨ 26.
ਦੇਸ਼ ਦੇ ਕਿਸ ਰਾਜ ਵਿਚ ਮੁੱਖ ਕਾਮਿਆਂ ਦੀ ਪ੍ਰਤੀਸ਼ਤ ਮਾਤਰਾ ਸਭ ਤੋਂ ਵੱਧ ਹੈ ?
ਉੱਤਰ-
ਦੇਸ਼ ਵਿਚ ਮੁੱਖ ਕਾਮਿਆਂ ਦੀ ਸਭ ਤੋਂ ਵੱਧ ਪ੍ਰਤੀਸ਼ਤ ਮਾਤਰਾ ਆਂਧਰਾ ਪ੍ਰਦੇਸ਼ ਵਿਚ ਹੈ ।
ਪ੍ਰਸ਼ਨ 27.
ਕੰਮ ਦੇ ਆਧਾਰ ‘ਤੇ ਜਨਸੰਖਿਆ ਦਾ ਕਾਮਿਆਂ ਅਤੇ ਅਕਾਮਿਆਂ ਦੇ ਵਰਗਾਂ ਵਿਚ ਵੰਡਣ ਦਾ ਵਿਚਾਰ ਭਾਰਤੀ ਲੋਕ ਗਿਣਤੀ ਵਿਚ ਪਹਿਲੀ ਵਾਰ ਕਿਸ ਸਾਲ ਵਿਚ ਆਇਆ ?
ਉੱਤਰ-
ਕੰਮ ਦੇ ਆਧਾਰ ‘ਤੇ ਜਨਸੰਖਿਆ ਦਾ ਕਾਮਿਆਂ ਅਤੇ ਅਕਾਮਿਆਂ ਵਿਚ ਵੰਡਣ ਦਾ ਵਿਚਾਰ ਪਹਿਲੀ ਵਾਰ 1961 ਦੀ ਗਣਨਾ ਦੇ ਸਮੇਂ ਆਇਆ।
ਪ੍ਰਸ਼ਨ 28.
ਪੇਂਡੂ ਖੇਤਰਾਂ ਵਿਚ ਮਜ਼ਦੂਰਾਂ ਦੀ ਕਿੰਨੇ ਪ੍ਰਤੀਸ਼ਤ ਮਾਤਰਾ ਹੈ ?
ਉੱਤਰ-
ਪੇਂਡੂ ਖੇਤਰਾਂ ਵਿਚ ਮਜ਼ਦੂਰਾਂ ਦਾ ਪ੍ਰਤੀਸ਼ਤ 40.1% ਹੈ ।
II. ਹੇਠਾਂ ਲਿਖੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ ਲਗਪਗ 50-60 ਸ਼ਬਦਾਂ ਵਿਚ ਦਿਓ-
ਪ੍ਰਸ਼ਨ 1.
ਰਾਜਾਂ ਵਿਚ ਬਹੁਤ ਜ਼ਿਆਦਾ ਅਸਮਾਨ ਜਨਸੰਖਿਅਕ ਵੰਡ ਨਾਲ ਦੇਸ਼ ਵਿਚ ਕਿਹੜੀਆਂ ਸਮੱਸਿਆਵਾਂ ਪੈਦਾ ਹੋ ਰਹੀਆਂ ਹਨ ?
ਉੱਤਰ-
ਭਾਰਤ ਵਿਚ 28 ਰਾਜ ਹਨ । ਇਨ੍ਹਾਂ ਰਾਜਾਂ ਵਿਚ ਬਹੁਤ ਜ਼ਿਆਦਾ ਅਸਮਾਨ ਜਨਸੰਖਿਆ ਵੰਡ ਹੈ । ਜਨਸੰਖਿਆ ਦੀ ਅਸਮਾਨ ਵੰਡ ਦੇ ਕਾਰਨ ਅਨੇਕਾਂ ਸਮੱਸਿਆਵਾਂ ਪੈਦਾ ਹੋ ਗਈਆਂ ਹਨ ਜਿਨ੍ਹਾਂ ਦਾ ਵਰਣਨ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹੈ-
- ਦੂਰ-ਦੂਰ ਤਕ ਫੈਲੀਆਂ ਪੇਂਡੂ ਬਸਤੀਆਂ ਨੂੰ ਆਪਸ ਵਿਚ ਸੜਕਾਂ ਦੁਆਰਾ ਅਤੇ ਨੇੜਲੇ ਸ਼ਹਿਰਾਂ ਦੇ ਨਾਲ ਜੋੜਨ ਦੀ ਵੱਡੀ ਸਮੱਸਿਆ ਹੈ ।
- ਇਨ੍ਹਾਂ ਪੇਂਡੂ ਬਸਤੀਆਂ ਦੇ ਨਿਵਾਸੀਆਂ ਨੂੰ ਮੁੱਢਲੀਆਂ ਸਹੂਲਤਾਂ ਪ੍ਰਦਾਨ ਕਰਨਾ ਬਹੁਤ ਮੁਸ਼ਕਿਲ ਅਤੇ ਮਹਿੰਗਾ ਕੰਮ ਹੈ ।
- ਵੱਡੇ-ਵੱਡੇ ਸ਼ਹਿਰਾਂ ਵਿਚ ਪ੍ਰਦੂਸ਼ਣ, ਆਵਾਜਾਈ, ਮਕਾਨਾਂ ਦੀ ਘਾਟ ਵਰਗੀਆਂ ਹੋਰ ਸਮੱਸਿਆਵਾਂ ਪੈਦਾ ਹੋ ਗਈਆਂ ਹਨ ।
ਪ੍ਰਸ਼ਨ 2.
ਭਾਰਤ ਵਿਚ ਜਨਸੰਖਿਆ ਦੀ ਵੰਡ ਤੇ ਕਿਹੜੇ-ਕਿਹੜੇ ਤੱਤਾਂ ਦਾ ਜ਼ਿਆਦਾ ਪ੍ਰਭਾਵ ਹੈ ? ਕੋਈ ਤਿੰਨ ਤੱਥ (ਪ੍ਰਭਾਵ ਲਿਖੋ ।
ਉੱਤਰ-
ਭਾਰਤ ਵਿਚ ਜਨਸੰਖਿਆ ਦੀ ਵੰਡ ਬਰਾਬਰ ਨਹੀਂ ਹੈ । ਇਸੇ ਦੇ ਲਈ ਅੱਗੇ ਲਿਖੇ ਅਨੇਕਾਂ ਤੱਤ ਜ਼ਿੰਮੇਵਾਰ ਹਨ-
- ਭੂਮੀ ਦੀ ਉਪਜਾਊਪਨ – ਭਾਰਤ ਵਿਚ ਜਿਨ੍ਹਾਂ ਰਾਜਾਂ ਵਿਚ ਉਪਜਾਊ ਭੂਮੀ ਦਾ ਜ਼ਿਆਦਾ ਵਿਸਥਾਰ ਹੈ, ਉੱਥੇ ਜਨਸੰਖਿਆ ਦੀ ਘਣਤਾ ਵੱਧ ਹੈ । ਉੱਤਰ ਪ੍ਰਦੇਸ਼ ਅਤੇ ਬਿਹਾਰ ਅਜਿਹੇ ਹੀ ਰਾਜ ਹਨ ।
- ਵਰਖਾ ਦੀ ਮਾਤਰਾ – ਵੱਧ ਵਰਖਾ ਵਾਲੇ ਭਾਗਾਂ ਵਿਚ ਜਨਸੰਖਿਆ ਦੀ ਘਣਤਾ ਵੱਧ ਹੁੰਦੀ ਹੈ । ਉੱਤਰੀ ਭਾਰਤ ਵਿਚ ਪੂਰਬ ਤੋਂ ਪੱਛਮ ਨੂੰ ਜਾਂਦੇ ਹੋਏ ਵਰਖਾ ਦੀ ਮਾਤਰਾ ਘੱਟ ਹੁੰਦੀ ਹੈ । ਇਸ ਲਈ ਜਨਸੰਖਿਆ ਦੀ ਘਣਤਾ ਵੀ ਘੱਟਦੀ ਜਾਂਦੀ ਹੈ ।
- ਜਲਵਾਯੂ – ਜਿੱਥੋਂ ਦੀ ਜਲਵਾਯੂ ਸਿਹਤ ਦੇ ਲਈ ਠੀਕ ਹੈ ਉੱਥੇ ਵੀ ਜਨਸੰਖਿਆ ਦੀ ਘਣਤਾ ਵੱਧ ਹੁੰਦੀ ਹੈ । ਇਸ ਦੇ ਉਲਟ ਅਜਿਹੇ ਦੇਸ਼ਾਂ ਵਿਚ ਜਨਸੰਖਿਆ ਦੀ ਘਣਤਾ ਘੱਟ ਹੁੰਦੀ ਹੈ ਜਿੱਥੋਂ ਦੀ ਜਲਵਾਯੂ ਸਿਹਤ ਲਈ ਠੀਕ ਨਾ ਹੋਵੇ | ਆਸਾਮ ਵਿਚ ਵਰਖਾ ਵੱਧ ਹੋਣ ਤੇ ਵੀ ਜਨਸੰਖਿਆ ਦੀ ਘਣਤਾ ਘੱਟ ਹੈ ਕਿਉਂਕਿ ਉੱਥੇ ਜ਼ਿਆਦਾ ਨਮੀ ਦੇ ਕਾਰਨ ਮਲੇਰੀਏ ਦਾ ਪ੍ਰਕੋਪ ਜ਼ਿਆਦਾ ਰਹਿੰਦਾ ਹੈ ।
- ਆਵਾਜਾਈ ਦੇ ਉੱਨਤ ਸਾਧਨ – ਆਵਾਜਾਈ ਦੇ ਸਾਧਨਾਂ ਦੇ ਵੱਧ ਵਿਕਾਸ ਦੇ ਕਾਰਨ ਵਪਾਰ ਵਿਚ ਉੱਨਤੀ ਤੇਜ਼ ਹੋ ਜਾਂਦੀ ਹੈ, ਜਿਸ ਨਾਲ ਜਨਸੰਖਿਆ ਦੀ ਘਣਤਾ ਵੀ ਜ਼ਿਆਦਾ ਹੋ ਜਾਂਦੀ ਹੈ । ਉੱਤਰ ਪ੍ਰਦੇਸ਼, ਪੱਛਮੀ ਬੰਗਾਲ, ਬਿਹਾਰ ਅਤੇ ਝਾਰਖੰਡ ਆਦਿ ਰਾਜਾਂ ਵਿਚ ਜ਼ਿਆਦਾ ਜਨਸੰਖਿਆ ਹੋਣ ਦਾ ਇਕ ਕਾਰਨ ਆਵਾਜਾਈ ਦੇ ਸਾਧਨਾਂ ਦਾ ਵਿਕਾਸ ਹੈ ।
- ਉਦਯੋਗਿਕ ਵਿਕਾਸ – ਜਿਨ੍ਹਾਂ ਸਥਾਨਾਂ ਤੇ ਉਦਯੋਗ ਸਥਾਪਿਤ ਹੋ ਜਾਂਦੇ ਹਨ ਉੱਥੇ ਜਨਸੰਖਿਆ ਦੀ ਘਣਤਾ ਵੱਧ ਜਾਂਦੀ ਹੈ । ਇਸ ਦਾ ਕਾਰਨ ਇਹ ਹੈ ਕਿ ਉਦਯੋਗਿਕ ਖੇਤਰਾਂ ਵਿਚ ਰੋਜ਼ੀ ਕਮਾਉਣਾ ਸਰਲ ਹੁੰਦਾ ਹੈ । ਦਿੱਲੀ, ਕੋਲਕਾਤਾ, ਮੁੰਬਈ ਆਦਿ ਨਗਰਾਂ ਵਿਚ ਉਦਯੋਗਿਕ ਵਿਕਾਸ ਦੇ ਕਾਰਨ ਹੀ ਜਨਸੰਖਿਆ ਜ਼ਿਆਦਾ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 3.
ਜਨਸੰਖਿਆ ਦੇ ਆਰਥਿਕ ਢਾਂਚੇ ਦੇ ਅਧਿਐਨ ਦਾ ਕੀ ਮਹੱਤਵ ਹੈ ?
ਉੱਤਰ-
ਜਨਸੰਖਿਆ ਦੇ ਆਰਥਿਕ ਢਾਂਚੇ ਦਾ ਵਿਸ਼ੇਸ਼ ਮਹੱਤਵ ਹੈ-
- ਇਸ ਤੋਂ ਸਾਨੂੰ ਪਤਾ ਲੱਗਦਾ ਹੈ ਕਿ ਦੇਸ਼ ਦੀ ਜਨਸੰਖਿਆ ਦਾ ਕਿੰਨਾ ਹਿੱਸਾ ਕਾਰਜਸ਼ੀਲ ਹੈ ਅਤੇ ਉਹ ਕਿਸ ਕੰਮ ਵਿਚ ਲੱਗਾ ਹੋਇਆ ਹੈ ।
- ਇਹ ਢਾਂਚਾ ਕਿਸੇ ਖੇਤਰ ਦੀ ਜਨਸੰਖਿਅਕ ਅਤੇ ਸੱਭਿਆਚਾਰ ਨੂੰ ਪ੍ਰਗਟ ਕਰਦੀ ਹੈ । ਇਸ ’ਤੇ ਹੀ ਉਸ ਦੇਸ਼ ਦੇ ਭਵਿੱਖ ਦਾ ਸਮਾਜਿਕ ਅਤੇ ਆਰਥਿਕ ਵਿਕਾਸ ਦਾ ਪੱਧਰ ਆਧਾਰਿਤ ਹੁੰਦਾ ਹੈ ।
- ਆਰਥਿਕ ਢਾਂਚੇ ਤੋਂ ਸਾਨੂੰ ਪਤਾ ਲਗਦਾ ਹੈ ਕਿ ਦੇਸ਼ ਕਿਸ ਆਰਥਿਕ ਖੇਤਰ ਵਿਚ ਪੱਛੜਿਆ ਹੋਇਆ ਹੈ । ਇਸ ਲਈ ਉਸ ਖੇਤਰ ਦੇ ਵਿਕਾਸ ਲਈ ਉੱਚਿਤ ਯੋਜਨਾ ਬਣਾ ਸਕਦੇ ਹਾਂ ।
ਪ੍ਰਸ਼ਨ 4.
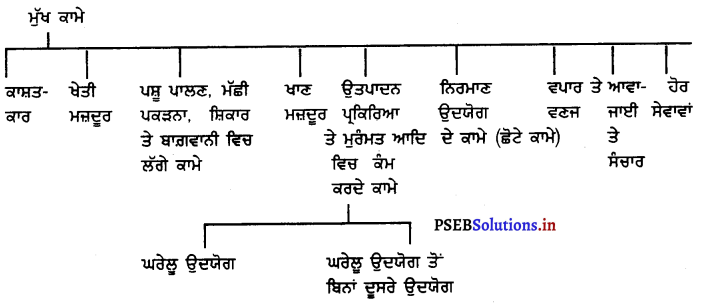
ਮੁੱਖ ਮਜ਼ਦੂਰਾਂ ਨੂੰ ਕਿੰਨੀਆਂ ਉਦਯੋਗਿਕ ਸ਼੍ਰੇਣੀਆਂ ਵਿਚ ਵੰਡਿਆ ਜਾ ਸਕਦਾ ਹੈ ? ਉਹਨਾਂ ਦੇ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਹੇਠ ਲਿਖੀ ਸਾਰਣੀ ਤੋਂ ਮਜ਼ਦੂਰ ਸ਼੍ਰੇਣੀਆਂ ਸਪੱਸ਼ਟ ਹੋ ਜਾਣਗੀਆਂ
(ਦੋ ਉਦਯੋਗਿਕ ਸ਼੍ਰੇਣੀਆਂ-ਮੁੱਖ ਕਾਮੇ ਅਤੇ ਛੋਟੇ ਕਾਮੇ)
ਪ੍ਰਸ਼ਨ 5.
ਭਾਰਤ ਵਿਚ ਇਸਤਰੀ ਮਜ਼ਦੂਰਾਂ ਦੀ ਪ੍ਰਤੀਸ਼ਤ ਮਾਤਰਾ ਮਰਦ ਮਜ਼ਦੂਰਾਂ ਤੋਂ ਘੱਟ ਕਿਉਂ ਹੈ ?
ਉੱਤਰ-
ਦੇਸ਼ ਵਿਚ ਸਭ ਮਜ਼ਦੂਰਾਂ ਦਾ ਪ੍ਰਤੀਸ਼ਤ (ਅਸਮ ਅਤੇ ਜੰਮੂ-ਕਸ਼ਮੀਰ ਨੂੰ ਛੱਡ ਕੇ) 37.50 ਪ੍ਰਤੀਸ਼ਤ ਹੈ । ਦੂਸਰੇ ਸ਼ਬਦਾਂ ਵਿਚ ਅਸੀਂ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਦੇਸ਼ ਦੀ ਕੁੱਲ ਜਨਸੰਖਿਆ ਦਾ ਲਗਪਗ ਇਕ-ਤਿਹਾਈ ਭਾਗ ਹੀ ਆਰਥਿਕ ਰੂਪ ਵਿਚ ਕਾਰਜ਼ਸ਼ੀਲ ਹੈ । ਇਸ ਦੇ ਮੁੱਖ ਕਾਰਨ ਹੇਠ ਲਿਖੇ ਹਨ-
- ਤੇਜ਼ੀ ਨਾਲ ਵੱਧ ਰਹੀ ਜਨਸੰਖਿਆ ਦੇ ਕਾਰਨ ਭਾਰਤ ਵਿੱਚ ਬੱਚਿਆਂ (ਗੈਰ-ਮਜ਼ਦੂਰਾਂ ਦਾ ਅਨੁਪਾਤ ਵਧੇਰੇ ਬਣਿਆ ਰਹਿੰਦਾ ਹੈ । ਇਸ ਨਾਲ ਮਜ਼ਦੂਰਾਂ ਦਾ ਪਤੀਸ਼ਤ ਘੱਟ ਹੋ ਜਾਂਦਾ ਹੈ ਇਸ ਦਾ ਮੁੱਖ ਕਾਰਨ ਹੈ । ਬੱਚਿਆਂ ਦੀ ਸੰਖਿਆ ਵਧਣ ਨਾਲ ਨਿਰਭਰਾਂ ਦੀ ਸੰਖਿਆ ਵੀ ਵੱਧ ਜਾਂਦੀ ਹੈ ।
- ਸਾਡੀਆਂ ਸਮਾਜਿਕ ਸਮਾਨਤਾਵਾਂ ਦੇ ਕਾਰਨ ਇਸਤਰੀਆਂ ਨੂੰ ਘਰ ਤੋਂ ਬਾਹਰ ਕੰਮ ਨਹੀਂ ਕਰਨ ਦਿੱਤਾ ਜਾਂਦਾ ।
- ਇਸਤਰੀਆਂ ਵਿਚ ਸਿੱਖਿਆ ਅਤੇ ਜਾਗਰੂਕਤਾ ਦੀ ਘਾਟ ਵੀ ਇਸ ਦਾ ਕਾਰਨ ਹੈ ।
ਪ੍ਰਸ਼ਨ 6.
ਭਾਰਤ ਨੂੰ ਪਿੰਡਾਂ ਦਾ ਦੇਸ਼ ਕਿਉਂ ਕਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਇਸ ਵਿਚ ਕੋਈ ਸ਼ੱਕ ਨਹੀਂ ਹੈ ਕਿ ਭਾਰਤ ਪਿੰਡਾਂ ਦਾ ਦੇਸ਼ ਹੈ । ਹੇਠ ਲਿਖੇ ਤੱਥਾਂ ਤੋਂ ਇਹ ਗੱਲ ਸਪੱਸ਼ਟ ਹੋ ਜਾਵੇਗੀ-
- ਦੇਸ਼ ਦੀ ਜ਼ਿਆਦਾਤਰ ਜਨਸੰਖਿਆ ਪੇਂਡੂ ਖੇਤਰਾਂ ਵਿਚ ਰਹਿੰਦੀ ਹੈ ।
- ਦੇਸ਼ ਦੀ ਕੁੱਲ ਜਨਸੰਖਿਆ ਦਾ ਲਗਪਗ 71% ਭਾਗ ਪੇਂਡੂ ਖੇਤਰਾਂ ਵਿਚ ਰਹਿੰਦਾ ਹੈ ।
- ਦੇਸ਼ ਵਿਚ 5 ਲੱਖ 50 ਹਜ਼ਾਰ ਤੋਂ ਜ਼ਿਆਦਾ ਪੇਂਡੂ ਬਸਤੀਆਂ (Rural settlements) ਹਨ ਜਦ ਕਿ ਕੁੱਲ ਸ਼ਹਿਰੀ ਜਨਸੰਖਿਆ ਦਾ ਦੋ-ਤਿਹਾਈ ਭਾਗ ਦੇਸ਼ ਦੇ ਵੱਡੇ ਨਗਰਾਂ ਵਿਚ ਵੱਸਿਆ ਹੋਇਆ ਹੈ ।
- ਦੇਸ਼ ਵਿਚ ਕੁੱਲ ਮਜ਼ਦੂਰਾਂ ਦਾ 40.1 ਪ੍ਰਤੀਸ਼ਤ ਪੇਂਡੂ ਖੇਤਰਾਂ ਵਿਚ 30.2 ਪ੍ਰਤੀਸ਼ਤ ਨਗਰਾਂ ਵਿਚ ਨਿਵਾਸ ਕਰਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 7.
ਦੇਸ਼ ਵਿਚ ਬੋਲੀਆਂ ਜਾਣ ਵਾਲੀਆਂ ਮੁੱਖ ਭਾਸ਼ਾਵਾਂ ਦੇ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਭਾਰਤ ਵਿਚ ਅਨੇਕਾਂ ਭਾਸ਼ਾਵਾਂ ਬੋਲੀਆਂ ਜਾਂਦੀਆਂ ਹਨ | ਅਸਾਮੀ, ਉੜੀਆ, ਊਰਦੂ, ਕੰਨੜ, ਕਸ਼ਮੀਰੀ, ਗੁਜਰਾਤੀ, ਤਾਮਿਲ, ਤੇਲਗੂ, ਪੰਜਾਬੀ, ਬੰਗਲਾ, ਮਰਾਠੀ, ਮਲਿਆਲਮ, ਸੰਸਕ੍ਰਿਤ, ਸਿੰਧੀ ਅਤੇ ਹਿੰਦੀ ਭਾਰਤ ਦੀਆਂ ਮੁੱਖ ਭਾਸ਼ਾਵਾਂ ਹਨ । ਇਹਨਾਂ ਸਭ ਭਾਸ਼ਾਵਾਂ ਨੂੰ ਸੰਵਿਧਾਨਿਕ ਦਰਜਾ ਦਿੱਤਾ ਗਿਆ ਹੈ । ਦੱਖਣ ਭਾਰਤ ਦੀਆਂ ਚਾਰ ਭਾਸ਼ਾਵਾਂ ਤਮਿਲ, ਤੇਲਗੂ, ਕੰਨੜ ਅਤੇ ਮਲਿਆਲਮ ਦੀ ਉਤਪੱਤੀ ਵਿੜ ਤੋਂ ਹੋਈ ਹੈ ।
ਭਾਰਤ ਵਿਚ ਬਹੁਤ ਵੱਡੀ ਸੰਖਿਆ ਵਿਚ ਲੋਕ ਹਿੰਦੀ ਬੋਲਦੇ ਹਨ । ਨਾਲ ਹੀ ਅਨੇਕਾਂ ਲੋਕ ਇਸ ਭਾਸ਼ਾ ਨੂੰ ਸਮਝ ਲੈਂਦੇ ਹਨ, ਭਾਵੇਂ ਇਹ ਉਹਨਾਂ ਦੀ ਮਾਤ-ਭਾਸ਼ਾ ਨਹੀਂ ਹੈ । ਹਿੰਦੀ ਨੂੰ ਰਾਜ ਭਾਸ਼ਾ ਦਾ ਸਥਾਨ ਮਿਲਿਆ ਹੋਇਆ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 8.
ਭਾਰਤ ਵਿਚ ਜਨਸੰਖਿਆ ਦੇ ਖੇਤਰੀ ਵੰਡ ਦੀਆਂ ਮਹੱਤਵਪੂਰਨ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਕੀ ਹਨ ?
ਉੱਤਰ-
ਭਾਰਤ ਵਿਚ ਜਨਸੰਖਿਆ ਵੰਡ ਦੀਆਂ ਕੁੱਝ ਮਹੱਤਵਪੂਰਨ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਅੱਗੇ ਲਿਖੀਆਂ ਹਨ-
- ਭਾਰਤ ਵਿਚ ਜਨਸੰਖਿਆ ਦੀ ਵੰਡ ਬਹੁਤ ਅਸਮਾਨ ਹੈ । ਨਦੀਆਂ ਦੀਆਂ ਘਾਟੀਆਂ ਅਤੇ ਸਮੁੰਦਰ ਤੇ ਤਟਵਰਤੀ ਮੈਦਾਨਾਂ ਵਿਚ ਜਨਸੰਖਿਆ ਦੀ ਵੰਡ ਬਹੁਤ ਸੰਘਣੀ ਹੈ, ਪਰੰਤੂ ਪਰਬਤੀ ਮਾਰੂਥਲੀ ਅਤੇ ਕਾਲ-ਪੀੜਤ ਖੇਤਰਾਂ ਵਿਚ ਜਨਸੰਖਿਆ ਵੰਡ ਬਹੁਤ ਵਿਰਲੀ ਹੈ ।
- ਦੇਸ਼ ਦੀ ਕੁੱਲ ਜਨਸੰਖਿਆ ਦਾ ਲਗਪਗ 71% ਭਾਗ ਪੇਂਡੂ ਖੇਤਰਾਂ ਵਿਚ ਅਤੇ 29% ਸ਼ਹਿਰਾਂ ਵਿਚ ਰਹਿੰਦਾ ਹੈ ।
ਸ਼ਹਿਰੀ ਜਨਸੰਖਿਆ ਦਾ ਭਾਰੀ ਜਮਾਅ ਵੱਡੇ ਸ਼ਹਿਰਾਂ ਵਿਚ ਹੈ । ਕੁੱਲ ਸ਼ਹਿਰੀ ਜਨਸੰਖਿਆ ਦਾ ਦੋ ਤਿਹਾਈ ਭਾਗ ਇਕ ਲੱਖ ਜਾਂ ਇਸ ਤੋਂ ਵੱਧ ਆਬਾਦੀ ਵਾਲੇ ਪਹਿਲੀ ਸ਼੍ਰੇਣੀ ਦੇ ਸ਼ਹਿਰਾਂ ਵਿਚ ਰਹਿੰਦਾ ਹੈ । - ਦੇਸ਼ ਦੇ ਘੱਟ ਗਿਣਤੀ ਫ਼ਿਰਕਿਆਂ ਦਾ ਬਹੁਤ ਸੰਵੇਦਨਸ਼ੀਲ ਤੇ ਮਹੱਤਵਪੂਰਨ ਬਾਹਰਲੇ ਸਰਹੱਦੀ ਖੇਤਰਾਂ ਵਿਚ ਵਸਣਾ ਹੈ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ‘ਤੇ ਉੱਤਰ-ਪੱਛਮੀ ਭਾਰਤ ਵਿਚ ਭਾਰਤ-ਪਾਕਿ ਸਰਹੱਦ ਦੇ ਕੋਲ ਪੰਜਾਬ ਵਿਚ ਸਿੱਖਾਂ ਅਤੇ ਜੰਮੂਕਸ਼ਮੀਰ ਦੇ ਮੁਸਲਮਾਨਾਂ ਦੀ ਗਿਣਤੀ ਵੱਧ ਹੈ ।
- ਇਕ ਪਾਸੇ ਤਟਵਰਤੀ ਮੈਦਾਨਾਂ ‘ਤੇ ਨਦੀਆਂ ਦੀਆਂ ਘਾਟੀਆਂ ਵਿਚ ਜਨਸੰਖਿਆ ਦਾ ਭਾਰੀ ਜਮਾਓ ਮਿਲਦਾ ਹੈ ਤਾਂ ਦੂਸਰੇ ਪਾਸੇ ਪਹਾੜੀ, ਪਠਾਰੀ ਤੇ ਰੇਗਿਸਤਾਨੀ ਭਾਗਾਂ ਵਿਚ ਜਨਸੰਖਿਆ ਵਿਰਲੀ ਹੈ । ਇਹ ਵੰਡ ਇਕ ਜਨਸੰਖਿਅਕੀ ਵੰਡ (demographic divide) ਵਰਗੀ ਲਗਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 9.
ਦੇਸ਼ ਦੇ ਵੱਧ ਜਨਸੰਖਿਅਕ ਘਣਤਾ ਵਾਲੇ ਖੇਤਰ ਕਿਹੜੇ ਹਨ ?
ਉੱਤਰ-
ਉੱਤਰੀ ਮੈਦਾਨ, ਪੱਛਮੀ ਤਟਵਰਤੀ ਮੈਦਾਨ ਅਤੇ ਪੂਰਬੀ ਤਟਵਰਤੀ ਮੈਦਾਨ ਦੇ ਡੈਲਟਾਈ ਖੇਤਰਾਂ ਵਿਚ ਜਨਸੰਖਿਆ ਸੰਘਣੀ ਵਸੀ ਹੋਈ ਹੈ । ਉਹਨਾਂ ਦੇਸ਼ਾਂ ਦੀ ਭੂਮੀ ਉਪਜਾਉ ਹੈ ਅਤੇ ਖੇਤੀ ਦੀਆਂ ਸਹੂਲਤਾਂ ਪ੍ਰਾਪਤ ਹਨ । ਇਸ ਲਈ ਇਨ੍ਹਾਂ ਦੀ ਜਨਸੰਖਿਆ ਸੰਘਣੀ ਹੈ । ਇਕ ਗੱਲ ਹੋਰ ਜਿਉਂ-ਜਿਉਂ ਅਸੀਂ ਪੂਰਬ ਤੋਂ ਪੱਛਮ ਵੱਲ ਜਾਂਦੇ ਹਾਂ, ਸੁੱਕਾਪਨ ਵੱਧਦਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਜਨ-ਘਣਤਾ ਘਟਦੀ ਜਾਂਦੀ ਹੈ । ਇਹੀ ਕਾਰਨ ਹੈ ਕਿ ਪੁਰਬ ਵਿਚ ਸਥਿਤ ਪੱਛਮੀ ਬੰਗਾਲ ਦੀ ਘਣਤਾ ਪੰਜਾਬ ਅਤੇ ਹਰਿਆਣਾ ਦੀ ਬਜਾਏ ਪੱਛਮ ਦੀ ਸਥਿਤੀ ਦੀ ਤੁਲਨਾ ਵਿਚ ਜ਼ਿਆਦਾ ਹੈ । ਕੇਰਲ ਵਿਚ ਜਨ-ਘਣਤਾ ਸਭ ਤੋਂ ਜ਼ਿਆਦਾ ਹੈ ਕਿਉਂਕਿ ਭਾਰੀ ਵਰਖਾ ਦੇ ਕਾਰਨ ਇੱਥੇ ਸਾਲ ਵਿਚ ਦੋ ਜਾਂ ਤਿੰਨ ਫ਼ਸਲਾਂ ਪੈਦਾ ਕੀਤੀਆਂ ਜਾਂਦੀਆਂ ਹਨ ।
ਪ੍ਰਸ਼ਨ 10.
ਦੇਸ਼ ਦੇ ਮੈਦਾਨੀ ਭਾਗਾਂ ਵਿਚ ਜਨਸੰਖਿਆ-ਘਣਤਾ ਵੱਧ ਹੋਣ ਦੇ ਕੀ ਕਾਰਨ ਹਨ ?
ਉੱਤਰ-
ਦੇਸ਼ ਦੇ ਮੈਦਾਨੀ ਭਾਗਾਂ ਵਿਚ ਜਨਸੰਖਿਆ-ਘਣਤਾ ਬਹੁਤ ਜ਼ਿਆਦਾ ਹੈ । ਇਸ ਦੇ ਮੁੱਖ ਕਾਰਨ ਹੇਠ ਲਿਖੇ ਹਨ-
- ਭਾਰਤ ਦਾ ਉੱਤਰੀ ਮੈਦਾਨ ਵਿਸ਼ਾਲ ਅਤੇ ਉਪਜਾਊ ਹੈ ।
- ਇੱਥੇ ਵਰਖਾ ਵੀ ਕਾਫ਼ੀ ਹੁੰਦੀ ਹੈ ।
- ਇੱਥੇ ਉਦਯੋਗ ਦੇ ਵੱਡੇ-ਵੱਡੇ ਕੇਂਦਰ ਹਨ ।
- ਇੱਥੇ ਆਵਾਜਾਈ ਦੇ ਸਾਧਨ ਉੱਨਤ ਹਨ ।
- ਤਟਵਰਤੀ ਮੈਦਾਨੀ ਦੇਸ਼ਾਂ ਵਿਚ ਮੱਛੀ ਫੜਨ ਅਤੇ ਵਿਦੇਸ਼ੀ ਵਪਾਰ ਦੀਆਂ ਸਹੂਲਤਾਂ ਹਨ | ਫਲਸਰੂਪ ਲੋਕਾਂ ਦੇ ਲਈ ਰੋਜ਼ੀ ਕਮਾਉਣਾ ਸੌਖਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 11.
ਦੇਸ਼ ਵਿਚ ਘੱਟ ਜਨਸੰਖਿਆ ਵਾਲੇ ਖੇਤਰ ਕਿਹੜੇ ਹਨ ?
ਉੱਤਰ-ਭਾਰਤ ਦੇ ਥਾਰ-ਮਾਰੂਥਲ, ਪੂਰਬੀ ਹਿਮਾਲਿਆ ਪ੍ਰਦੇਸ਼ ਅਤੇ ਛੋਟਾ ਨਾਗਪੁਰ ਦੇ ਪਠਾਰ ਵਿਚ ਜਨਸੰਖਿਆ ਘੱਟ ਹੈ ।
ਕਾਰਨ-
- ਜਿਨ੍ਹਾਂ ਦੇਸ਼ਾਂ ਦੀ ਭੂਮੀ ਉਪਜਾਊ ਨਹੀਂ ਹੈ । ਇਹ ਜਾਂ ਤਾਂ ਰੇਤਲੀ ਹੈ ਜਾਂ ਪਥਰੀਲੀ ।
- ਇੱਥੇ ਆਵਾਜਾਈ ਦੇ ਸਾਧਨਾਂ ਦਾ ਵਿਕਾਸ ਨਹੀਂ ਹੋ ਸਕਿਆ ਹੈ ।
- ਇੱਥੇ ਦੀ ਜਲਵਾਯੂ ਸਿਹਤ ਦੇ ਅਨੁਕੂਲ ਨਹੀਂ ਹੈ । ਇਹ ਜਾਂ ਤਾਂ ਬਹੁਤ ਜ਼ਿਆਦਾ ਗਰਮ ਹੈ ਜਾਂ ਬਹੁਤ ਜ਼ਿਆਦਾ ਠੰਢੀ । ਹਿਮਾਲਿਆ ਖੇਤਰ ਵਿਚ ਜ਼ਰੂਰਤ ਤੋਂ ਜ਼ਿਆਦਾ ਵਰਖਾ ਹੁੰਦੀ ਹੈ ।
- ਛੋਟਾ ਨਾਗਪੁਰ ਖੇਤਰ ਨੂੰ ਛੱਡ ਕੇ ਹੋਰ ਭਾਗਾਂ ਵਿਚ ਨਿਰਮਾਣ ਉਦਯੋਗ ਵਿਕਸਿਤ ਨਹੀਂ ਹੈ ।
ਪ੍ਰਸ਼ਨ 12.
ਦੇਸ਼ ਦੇ ਚੌਲ ਉਤਪਾਦਕ ਖੇਤਰਾਂ ਵਿਚ ਜਨਸੰਖਿਆ ਦੀ ਘਣਤਾ ਵੱਧ ਕਿਉਂ ਹੈ ?
ਉੱਤਰ-
ਦੇਸ਼ ਦੇ ਪਰੰਪਰਾਗਤ ਚੌਲ ਉਤਪਾਦਕ ਖੇਤਰ ਤਾਮਿਲਨਾਡੂ, ਪੱਛਮੀ ਬੰਗਾਲ ਆਦਿ ਸਭ ਤੋਂ ਵੱਧ ਸੰਘਣੀ ਜਨਸੰਖਿਆ ਘਣਤਾ ਵਾਲੇ ਖੇਤਰ ਹਨ। ਇਸ ਦਾ ਕਾਰਨ ਇਹ ਹੈ ਕਿ ਇਹ ਖੇਤਰ ਬਹੁਤ ਉਪਜਾਊ ਹਨ ਅਤੇ ਇੱਥੇ ਕਾਫ਼ੀ ਵਰਖਾ ਹੁੰਦੀ ਹੈ । ਦੂਸਰੇ ਚੌਲ ਦੀ ਖੇਤੀ ਨਾਲ ਸੰਬੰਧਿਤ ਜ਼ਿਆਦਾਤਰ ਕੰਮ ਹੱਥਾਂ ਨਾਲ ਕਰਨੇ ਪੈਂਦੇ ਹਨ । ਇਸ ਲਈ ਜ਼ਿਆਦਾ ਸੰਖਿਆ ਵਿਚ ਮਜ਼ਦੂਰਾਂ ਦੀ ਜ਼ਰੂਰਤ ਅਨੁਭਵ ਕੀਤੀ ਜਾਂਦੀ ਹੈ, ਜਿਸ ਨਾਲ ਲੋਕਾਂ ਲਈ ਰੋਜ਼ੀ ਕਮਾਉਣ ਦੇ ਮੌਕੇ ਵੱਧ ਜਾਂਦੇ ਹਨ । ਤੀਸਰਾ ਚੌਲ ਦਾ ਉਤਪਾਦਨ ਜ਼ਿਆਦਾ ਹੋਣ ਨਾਲ ਲੋਕਾਂ ਨੂੰ ਸਸਤਾ ਭੋਜਨ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ । ਨੇੜੇ ਵੀ ਮੱਛੀ ਫੜਨ ਦੇ ਖੇਤਰ ਹੋਣ ਦੇ ਕਾਰਨ ਪ੍ਰੋਟੀਨ-ਯੁਕਤ ਭੋਜਨ ਵੀ ਮਿਲ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 13.
ਦੇਸ਼ ਦੀ ਜਨਸੰਖਿਆ ਦੀ ਬਣਤਰ ਦਾ ਅਧਿਐਨ ਕਰਨਾ ਕਿਉਂ ਜ਼ਰੂਰੀ ਹੈ ?
ਉੱਤਰ-
ਕਿਸੇ ਦੇਸ਼ ਦੀ ਜਨਸੰਖਿਆ ਦੀ ਬਣਤਰ ਨੂੰ ਜਾਣਨਾ ਕਿਉਂ ਜ਼ਰੂਰੀ ਹੈ, ਇਸ ਦੇ ਕਈ ਕਾਰਨ ਹਨ-
(1) ਸਮਾਜਿਕ ਤੇ ਆਰਥਿਕ ਨਿਯੋਜਨ ਦੇ ਲਈ ਕਿਸੇ ਵੀ ਦੇਸ਼ ਦੀ ਜਨਸੰਖਿਆ ਦੇ ਭਿੰਨ-ਭਿੰਨ ਲੱਛਣਾਂ ਜਿਵੇਂਜਨਸੰਖਿਆ ਦੀ ਉਮਰ, ਬਣਤਰ, ਲਿੰਗ ਬਣਤਰ, ਕਿੱਤਾ ਬਣਤਰ ਆਦਿ ਅੰਕੜਿਆਂ ਦੀ ਜ਼ਰੂਰਤ ਪੈਂਦੀ ਹੈ ।
(2) ਜਨਸੰਖਿਆ ਦੀ ਬਣਤਰ ਦੇ ਭਿੰਨ-ਭਿੰਨ ਘਟਕਾਂ ਦਾ ਦੇਸ਼ ਦੇ ਆਰਥਿਕ ਵਿਕਾਸ ਨਾਲ ਡੂੰਘਾ ਸੰਬੰਧ ਹੈ । ਜਿੱਥੇ ਇਕ ਪਾਸੇ ਇਹ ਜਨਸੰਖਿਆ ਬਣਤਰ ਘਟਕ ਆਰਥਿਕ ਵਿਕਾਸ ਤੋਂ ਪ੍ਰਭਾਵਿਤ ਹੁੰਦੇ ਹਨ, ਉੱਥੇ ਇਹ ਆਰਥਿਕ ਵਿਕਾਸ ਦੀ ਉੱਨਤੀ ਦੇ ਪੱਧਰ ਤੇ ਪ੍ਰਭਾਵ ਤੋਂ ਵੀ ਅਣਛੂਹੇ ਨਹੀਂ ਰਹਿ ਜਾਂਦੇ । ਉਦਾਹਰਨ ਦੇ ਲਈ ਜਦੋਂ ਕਿਸੇ ਦੇਸ਼ ਦੀ ਜਨਸੰਖਿਆ ਦੀ ਉਮਰ ਬਣਤਰ ਵਿਚ ਬੱਚਿਆਂ ਅਤੇ ਬੁੱਢੇ ਲੋਕਾਂ ਦਾ ਪ੍ਰਤੀਸ਼ਤ ਬਹੁਤ ਵੱਧ ਹੈ ਤਾਂ ਦੇਸ਼ ਨੂੰ ਸਿੱਖਿਆ ਤੇ ਸਿਹਤ ਵਰਗੀਆਂ ਮੁੱਢਲੀਆਂ ਸਹੂਲਤਾਂ ਉੱਤੇ ਜ਼ਿਆਦਾਤਰ ਵਿੱਤੀ ਸਾਧਨਾਂ ਨੂੰ ਖ਼ਰਚ ਕਰਨਾ ਪਵੇਗਾ । ਦੂਸਰੇ ਪਾਸੇ ਉਮਰ ਬਣਤਰ ਵਿਚ ਕਾਮੇ ਲੋਕਾਂ ਦੇ ਉਮਰ-ਵਰਗਾਂ (Working age-groups) ਦਾ ਭਾਗ ਜ਼ਿਆਦਾ ਹੋਣ ਨਾਲ ਦੇਸ਼ ਦੇ ਆਰਥਿਕ ਵਿਕਾਸ ਦੀ ਦਰ ਤੇਜ਼ ਹੋ ਜਾਂਦੀ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 14.
ਉਮਰ ਬਣਤਰ ਦੇ ਅਧਿਐਨ ਤੋਂ ਕੀ ਲਾਭ ਹੈ ?
ਉੱਤਰ-
ਉਮਰ-ਬਣਤਰ ਦੇ ਅਧਿਐਨ ਦੇ ਅਨੇਕਾਂ ਲਾਭ ਹਨ-
(1) ਬਾਲ ਉਮਰ ਵਰਗ (0-14) ਦੀ ਕੁੱਲ ਜਨਸੰਖਿਆ ਪ੍ਰਾਪਤ ਹੋਣ ਨਾਲ ਸਰਕਾਰ ਨੂੰ ਇਨ੍ਹਾਂ ਗੱਲਾਂ ਦਾ ਸਪੱਸ਼ਟ ਪਤਾ ਲੱਗ ਸਕਦਾ ਹੈ ਕਿ ਸਿੱਖਿਆ, ਸਿਹਤ ਅਤੇ ਸਮਾਜਿਕ ਸੇਵਾਵਾਂ ਵਿਚ ਕਿੰਨੀਆਂ ਸਹੂਲਤਾਂ ਦੀ ਜ਼ਰੂਰਤ ਹੈ । ਉਸੇ ਅਨੁਸਾਰ ਨਵੇਂ ਸਕੂਲਾਂ, ਸਿਹਤ ਕੇਂਦਰਾਂ, ਸਮੁਦਾਇਕ ਕੇਂਦਰਾਂ ਆਦਿ ਦਾ ਨਿਰਮਾਣ ਕਰਾਇਆ ਜਾਂਦਾ ਹੈ ।
(2) ਦੇਸ਼ ਵਿਚ ਕਿੰਨੇ ਲੋਕ ਵੋਟਰ ਵਰਗ ਵਿਚ ਹਨ, ਇਸ ਗੱਲ ਦੀ ਜਾਣਕਾਰੀ ਵੀ ਹੋ ਸਕਦੀ ਹੈ । ਵੋਟਰ ਵਰਗ ਦੇ ਲੋਕਾਂ ਦੀ ਜਾਣਕਾਰੀ ਹੋਣਾ ਪਰਜਾਤੰਤਰ ਵਿਚ ਬਹੁਤ ਜ਼ਰੂਰੀ ਹੈ । ਉਮਰ ਬਣਤਰ ਦੇ ਅੰਕੜਿਆਂ ਦੇ ਹਿਸਾਬ ਨਾਲ ਲਗਪਗ 58 ਪ੍ਰਤੀਸ਼ਤ ਮਤਦਾਤਾ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ, ਪਰੰਤੁ ਦੇਸ਼ ਵਿਚ ਮਤਦਾਤਾ 60 ਪ੍ਰਤੀਸ਼ਤ ਹਨ ।
ਪ੍ਰਸ਼ਨ 15.
ਭਾਰਤ ਵਿਚ ਲਿੰਗ-ਅਨੁਪਾਤ ਘੱਟ ਹੋਣ ਦੇ ਕੀ ਕਾਰਨ ਹਨ ?
ਉੱਤਰ-
ਭਾਰਤ ਵਿਚ ਲਿੰਗ-ਅਨੁਪਾਤ ਘੱਟ ਹੋਣ ਦੇ ਕਾਰਨਾਂ ਬਾਰੇ ਨਿਸ਼ਚਿਤ ਤੌਰ ‘ਤੇ ਕੁਝ ਵੀ ਕਹਿਣਾ ਸੰਭਵ ਨਹੀਂ ਹੈ । ਪਰੰਤੁ ਭਾਰਤੀ ਸਮਾਜ ਵਿਚ ਇਸਤਰੀ ਦਾ ਦਰਜਾ ਹੇਠਾਂ ਹੋਣਾ ਇਸ ਦਾ ਇਕ ਮੁੱਖ ਕਾਰਨ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ । ਪਰਿਵਾਰ ਪ੍ਰਣਾਲੀ ਵਿਚ ਉਸ ਨੂੰ ਹੇਠਲਾ ਦਰਜਾ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਮਰਦ ਨੂੰ ਉੱਚਾ ।’ਇਸ ਕਾਰਨ ਘੱਟ ਉਮਰ ਵਰਗ ਵਿਚ ਲੜਕੀਆਂ ਦੀ ਸਿਹਤ, ਖਾਣ-ਪੀਣ ਅਤੇ ਦੇਖ-ਭਾਲ ਦੇ ਵੱਲ ਘੱਟ ਧਿਆਨ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਫਲਸਰੂਪ ਉਮਰ ਵਰਗ (06 ਸਾਲ ਵਿਚ ਲੜਕਿਆਂ ਦੀ ਬਜਾਏ ਲੜਕੀਆਂ ਦੀ ਮੌਤ-ਦਰ ਵੱਧ ਹੈ । ਇਸ ਉਮਰ ਵਿਚ ਲਿੰਗ ਅਨੁਪਾਤ ਜੋ ਸਾਲ 1961 ਵਿਚ 976 ਸੀ ਘੱਟ ਕੇ ਸਾਲ 2001 ਵਿਚ 933 ‘ਤੇ ਪਹੁੰਚ ਗਿਆ । ਲਿੰਗ-ਅਨੁਪਾਤ ਘੱਟ ਹੋਣ ਦੇ ਹੋਰ ਮੁੱਖ ਕਾਰਨ ਹਨਜਨਗਣਨਾ ਦੇ ਸਮੇਂ ਇਸਤਰੀਆਂ ਦੀ ਨਿਸਬਤ ਘੱਟ ਗਣਨਾ ਕਰਨਾ ਜਾਂ ਮਰਦਾਂ ਦੀ ਗਣਨਾ ਵੱਧ ਕਰਨਾ, ਲੜਕੀਆਂ ਦੀ ਜਨਮ-ਦਰ ਘੱਟ ਹੋਣਾ ਅਤੇ ਇਸਤਰੀ ਗਰਭ-ਹੱਤਿਆ (Female Foeticide) ।
ਪ੍ਰਸ਼ਨ 16.
ਭਾਰਤ ਵਿਚ ਸ਼ਹਿਰੀ ਆਬਾਦੀ ਦੇ ਪਿਛਲੇ ਸਾਲਾਂ ਵਿਚ ਤੇਜ਼ੀ ਨਾਲ ਵਧਣ ਦੇ ਕੀ ਕਾਰਨ ਹਨ ?
ਉੱਤਰ-ਉੱਤਰ ਲਈ ਭਾਗ III) ਦਾ ਪ੍ਰਸ਼ਨ ਨੰ: 4 ਪੜ੍ਹੋ : MISSING
III. ਹੇਠ ਲਿਖੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ ਲਗਪਗ 125-130 ਸ਼ਬਦਾਂ ਵਿਚ ਦਿਓ-
ਪ੍ਰਸ਼ਨ 1.
ਭਾਰਤ ਵਿਚ ਜਨਸੰਖਿਆ ਦੀ ਘਣਤਾ ਦੇ ਖੇਤਰੀ ਰੂਪ ਦਾ ਵਰਣਨ ਕਰੋ ।
ਉੱਤਰ-
2011 ਦੀ ਜਨਗਣਨਾ ਦੇ ਅਨੁਸਾਰ ਭਾਰਤ ਵਿਚ ਜਨਸੰਖਿਆ ਘਣਤਾ 382 ਵਿਅਕਤੀ ਪ੍ਰਤੀ ਵਰਗ ਕਿਲੋਮੀਟਰ ਹੈ । ਪਰੰਤੁ ਦੇਸ਼ਿਕ ਪੱਧਰ ‘ਤੇ ਜਨਸੰਖਿਆਂ ਘਣਤਾ ਵਿਚ ਭਾਰੀ ਅੰਤਰ ਹੈ । ਜਨਸੰਖਿਆ ਘਣਤਾ ਬਿਹਾਰ ਵਿਚ ਸਭ ਤੋਂ ਵੱਧ ਹੈ ਅਤੇ ਸਭ ਤੋਂ ਘੱਟ ਅਰੁਣਾਚਲ ਪ੍ਰਦੇਸ਼ ਵਿਚ ਹੈ । ਕੇਂਦਰ ਸ਼ਾਸਿਤ ਪ੍ਰਦੇਸ਼ਾਂ ਵਿਚ ਇਹ ਅੰਤਰ ਹੋਰ ਵੀ ਜ਼ਿਆਦਾ ਹੈ ।
ਰਾਸ਼ਟਰੀ ਖੇਤਰ ਰਾਜਧਾਨੀ ਖੇਤਰ ਦਿੱਲੀ ਵਿਚ ਜਨਸੰਖਿਆ ਘਣਤਾ ਸਭ ਤੋਂ ਵੱਧ (9340) ਵਿਅਕਤੀ ਹੈ, ਜਦਕਿ ਅੰਡੇਮਾਨ ਤੇ ਨਿਕੋਬਾਰ ਦੀਪ ਸਮੂਹ ਵਿਚ ਇਹ ਕੇਵਲ 46 ਵਿਅਕਤੀ ਪ੍ਰਤੀ ਵਰਗ ਕਿਲੋਮੀਟਰ ਹੈ ।
1. ਜ਼ਿਆਦਾ ਜਨਸੰਖਿਆ ਘਣਤਾ – ਪ੍ਰਦੇਸ਼ਿਕ ਪੱਧਰ ‘ਤੇ ਵੱਧ ਜਨਸੰਖਿਆ ਘਣਤਾ (400 ਪ੍ਰਤੀ ਵਿਅਕਤੀ ਵਰਗ ਕਿਲੋਮੀਟਰ ਤੋਂ ਜ਼ਿਆਦਾ ਵਾਲੇ ਖੇਤਰ ਸਤਲੁਜ, ਗੰਗਾ, ਬ੍ਰਹਮਪੁੱਤਰ, ਮਹਾਂਨਦੀ, ਗੋਦਾਵਰੀ, ਭ੍ਰਿਸ਼ਨਾ ਤੇ ਕਾਵੇਰੀ ਨਦੀਆਂ ਦੇ ਡੈਲਟੇ ਹਨ ਤੇ ਉਪਜਾਊ ਮਿੱਟੀ ਅਤੇ ਚੰਗੀ ਵਰਖਾ ਦੇ ਕਾਰਨ ਖੇਤੀ ਦਾ ਵਿਕਾਸ ਚੰਗਾ ਹੈ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਵੱਡੇ ਉਦਯੋਗਿਕ ਤੇ ਪ੍ਰਸ਼ਾਸਨਿਕ ਨਗਰਾਂ; ਜਿਵੇਂ-ਲੁਧਿਆਣਾ, ਗੁੜਗਾਓਂ, ਰਾਸ਼ਟਰੀ ਰਾਜਧਾਨੀ ਖੇਤਰ ਦਿੱਲੀ, ਕਾਨਪੁਰ, ਪਟਨਾ, ਕੋਲਕਾਤਾ, ਮੁੰਬਈ, ਚੇਨੱਈ, ਅਹਿਮਦਾਬਾਦ, ਬੰਗਲੌਰ ਤੇ ਹੈਦਰਾਬਾਦ ਦੇ ਆਸ-ਪਾਸ ਵੀ ਜ਼ਿਆਦਾ ਜਨਸੰਖਿਆ ਦੀ ਘਣਤਾ ਪਾਈ ਜਾਂਦੀ ਹੈ ।
2. ਘੱਟ ਜਨਸੰਖਿਆ ਘਣਤਾ – ਘੱਟ ਜਨਸੰਖਿਆ ਘਣਤਾ (200 ਵਿਅਕਤੀ ਵਰਗ ਕਿਲੋਮੀਟਰ ਤੋਂ ਘੱਟ ਵਾਲੇ ਖੇਤਰ ਅਜਿਹੇ ਹਨ ਜੋ ਭੌਤਿਕ ਕਮਜ਼ੋਰੀਆਂ ਨਾਲ ਭਰੇ (Physical handicapped) ਪਏ ਹਨ । ਅਜਿਹੇ ਖੇਤਰ
- ਉੱਤਰ ਵਿਚ ਹਿਮਾਲਿਆ ਪਰਬਤ ਦੀਆਂ ਸ਼੍ਰੇਣੀਆਂ ਵਿਚ ਜੰਮੂ-ਕਸ਼ਮੀਰ, ਹਿਮਾਚਲ ਪ੍ਰਦੇਸ਼, ਉੱਤਰਾਖੰਡ ਦੇ ਪਹਾੜੀ ਭਾਗ,
- ਪੁਰਬ ਵਿਚ ਅਰੁਣਾਚਲ ਪ੍ਰਦੇਸ਼, ਨਾਗਾਲੈਂਡ, ਮਨੀਪੁਰ, ਮਿਜ਼ੋਰਮ, ਮੇਘਾਲਿਆ ਅਤੇ ਤਿਪੁਰਾ ਰਾਜ,
- ਪੱਛਮੀ ਰਾਜਸਥਾਨ ਦੇ ਮਾਰੂਥਲੀ ਭਾਗਾਂ, ਗੁਜਰਾਤ ਦੇ ਦਲਦਲੀ ਖੇਤਰਾਂ ਅਤੇ
- ਦੱਖਣ ਅੰਤਰਿਕ ਪ੍ਰਾਇਦੀਪੀ ਪਠਾਰ ਵਿਚ ਮੱਧ ਪ੍ਰਦੇਸ਼ । ਪੂਰਬੀ ਮਹਾਂਰਾਸ਼ਟਰ, ਪੂਰਬੀ ਕਰਨਾਟਕ, ਤੇਲੰਗਾਨਾ ਅਤੇ ਤਾਮਿਲਨਾਡੂ ਦੇ ਕੁੱਝ ਭਾਗ ਸ਼ਾਮਲ ਹਨ ।
3. ਔਸਤ ਜਨਸੰਖਿਆ ਘਣਤਾ-ਜ਼ਿਆਦਾ ਜਨਸੰਖਿਆ ਘਣਤਾ ਵਿਚ ਖੇਤਰਾਂ ਦੇ ਖੱਬੇ ਭਾਗ ਔਸਤ ਜਨਸੰਖਿਆ ਘਣਤਾ (200 ਤੋਂ 300 ਵਿਅਕਤੀ ਪ੍ਰਤੀ ਵਰਗ ਕਿਲੋਮੀਟਰ ਦੇ ਖੇਤਰ ਕਹਾਉਂਦੇ ਹਨ । ਆਮ ਤੌਰ ‘ਤੇ ਇਹ ਖੇਤਰ ਘੱਟ ਅਤੇ ਵੱਧ ਜਨਸੰਖਿਆ ਘਣਤਾ ਦੇ ਖੇਤਰਾਂ ਦੇ ਵਿਚਕਾਰ ਪੈਂਦੇ ਹਨ । ਇਹਨਾਂ ਦੀ ਸੰਖਿਆ ਘੱਟ ਹੈ ।
ਇਸ ਤੋਂ ਇਸ ਗੱਲ ਦਾ ਪਤਾ ਲੱਗ ਜਾਂਦਾ ਹੈ ਕਿ ਭਾਰਤ ਵਿਚ ਜਨਸੰਖਿਆ ਵੰਡ ਅਤੇ ਘਣਤਾ ਵਿਚ ਭਾਰੀ ਦੇਸ਼ਿਕ ਅਸਮਾਨਤਾਵਾਂ ਹਨ ।
![]()
ਪ੍ਰਸ਼ਨ 2.
ਭਾਰਤ ਵਿਚ ਲਿੰਗ-ਅਨੁਪਾਤ ਦੇ ਰਾਜ ਪੱਧਰ ਦੇ ਰੂਪ ਦਾ ਵਿਸਥਾਰਪੂਰਵਕ ਵਰਣਨ ਕਰੋ |
ਉੱਤਰ-
ਲਿੰਗ – ਅਨੁਪਾਤ ਤੋਂ ਭਾਵ ਹੈ ਪ੍ਰਤੀ ਹਜ਼ਾਰ ਆਦਮੀਆਂ ਪਿੱਛੇ ਇਸਤਰੀਆਂ ਦੀ ਔਸਤ ਸੰਖਿਆ । ਅੱਜ-ਕਲ੍ਹ ਸਮਾਜ ਵਿਚ ਇਸਤਰੀਆਂ ਨੂੰ ਇਕ ਸਮਾਨ ਨਜ਼ਰ ਨਾਲ ਵੇਖਿਆ ਜਾਂਦਾ ਹੈ । ਜ਼ਿਆਦਾਤਰ ਅਮੀਰ ਦੇਸ਼ਾਂ ਵਿਚ ਇਸਤਰੀਆਂ ਦੀ ਸੰਖਿਆ ਆਦਮੀਆਂ ਦੇ ਬਰਾਬਰ ਹੈ ਜਾਂ ਉਸ ਤੋਂ ਜ਼ਿਆਦਾ ਵਿਕਸਿਤ ਦੇਸ਼ਾਂ ਦਾ ਔਸਤ 1050 ਇਸਤਰੀਆਂ ਪ੍ਰਤੀ 1000 ਆਦਮੀ ਹਨ ਜਦ ਕਿ ਵਿਕਾਸਸ਼ੀਲ ਦੇਸ਼ਾਂ ਵਿੱਚ ਇਹ ਔਸਤ 964 ਇਸਤਰੀਆਂ ਪ੍ਰਤੀ 1000 ਆਦਮੀ ਹੈ । ਭਾਰਤ ਵਿਚ 2011 ਦੀ ਜਣਗਣਨਾ ਦੇ ਅਨੁਸਾਰ ਲਿੰਗ-ਅਨੁਪਾਤ 944 ਇਸਤਰੀਆਂ ਪ੍ਰਤੀ ਹਜ਼ਾਰ ਆਦਮੀ ਹੈ । ਇਹ ਔਸਤ ਸੰਸਾਰ ਵਿਚ ਸਭ ਤੋਂ ਘੱਟ ਔਸਤਾਂ ਵਿੱਚੋਂ ਇਕ ਹੈ ।
ਰਾਜ ਪੱਧਰੀ ਰੂਪ – ਦੇਸ਼ ਦੇ ਸਭ ਰਾਜਾਂ ਵਿਚ ਲਿੰਗ-ਅਨੁਪਾਤ ਇਕ ਸਮਾਨ ਨਹੀਂ ਹੈ । ਭਾਰਤ ਦੇ ਕੇਵਲ ਦੋ ਹੀ ਰਾਜ ਅਜਿਹੇ ਹਨ, ਜਿੱਥੇ ਲਿੰਗ-ਅਨੁਪਾਤ ਇਸਤਰੀਆਂ ਦੇ ਪੱਖ ਵਿਚ ਹੈ । ਇਹ ਰਾਜ ਹਨ-ਕੇਰਲ ਅਤੇ ਤਾਮਿਲਨਾਡੂ । ਕੇਰਲ ਵਿਚ ਪ੍ਰਤੀ ਹਜ਼ਾਰ ਆਦਮੀਆਂ ਪਿੱਛੇ 1099 ਇਸਤਰੀਆਂ ਹਨ, (2011 ਵਿਚ | ਦੇਸ਼ ਦੇ ਹੋਰ ਰਾਜਾਂ ਵਿਚ ਅਨੁਪਾਤ ਆਦਮੀਆਂ ਦੇ ਪੱਖ ਵਿੱਚ ਹੈ ਜਾਂ ਇਹਨਾਂ ਰਾਜਾਂ ਵਿਚ ਪ੍ਰਤੀ ਹਜ਼ਾਰ, ਆਦਮੀਆਂ ਪਿੱਛੇ ਇਸਤਰੀਆਂ ਦੀ ਸੰਖਿਆ ਘੱਟ ਹੈ, ਜੋ ਹੇਠ ਲਿਖੀਆਂ ਉਦਾਹਰਨਾਂ ਤੋਂ ਸਪੱਸ਼ਟ ਹੈ-
- ਪੰਜਾਬ ਦੇ – 899
- ਹਰਿਆਣਾ – 885
- ਰਾਜਸਥਾਨ – 935
- ਬਿਹਾਰ – 912
- ਉੱਤਰ ਪ੍ਰਦੇਸ਼ – 910
- ਤਾਮਿਲਨਾਡੂ – 1000
ਲਿੰਗ-ਅਨੁਪਾਤ – ਅਨੁਪਾਤ ਦੇ ਰਾਜ ਰੂਪ ਨਾਲ ਇਕ ਹੋਰ ਗੱਲ ਵੀ ਸਪੱਸ਼ਟ ਹੋ ਜਾਂਦੀ ਹੈ ਕਿ ਦੇਸ਼ ਦੇ ਉੱਤਰੀ ਰਾਜਾਂ ਵਿਚ ਦੱਖਣੀ ਰਾਜਾਂ ਦੀ ਤੁਲਨਾ ਵਿਚ ਲਿੰਗ-ਅਨੁਪਾਤ ਘੱਟ ਹੈ । ਇਹ ਗੱਲ ਸਮਾਜ ਵਿਚ ਇਸਤਰੀ ਦੇ ਘੱਟ ਅਨੁਪਾਤ ਨੂੰ ਦਿਖਾਉਂਦੀ ਹੈ । ਇਹ ਨਿਰਸੰਦੇਹ ਇਕ ਚਿੰਤਾ ਦਾ ਵਿਸ਼ਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 3.
ਦੇਸ਼ ਵਿਚ ਜਨਸੰਖਿਆ ਦੀ ਵੰਡ ਦੇ ਖੇਤਰੀ ਰੂਪ ਦੀਆਂ ਮੁੱਖ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਸਹਿਤ ਵਿਆਖਿਆ ਕਰੋ ।
ਉੱਤਰ-
ਭਾਰਤ ਵਿਚ ਜਨਸੰਖਿਆ ਦੀ ਵੰਡ ਦੇ ਖੇਤਰੀ ਰੂਪ ਅਤੇ ਉਸ ਦੀਆਂ ਕੁੱਝ ਮਹੱਤਵਪੂਰਨ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਹੇਠ ਲਿਖੀਆਂ ਹਨ-
(1) ਭਾਰਤ ਵਿਚ ਜਨਸੰਖਿਆ ਦੀ ਵੰਡ ਬਹੁਤ ਅਸਮਾਨ ਹੈ । ਨਦੀਆਂ ਦੀਆਂ ਘਾਟੀਆਂ ਅਤੇ ਸਮੁੰਦਰ ਤੇ ਤਟਵਰਤੀ ਮੈਦਾਨਾਂ ਵਿਚ ਜਨਸੰਖਿਆ ਬਹੁਤ ਸੰਘਣੀ ਹੈ, ਪਰੰਤੂ ਪਰਬਤੀ, ਮਾਰੂਥਲੀ ਅਤੇ ਕਾਲੇ-ਪੀੜਤ ਖੇਤਰਾਂ ਵਿਚ ਜਨਸੰਖਿਆ ਬਹੁਤ ਵਿਰਲੀ ਹੈ ਉੱਤਰ ਦੇ ਪਹਾੜੀ ਦੇਸ਼ਾਂ ਵਿਚ ਦੇਸ਼ ਦੇ 16 ਪ੍ਰਤੀਸ਼ਤ ਭੂ-ਭਾਗ ਉੱਤੇ ਕੇਵਲ 3 ਪ੍ਰਤੀਸ਼ਤ ਜਨਸੰਖਿਆ ਰਹਿੰਦੀ ਹੈ, ਜਦਕਿ ਉੱਤਰੀ ਮੈਦਾਨਾਂ ਵਿਚ ਦੇਸ਼ ਦੀ 18 ਪ੍ਰਤੀਸ਼ਤ ਭੂਮੀ ਤੇ 40 ਪ੍ਰਤੀਸ਼ਤ ਜਨਸੰਖਿਆ ਰਹਿੰਦੀ ਹੈ । ਰਾਜਸਥਾਨ ਵਿਚ ਦੇਸ਼ ਦੇ ਕੇਵਲ 6% ਭੂ-ਭਾਗ ਉੱਤੇ 6% ਜਨਸੰਖਿਆ ਰਹਿੰਦੀ ਹੈ ।
(2) ਜ਼ਿਆਦਾਤਰ ਜਨਸੰਖਿਆ ਪੇਂਡੂ ਖੇਤਰਾਂ ਵਿਚ ਵਸੀ ਹੈ ।ਦੇਸ਼ ਦੀ ਕੁੱਲ ਜਨਸੰਖਿਆ ਦਾ ਲਗਪਗ 71% ਭਾਗ ਪੇਂਡੂ ਖੇਤਰਾਂ ਵਿਚ ਅਤੇ ਲਗਪਗ 29% ਭਾਗ ਸ਼ਹਿਰਾਂ ਵਿਚ ਰਹਿੰਦਾ ਹੈ |
ਸ਼ਹਿਰੀ ਜਨਸੰਖਿਆ ਦਾ ਭਾਰੀ ਜਮਾਅ ਵੱਡੇ ਸ਼ਹਿਰਾਂ ਵਿਚ ਹੈ । ਕੁੱਲ ਸ਼ਹਿਰੀ ਜਨਸੰਖਿਆ ਦਾ ਦੋ-ਤਿਹਾਈ ਭਾਗ ਇਕ ਲੱਖ ਜਾਂ ਇਸ ਤੋਂ ਵੱਧ ਆਬਾਦੀ ਵਾਲੇ ਪਹਿਲੀ ਸ਼੍ਰੇਣੀ ਦੇ ਸ਼ਹਿਰਾਂ ਵਿਚ ਰਹਿੰਦਾ ਹੈ ।
(3) ਦੇਸ਼ ਦੇ ਘੱਟ ਗਿਣਤੀ ਫ਼ਿਰਕਿਆਂ ਦਾ ਬਹੁਤ ਸੰਵੇਦਨਸ਼ੀਲ ਤੇ ਮਹੱਤਵਪੂਰਨ ਬਾਹਰਲੇ ਸਰਹੱਦੀ ਖੇਤਰਾਂ ਵਿਚ ਵਸਣਾ ਹੈ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ‘ਤੇ ਉੱਤਰ-ਪੱਛਮੀ ਭਾਰਤ ਵਿਚ ਭਾਰਤ-ਪਾਕਿ ਸਰਹੱਦ ਦੇ ਕੋਲ ਪੰਜਾਬ ਵਿਚ ਸਿੱਖਾਂ ਅਤੇ ਜੰਮੂਕਸ਼ਮੀਰ ਵਿਚ ਮੁਸਲਮਾਨਾਂ ਦੀ ਗਿਣਤੀ ਵੱਧ ਹੈ । ਇਸੇ ਤਰ੍ਹਾਂ ਉੱਤਰ-ਪੂਰਬ ਵਿਚ ਚੀਨ ਤੇ ਬਰਮਾ (ਮਿਆਂਮਾਰ) ਦੀਆਂ ਸਰਹੱਦਾਂ ਦੇ ਨਾਲ ਈਸਾਈ ਧਰਮ ਦੇ ਲੋਕਾਂ ਦਾ ਵਧੇਰੇ ਇਕੱਠ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਦੀ ਵੰਡ ਤੋਂ ਅਨੇਕਾਂ ਸਮਾਜਿਕ, ਆਰਥਿਕ ਤੇ ਰਾਜਨੀਤਿਕ ਮੁਸ਼ਕਿਲਾਂ ਸਾਹਮਣੇ ਆਉਂਦੀਆਂ ਹਨ ।
(4) ਇਕ ਪਾਸੇ ਤਟਵਰਤੀ ਮੈਦਾਨਾਂ ਤੇ ਨਦੀਆਂ ਦੀਆਂ ਘਾਟੀਆਂ ਵਿਚ ਜਨਸੰਖਿਆ ਸੰਘਣੀ ਹੈ ਤਾਂ ਦੂਸਰੇ ਪਾਸੇ ਪਹਾੜੀ, ਪਠਾਰੀ ਤੇ ਰੇਗਿਸਤਾਨੀ ਭਾਗਾਂ ਵਿਚ ਜਨਸੰਖਿਆ ਵਿਰਲੀ ਹੈ । ਇਹ ਵੰਡ ਇਕ ਜਨਸੰਖਿਅਕੀ ਵੰਡ (Demographic divide) ਵਰਗੀ ਲਗਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 4.
ਮੈਟਰੋ ਸ਼ਹਿਰਾਂ ਵਿਚ ਆਬਾਦੀ ਦੇ ਵਧਣ ਨਾਲ ਕਿਹੜੀਆਂ-ਕਿਹੜੀਆਂ ਸਮੱਸਿਆਵਾਂ ਪੈਦਾ ਹੋ ਰਹੀਆਂ ਹਨ ?
ਉੱਤਰ-
ਵੱਖ-ਵੱਖ ਦੇਸ਼ਾਂ ਵਿਚ ਤੇਜ਼ੀ ਨਾਲ ਆਬਾਦੀ ਦੇ ਵਧਣ ਨਾਲ ਬਹੁਤ ਸਾਰੀਆਂ ਸਮਾਜਿਕ-ਆਰਥਿਕ ਸਮੱਸਿਆਵਾਂ ਪੈਦਾ ਹੋ ਰਹੀਆਂ ਹਨ । ਅਜਿਹੀਆਂ ਸਮੱਸਿਆਵਾਂ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹਨ-
- ਖਾਧ ਪਦਾਰਥਾਂ ਦੀ ਸਮੱਸਿਆ – ਬਹੁਤ ਸਾਰੇ ਇਲਾਕਿਆਂ ਵਿਚ ਵਸੋਂ ਦੇ ਵਾਧੇ ਨਾਲ ਖਾਧ/ਅਨਾਜ ਦੀ ਕਮੀ ਹੋ ਰਹੀ ਹੈ । ਨਵੀਆਂ ਤਕਨੀਕਾਂ ਦੇ ਸਦਕੇ ਖੇਤੀਬਾੜੀ ਦੀ ਪੈਦਾਵਾਰ ਵਿਚ ਵਾਧਾ ਹੋਇਆ ਹੈ, ਹਾਲਾਂਕਿ ਕਈ ਦੇਸ਼ਾਂ ਨੂੰ ਖੇਤੀਬਾੜੀ ਪੈਦਾਵਾਰ ਦਾ ਆਯਾਤ ਕਰਨਾ ਪਿਆ ਹੈ ।
- ਮਕਾਨਾਂ ਦੀ ਸਮੱਸਿਆ – ਵੱਧ ਵਸੋਂ ਵਾਲੇ ਦੇਸ਼ਾਂ ਵਿਚ ਰਹਿਣ ਵਾਲੇ ਮਕਾਨਾਂ ਦੀ ਸਥਿਤੀ ਬਹੁਤ ਹੀ ਮਾੜੀ ਹੈ । ਇਹਨਾਂ ਦੇਸ਼ਾਂ ਦੇ ਲੋਕ ਗੰਦੀਆਂ ਬਸਤੀਆਂ ਵਿਚ ਰਹਿੰਦੇ ਹਨ । ਕਈ ਮੈਟਰੋ ਪੋਲੀਟਨ ਸ਼ਹਿਰਾਂ ਵਿਚ ਆਸਮਾਨ ਨੂੰ ਛੂੰਹਦੀਆਂ ਇਮਾਰਤਾਂ ਦੀ ਉਸਾਰੀ ਹੋ ਰਹੀ ਹੈ ।
- ਬੇਰੁਜ਼ਗਾਰੀ – ਤੇਜ਼ੀ ਨਾਲ ਵੱਧ ਰਹੀ ਵਸੋਂ ਦੇ ਕਾਰਨ ਬੇਰੁਜ਼ਗਾਰੀ ਬਹੁਤ ਵਧਦੀ ਹੈ । ਭਾਰੀ ਵਸੋਂ ਵਾਲੇ ਦਿਹਾਤੀ ਇਲਾਕਿਆਂ ਤੋਂ ਲੋਕਾਂ ਦੇ ਆਵਾਸ ਕਰਨ ਨਾਲ ਬੇਰੁਜ਼ਗਾਰੀ ਵਿਚ ਵਾਧਾ ਹੋਇਆ ਹੈ ।
- ਨੀਵਾਂ ਜੀਵਨ ਪੱਧਰ – ਵਸੋਂ ਦੀ ਭਰਮਾਰ ਵਾਲੇ ਇਲਾਕਿਆਂ ਵਿਚ ਪ੍ਰਤੀ ਜੀਅ ਆਮਦਨ ਬਹੁਤ ਹੀ ਘੱਟ ਹੈ । ਇਸ ਲਈ ਜੀਵਨ ਪੱਧਰ ਬਹੁਤ ਨੀਵਾਂ ਹੈ । ਅਜਿਹਾ ਹੋਣ ਨਾਲ ਲੋਕ ਜੀਵਨ ਦੀਆਂ ਮੁੱਢਲੀਆਂ ਸਹੂਲਤਾਂ ਤੋਂ ਵਾਂਝੇ ਰਹਿ ਜਾਂਦੇ ਹਨ । ਵਧਦੀ ਹੋਈ ਵਸੋਂ ਨਾਲ ਗ਼ਰੀਬੀ ਵਧੀ ਹੈ ਅਤੇ ਜੀਵਨ ਪੱਧਰ ਬਹੁਤ ਨੀਵਾਂ ਹੋਇਆ ਹੈ ।
- ਨਿਰਭਰ ਜਨਸੰਖਿਆ – ਨੌਜਵਾਨ ਵਰਗ ਦਾ ਬਹੁਤ ਵੱਡਾ ਪ੍ਰਤੀਸ਼ਤ ਬਹੁਤ ਘੱਟ ਕਾਰਜਸ਼ੀਲ ਜਨਸੰਖਿਆ ਉੱਤੇ ਨਿਰਭਰ ਹੈ ।
- ਸਮਾਜਿਕ ਸਮੱਸਿਆਵਾਂ – ਵਸੋਂ ਦੇ ਵਧਣ ਨਾਲ ਬਹੁਤ ਸਾਰੀਆਂ ਸਮਾਜਿਕ ਸਮੱਸਿਆਵਾਂ ਪੈਦਾ ਹੁੰਦੀਆਂ ਹਨ । ਮਾੜੀ ਸਿਹਤ ਅਤੇ ਭੈੜੀਆਂ ਸਫ਼ਾਈ ਸਥਿਤੀਆਂ ਕਰਕੇ ਮਹਾਂਮਾਰੀਆਂ ਫੈਲਦੀਆਂ ਹਨ ।
![]()
ਪ੍ਰਸ਼ਨ 5.
ਭਾਰਤ ਦੀ ਜਨਸੰਖਿਆ ਦੀ ਸੰਸਕ੍ਰਿਤਕ ਬਣਤਰ ‘ ਤੇ ਇਕ ਨੋਟ ਲਿਖੋ ।
ਉੱਤਰ-
1. ਅਨੇਕ ਜਾਤੀਆਂ – ਭਾਰਤ ਵਿਚ ਅਨੇਕਾਂ ਜਾਤੀਆਂ ਦੇ ਲੋਕ ਰਹਿੰਦੇ ਹਨ । ਦਰਾਵਿੜ, ਮੰਗੋਲ, ਆਰੀਆ ਆਦਿ । ਇਨ੍ਹਾਂ ਦੇ ਇਲਾਵਾ ਕੁਝ ਕਾਕੇਸ਼ੀਅਨ ਵੀ ਹਨ । ਸਮੇਂ ਦੇ ਨਾਲ-ਨਾਲ ਇਹ ਜਾਤੀਆਂ ਆਪਸ ਵਿਚ ਇਕ-ਦੂਸਰੇ ਨਾਲ ਇਸ ਤਰ੍ਹਾਂ ਘੁਲ-ਮਿਲ ਗਈਆਂ ਹਨ ਕਿ ਹੁਣ ਉਹਨਾਂ ਦੇ ਅਸਲ ਚਿੰਨ ਖ਼ਤਮ ਹੋ ਗਏ ਹਨ । ਫਿਰ ਵੀ ਭਾਰਤ ਦੇ ਲੋਕਾਂ ਵਿਚ ਕਾਫ਼ੀ ਭਿੰਨਤਾ ਦਿਖਾਈ ਦਿੰਦੀ ਹੈ । ਅਸਲ ਵਿਚ ਭਾਰਤੀ ਸੰਸਕ੍ਰਿਤੀ ਦੀ ਪੂਰਨਤਾ ਇਸ ਦੀ ਅਨੇਕਤਾ ਵਿਚ ਹੀ ਮੌਜੂਦ ਹੈ । ਸਹਿਗੁਣਾਂ ਦੀ ਭਾਵਨਾ, ਅਦਾਨ-ਪ੍ਰਦਾਨ ਅਤੇ ਸਭ ਨੂੰ ਆਪਣੇ ਵਿਚ ਮਿਲਾਉਣ ਦੀ ਪ੍ਰਵਿਰਤੀ ਭਾਰਤੀ ਸੰਸਕ੍ਰਿਤੀ ਦੇ ਵਿਲੱਖਣ ਗੁਣ ਹਨ ।
2. ਭਿੰਨ-ਭਿੰਨ ਧਰਮ ਤੇ ਭਾਸ਼ਾਵਾਂ-
(i) ਭਾਰਤ ਦੇ ਲੋਕ ਭਿੰਨ-ਭਿੰਨ ਧਰਮਾਂ ਦਾ ਪਾਲਣ ਕਰਦੇ ਹਨ ਉਹ ਧਰਮ, ਦੇਸ਼, ਰਾਜਨੀਤਿਕ ਅਤੇ ਭਾਸ਼ਾ ਦੇ ਬੰਧਨਾਂ ਤੋਂ ਮੁਕਤ ਹਨ । ਇਕ ਹੀ ਧਰਮ ਨੂੰ ਮੰਨਣ ਵਾਲੇ ਲੋਕ ਭਿੰਨ-ਭਿੰਨ ਭਾਸ਼ਾਵਾਂ ਬੋਲਦੇ ਹਨ । ਭਾਸ਼ਾ, ਜਾਤੀਆਂ, ਧਰਮਾਂ ਅਤੇ ਦੇਸ਼ਾਂ ਦੀਆਂ ਸਰਹੱਦਾਂ ਵਿਚ ਨਹੀਂ ਬੰਨ੍ਹੀਆਂ ਹੋਈਆਂ ਹਨ । ਇਹਨਾਂ ਜਾਤੀ, ਧਾਰਮਿਕ, ਭਾਸ਼ਾਈ ਅਤੇ ਪ੍ਰਦੇਸ਼ਿਕ ਭਿੰਨਤਾਵਾਂ ਦੇ ਬਾਵਜੂਦ ਅਸੀਂ ਸਭ ਭਾਰਤੀ ਹਾਂ ।
(ii) ਭਾਰਤ ਹਿੰਦੂ, ਇਸਲਾਮ, ਸਿੱਖ, ਈਸਾਈ, ਬੁੱਧ, ਜੈਨ, ਪਾਰਸੀ ਅਤੇ ਹੋਰ ਕਈ ਧਰਮਾਂ ਨੂੰ ਮੰਨਣ ਵਾਲੇ ਲੋਕਾਂ ਦਾ ਘਰ ਹੈ । ਇੱਥੇ ਕਿਸੇ ਵੀ ਵਿਅਕਤੀ ਨੂੰ ਧਰਮ ਦੇ ਆਧਾਰ ‘ਤੇ ਕੋਈ ਵਿਸ਼ੇਸ਼ ਅਧਿਕਾਰ ਨਹੀਂ ਮਿਲੇ ਹਨ ਅਤੇ ਨਾ ਹੀ ਉਸ ਨੂੰ ਕਿਸੇ ਵਿਸ਼ੇਸ਼ ਧਰਮ ਦੇ ਕਾਰਨ ਆਰਥਿਕ, ਰਾਜਨੀਤਿਕ ਜਾਂ ਸਮਾਜਿਕ ਖੇਤਰ ਵਿਚ ਕੋਈ ਹਾਨੀ ਹੀ ਉਠਾਉਣੀ ਪੈਂਦੀ ਹੈ ।
(iii) ਭਾਰਤ ਵਿਚ ਅਨੇਕਾਂ ਭਾਸ਼ਾਵਾਂ ਬੋਲੀਆਂ ਜਾਂਦੀਆਂ ਹਨ । ਇਹਨਾਂ ਵਿਚੋਂ ਕੁੱਝ ਦਾ ਜਨਮ ਸੰਸਕ੍ਰਿਤ ਤੋਂ ਅਤੇ ਕੁੱਝ ਦਾ ਦਾਵਿੜ ਤੋਂ ਹੋਇਆ ਹੈ । ਅਸਮੀ, ਉੜੀਆ, ਉਰਦੂ, ਕੰਨੜ, ਕਸ਼ਮੀਰੀ, ਗੁਜਰਾਤੀ, ਤਾਮਿਲ, ਤੇਲਗੂ, ਪੰਜਾਬੀ, ਬੰਗਲਾ, ਮਰਾਠੀ, ਮਲਿਆਲਮ, ਸੰਸਕ੍ਰਿਤ, ਸਿੰਧੀ ਅਤੇ ਹਿੰਦੀ ਭਾਰਤ ਦੀਆਂ ਮੁੱਖ ਭਾਸ਼ਾਵਾਂ ਹਨ । ਇਨ੍ਹਾਂ ਵਿਚੋਂ ਦੱਖਣ ਭਾਰਤ ਦੀਆਂ ਚਾਰ ਭਾਸ਼ਾਵਾਂ-ਤਮਿਲ, ਤੇਲਗੂ, ਕੰਨੜ ਅਤੇ ਮਲਿਆਲਮ ਦੀ ਉਤਪੱਤੀ ਦਾਵਿੜ ਭਾਸ਼ਾ ਤੋਂ ਹੋਈ ਹੈ ।
3. ਭਾਸ਼ਾਈ ਅਤੇ ਸਾਹਿਤਕ – ਸਮਾਨਤਾਵਾਂ-ਭਾਸ਼ਾ ਵਿਗਿਆਨੀਆਂ ਦਾ ਮਤ ਹੈ ਕਿ ਭਾਰਤ ਦੀਆਂ ਵਿਭਿੰਨ ਭਾਸ਼ਾਵਾਂ ਅਤੇ ਉਹਨਾਂ ਦੇ ਸਾਹਿਤ ਵਿਚ ਉੱਪਰਲੇ ਅੰਤਰ ਦੇ ਬਾਵਜੂਦ ਕਈ ਗੱਲਾਂ ਵਿਚ ਬਹੁਤ ਹੀ ਸਮਾਨਤਾਵਾਂ ਹਨ । ਸਾਰੀਆਂ ਭਾਰਤੀ ਭਾਸ਼ਾਵਾਂ ਦਾ ਸੰਬੰਧ ਧੁਨੀ ਤੋਂ ਹੈ । ਸਭ ਦੀ ਬਣਤਰ ਵੀ ਲਗਪਗ ਇੱਕੋ-ਜਿਹੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 6.
ਭਾਰਤ ਵਿਚ ਜਨਸੰਖਿਆ ਦੇ ਵਾਧੇ ਦੀ ਸਮੱਸਿਆ ‘ਤੇ ਇਕ ਲੇਖ ਲਿਖੋ ਅਤੇ ਇਸ ਸਮੱਸਿਆ ਦੇ ਹੱਲ ਬਾਰੇ ਵੀ ਚਾਨਣਾ ਪਾਓ ।
ਉੱਤਰ-
ਭਾਰਤ ਦੀ ਵਸੋਂ ਬੜੀ ਤੇਜ਼ ਗਤੀ ਨਾਲ ਵੱਧ ਰਹੀ ਹੈ । ਵਸੋਂ ਦੇ ਇਸ ਵਾਧੇ ਦੇ ਕਾਰਨ ਕਈ ਸਮੱਸਿਆਵਾਂ ਪੈਦਾ ਹੋ ਗਈਆਂ ਹਨ, ਜਿਨ੍ਹਾਂ ਦਾ ਵਰਣਨ ਇਸ ਪ੍ਰਕਾਰ ਹੈ-
- ਨੀਵਾਂ ਜੀਵਨ ਪੱਧਰ-ਦੂਸਰੇ ਦੇਸ਼ਾਂ ਦੇ ਜੀਵਨ ਪੱਧਰ ਦੇ ਮੁਕਾਬਲੇ ਵਿਚ ਭਾਰਤੀ ਲੋਕਾਂ ਦਾ ਜੀਵਨ ਪੱਧਰ ਬਹੁਤ ਨੀਵਾਂ ਹੈ । ਇਹ ਸਮੱਸਿਆ ਅਸਲ ਵਿਚ ਵਸੋਂ ਦੇ ਵਾਧੇ ਦੇ ਕਾਰਨ ਹੀ ਪੈਦਾ ਹੋਈ ਹੈ ।
- ਜੰਗਲਾਂ ਦੀ ਕਟਾਈ – ਵਧਦੀ ਹੋਈ ਵਸੋਂ ਨੂੰ ਘਰ ਤੇ ਭੋਜਨ ਮੁਹੱਇਆ ਕਰਵਾਉਣ ਵਾਸਤੇ ਵਾਧੂ ਜ਼ਮੀਨ ਦੀ ਜ਼ਰੂਰਤ ਹੁੰਦੀ ਹੈ ਤਾਂ ਜੋ ਖੇਤੀ ਦਾ ਵਿਕਾਸ ਕੀਤਾ ਜਾ ਸਕੇ । ਇਹ ਭੂਮੀ ਜੰਗਲਾਂ ਨੂੰ ਕੱਟ ਕੇ ਪ੍ਰਾਪਤ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ । ਇਸ ਕਾਰਨ ਜੰਗਲਾਂ ਦੀ ਕਟਾਈ ਦੇ ਕਾਰਨ ਹੋਰ ਕਈ ਸਮੱਸਿਆਵਾਂ ਪੈਦਾ ਹੋ ਜਾਂਦੀਆਂ ਹਨ, ਜਿਵੇਂ ਭੋਂ-ਖੋਰ, ਨਦੀਆਂ ਵਿਚ ਹੜਾਂ ਦਾ ਆਉਣਾ, ਵਾਤਾਵਰਨ ਦਾ ਪ੍ਰਦੂਸ਼ਿਤ ਹੋਣਾ ਅਤੇ ਜੰਗਲ ਸੰਪਦਾ ਦੀ ਹਾਨੀ ।
- ਪਸ਼ੂਆਂ ਲਈ ਚਾਰੇ ਦੀ ਘਾਟ – ਭਾਰਤ ਵਿਚ ਕੇਵਲ 4% ਭਾਗ ‘ਤੇ ਚਰਾਂਦਾਂ ਹਨ । ਵਸੋਂ ਦੀ ਸਮੱਸਿਆ ਦੇ ਕਾਰਨ ਜੇਕਰ ਇਹਨਾਂ ਨੂੰ ਖੇਤੀ ਜਾਂ ਰਹਿਣ-ਸਹਿਣ ਦੇ ਨਿਰਮਾਣ ਲਈ ਵਰਤਿਆ ਗਿਆ ਤਾਂ ਪਸ਼ੂਆਂ ਲਈ ਚਾਰੇ ਦੀ ਸਮੱਸਿਆ ਹੋਰ ਵੀ ਜਟਿਲ ਹੋ ਜਾਵੇਗੀ ।
- ਭੂਮੀ ‘ਤੇ ਦਬਾਓ – ਵਸੋਂ ਦੇ ਵਾਧੇ ਦਾ ਸਿੱਧਾ ਪ੍ਰਭਾਵ ਭੂਮੀ ‘ਤੇ ਪੈਂਦਾ ਹੈ । ਭੂਮੀ ਇਕ ਅਜਿਹਾ ਸਾਧਨ ਹੈ ਜਿਸ ਨੂੰ ਵਧਾਇਆ ਨਹੀਂ ਜਾ ਸਕਦਾ | ਜੇਕਰ ਭਾਰਤ ਦੀ ਵਸੋਂ ਇਸ ਤਰ੍ਹਾਂ ਵਧਦੀ ਗਈ ਤਾਂ ਭੂਮੀ ‘ਤੇ ਦਬਾਓ ਪਵੇਗਾ । ਇਸ ਦੇ ਨਤੀਜੇ ਵਜੋਂ ਖੇਤੀ ਉਤਪਾਦਾਂ ਦਾ ਹੋਰ ਵੀ ਜ਼ਿਆਦਾ ਦਬਾਓ ਹੋ ਜਾਵੇਗਾ ।
- ਖਣਿਜਾਂ ਦੀ ਘਾਟ – ਅਸੀਂ ਵਧਦੀ ਹੋਈ ਵਸੋਂ ਦੀਆਂ ਲੋੜਾਂ ਨੂੰ ਉਦਯੋਗਾਂ ਦਾ ਵਿਕਾਸ ਕਰਕੇ ਪੂਰਾ ਕਰ ਰਹੇ ਹਾਂ । ਪਰ ਉਦਯੋਗਾਂ ਦੇ ਵਿਕਾਸ ਦੇ ਲਈ ਖਣਿਜਾਂ ਦੀ ਹੋਰ ਵੀ ਜ਼ਿਆਦਾ ਲੋੜ ਹੈ । ਨਤੀਜੇ ਵਜੋਂ ਸਾਡੇ ਖਣਿਜਾਂ ਦੇ ਭੰਡਾਰ ਜਲਦੀ ਖ਼ਤਮ ਹੋ ਜਾਣਗੇ ।
- ਵਾਤਾਵਰਨ ਦੀ ਸਮੱਸਿਆ – ਵਸੋਂ ਵਿਚ ਵਾਧੇ ਦੇ ਕਾਰਨ ਵਾਤਾਵਰਨ ‘ਤੇ ਵੀ ਬੁਰਾ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ । ਇਸ ਲਈ ਸਾਫ਼ ਜਲ, ਸਾਫ਼ ਹਵਾ ਦੀ ਘਾਟ ਇਕ ਸਮੱਸਿਆ ਬਣ ਗਈ ਹੈ । ਬਨਸਪਤੀ ਦੀ ਕਮੀ ਦੇ ਕਾਰਨ ਆਕਸੀਜਨ ਦੀ ਵੀ ਘਾਟ ਹੋ ਰਹੀ ਹੈ ।
ਸਮੱਸਿਆ ਦਾ ਹੱਲ – ਜਨਸੰਖਿਆ ਦੇ ਵਾਧੇ ਦੀ ਸਮੱਸਿਆ ਨਾਲ ਨਿਪਟਣ ਲਈ ਹੇਠ ਲਿਖੇ ਉਪਾਅ ਕਰਨੇ ਚਾਹੀਦੇ ਹਨ-
- ਸੀਮਿਤ ਪਰਿਵਾਰ ਯੋਜਨਾਵਾਂ ਨੂੰ ਜ਼ਿਆਦਾ ਮਹੱਤਵ ਦੇਣਾ ਚਾਹੀਦਾ ਹੈ ।
- ਲੋਕਾਂ ਨੂੰ ਫ਼ਿਲਮਾਂ, ਨਾਟਕਾਂ ਅਤੇ ਹੋਰ ਸਾਧਨਾਂ ਦੁਆਰਾ ਸੀਮਿਤ ਪਰਿਵਾਰ ਦਾ ਮਹੱਤਵ ਸਮਝਾਇਆ ਜਾਵੇ ।
- ਦੇਸ਼ ਵਿਚੋਂ ਅਨਪੜ੍ਹਤਾ ਨੂੰ ਦੂਰ ਕਰਨ ਦਾ ਜਤਨ ਕੀਤਾ ਜਾਵੇ ਤਾਂ ਕਿ ਲੋਕ ਆਪ ਵੀ ਵੱਧਦੀ ਹੋਈ ਜਨਸੰਖਿਆ ਦੀਆਂ ਹਾਨੀਆਂ ਨੂੰ ਸਮਝ ਸਕਣ ।
- ਇਸਤਰੀ ਸਿੱਖਿਆ ‘ਤੇ ਵਿਸ਼ੇਸ਼ ਜ਼ੋਰ ਦਿੱਤਾ ਜਾਵੇ । ਵਿਆਹ ਦੀ ਉਮਰ ਵਿਚ ਵਾਧਾ ਕੀਤਾ ਜਾਵੇ ਤਾਂ ਕਿ ਵਿਆਹ ਛੋਟੀ ਉਮਰ ਵਿਚ ਨਾ ਹੋ ਸਕੇ ।
ਪ੍ਰਸ਼ਨ 7.
ਦੇਸ਼ ਵਿਚ ਸਿੱਖਿਆ ਦੇ ਫੈਲਾਅ ਲਈ ਕੀਤੀਆਂ ਗਈਆਂ ਕੋਸ਼ਿਸ਼ਾਂ ਦਾ ਆਲੋਚਨਾਤਮਕ ਅਧਿਐਨ ਕਰੋ ।
ਉੱਤਰ-
ਸਿੱਖਿਆ ਮਨੁੱਖ ਦੇ ਪੂਰਨ ਵਿਕਾਸ ਲਈ ਬਹੁਤ ਜ਼ਰੂਰੀ ਹੈ | ਆਜ਼ਾਦੀ ਦੇ ਸਮੇਂ ਦੇਸ਼ ਵਿਚ ਕੇਵਲ 14 ਪ੍ਰਤੀਸ਼ਤ ਲੋਕ ਹੀ ਸਾਖ਼ਰ ਹਨ | ਸਾਖ਼ਰਤਾ ਦਾ ਅਰਥ ਘੱਟ ਤੋਂ ਘੱਟ ਨਾਂ ਲਿਖਣ ਅਤੇ ਪੜ੍ਹਨ ਤਕ ਹੀ ਸੀਮਿਤ ਹੈ । ਸਾਲ 2001 ਵਿਚ ਹੋਈ ਜਨਗਣਨਾ ਦੇ ਅਨੁਸਾਰ ਸਾਖ਼ਰਤਾ ਪ੍ਰਤੀਸ਼ਤ 74.01 ਪ੍ਰਤੀਸ਼ਤ ਸੀ | ਪਹਿਲਾਂ ਸਾਡੇ ਦੇਸ਼ ਵਿਚ ਕੇਵਲ 6 ਕਰੋੜ ਵਿਅਕਤੀ ਹੀ ਪੜ੍ਹੇ-ਲਿਖੇ ਸਨ, ਪਰੰਤੂ ਹੁਣ ਇਹਨਾਂ ਦੀ ਸੰਖਿਆ ਵੱਧ ਕੇ 70 ਕਰੋੜ ਤੋਂ ਵੀ ਵੱਧ ਹੋ ਗਈ ਹੈ । ਇਸ ਪ੍ਰਕਾਰ ਸਾਖ਼ਰਤਾ ਵਿਚ ਸੱਤ ਗੁਣਾ ਵਾਧਾ ਹੋਇਆ ਹੈ । ਪਰੰਤੁ ਵਿਚਾਰ ਕਰਨ ਵਾਲੀ ਗੱਲ ਇਹ ਹੈ ਕਿ ਇਸ ਸਮੇਂ ਦੌਰਾਨ ਅਨਪੜ੍ਹ ਲੋਕਾਂ ਦੀ ਸੰਖਿਆ ਵੀ ਦੇਸ਼ ਵਿਚ ਵੱਧ ਗਈ ਹੈ ।
ਸਾਡੇ ਦੇਸ਼ ਦੇ ਸੰਵਿਧਾਨ ਅਨੁਸਾਰ ਚੌਦਾਂ ਸਾਲ ਤਕ ਦੀ ਉਮਰ ਦੇ ਸਾਰੇ ਬੱਚਿਆਂ ਲਈ ਮੁਫ਼ਤ ਅਤੇ ਲਾਜ਼ਮੀ ਸਿੱਖਿਆ ਦੀ ਵਿਵਸਥਾ ਕੀਤੀ ਗਈ ਹੈ । ਪਰ ਅਜੇ ਵੀ ਇਸ ਟੀਚੇ ਨੂੰ ਪੂਰਾ ਨਹੀਂ ਕੀਤਾ ਜਾ ਸਕਿਆ ਹੈ । ਇਸ ਦਾ ਕਾਰਨ ਇਹ ਹੈ ਕਿ ਦੇਸ਼ ਦੇ ਹਰ ਪਿੰਡ ਵਿਚ ਸਕੂਲ ਖੋਲ੍ਹਣਾ ਅਤੇ ਹਰ ਮਾਤਾ-ਪਿਤਾ ਨੂੰ ਆਪਣੇ ਬੱਚਿਆਂ ਨੂੰ ਸਕੂਲ ਭੇਜਣ ਲਈ ਮਨਾਉਣਾ ਇਕ ਬਹੁਤ ਹੀ ਮੁਸ਼ਕਿਲ ਕੰਮ ਹੈ ।
ਪਹਿਲਾਂ 15 ਪ੍ਰਾਇਮਰੀ ਸਕੂਲਾਂ ਪਿੱਛੇ ਇਕ ਮਿਡਲ ਸਕੂਲ ਸੀ, ਹੁਣ ਚਾਰ ਦੇ ਪਿੱਛੇ ਇਕ ਮਿਡਲ ਸਕੂਲ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਕਈ ਰਾਜ ਸਰਕਾਰਾਂ ਨੇ ਚਲਦੇ-ਫਿਰਦੇ ਸਕੂਲਾਂ ਅਤੇ ਰਾਤ ਦੇ ਸਕੂਲਾਂ ਦਾ ਵੀ ਪ੍ਰਬੰਧ ਕੀਤਾ ਹੈ ।
ਲੜਕੀਆਂ ਦੀ ਸਿੱਖਿਆ ‘ਤੇ ਵਿਸ਼ੇਸ਼ ਜ਼ੋਰ ਦੇਣ ਲਈ ਲੜਕੀਆਂ ਲਈ ਹੋਸਟਲ ਆਦਿ ਦਾ ਵੀ ਪ੍ਰਬੰਧ ਅਤੇ ਵਜ਼ੀਫ਼ਿਆਂ ਦਾ ਆਕਰਸ਼ਣ ਦਿੱਤਾ ਗਿਆ ਹੈ । ਪਰੰਤੂ ਕਈ ਰਾਜਾਂ ਵਿਚ ਬੱਚਿਆਂ ਦਾ ਅੱਧ ਵਿਚਕਾਰ ਹੀ ਸਕੂਲੀ ਸਿੱਖਿਆ ਛੱਡ ਦੇਣਾ ਚਿੰਤਾ ਦਾ ਵਿਸ਼ਾ ਬਣਿਆ ਹੋਇਆ ਹੈ । ਇਹ ਗੱਲ ਉੱਤਰ ਪ੍ਰਦੇਸ਼, ਮੱਧ ਪ੍ਰਦੇਸ਼, ਬਿਹਾਰ ਅਤੇ ਰਾਜਸਥਾਨ ਵਿਚ ਆਮ ਹੈ । ਇਹਨਾਂ ਚਾਰੇ ਰਾਜਾਂ ਵਿਚ ਸਾਖ਼ਰਤਾ ਪ੍ਰਤੀਸ਼ਤ ਦੇਸ਼ ਦੇ ਸਭ ਰਾਜਾਂ ਨਾਲੋਂ ਘੱਟ ਹੈ । ਇਸ ਦੇ ਉਲਟ ਕੇਰਲ ਦੇਸ਼ ਦਾ ਇਕ ਅਜਿਹਾ ਰਾਜ ਹੈ, ਜਿੱਥੇ ਸਾਖ਼ਰਤਾ ਦਰ ਨਾ ਕੇਵਲ ਸਭ ਤੋਂ ਵੱਧ ਹੈ ਬਲਕਿ ਬਹੁਤ ਉੱਚੀ ਹੈ ।
ਹੁਣ ਵੀ ਦੇਸ਼ ਵਿਚ 100 ਬੱਚਿਆਂ ਵਿਚੋਂ ਕੇਵਲ 25 ਬੱਚੇ ਹੀ ਅੱਠਵੀਂ ਜਮਾਤ ਤਕ ਪਹੁੰਚਦੇ ਹਨ । ਇਸ ਪ੍ਰਕਾਰ ਤਿੰਨਚੌਥਾਈ ਬੱਚੇ ਸਿੱਖਿਆ ਦੇ ਅਸਲੀ ਲਾਭ ਤੋਂ ਵਾਂਝੇ ਰਹਿ ਜਾਂਦੇ ਹਨ । ਦੇਸ਼ ਵਿਚ ਉੱਚ ਅਤੇ ਉਦਯੋਗਿਕ ਸਿੱਖਿਆ ਦੀ ਭਾਰੀ ਘਾਟ ਹੈ ।
II. ਹੇਠਾਂ ਲਿਖਿਆਂ ਨੂੰ ਭਾਰਤ ਦੇ ਨਕਸ਼ੇ ਵਿਚ ਦਰਸਾਉ-
(1) ਵੱਧ ਜਨਸੰਖਿਆ ਦੀ ਘਣਤਾ ਵਾਲੇ ਖੇਤਰ ।
(2) ਵੱਧ ਸਾਖ਼ਰਤਾ ਦੀ ਦਰ ਵਾਲੇ ਦੋ ਰਾਜ ।
(3) ਸਭ ਤੋਂ ਵੱਧ ਅਤੇ ਸਭ ਤੋਂ ਘੱਟ ਆਬਾਦੀ ਵਾਲੇ ਦੋ ਰਾਜ ।
(4) ਵੱਧ ਜਨਸੰਖਿਅਕ ਵਾਧਾ ਦਰ ਵਾਲੇ ਖੇਤਰ ।
PSEB 10th Class Social Science Guide ਜਨਸੰਖਿਆ Important Questions and Answers
ਵਸਤੂਨਿਸ਼ਠ ਪ੍ਰਸ਼ਨ (Objective Type Questions)
I. ਉੱਤਰ ਇਕ ਲਾਈਨ ਜਾਂ ਇਕ ਸ਼ਬਦ ਵਿਚ-
ਪ੍ਰਸ਼ਨ 1.
ਜਨਸੰਖਿਆ ਵੰਡ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਜਨਸੰਖਿਆ ਵੰਡ ਤੋਂ ਭਾਵ ਹੈ ਕਿ ਕਿਸੇ ਖੇਤਰ ਵਿਚ ਜਨਸੰਖਿਆ ਦਾ ਕਿਸ ਤਰ੍ਹਾਂ ਦਾ ਸਰੂਪ ਫ਼ੈਲਿਆ ਹੋਇਆ ਹੈ ਜਾਂ ਉਸ ਦਾ ਇਕ ਹੀ ਜਗ੍ਹਾ ਉੱਤੇ ਕਿੰਨਾ ਜਮਾਅ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 2.
ਜਨਸੰਖਿਆ ਘਣਤਾ ਦਾ ਕੀ ਅਰਥ ਹੈ ?
ਉੱਤਰ-
ਕਿਸੇ ਖੇਤਰ ਦੇ ਇਕ ਵਰਗ ਕਿਲੋਮੀਟਰ ਖੇਤਰ ਵਿਚ ਰਹਿਣ ਵਾਲੇ ਲੋਕਾਂ ਦੀ ਔਸਤ ਗਿਣਤੀ ਨੂੰ ਉਸ ਖੇਤਰ ਦੀ ਜਨਸੰਖਿਆ ਘਣਤਾ ਆਖਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 3.
ਭਾਰਤ ਵਿਚ ਜਨਸੰਖਿਆ ਵੰਡ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਨ ਵਾਲਾ ਮੁੱਖ ਤੱਤ ਕਿਹੜਾ ਹੈ ਅਤੇ ਕਿਉਂ ?
ਉੱਤਰ-
ਖੇਤੀ ਉਤਪਾਦਕਤਾ ।
ਪ੍ਰਸ਼ਨ 4.
(i) ਭਾਰਤ ਦੇ ਕਿਹੜੇ ਧਰਮ ਦੇ ਲੋਕਾਂ ਵਿਚ ਲਿੰਗ-ਅਨੁਪਾਤ ਸਭ ਤੋਂ ਵੱਧ ਅਤੇ
(i) ਕਿਹੜੇ ਧਰਮ ਦੇ ਲੋਕਾਂ ਵਿਚ ਸਭ ਤੋਂ ਘੱਟ ਹੈ ?
ਉੱਤਰ-
(i) ਭਾਰਤ ਵਿਚ ਇਸਾਈ ਧਰਮ ਦੇ ਲੋਕਾਂ ਵਿਚ ਲਿੰਗ-ਅਨੁਪਾਤ ਸਭ ਤੋਂ ਵੱਧ (994 ਔਰਤਾਂ ਪ੍ਰਤੀ ਹਜ਼ਾਰ ਮਰਦ ਅਤੇ
(ii) ਸਿੱਖਾਂ ਵਿਚ ਸਭ ਤੋਂ ਘੱਟ (888 ਪ੍ਰਤੀ ਹਜ਼ਾਰ ਮਰਦ ਹੈ ।
ਪ੍ਰਸ਼ਨ 5.
ਭਾਰਤ ਦੇ ਬਹੁਤ ਸੰਘਣੀ ਆਬਾਦੀ ਵਾਲੇ ਦੋ ਹਿੱਸੇ ਦੱਸੋ ।
ਉੱਤਰ-
ਭਾਰਤ ਵਿਚ ਉੱਪਰਲੀ ਗੰਗਾ ਘਾਟੀ ਅਤੇ ਮਾਲਾਬਾਰ ਵਿਚ ਬਹੁਤ ਸੰਘਣੀ ਜਨਸੰਖਿਆ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 6.
ਭਾਰਤ ਦੇ ਕਿਹੜੇ ਦੇਸ਼ਾਂ ਵਿਚ ਵਸੋਂ ਦੀ ਘਣਤਾ ਘੱਟ ਹੈ ?
ਉੱਤਰ-
ਭਾਰਤ ਦੇ ਉੱਤਰ-ਪੂਰਬਤੀ ਦੇਸ਼, ਸੰਘਣੀ ਵਰਖਾ ਕਰਨ ਵਾਲੇ
ਉੱਤਰ-
ਪੂਰਬੀ ਦੇਸ਼, ਪੱਛਮੀ ਰਾਜਸਥਾਨ ਦੇ ਬੇਹੱਦ ਖ਼ੁਸ਼ਕ ਖੇਤਰ ਅਤੇ ਗੁਜਰਾਤ ਦੇ ਕੁਝ ਖੇਤਰਾਂ ਵਿਚ ਵਸੋਂ ਘਣਤਾ ਘੱਟ ਹੈ |
ਪ੍ਰਸ਼ਨ 7.
ਸ਼ਹਿਰਾਂ ਵਿਚ ਵਸੋਂ ਦੇ ਬਹੁਤ ਤੇਜ਼ੀ ਨਾਲ ਵਧਣ ਦੇ ਕੀ ਬੁਰੇ ਨਤੀਜੇ ਹੋਏ ਹਨ ?
ਉੱਤਰ-
ਸ਼ਹਿਰਾਂ ਵਿਚ ਵਸੋਂ ਦੇ ਬਹੁਤ ਤੇਜ਼ੀ ਨਾਲ ਵਧਣ ਦੇ ਕਾਰਨ ਉਪਲੱਬਧ ਸਾਧਨਾਂ ਅਤੇ ਜਨ-ਸਹੂਲਤਾਂ ਉੱਤੇ ਦਬਾਅ ਵਧਿਆ ਹੈ ।
ਪ੍ਰਸ਼ਨ 8.
ਔਰਤ-ਮਰਦ ਜਾਂ ਲਿੰਗ-ਅਨੁਪਾਤ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਪ੍ਰਤੀ ਹਜ਼ਾਰ ਮਰਦਾਂ ਦੇ ਪਿੱਛੇ ਔਰਤਾਂ ਦੀ ਗਿਣਤੀ ਨੂੰ ਲਿੰਗ ਅਨੁਪਾਤ ਕਹਿੰਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 9.
ਕਮਾਊ ਜਨਸੰਖਿਆ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਕਮਾਊ ਜਨਸੰਖਿਆ ਤੋਂ ਭਾਵ ਉਨ੍ਹਾਂ ਲੋਕਾਂ ਤੋਂ ਹੈ ਜਿਹੜੇ ਵੱਖ-ਵੱਖ ਕਿੱਤਿਆਂ ਵਿਚ ਕੰਮ ਕਰਕੇ ਧਨ ਕਮਾਉਂਦੇ ਹਨ ।
![]()
ਪ੍ਰਸ਼ਨ 10.
ਨਿਰਭਰ ਜਨਸੰਖਿਆ ਕੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਨਿਰਭਰ ਜਨਸੰਖਿਆ ਵਿਚ ਉਹ ਬੱਚੇ ਅਤੇ ਬੁੱਢੇ ਆਉਂਦੇ ਹਨ ਜਿਹੜੇ ਕੰਮ ਨਹੀਂ ਕਰ ਸਕਦੇ ਪਰ ਕਮਾਊ ਜਨਸੰਖਿਆ ਉੱਤੇ ਨਿਰਭਰ ਰਹਿੰਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 11.
ਭਾਰਤ ਵਿਚ ਰਹਿਣ ਵਾਲੀਆਂ ਚਾਰ ਪ੍ਰਜਾਤੀਆਂ ਦੇ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਭਾਰਤ ਵਿਚ ਰਹਿਣ ਵਾਲੀਆਂ ਚਾਰ. ਮੁੱਖ ਪ੍ਰਜਾਤੀਆਂ ਹਨ-ਦਾਵਿੜ, ਮੰਗੋਲ, ਆਰੀਆ ਅਤੇ ਕਾਕੇਸ਼ੀਅਨ ।
ਪ੍ਰਸ਼ਨ 12.
ਉਹ ਕਿਹੜੀਆਂ ਚਾਰ ਭਾਸ਼ਾਵਾਂ ਹਨ ਜਿਨ੍ਹਾਂ ਦੀ ਉਤਪੱਤੀ ਦਾਵਿੜ ਭਾਸ਼ਾ ਤੋਂ ਹੋਈ ?
ਉੱਤਰ-
ਤਾਮਿਲ, ਤੇਲਗੂ, ਕੰਨੜ ਅਤੇ ਮਲਿਆਲਮ ਭਾਸ਼ਾਵਾਂ ਦੀ ਉਤਪੱਤੀ ਦਾਵਿੜ ਭਾਸ਼ਾ ਤੋਂ ਹੋਈ ।
ਪ੍ਰਸ਼ਨ 13.
ਮੌਤ-ਦਰ ਦੇ ਤੇਜ਼ੀ ਨਾਲ ਘਟਣ ਦਾ ਮੁੱਖ ਕਾਰਨ ਦੱਸੋ ।
ਉੱਤਰ-
ਮੌਤ-ਦਰ ਦੇ ਤੇਜ਼ੀ ਨਾਲ ਘਟਣ ਦਾ ਮੁੱਖ ਕਾਰਨ ਸਿਹਤ ਸੇਵਾਵਾਂ ਦਾ ਪ੍ਰਸਾਰ ਹੈ ।
ਪ੍ਰਸ਼ਨ 14.
ਭਾਰਤ ਵਿਚ ਸਭ ਤੋਂ ਘੱਟ ਜਨਸੰਖਿਆ ਵਾਲਾ ਰਾਜ ਹੈ ?
ਉੱਤਰ-
ਸਿੱਕਿਮ ।
![]()
ਪ੍ਰਸ਼ਨ 15.
ਭਾਰਤ ਵਿਚ ਜਨਸੰਖਿਆ ਘਣਤਾ ਕਿੰਨੀ ਹੈ ?
ਉੱਤਰ-
382 ਵਿਅਕਤੀ ਪ੍ਰਤੀ ਵਰਗ ਕਿਲੋਮੀਟਰ ।
ਪ੍ਰਸ਼ਨ 16.
ਪੱਛਮੀ ਬੰਗਾਲ ਵਿਚ ਜਨਸੰਖਿਆ ਘਣਤਾ ਕਿੰਨੀ ਹੈ ?
ਉੱਤਰ-
1082 ਵਿਅਕਤੀ ਪ੍ਰਤੀ ਵਰਗ ਕਿਲੋਮੀਟਰ ।
ਪ੍ਰਸ਼ਨ 17.
ਭਾਰਤ ਵਿਚ ਸਭ ਤੋਂ ਵਧੇਰੇ ਜਨਸੰਖਿਆ ਘਣਤਾ ਵਾਲੇ ਰਾਜ ਦਾ ਨਾਂ ਦੱਸੋ । .
ਉੱਤਰ-
ਬਿਹਾਰ ।
ਪ੍ਰਸ਼ਨ 18.
ਭਾਰਤ ਵਿਚ ਸਭ ਤੋਂ ਵਧੇਰੇ ਜਨਸੰਖਿਆ ਵਾਲਾ ਰਾਜ ਕਿਹੜਾ ਹੈ ?
ਉੱਤਰ-
ਉੱਤਰ-ਪ੍ਰਦੇਸ਼ ।
ਪ੍ਰਸ਼ਨ 19.
ਦਿੱਲੀ ਵਿਚ ਜਨਸੰਖਿਆ ਘਣਤਾ ਕਿੰਨੀ ਹੈ ?
ਉੱਤਰ-
9294 ਵਿਅਕਤੀ ਪ੍ਰਤੀ ਵਰਗ ਕਿਲੋਮੀਟਰ ।
![]()
ਪ੍ਰਸ਼ਨ 20.
ਭਾਰਤ ਵਿਚ 2001 ਦੀ ਜਨਗਣਨਾ ਅਨੁਸਾਰ ਲਿੰਗ ਅਨੁਪਾਤ ਕਿੰਨਾ ਹੈ ?
ਉੱਤਰ-
933 ਔਰਤਾਂ ਪ੍ਰਤੀ ਇਕ ਹਜ਼ਾਰ ਮਰਦ ।
ਪ੍ਰਸ਼ਨ 21.
ਭਾਰਤ ਵਿਚ ਸਭ ਤੋਂ ਵਧੇਰੇ ਸਾਖਰਤਾ ਦਰ ਵਾਲਾ ਰਾਜ ਕਿਹੜਾ ਹੈ ?
ਉੱਤਰ-
ਕੇਰਲਾ ।
ਪ੍ਰਸ਼ਨ 22.
ਭਾਰਤ ਵਿਚ ਸਭ ਤੋਂ ਘੱਟ ਜਨਸੰਖਿਆ ਘਣਤਾ ਵਾਲਾ ਰਾਜ ਕਿਹੜਾ ਹੈ ?
ਉੱਤਰ-
ਅਰੁਣਾਚਲ ਪ੍ਰਦੇਸ਼ ।
II. ਖ਼ਾਲੀ ਥਾਂਵਾਂ ਭਰੋ-
1. 2011 ਦੀ ਮਰਦਮ-ਸ਼ੁਮਾਰੀ ਦੇ ਅਨੁਸਾਰ ਭਾਰਤ ਵਿਚ ਕੁੱਲ ਸ਼ਹਿਰੀ ਵਸੋਂ ਲਗਪਗ …………………….. ਹੈ ।
2. ਪੇਂਡੂ ਖੇਤਰਾਂ ਵਿਚ ਮਜ਼ਦੂਰਾਂ ਦਾ ਪ੍ਰਤੀਸ਼ਤ ……………………….. ਹੈ ।
3. 2011 ਦੀ ਮਰਦਮ-ਸ਼ੁਮਾਰੀ ਅਨੁਸਾਰ ਭਾਰਤ ਵਿਚ ਵਸੋਂ ਘਣਤਾ …………………….: ਪ੍ਰਤੀ ਵਰਗ ਕਿਲੋਮੀਟਰ ਹੈ ।
4. ਦੇਸ਼ ਵਿਚ ਮੁੱਖ ਮਜ਼ਦੂਰਾਂ ਦਾ ਪ੍ਰਤੀਸ਼ਤ ………………………. ਹੈ ।
5. ਦੇਸ਼ ਵਿਚ ਮੁੱਖ ਮਜ਼ਦੂਰਾਂ ਦਾ ਸਭ ਤੋਂ ਵੱਧ ਪ੍ਰਤੀਸ਼ਤ ……………………….. ਵਿਚ ਹੈ ।
6. ਦੇਸ਼ ਵਿਚ 15-16 ਉਮਰ ਵਰਗ ਵਿਚ ……………………….. ਪ੍ਰਤੀਸ਼ਤ ਵਸੋਂ ਹੈ ।
ਉੱਤਰ-
1. 35 ਕਰੋੜ
2. 40.1
3. 382
4. 37.50
5. ਆਂਧਰ ਪ੍ਰਦੇਸ਼
6. 58.4.
II. ਬਹੁਵਿਕਲਪੀ ਪ੍ਰਸ਼ਨ-
ਪ੍ਰਸ਼ਨ 1.
ਵਸੋਂ ਦੇ ਪੱਖੋਂ ਭਾਰਤ ਦਾ ਸੰਸਾਰ ਵਿਚ ਸਥਾਨ ਹੈ-
(A) ਦੂਸਰਾ
(B) ਚੌਥਾ
(C) ਪੰਜਵਾਂ
(D) ਨੌਵਾਂ ।
ਉੱਤਰ-
(A) ਦੂਸਰਾ
ਪ੍ਰਸ਼ਨ 2.
ਪੰਜਾਬ ਵਿਚ ਪੂਰੇ ਦੇਸ਼ ਦੀ ਲਗਪਗ ਵਜੋਂ ਨਿਵਾਸ ਕਰਦੀ ਹੈ ।
(A) 1.3 ਪ੍ਰਤੀਸ਼ਤ
(B) 2.3 ਪ੍ਰਤੀਸ਼ਤ
(C) 3.2 ਪ੍ਰਤੀਸ਼ਤ
(D) 1.2 ਪ੍ਰਤੀਸ਼ਤ ।
ਉੱਤਰ-
(B) 2.3 ਪ੍ਰਤੀਸ਼ਤ
![]()
ਪ੍ਰਸ਼ਨ 3.
ਦੇਸ਼ ਦੀ ਕਿੰਨੇ ਪ੍ਰਤੀਸ਼ਤ ਵਜੋਂ ਪੇਂਡੂ ਖੇਤਰਾਂ ਵਿਚ ਨਿਵਾਸ ਕਰਦੀ ਹੈ-
(A) 70
(B) 75
(C) 78
(D) 71
ਉੱਤਰ-
(D) 71
ਪ੍ਰਸ਼ਨ 4.
2011 ਦੀ ਮਰਦ-ਸ਼ੁਮਾਰੀ ਅਨੁਸਾਰ ਪੰਜਾਬ ਵਿਚ ਵਸੋਂ ਘਣਤਾ ਹੈ-
(A) 888
(B) 944
(C) 550
(D) 933
ਉੱਤਰ-
(C) 550
ਪ੍ਰਸ਼ਨ 5.
2011 ਦੀ ਮਰਦਮ-ਸ਼ੁਮਾਰੀ ਅਨੁਸਾਰ ਦੇਸ਼ ਵਿਚ ਪ੍ਰਤੀ 1000 ਮਰਦਾਂ ਪਿੱਛੇ ਔਰਤਾਂ ਦੀ ਸੰਖਿਆ ਹੈ-
(A) 944
(B) 933
(C) 939
(D) 894.
ਉੱਤਰ-
(A) 944
IV ਸਹੀ-ਗਲਤ ਕਥਨ-
ਪ੍ਰਸ਼ਨ-ਸਹੀ ਕਥਨਾਂ ‘ਤੇ (√) ਅਤੇ ਗਲਤ ਕਥਨਾਂ ਉੱਪਰ (×) ਦਾ ਨਿਸ਼ਾਨ ਲਗਾਓ :
1. ਜਨਸੰਖਿਆ ਦੀ ਦ੍ਰਿਸ਼ਟੀ ਤੋਂ ਸੰਸਾਰ ਵਿਚ ਭਾਰਤ ਦਾ ਪਹਿਲਾ ਸਥਾਨ ਹੈ ।
2. ਦੇਸ਼ ਦੇ ਪਰਬਤੀ ਅਤੇ ਮਾਰੁਸਥਲ ਖੇਤਰਾਂ ਵਿਚ ਜਨਸੰਖਿਆ ਬਹੁਤ ਸੰਘਣੀ ਹੈ ।
3. ਨਿਰਧਨ ਦੇਸ਼ਾਂ ਵਿਚ ਬਚਪਨ ਉਮਰ ਵਰਗ 10-14 ਸਾਲ ਦੀ ਜਨਸੰਖਿਆ ਦਾ ਪ੍ਰਤੀਸ਼ਤ ਜ਼ਿਆਦਾ ਹੈ ।
4. ਭਾਰਤ ਵਿਚ ਲਿੰਗ-ਅਨੁਪਾਤ ਘੱਟ ਜਾਂ ਪ੍ਰਤੀਕੂਲ ਹੈ ।
5. ਜਨਸੰਖਿਆ ਦੀ ਕੁਦਰਤੀ ਵਾਧਾ ਦਰ ਜਨਮ-ਦਰ ਅਤੇ ਮੌਤ ਦਰ ਦੇ ਅੰਤਰ ‘ਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ ।
ਉੱਤਰ-
1. ×
2. ×
3. √
4. √
5. √
V. ਸਹੀ-ਮਿਲਾਨ ਕਰੈ-
1. ਪ੍ਰਤੀ ਹਜ਼ਾਰ ਆਦਮੀ ਦੇ ਪਿੱਛੇ ਔਰਤਾਂ ਦੀ ਸੰਖਿਆ-ਨਿਰਭਰ ਜਨਸੰਖਿਆ
2. ਬੱਚੇ ਅਤੇ ਬੁੱਢੇ-ਬਿਹਾਰ
3. ਭਾਰਤ ਦਾ ਸਭ ਤੋਂ ਜ਼ਿਆਦਾ ਜਨਸੰਖਿਆ ਘਣਤਾ ਵਾਲਾ ਰਾਜ-ਉੱਤਰ ਪ੍ਰਦੇਸ਼
4. ਭਾਰਤ ਦਾ ਸਭ ਤੋਂ ਜ਼ਿਆਦਾ ਜਨਸੰਖਿਆ ਵਾਲਾ ਰਾਜ-ਲਿੰਗ ਅਨੁਪਾਤ ।
ਉੱਤਰ-
1. ਪ੍ਰਤੀ ਹਜ਼ਾਰ ਆਦਮੀ ਦੇ ਪਿੱਛੇ ਔਰਤਾਂ ਦੀ ਸੰਖਿਆ-ਲਿੰਗ ਅਨੁਪਾਤ,
2. ਬੱਚੇ ਅਤੇ ਬੁੱਢੇ-ਨਿਰਭਰ ਜਨਸੰਖਿਆ,
3. ਭਾਰਤ ਦਾ ਸਭ ਤੋਂ ਜ਼ਿਆਦਾ ਜਨਸੰਖਿਆ ਘਣਤਾ ਵਾਲਾ ਰਾਜ-ਬਿਹਾਰ,
4. ਭਾਰਤ ਦਾ ਸਭ ਤੋਂ ਜ਼ਿਆਦਾ ਜਨਸੰਖਿਆ ਵਾਲਾ ਰਾਜ-ਉੱਤਰ ਪ੍ਰਦੇਸ਼ ।
![]()
ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Short Answer Type Questions)
ਪ੍ਰਸ਼ਨ 1
ਭਾਰਤ ਵਿਚ ਅਸਮਾਨ ਜਨਸੰਖਿਆ ਵੰਡ ਦੇ ਤਿੰਨ ਕਾਰਨ ਦਿਓ ।
ਉੱਤਰ-
ਭਾਰਤ ਵਿਚ ਅਸਮਾਨ ਜਨਸੰਖਿਆਂ ਵੰਡ ਦੇ ਤਿੰਨ ਕਾਰਨ ਹੇਠ ਲਿਖੇ ਹਨ-
- ਭੂਮੀ ਦਾ ਉਪਜਾਊਪਨ – ਭਾਰਤ ਦੇ ਜਿਨ੍ਹਾਂ ਰਾਜਾਂ ਵਿਚ ਉਪਜਾਊ ਭੂਮੀ ਦਾ ਵਧੇਰੇ ਵਿਸਥਾਰ ਹੈ, ਉੱਥੇ ਜਨਸੰਖਿਆ ਦੀ ਘਣਤਾ ਵਧੇਰੇ ਹੈ । ਉੱਤਰ ਪ੍ਰਦੇਸ਼ ਅਤੇ ਬਿਹਾਰ ਅਜਿਹੇ ਹੀ ਰਾਜ ਹਨ ।
- ਵਰਖਾ ਦੀ ਮਾਤਰਾ – ਵਧੇਰੇ ਵਰਖਾ ਵਾਲੇ ਹਿੱਸਿਆਂ ਵਿਚ ਜਨਸੰਖਿਆ ਦੀ ਘਣਤਾ ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ, ਉੱਤਰੀ ਭਾਰਤ ਵਿਚ ਪੂਰਬ ਤੋਂ ਪੱਛਮ ਵੱਲ ਜਾਂਦੇ ਹੋਇਆਂ ਵਰਖਾ ਦੀ ਮਾਤਰਾ ਘਟਦੀ ਜਾਂਦੀ ਹੈ । ਇਸ ਲਈ ਜਨਸੰਖਿਆ ਦੀ ਘਣਤਾ ਵੀ ਘਟਦੀ ਜਾਂਦੀ ਹੈ ।
- ਜਲਵਾਯੂ – ਜਿੱਥੇ ਜਲਵਾਯੂ ਸਿਹਤ ਲਈ ਅਨੁਕੂਲ ਹੁੰਦੀ ਹੈ, ਉੱਥੇ ਵੀ ਜਨਸੰਖਿਆ ਘਣਤਾ ਵਧੇਰੇ ਹੁੰਦੀ ਹੈ । ਆਸਾਮ ਵਿਚ ਵਰਖਾ ਵਧੇਰੇ ਹੁੰਦੇ ਹੋਇਆਂ ਵੀ ਵਧੇਰੇ ਨਮੀ ਦੇ ਕਾਰਨ ਮਲੇਰੀਏ ਦਾ ਜ਼ੋਰ ਬਣਿਆ ਰਹਿੰਦਾ ਹੈ । ਇਹੀ ਕਾਰਨ ਹੈ ਕਿ ਉੱਥੇ ਜਨਸੰਖਿਆ ਦੀ ਘਣਤਾ ਘੱਟ ਹੈ ।
ਪ੍ਰਸ਼ਨ 2.
ਭਾਰਤੀ ਜਨਸੰਖਿਆ ਦਾ ਵਾਧਾ ਭਾਰਤ ਲਈ ਸਮੱਸਿਆ ਕਿਉਂ ਬਣ ਗਈ ਹੈ ?
ਉੱਤਰ-
ਆਜ਼ਾਦੀ ਤੋਂ ਬਾਅਦ ਭਾਰਤ ਦਾ ਖੇਤਰਫਲ ਤਾਂ ਉੱਨਾ ਹੀ ਹੈ ਪਰ ਸੁਤੰਤਰਤਾ ਤੋਂ ਬਾਅਦ ਦੇਸ਼ ਦੀ ਜਨਸੰਖਿਆ ਲਗਪਗ ਤਿਗੁਣੀ ਹੋ ਗਈ ਹੈ । ਅੱਜ ਜਨਸੰਖਿਆ 1.95 ਪ੍ਰਤੀਸ਼ਤ ਦੀ ਰਫ਼ਤਾਰ ਨਾਲ ਵੱਧ ਰਹੀ ਹੈ । ਇੰਨੀ ਵੱਡੀ ਜਨਸੰਖਿਆ ਦੀਆਂ ਮੂਲ ਜ਼ਰੂਰਤਾਂ ਪੂਰੀਆਂ ਕਰਨੀਆਂ ਬਹੁਤ ਵੱਡੀ ਸਮੱਸਿਆ ਬਣੀ ਹੋਈ ਹੈ । ਦੇਸ਼ ਦੇ ਇਨ੍ਹਾਂ ਲੋਕਾਂ ਲਈ ਸਕੂਲਾਂ, ਹਸਪਤਾਲਾਂ ਅਤੇ ਹੋਰ ਸੇਵਾਵਾਂ ਦਾ ਪ੍ਰਬੰਧ ਕਰਨਾ ਸੌਖਾ ਨਹੀਂ ਹੈ । ਜਨਸੰਖਿਆ ਦੇ ਵਾਧੇ ਦੇ ਨਾਲ-ਨਾਲ ਸੰਚਾਰ ਅਤੇ ਆਵਾਜਾਈ ਦੀਆਂ ਸੇਵਾਵਾਂ ਵਿਚ ਵੀ ਵਾਧਾ ਕਰਨਾ ਹੋਵੇਗਾ | ਸਭ ਤੋਂ ਵੱਡੀ ਸਮੱਸਿਆ ਮਨੁੱਖੀ ਸਾਧਨਾਂ ਵਿਚ-ਗੁਣਵਤਾ ਦਾ ਪੈਦਾ ਕਰਨਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 3.
ਭਾਰਤ ਵਿਚ ਜਨਸੰਖਿਆ ਵਾਧੇ ਦੇ ਤਿੰਨ ਬੁਰੇ ਪ੍ਰਭਾਵ ਦੱਸੋ ।
ਉੱਤਰ-
ਭਾਰਤ ਵਿਚ ਜਨਸੰਖਿਆ ਵਾਧੇ ਦੇ ਤਿੰਨ ਬੁਰੇ ਪ੍ਰਭਾਵ ਅੱਗੇ ਲਿਖੇ ਹਨ
- ਲੋਕਾਂ ਨੂੰ ਜੀਵਨ ਦੀਆਂ ਜ਼ਰੂਰੀ ਲੋੜਾਂ ਉਪਲੱਬਧ ਨਹੀਂ ਹੋ ਰਹੀਆਂ ਹਨ ਅਤੇ ਉਨ੍ਹਾਂ ਦਾ ਜੀਵਨ ਪੱਧਰ ਦਿਨੋ-ਦਿਨ ਡਿੱਗਦਾ ਜਾ ਰਿਹਾ ਹੈ ।
- ਭਾਰਤ ਵਿਚ ਬੇਰੁਜ਼ਗਾਰੀ ਦੀ ਸਮੱਸਿਆ ਗੰਭੀਰ ਰੂਪ ਧਾਰਨ ਕਰ ਰਹੀ ਹੈ ।
- ਜਨਸੰਖਿਆ ਵਾਧੇ ਨਾਲ ਖੇਤੀ ਉੱਤੇ ਦਬਾਅ ਵਧ ਰਿਹਾ ਹੈ । ਇਸ ਦੇ ਫਲਸਰੂਪ ਲੋਕ ਪਿੰਡਾਂ ਤੋਂ ਸ਼ਹਿਰਾਂ ਵੱਲ ਹਿਜ਼ਰਤ ਕਰ ਰਹੇ ਹਨ । ਇਸ ਨਾਲ ਸ਼ਹਿਰਾਂ ਵਿਚ ਪ੍ਰਦੂਸ਼ਣ, ਬੇਰੁਜ਼ਗਾਰੀ ਅਤੇ ਅਪਰਾਧਾਂ ਦੀ ਦਰ ਵਿਚ ਵਾਧਾ ਹੋਇਆ ਹੈ ।
ਪ੍ਰਸ਼ਨ 4.
ਭਾਰਤ ਦੀ ਜਨਸੰਖਿਆ ਦੀ ਪੇਸ਼ਾਵਰੀ ਬਣਤਰ ਕਿਉਂ ਅਸੰਤੁਲਿਤ ਹੈ ?
ਉੱਤਰ-
ਭਾਰਤ ਦੀ ਜਨਸੰਖਿਆ ਦਾ ਦੋ-ਤਿਹਾਈ ਹਿੱਸਾ ਖੇਤੀ ਉੱਤੇ ਨਿਰਭਰ ਹੈ । ਭਾਰਤ ਵਿਚ ਕੁੱਲ ਕਮਾਊ ਜਨਸੰਖਿਆ ਦਾ ਸਿਰਫ਼ 10 ਪ੍ਰਤੀਸ਼ਤ ਭਾਗ ਹੀ ਉਦਯੋਗਾਂ ਵਿਚ ਲੱਗਿਆ ਹੋਇਆ ਹੈ । ਜਨਸੰਖਿਆ ਦਾ ਬਾਕੀ ਇਕ-ਚੌਥਾਈ ਭਾਗ ਤੀਸਰੇ ਕਿੱਤਿਆਂ ਭਾਵ ਸੇਵਾਵਾਂ ਵਿਚ ਲੱਗਾ ਹੋਇਆ ਹੈ । ਇਸ ਪੇਸ਼ਾਵਰੀ ਰਚਨਾ ਵਿਚ ਇਕ ਗੱਲ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਸਾਡੀ ਜਨਸੰਖਿਆ ਦਾ ਬਹੁਤ ਵੱਡਾ ਹਿੱਸਾ ਅਰਥ-ਪ੍ਰਬੰਧ ਦੇ ਹਲਕੇ ਖੇਤਰ ਵਿਚ ਕੰਮ ਕਰਦਾ ਹੈ । ਹਲਕੇ ਖੇਤਰ ਵਿਚ ਨਿਰਮਾਣ ਉਦਯੋਗ ਆਉਂਦੇ ਹਨ ਜਿਨ੍ਹਾਂ ਰਾਹੀਂ ਅਸੀਂ ਕੱਚੇ ਮਾਲ ਤੋਂ ਲਾਭਕਾਰੀ ਵਸਤਾਂ ਬਣਾ ਕੇ ਰਾਸ਼ਟਰੀ ਆਮਦਨ ਵਿਚ ਵਾਧਾ ਕਰਦੇ ਹਾਂ । ਇਸ ਲਈ ਜਿਨ੍ਹਾਂ ਖੇਤਰਾਂ ਵਿਚ ਵਧੇਰੇ ਲੋਕ ਲੱਗੇ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ, ਉੱਥੇ ਨਹੀਂ ਲੱਗੇ ਹੋਏ ਹਨ । ਇਸ ਲਈ ਸਾਡੀ ਜਨਸੰਖਿਆ ਦੀ ਪੇਸ਼ਾਵਰੀ ਬਣਤਰ ਅਸੰਤੁਲਿਤ ਹੈ ।
ਪ੍ਰਸ਼ਨ 5.
ਉੱਤਰੀ ਭਾਰਤ ਦਾ ਮੈਦਾਨ ਸੰਘਣਾ ਆਬਾਦ ਕਿਉਂ ਹੈ ? ਦੋ ਕਾਰਨ ਲਿਖੋ ।
ਉੱਤਰ-
ਉੱਤਰੀ ਭਾਰਤ ਦੇ ਮੈਦਾਨ ਵਧੇਰੇ ਸੰਘਣੇ ਆਬਾਦ ਹੋਣ ਦੇ ਦੋ ਹੇਠ ਲਿਖੇ ਕਾਰਨ ਹਨ-
- ਇਨ੍ਹਾਂ ਦੇਸ਼ਾਂ ਦਾ ਜਲਵਾਯੂ ਸਿਹਤ ਲਈ ਠੀਕ ਹੈ ਅਤੇ ਇੱਥੋਂ ਦੀ ਮਿੱਟੀ ਉਪਜਾਊ ਹੈ ਤੇ ਖੇਤੀ ਕਿੱਤਾ ਉੱਨਤ ਹੈ ।
- ਇੱਥੇ ਆਵਾਜਾਈ ਦੇ ਸਾਧਨ ਉੱਨਤ ਹਨ ਅਤੇ ਇਹ ਦੇਸ਼ ਉਦਯੋਗਿਕ ਪੱਖੋਂ ਵੀ ਕਾਫ਼ੀ ਉੱਨਤ ਹਨ ।
ਪ੍ਰਸ਼ਨ 6.
ਭਾਰਤ ਦੇ ਕਿਹੜੇ ਤਿੰਨ ਹਿੱਸੇ ਵਿਰਲੇ ਆਬਾਦ ਹਨ ? ਇਸ ਦੇ ਲਈ ਜ਼ਿੰਮੇਵਾਰ ਤਿੰਨ ਮਹੱਤਵਪੂਰਨ ਕਾਰਨ ਵੀ ਦੱਸੋ ।
ਉੱਤਰ-
ਭਾਰਤ ਦੇ ਥਾਰ ਮਾਰੂਥਲ, ਪੱਛਮੀ ਹਿਮਾਲਾ ਦੇਸ਼ ਅਤੇ ਛੋਟਾ ਨਾਗਪੁਰ ਦੇ ਪਠਾਰ ਵਿਚ ਜਨਸੰਖਿਆ ਵਿਰਲੀ ਆਬਾਦ ਹੈ ।
ਕਾਰਨ-
- ਇਨ੍ਹਾਂ ਦੇਸ਼ਾਂ ਦੀ ਭੂਮੀ ਉਪਜਾਊ ਨਹੀਂ ਹੈ । ਇਹ ਜਾਂ ਤਾਂ ਰੇਤਲੀ ਹੈ ਜਾਂ ਪਥਰੀਲੀ ।
- ਇੱਥੇ ਆਵਾਜਾਈ ਦੇ ਸਾਧਨਾਂ ਦਾ ਵਿਕਾਸ ਨਹੀਂ ਹੋ ਸਕਿਆ ਹੈ ।
- ਇੱਥੋਂ ਦਾ ਜਲਵਾਯੂ ਸਿਹਤ ਲਈ ਢੁੱਕਵਾਂ ਨਹੀਂ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 7.
ਭਾਰਤ ਨੂੰ ਧਿਆਨ ਵਿਚ ਰੱਖਦੇ ਹੋਇਆਂ ਹੇਠ ਲਿਖਿਆਂ ਦੀ ਵਿਆਖਿਆ ਕਰੋ-
(ਉ) ਜਨਗਣਨਾ
(ਅ) ਜਨਸੰਖਿਆ ਦੀ ਔਸਤ ਘਣਤਾ
(ੲ) ਮੌਤ-ਦਰੇ ।
ਉੱਤਰ-
(ਉ) ਜਨਗਣਨਾ – ਸਰਕਾਰ ਹਰੇਕ 10 ਸਾਲ ਬਾਅਦ ਦੇਸ਼ ਦੇ ਸਾਰੇ ਲੋਕਾਂ ਦੀ ਗਿਣਤੀ ਕਰਵਾਉਂਦੀ ਹੈ । ਇਸ ਪ੍ਰਕਿਰਿਆ ਨੂੰ ਜਨਗਣਨਾ ਆਖਦੇ ਹਨ । ਇਸ ਵਿਚ ਕੁਝ ਸਮਾਜਿਕ ਅਤੇ ਆਰਥਿਕ ਅੰਕੜੇ ਵੀ ਇਕੱਠੇ ਕੀਤੇ ਜਾਂਦੇ ਹਨ । ਭਾਰਤ ਵਿਚ ਆਖ਼ਰੀ ਜਨਗਣਨਾ 2011 ਈ. ਵਿਚ ਹੋਈ ਸੀ ।
(ਅ) ਜਨਸੰਖਿਆ ਦੀ ਔਸਤ ਘਣਤਾ – ਕਿਸੇ ਦੇਸ਼ ਦੇ ਇਕ-ਤਿਹਾਈ ਖੇਤਰ ਵਿਚ ਰਹਿਣ ਵਾਲੇ ਲੋਕਾਂ ਦੀ ਔਸਤ ਸੰਖਿਆ ਉਸ ਦੇਸ਼ ਦੀ ਜਨਸੰਖਿਆ ਦੀ ਔਸਤ ਘਣਤਾ ਅਖਵਾਉਂਦੀ ਹੈ । ਇਸ ਨੂੰ ਅਕਸਰ ਵਿਅਕਤੀ ਪ੍ਰਤੀ ਵਰਗ ਕਿਲੋਮੀਟਰ ਜਨਸੰਖਿਆ ਵਿਚ ਪ੍ਰਗਟ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । 2011 ਈ: ਦੀ ਜਨਗਣਨਾ ਦੇ ਅਨੁਸਾਰ ਭਾਰਤ ਵਿਚ ਜਨਸੰਖਿਆ ਦੀ ਔਸਤ ਘਣਤਾ 382 ਵਿਅਕਤੀ ਪ੍ਰਤੀ ਵਰਗ ਕਿਲੋਮੀਟਰ ਹੈ ।
(ੲ) ਮੌਤ-ਦਰ – ਮੌਤ-ਦਰ ਤੋਂ ਸਾਡਾ ਭਾਵ ਮਰਨ ਵਾਲਿਆਂ ਦੀ ਗਿਣਤੀ ਤੋਂ ਹੈ । ਜਨਮ-ਦਰ ਵਾਂਗ ਮਰਨ ਵਾਲਿਆਂ ਦੀ ਗਿਣਤੀ ਨੂੰ ਵੀ ਅਸੀਂ ਪ੍ਰਤੀ ਹਜ਼ਾਰ ਵਿਚ ਬਿਆਨ ਕਰਦੇ ਹਾਂ । ਪ੍ਰਤੀ ਹਜ਼ਾਰ ਵਿਅਕਤੀ ਦੇ ਪਿੱਛੇ ਜਿੰਨੇ ਵਿਅਕਤੀਆਂ ਦੀ ਮੌਤ ਹੁੰਦੀ ਹੈ, ਉਸ ਨੂੰ ਮੌਤ-ਦਰ ਆਖਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 8.
ਨਿਰਭਰ-ਅਨੁਪਾਤ ਦਾ ਕੀ ਅਰਥ ਹੈ ? ਭਾਰਤ ਵਿਚ ਨਿਰਭਰ-ਅਨੁਪਾਤ ਮੁਕਾਬਲੇ ਵਿਚ ਵਧੇਰੇ ਕਿਉਂ ਹੈ ? ਦੋ ਕਾਰਨ ਦਿਓ ।
ਉੱਤਰ-
ਨਿਰਭਰ ਅਨੁਪਾਤ ਤੋਂ ਭਾਵ ਜਨਸੰਖਿਆ ਦਾ ਉਹ ਹਿੱਸਾ ਹੈ, ਜਿਹੜਾ ਖ਼ੁਦ ਕਮਾਈ ਨਹੀਂ ਕਰਦਾ । ਕੰਮ ਨਾ ਕਰਨ ਵਾਲੇ ਬੁੱਢੇ ਅਤੇ ਬੱਚੇ ਨਿਰਭਰ ਜਨਸੰਖਿਆ ਵਿਚ ਗਿਣੇ ਜਾਂਦੇ ਹਨ | ਕੁੱਲ ਜਨਸੰਖਿਆ ਦਾ ਜਿੰਨੇ ਪ੍ਰਤੀਸ਼ਤ ਹਿੱਸਾ ਨਿਰਭਰ ਜਨਸੰਖਿਆ ਹੁੰਦੀ ਹੈ, ਉਸ ਦਾ ਅਨੁਪਾਤ ਹੀ ਨਿਰਭਰ ਅਨੁਪਾਤ ਅਖਵਾਉਂਦਾ ਹੈ ।
ਕਾਰਨ-
- ਭਾਰਤ ਵਿਚ ਪਰੰਪਰਾਗਤ ਰੂਪ ਤੋਂ ਸੰਯੁਕਤ ਪਰਿਵਾਰ ਪ੍ਰਣਾਲੀ ਚਲੀ ਆ ਰਹੀ ਹੈ । ਇਸ ਲਈ ਇੱਥੇ ਬੁੱਢੇ ਅਤੇ ਬੱਚਿਆਂ ਨੂੰ ਦੁਸਰੇ ਦੇਸ਼ਾਂ ਦੇ ਮੁਕਾਬਲੇ ਵਿਚ ਰੋਜ਼ੀ ਰੋਟੀ ਦੀ ਗਾਰੰਟੀ ਹੁੰਦੀ ਹੈ ।
- ਅਨਪੜ੍ਹਤਾ ਅਤੇ ਰੂੜੀਵਾਦ ਨੇ ਵੀ ਇਸ ਗੱਲ ਨੂੰ ਬੜਾਵਾ ਦਿੱਤਾ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 9.
ਭਾਰਤੀ ਯੋਜਨਾ ਦੀ ਸਭ ਤੋਂ ਵੱਡੀ ਭੁੱਲ ਕਿਹੜੀ ਹੈ ? ਇਸ ਦੇ ਕੀ ਸਿੱਟੇ ਨਿਕਲਦੇ ਹਨ ?
ਉੱਤਰ-
ਅਰਥ-ਸ਼ਾਸਤਰੀ ਪ੍ਰੋ: ਅਮਰੱਤਿਆ ਸੈਨ ਦੇ ਅਨੁਸਾਰ ਮਨੁੱਖੀ ਸਾਧਨਾਂ ਦੇ ਵਿਕਾਸ ਵੱਲ ਉੱਚਿਤ ਧਿਆਨ ਨਾ ਦੇਣਾ ਭਾਰਤੀ ਯੋਜਨਾ (Indian Planning) ਦੀ ਵੱਡੀ ਭੁੱਲ ਹੈ । ਇਹ ਸਾਡੀਆਂ ਆਰਥਿਕ ਨਾਕਾਮਯਾਬੀਆਂ ਦਾ ਮੂਲ ਕਾਰਨ ਹੈ । ਅਜਿਹਾ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ ਕਿ ਸਮਾਜਿਕ ਨਿਆਂ ਦੇ ਪਹਿਲੂਆਂ ਵੱਲ ਉੱਚਿਤ ਧਿਆਨ ਨਾ ਦੇਣ ਦੇ ਕਾਰਨ ਭਾਰਤ ਵਿਚ ਹੋਏ ਆਰਥਿਕ ਵਿਕਾਸ ਦਾ ਲਾਭ ਗ਼ਰੀਬਾਂ, ਔਰਤਾਂ ਅਤੇ ਸਮਾਜ ਦੇ ਕਮਜ਼ੋਰ ਵਰਗਾਂ ਅਤੇ ਦੱਬੇ ਹੋਏ ਵਰਗਾਂ ਤਕ ਨਹੀਂ ਪਹੁੰਚ ਸਕਿਆ ਹੈ । ਫਲਸਰੂਪ ਆਰਥਿਕ ਵਿਕਾਸ ਦੇ ਨਾਲ-ਨਾਲ ਡੂੰਘੀਆਂ ਸਮਾਜਿਕ, ਆਰਥਿਕ, ਭੂਗੋਲਿਕ ਅਤੇ ਰਾਜਨੀਤਿਕ ਸਮੱਸਿਆਵਾਂ ਪੈਦਾ ਹੋ ਗਈਆਂ ਹਨ। ਅੱਜ-ਕਲ੍ਹ ਦੇਸ਼ ਵਿਚ ਜਿਹੜੇ ਜਾਤੀ, ਧਾਰਮਿਕ ਅਤੇ ਖੇਤਰੀ ਸੰਘਰਸ਼ ਨਜ਼ਰ ਆ ਰਹੇ ਹਨ ਉਨ੍ਹਾਂ ਦੇ ਮੂਲ ਵਿਚ ਮਨੁੱਖੀ ਸਾਧਨਾਂ ਦੇ ਵਿਕਾਸ ਦੀ ਭੁੱਲ ਹੈ ।
ਪ੍ਰਸ਼ਨ 10.
ਜਨਸੰਖਿਆ ਵੰਡ ਅਤੇ ਜਨਸੰਖਿਆ ਘਣਤਾ ਵਿਚ ਫ਼ਰਕ ਸਪੱਸ਼ਟ ਕਰੋ ।
ਉੱਤਰ-
ਜਨਸੰਖਿਆ ਵੰਡ ਦਾ ਸੰਬੰਧ ਸਥਾਨ ਨਾਲ ਹੈ ਅਤੇ ਜਨਸੰਖਿਆ ਘਣਤਾ ਦਾ ਸੰਬੰਧ ਅਨੁਪਾਤ ਨਾਲ ਹੈ । ਜਨਸੰਖਿਆ ਵੰਡ ਦਾ ਅਰਥ ਇਹ ਹੈ ਕਿ ਦੇਸ਼ ਦੇ ਕਿਸੇ ਇਕ ਹਿੱਸੇ ਵਿਚ ਜਨਸੰਖਿਆ ਖੇਤਰੀ ਪੱਧਰ (Pattern) ਕਿਹੋ ਜਿਹਾ ਹੈ । ਅਸੀਂ ਇਹ ਵੀ ਆਖ ਸਕਦੇ ਹਾਂ ਕਿ ਜਨਸੰਖਿਆ ਵੰਡ ਵਿਚ ਇਸ ਗੱਲ ਦੀ ਜਾਣਕਾਰੀ ਪ੍ਰਾਪਤ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ਕਿ ਜਨਸੰਖਿਆ ਪੱਧਰ ਫੈਲਾਅ ਲਈ ਹੈ ਜਾਂ ਇਸ ਦਾ ਇਕ ਹੀ ਥਾਂ ਉੱਤੇ ਵਧੇਰੇ ਜਮਾਅ ਹੈ । ਇਸ ਦੇ ਉਲਟ ਜਨਸੰਖਿਆ ਘਣਤਾ ਵਿਚ ਇਸ ਦਾ ਸੰਬੰਧ ਜਨਸੰਖਿਆ ਆਕਾਰ ਅਤੇ ਖੇਤਰ ਨਾਲ ਹੁੰਦਾ ਹੈ, ਮਨੁੱਖ ਅਤੇ ਖੇਤਰ ਦੇ ਅਨੁਪਾਤ ਉੱਤੇ ਧਿਆਨ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 11.
ਸਾਧਨਾਂ ਦੀ ਸੁਰੱਖਿਆ ਕਿਉਂ ਜ਼ਰੂਰੀ ਹੈ ? ਦੋ ਕਾਰਨ ਦੱਸੋ ।
ਉੱਤਰ-
ਜਨਸੰਖਿਆ ਦੇ ਵਾਧੇ ਅਤੇ ਆਰਥਿਕ ਵਿਕਾਸ ਦੇ ਕਾਰਨ ਸਾਧਨਾਂ ਦੀ ਨਿਰੰਤਰ ਵਰਤੋਂ ਹੋਈ ਹੈ । ਜੇ ਸਾਧਨਾਂ ਦੀ ਵਰਤੋਂ ਦੀ ਇਹੀ ਰਫ਼ਤਾਰ ਰਹੀ ਤਾਂ ਇਕ ਦਿਨ ਆਰਥਿਕ ਵਿਕਾਸ ਰੁਕ ਜਾਵੇਗਾ ਅਤੇ ਮਾਨਵ ਸਾਧਨਾਂ ਦੀ ਹੋਂਦ ਖ਼ਤਰੇ ਵਿਚ ਪੈ ਜਾਵੇਗੀ । ਇਸ ਲਈ ਸਾਧਨਾਂ ਦੀ ਸੁਰੱਖਿਆ ਲਾਜ਼ਮੀ ਹੋ ਗਈ ਹੈ । ਹੇਠ ਲਿਖੇ ਤੱਥਾਂ ਤੋਂ ਸਪੱਸ਼ਟ ਹੋ ਜਾਵੇਗਾ ਕਿ ਸਾਧਨਾਂ ਦੀ ਸੁਰੱਖਿਆ ਕਿਉਂ ਜ਼ਰੂਰੀ ਹੈ-
- ਅੱਜ ਮਨੁੱਖਾ-ਨਿਵਾਸ ਦੇ ਕਾਰਨ ਸੰਘਣੇ ਵੱਸੇ ਦੇਸ਼ਾਂ ਵਿਚ ਭੂਮੀ ਦੁਰਲਭ ਹੋ ਗਈ ਹੈ । ਖੇਤੀ ਦੇ ਲਈ ਲਾਭਦਾਇਕ ਭੂਮੀ ਉੱਤੇ ਵੀ ਮਕਾਨ ਬਣ ਰਹੇ ਹਨ । ਇਸ ਲਈ ਇਹ ਜ਼ਰੂਰੀ ਹੋ ਗਿਆ ਹੈ ਕਿ ਉਪਲੱਬਧ ਭੂਮੀ ਦੀ ਸਰਵ-ਉੱਤਮ ਵਰਤੋਂ ਕੀਤੀ ਜਾਵੇ ।
- ਭੂਮੀ ਹੇਠਲੇ ਪਾਣੀ ਦੀ ਨਿਰੰਤਰ ਵਰਤੋਂ ਨਾਲ ਪਾਣੀ ਦਾ ਪੱਧਰ ਨੀਵਾਂ ਹੋ ਗਿਆ ਹੈ ਜਿਸ ਨਾਲ ਖੇਤੀ ਉੱਤੇ ਬਹੁਤ ਬੁਰਾ ਅਸਰ ਪੈ ਰਿਹਾ ਹੈ । ਇਸ ਲਈ ਭੂਮੀ: ਹੇਠਲੇ ਪਾਣੀ ਦੀ ਸੰਭਾਲ ਵੀ ਜ਼ਰੂਰੀ ਹੋ ਗਈ ਹੈ ।
ਪ੍ਰਸ਼ਨ 12.
ਰਾਜਸਥਾਨ ਅਤੇ ਅਰੁਣਾਚਲ ਪ੍ਰਦੇਸ਼ ਵਿਚ ਜਨਸੰਖਿਆ ਘੱਟ ਕਿਉਂ ਹੈ ?
ਉੱਤਰ-
ਭਾਰਤ ਵਿਚ ਕੁਝ ਅਜਿਹੇ ਖੇਤਰ ਹਨ ਜਿੱਥੇ ਜੀਵਨ ਦੀਆਂ ਸਹੂਲਤਾਂ ਬੜੀ ਮੁਸ਼ਕਿਲ ਨਾਲ ਪ੍ਰਾਪਤ ਹੁੰਦੀਆਂ ਹਨ । ਇਨ੍ਹਾਂ ਖੇਤਰਾਂ ਵਿਚ ਜਾਂ ਤਾਂ ਜਲਵਾਯੂ ਬੜਾ ਕਠੋਰ ਹੈ ਜਾਂ ਭੂਮੀ ਉਪਜਾਊ ਨਹੀਂ ਹੈ ਜਾਂ ਇਹ ਖੇਤਰ ਪਹਾੜੀ ਹਨ । ਅਜਿਹੇ ਖੇਤਰਾਂ ਵਿਚ ਖੇਤੀ ਕਰਨੀ ਬਹੁਤ ਮੁਸ਼ਕਿਲ ਕੰਮ ਹੈ । ਇਸ ਦੇ ਇਲਾਵਾ ਸਿੰਜਾਈ ਦੀਆਂ ਸਹੂਲਤਾਂ ਵੀ ਬਹੁਤ ਘੱਟ ਹਨ । ਇਸ ਦੇ ਕਾਰਨ ਉਤਪਾਦਨ ਵੀ ਘੱਟ ਹੁੰਦਾ ਹੈ । ਅਜਿਹੇ ਖੇਤਰਾਂ ਵਿਚ ਉਦਯੋਗ ਵੀ ਤਰੱਕੀ ਨਹੀਂ ਕਰ ਸਕਦੇ । ਰਾਜਸਥਾਨ ਅਤੇ ਅਰੁਣਾਚਲ ਪ੍ਰਦੇਸ਼ ਵਿਚ ਜਨਸੰਖਿਆ ਘੱਟ ਹੋਣ ਦੇ ਇਹੀ ਕਾਰਨ ਹਨ ।
ਵੱਡੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Long Answer Type Questions)
ਪ੍ਰਸ਼ਨ 1.
ਭਾਰਤ ਵਿਚ ਜਨਸੰਖਿਆ ਦੀ ਅਸਮਾਨ ਵੰਡ ਲਈ ਜ਼ਿੰਮੇਵਾਰ ਕਿਸੇ ਪੰਜ ਕਾਰਕਾਂ ਨੂੰ ਸਪੱਸ਼ਟ ਕਰੋ ।
ਉੱਤਰ-
ਭਾਰਤ ਵਿਚ ਜਨਸੰਖਿਆ ਦੀ ਵੰਡ ਇੱਕੋ ਜਿਹੀ ਨਹੀਂ ਹੈ । ਇਸ ਦੇ ਲਈ ਅਨੇਕਾਂ ਤੱਤ ਜ਼ਿੰਮੇਵਾਰ ਹਨ-
- ਭੂਮੀ ਦੀ ਉਪਜਾਊਪਨ-ਭਾਰਤ ਦੇ ਜਿਹੜੇ ਰਾਜਾਂ ਵਿਚ ਉਪਜਾਊ ਭੂਮੀ ਦਾ ਜ਼ਿਆਦਾ ਵਿਸਤਾਰ ਹੈ, ਉੱਥੇ ਜਨਸੰਖਿਆ ਦੀ ਘਣਤਾ ਜ਼ਿਆਦਾ ਹੈ । ਜਿਵੇਂ ਉੱਤਰ ਪ੍ਰਦੇਸ਼ ਅਤੇ ਬਿਹਾਰ ਅਜਿਹੇ ਹੀ ਰਾਜ ਹਨ ।
- ਵਰਖਾ ਦੀ ਮਾਤਰਾ-ਵਧੇਰੇ ਵਰਖਾ ਵਾਲੇ ਭਾਗਾਂ ਵਿਚ ਆਮ ਤੌਰ ‘ਤੇ ਜਨਸੰਖਿਆ ਦੀ ਘਣਤਾ ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ । ਉੱਤਰੀ ਭਾਰਤ ਵਿਚ ਪੂਰਬ ਤੋਂ ਪੱਛਮ ਨੂੰ ਜਾਂਦੇ ਹੋਏ ਵਰਖਾ ਦੀ ਮਾਤਰਾ ਘੱਟ ਹੁੰਦੀ ਜਾਂਦੀ ਹੈ । ਇਸ ਲਈ ਜਨਸੰਖਿਆ ਦੀ ਘਣਤਾ ਵੀ ਘਟਦੀ ਜਾਂਦੀ ਹੈ ।
- ਜਲਵਾਯੂ-ਜਿੱਥੇ ਜਲਵਾਯੂ ਸਿਹਤ ਲਈ ਅਨੁਕੂਲ ਹੈ, ਉੱਥੇ ਵੀ ਜਨਸੰਖਿਆ ਦੀ ਘਣਤਾ ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ, ਇਸ ਦੇ ਉਲਟ ਜਿਹੜੇ ਦੇਸ਼ਾਂ ਵਿਚ ਜਲਵਾਯੂ ਸਿਹਤ ਲਈ ਚੰਗੀ ਨਾ ਹੋਵੇ, ਉੱਥੇ ਜਨਸੰਖਿਆ ਦੀ ਘਣਤਾ ਬਹੁਤ ਘੱਟ ਹੁੰਦੀ ਹੈ । ਆਸਾਮ ਵਿਚ ਵਰਖਾ ਜ਼ਿਆਦਾ ਹੁੰਦੇ ਹੋਏ ਵੀ ਜਨਸੰਖਿਆ ਦੀ ਘਣਤਾ ਘੱਟ ਹੈ, ਕਿਉਂਕਿ ਉੱਥੇ ਵਧੇਰੇ ਨਮੀ ਦੇ ਕਾਰਨ ਮਲੇਰੀਆ ਦਾ ਖ਼ਤਰਾ ਜ਼ਿਆਦਾ ਰਹਿੰਦਾ ਹੈ ।
- ਆਵਾਜਾਈ ਦੇ ਉੱਨਤ ਸਾਧਨ – ਆਵਾਜਾਈ ਦੇ ਸਾਧਨਾਂ ਦੇ ਵਧੇਰੇ ਵਿਕਾਸ ਦੇ ਕਾਰਨ ਵਪਾਰ ਦੀ ਪ੍ਰਗਤੀ ਤੇਜ਼ ਹੋ ਜਾਂਦੀ ਹੈ ਜਿਸ ਨਾਲ ਜਨਸੰਖਿਆ ਦੀ ਘਣਤਾ ਵੀ ਜ਼ਿਆਦਾ ਹੋ ਜਾਂਦੀ ਹੈ । ਉੱਤਰ ਪ੍ਰਦੇਸ਼, ਬੰਗਾਲ, ਬਿਹਾਰ ਆਦਿ ਰਾਜਾਂ ਵਿਚ ਵਧੇਰੇ ਜਨਸੰਖਿਆ ਹੋਣ ਦਾ ਇਕ ਕਾਰਨ ਆਵਾਜਾਈ ਦੇ ਸਾਧਨਾਂ ਦਾ ਵਿਕਾਸ ਹੈ ।
- ਉਦਯੋਗਿਕ ਵਿਕਾਸ – ਜਿਹੜੇ ਸਥਾਨਾਂ ‘ਤੇ ਉਦਯੋਗ ਸਥਾਪਿਤ ਹੋ ਜਾਂਦੇ ਹਨ ਉੱਥੇ ਵੀ ਜਨਸੰਖਿਆ ਦੀ ਘਣਤਾ ਵਧ ਜਾਂਦੀ ਹੈ । ਇਸ ਦਾ ਕਾਰਨ ਇਹ ਹੈ ਕਿ ਉਦਯੋਗਿਕ ਖੇਤਰਾਂ ਵਿਚ ਰੋਜ਼ੀ-ਰੋਟੀ ਕਮਾਉਣਾ ਆਸਾਨ ਹੁੰਦਾ ਹੈ । ਦਿੱਲੀ, ਮੁੰਬਈ, ਕੋਲਕਾਤਾ ਆਦਿ ਨਗਰਾਂ ਵਿਚ ਉਦਯੋਗਿਕ ਵਿਕਾਸ ਦੇ ਕਾਰਨ ਹੀ ਜਨਸੰਖਿਆ ਜ਼ਿਆਦਾ ਹੈ ।
ਇਸ ਦੇ ਇਲਾਵਾ ਅਜਿਹੇ ਖੇਤਰਾਂ ਵਿਚ ਜਿੱਥੇ ਕੁਦਰਤੀ ਸਾਧਨ ਵਧੇਰੇ ਹੁੰਦੇ ਹਨ, ਉੱਥੇ ਵੀ ਜਨਸੰਖਿਆ ਜ਼ਿਆਦਾ ਹੁੰਦੀ
ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 2.
ਹੇਠਾਂ ਭਾਰਤ ਦੀ ਜਨਸੰਖਿਆ ਨਾਲ ਸੰਬੰਧਿਤ ਪੰਜ ਸਮੱਸਿਆਵਾਂ ਦਿੱਤੀਆਂ ਗਈਆਂ ਹਨ । ਹੇਠਾਂ ਲਿਖੀ ਹਰੇਕ ਸਮੱਸਿਆ ਨਾਲ ਸੰਬੰਧਿਤ ਇਕ ਬੁਰਾ ਪ੍ਰਭਾਵ ਦੱਸੋ ਅਤੇ ਹਰੇਕ ਬੁਰੇ ਪ੍ਰਭਾਵ ਦੀ ਇਕ ਵਿਹਾਰਕ ਹੱਲ ਸੁਝਾਓ ।
(i) ਜਨਸੰਖਿਆ ਦੀ ਉੱਚ ਘਣਤਾ
(ii) ਅਸੰਤੁਲਿਤ ਔਰਤ-ਮਰਦ ਅਨੁਪਾਤ
(iii) ਸਾਰਿਆਂ ਲਈ ਸਿਹਤ ਸਹੂਲਤਾਂ
(iv) ਵਾਤਾਵਰਨ (ਵਧਦੀ ਹੋਈ ਜਨਸੰਖਿਆ ਦੇ ਸੰਦਰਭ ਵਿਚ
(v) ਔਰਤਾਂ ਦੀ ਆਰਥਿਕ ਸਹਿਭਾਗਤਾ ।
ਉੱਤਰ-
(i) ਜਨਸੰਖਿਆ ਦੀ ਉੱਚ ਘਣਤਾ – ਜਨਸੰਖਿਆ ਦੀ ਉੱਚ ਘਣਤਾ ਨਾਲ ਭੋਜਨ ਅਤੇ ਆਵਾਸ ਦੀ ਸਮੱਸਿਆ ਪੈਦਾ ਹੁੰਦੀ ਹੈ । ਇਸ ਸਮੱਸਿਆ ਦੇ ਹੱਲ ਲਈ ਪਰਿਵਾਰ ਨਿਯੋਜਨ ਕਾਰਜਕ੍ਰਮਾਂ ਨੂੰ ਵੱਧ ਤੋਂ ਵੱਧ ਲੋਕਪ੍ਰਿਆ ਬਣਾਉਣਾ ਚਾਹੀਦਾ ਹੈ ।
(ii) ਅਸੰਤੁਲਿਤ ਔਰਤ-ਮਰਦ ਅਨੁਪਾਤ – ਇਹ ਅਨੁਪਾਤ ਮਰਦਾਂ ਦੇ ਪੱਖ ਵਿਚ ਹੋਣ ਦੇ ਕਾਰਨ ਦੇਸ਼ ਵਿਚ ਅੱਜ ਵੀ ਔਰਤਾਂ ਦੀ ਸਥਿਤੀ ਕਮਜ਼ੋਰ ਬਣੀ ਹੋਈ ਹੈ । ਇਸ ਸਮੱਸਿਆ ਨਾਲ ਨਿਪਟਣ ਲਈ ਲੋਕਾਂ ਵਿਚ ਇਸ ਗੱਲ ਦੀ ਜਾਗ੍ਰਿਤੀ ਪੈਦਾ ਕਰਨਾ ਜ਼ਰੂਰੀ ਹੈ ਕਿ ਕੰਨਿਆ-ਜਨਮ ਨੂੰ ਅਸ਼ੁੱਭ ਨਾ ਮੰਨਣ ਅਤੇ ਉਨ੍ਹਾਂ ਦੇ ਪਾਲਣ-ਪੋਸ਼ਣ ਵਲ ਉੱਚਿਤ ਧਿਆਨ ਦੇਣ ।
(iii) ਸਾਰਿਆਂ ਲਈ ਸਿਹਤ ਸਹੂਲਤਾਂ – ਜਨਸੰਖਿਆ ਦੇ ਤੇਜ਼ ਵਾਧੇ ਦੇ ਕਾਰਨ ਦੇਸ਼ ਵਿਚ ਸਾਰਿਆਂ ਲਈ ਉੱਚਿਤ ਸਿਹਤ ਸੇਵਾਵਾਂ ਜੁਟਾ ਪਾਉਣਾ ਅਸੰਭਵ ਹੈ । ਇਸ ਲਈ ਦੇਸ਼ ਵਿਚ ਅਨੇਕ ਰੋਗਗ੍ਰਸਤ ਲੋਕ ਚਿਕਿਤਸਾ ਦੀ ਘਾਟ ਵਿਚ ਦਮ ਤੋੜ ਦਿੰਦੇ ਹਨ । ਇਸ ਸਮੱਸਿਆ ਨਾਲ ਨਿਪਟਣ ਦੇ ਲਈ ਸਾਨੂੰ ਸਿਹਤ ਸੇਵਾਵਾਂ ਦਾ ‘ਸਰਲ ਸਾਧਨਾਂ ਅਤੇ ਹੋਰਨਾਂ ਤਰੀਕਿਆਂ ਦੁਆਰਾ ਵਿਸਤਾਰ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ।
(iv) ਵਾਤਾਵਰਨ ਦੀ ਸਮੱਸਿਆ – ਵਧਦੀ ਹੋਈ ਆਬਾਦੀ ਦੇ ਕਾਰਨ ਵਾਤਾਵਰਨ ਸੰਤੁਲਨ ਵਿਗੜ ਰਿਹਾ ਹੈ ਅਤੇ ਵਾਤਾਵਰਨ ਦੂਸ਼ਿਤ ਹੋ ਰਿਹਾ ਹੈ । ਵਾਤਾਵਰਨ ਦੇ ਬਚਾਓ ਲਈ ਜਨਸੰਖਿਆ ਦੇ ਵਾਧੇ ‘ਤੇ ਰੋਕ ਲਗਾਉਣੀ ਚਾਹੀਦੀ ਹੈ ਅਤੇ ਵਣ ਖੇਤਰਾਂ ਦਾ ਵਿਸਥਾਰ ਕਰਨਾਂ ਚਾਹੀਦਾ ਹੈ ।
(v) ਔਰਤਾਂ ਦੀ ਆਰਥਿਕ ਸਹਿਭਾਗਤਾ – ਭਾਰਤ ਵਿਚ ਜ਼ਿਆਦਾਤਰ ਔਰਤਾਂ ਹੁਣ ਵੀ ਘਰ ਦੇ ਕੰਮ-ਕਾਜ ਤਕ ਸੀਮਿਤ ਹਨ ਅਤੇ ਉਨ੍ਹਾਂ ਦੀ ਆਰਥਿਕ ਸਹਿਭਾਗਤਾ ਨਾਂ-ਮਾਤਰ ਹੈ । ਇਸ ਲਈ ਜ਼ਿਆਦਾਤਰ ਪਰਿਵਾਰਾਂ ਦੀ ਸਾਲਾਨਾ ਆਮਦਨ ਸੀਮਿਤ ਹੈ । ਇਸ ਲਈ ਔਰਤ-ਸਿੱਖਿਆ ਦੇ ਵਿਸਥਾਰ ਨਾਲ ਔਰਤਾਂ ਦੀ ਆਰਥਿਕ ਸਹਿਭਾਗਤਾ ਨੂੰ ਵਧਾਉਣਾ ਚਾਹੀਦਾ ਹੈ ।