Punjab State Board PSEB 10th Class Physical Education Book Solutions ਬਾਸਕਟ ਬਾਲ (Basket Ball) Game Rules.
ਬਾਸਕਟ ਬਾਲ (Basket Ball) Game Rules – PSEB 10th Class Physical Education
ਯਾਦ ਰੱਖਣ ਵਾਲੀਆਂ ਗੱਲਾਂ
(Points to Remember)
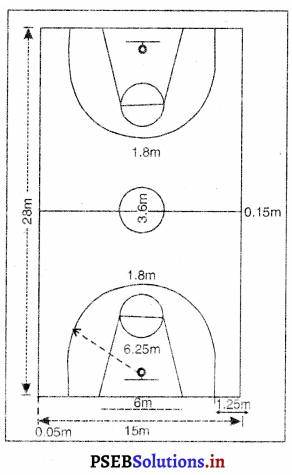
- ਬਾਸਕਟ ਬਾਲ ਕੋਰਟ ਦੀ ਲੰਬਾਈ ਅਤੇ ਚੌੜਾਈ = 28 ਮੀਟਰ × 15 ਮੀਟਰ
- ਬਾਸਕਟ ਬਾਲ ਟੀਮ ਦੇ ਖਿਡਾਰੀ = 12, 5 ਖੇਡਦੇ ਹਨ ਅਤੇ 7 ਬਦਲਵੇਂ ਖਿਡਾਰੀ
- ਕੋਰਟ ਦੇ ਕੇਂਦਰੀ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ = 1.80 ਮੀਟਰ
- ਰੇਖਾਵਾਂ ਦੀ ਚੌੜਾਈ = 5 ਸੈਂ.ਮੀ.
- ਬੋਰਡ ਦੀ ਮੋਟਾਈ = 3 ਸੈਂ.ਮੀ.
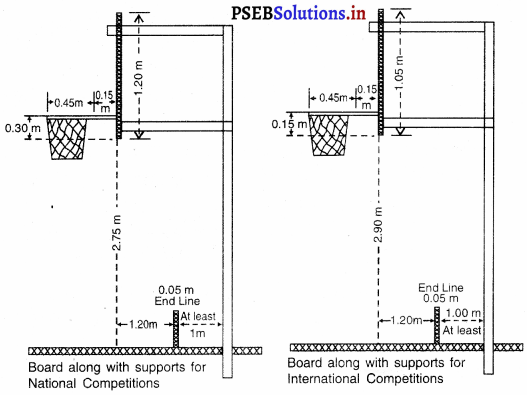
- ਬੋਰਡ ਦੇ ਹੇਠਲੇ ਹਿੱਸੇ ਦੀ ਜ਼ਮੀਨ ਤੋਂ ਉਚਾਈ = 2.90 ਮੀਟਰ
- ਬੋਰਡ ਦਾ ਆਕਾਰ = 180 × 120 ਮੀਟਰ
- ਬਾਲ ਦਾ ਘੇਰਾ = 75 ਤੋਂ 78 ਸੈਂ. ਮੀ.
- ਬਾਲ ਦਾ ਭਾਰ = 600 ਤੋਂ 650 ਗਰਾਮ
- ਬੋਰਡ ਤੇ ਆਇਤ ਦਾ ਸਾਈਜ਼ = 49 × 45 ਸੈਂ. ਮੀਟਰ
- ਪੋਲਾਂ ਦੀ ਦੂਰੀ = 2 ਮੀਟਰ
- ਖੇਡ ਦਾ ਸਮਾਂ = 40 ਮਿੰਟ ਦੇ ਚਾਰ ਕਵਾਟਰ 10-2-10 (10) 10-2-10
- ਬਾਸਕਟ ਬਾਲ ਦੇ ਅਧਿਕਾਰੀ = 1 ਟੇਬਲ ਕਮਿਸ਼ਨਰ, 1 ਰੈਫ਼ਰੀ, 1 ਅੰਪਾਇਰ, 1 ਚੀਫ਼ ਰੈਫ਼ਰੀ, 1 ਟਾਈਮ ਕੀਪਰ, 1 ਸਕੋਰਰ, 24 ਸੈਕਿੰਡ ਆਪਰੇਟਰ ਇਕ
- ਦੋ ਪਾਸਿਆਂ ਦੇ ਵਿਚਕਾਰ ਆਰਾਮ ਦਾ ਸਮਾਂ = 10 ਮਿੰਟ
![]()
ਖੇਡਾ ਸੰਬੰਧੀ ਮਹੰਝਵਪੂਰਨ ਜਾਣਕਾਰੀ
- ਬਾਸਕਟ ਬਾਲ ਦਾ ਮੈਚ ਦੋ ਟੀਮਾਂ ਵਿਚਕਾਰ ਹੁੰਦਾ ਹੈ । ਦੋਹਾਂ ਟੀਮਾਂ ਵਿਚ 5-5 ਖਿਡਾਰੀ ਹੁੰਦੇ ਹਨ ਅਤੇ ਪੰਜ ਜਾਂ ਸੱਤ ਬਦਲਵੇਂ (Substitutes) ਖਿਡਾਰੀ ਹੁੰਦੇ ਹਨ ।
- ਬਾਸਕਟ ਬਾਲ ਖੇਡ ਦਾ ਮੈਦਾਨ ਆਇਤਾਕਾਰ ਹੁੰਦਾ ਹੈ । ਮੈਦਾਨ ਦੀ ਲੰਬਾਈ 28 ਮੀਟਰ ਅਤੇ ਚੌੜਾਈ 15 ਮੀਟਰ ਹੁੰਦੀ ਹੈ । ਮੈਦਾਨ ਲੱਕੜੀ ਜਾਂ ਸੀਮਿੰਟ ਦਾ ਹੋਣਾ ਜ਼ਰੂਰੀ ਹੈ ।
- ਟੀਮ ਦੇ ਹਰੇਕ ਖਿਡਾਰੀ ਦੀ ਬੁਨੈਣ ਦੇ ਸਾਹਮਣੇ ਅਤੇ ਪਿੱਛੇ ਕੱਪੜੇ ਦੇ 4 ਤੋਂ 15 | ਤਕ ਨੰਬਰ ਜੋ ਕਿ ਸਾਹਮਣੇ 6” ਲੰਬੇ ਅਤੇ ਪਿਛਲੇ 15” ਹੋਣੇ ਜ਼ਰੂਰੀ ਹਨ ।
- ਖੇਡ ਦਾ ਸਮਾਂ 10-2-10; 10, 10-2-10 ਮਿੰਟ ਦੀਆਂ ਚਾਰ ਅਵਧੀਆਂ ਦਾ ਹੁੰਦਾ ਹੈ । ਜਦੋਂ ਤਕ ਇੰਟਰਵਲ ਨਾ ਹੋਵੇ, ਜੋ ਕਿ ਦਸ ਮਿੰਟ ਦਾ ਹੁੰਦਾ ਹੈ ਕੋਈ ਖਿਡਾਰੀ ਬਿਨਾਂ ਅਧਿਕਾਰੀ ਦੀ ਆਗਿਆ ਤੋਂ ਬਿਨਾਂ ਮੈਦਾਨ ਛੱਡ ਨਹੀਂ ਸਕਦਾ ।
- ਖੇਡ ਵਿਚ ਖਿਡਾਰੀਆਂ ਨੂੰ ਜਿੰਨੀ ਵਾਰੀ ਮਰਜ਼ੀ ਚਾਹੇ ਬਦਲਿਆ ਜਾ ਸਕਦਾ ਹੈ, ਪਰ | ਉਨ੍ਹਾਂ ਦਾ ਨਾਮ ਸਕੋਰ ਸ਼ੀਟ ‘ਤੇ ਲਿਖਿਆ ਹੋਣਾ ਜ਼ਰੂਰੀ ਹੈ ਅਤੇ ਬਦਲੁ ਟੀਮ ਦੀ ਥਰੋ ਜਾਂ (Watch) ਅਤੇ ਬਾਲ ਡੈੱਡ ਹੋਣ ‘ਤੇ ਹੋ ਸਕਦਾ ਹੈ ।
- ਕਿਸੇ ਟੀਮ ਦੇ ਇਕ ਹਾਫ਼ ਵਿਚ 4 ਫਾਉਲ ਹੋਣ ਮਗਰੋਂ ਹੋਣ ਵਾਲੇ ਫਾਉਲ ਤੇ ਦੋ ਜਾਂ ਤਿੰਨ ਫਰੀ ਥਰੋ ਹਾਲਤ ਅਨੁਸਾਰ ਮਿਲਦੀਆਂ ਹਨ ।
- ਟੀਮ ਦੇ ਕਿਸੇ ਖਿਡਾਰੀ ਦੇ ਪੰਜ ਫਾਊਲ ਹੋਣ ਪਿੱਛੋਂ ਉਸ ਨੂੰ ਉਸ ਮੈਚ ਵਿਚੋਂ ਬਾਹਰ ਕੱਢ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
- ਬਾਸਕਟ ਬਾਲ ਦਾ ਭਾਰ 60 ਤੋਂ 650 ਗ੍ਰਾਮ ਅਤੇ ਗੇਂਦ ਦੀ ਪਰਿਧੀ 75 ਤੋਂ 78 ਸੈਂਟੀਮੀਟਰ ਹੁੰਦੀ ਹੈ ।
- ਹਰੇਕ ਟੀਮ ਦਾ ਕੋਚ ਇੱਕੋ ਮੈਚ ਦੇ ਖੇਡ ਵਿਚ ਦੋ ਵਾਰ ਆਰਾਮ ਕਰਨ ਲਈ ਟਾਈਮ ਆਊਟ ਲੈ ਸਕਦਾ ਹੈ, ਜੋ ਕਿ ਇਕ ਮਿੰਟ ਦਾ ਹੁੰਦਾ ਹੈ ।
- ਬਾਸਕਟ ਬਾਲ ਕੋਰਟ ਦੇ ਕੇਂਦਰੀ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ 180 ਮੀਟਰ, ਬੋਰਡ ਦੀ ਮੋਟਾਈ 3 ਸੈਂ.ਮੀ., ਬੋਰਡ ਦੇ ਹੇਠਲੇ ਕਿਨਾਰੇ ਦੀ ਜ਼ਮੀਨ ਤੋਂ ਉਚਾਈ 2.75
ਮੀਟਰ, ਰਿੰਗ ਦੀ ਉਚਾਈ 3.05 ਮੀਟਰ, ਚਿੱਟੀ ਨੈੱਟ ਦੀ ਲੰਬਾਈ 40 ਸੈਂ. ਮੀ. ਹੁੰਦੀ ਹੈ । ਸਾਰੀਆਂ ਸੀਮਾਵਾਂ ਦੀ ਚੌੜਾਈ 5 ਸੈਂ.ਮੀ. ਹੁੰਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 1.
ਬਾਸਕਟ ਬਾਲ ਖੇਡ ਦਾ ਸੰਖੇਪ ਹਾਲ, ਇਸ ਦੀ ਕੋਰਟ ਅਤੇ ਰਿਸਟਰਿਕਟਿਡ ਏਰੀਆ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
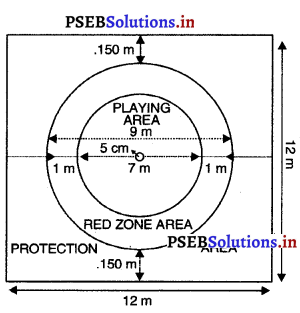
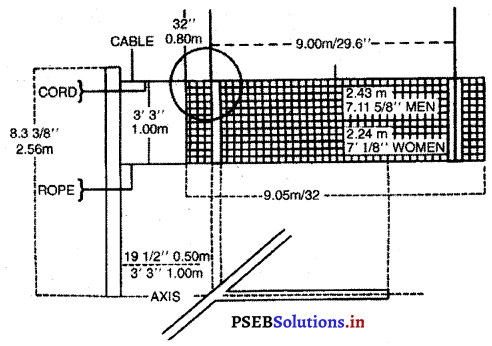
ਬਾਸਕਟ ਬਾਲ ਖੇਡ ਦੋ ਟੀਮਾਂ ਵਿਚਕਾਰ ਖੇਡੀ ਜਾਂਦੀ ਹੈ । ਹਰੇਕ ਟੀਮ ਦੇ 5-5 ਖਿਡਾਰੀ ਖੇਡਦੇ ਹਨ ਅਤੇ 7-7 ਜਾਂ 5-5 ਬਦਲਵੇਂ ਹੁੰਦੇ ਹਨ । ਹਰੇਕ ਟੀਮ ਵਿਰੋਧੀ ਟੀਮ ਦੀ ਬਾਸਕਟ ਵਿਚ ਬਾਲ ਪਾਉਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦੀ ਹੈ ਅਤੇ ਦੂਸਰੀ ਟੀਮ ਨੂੰ ਆਪਣੀ ਬਾਸਕਟ ਵਿਚ ਗੋਲ ਕਰਨ ਤੋਂ ਰੋਕਦੀ ਹੈ ! ਬਾਸਕਟ ਬਾਲ ਕੋਰਟ 28 ਮੀਟਰ ਲੰਬਾ ਅਤੇ 15 ਮੀਟਰ ਚੌੜਾ ਹੁੰਦਾ ਹੈ । ਇਸ ਦੀ ਲੰਬਾਈ 2 ਮੀਟਰ ਅਤੇ ਚੌੜਾਈ 5 ਮੀਟਰ ਦੋਵੇਂ ਸਾਈਡਾਂ ਦੇ ਅਨੁਪਾਤ ਨਾਲ ਘਟਾਈ ਜਾ ਸਕਦੀ ਹੈ । ਹਾਲ ਦੀ ਉਚਾਈ 7 ਮੀਟਰ ਅਤੇ ਇੱਕੋ ਜਿਹੀ ਰੌਸ਼ਨੀ ਹੋਣੀ ਜ਼ਰੂਰੀ ਹੈ । ਇਸ ਦਾ ਫਰਸ਼ ਲੱਕੜੀ ਜਾਂ ਸੀਮਿੰਟ ਦਾ ਹੋਣਾ ਜ਼ਰੂਰੀ ਹੈ । ਸਿੰਥੇਟਿਕ ਰਬੜ ਦਾ ਫਰਸ਼ ਵੀ ਹੋ ਸਕਦਾ ਹੈ । FIBA (International Amateur Basket Federation) ਦੇ ਮੁਕਾਬਲੇ ਲਈ ਕੋਰਟ ਦਾ ਮਾਪ ਕੋਡ ਜ਼ਰੂਰੀ ਹੁੰਦਾ ਹੈ । ਬਾਸਕਟ ਬਾਲ ਕੋਰਟ ਦੀਆਂ ਸੀਮਾ ਰੇਖਾਵਾਂ ਹਰੇਕ ਥਾਂ ਤੋਂ ਘੱਟ ਤੋਂ ਘੱਟ ਦੋ ਮੀਟਰ ਤਕ ਬਿਨਾਂ ਕਿਸੇ ਰੁਕਾਵਟ ਅੰਕਿਤ ਕੀਤੀਆਂ ਜਾਣਗੀਆਂ । ਰੇਖਾਵਾਂ ਦੀ ਚੌੜਾਈ 5 ਸੈਂਟੀਮੀਟਰ ਹੋਵੇਗੀ ।
ਬੋਰਡ – ਬੋਰਡ ਸਖ਼ਤ ਲੱਕੜ ਜਾਂ ਕਿਸੇ ਪਾਰਦਰਸ਼ੀ ਪਦਾਰਥ ਦੇ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ, ਜਿਸ ਦੀ ਮੋਟਾਈ 2 ਸੈਂਟੀਮੀਟਰ ਹੋਵੇ । ਗਿੰਗ ਦੀ ਕਿੱਲੀ ਨਾਲ ਬੋਰਡ ਦੇ ਉੱਪਰ 59 ਸੈਂਟੀਮੀਟਰ × 45 ਸੈਂਟੀਮੀਟਰ ਦੀ ਆਇਤ 5 ਸੈਂਟੀਮੀਟਰ ਦੀ ਚੌੜਾਈ ਦੀ ਲਾਈਨ ਨਾਲ ਬਣਾਈ ਜਾਂਦੀ ਹੈ । ਬੋਰਡ ਦੀ ਸੀਮਾ ਵੀ 5 ਸੈਂਟੀਮੀਟਰ ਮੋਟਾਈ ਦੀਆਂ ਰੇਖਾਵਾਂ ਨਾਲ ਮਾਰਕ ਕੀਤੀ ਜਾਂਦੀ ਹੈ | ਬੋਰਡ ਦਾ ਹੇਠਲਾ ਕੰਢਾ ਧਰਤੀ ਤੋਂ 2.75 ਮੀਟਰ ਉੱਚਾ ਹੁੰਦਾ ਹੈ ।
ਬਾਸਕਟ (Basket) – ਇਹ ਲੋਹੇ ਦੇ ਰਿੰਗ ਨਾਲ ਚਿੱਟੇ ਰੰਗ ਦੀ ਨੈਟ ਲਾ ਕੇ ਬਣਾਈ ਜਾਂਦੀ ਹੈ । ਨੈਟ 40 ਸੈਂਟੀਮੀਟਰ ਲੰਮੀ ਅਤੇ ਰਿੰਗ ਦਾ ਅਰਧ ਵਿਆਸ 45 ਸੈਂਟੀਮੀਟਰ ਅਤੇ ਰਿੰਗ ਦੀ ਮੋਟਾਈ 20 ਮਿਲੀਮੀਟਰ ਹੁੰਦੀ ਹੈ ।
ਕੇਂਦਰੀ ਰੇਖਾ (Centre Line) – ਕੋਰਟ ਦੇ ਠੀਕ ਅੱਧ ਵਿਚ ਅੰਤਲੀਆਂ ਰੇਖਾਵਾਂ ਦੇ ਸਮਾਨ ਅੰਤਰ ਕੇਂਦਰੀ ਰੇਖਾ ਖਿੱਚੀ ਜਾਵੇਗੀ ਜਿਹੜੀ ਕੋਰਟ ਨੂੰ ਅੱਗੇ ਵਾਲੇ ਅਤੇ ਪਿੱਛੇ ਵਾਲੇ ਕੋਰਟ ਵਿਚ ਵੰਡੇਗੀ । ਇਹ ਰੇਖਾ ਕੋਰਟ ਦੇ ਬਾਹਰ 15 ਸੈਂਟੀਮੀਟਰ ਦੋਵੇਂ ਪਾਸੇ ਹੋਵੇਗੀ ।
ਮੱਧ ਦਾ ਘੇਰਾ (Centre Line) – ਕੋਰਟ ਦੇ ਠੀਕ ਦਰਮਿਆਨ 1.80 ਮੀਟਰ ਅਰਧ ਵਿਆਸ ਦਾ ਚੱਕਰ ਹੋਵੇਗਾ । ਇਸ ਦੀ ਮਿਣਤੀ ਘੇਰੇ ਦੀ ਬਾਹਰਲੀ ਰੇਖਾ ਤੋਂ ਹੋਵੇਗੀ ।
ਤਿੰਨ ਨੰਬਰੀ ਗੋਲ ਏਰੀਆ (Three point Field goal Area) – ਤਿੰਨ ਨੰਬਰੀ ਗੋਲ ਏਰੀਆ ਦੇ ਬੰਦ ਚਾਪਾਂ ਨਾਲ ਮਾਰਕ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਜੋ ਕਿ ਸਾਈਡ ਲਾਈਨ ਦੇ ਕੇਂਦਰ ਬਿੰਦੂ ਦੇ ਬਾਹਰਲੇ ਕਿਨਾਰਿਆਂ ਤੋਂ 6.25 ਮੀਟਰ ਦੇ ਅਰਧ ਵਿਆਸ ‘ਤੇ ਹੁੰਦਾ ਹੈ । ਇਹ ਟੋਕਰੀ ਦੇ ਕੇਂਦਰ ਦੇ ਬਿਲਕੁਲ ਲੰਬ ਹੁੰਦਾ ਹੈ । ਕਿਨਾਰੇ ਵਾਲੀਆਂ ਲਕੀਰਾਂ ਸਾਈਡ ਲਕੀਰਾਂ ਦੇ ਸਮਾਨੰਤਰ ਹੁੰਦੀਆਂ ਹਨ । ਕਿਨਾਰੇ ਵਾਲੀ ਲਕੀਰ ਅਤੇ ਤਿੰਨ ਨੰਬਰੀ ਗੋਲ ਏਰੀਆ ਦੀਆਂ ਲਕੀਰਾਂ ਵਿਚ ਫਰਕ 1.25 ਮੀਟਰ ਹੁੰਦਾ ਹੈ ! ਸਾਈਡ ਲਾਈਨ ਦੇ ਕੇਂਦਰ ਤੋਂ ਫਾਸਲਾ ਕੇਂਦਰ ਪੁਆਇੰਟ ਦੀ ਚਾਪ ਵਿਚ 1.575 ਮੀਟਰ ਹੋਵੇਗਾ । ਚਾਪ ਅੱਧੇ ਚੱਕਰ ਤੁਕ ਹੈ ਅਤੇ ਇਸ ਦੇ ਪਿੱਛੇ ਪਾਸੇ ਦੀ ਲਕੀਰ ਦੇ ਸਮਾਨੰਤਰ ਹੁੰਦੀ ਹੈ ।
ਫਰੀ ਥਰੋ ਲਾਈਨਾਂ ਅਤੇ ਪ੍ਰਤੀਬੱਧ ਖੇਤਰ (Restricted Area, Free Throw Lines) – ਹਰੇਕ ਅੰਤ ਰੇਖਾ ਦੇ ਸਮਾਨੰਤਰ ਅੰਦਰਲੇ ਕਿਨਾਰੇ ਤੋਂ 5.80 ਮੀਟਰ ਦੀ ਦੂਰੀ ਤੇ ਫ਼ਰੀ ਥਰੋ ਲਾਈਨ ਖਿੱਚੀ ਜਾਂਦੀ ਹੈ । ਫ਼ਰੀ ਥਰੋ ਰੇਖਾ ਦੀ ਲੰਬਾਈ 3.60 ਮੀਟਰ ਅਤੇ ਕੇਂਦਰ ਬਿੰਦੁ ਅੰਤ ਰੇਖਾਵਾਂ ਨੂੰ ਦਰਮਿਆਨ ਬਿੰਦੁਆਂ ਨੂੰ ਜੋੜਨ ਵਾਲੀ ਰੇਖਾ ਉੱਤੇ ਹੋਵੇਗਾ | ਪਤੀਬੱਧ ਖੇਤਰ ਫ਼ਰੀ ਥਰੋ ਅਤੇ ਅੰਤ ਰੇਖਾਵਾਂ ਤੋਂ ਨਿਕਲਣ ਵਾਲੀਆਂ ਰੇਖਾਵਾਂ ਤੋਂ ਬਣਦਾ ਹੈ । ਸਿਰਿਆਂ ਵਾਲੀਆਂ ਫ਼ਰੀ ਥਰੋ ਰੇਖਾਵਾਂ ਇਸ ਦੇ ਅੱਧ ਵਿਆਸ ਨੂੰ ਅੰਕਿਤ ਕਰਦੀਆਂ ਹਨ । ਇਹਨਾਂ ਰੇਖਾਵਾਂ ਦਾ ਬਾਹਰੀ ਕਿਨਾਰਾ ਅੰਤ ਰੇਖਾਵਾਂ ਦੇ ਮੱਧ ਬਿੰਦੂ ਤੋਂ ਤਿੰਨ ਮੀਟਰ ਦੇ ਫਾਸਲੇ ਅਤੇ ਫ਼ਰੀ ਥਰੋ ਰੇਖਾਵਾਂ ਦੇ ਸਿਰਿਆਂ ਉੱਤੇ ਆ ਕੇ ਖ਼ਤਮ ਹੁੰਦਾ ਹੈ । ਇਹ ਰੇਖਾ ਕੋਰਟ ਵਿਚ 1.80 ਦੇ ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਅਰਧ ਚੱਕਰ ਵਿਚ ਲੱਗੀ ਹੁੰਦੀ ਹੈ ।
RESTRICTED AREA REGULATION FREE THROW LINE

ਪਹਿਲੀ ਲਕੀਰ ਸਿਰੇ ਵਾਲੀ ਲਕੀਰ ਦੇ ਕਿਨਾਰੇ ‘ਤੇ 1.75 ਮੀਟਰ ਦੀ ਦੂਰੀ ‘ਤੇ ਹੋਵੇਗੀ । ਪਹਿਲੇ ਖਿਡਾਰੀ ਦੇ ਖੜੇ ਹੋਣ ਵਾਲੀ ਥਾਂ 85 ਸੈਂਟੀਮੀਟਰ ਦੂਰ ਲਕੀਰ ਨਾਲ ਬੰਨੀ ਜਾਵੇਗੀ । ਇਸ ਥਾਂ ਤੋਂ ਅੱਗੇ ਇਕ ਉਦਾਸੀਨ ਦੇਸ਼ ਹੁੰਦਾ ਹੈ, ਜਿਸ ਦੀ ਚੌੜਾਈ 30 ਸੈਂਟੀਮੀਟਰ ਹੁੰਦੀ ਹੈ । ਦੂਜੇ ਖਿਡਾਰੀ ਦੀ ਥਾਂ ਵੀ 35 ਸੈਂਟੀਮੀਟਰ ਚੌੜੀ ਹੁੰਦੀ ਹੈ ਤੇ ਉਦਾਸੀਨ ਖੇਤਰ ਵੀ ਇਸ ਦੇ ਨਾਲ ਹੀ ਲੱਗਦਾ ਹੈ । ਤੀਜੇ ਖਿਡਾਰੀ ਦੀ ਥਾਂ ਵੀ ਦੂਜੇ ਖਿਡਾਰੀ ਦੇ ਨਾਲ ਹੀ ਲੱਗਦੀ ਹੈ । ਇਸ ਦੀ ਚੌੜਾਈ 85 ਸੈਂਟੀਮੀਟਰ ਹੁੰਦੀ ਹੈ । ਟੁੱਟੇ ਹੋਏ ਅੱਧੇ ਚੱਕਰ ਦਾ ਹਰੇਕ ਚਿੰਨਿਤ ਹਿੱਸੇ ਦੀ ਲੰਬਾਈ 35 ਸੈਂਟੀਮੀਟਰ ਹੁੰਦੀ ਹੈ ਅਤੇ ਦੋਵੇਂ ਹਿੱਸਿਆਂ ਦੇ ਵਿਚਕਾਰ ਫ਼ਾਸਲਾ 40 ਸੈਂਟੀਮੀਟਰ ਹੁੰਦਾ ਹੈ ।
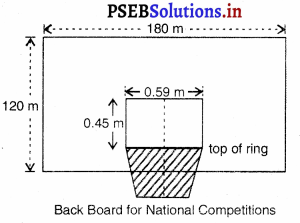
ਪਿਛਲੇ ਬੋਰਡ ਦਾ ਆਕਾਰ ਅਤੇ ਪਦਾਰਥ (Back Board-Size, Material and Position) –
ਪਿਛਲੇ ਵਾਲੇ ਬੋਰਡ ਸਖ਼ਤ ਲੱਕੜ ਜਾਂ ਕਿਸੇ ਪਾਰਦਰਸ਼ੀ ਪਦਾਰਥ ਦੇ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ । ਇਹਨਾਂ ਦੀਆਂ ਮੋਟਾਈ ਤਿੰਨ ਸੈਂਟੀਮੀਟਰ ਹੁੰਦੀ ਹੈ । ਇਹ ਆਡੇ ਰੁੱਖ 1.80 ਮੀਟਰ ਅਤੇ ਖੜੇ ਰੁੱਖ 1.05 ਮੀਟਰ ਹੁੰਦੇ ਹਨ । ਜਿੱਥੇ ਰਿੰਗ ਲੱਗਦਾ ਹੈ, ਉਸ ਦੇ ਪਿੱਛੇ ਬੋਰਡ ਉੱਤੇ ਇਕ 59 ਸੈਂਟੀਮੀਟਰ x45 ਸੈਂਟੀਮੀਟਰ ਆਇਤ ਬਣਾਈ ਜਾਂਦੀ ਹੈ । ਇਸ ਦੀਆਂ ਰੇਖਾਵਾਂ ਦੀ ਚੌੜਾਈ 5 ਸੈਂਟੀਮੀਟਰ ਹੁੰਦੀ ਹੈ । ਇਸ ਰੇਖਾ ਦਾ ਉੱਪਰ ਵਾਲਾ ਕਿਨਾਰਾ ਰਿੰਗ ਦੀ ਸਤਹਿ ਦੇ ਬਰਾਬਰ ਹੋਵੇਗਾ | ਬੋਰਡ ਦੀ ਸੀਮਾ 5 ਸੈਂਟੀਮੀਟਰ ਮੋਟਾਈ ਦੀਆਂ ਰੇਖਾਵਾਂ ਨਾਲ ਮਾਰਕ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਬੋਰਡ ਦਾ ਹੇਠਲਾ ਕੰਢਾ ਧਰਤੀ ਤੋਂ 2.75 ਮੀਟਰ ਉੱਚਾ ਹੁੰਦਾ ਹੈ । ਇਹਨਾਂ ਬੋਰਡਾਂ ਨੂੰ ਸਹਾਰਾ ਦੇਣ ਵਾਲੀਆਂ ਭੁਜਾਵਾਂ ਆਖਰੀ ਰੇਖਾ ਦੇ ਇਕ ਮੀਟਰ ਦੀ ਦੂਰੀ ਤੇ ਪ੍ਰਤੀਬੰਧ ਖੇਤਰ ਵਿਚ ਹੁੰਦੀਆਂ ਹਨ ।
ਬਾਸਕਟ (Basket) – ਬਾਸਕਟ ਛੱਲਿਆਂ ਅਤੇ ਜਾਲੀ ਦੀ ਬਣੀ ਹੁੰਦੀ ਹੈ । ਇਸ ਦੀ ਲੰਬਾਈ 40 ਸੈਂਟੀਮੀਟਰ ਹੁੰਦੀ ਹੈ । ਇਹ ਲੋਹੇ ਦੇ ਰਿੰਗ ਨਾਲ ਲਾਈ ਜਾਂਦੀ ਹੈ । ਰੰਗ ਦਾ ਅੰਦਰੂਨੀ ਹਿੱਸਾ 45 ਸੈਂਟੀਮੀਟਰ ਹੁੰਦਾ ਹੈ । ਇਸ ਨਾਰੰਗੀ ਰੰਗ ਵਾਲੇ ਬਾਸਕਟ ਦਾ ਅਰਧ ਵਿਆਸ 45 ਸੈਂਟੀਮੀਟਰ ਹੁੰਦਾ ਹੈ | ਘੇਰੇ ਦੀ ਧਾਤ 20 ਮਿਲੀਮੀਟਰ ਮੋਟੀ ਹੁੰਦੀ ਹੈ । ਇਸ ਦੇ ਹੇਠਾਂ ਇਕ ਜਾਲੀ ਲਾਈ ਜਾਂਦੀ ਹੈ, ਜੋ ਕਿ ਚਿੱਟੀ ਰੱਸੀ ਦੀ ਬਣੀ ਹੁੰਦੀ ਹੈ ਅਤੇ ਉਹ ਛੱਲਿਆਂ ਨਾਲ ਲਟਕਦੀ ਹੈ । ਇਹ ਛੱਲੇ ਇਸ ਤਰ੍ਹਾਂ ਦੇ ਬਣੇ ਹੁੰਦੇ ਹਨ ਕਿ ਜਦ ਗੇਂਦ ਉਸ ਤੋਂ ਲੰਘਦੀ ਹੈ ਉਹ ਇਸ ਨੂੰ ਥੋੜ੍ਹੀ ਦੇਰ ਲਈ ਰੋਕ ਦਿੰਦੇ ਹਨ । ਜਾਲੀ ਦੀ ਲੰਬਾਈ 0.40 ਸੈਂਟੀਮੀਟਰ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ।
ਗੇਂਦ (Ball) – ਗੇਂਦ ਗੋਲਾਕਾਰ ਹੁੰਦੀ ਹੈ । ਇਹ ਚਮੜੇ ਦੀ ਬਣੀ ਹੁੰਦੀ ਹੈ ਅਤੇ ਇਸ ਦੇ ਅੰਦਰ ਦਾ ਬਲੈਡਰ ਰਬੜ ਦਾ ਹੁੰਦਾ ਹੈ । ਇਸ ਦੀ ਪਰਿਧੀ 75 ਸੈਂਟੀਮੀਟਰ ਤੋਂ 78 ਸੈਂਟੀਮੀਟਰ ਹੁੰਦੀ ਹੈ । ਇਸ ਦਾ ਭਾਰ 600 ਗ੍ਰਾਮ ਤੋਂ 650 ਗ੍ਰਾਮ ਹੁੰਦਾ ਹੈ । ਹੁਣ ਕਾਨੂੰਨ ਇਹ ਆਗਿਆ ਦਿੰਦਾ ਹੈ ਕਿ ਵਰਤੋਂ ਕੀਤੀ ਹੋਈ ਗੇਂਦ ਵੀ ਵਰਤੀ ਜਾ ਸਕਦੀ ਹੈ । ਰੈਫ਼ਰੀ ਵਰਤੀ ਹੋਈ ਗੇਂਦ ਚੁਣ ਸਕਦਾ ਹੈ । ਕੇਂਦਰ ਵਿਚ ਹਵਾ ਇੰਨੀ ਚਾਹੀਦੀ ਹੈ ਕਿ 1.80 ਮੀਟਰ ਦੀ ਉਚਾਈ ਤੋਂ ਲੱਕੜੀ ਦੇ ਠੋਸ ਫ਼ਰਸ਼ ਤੇ ਸੁੱਟੇ ਜਾਣ ਤੇ ਇਹ ਗੇਂਦ ਦੇ ਉੱਪਰਲੇ ਸਿਰੇ ਤੋਂ ਲੈ ਕੇ 1.20 ਮੀਟਰ ਤੋਂ ਘੱਟ ਅਤੇ 1.40 ਮੀਟਰ ਤੋਂ ਵੱਧ ਨਾ ਉਛਲੇ : ਜਿਹੜੀ ਗੇਂਦ ਇਕ ਵਾਰੀ ਚੁਣ ਲਈ ਜਾਵੇ, ਦੋਹਾਂ ਟੀਮਾਂ ਦਾ ਕੋਈ ਵੀ ਖਿਡਾਰੀ ਖੇਡਣ ਤੋਂ ਪਹਿਲਾਂ ਉਸ ਦੀ ਵਰਤੋਂ ਨਹੀਂ ਕਰ ਸਕਦਾ । ਜੇਕਰ ਪੁਰਾਣੀ ਗੇਂਦ ਨਾ ਮਿਲ ਸਕਦੀ ਹੋਵੇ ਤਾਂ ਨਵੀਂ ਗੇਂਦ ਵਰਤੀ ਜਾ ਸਕਦੀ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 2.
ਬਾਸਕਟਬਾਲ ਖੇਡ ਦਾ ਤਕਨੀਕੀ ਸਮਾਨ ਕੀ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
(ਉ) ਤਕਨੀਕੀ ਸਮਾਨ (Technical Equipment)
- ਖੇਡ ਦੀ ਘੜੀ (Game watch)
- ਟਾਈਮ ਆਊਟ ਲਈ ਘੜੀ (Time Out watch)
- ਸਟਾਪ ਘੜੀਆਂ (Stop watch)
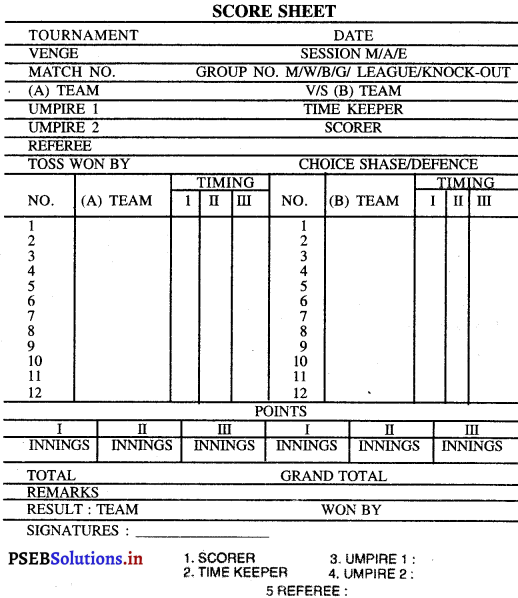
(ਅ) ਸਕੋਰ ਸ਼ੀਟ
(ੲ) ਘੱਟ ਤੋਂ ਘੱਟ 20 ਸਮ × 10 ਸਮ ਇਕ ਤੋਂ ਪੰਜ ਤਕ ਅੰਕ । ਇਕ ਤੋਂ ਚਾਰ ਤਕ ਕਾਲੇ ਰੰਗ ਦੇ ਅੰਕ ਅਤੇ ਪੰਜ ਦੇ ਲਈ ਲਾਲ ਰੰਗ ਦੇ ਅੰਕ |

(ਸ) 24 ਸੈਕਿੰਡ ਨਿਯਮ ਦੇ ਪ੍ਰਬੰਧ ਲਈ ਇਕ ਯੋਗ ਯੰਤਰ ਜਿਸ ਨੂੰ ਖਿਡਾਰੀ ਅਤੇ ਦਰਸ਼ਕ ਦੇਖ ਸਕਣ |
(ਹ) ਸਾਰਿਆਂ ਨੂੰ ਦਿੱਸਣ ਵਾਲਾ ਇਕ ਖੇਡ ਅੰਕ ਫੱਟਾ (Score Board) ਹੋਵੇਗਾ, ਜਿਸ ਤੇ ਦੋਵੇਂ ਟੀਮਾਂ ਦੇ ਖੇਡ ਅੰਕ ਲਿਖੇ ਜਾਣਗੇ ।
(ਕ) ਸਕੋਰਰ ਕੋਲ ਦੋ ਲਾਲ ਝੰਡੇ ਦੋਹਾਂ ਟੀਮਾਂ ਦੇ ਫਾਊਲ ਮਾਰਕਰ ਹੋਣਗੇ, ਜੋ ਕਿ ਟੀਮ ਦੇ ਅੱਠ ਫਾਊਲ ਇਕ ਮਿਆਦ ਵਿਚ ਹੋਣ ਦੀ ਸੂਰਤ ਵਿਚ ਉਸ ਟੀਮ ਵੱਲ ਲਿਆ ਜਾਵੇਗਾ, ਜੋ ਕਿ ਖਿਡਾਰੀਆਂ, ਕੋਚ ਸਾਹਿਬਾਨ ਅਤੇ ਖੇਡ ਅਧਿਕਾਰੀਆਂ ਨੂੰ ਦਿਖਾਈ ਦੇ ਸਕੇ ।
ਪਸ਼ਨ 3.
ਬਾਸਕਟ ਬਾਲ ਖੇਡ ਦੇ ਅਧਿਕਾਰੀ ਅਤੇ ਉਹਨਾਂ ਦੇ ਸਹਾਇਕਾਂ ਦੇ ਕਰਤੱਵ ਲਿਖੋ ।
ਉੱਤਰ-
ਬਾਸਕਟ ਬਾਲ ਖੇਡ ਦੇ ਅਧਿਕਾਰੀ ਅਤੇ ਉਹਨਾਂ ਦੇ ਸਹਾਇਕਾਂ ਦੇ ਕਰਤੱਵ (Officials and their assistants and their Duties)
ਰੈਫ਼ਰੀ ਦਾ ਕਰਤੱਵ (Referees Duty) –
- ਗਰਾਊਂਡ ਵਿਚ ਸਮੁੱਚੇ ਸਮਾਨ ਦੀ ਜ਼ਿੰਮੇਵਾਰੀ ਅਤੇ ਸਭ ਖਿਡਾਰੀਆਂ ਨੂੰ ਸੰਕੇਤ ਨਾਲ ਸਮਝਾਉਣ ਦੀ ਜ਼ਿੰਮੇਵਾਰੀ ।
- ਇਸ ਦੇ ਬਾਕੀ ਸਹਾਇਕ ਕੰਮ ਦਿੱਤੇ ਗਏ ਆਦੇਸ਼ਾਂ ਅਨੁਸਾਰ ਕਰਨਾ ।
- ਰੈਫ਼ਰੀ ਦਾ ਕਰਤੱਵ ਹੈ ਸਕੋਰਰ ਤੋਂ ਰਿਕਾਰਡ ਸ਼ੀਟ ਭਰਵਾਏ ।
- ਇਹ ਮੱਧ ਵਿਚ ਬਾਲ ਦੀ ਟਾਸ ਕਰਦਾ ਹੈ ।
- ਪੂਰੀ ਗੇਮ ਨੂੰ ਆਪਣੀ ਦੇਖ-ਭਾਲ ਵਿਚ ਖਿਡਾਉਂਦਾ ਹੈ । ਇਹ ਦੋਨਾਂ ਟੀਮਾਂ ਨੂੰ ਉੱਚਿਤ ਫੈਸਲਾ ਦਿੰਦਾ ਹੈ । ਜੋ ਇਹ ਫੈਸਲਾ ਦਿੰਦਾ ਹੈ, ਉਹ ਸਾਰਿਆਂ ਨੂੰ ਮੰਨਣਾ ਪੈਂਦਾ ਹੈ ।
- ਖਿਡਾਰੀਆਂ ਵਿਚ ਕਿਸੇ ਤਰ੍ਹਾਂ ਦੇ ਮਤਭੇਦ ਨੂੰ ਦੂਰ ਕਰਨ ਲਈ ਵੀ ਇਹ ਆਪਣਾ ਫੈਸਲਾ ਦਿੰਦਾ ਹੈ ਤੇ ਖੇਡ ਨੂੰ ਨਿਯਮ ਅਨੁਸਾਰ ਚਲਾਉਂਦਾ ਹੈ ।
- ਜੇ ਕੋਈ ਗ਼ਲਤ ਖੇਡ ਖੇਡਦਾ ਹੈ, ਤਾਂ ਉਸ ਨੂੰ ਦੰਡ ਪੈਨਲਟੀ ਫਾਊਲ ਦੇ ਰੂਪ ਵਿਚ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ ।
- ਅੰਤ ਵਿਚ ਰੈਫ਼ਰੀ ਸਕੋਰ ਸ਼ੀਟ ਦੇਖਦਾ ਹੈ ਤੇ ਉਸ ਦੇ ਉੱਪਰ ਆਪਣੇ ਦਸਖਤ ਕਰਕੇ ਹਾਰ ਜਿੱਤ ਦਾ ਫੈਸਲਾ ਦਿੰਦਾ ਹੈ ।
ਟਾਈਮ ਕੀਪਰ (Time Keeper)-
- ਇਸ ਦਾ ਕੰਮ ਸਮੇਂ ‘ਤੇ ਕੰਟਰੋਲ ਕਰਨਾ ਹੈ । ਖੇਡ ਆਰੰਭ ਹੋਣ ਤੋਂ ਪਹਿਲਾਂ ਟਾਈਮ ਕੀਪਰ ਰੈਫ਼ਰੀ ਨੂੰ ਦੱਸ ਦਿੰਦਾ ਹੈ ਕਿ ਖੇਡ ਸ਼ੁਰੂ ਹੋਣ ਵਿਚ ਤਿੰਨ ਮਿੰਟ ਬਾਕੀ ਹਨ, ਤਾਂ ਜੋ ਉਹ ਟੀਮਾਂ ਨੂੰ ਸੂਚਿਤ ਕਰ ਸਕੇ : ਖੇਡ ਦੇ ਅੱਧੇ ਸਮੇਂ ਬਾਅਦ ਵੀ ਇਹ ਰੈਫ਼ਰੀ ਨੂੰ ਯਾਦ ਕਰਵਾਉਂਦਾ ਹੈ ਕਿ ਖੇਡ ਆਰੰਭ ਹੋਣ ਵਿਚ ਦੋ ਮਿੰਟ ਬਾਕੀ ਹਨ ।
- ਇਹ ਖੇਡ ਦੇ ਆਰੰਭ ਤੋਂ ਅੰਤ ਤੱਕ ਦਾ ਪੂਰਾ ਹਿਸਾਬ ਕਿਤਾਬ ਰੱਖਦਾ ਹੈ । ਉਸ ਨੂੰ ਇਹ ਦੇਖਣਾ ਪੈਂਦਾ ਹੈ ਕਿ ਖੇਡ ਕਿੰਨੇ ਸਮ ਤਕ ਬੰਦ ਰਹੀ । ਟਾਈਮ ਕੀਪਰ ਜਦ ਘੰਟੀ ਵਜਾਉਂਦਾ ਹੈ, ਤਾਂ ਉਸ ਦੇ ਨਾਲ ਰੈਫ਼ਰੀ ਵੀ ਆਪਣੀ ਵਿਸਲ ਵਜਾ ਕੇ ਸਮਾਂ ਖ਼ਤਮ ਕਰਨ ਦਾ ਐਲਾਨ ਕਰਦਾ ਹੈ ।
ਸਕੋਰਰ (Scorer)-
- ਇਸ ਦਾ ਕੰਮ ਜਿੰਨੇ ਵੀ ਕੋਈ ਖਿਡਾਰੀ ਨੰਬਰ ਲਵੇ, ਉਸ ਨੂੰ ਇਕ ਸਕੋਰ ਸ਼ੀਟ ਤੋਂ ਨੋਟ ਕਰਨਾ ਹੁੰਦਾ ਹੈ ।
- ਖੇਡ ਦਾ ਆਰੰਭ ਹੋਣ ਤੋਂ ਪਹਿਲਾਂ ਉਹ ਸਾਰੇ ਖਿਡਾਰੀਆਂ ਦੇ ਨਾਮ ਸਕੋਰ ਸ਼ੀਟ ‘ਤੇ ਲਿਖ ਲੈਂਦਾ ਹੈ ।
- ਸਕੋਰਰ ਨੂੰ ਪਤਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ਕਿ ਕਿਸ ਖਿਡਾਰੀ ਨੇ ਕਿੰਨੇ ਨੰਬਰ ਲਏ ਹਨ ।
- ਉਹ ਹਰੇਕ ਨੰਬਰ ਨੂੰ ਬਹੁਤ ਸਾਵਧਾਨੀ ਨਾਲ ਹਰੇਕ ਖਿਡਾਰੀ ਦੇ ਬਣੇ ਹੋਏ ਖਾਤੇ ਵਿਚ ਜੋੜ ਦਿੰਦਾ ਹੈ ।
- ਉਸ ਨੂੰ ਹਰੇਕ ਖਿਡਾਰੀ ਦੇ ਫਾਉਲ ਵਾਲੇ ਪਾਸੇ ਫਾਉਲ ਨੋਟ ਕਰਨੇ ਚਾਹੀਦੇ ਹਨ । ਜਦੋਂ ਕੋਈ ਖਿਡਾਰੀ ਪੰਜ ਫਾਊਲ ਕਰ ਲੈਂਦਾ ਹੈ, ਤਾਂ ਉਸ ਸਮੇਂ ਸਕੋਰਰ ਰੈਫ਼ਰੀ ਨੂੰ ਦੱਸ ਦੇਵੇ ਕਿ ਇਸ ਖਿਡਾਰੀ ਦੇ ਪੰਜ ਫਾਉਲ ਹੋ ਗਏ ਹਨ ਤਾਂ ਉਸ ਖਿਡਾਰੀ ਨੂੰ ਖੇਡ ਤੋਂ ਬਾਹਰ ਕਰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
- ਖੇਡ ਸਮਾਪਤ ਹੋਣ ਦੇ ਬਾਅਦ ਸਕੋਰਰ ਰੈਫ਼ਰੀ ਤੋਂ ਸਕੋਰ ਸ਼ੀਟ ਤੇ ਦਸਤਖ਼ਤ ਕਰਵਾਉਂਦਾ ਹੈ । ਜੇ ਖੇਡਦੇ ਸਮੇਂ ਬਾਲ ਟੋਕਰੀ ਵਿਚ ਉੱਪਰ ਤੋਂ ਹੇਠਾਂ ਦਿੱਤਾ ਜਾਵੇ ਤਾਂ ਦੇ ਸਕੋਰ ਹੁੰਦੇ ਹਨ । ਜੇ ਫਰੀ ਥਰੋ ਦਿੱਤੀ ਜਾਵੇ, ਤਾਂ ਇਕ ਸਕੋਰ ਹੁੰਦਾ ਹੈ ।
ਖਿਡਾਰੀ ਵੱਲੋਂ ਕੋਰਟ ਛੱਡਣਾ (Player Leaving Court) – ਜਦ ਤਕ ਅੱਧਾ ਸਮਾਂ (interval) ਨਾ ਹੋਵੇ ਜਾਂ ਨਿਯਮ ਪ੍ਰਵਾਨਗੀ ਨਾ ਦੇਣ ਤਦ ਤਕ ਕੋਈ ਵੀ ਖਿਡਾਰੀ ਅਧਿਕਾਰੀਆਂ ਦੇ ਹੁਕਮ ਤੋਂ ਬਿਨਾਂ ਕੋਰਟ ਛੱਡ ਕੇ ਬਾਹਰ ਨਹੀਂ ਜਾ ਸਕਦਾ ।
ਕਪਤਾਨ (Captain) – ਸਿਰਫ ਕਪਤਾਨ ਹੀ ਸੂਚਨਾ ਲੈਣ ਲਈ ਜਾਂ ਕਿਸੇ ਤਰ੍ਹਾਂ ਦੀ ਵਿਆਖਿਆ ਲਈ ਅਧਿਕਾਰੀ ਨਾਲ ਗੱਲਬਾਤ ਕਰ ਸਕਦਾ ਹੈ । ਖਿਡਾਰੀ ਬਦਲਣ ਦਾ ਅਧਿਕਾਰ ਕੋਚ ਜਾਂ ਕੋਚ ਦੀ ਥਾਂ ਉੱਤੇ ਕੰਮ ਕਰ ਰਹੇ ਕਪਤਾਨ ਨੂੰ ਹੁੰਦਾ ਹੈ ।
ਖੇਡ ਦੀ ਮਿਆਦ (Duration of Play) – ਖੇਡ 10-2-10-10,10-2-10 ਮਿੰਟ ਦੀਆਂ ਚਾਰ ਮਿਆਦਾਂ ਵਿਚ ਖੇਡੀ ਜਾਵੇਗੀ । ਦੋ ਮਿਆਦਾਂ ਮਗਰੋਂ 10 ਮਿੰਟ ਆਰਾਮ ਦਾ ਸਮਾਂ ਹੋਵੇਗਾ ।
ਖੇਡ ਦਾ ਆਰੰਭ (Start of Play) – ਖੇਡ ਦਾ ਆਰੰਭ ਰੈਫ਼ਰੀ ਵੱਲੋਂ ਕੀਤਾ ਜਾਵੇਗਾ । ਉਹ ਦੋਵੇਂ ਵਿਰੋਧੀਆਂ ਦਰਮਿਆਨ ਕੇਂਦਰ ਵਿਚ ਗੇਂਦ ਨੂੰ ਉੱਪਰ ਸੁੱਟੇਗਾ | ਖੇਡ ਉਸ ਵੇਲੇ ਤਕ ਸ਼ੁਰੂ ਨਹੀਂ ਹੋਵੇਗੀ ਜਦ ਤਕ ਕਿ ਇਹ ਟੀਮ ਆਪਣੇ ਪੰਜ ਖਿਡਾਰੀਆਂ ਸਮੇਤ ਮੈਦਾਨ ਵਿਚ ਨਾ ਆ ਜਾਵੇ । ਜੇ ਖੇਡ ਸ਼ੁਰੂ ਹੋਣ ਦੇ ਸਮੇਂ ਤਕ ਦੂਜੀ ਟੀਮ ਮੈਦਾਨ ਵਿਚ ਨਹੀਂ ਪਹੁੰਚਦੀ ਤਾਂ ਵਿਰੋਧੀ ਟੀਮ ਨੂੰ ਵਾਕ ਓਵਰ ਮਿਲ ਜਾਂਦਾ ਹੈ ਅਰਥਾਤ ਉਸ ਨੂੰ ਬਿਨਾਂ ਖੇਡੇ ਹੀ ਜੇਤੂ ਕਰਾਰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 4.
ਜੰਪ ਬਾਲ ਅਤੇ ਜੰਪ ਬਾਲ ਸਮੇਂ ਫਾਊਲਾਂ ਦਾ ਵਰਣਨ ਕਰੋ ।
ਉੱਤਰ-
ਜੰਪ ਬਾਲ (Jump Ball) – ਜੇ ਬਾਲ ਦੇ ਸਮੇਂ ਦੋ ਖਿਡਾਰੀ ਅਰਧ ਗੋਲੇ ਦੇ ਅੰਦਰ ਪੈਰ ਰੱਖ ਕੇ ਆਪਣੀ-ਆਪਣੀ ਬਾਸਕਟ ਦੇ ਨੇੜੇ ਖੜੇ ਹੋਣਗੇ ਅਤੇ ਉਨ੍ਹਾਂ ਦਾ ਇਕ ਪੈਰ ਦਰਮਿਆਨ ਵਿਚ ਬਣੀ ਲਾਈਨ ਦੇ ਕੇਂਦਰ ਦੇ ਪਾਰ ਹੋਵੇਗਾ, ਉਸ ਸਮੇਂ ਕੋਈ ਅਧਿਕਾਰੀ ਗੇਂਦ ਨੂੰ ਇੰਨੀ ਉੱਚਾਈ ਤੋਂ ਉੱਪਰ ਸੁੱਟੇਗਾ ਕਿ ਉਨ੍ਹਾਂ ਵਿਚ ਕੋਈ ਖਿਡਾਰੀ ਉਛਲ ਕੇ ਗੇਂਦ ਨਾ ਫੜ ਸਕੇ ਅਤੇ ਗੇਂਦ ਉਨ੍ਹਾਂ ਦੋਹਾਂ ਦੇ ਦਰਮਿਆਨ ਵਿਚ ਡਿਗੇ । ਕੋਈ ਵੀ ਖਿਡਾਰੀ ਗੇਂਦ ਨੂੰ ਤਦ ਤਕ ਥਪਥਪਾਉਣ ਦਾ ਯਤਨ ਨਹੀਂ ਕਰੇਗਾ, ਜਦ ਤਕ ਕਿ ਉਹ ਵੱਧ ਤੋਂ ਵੱਧ ਉੱਚਾ ਨਾ ਚਲਾ ਜਾਵੇ । ਟਪਾਉਣ ਵਾਲਾ ਖਿਡਾਰੀ ਸਿਰਫ਼ ਦੋ ਵਾਰੀ ਗੇਂਦ ਥਪਥਪਾ ਸਕਦਾ ਹੈ । ਜਿਸ ਵੇਲੇ ਜੰਪ ਬਾਲ ਵਿਚ ਕਾਨੂੰਨ ਤੋੜਿਆ ਜਾਂਦਾ ਹੈ ਤਾਂ ਇਸ ਦਾ ਦੰਡ ਸਾਈਡ ਲਾਈਨ ਤੋਂ ਥਰੋ-ਇਨ (Throw-in) ਦੇ ਕੇ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਇਹ ਵਿਰੋਧੀਆਂ ਲਈ ਵਿਚਕਾਰਲਾ ਬਿੰਦੂ ਹੁੰਦਾ ਹੈ ।
ਗੋਲ ਬਾਰੇ ਜਾਣਕਾਰੀ: (Goal) – ਜਦੋਂ ਗੇਂਦ ਬਾਸਕਟ ਵਿਚ ਉੱਪਰ ਜਾ ਕੇ ਰੁਕ ਜਾਵੇ, ਜਾਂ ਨਿਕਲ ਜਾਵੇ ਤਦ ਗੋਲ ਬਣ ਜਾਂਦਾ ਹੈ । ਤਿੰਨ ਅੰਕ ਰੇਖਾ ਦੇ ਖੇਤਰ ‘ਤੇ ਕੀਤੇ ਗਏ ਗੋਲ ਦੇ ਦੋ ਅੰਕ ਅਤੇ ਫ਼ਰੀ ਥਰੋ ਰਾਹੀਂ ਕੀਤੇ ਗਏ ਗੋਲ ਦਾ ਇਕ ਅੰਕ ਹੋਵੇਗਾ । ਤਿੰਨ ਪੁਆਇੰਟ ਲਾਈਨ ਤੋਂ ਪਰੇ ਫ਼ੀਲਡ ਗੋਲ ਲਗਾਉਣ ਲਈ ਯਤਨ ਕਰਨ ਦੇ ਦਿੱਤੇ ਜਾਣਗੇ ।
ਹਮਲੇ ਸਮੇਂ ਰੁਕਾਵਟ ਪੈਦਾ ਕਰਨਾ (Obstacle during attack) – ਜਿਸ ਵੇਲੇ ਗੇਂਦ ਬਾਸਕਟ ਦੇ ਉੱਪਰੋਂ ਹੇਠਾਂ ਵਲ ਆਉਂਦੀ ਹੈ ਤਾਂ ਕੋਈ ਖਿਡਾਰੀ ਆਪਣੇ ਸੀਮਿਤ ਖੇਤਰ ਵਿਚ ਨਾ ਤਾਂ ਗੇਂਦ ਨੂੰ ਛੂਹ ਸਕਦਾ ਹੈ, ਅਤੇ ਨਾ ਹੀ ਉਹ ਇਸ ਨੂੰ ਫੜ ਸਕਦਾ ਹੈ ਭਾਵੇਂ ਉਹ ਗੋਲ ਬਣਾਉਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਵਿਚ ਹੋਵੇ ।
ਰੱਖਿਆ ਸਮੇਂ ਗੱਦ ਵਿਚ ਰੁਕਾਵਟ (Obstacle (during Defence) – ਜਦ ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਗੋਲ ਕਰਨ ਲਈ ਗੇਂਦ ਸੁੱਟਦਾ ਹੈ ਅਤੇ ਸਾਰੀ ਗੇਂਦ ਬਾਸਕਟ ਦੇ ਘੇਰੇ ਦੀ ਤਹਿ ਦੇ ਉੱਪਰੋਂ ਹੋਵੇ, ਉਸ ਵੇਲੇ ਤਕ ਜਿਉਂ ਹੀ ਗੇਂਦ ਹੇਠਾਂ ਆਉਣੀ ਸ਼ੁਰੂ ਕਰੇ, ਰੱਖਿਅਕ ਖਿਡਾਰੀ
ਅੱਠ ਸੈਕਿੰਡ ਦਾ ਨਿਯਮ (Eight Second Rule) – ਜਦ ਕਿਸੇ ਟੀਮ ਨੂੰ ਮੈਦਾਨ ਦੇ ਪਿਛਲੇ ਹਿੱਸੇ ਵਿਚ ਗੇਂਦ ਪ੍ਰਾਪਤ ਹੋਏ, ਤਾਂ ਉਸ ਨੂੰ ਅੱਠ ਸੈਕਿੰਡ ਦੇ ਅੰਦਰ ਗੇਂਦ ਨੂੰ ਅਗਲੇ ਹਿੱਸੇ ਵਿਚ ਰੱਖਣਾ ਪੈਂਦਾ ਹੈ ।
ਚੌਵੀ (2) ਸੈਕਿੰਡ ਦਾ ਨਿਯਮ (Twenty Four Second Rule) – ਨਵੇਂ ਕਾਨੂੰਨ ਅਨੁਸਾਰ ਸਾਈਡ ਲਾਈਨ (Side Line) ਤੇ ਆਊਟ ਆਫ਼ ਬਾਉਂਡਜ਼ (Out line bounds) ਤੋਂ ਥਰੋ-ਇਨ (Throw-in) ਤੋਂ ਬਾਅਦ ਇਕ ਨਵਾਂ ਚੌਵੀ ਸੈਕਿੰਡ ਪੀਰਿਅਡ ਤਦ ਤਕ ਸ਼ੁਰੂ ਨਹੀਂ ਹੁੰਦਾ, ਜਦੋਂ ਤਕ-() ਗੇਂਦ ਆਉਟ ਆਫ਼ ਬਾਉਂਡਜ਼ ਨਹੀਂ ਜਾਂਦੀ ਅਤੇ ਉਸ ਟੀਮ ਦੇ ਖਿਡਾਰੀ ਰਾਹੀਂ ਰੋਇਨ ਨਹੀਂ ਕੀਤੀ ਜਾਂਦੀ । (ਅ) ਅਫ਼ਸਰਾਂ (Officials) ਨੇ ਕਿਸੇ ਜ਼ਖ਼ਮੀ ਨੂੰ ਬਚਾਉਣ ਲਈ ਖੇਡ ਨੂੰ ਰੋਕ (Suspend) ਦਿੱਤਾ ਹੋਵੇ ਅਤੇ ਜ਼ਖ਼ਮੀ ਖਿਡਾਰੀ ਵਾਲੀ ਟੀਮ ਦੇ ਖਿਡਾਰੀ ਨੇ ਥਰੋ-ਇਨ (Throw-in) ਲਈ ਹੋਵੇ ।24 ਸੈਕਿੰਡ ਪਿੱਛੋਂ ਓਪਰੇਟਰ (Operator) ਉਸ ਸਮੇਂ ਤੋਂ ਘੜੀ ਨੂੰ ਰੋਕੇ ਹੋਏ ਸਮੇਂ ਤੋਂ ਚਲਾਵੇਗਾ, ਜਦ ਉਹ ਟੀਮ ਥਰੋ-ਇਨ (Throwin) ਕੀਤੇ ਜਾਣ ਤੋਂ ਬਾਅਦ ਦੋਬਾਰਾ ਕਾਬੂ ਪਾ ਲੈਂਦੀ ਹੈ ।
ਖੇਡ ਦੀ ਸਮਾਪਤੀ (Termination of Play) – ਟਾਈਮ ਕੀਪਰ ਵੱਲੋਂ ਖੇਡ ਦੀ ਸਮਾਪਤੀ ਦੀ ਸੂਚਨਾ ਦਿੱਤੇ ਜਾਣ ਉੱਤੇ ਖੇਡ ਖ਼ਤਮ ਕਰ ਦਿੱਤੀ ਜਾਵੇਗੀ ।
ਖਿਡਾਰੀ ਦਾ ਬਦਲਣਾ (Substitution of Play) – ਬਦਲਵਾਂ (Substitute) ਖਿਡਾਰੀ ਮੈਦਾਨ ਵਿਚ ਉਤਰਨ ਤੋਂ ਪਹਿਲਾਂ ਸਕੋਰਰ ਕੋਲ ਰਿਪੋਰਟ ਕਰੇਗਾ ਅਤੇ ਤੁਰੰਤ ਖੇਡਣ ਲਈ ਹਾਜ਼ਰ ਰਹੇਗਾ | ਅਧਿਕਾਰੀ ਦਾ ਇਸ਼ਾਰਾ ਮਿਲਦੇ ਹੀ ਉਹ ਮੈਦਾਨ ਵਿਚ ਉਤਰੇਗਾ | ਬਦਲਵੇਂ ਖਿਡਾਰੀ ਨੂੰ ਮੈਦਾਨ ਵਿਚ ਉਤਰਨ ਲਈ ਵੀਹ ਸੈਕਿੰਡ ਤੋਂ ਵੱਧ ਸਮਾਂ ਨਹੀਂ ਲਗਣਾ ਚਾਹੀਦਾ । ਜੇ ਉਸ ਨੂੰ ਜ਼ਿਆਦਾ ਸਮਾਂ ਲਗਦਾ ਹੈ, ਤਾਂ ਇਹ ਟਾਈਮ ਆਊਟ ਮੰਨਿਆ ਜਾਵੇਗਾ ਅਤੇ ਵਿਰੋਧੀ ਪਾਰਟੀ ਦੇ ਵਿਰੁੱਧ ਅੰਕਿਤ ਕਰ ਦਿੱਤਾ ਜਾਵੇਗਾ ।
ਮੁਰਦਾ ਗੇਂਦ (Dead Bally) – ਗੇਂਦ ਉਸ ਵਕਤ ਹੀ ਮੁਰਦਾ ਹੁੰਦੀ ਹੈ, ਜਦ ਗੇਂਦ ਜੋ ਪਹਿਲਾਂ ਹੀ ਗੋਲ ਲਈ ਸ਼ੌਟ ਦੇ ਲਈ ਉੜਾਨ ਵਿਚ ਹੁੰਦੀ ਹੈ ਅਤੇ ਖਿਡਾਰੀ ਦੇ ਦੁਆਰਾ ਉਸ ਸਮੇਂ ਤੋਂ ਬਾਅਦ ਛੂਹੀ ਜਾਂਦੀ ਹੈ, ਜਦ ਅੱਧਾ ਜਾਂ ਫਾਲਤੂ ਸਮਾਂ ਪੂਰਾ ਹੋ ਚੁੱਕਾ ਹੁੰਦਾ ਹੈ ਜਾਂ ਜਦ ਫਾਉਲ ਬੁਲਾਇਆ ਜਾ ਚੁੱਕਿਆ ਹੁੰਦਾ ਹੈ ।
ਤਿੰਨ ਸੈਕਿੰਡ ਦਾ ਨਿਯਮ (Three Second Rule) – ਜਦ ਗੇਂਦ ਕਿਸੇ ਟੀਮ ਦੇ ਅਧਿਕਾਰ ਵਿਚ ਹੋਵੇ ਤਾਂ ਇਸ ਟੀਮ ਦਾ ਕੋਈ ਵੀ ਖਿਡਾਰੀ ਪ੍ਰਤੀਬੰਧਿਤ ਖੇਤਰ ਵਿਚ ਤਿੰਨ ਸੈਕਿੰਡ ਤੋਂ ਵੱਧ ਨਹੀਂ ਰਹਿ ਸਕਦਾ ।
ਡਰਿਬਲਿੰਗ (Dribbling) – ਬਾਸਕਟ ਬਾਲ ਵਿਚ ਡਰਿਬਲਿੰਗ ਦਾ ਖਾਸ ਮਹੱਤਵ ਹੈ । ਜਦ ਕੋਈ ਖਿਡਾਰੀ ਪੂਰਾ-ਪੂਰਾ ਕੰਟਰੋਲ ਕਰਨਾ ਸਿੱਖ ਜਾਵੇ ਅਤੇ ਠੀਕ ਡਰਿਬਲਿੰਗ ਕਰੇ, ਤਾਂ ਉਹ ਅੱਧੀ ਖੇਡ ਸਿੱਖ ਜਾਂਦਾ ਹੈ । ਡਰਿਬਲਿੰਗ ਉਸ ਨੂੰ ਕਹਿੰਦੇ ਹਨ ਜਦ ਕਿ ਖਿਡਾਰੀ ਬਾਲ ਹਵਾ ਵਿਚ ਉਛਾਲ ਕੇ ਫਿਰ ਧਰਤੀ ‘ਤੇ ਸੁੱਟਦਾ ਹੈ ਜਾਂ ਚੁੱਕਦਾ ਜਾਂਦਾ ਹੈ ।
ਉਸ ਨੂੰ ਛੂਹਣ ਦੀ ਬਿਲਕੁਲ ਕੋਸ਼ਿਸ਼ ਨਹੀਂ ਕਰੇਗਾ । ਉਲੰਘਣਾ ਹੋਣ ਉੱਤੇ ਗੇਂਦ ਮ੍ਰਿਤ ਹੋ ਜਾਂਦੀ ਹੈ । ਜੇ ਫ਼ਰੀ ਥਰੋ ਸਮੇਂ ਉਲੰਘਣਾ ਹੋਣ ਤੇ ਸੁੱਟਣ ਵਾਲੇ ਦੇ ਪੱਖ ਵਿਚ ਇਕ ਅੰਕ ਅਤੇ ਜੋ ਗੋਲ ਦੀ ਕੋਸ਼ਿਸ਼ ਦੇ ਸਮੇਂ ਹੋਵੇ ਤਾਂ ਦੋ ਅੰਕ ਜਮ੍ਹਾਂ ਕਰ ਦਿੱਤੇ ਜਾਂਦੇ ਹਨ ।
ਗੋਲ ਤੋਂ ਬਾਅਦ ਗੇਂਦ ਖੇਡ ਵਿਚ (Ball in Play after Goal) – ਗੋਲ ਬਣਨ ਤੋਂ ਪੰਜ ਸੈਕਿੰਡ ਬਾਅਦ ਵਿਰੋਧੀ ਟੀਮ ਦਾ ਕੋਈ ਖਿਡਾਰੀ ਕੋਰਟ ਦੇ ਅੰਤ ਵਿਚ ਪਰਿਧੀ ਤੋਂ ਬਾਹਰ ਕਿਸੇ ਵੀ ਬਿੰਦੂ ਤੋਂ ਜਿੱਥੇ ਗੋਲ ਬਣਿਆ ਸੀ, ਗੇਂਦ ਖੇਡ ਵਿਚ ਸੁੱਟੇਗਾ ।
ਬਾਸਕਟ ਬਾਲ ਖੇਡ ਦਾ ਫੈਸਲਾ (Decision of Play) – ਖੇਡ ਵਿਚ ਵਧੇਰੇ ਅੰਕ ਪ੍ਰਾਪਤ ਕਰਨ ਵਾਲੀ ਟੀਮ ਨੂੰ ਜੇਤੂ ਘੋਸ਼ਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
ਖੇਡ ਦਾ ਅਧਿਕਾਰ ਖੋਹਿਆ ਜਾਣਾ (Forfeit of Play) – ਜੇ ਅੱਧੇ ਸਮੇਂ ਜਾਂ ਟਾਈਮ ਆਉਟ ਤੋਂ ਬਾਅਦ ਕੋਈ ਟੀਮ ਰੈਫ਼ਰੀ ਦੇ ਬੁਲਾਉਣ ਤੋਂ ਬਾਅਦ ਖੇਡ ਲਈ ਮੈਦਾਨ ਵਿਚ ਨਹੀਂ ਆਉਂਦੀ ਤਾਂ ਗੇਂਦ ਮੈਦਾਨ ਵਿਚ ਲਿਆਂਦੀ ਜਾਵੇਗੀ ਅਤੇ ਗ਼ੈਰ ਹਾਜ਼ਿਰ ਟੀਮ ਖੇਡ ‘ ਦਾ ਹੱਕ ਗੁਆ ਲੈਂਦੀ ਹੈ । ਜੇ ਖੇਡ ਦੇ ਦੌਰਾਨ ਕਿਸੇ ਟੀਮ ਦੇ ਖਿਡਾਰੀਆਂ ਦੀ ਗਿਣਤੀ ਦੋ ਤੋਂ ਘੱਟ ਰਹਿ ਜਾਵੇ, ਤਾਂ ਖੇਡ ਖ਼ਤਮ ਹੋ ਜਾਵੇਗੀ ਅਤੇ ਉਹ ਟੀਮ ਖੇਡ ਦਾ ਅਧਿਕਾਰ ਗੁਆ ਲਵੇਗੀ ।
ਸਕੋਰ ਅਤੇ ਵਾਧੂ ਸਮਾਂ (Score and Extra Time) – ਜੇ ਚੌਥੇ ਖੇਡ ਦੇ ਅਵਧੀ ਦੀ ਸਮਾਪਤੀ ਤਕ ਦੋਵੇਂ ਟੀਮਾਂ ਦੇ ਅੰਕ ਬਰਾਬਰ ਹੋਣ ਤਾਂ ਪੰਜ ਮਿੰਟਾਂ ਦੀ ਅਧਿਕ ਮਿਆਦ ਦਿੱਤੀ ਜਾਵੇਗੀ ਅਤੇ ਅਜਿਹੀ ਮਿਆਦ ਜਦ ਤਕ ਖੇਡ ਦਾ ਫ਼ੈਸਲਾ ਨਾ ਹੋਵੇ, ਦਿੱਤੀ ਜਾਵੇਗੀ । ਪਹਿਲੇ ਵਾਧੂ ਸਮੇਂ ਬਾਸਕਟ ਦੀ ਚੋਣ ਲਈ ਟਾਸ ਹੋਵੇਗੀ ਅਤੇ ਉਸ ਦੇ ਬਾਅਦ ਹਰੇਕ ਵਾਧੂ ਸਮੇਂ ਲਈ ਬਾਸਕਟ ਬਦਲ ਲਈ ਜਾਵੇਗੀ ।
ਟਾਈਮ ਆਊਟ (Time Out) – ਅੱਧੇ ਸਮੇਂ ਤਕ ਹਰੇਕ ਟੀਮ ਨੂੰ ਦੋ ਟਾਈਮ ਆਊਟ ਮਿਲ ਸਕਦੇ ਹਨ ਅਤੇ ਵਾਧੂ ਸਮੇਂ ਵਿਚ ਇਕ ਟਾਈਮ ਆਉਟ ਮਿਲ ਸਕਦਾ ਹੈ ਕਿਸੇ ਖਿਡਾਰੀ ਨੂੰ ਸੱਟ ਲੱਗਣ ਦੀ ਦਸ਼ਾ ਵਿਚ ਇਕ ਮਿੰਟ ਦਾ ਟਾਈਮ ਆਊਟ ਮਿਲਦਾ ਹੈ । ਜੇ ਇਸ ਦੌਰਾਨ ਜ਼ਖ਼ਮੀ ਖਿਡਾਰੀ ਠੀਕ ਨਹੀਂ ਹੁੰਦਾ, ਤਾਂ ਉਸ ਦੀ ਥਾਂ ਨਵਾਂ ਖਿਡਾਰੀ ਲੈ ਲਿਆ ਜਾਂਦਾ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 5.
ਬਾਸਕਟ ਬਾਲ ਵਿਚ ਪੰਜ ਸੈਕਿੰਡ ਦਾ ਨਿਯਮ, ਤਿੰਨ ਸੈਕਿੰਡ, ਅੱਠ ਸੈਕਿੰਡ ਦਾ ਨਿਯਮ ਅਤੇ ਚੌਵੀ ਸੈਕਿੰਡ ਦਾ ਨਿਯਮ ਕੀ ਹਨ ?
ਉੱਤਰ-
ਪੰਜ ਸੈਕਿੰਡ ਦਾ ਨਿਯਮ (Five Second Rule) – ਜਦ ਨੇੜੇ ਦਾ ਕੋਈ ਰੱਖਿਅਕ ਖਿਡਾਰੀ ਗੇਂਦ ਨੂੰ ਖੇਡਣ ਤੋਂ ਰੋਕਦਾ ਹੈ ਅਤੇ ਉਹ ਪੰਜ ਸੈਕਿੰਡ ਅੰਦਰ ਗੇਂਦ ਨੂੰ ਖੇਡ ਵਿਚ ਦੁਬਾਰਾ ਸੁੱਟਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਨਹੀਂ ਕਰਦਾ, ਤਾਂ ਇਸ ਨੂੰ ਬਲਾਕਿੰਗ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
ਪੀਵਟ ਫੁਟ (Pivot foot) – ਜਦ ਕੋਈ ਖਿਡਾਰੀ ਬਾਲ ਲੈ ਕੇ ਇਸ ਤਰ੍ਹਾਂ ਘੁੰਮਦਾ ਹੈ ਕਿ ਉਸ ਦਾ ਇਕ ਪੈਰ ਫਰਸ਼ ਉੱਤੇ ਇਕ ਪੈਰ ਬਿੰਦੂ ਉੱਤੇ ਘੁੰਮਦਾ ਨਜ਼ਰ ਆਵੇ, ਤਾਂ ਉਸ ਨੂੰ ਪੀਵਟ ਫੁਟ (Pivot foot) ਕਹਿੰਦੇ ਹਨ ।
ਬਾਸਕਟ ਬਾਲ ਵਿਚ ਫਾਉਲ ਹੋਣ ਤੋਂ ਬਾਅਦ ਦ ਖੇਡ ਵਿਚ (Ball in play after Foul) – ਗੇਂਦ ਕਿਸੇ ਫਾਊਲ ਦੇ ਨਾਲ ਖੇਡ ਤੋਂ ਬਾਹਰ ਹੋ ਜਾਵੇ, ਤਾਂ ਇਸ ਸਥਿਰ ਗੇਂਦ ਨੂੰ ਫਿਰ ਖੇਡ ਵਿਚ ਲਿਆਂਦਾ ਜਾਵੇਗਾ-
- ਬਾਹਰ ਤੋਂ ਥਰੋ ਕਰਕੇ ਜਾਂ,
- ਕਿਸੇ ਇਕ ਚੱਕਰ ਵਿਚ ਜੰਪ ਬਾਲ ਰਾਹੀਂ ਜਾਂ
- ਇਕ ਜਾਂ ਵਧੇਰੇ ਫ਼ਰੀ ਥਰੋ ਰਾਹੀਂ ।
ਥਰੋ-ਇਨ (Throw-in) – ਜਦ ਕਿਸੇ ਨਿਯਮ ਦੀ ਉਲੰਘਣਾ ਹੋ ਜਾਵੇ, ਤਾਂ ਗੇਂਦ ਸਥਿਰ ਸਮਝੀ ਜਾਂਦੀ ਹੈ ਅਤੇ ਵਿਰੋਧੀ ਟੀਮ ਨੂੰ ਸਾਈਡ ਲਾਈਨ ਦੇ ਨੇੜੇ ਦੇ ਬਿੰਦੂ ਤੋਂ ਥਰੋ-ਇਨ ਲਈ ਜਾਂਦੀ ਹੈ । ਹੁਣ ਰੂਲ ਉਸ ਖਿਡਾਰੀ ਨੂੰ ਆਗਿਆ ਦਿੰਦਾ ਹੈ, ਜਿਸ ਨੇ ਥਰੋ-ਇਨ (Throwin) ਕਰਨਾ ਹੈ ਕਿ ਉਹ ਸਮਾਪਤੀ ਲਕੀਰ (End line) ਨੂੰ ਛੂਹੇ ਇਹ ਕਾਨੂੰਨ ਨੂੰ ਤੋੜਨਾ ਨਹੀਂ ਹੈ ।
ਫ਼ਰੀ ਥਰੋ (Free throw) – ਜਿਸ ਖਿਡਾਰੀ ਉੱਤੇ ਫਾਉਲ ਕੀਤਾ ਗਿਆ ਹੋਵੇ, ਉਹ | ਫ਼ਰੀ ਥਰੋ ਲੈਂਦਾ ਹੈ । ਪਰ ਕਿਸੇ ਤਕਨੀਕੀ ਫਾਊਲ ਦੀ ਹਾਲਤ ਵਿਚ ਕੋਈ ਵੀ ਖਿਡਾਰੀ ਫ਼ਰੀ| ਥਰੋ ਲੈ ਸਕਦਾ ਹੈ, ਜਦ ਫ਼ਰੀ ਥਰੋ ਲਈ ਜਾਂਦੀ ਹੈ ਤਾਂ ਖਿਡਾਰੀਆਂ ਦੀ ਸਥਿਤੀ ਇਸ ਤਰ੍ਹਾਂ ਹੁੰਦੀ ਹੈ-
- ਵਿਰੋਧੀ ਟੀਮ ਦੇ ਦੋ ਖਿਡਾਰੀ ਬਾਸਕਟ ਦੇ ਨੇੜੇ ਖੜ੍ਹੇ ਹੋਣਗੇ ।
- ਦੂਜੇ ਖਿਡਾਰੀ ਵੱਖ-ਵੱਖ ਪੁਜ਼ੀਸ਼ਨਾਂ ਲੈਣਗੇ ।
- ਬਾਕੀ ਦੇ ਖਿਡਾਰੀ ਕੋਈ ਵੀ ਪੁਜ਼ੀਸ਼ਨ ਲੈ ਸਕਦੇ ਹਨ, ਪਰ ਉਹ ਫ਼ਰੀ-ਥਰੋ ਸਮੇਂ ਰੁਕਾਵਟ ਨਹੀਂ ਬਣਨੇ ਚਾਹੀਦੇ ।
ਫ਼ਰੀ-ਥਰੋ ਨਿਯਮਾਂ ਦੀ ਉਲੰਘਣਾ (Violation of Free Throw Rules) – ਫ਼ਰੀਬਰੋ ਕਾਰਨ ਖਿਡਾਰੀ ਦੇ ਅਧਿਕਾਰ ਵਾਲੇ ਖੇਤਰ ਵਿਚ ਗੇਂਦ ਦੇਣ ਤੋਂ ਬਾਅਦ
(ਉ) ਉਹ ਪੰਜ ਸੈਕਿੰਡ ਦੇ ਅੰਦਰ ਗੇਂਦ ਨੂੰ ਇਸ ਤਰ੍ਹਾਂ ਸੁੱਟੇਗਾ ਕਿ ਖਿਡਾਰੀ ਰਾਹੀਂ ਛੂਹੇ | ਜਾਣ ਤੋਂ ਪਹਿਲਾਂ ਗੇਂਦ ਬਾਸਕਟ ਵਿਚ ਚਲੀ ਜਾਵੇ ਜਾਂ ਘੇਰੇ ਨੂੰ ਛੂਹ ਲਵੇ ।
(ਅ) ਗੇਂਦ ਦੇ ਬਾਸਕਟ ਵਲ ਜਾਂਦੇ ਸਮੇਂ ਜਾਂ ਅੰਦਰ ਪਹੁੰਚਣ ਉੱਤੇ ਨਾ ਤਾਂ ਉਹ ਖਿਡਾਰੀ | ਅਤੇ ਨਾ ਹੀ ਕੋਈ ਦੂਜਾ ਖਿਡਾਰੀ ਗੇਂਦ ਬਾਸਕਟ ਨੂੰ ਛੂਹ ਸਕਦਾ ਹੈ ।
(ੲ) ਉਹ ਫ਼ਰੀ-ਬਰੋ ਲਾਈਨ ਜਾਂ ਉਸ ਦੇ ਪੂਰੇ ਜ਼ਮੀਨ ਨੂੰ ਨਹੀਂ ਛੂਹੇਗਾ | ਨਾ ਹੀ ਕਿਸੇ ਟੀਮ ਦਾ ਕੋਈ ਦੂਜਾ ਖਿਡਾਰੀ ਫ਼ਰੀ-ਬਰੋ ਲਾਈਨ ਨੂੰ ਛੂਹੇਗਾ ਜਾਂ ਫ਼ਰੀ ਥਰੋ ਕਰਨ ਵਾਲੇ ਖਿਡਾਰੀ ਲਈ ਰੁਕਾਵਟ ਖੜੀ ਕਰੇਗਾ ।
ਖੇਡ ਜ਼ਬਤ ਹੋਣਾ (Game to be forfeited) – ਨਵੇਂ ਕਾਨੂੰਨ ਦੇ ਅਨੁਸਾਰ ਰੈਫ਼ਰੀ ਨੂੰ ਹੁਣ ਇਹ ਜ਼ਰੂਰੀ ਨਹੀਂ ਹੈ ਕਿ ਗੇਂਦ ਨੂੰ ਉਸ ਢੰਗ ਨਾਲ ਖੇਡ ਵਿਚ ਰੱਖੇ, ਜਿਵੇਂ ਕਿ ਦੋਨੋਂ ਟੀਮਾਂ ਫਰਸ਼ ‘ਤੇ ਖੇਡਣ ਲਈ ਅਤੇ ਖੇਡ ਨੂੰ ਜ਼ਬਤ ਕਰਨ ਲਈ ਤਿਆਰ ਹੋਣ । ਤੁਸੀਂ ਰੈਫ਼ਰੀ (Referee) ਦੇ ਖੇਡ ਬੁਲਾਉਣ ਦੇ ਮਗਰੋਂ ਜੇਕਰ ਇਕ ਟੀਮ ਖੇਡਣ ਤੋਂ ਇਨਕਾਰ ਕਰ ਦਿੰਦੀ ਹੈ, ਤਾਂ ਖੇਡ ਜ਼ਬਤ ਹੋ ਜਾਂਦੀ ਹੈ ।
ਗੇਂਦ ਦਾ ਪਿਛਲੀ ਕੋਰਟ ਨੂੰ ਵਾਪਸ ਜਾਣਾ (Ball return to Back Court) – ਨਵੇਂ ਰੁਲ ਦੇ ਅਨੁਸਾਰ ਗੇਂਦ ਨੂੰ ਟੀਮ (A) ਦੀ ਪਿਛਲੀ ਕੋਰਟ ਵਲ ਭੇਜਿਆ ਜਾਂਦਾ ਹੈ, ਸ਼ਰਤ ਇਹ ਹੈ ਕਿ ਇਸ ਨੂੰ ਟੀਮ ਏ (A) ਦਾ ਇਕ ਖਿਡਾਰੀ ਛੂਹਦਾ ਹੈ, ਜਦ ਟੀਮ ਏ ਸਾਹਮਣੇ ਦੀ ਕੋਰਟ ਵਿਚ ਗੇਂਦ ਨੂੰ ਕਾਬੂ ਰੱਖਦੀ ਹੈ । ਇਸ ਦੇ ਅਨੁਸਾਰ A ਦੇ ਖਿਡਾਰੀ ਵਲੋਂ ਛੂਹਣਾ ਜਦ ਕਿ ਗੇਂਦ ਟੀਮ ਏ ਦੇ ਸਾਹਮਣੇ ਦੀ ਕੋਰਟ ਵਿਚ ਟੀਮ ਬੀ ਦੇ ਕਾਬੂ ਵਿਚ ਹੈ, ਜੇਕਰ ਟੀਮ ਏ ਦੀ ਪਿਛਲੀ ਕੋਰਟ ਵਿਚ ਗੇਂਦ ਜਾਣ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਉਸ ਨੂੰ ਇਸ ਤਰ੍ਹਾਂ ਨਹੀਂ ਸਮਝਾਇਆ ਜਾਂਦਾ ਕਿ ਗੇਂਦ ਪਿਛਲੀ ਕੋਰਟ ਵਿਚ ਜਾਣ ਦਿੱਤਾ ਜਾਵੇ । ਇਸ ਦੇ ਅੱਗੇ ਕੇਂਦਰ (Midpoint) ਤੋਂ ਥਰੋ-ਇਨ (Throw-in) ਦੇ ਦੌਰਾਨ ਅਫ਼ਸਰ (Official) ਇਹ ਨਿਸ਼ਚਿਤ ਬਣਾਏਗਾ ਕਿ ਖਿਡਾਰੀ ਵਧਾਈ ਗਈ ਸਾਈਡ ਲਾਈਨ (Side line) ਦੇ ਦੋਨੋਂ ਪਾਸੇ ਇਕ ਪੈਰ ਵੱਖ ਰੱਖ ਕੇ ਪੋਜ਼ੀਸ਼ਨ ਬਣਾ ਲੈਂਦਾ ਹੈ ।
ਆਉਟ ਆਫ਼ ਬਾਉਂਡਜ਼ ਖੇਡ ਤੋਂ ਕਾਨੂੰਨ ਤੋੜਨਾ (Violation on out of bounds play – ਇਹ ਕਾਨੂੰਨ ਤੋੜਨਾ ਨਹੀਂ ਹੈ । ਜਦ ਕਿ ਖਿਡਾਰੀ ਜਿਸ ਨੂੰ ਥਰੋ-ਇਨ (Throwin) ਦਿੱਤੀ ਗਈ ਹੈ, ਗੇਂਦ ਨੂੰ ਛੱਡਣ ਵੇਲੇ ਲਕੀਰ ‘ਤੇ ਪੈਰ ਰੱਖਦਾ ਹੈ ।
ਸਜ਼ਾ (Penalty) –
- ਉਲੰਘਣਾ ਫ਼ਰੀ-ਥਰੋ ਕਰਨ ਵਾਲੇ ਖਿਡਾਰੀ ਦੁਆਰਾ ਹੋਣ ‘ਤੇ ਕੋਈ ਅੰਕ ਰਿਕਾਰਡ ਨਹੀਂ ਹੋਵੇਗਾ । ਗੇਂਦ ਫ਼ਰੀ-ਥਰੋ ਕਰਨ ਵਾਲੇ ਖਿਡਾਰੀ ਦੇ ਵਿਰੋਧੀ ਨੂੰ ਫ਼ਰੀ ਥਰੋ ਲਾਈਨ ਦੇ ਸਾਹਮਣੇ ਦੇ ਦਿੱਤੀ ਜਾਵੇਗੀ ।
- ਉਲੰਘਣਾ ਫ਼ਰੀ ਥਰੋ ਕਰਨ ਵਾਲੇ ਖਿਡਾਰੀ ਦੀ ਟੀਮ ਦੇ ਹੋਰ ਖਿਡਾਰੀ ਰਾਹੀਂ ਹੋਣ ਉੱਤੇ ਵੀ ਅੰਕ ਰਿਕਾਰਡ ਹੋਵੇਗਾ । ਜੇ ਨਿਯਮ ਦੀ ਉਲੰਘਣਾ ਦੋਵੇਂ ਟੀਮਾਂ ਵਲੋਂ ਹੁੰਦੀ ਹੈ, ਤਾਂ ਕੋਈ ਅੰਕ ਦਰਜ ਨਹੀਂ ਹੋਵੇਗਾ ਅਤੇ ਫ਼ਰੀ ਥਰੋ ਲਾਈਨ ਉੱਤੇ ਜੰਪ ਬਾਲ ਰਾਹੀਂ ਖੇਡ ਜਾਰੀ ਕੀਤੀ ਜਾਵੇਗੀ ।
- ਜੇ ਨਿਯਮ (ਇ) ਦੀ ਉਲੰਘਣਾ ਫ਼ਰੀ ਥਰੋ ਕਰਨ ਵਾਲੇ ਖਿਡਾਰੀ ਦੇ ਸਾਥੀ ਰਾਹੀਂ ਹੁੰਦੀ ਹੈ ਅਤੇ ਫ਼ਰੀ ਥਰੋ ਸਫਲ ਹੋ ਜਾਂਦੀ ਹੈ, ਤਾਂ ਉਲੰਘਣਾ ਨੂੰ ਅੱਖੋਂ ਉਹਲੇ ਕਰਕੇ ਗੋਲ ਗਿਣ ਲਿਆ ਜਾਵੇਗਾ । ਜੇ ਫ਼ਰੀ-ਬਰੋ ਸਫਲ ਨਹੀਂ ਹੁੰਦੀ ਤਾਂ ਇਸ ਦਾ ਦੰਡ ਦਿੱਤਾ ਜਾਵੇਗਾ ।
- ਜੇ ਨਿਯਮ (ਇ) ਦੀ ਉਲੰਘਣਾ ਫ਼ ਥਰੇ ਕਰਨ ਵਾਲੇ ਖਿਡਾਰੀ ਦੇ ਵਿਰੋਧੀਆਂ ਵਲੋਂ ਹੁੰਦੀ ਹੈ, ਤਾਂ ਫ਼ਰੀ ਥਰੋ ਸਫਲ ਨਹੀਂ ਹੋਣ ਉੱਤੇ ਉਲੰਘਣਾ ਨੂੰ ਅੱਖੋਂ ਉਹਲੇ ਕਰਕੇ ਗੋਲ ਗਿਣਿਆ ਜਾਵੇਗਾ ।
- ਜੇ ਨਿਯਮ (ਇ) ਦੀ ਉਲੰਘਣਾ ਦੋਵੇਂ ਟੀਮਾਂ ਰਾਹੀਂ ਹੁੰਦਾ ਹੈ ਅਤੇ ਫ਼ਰੀ ਥਰੋ ਸਫਲ ਹੋ ਜਾਂਦੀ ਹੈ ਤਾਂ ਉਲੰਘਣਾ ਨੂੰ ਨਜ਼ਰ ਅੰਦਾਜ਼ ਕਰਕੇ ਗੋਲ ਗਿਣ ਲਿਆ ਜਾਵੇਗਾ । ਫ਼ਰੀ ਥਰੋ ਸਫਲ ਨਾ ਹੋਣ ਦੀ ਦਿਸ਼ਾ ਵਿਚ ਫ਼ਰੀ ਥਰੋ ਲਾਈਨ ਉੱਤੇ ਜੰਪ ਬਾਲ ਦੇ ਨਾਲ ਖੇਡ ਦੁਬਾਰਾ ਜਾਰੀ ਕੀਤੀ ਜਾਵੇਗੀ ।
![]()
ਪ੍ਰਸ਼ਨ 6.
ਬਾਸਕਟ ਬਾਲ ਖੇਡ ਵਿਚ ਖਿਡਾਰੀਆਂ ਦੇ ਤਕਨੀਕੀ ਫਾਉਲ ਲਿਖੋ ।
ਉੱਤਰ-
ਬਾਸਕਟ ਬਾਲ ਖੇਡ ਵਿਚ ਖਿਡਾਰੀ ਵਲੋਂ ਤਕਨੀਕੀ ਫਾਊਲ (Technical Foul by Player) – ਕੋਈ ਵੀ ਖਿਡਾਰੀ ਅਧਿਕਾਰੀਆਂ ਵਲੋਂ ਦਿੱਤੀ ਚੇਤਾਵਨੀ ਨੂੰ ਨਜ਼ਰ ਅੰਦਾਜ਼ ਨਹੀਂ ਕਰੇਗਾ ਅਤੇ ਨਾ ਹੀ ਅਜਿਹਾ ਵਤੀਰਾ ਕਰੇਗਾ, ਜਿਹੜਾ ਇਕ ਖਿਡਾਰੀ ਨੂੰ ਸ਼ੋਭਾ ਨਾ ਦੇਵੇ, ਜਿਵੇਂ-
- ਅਧਿਕਾਰੀ ਨੂੰ ਅਪਮਾਨਜਨਕ ਢੰਗ ਨਾਲ ਸੰਬੋਧਿਤ ਕਰਨਾ ਜਾਂ ਮਿਲਣਾ ।
- ਗ਼ਲਤ ਵਤੀਰਾ ਕਰਨਾ ।
- ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਨੂੰ ਤੰਗ ਕਰਨਾ ਜਾਂ ਉਸ ਦੀਆਂ ਅੱਖਾਂ ਅੱਗੇ ਹੱਥ ਕਰਕੇ ਉਸ ਨੂੰ ਦੇਖਣ ਵਿਚ ਰੁਕਾਵਟ ਪਾਉਣਾ ।
- ਖੇਡ ਵਿਚ ਅਨੁਚਿਤ ਢੰਗ ਨਾਲ ਰੁਕਾਵਟ ਪਾਉਣਾ ।
- ਫਾਊਲ ਦਾ ਸੰਕੇਤ ਮਿਲਣ ਉੱਤੇ ਠੀਕ ਢੰਗ ਨਾਲ ਬਾਂਹ ਉੱਤੇ ਨਾ ਕਰਨਾ ।
- ਸਕੋਰਰ ਜਾਂ ਰੈਫ਼ਰੀ ਨੂੰ ਬਿਨਾਂ ਸੂਚਿਤ ਕੀਤੇ ਆਪਣੇ ਨੰਬਰ ਬਦਲਣਾ ।
- ਸਕੋਰਰ ਨੂੰ ਸੂਚਿਤ ਕੀਤੇ ਬਿਨਾਂ ਬਦਲਵੇਂ ਖਿਡਾਰੀ (Substitute) ਨੂੰ ਕੋਰਟ ਵਿਚ ਭੇਜਣਾ ।
ਸਜ਼ਾ (Penalty) – ਹਰੇਕ ਜੁਰਮ ਦਾ ਇਕ ਫਾਉਲ ਮੰਨਿਆ ਜਾਵੇਗਾ ਅਤੇ ਹਰੇਕ ਫਾਉਲ ਲਈ ਵਿਰੋਧੀ ਨੂੰ ਦੋ ਫ਼ਰੀ ਥਰੋਆਂ ਦਿੱਤੀਆਂ ਜਾਣਗੀਆਂ । ਇਸ ਨਿਯਮ ਦੀ ਘੜੀ-ਮੁੜੀ ਉਲੰਘਣਾ ਕੀਤੇ ਜਾਣ ਉੱਤੇ ਖਿਡਾਰੀ ਨੂੰ ਆਯੋਗ ਘੋਸ਼ਿਤ ਕਰਕੇ ਖੇਡ ਵਿਚੋਂ ਕੱਢ ਦਿੱਤਾ ਜਾਵੇਗਾ ।
ਕੋਚ ਜਾਂ ਬਦਲਵੇਂ ਖਿਡਾਰੀ ਵਲੋਂ ਤਕਨੀਕੀ ਫਾਊਲ (Technical foul by Coach or Substitute Player) – ਕੋਈ ਕੋਚ ਜਾਂ ਬਦਲਵਾਂ ਖਿਡਾਰੀ ਬਿਨਾਂ ਅਧਿਕਾਰੀ ਦੇ ਹੁਕਮ ਦੇ ਕੋਰਟ ਵਿਚ ਦਾਖਲ ਨਹੀਂ ਹੋ ਸਕਦਾ, ਨਾ ਹੀ ਕੋਰਟ ਦੇ ਕੰਮਾਂ ਨੂੰ ਜਾਣਨ ਲਈ ਆਪਣੀ ਥਾਂ ਛੱਡ ਸਕਦਾ ਹੈ ਅਤੇ ਨਾ ਹੀ ਕਿਸੇ ਅਧਿਕਾਰੀ ਜਾਂ ਵਿਰੋਧੀ ਨੂੰ ਅਪਮਾਨਜਨਕ ਢੰਗ ਨਾਲ ਬੁਲਾ ਸਕਦਾ ਹੈ ।
ਸਜ਼ਾ (Penalty) – ਕੋਚ ਵਲੋਂ ਇਸ ਨਿਯਮ ਦੀ ਉਲੰਘਣਾ ਕਰਨ ਉੱਤੇ ਉਸ ਦੇ ਨਾਂ ਫਾਊਲ ਦਰਜ ਕੀਤਾ ਜਾਵੇਗਾ | ਹਰੇਕ ਜੁਰਮ ਦੇ ਲਈ ਦੋ ਫਰੀ ਥਰੋ ਦਿੱਤੀ ਜਾਵੇਗੀ ਅਤੇ ਬਾਲ ਉਸੋ ਟੀਮ ਨੂੰ ਕੇਂਦਰੀ ਰੇਖਾ ਕੋਲੋਂ ਥਰੋ-ਇਨ ਕਰਨ ਲਈ ਮਿਲੇਗਾ। ਇਸ ਨਿਯਮ ਦੀ ਘੜੀ-ਮੁੜੀ ਉਲੰਘਣਾ ਕੀਤੇ ਜਾਣ ਉੱਤੇ ਕੋਚ ਨੂੰ ਖੇਡ ਦੀਆਂ ਸੀਮਾਵਾਂ ਤੋਂ ਬਾਹਰ ਵੀ ਕੱਢਿਆ ਜਾ ਸਕਦਾ ਹੈ ।
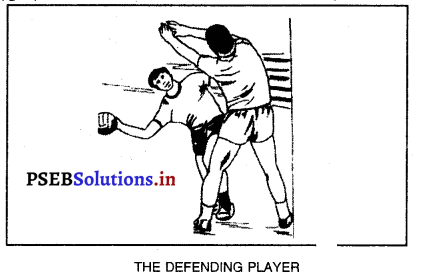
ਨਿੱਜੀ ਫਾਊਲ (Personal foul) – ਨਿੱਜੀ ਫਾਊਲ ਉਸ ਖਿਡਾਰੀ ਦਾ ਹੁੰਦਾ ਹੈ, ਜਿਹੜਾ ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਨੂੰ ਬਲਾਕ ਕਰਦਾ ਹੈ ਜਦ ਕਿ ਇਸ ਪਾਸੇ ਦਾ ਖਿਡਾਰੀ ਅਰਾਮ ਨਾਲ ਬਾਲ ਲੈ ਕੇ ਜਾ ਰਿਹਾ ਹੋਵੇ ਅਤੇ ਦੂਸਰੇ ਪਾਸੇ ਦਾ ਖਿਡਾਰੀ ਉਸ ‘ਤੇ ਹਮਲਾ ਕਰ ਦੇਵੇ ਜਾਂ ਉਸ ਨੂੰ ਫੜਦਾ ਹੈ ਜਾਂ ਧੱਕ ਦਿੰਦਾ ਹੈ ਇਸ ਸਮੇਂ ਰੈਫ਼ਰੀ ਸੀਟੀ ਵਜਾਉਂਦਾ ਹੈ ਤੇ ਸਜ਼ਾ ਦਿੰਦਾ ਹੈ ।
ਸਜ਼ਾ (Penalty)-
- ਜੇ ਸ਼ੂਟਿੰਗ ਕਰਦੇ ਸਮੇਂ ਖਿਡਾਰੀ ਉੱਤੇ ਫਾਉਲ ਹੁੰਦਾ ਹੈ ਤਾਂ
- ਗੋਲ ਹੋ ਜਾਂਦਾ ਹੈ ਤਾਂ ਉਸ ਦੀ ਗਿਣਤੀ ਕੀਤੀ ਜਾਵੇਗੀ ਅਤੇ ਇਕ ਫ਼ਰੀ-ਥਰੋ ਦਿੱਤੀ ਜਾਵੇਗੀ ।
- ਜੋ ਗੋਲ (ਦੋ ਅੰਕ) ਨਹੀਂ ਹੁੰਦਾ ਜਾਂ ਅਸਫਲ ਹੋਵੇ ਤਾਂ ਦੋ ਫ਼ਰੀ ਥਰੋ ਦਿੱਤੇ ਜਾਣਗੇ ।
- ਜੇਕਰ ਗੋਲ (Goal) ਦੇ ਲਈ ਸ਼ੌਟ (Shot) ਅਸਫਲ ਹੁੰਦਾ ਹੈ, ਤਾਂ ਤਿੰਨ ਫ਼ਰੀ ਥਰੋ (Free Throws) ਦਿੱਤੇ ਜਾਣਗੇ ।
ਜਾਣ ਬੁੱਝ ਕੇ ਫਾਊਲ ਕਰਨਾ (Intentional foul) – ਇਹ ਉਹ ਸਰੀਰਕ ਫਾਉਲ ਹੈ, ਜਿਹੜਾ ਕਿਸੇ ਖਿਡਾਰੀ ਵਲੋਂ ਜਾਣ ਬੁੱਝ ਕੇ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਜਿਹੜਾ ਖਿਡਾਰੀ ਘੜੀ-ਮੁੜੀ ਅਜਿਹਾ ਫਾਊਲ ਕਰਦਾ ਹੈ ਉਸ ਨੂੰ ਅਯੋਗ ਘੋਸ਼ਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਖੇਡ ਵਿਚੋਂ ਬਾਹਰ ਕੱਢ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
ਸਜ਼ਾ (Penalty) – ਅਪਰਾਧੀ ਉੱਤੇ ਸਰੀਰਕ ਫਾਊਲ ਦਾ ਦੋਸ਼ ਲਗਾਇਆ ਜਾਵੇਗਾ ਤੇ ਦੋ ਫ਼ਰੀ ਥਰੋਆਂ ਦਿੱਤੀਆਂ ਜਾਣਗੀਆਂ ਜੇ ਇਹ ਫਾਊਲ ਅਜਿਹੇ ਖਿਡਾਰੀ ਦੁਆਰਾ ਹੁੰਦਾ ਹੈ, ਜਿਹੜਾ ਗੋਲ ਕਰਦਾ ਹੈ ਤਾਂ ਇਹ ਗੋਲ ਮੰਨਿਆ ਜਾਵੇਗਾ ਅਤੇ ਇਕ ਵਾਧੂ ਫ਼ਰੀ ਥਰੋ ਦਿੱਤੀ ਜਾਵੇਗੀ ।
ਡਬਲ ਫਾਉਲ (Double foul) – ਡਬਲ ਫਾਉਲ ਉਸ ਸਥਿਤੀ ਵਿਚ ਹੁੰਦਾ ਹੈ, ਜਦ ਦੋ ਖਿਡਾਰੀ ਖੇਡਦੇ-ਖੇਡਦੇ ਆਪਸ ਵਿਚ ਟਕਰਾ ਜਾਣ, ਜਿਸ ਵਿਚ ਦੋਸ਼ ਦੋਹਾਂ ਦਾ ਹੋਵੇ, ਉਸ ਸਮੇਂ ਡਬਲ ਫਾਉਲ ਗਿਣਿਆ ਜਾਂਦਾ ਹੈ । ਇਹ ਫਾਉਲ ਦੋਹਾਂ ਖਿਡਾਰੀਆਂ ਦੇ ਨਾਂ ਦਰਜ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਡਬਲ ਫਾਊਲ ਹੋਣ ਉੱਤੇ ਨਜ਼ਦੀਕੀ ਚੱਕਰ ਤੋਂ ਜੰਪ ਬਾਲ ਰਾਹੀਂ ਖੇਡ ਦੁਬਾਰਾ ਸ਼ੁਰੂ ਕਰਵਾ ਦਿੱਤੀ ਜਾਵੇਗੀ ।
ਬਹੁਪੱਖੀ ਫਾਊਲ (Multiple foul) – ਬਹੁਪੱਖੀ ਫਾਉਲ ਉਸ ਵੇਲੇ ਹੁੰਦਾ ਹੈ, ਜਦ ਇਕ ਟੀਮ ਦੇ ਦੋ ਜਾਂ ਤਿੰਨ ਖਿਡਾਰੀ ਇਕ ਹੀ ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਉੱਤੇ ਨਿੱਜੀ ਫਾਊਲ ਕਰ ਦਿੰਦੇ ਹਨ । ਇਸ ਸਥਿਤੀ ਵਿਚ ਹਰੇਕ ਅਪਰਾਧੀ ਖਿਡਾਰੀ ਉੱਤੇ ਇਕ ਫਾਉਲ ਲਗੇਗਾ ਅਤੇ ਜਿਸ ਖਿਡਾਰੀ ਪ੍ਰਤੀ ਅਪਰਾਧ ਹੋਇਆ ਹੈ, ਉਸ ਨੂੰ ਫ਼ਰੀ-ਥਰੋ ਦਿੱਤੀ ਜਾਵੇਗੀ । ਜੇ ਸੁੱਟਣ ਦੀ ਕਿਰਿਆ ਵਿਚ ਕਿਸੇ ਖਿਡਾਰੀ ਪ੍ਰਤੀ ਫਾਉਲ ਹੋਇਆ ਹੈ, ਤਾਂ ਗੋਲ ਹੋਣ ਉੱਤੇ ਗਿਣਿਆ ਜਾਵੇਗਾ ਅਤੇ ਇਕ ਫ਼ਰੀ ਥਰੋ ਦਿੱਤੀ ਜਾਵੇਗੀ ।
ਪੰਜ ਫਾਊਲ (Five foul) – ਜਦ ਕੋਈ ਖਿਡਾਰੀ ਪੰਜ ਫਾਊਲ (ਨਿੱਜੀ ਜਾਂ ਤਕਨੀਕੀ ਕਰਦਾ ਹੈ ਤਾਂ ਉਸ ਨੂੰ ਬਾਹਰ ਕੱਢ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
ਥਰੀ ਫ਼ਾਰ ਟੂ ਰੂਲ (Three for two rule) – ਜਦੋਂ ਖਿਡਾਰੀ ਗੋਲ ਕਰਨ ਲੱਗਾ ਹੋਵੇ ਅਤੇ ਉਸ ਉੱਪਰ ਵਿਰੋਧੀ ਟੀਮ ਦਾ ਖਿਡਾਰੀ ਫਾਉਲ ਕਰ ਦੇਵੇ, ਜੇ ਗੋਲ ਬਣ ਜਾਵੇ ਤਾਂ ਇਕ ਹੋਰ ਫ਼ਰੀ-ਥਰੋ ਮਿਲੇਗਾ | ਗੋਲ ਨਾ ਹੋਣ ਦੀ ਸੂਰਤ ਵਿਚ ਦੋਹਾਂ ਫ਼ਰੀ ਬਰੋਆਂ ਵਿਚੋਂ ਇਕ ਵੀ ਨਾ ਹੋਣ ‘ਤੇ ਵਾਧੂ ਫ਼ਰੀ ਥਰੋ ਮਿਲੇਗੀ ।
ਚੋਣ ਦਾ ਹੱਕ (Right of option) – ਕੇਂਦਰ (mid point) ਤੋਂ ਥਰੋ-ਇਨ ਦੇ ਲਈ ਚੋਣ ਦਾ ਹੱਕ ਇਕ, ਦੋ ਥਰੋ ਦੀ ਹਾਲਤ ਵਿਚ ਲਾਗੂ ਹੁੰਦਾ ਹੈ । ਚੋਣ ਕਰਨ ਤੋਂ ਪਹਿਲਾਂ ਕਪਤਾਨ ਨੂੰ ਕੋਚ ਦੇ ਨਾਲ ਸੰਖੇਪ ਮਸ਼ਵਰਾ ਕਰਨ ਦੀ ਆਗਿਆ ਹੁੰਦੀ ਹੈ
ਟੀਮ ਰਾਹੀਂ ਚਾਰ ਫਾਊਲ (Four fouls by team) – ਜਦ ਟੀਮ ਇਕ ਕੁਆਟਰ ਵਿਚ ਚਾਰ ਤੋਂ ਵੱਧ ਖਿਡਾਰੀਆਂ ਦਾ ਫਾਊਲ (ਨਿੱਜੀ ਅਤੇ ਤਕਨੀਕੀ) ਕਰ ਚੁੱਕਦੀ ਹੈ, ਤਾਂ ਉਸ ਦੇ ਮਗਰੋਂ ਹੋਣ ਵਾਲੇ ਹਰ ਫਾਊਲ ਤੇ ਦੋ ਫਰੀ ਥਰੋ ਮਿਲਣਗੀਆਂ ।
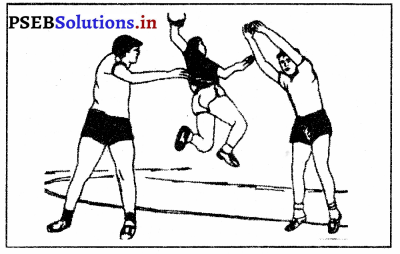
ਜੰਪ ਬਾਲ (Jump Ball) – ਜਦ ਖੇਡ ਸ਼ੁਰੂ ਹੁੰਦੀ ਹੈ ਜਾਂ ਮੱਧਅੰਤਰ (Interval) ਦੇ ਪਿੱਛੋਂ ਸ਼ੁਰੂ ਹੁੰਦੀ ਹੈ ਜਾਂ ਦੋਹਰਾ ਜਾਂ ਬਹੁਪੱਖੀ ਫਾਊਲ ਹੋ ਜਾਂਦਾ ਹੈ, ਤਦ ਖੇਡ ਜੰਪ ਬਾਲ ਤੋਂ ਸ਼ੁਰੂ ਹੁੰਦੀ ਹੈ । ਰੈਫ਼ਰੀ ਵਿਰੋਧੀ ਖਿਡਾਰੀਆਂ ਦੇ ਵਿਚਕਾਰ ਬਾਲ ਨੂੰ ਕੇਂਦਰੀ ਚੱਕਰ ਵਿਚੋਂ ਉੱਪਰ ਨੂੰ ਉਛਾਲਦਾ ਹੈ । ਦੋਵੇਂ ਹੀ ਖਿਡਾਰੀ ਉਛਲੇ ਹੋਏ ਬਾਲ ਨੂੰ ਜੰਪ ਕਰਕੇ ਫੜਨ ਦਾ ਯਤਨ ਕਰਦੇ ਹਨ । ਕਿਸੇ ਇਕ ਖਿਡਾਰੀ ਦੇ ਗੇਂਦ ਨੂੰ ਛੂਹ ਦੇਣ ਨਾਲ ਖੇਡ ਸ਼ੁਰੂ ਹੋ ਜਾਂਦੀ ਹੈ ।
ਜੰਪ ਬਾਲ ਕਰਦੇ ਸਮੇਂ ਫਾਊਲ (Fouls during Jump ball) – ਜੰਪ ਬਾਲ ਕਰਦੇ ਸਮੇਂ ਕਈ ਖਿਡਾਰੀ ਹੇਠ ਲਿਖੇ ਪ੍ਰਕਾਰ ਦੇ ਫਾਊਲ ਅਕਸਰ ਕਰ ਦਿੰਦੇ ਹਨ
- ਇਕ ਦੂਸਰੇ ‘ਤੇ ਜੰਪ ਕਰ ਜਾਣਾ ।
- ਲਾਈਨ ਨੂੰ ਛੂਹਣਾ (Touch) ।
- ਰੈਫ਼ਰੀ ਜਦ ਬਾਲ ਉੱਪਰ ਸੁੱਟਦਾ ਹੈ ਤਾਂ ਉੱਪਰ ਜਾਂਦੇ ਬਾਲ ਨੂੰ ਛੂਹ ਦੇਣਾ ਵੀ ਫਾਉਲ ਹੈ ।
- ਜੰਪ ਕਰਦੇ ਸਮੇਂ ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਨੂੰ ਕੂਹਣੀ ਮਾਰਨਾ ਜਾਂ ਧੱਕਾ ਦੇ ਦੇਣਾ ਤਾਂ ਜੋ ਜੰਪ ਨਾ ਕਰ ਸਕੇ ।
- ਜੰਪ ਕਰਦੇ ਸਮੇਂ ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਦੇ ਪੈਰ ‘ਤੇ ਪੈਰ ਰੱਖ ਕੇ ਉਸ ਨੂੰ ਜੰਪ ਕਰਨ ਤੋਂ ਰੋਕਣਾ ।
- ਜੰਪ ਕਰਦੇ ਸਮੇਂ ਅਰਧ ਵਿਆਸ ਦੀਆਂ ਲਾਈਨਾਂ ਨੂੰ ਛੂਹਣਾ ।
- ਜੰਪ ਬਾਲ ਕਰਦੇ ਸਮੇਂ ਖਿਡਾਰੀਆਂ ਦਾ ਇਕ ਥਾਂ ਤੋਂ ਦੂਜੇ ਥਾਂ ‘ਤੇ ਜਾਣਾ ।
![]()
ਪ੍ਰਸ਼ਨ 7.
ਬਾਸਕਟ ਬਾਲ ਦੇ ਮਹੱਤਵਪੂਰਨ ਪਾਸ ਲਿਖੋ ।
ਉੱਤਰ-
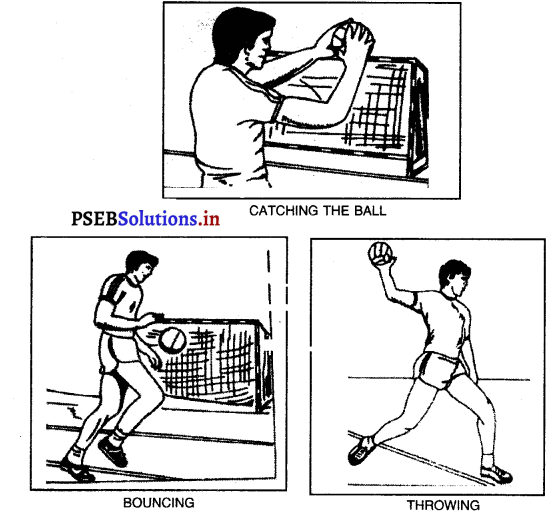
ਬਾਸਕਟ ਬਾਲ ਦੇ ਮਹੱਤਵਪੂਰਨ ਪਾਸ-
1. ਦੋਹਾਂ ਹੱਥਾਂ ਨਾਲ ਛਾਤੀ ਦੇ ਸਾਹਮਣੇ ਪਾਸ (Two Hands Chest Pass) – ਦੋਹਾਂ ਹੱਥਾਂ ਨਾਲ ਛਾਤੀ ਦੇ ਸਾਹਮਣੇ ਕਰਕੇ ਪਾਸ ਬਹੁਤ ਫੁਰਤੀ ਨਾਲ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਇਹ ਪਾਸ ਤਦ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ਜਦ ਸਾਹਮਣੇ ਖਿਡਾਰੀ ਦੇ ਕੋਲ ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਨਾ ਹੋਵੇ | ਬਾਲ ਦੋਨਾਂ ਹੱਥਾਂ ਨਾਲ ਫੜ ਕੇ ਮੋਢਿਆਂ ਤੇ ਬਾਹਾਂ ਉਠਾ ਕੇ ਥੋੜ੍ਹਾ ਜਿਹਾ ਸਰੀਰ ਨੂੰ ਝੁਕਾ ਕੇ ਆਪਣੇ ਇਕ ਪੈਰ ‘ਤੇ ਜ਼ੋਰ ਦੇ ਕੇ ਪੂਰੀ ਤਾਕਤ ਨਾਲ ਆਪਣੇ ਖਿਡਾਰੀ ਨੂੰ ਦਿੰਦੇ ਹਨ । ਖੇਡ ਵਿਚ ਇਹ ਵਿਧੀ ਆਮ ਪ੍ਰਚੱਲਿਤ ਹੈ ।
2. ਬਾਂਹ ਇਕ ਪਾਸੇ ਕਰਕੇ ਪਾਸ ਦੇਣਾ (Side Arm Pass) – ਬਾਂਹ ਲੰਬੀ ਕਰਕੇ ਜਾਂ ਹੱਥ ਨਾਲ ਉੱਚੀ ਕਰਕੇ ਆਪਣੀ ਹੀ ਟੀਮ ਦੇ ਖਿਡਾਰੀ ਨੂੰ ਪਾਸ ਦਿੰਦੇ ਹਨ । ਜਦ ਸਾਥੀ ਦੂਰ ਹੋਵੇ ਅਤੇ ਦੂਸਰਾ ਖਿਡਾਰੀ ਉਸ ਨੂੰ ਪਾਸ ਦੇਣਾ ਚਾਹੇ ਤਾਂ ਇਹ ਢੰਗ ਅਪਣਾਇਆ ਜਾਂਦਾ ਹੈ । ਇਹ ਪਾਸ ਉਸ ਵੇਲੇ ਦਿੱਤਾ ਜਾ ਸਕਦਾ ਹੈ, ਜਦ Dribble ਪ੍ਰਕਿਰਿਆ ਨਾਲ ਰਾਹ ਵਿਚ ਕੋਈ ਰੋਕ ਆ ਜਾਵੇ, ਤਾਂ ਇਕ ਖਿਡਾਰੀ ਆਪਣੇ ਦੁਸਰੇ ਖਿਡਾਰੀ ਨੂੰ ਬਾਂਹ ਲੰਬੀ ਕਰਕੇ ਪਾਸ ਦਿੰਦਾ ਹੈ । ਕਈ ਟੀਮਾਂ ਸੈਂਟਰ ਵਿਚੋਂ ਹੀ ਰਿੰਗ ਵਿਚ ਬਾਲ ਪਾਉਣ ਲਈ ਇਹ ਢੰਗ ਵਰਤਣ ਵਿਚ ਬਹੁਤ ਨਿਪੁੰਨ ਹੁੰਦੀਆਂ ਹਨ ।
3. ਸਿਰ ਦੇ ਉੱਪਰ ਤੋਂ ਪਾਸ (Over Head Pass) – ਇਹ ਪਾਸ ਬਾਂਹ ਉੱਪਰ ਚੁੱਕ ਕੇ ਦੁਸਰੇ ਸਾਥੀਆਂ ਨੂੰ ਦਿੰਦੇ ਹਨ । ਇਹ ਪਾਸ ਉਸ ਸਮੇਂ ਠੀਕ ਸਮਝਿਆ ਜਾਂਦਾ ਹੈ, ਜਦ ਖਿਡਾਰੀ ਬਹੁਤ ਸਾਰੇ ਵਿਰੋਧੀ ਖਿਡਾਰੀਆਂ ਦੇ ਘੇਰੇ ਵਿਚ ਹੋਵੇ ਅਤੇ ਉਹ ਇਹ ਪਾਸ ਬਾਂਹ ਉੱਪਰ ਉਠਾ ਕੇ ਸਭ ਸਿਰਾਂ ਦੇ ਉੱਪਰ ਤੋਂ ਬਾਲ ਖ਼ਾਸ ਕਰਕੇ ਪਾਸ ਦੇਵੇ । ਇਸ ਨਾਲ ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਨੂੰ ਬਾਲ ਰੋਕਣ ਲਈ ਬਹੁਤ ਯਤਨ ਕਰਨਾ ਪੈਂਦਾ ਹੈ ।
4. ਧਰਤੀ ਦਾ ਪਾਸ (Ground Pass) – ਇਹ ਪਾਸ ਉਸ ਸਮੇਂ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ, ਜਿਸ ਸਮੇਂ ਸਾਹਮਣੇ ਦਾ ਖਿਡਾਰੀ ਲੰਬਾ ਹੋਵੇ ਅਤੇ ਬਾਲ ਉਸ ਦੇ ਸਿਰ ਤੋਂ ਕਾਸ ਨਾ ਕੀਤਾ ਜਾ ਸਕੇ । ਉਸ ਸਮੇਂ ਬਾਲ ਨੂੰ ਧਰਤੀ ‘ਤੇ ਸੁੱਟ ਕੇ ਪਾਸ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
5. ਪਿੱਛੇ ਦਾ ਪਾਸ (Back Pass) – ਇਹ ਪਾਸ Back Side ਤੋਂ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਖਿਡਾਰੀ ਬਾਲ ਨੂੰ ਹੱਥ ‘ਤੇ ਉਛਾਲਦਾ ਹੋਇਆ ਜਾਂਦਾ ਹੈ ਅਤੇ ਸਾਹਮਣੇ ਜੇਕਰ ਕੋਈ ਰੁਕਾਵਟ ਹੋਵੇ, ਤਾਂ ਉਹ ਬਾਲ ਪਿੱਛੇ ਖੜ੍ਹੇ ਖਿਡਾਰੀ ਨੂੰ Back Pass ਦੇ ਦਿੰਦਾ ਹੈ ।