Class 12

Punjab State Board PSEB 12th Class Physics Book Solutions Chapter 13 Nuclei Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Physics Chapter 13 Nuclei

PSEB 12th Class Physics Guide Nuclei Textbook Questions and Answers

Question 1.
(a) Two stable isotopes of lithium ₃⁶Li and ₃⁷Li have respective
abundances of 7.5% and 92.5%. These isotopes have masses 6.01512 u and 7.01600 u, respectively. Find the atomic mass of lithium.
Boron has two stable isotopes, ₅¹⁰B and ₅¹¹B. Their respective masses are 10.01294 u and 11.00931 u, and the atomic mass of boron is 10.811 u. Find the abundances of ₅¹⁰B and ₅¹¹B.
Answer:
(a) Mass of ₃⁶Li lithium isotope, m₁ = 6.01512 u
Mass of ₃⁷Li lithium isotope, m₂ = 7.01600 u
Abundance of ₃⁶Li, n₁ = 7.5%
Abundance of ₃⁷Li, n₂ = 92.5%
The atomic mass of lithium atom is given as
m = \(\frac{m_{1} n_{1}+m_{2} n_{2}}{n_{1}+n_{2}}\)
= \(\frac{6.01512 \times 7.5+7.01600 \times 92.5}{7.5+92.5}\) = 6.940934 u
Mass of boron isotope ₅¹⁰B, m₁=10.01294 u
Mass of boron isotope ₅¹¹B, m₂ = 11.00931 u
Abundance of ₅¹⁰B,n₁ = x%
Abundance of ₅¹¹B, n₂ = (100 – x)%

Atomic mass of boron, m = 10.811 u.
The atomic mass of boron atom is given as
m = \(\frac{m_{1} n_{1}+m_{2} n_{2}}{n_{1}+n_{2}}\)
10.811 = \(\frac{10.01294 \times x+11.00931 \times(100-x)}{x+100-x}\)
1081.11 = 10.01294 x + 1100.931 – 11.00931 x
∴ x = \(\frac{19.821}{0.99637}\) = 19.89%
And 100 – x = 100 -19.89 = 80.11%
Hence, the abundance of ₅¹⁰B is 19.89% and that of ₅¹¹B is 80.11%.

Question 2.
The three stable isotopes of neon: ₁₀²⁰Ne, ₁₀²¹Ne and ₁₀²²Ne have respective abundances of 90.51%, 0.27%, and 9.22%. The atomic masses of the three isotopes are 19.99 u, 20.99 u, and 21.99 u, respectively. Obtain the average atomic mass of neon.
Answer:
Atomic mass of ₁₀²⁰Ne,m₁ = 19.99%u
Abundance of ₁₀²⁰Ne,n₁ = 90.51%
Atomic mass of ₁₀²¹Ne, m₂ = 20.99u
Abundance of ₁₀²¹Ne,n₂ = 0.27%
Atomic mass of ₁₀²²Ne,m₃ = 21.99u
Abundance of ₁₀²²Ne,n₃ = 9.22%
m = \(\frac{m_{1} n_{1}+m_{2} n_{2}+m_{3} n_{3}}{n_{1}+n_{2}+n_{3}} \)
= \(\frac{19.99 \times 90.51+20.99 \times 0.27+21.99 \times 9.22}{90.51+0.27+9.22}\)
= 20.1771 u

Question 3.
Obtain the binding energy (in MeV) of a nitrogen nucleus (₇¹⁴ N), given m (₇¹⁴ N) = 14.00307 u.
Answer:
Atomic mass of (₇N¹⁴) nitrogen, m = 14.00307 u
A nucleus of ₇N¹⁴ nitrogen contains 7 protons and 7 neutrons.
Hence, the mass defect of this nucleus, Δ m = 7 m_H +7m_n -m
where, Mass of a proton, m_H = 1.007825 u (∵ m_p = m_H)
Mass of a neutron, m_n = 1.008665 u
∴ Δm = 7 x 1.007825 + 7 x 1.008665 -14.00307
= 7.054775 + 7.06055 -14.00307
= 0.112255 u
But 1 u = 931.5 MeV/c²

Δm = 0.112255 x 931.5 MeV/c²
Hence, the binding energy of the nucleus is given as
E_b = Δ mc² .
where, c = speed of light
∴ E_b = 0.112255 x 93.15 \(\left(\frac{\mathrm{MeV}}{\mathrm{c}^{2}}\right)\) x c²
= 104.565532 MeV
Hence, the binding energy of a nitrogen nucleus is 104.565532 MeV.

Question 4.
Obtain the binding energy of the nuclei _56²⁶Fe and _83²⁰⁹Bi in units of MeV from the following data : m (_56²⁶Fe) = 55.934939 u, m (_83²⁰⁹Bi) = 208.980388 u
Answer:
Atomic mass of _56²⁶Fe, m₁ = 55.934939 u
_56²⁶Fe nucleus has 26 protons and (56 -26) = 30 neutrons
Hence, the mass defect of the nucleus, Δ m = 26 x m_H +30 x m_n – m₁
where, mass of a proton, m_H = 1.007825 u
Mass of a neutron, m_n = 1.008665 u
∴Δm = 26 x 1.007825 + 30 x 1.008665 – 55.934939
= 26.20345 + 30.25995 – 55.934939
= 0.528461 u
But 1u = 931.5 MeV/c²
∴ Δm = 0.528461×931.5 MeV/c²

The binding energy of this nucleus is given as
E_b1 = Δmc²
Where, c = speed of light
∴ E_b1 = 0.528461 x 931.5 \(\left(\frac{\mathrm{MeV}}{\mathrm{c}^{2}}\right)\) x c²
= 492.26 MeV
Average binding energy per nucleon = \(\frac{492.26}{56}\) = 8.79 MeV

Atomic mass of _83²⁰⁹Bi, m₂ = 208.980388 u
_83²⁰⁹Bi nucleus has 83 protons and (209 -83) 126 neutrons.
Hence, the mass defect of this nucleus is given as
Δm’ = 83 x m_H +126 x m_n -m₂
where, mass of a proton, m_H = 1.007825 u
Mass of a neutron, m_n = 1.008665 u
∴Δm’ = 83 x 1.007825 +126 x 1.008665 – 208.980388
= 83.649475 + 127.091790 – 208.980388
= 1.760877 u

But 1u = 931.5 MeV/c²
∴Δm’=1.760877×931.5 MeV/c²
Hence, the binding energy of this nucleus is given as
Eb₂ =Δ m’c²
∴ Eb₂ =1.760877 x 931.5 \(\left(\frac{\mathrm{MeV}}{\mathrm{c}^{2}}\right)\) x c²
= 1640.26 MeV
Average binding energy per nucleon = \(\frac{1640.26}{209}\) =7.848 MeV.

Question 5.
A given coin has a mass of 3.0 g. Calculate the nuclear energy that would be required to separate all the neutrons and protons from each other. For simplicity assume that the coin is entirely made of _29⁶³Cu atoms (of mass 62.92960 u).
Answer:
Mass of the copper coin, m’ = 3 g
Atomic mass of 29 Cu⁶³ atom, m = 62.92960 u
The total number of 29Cu⁶³ atoms in the coin, N = \(\frac{N_{A} \times m^{\prime}}{\text { Mass number }}\)
where, NA = Avogadro’s number = 6.023 x 1023 atoms/g
Mass number =63 g
∴N = \(\frac{6.023 \times 10^{23} \times 3}{63}\) = 2.868 x 10²² atoms

29Cu⁶³ nucleus has 29 protons and (63 -29)34 neutrons
∴ Mass defect of this nucleus, Δ m’ = 29 x m_H +34 x m_n -m
where, mass of a proton, m_H = 1.007825 u
Mass of a neutron, m_n = 1.008665 u
∴Δ m’ = 29 x 1.007825 + 34 x 1.008665 – 62.92960
= 29.226925 + 34.29461 – 62.92960 = 0.591935 u

Mass defect of all the atoms present in the coin,
Δm = 0.591935 x 2.868 x 10²²
= 1.69766958 x 10²² u
But 1 u = 931.5MeV/c²
∴ Δm =1.69766958 x 10²² x 931.5MeV/c²

Hence, the binding energy of the nuclei of the coin is given as
E_b = Δmc²
E_b = 1.69766958 x 10²² x 93.15 \(\left(\frac{\mathrm{MeV}}{\mathrm{c}^{2}}\right)\) x c²
= 1.581 x 10²⁵ MeV
But 1 MeV =1.6 x 10^-13 J
E_b= 1.581 x 10²⁵ x 1.6x 10^-13
= 2.53026 x 10¹² J
This much energy is required to separate all the neutrons and protons from the given coin.

Question 6.
Write nuclear reaction equations for
(i) α-decay of _88²²⁶Ra
(ii) α-decay of \(\frac{242}{94}\) Pu
(iii) β^– – decay of _15³²P
(iv) β^– -decay of _83²¹⁰Bi
(y) β⁺ -decay of _6¹¹C
(vi) β⁺ -decay of _43⁹⁷ Tc
(vii) Electron capture of _54¹²⁰ Xe
Answer:

Question 7.
A radioactive isotope has a half-life of T years. How long will it take the activity to reduce to (a) 3.125% (b) 1% of its original value?
Answer:
Half-life of the radioactive isotope = T years
Original amount of the radioactive isotope = N₀
(a) After decay, the amount of the radioactive isotope = N
It is given that only 3.125% of N₀ remains after decay. Hence, we can write
\(\frac{N}{N_{0}}\) = 3.125% = \(\frac{3.125}{100}=\frac{1}{32}\)
But \(\frac{N}{N_{0}}=e^{-\lambda t}\)
where, λ = Decay constant t = Time

Hence, the isotope will take about 5T years to reduce to 3.125% of its original value.

(b) After decay, the amount of the radioactive isotope = N
It is given that only 1% of N₀ remains after decay. Hence, we can write

Hence, the isotope will take about 6.645 T years to reduce to 1% of its original value.

Question 8.
The normal activity of living carbon-containing matter is found to be about 15 decays per minute for every gram of carbon. This activity arises from the small proportion of radioactive _6¹⁴C present with the stable carbon isotope _6¹⁴C. When the organism is dead, its interaction with the atmosphere (which maintains the above equilibrium activity) ceases and its activity begins to drop. From the known half-life (5730 years) of _6¹²C, and the measured activity, the age of the specimen can be approximately estimated. This is the principle of dating _6¹²C used in archaeology. Suppose a specimen from Mohenjodaro gives an activity of 9 decays per minute per gram of carbon. Estimate the approximate age of the Indus-Valley civilization.
Answer:
Decay rate of living carbon-containing matter, R = 15 decays/min
Let N be the number of radioactive atoms present in a normal carbon-containing matter.
Half-life of _6¹²C, T_1/2 = 5730 years
The decay rate of the specimen obtained from the Mohenjodaro site
R’ = 9 decays/min
Let N be the number of radioactive atoms present in the specimen during the Mohenjodaro period.
Therefore, we can relate the decay constant, λ and time, t as

Hence, the approximate age of the Indus-Valley civilization is 4223.5 years.

Question 9.
Obtain the amount of _27⁶⁰Co necessary to provide a radioactive source of 8.0 mCi strength.
The half-life of _27⁶⁰Co is 5.3 years.
Answer:
The strength of the radioactive source is given as
\(\frac{d N}{d t}\) = 8.0 mCi
= 8 x 10^-3 x 3.7 x 10¹⁰
= 29.6 x 10⁷ decay/s
where, N = Required number of atoms
Half-life of _27⁶⁰Co, T_1/2 = 5.3 years
= 5.3 x 365 x 24 x 60 x 60
= 1.67 x 10⁸ s
For decay constant λ, we have the rate of decay as \(\frac{d N}{d t}\) =λN
Where λ = \(\frac{0.693}{T_{1 / 2}}=\frac{0.693}{1.67 \times 10^{8}} \mathrm{~s}^{-1}\)
∴ N = \(\frac{1}{\lambda} \frac{d N}{d t} \)
= \(\frac{\frac{29.6 \times 10^{7}}{0.693}}{1.67 \times 10^{8}}\) = 7.133 x 10¹⁶ atoms
For ₂₇Co⁶⁰
Mass of 6.023 x 10²³ (Avogadro’s number) atoms = 60 g
∴ Mass of 7.133 x 10¹⁶ atoms = \(\frac{60 \times 7.133 \times 10^{16}}{6.023 \times 10^{23}}\) = 7.106 x 10^-6g
Hence, the amount of ₂₇Co⁶⁰ necessary for the purpose is 7.106 x 10^-6g.

Question 10.
The half-life of _38⁹⁰Sr is 28 years. What is the disintegration rate of 15 mg of this isotope?
Answer;
Half-life of _38⁹⁰Sr, t_1/2 = 28 years
= 28 x 365 x 24 x 60 x 60
= 8.83 x 10⁸s
Mass of the isotope, m = 15 mg
90 g of _38⁹⁰Sr atom contains 6.023 x 10²³ (Avogadro’s number) atoms.
Therefore 15 mg of _38⁹⁰ Sr contains \(\frac{6.023 \times 10^{23} \times 15 \times 10^{-3}}{90}\)
i. e.,1.0038 x 10²⁰ number of atoms
Rate of disintegration, = \(\frac{d N}{d t}=\lambda N\)
where, λ = Decay constant = \(\frac{0.693}{8.83 \times 10^{8}} \mathrm{~s}^{-1}\)
∴ \(\frac{d N}{d t}=\frac{0.693 \times 1.0038 \times 10^{20}}{8.83 \times 10^{8}}\)
= 7.878 x 10¹⁰ atoms/s
Hence, the disintegration rate of 15 mg of the given isotope is 7.878 x 10¹⁰ atoms/s.

Question 11.
Obtain approximately the ratio of the nuclear radii of the gold isotope _79¹⁹⁷Au and the silver isotope _47¹⁰⁷Ag.
Answer:
Nuclear radius of the gold isotope _79¹⁹⁷Au = R_Au
Nuclear radius of the silver isotope _47¹⁰⁷Ag =R_Ag
Mass number of gold, A_AU = 197
Mass number of silver, A_Ag =107
The ratio of the radii of the two nuclei is related with their mass numbers as
\(\frac{R_{\mathrm{Au}}}{R_{\mathrm{Ag}}}=\left(\frac{A_{\mathrm{Au}}}{A_{\mathrm{Ag}}}\right)^{1 / 3}\)
= \(=\left(\frac{197}{107}\right)^{1 / 3}\) = 1.2256
Hence, the ratio of the nuclear radii’of the gold and silver isotopes is about 1.23.

Question 12.
Find the Q- value and the kinetic energy of the emitted α-particle in the a-decay of
(a) _88²²⁶ Ra and (b) _86²²⁰ Rn.
Given m (_88²²⁶Ra) = 226.02540u, m (_86²²²Rn) = 222.01750u,
m(_86²²⁶Rn) = 220.01137 u, (_84²¹⁶Po) = 216.00189 u.
Answer:
(a) Alpha particle decay of _88²²⁶Ra emits a helium nucleus. As a result, its
mass number reduces to (226 – 4) 222 and its atomic number reduces to (88 – 2) 86.
This is shown in the following nuclear reaction
_88²²⁶Ra → _86²²²Rn+ _2⁴He

Q-value of emitted α-particle
= (Sum of initial mass – Sum of final mass) c²
where c = speed of light It is given that
m (_88²²⁶Ra) =226.02540 u
m (_86²²²Rn) = 222.01750 u
m (_2⁴He) = 4.002603 u
Q-value =[226.02540 – (222.01750 + 4.002603)] u c²
= 0.005297 u c²
But 1 u = 931.5 MeV/c²
∴ Q = 0.005297 x 931.5 ≈ 4.94 MeV
I Mass number after decay
Kinetic energy of the α -particle = \(\left(\frac{\text { Mass number after decay }}{\text { Mass number before decay }}\right)\) x Q
=\(\frac{222}{226}\) x 4.94=4.85MeV ,

(b) Alpha particle decay of (_86²²²Rn)
_86²²²Rn + _84²¹⁶Po + _2⁴He
It is given that
Mass of (_86²²⁰Rn) = 220.01137 u
Mass of (_84²¹⁶P0) = 216.00189 u
∴ Q-value =[220.01137 – (216.00189 + 4.002603)] x 931.5 ≈ 641 MeV
Kinetic energy of the α -particle = \(\left(\frac{220-4}{220}\right)\) x 6.41 = 6.29 MeV

Question 13.
The radionuclide ¹¹C decays according to _6¹¹C → _5¹¹B + e⁺ + v: T_1/2 = 20.3 min
The maximum energy of the emitted positron is 0.960 MeV. Given the mass values.
m (_6¹¹C) = 11.011434 u and (_5¹¹B) = 11.009305 u,
calculate Q and compare it with the maximum energy of the positron emitted.
Answer:
Mass difference Δm = m_N(_6¹¹C) – {m_N(_5¹¹B) + m_e}
where, m_N denotes that masses of atomic nuclei.
If we take the masses of atoms, then we have to add 6m_e for ¹¹C and 5m_e
for ¹¹B, then Mass difference
= m(_6¹¹C -6m_e) -{m(_5¹¹B – 5m_e + m_e)}
= {m(¹¹C)-m(_6¹¹B)-2m_e}
= 11.011434 -11.009305 – 2 x 0.000548
= 0.001033 u
Q = 0.001033 x 931.5 MeV
= 0.962 MeV
This energy is nearly the same as energy carried by positron (0.960 MeV). The reason is that the daughter nucleus is too heavy as compared to e⁺ and v, so it carries negligible kinetic energy. Total kinetic energy is shared by positron and neutrino; here energy carried by neutrino (E_v) is minimum so that energy carried by positron (E_e) is maximum (practically, E_e ≈ Q).

Question 14.
The nucleus _10²³Ne decays by β^– emission. Write down the β decay equation and determine the maximum kinetic energy of the electrons emitted. Given that: m (_10²³Ne) = 22.994466 u m (_11²³Na) = 22.089770 u
Answer:
In β^– emission, the number of protons increases by 1, and one electron and an antineutrino are emitted from the parent nucleus. β^– emission of the nucleus _10²³Ne
_10²³Ne → _11²³Na +e^–+\(\bar{v}\) +Q
It is given that
Atomic mass m of (_10²³Ne) = 22.994466 u
Atomic mass m of (_11²³ Na) = 22.089770 u
Mass of an electron, m_e = 0.000548 u
Q-value of the given reaction is given as
Q = [m(_10²³Ne)-{m(_11²³Na) + m_e}]c²
There are 10 electrons in _10²³Ne and 11 electrons in _11²³Na.
Hence, the mass of the electron is cancelled in the Q-value equation.
∴ Q = [22.994466 -22.089770] c²
= 0.004696 uc²
But 1 u = 981.5 MeV/c²
∴ Q = 0.004696 uc² x 931.5 = 4.374 MeV
The daughter nucleus is too fifeavy as compared to e^– and \(\bar{v}\).
Hence, it carries negligible energy. The kinetic energy of the antineutrino is nearly zero.
Hence, the maximum kinetic energy of the emitted electrons is almost equal to the Q-value, i. e., 4.374 MeV.

Question 15.
The Q value of a nuclear reaction A + b → C + d is defined by Q = [m_A + m_b -m_c -m_d]c²
where the masses refer to the respective nuclei. Determine from the given data the Q-value of the following reactions and state whether the reactions are exothermic or endothermic.
(i) _1¹H + _1³H → _1²H + _1²H
(ii) _6¹² C + _6¹² C → _10²⁰Ne + ₂He
Atomic masses are given to be
m (₁₂H) = 2.014102 u
m(_1³H) = 3.016049 u
m(_6¹²C) = 12.000000 u
m(_10²⁰Ne) = 19.992439 u
Answer:
(i) The given nuclear reaction is
_1¹H + _1³H → _1²H + _1²H
It is given that
Atomic mass m of (_1¹H) = 1.007825 u
Atomic mass m of (_1³H) = 3.016049 u
Atomic mass m of (_1²H) = 2.014102 u

According to the question, the Q-value of the reaction can be written as
Q = [m (_1¹H) + m (_1³H) -2m (_1²H)] c²
= [1.007825 + 3.016049 – 2 x 2.014102] c²
Q = (-0.00433 c²)u
But 1 u = 931.5MeV/c²
∴ Q = -0.00433 x 931.5 = -4.0334 MeV
The negative Q-value of the reaction shows that the reaction is endothermic.

(ii) The given nuclear reaction is
_12⁶C + _12⁶C → _10²⁰Ne + _2⁴He
It is given that
Atomic mass m of (_12⁶C) = 12.0 u
Atomic mass m of (_10²⁰Ne) = 19.992439 u
Atomic mass m of (_2⁴He) = 4.002603 u
The Q-value of this reaction is given as
Q = [2m (_12⁶C) – m (_10²⁰Ne) – m (_2⁴He)] c²
= [2 x 12.0 -19.992439 – 4.002603] c²
= (0.004958 c²) u
But 1 u = 931.5 MeV/c²
Q = 0.004958 x 931.5 = 4.618377 MeV
The positive Q-value of the reaction shows that the reaction is exothermic.

Question 16.
Suppose, we think of fission of a _26⁵⁶Fe nucleus into two equal fragments, _13²⁸Al. Is the fission energetically possible? Argue by working out Q of the process. Given m (_26⁵⁶Fe) = 55.93494 u and m(_13²⁸Al) = 27.98191 u.
Answer:
The fission of _26⁵⁶Fe can be given as
_26⁵⁶ Fe →2 _13²⁸Al
It is given that
Atomic mass m of (_26⁵⁶Fe) = 55.93494 u
Atomic mass m of (_13²⁸Al) = 27.98191 u
The Q-value of this nuclear reaction is given as
Q = [m (_26⁵⁶Fe) -2m (_13²⁸Al)] c²
= [55.93494 – 2 x 27.98191] c²
= (-0.02888 c²) u
Butl u = 931.5 MeV/c2
∴ Q =-0.02888 x 931.5 =-26.902 MeV
The Q-value of the fission is negative. Therefore, the fission is not possible energetically. For an energetically-possible fission reaction, the Q-value must be positive.

Question 17.
The fission properties of _94²³⁹Pu are very similar to those of _94²³⁹U. The average energy released per fission is 180 MeV. How much energy, in MeV, is released if all the atoms in 1 kg of pure _94²³⁹Pu undergo fission?
Answer:
Average energy released per fission of _94²³⁹Pu, E_av = 180 MeV
Amount of pure 94Pu²³⁹, m = 1 kg = 1000 g
N_A = Avogadro number = 6.023 x 10²³
Mass number of _94²³⁹Pu = 239 g

1 mole of ₉₄Pu²³⁹ contains N_A atoms
∴ 1 kg of 94Pu²³⁹ contains \(\left(\frac{N_{A}}{\text { Mass number }} \times m\right)\) atoms
= \(\frac{6.023 \times 10^{23}}{239} \times 1000\) = 2.52 x 10²⁴ atoms
∴ Total energy released during the fission of 1 kg of _94²³⁹ Pu is calculated as
E = E_av x 2.52 x10²⁴
= 180 x 2.52 x 10²⁴
= 4.536 x 10²⁶ MeV
Hence, 4.536 x10²⁶ MeV is released if all the atoms in 1 kg of pure ₉₄Pu²³⁹ undergo fission.

Question 18.
A 1000 MW fission reactor consumes half of its fuel in 5.00 y. How much _92²³⁵U did it contain initially? Assume that the reactor operates 80% of the time, that all the energy generated arises from the fission of _92²³⁵U, and that this nuclide is consumed only by the fission process.
Answer:
Half-life of the fuel of the fission reactor, t_1/2 =5 years.
= 5 x 365 x 24 x 60 x 60 s
We know that in the fission of 1 g of _92²³⁵ U nucleus, the energy released is equal to 200 MeV.
1 mole, i. e., 235 g of _92²³⁵ U contains 6.023 x 10²³ atoms.
∴ 1 g of _92²³⁵ U= \(\frac{6.023 \times 10^{23}}{235} \) atoms

The total energy generated per gram of _92²³⁵U is calculated as
E= \(\frac{6.023 \times 10^{23}}{235} \times 200 \mathrm{MeV} / \mathrm{g}\)
= \(\frac{200 \times 6.023 \times 10^{23} \times 1.6 \times 10^{-19} \times 10^{6}}{235}\)
= 8.20 x 10¹⁰ J/g
The reactor operates only 80% of the time.

Hence, the amount of _92²³⁵ U consumed in 5 years by the 1000 MW fission
reactor is calculated as
= \(\frac{5 \times 80 \times 60 \times 60 \times 365 \times 24 \times 1000 \times 10^{6}}{100 \times 8.20 \times 10^{10}} \mathrm{~g}\)
≈1538 kg
∴ Initial amount of _92²³⁵U = 2 x 1538 = 3076 kg.

Question 19.
How long can an electric lamp of 100 W be kept glowing by fusion of 2.0 kg of deuterium? Take the fusion reaction as The given fusion reaction is _1²H + _1²H → _2³He+n +3.27 MeV
Answer:
The given fusion reaction is
_1²H + _1²H → _2³He+n +3.27 MeV
Amount of deuterium, m = 2 kg
1 mole, i.e., 2 g of deuterium contains 6.023 x 10²³ atoms.
∴ 2.0 kg of deuterium contains = \(\frac{6.023 \times 10^{23}}{2} \times 2000\)
= 6.023 x 10 ²⁶ atoms

It can be inferred from the given reaction that ‘when two atoms of deuterium fuse, 3.27 MeV energy is released. ” ‘
∴ Total energy per nucleus released in the fusion reaction
E = \(\frac{3.27}{2} \times 6,023 \times 10^{26} \mathrm{MeV}\)
= \(\frac{3.27}{2} \times 6.023 \times 10^{26} \times 1.6 \times 10^{-19} \times 10^{6}\)
= 1.576 x 10¹⁴ J
Power of the electric lamp, P = 100 W = 100 J/s
Hence, the energy consumed by the lamp per second = 100 J
The total time for which the electric lamp will glow is calculated as \(\frac{1.576 \times 10^{14}}{100 \times 60 \times 60 \times 24 \times 365}\)
≈ 4.9 x 10⁴ years

Question 20.
Calculate the height of the potential harrier for a head-on collision of two deuterons. (Hint: The height of the potential barrier is given by the Coulomb repulsion between the two deuterons when they just touch each other. Assume that they can be taken as hard spheres of radius 2.0 fm).
Answer:
When two deuterons collide head-on, the distance between their centres, d is given as Radius of 1st deuteron + Radius of 2 nd deuteron
Radius of a deuteron nucleus = 2 fm =2 x 10^-15 m
∴ d = 2x 10^-15 +2 x 10^-15
=4 x 10^-15 m
Charge on a deuteron nucleus = Charge on an electron = e =1.6 x 10^-19C
Potential energy of the two-deuteron system
V = \(\frac{e^{2}}{4 \pi \varepsilon_{0} d} \)
where, \(\varepsilon_{0}\) = permittivity of free space


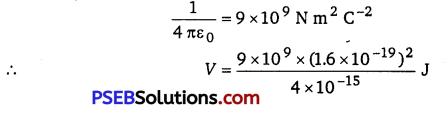
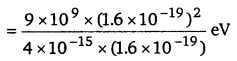
= 360 keV
Hence, the height of the potential barrier of the two-deuteron system is 360 keV.

Question 21.
From the relation R = R₀A^1/3, where R₀ is a constant and A is the mass number of a nucleus, show that the nuclear matter density is nearly constant (i. e., independent of A).
Answer:
We have the expression for nuclear radius as
R=R₀A^1/3
where, R0 = Constant.
Nuclear matter density, ρ = \(\frac{\text { Mass of the nucleus }}{\text { Volume of the nucleus }}\)
Let m be the average mass of the nucleus.
Hence, mass of the nucleus = mA

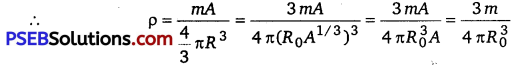
Hence, the nuclear matter density is independent; of A. It is nearly constant.

Question 22.
For the β⁺ (positron) emission from a nucleus, there is another competing process known as electron capture (electron from an inner orbit, say, the K-shell, is captured by the nucleus, and a neutrino is emitted.)
e⁺ + _A^Z X → _z-1^AY+ u
Show that if β⁺ emission is energetically allowed, electron capture is necessarily allowed but not vice-Versa.
Answer:
Let the amount of energy released during the electron capture process be Q₁.
The nuclear reaction can be written as
e⁺ + _A^Z X → _z-1Y+ v+ Q₁ …………..(1)
Let the amount of energy released during the positron capture process be Q₂.
The nuclear reaction can be written as
e⁺ + _A^Z X → _z-1Y+e⁺+ v+ Q₂ ……………………..(2)
m_N (_z^AX) = Nuclear mass of _z^A X
m_N (_z-1^AY) = Nuclear mass of ^z-1AY
m(_ZAX) = Atomic mass of _Z^A X
m (_z-1^A Y) = Atomic mass of _z-1^AY
m_e = Mass of an electron
c = Speed of light
Q-value of the electron capture reaction is given as


It can be inferred that if Q₂ > 0, then Q₁ > 0; Also, if Q₁> 0, it does not necessarily mean that Q₂ > 0.
In other words, this means that if β⁺ emission is energetically allowed, then the electron capture process is necessarily allowed, but not vice-versa. This is because the Q-value must be positive for an energetically-allowed nuclear reaction.

Additional Exercises

Question 23.
In a periodic table the average atomic mass of magnesium is given as 24.312 u. The average value is based on their relative natural abundance on earth. The three isotopes and their masses are _12²⁴ Mg (23.98504 u), _12²⁵Mg (24.98584 u) and _12²⁶Mg (25.98259 u). The natural abundance of _12²⁴Mg is 78.99% by mass. Calculate the abundances of other two isotopes.
Answer:
Average atomic mass of magnesium, m = 24.312 u
Mass of magnesium _12²⁴Mg isotope, m₁ = 23.98504 u
Mass of magnesium _12²⁵Mg isotope, m₂ = 24.98584 u
Mass of magnesium _12²⁶ Mg isotope, m₃ = 25.98259 u
Abundance of _12²⁴Mg, n₁ = 78.99%
Abundance of _12²⁵Mg, n₂ = x%
Hence, abundance of _12²⁶ Mg, n₃ = 100 – x- 78.99% = (21.01 – x)%

We have the relation for the average atomic mass as
m = \(\frac{m_{1} n_{1}+m_{2} n_{2}+m_{3} n_{3}}{n_{1}+n_{2}+n_{3}}\)
243.12 = \(\frac{23.98504 \times 78.99+24.98584 \times x+25.98259 \times(21.01-x)}{100}\)
2431.2 = 1894.5783096 + 24.98584x + 545.8942159- 25.98259 x
0.99675x =9.2725255
∴ x ≈ 9.3%
and 21.01-x =11.71%
Hence, the abundance of _12²⁵Mg is 9.3% and that of _12²⁶ Mg is 11.71%.

Question 24.
The neutron separation energy is defined as the energy required to remove a neutron from the nucleus.
Obtain the neutron separation energies of the nuclei _20⁴¹Ca and _13²⁷Al from
the following data:
m(_20⁴⁰Ca) = 39-962591u
m (_20⁴¹ Ca) = 40.962278 u
m (_26¹³Al) = 25.986895 u
m (_27¹³Al) = 26.981541 u
Answer:
For _20⁴¹Ca : Separation energy = 8.363007 MeV
For _27¹³ A1: Separation energy = 13.059 MeV
(_on¹) is removed from a _20⁴¹Ca.

Thus, the corresponding nuclear reaction can be written as
_20⁴¹Ca → _20⁴⁰Ca + _0¹n
It is given that
m(_20⁴⁰Ca) = 39.962591 u
m(_20⁴¹Ca )= 40.962278 u
m(_on¹) = 1.008665 u
The mass defect of this reaction is given as
Δm = m(_20⁴⁰Ca) + (_0¹n )-m(_20⁴¹Ca)
= 39.962591 +1.008665 – 40.962278
= 0.008978 u

But 1 u = 931.5 MeV/c²
∴ Δm = 0.008978×931.5 MeV/c²
Hence, the energy required for neutron removal is calculated as
E = Δmc²
= 0.008978 x 931.5 = 8.363007 MeV
For _13²⁷ Al, the neutron removal reaction can be written as
_13²⁷Al → _13²⁶ Al + _0¹n
It is given that
m (_13²⁷Al) = 26.981541 u
m (_13²⁶ Al) = 25.986895 u
The mass defect of this reaction is given as
Δm = m (_13²⁶ Al) + m (_0¹n) – m (_13²⁷ Al)
= 25.986895 +1.008665 – 26.981541
= 0.014019 u

But 1 u = 931.5 MeV/c2
∴ Δm = 0.014019 x 931.5 MeV/c²
Hence, the energy required for neutron removal is calculated as
E = Δmc²
= 0.014019 x 931.5 = 13.059 MeV

Question 25.
A source contains two phosphorous radio nudides _15³²P (TM_1/2 =14.3d)
and _15³³P (T_1/2 =253d). Initially, 10% of the
decays come from _15³³P. How long one must wait until 90% do so?
Answer:
Let radionuclide be represented as P₁ (T_1/2 =14.3 days) and
P₂(T_1/2 = 25.3 days).
Initial decay is 90% from P₁ and 10% from P₂. With the passage of rime,
amount of P₁ will decrease faster than that of P₂.

As rate of disintegration ∝ N or mass M. Initial ratio of P₁ to P₂ is 9: 1. Let mass of P₁ be 9x and that of P₂ be x. Let after t days mass of P₁ become y and that of P₂ become 9y.
Using half-life formula, \(\frac{M}{M_{0}}=\left(\frac{1}{2}\right)^{n}\) , where n is number of half lives,
n = \(\frac{t}{T_{1}}\)
\( \frac{y}{9 x}=\left(\frac{1}{2}\right)^{n_{i}}\) ……………………. (1)
Where, n₁ = \(\frac{t}{T_{2}}\)
\(\frac{9 y}{x}=\left(\frac{1}{2}\right)^{n_{2}}\) …………………………… (2)
On dividing eq.(1) by eq(2), we get

log 1- log 81 = t\(\left(\frac{1}{T_{1}}-\frac{1}{T_{2}}\right)\) \((\log 1-\log 2)\)

Question 26.
Under certain circumstances, a nucleus can decay by emitting a particle more massive than an a-particle. Consider the following decay processes:
_88²²³Ra → _82²⁰⁹Pb+ _6¹⁴C
_88²²³Ra → _86²¹⁹Rn + _2⁴He
Calculate the Q-values for these decays and determine that both are energetically allowed.
Answer:
Take a _6¹⁴C emission nuclear reaction
_88²²³Ra → _82²⁰⁹Pb+ _6¹⁴C
We know that
Mass of _88²²³Ra, m₁ = 223.01850 u
Mass of _82²⁰⁹ Pb, m₂ = 208.98107 u
Mass of _6¹⁴C, m₃ = 14.00324 u
Hence, the Q-value of the reaction is given as
Q = (m₁-m₂-m₃‘)c²
= (223.01850 -208.98107-14.00324)c²
= (0.03419 c²)u
But 1u = 931.5 MeV/c²
∴ Q = 0.03419 x 931.5 = 31.848 MeV

Hence, the Q-value of the nuclear reaction is 31.848 MeV. Since the value is positive, the reaction is energetically allowed.
Now take a _2⁴He emission nuclear reaction
_88²²³Ra → _86²¹⁹Rn + _2⁴He
We know that
Mass of _88²²³Ra, m₁ = 223.01850
Mass of _86²¹⁹Rn, m₂ = 219.00948
Mass of _2⁴He, m₃ = 4.00260
Q-value of this nuclear reaction is given as
Q = (m₁-m₂-m₃)c²
= (223.01850 -219.00948-4.00260)c²
= (0.00642 c²)u
= 0.00642 x 931.5 = 5.98 MeV
Hence, the Q value of the second nuclear reaction is 5.98 MeV. Since the value is positive, the reaction is energetically allowed.

Question 27.
Consider the fission of _92²³⁸U by fast neutrons. In one fission event, no neutrons are emitted and the final end products, after the beta decay of the primary fragments, are _58¹⁴⁰Ce and _44⁹⁹Ru.
Calculate Q for this fission process. The relevant atomic and particle masses are .
m = ( _92²³⁸U) = 238.05079 u
m = ( _58¹⁴⁰Ce) = 139.90543 u
m = ( _44⁹⁹Ru) = 98.90594 u
Answer:
In the fission of _92²³⁸U, 10β^– particles decay from the parent nucleus. The nuclear reaction can be written as
_92²³⁸U +_0¹n → _58¹⁴⁰Ce+_44⁹⁹Ru+10_-1⁰e

It is given that
Mass of a nucleus, m₁(_92²³⁸U) = 238.05079 u
Mass of a nucleus, m₂(_58¹⁴⁰Ce) = 139.90543 u
Mass of a nucleus,m₃ (_44⁹⁹Ru) = 98.90543 u
Mass of a neutron,m₄ (_0¹n) = 1.008665 u
Q-value of the above equation,
Q = [m'(_92²³⁸U) + m(_0¹n) – m'(_58¹⁴⁰Ce) – m'(_44⁹⁹Ru) -10 m_e]c²
Where, m’ represents the corresponding atomic masses of the nuclei,
m'(_92²³⁸U) = m1 – 92 m_e
m’ (_58¹⁴⁰Ce) = m₂ – 58m_e
m’ (_44⁹⁹Ru) = m₂ – 44 m_e
m(_0¹n) = m₄

But 1u = 931.5 MeV/c²
∴ Q = 0.247995 x 931.5 = 231.007 MeV
Hence, the Q-value of the fission process is 231.007 MeV.

Question 28.
Consider the D-T reaction (deuterium-tritium fusion)
_1²H +H _1³ →_2⁴He + n
(a) Calculate the energy released in MeV in this reaction from the data
m (_1²H) = 2.014102 u
m(H _1³) = 3.016049 u

(b) Consider the radius of both deuterium and tritium to be approximately 2.0 fm. What is the kinetic energy needed to overcome the coulomb repulsion between the two nuclei? To what temperature must the gas be heated to initiate the reaction? (Hint: Kinetic energy required for one fusion event = average thermal kinetic energy available with the interacting particles =2(3kT/2);k = Boltzman’s constant, T = absolute temperature.)
Answer:
(a) Take the D-T nuclear reaction :
_1²H +H _1³ →_2⁴He + n
It is given that
Mass of _1²H, m₁ = 2.014102 u
Mass of H _1³, m₂ = 3.016049 u
Mass of _2⁴He, m₃ = 4.002603 u
Mass of _0¹n, m₄ = 1.008665 u
Q-value of the given D-T reaction is
Q = [m₁ + m₂ – m₃ – m₄]c²
= [2.014102 + 3.016049 – 4.002603 -1.008665]c²
= [0.018883 c²]u
But 1 u = 931.5 MeV/c²
∴ Q = 0.018883 x 931.5 = 17.59 MeV

(b) Radius of deuterium and tritium, r ≈ 2.0 fm = 2 x 10^-15 m
Distance between the two nuclei at the moment when they touch each other,
d = r + r = 4 x 10^-15 m
Charge on the deuterium nucleus = e
Charge on the tritium nucleus = e
Hence, the repulsive potential energy between the two nuclei is given as
V = \(\frac{e^{2}}{4 \pi \varepsilon_{0}(d)}\)
Where, \(\varepsilon_{0}\) = Permittivity of free space

Hence, 5.76 x 10^-14 J or 360 key of kinetic energy (KE) is needed to overcome the Coulomb repulsion between the two nuclei.
However, it is given that
K.E = 2 x \(\frac{3}{2}\) kt
where, k = Boltzmann constant = 1.38 x 10^-23 m² kg s^-2 K^-1
T = Temperature required for triggering the reaction
T = \(\frac{K E}{3 K}\)
= \(\frac{5.76 \times 10^{-14}}{3 \times 1.38 \times 10^{-23}}\)
= 1.39 x 10⁹ K
Hence, the gas must be heated to a temperature of1.39 x 10⁹ K to initiate the reaction.

Question 29.
Obtain the maximum kinetic energy of β-particles, and the radiation frequencies of y decays in the decay scheme shown in Fig. 13.6. You are given that

It can be observed from the given γ-decay diagram that γ₁ decays from 1.088 MeV
energy level to the O’MeV energy level.
Hence, the energy corresponding to γ₁-decay is given as
E₁ =1.088-0 =1.088 MeV
hv₁ = 1.088 x 1.6 x 10^-19 x 10⁶
where, h = Planck’s constant = 6.63 x 10^-34 Js
v₁ = frequency of radiation radiated by γ₁ -decay.
∴ v₁ = \(\frac{E_{1}}{h}\)
= \(\frac{1.088 \times 1.6 \times 10^{-19} \times 10^{6}}{6.63 \times 10^{-34}}\)
= 2.637 x 10²⁰ Hz
It can be observed from the given γ-decay diagram that γ₂ decays from 0.412 MeV energy level to the 0 MeV energy level.
Hence, the energy corresponding to γ₂-decay is given as :
E₂ =0.412-0 =0.412 MeV
hv₂ = 0.412 x 1.6 x 10^-19 x 10⁶ J
where, v₂ = frequency of radiation radiated by γ₂-decay

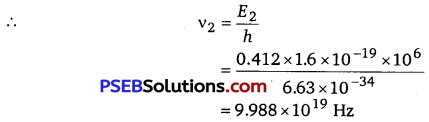
It can be observed from the given γ-decay diagram that γ₂ decays from the 1.088 MeV energy level to the 0.412 MeV energy level.
Hence, the energy corresponding to γ₃ -decay is given as
E₃ =1.088- 0.412 = 0.676 MeV
hv₃ = 0.676 x 1.6 x 10 ^-19 J

where, v₃ = frequency of radiation radiated by γ₃-decay
∴ v₃ = \(\frac{E_{3}}{h}=\frac{0.676 \times 1.6 \times 10^{-19} \times 10^{6}}{6.63 \times 10^{-34}}\)
= 1.639 x 10²⁰ Hz
Mass of m (_79¹⁹⁸ Au) = 197.968233 u
Mass of m (_80¹⁹⁸Hg) = 197.966760 u
1 u = 931.5 MeV/c²
Energy of the highest level is given as
E =[ (_79¹⁹⁸ Au) – m (_80¹⁹⁸Hg)]
= 197.968233 -197.966760
= 0.001473 u
= 0.001473 x 931.5 = 1.3720995 MeV
β₁ decays from the 1.3720995 MeV level to the 1.088 MeV level
Maximum kinetic energy of the β₁ particle = 1.3720995 – 1.088
= 0.2840995 MeV
β₂ decays from the 1.3720995.MeV level to the 0.412 MeV level ,
∴ Maximum kinetic energy of the β₂ particle = 1.3720995-0.412
= 0.9600995 MeV

Questions 30.
Calculate and compare the energy released by
(a) fusion of 1.0 kg of hydrogen deep within Sun and
(b) the fission of 1.0 kg of _92²³⁵U in a fission reactor.
Answer:
(a) Amount of hydrogen, m = 1 kg = 1000 g
1 mole, i. e, 1 g of hydrogen (_1¹H) contains 6.023 x 10²³ atoms.
∴ 1000 g of _1¹H contains 6.023 x 10²³ x 1000 atoms.
Within the sun, four _1¹H nuclei combine and form one _2⁴He nucleus. In this process 26 MeV of energy is released.
Hence, the energy released from the fusion of 1 kg _1¹H is
E₁ = \(\frac{6.023 \times 10^{23} \times 26 \times 10^{3}}{4}\)
= 39.1495 x 10²⁶MeV

(b) Amount of _92²³⁵U = 1 kg = 1000 g
1 mole, i. e., 235 g of _92²³⁵U contains 6.023 x 10²³ atoms.
∴1000 g of _92²³⁵U contains \(\frac{6.023 \times 10^{23} \times 1000}{235}\)atoms
It is known that the amount of energy released in the fission of one atom of _92²³⁵U is 200 MeV.
Hence, energy released from the fission of 1 kg of _92²³⁵U is
E₂ = \(\frac{6.023 \times 10^{23} \times 1000 \times 200}{235}\)
= 5.106 x 10²⁶ MeV
∴ \(\frac{E_{1}}{E_{2}}=\frac{39.1495 \times 10^{26}}{5.106 \times 10^{26}}\) = 7.67 ≈ 8
Therefore, the energy released in the fusion of 1 kg of hydrogen is nearly 8 times the energy released in the fission of 1 kg of uranium.

Question 31.
Suppose India had a target of producing by 2020 AD, 200,000 MW of electric power, ten percent of which was to be obtained from nuclear power plants. Suppose we are given that, on an average, the efficiency of utilization (i. e., conversion to electric energy) of thermal energy produced in a reactor was 25%. How much amount of fissionable uranium would our country need per year by 2020? Take the heat energy per fission of ²³⁵U to be about 200 MeV.
Answer:
Amount of electric power to be generated, P = 2 x10⁵ MW
10% of this amount has to be obtained from nuclear power plants.
P₁ = \(\frac{10}{100}\) x 2 x 10⁵
∴ Amount of nuclear power,
= 2 x 10⁴ MW
= 2x 104 x 10⁶ J/s
= 2 x 1010 x 60 x 60 x 24 x 365 J/y
Heat energy released per fission of a ²³⁵ U nucleus, E = 200 MeV
Efficiency of a reactor = 25%
Hence, the amount of energy converted into the electrical energy per fission is calculated as
\(\frac{25}{100} \times 200=50 \mathrm{MeV}=50 \times 1.6 \times 10^{-19} \times 10^{6}=8 \times 10^{-12} \mathrm{~J} \)
Number of atoms required for fission per year
\(\frac{2 \times 10^{10} \times 60 \times 60 \times 24 \times 365}{8 \times 10^{-12}}\) = 78840 x 10²⁴ atoms
1 mole, i. e., 235 g of U²³⁵ contains 6.023 x 10²³ atoms.
∴ Mass of 6.023 x 10²³ atoms of U²³⁵ = 235 g = 235 x 10^-3 kg
∴ Mass of 78840×10²⁴ atoms of U²³⁵ = \(\frac{235 \times 10^{-3}}{6.023 \times 10^{23}} \times 78840 \times 10^{24}\)
= 3.076 x10⁴ kg
Hence, the mass of uranium needed per year is 3.076 x 10⁴ kg.

Punjab State Board PSEB 12th Class Biology Book Solutions Chapter 12 Biotechnology and its Applications Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Biology Chapter 12 Biotechnology and its Applications

PSEB 12th Class Biology Guide Biotechnology and its Applications Textbook Questions and Answers

Question 1.
Crystals of Bt toxin produced by some bacteria do not kill the bacteria themselves because
(a) bacteria are resistant to the toxin,
(b) toxin is immature,
(c) toxin is inactive,
(d) bacteria encloses toxin in a special sac.
Answer:
Toxin is inactive: In bacteria, the toxin is present in an inactive form, called prototoxin, which gets converted into active form when it enters the body of an insect.

Question 2.
What are transgenic bacteria? Illustrate using any one example.
Answer:
Transgenic bacteria contain foreign gene that is intentionally introduced into its genome. They are manipulated to express the desirable gene for the production of various commercially important products.

An example of transgenic bacteria is E.coli. In the plasmid of E.coli, the two DNA sequences corresponding to A and B chain of human insulin are inserted, so as to produce the respective human insulin chains. Hence, after the insertion of insulin gene into the bacterium, it becomes transgenic and starts producing chains of human insulin. Later on, these chains are extracted from E.coli and combined to form human insulin.

Question 3.
Compare and contrast the advantages and disadvantages of production of genetically modified crops.
Answer:
The production of genetically modified (GM) or transgenic crops has several advantages.

• Most of the GM crops have been developed for pest resistance, which increases the crop productivity and therefore, reduces the reliance on chemical pesticides.
• Many varieties of GM food crops have been developed, which have enhanced nutritional quality. For example, golden rice is a transgenic variety of rice, which is rich in vitamin A.
• These plants prevent the loss of fertility of soil by increasing the ‘
  efficiency of mineral usage.
• They are highly tolerant to unfavourable abiotic conditions.
• The use of GM crops decreases the post harvesting loss of crops.

However, there are certain controversies regarding the use of genetically modified crops around the world. The use of these crops can affect the native biodiversity in an area. For example, the use of Bt toxin to decrease the amount of pesticide is posing a threat for beneficial insect pollinators such as honey bee. If the gene expressed for Bt toxin gets expressed in the pollen, then the honey bee might be affected. As a result, the process of pollination by honey bees would be affected. Also, genetically modified crops are affecting human health. They supply allergens and certain antibiotic resistance markers in the body. Also, they can cause genetic pollution in the wild relatives of the crop plants. Hence, it is affecting our natural environment.

Question 4.
What are Cry proteins? Name an organism that produce it. How has man exploited this protein to his benefit?
Answer:
Cry proteins are encoded by cry genes. These proteins are toxins, which are produced by Bacillus thuringiensis bacteria. This bacterium contains these proteins in their inactive form. When the inactive toxin protein is ingested by the insect, it gets activated by the alkaline pH of the gut. This results in the lysis of epithelial cell and eventually the death of the insect. Therefore, man has exploited this protein to develop certain transgenic crops with insect resistance such as Bt cotton, Bt corn, etc.

Question 5.
What is gene therapy? Illustrate using the example of adenosine deaminase (ADA) deficiency.
Answer:
Gene therapy is a technique for correcting a defective gene through gene manipulation. It involves the delivery of a normal gene into the individual to replace the defective gene, for example, the introduction of gene for adenosine deaminase (ADA) in ADA deficient individual. The adenosine deaminase enzyme is important for the normal functioning of the immune system. The individual suffering from this disorder can be cured by transplantation of bone marrow cells. The first step involves the extraction of lymphocyte from the patient’s bone marrow. Then, a functional gene for ADA is introduced into lymphocytes with the help of retrovirus. These treated lymphocytes containing ADA gene are then introduced into the patient’s bone . marrow. Thus, the gene gets activated producing functional T-lymphocytes and activating the patient’s immune system.

Question 6.
Diagrammatically represent the experimental steps in cloning and expressing an human gene (say the gene for growth hormone) into a bacterium like E. coli ?
Answer:
DNA cloning is a method of producing multiple identical copies of specific template DNA. It involves the use of a vector to carry the specific foreign DNA fragment into the host cell. The mechanism of cloning and transfer of gene for growth hormone into E.coli is represented below:

Question 7.
Can you suggest a method to remove oil (hydrocarbon) from seeds based on your understanding of rDNA technology and chemistry of oil?
Answer:
Recombinant DNA technology (rDNA) is a technique used for manipulating the genetic material of an organism to obtain the desired result. For example, this technology is used for removing oil from seeds. The constituents of oil are glycerol and fatty acids. Using rDNA, one can obtain oilless seeds by preventing the synthesis of either glycerol or fatty acids. This( is done by removing the specific gene responsible for the synthesis.

Question 8.
Find out from internet what is golden rice.
Answer:
Golden rice is a genetically modified variety of rice, Oryza sativa, which has been developed as a fortified food for areas where there is a shortage of dietary vitamin A. It contains a precursor of pro-vitamin A, called beta-carotene, which has been introduced into the rice through genetic engineering. The rice plant naturally produces beta-carotene pigment in its leaves. However, it is absent in the endosperm of the seed. This is because beta-carotene pigment helps in the process of photosynthesis while photosynthesis does not occur in endosperm.

Since beta-carotene is a precursor of pro-vitamin A, it is introduced into the rice variety to fulfil the shortage of dietary vitamin A. It is simple and a less expensive alternative to vitamin supplements. However, this variety of rice has faced a significant opposition from environment activists. Therefore, they are still not available in market for human consumption.

Question 9.
Does our blood have proteases and nucleases?
Answer:
No, human blood does not include the enzymes, nucleases and proteases. In human beings, blood serum contains different types of protease inhibitors, which protect the blood proteins from being broken down by the action of proteases. The enzyme, nucleases, catalyses the hydrolysis of nucleic acids that is absent in blood.

Question 10.
Consult internet and find out how to make orally active protein pharmaceutical. What is the major problem to be encountered?
Answer:
Orally active protein pharmaceutical can be made by lining it with a substance that will dissolve after it has passed through the stomach.
The major problem encountered is that the stomach enzymes and acids may denature the therapeutic protein and render it ineffective.

Punjab State Board PSEB 12th Class Physics Book Solutions Chapter 1 Electric Charges and Fields Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Physics Chapter 1 Electric Charges and Fields

PSEB 12th Class Physics Guide Electric Charges and Fields Textbook Questions and Answers

Question 1.
What is the force between two small charged spheres having charges of 2 × 10^-7 C and 3 × 10^-7 C placed 30 cm apart in air?
Answer:
Charge on the first sphere, q₁ = 2 × 10^-7 C
Charge on the second sphere, q₂ = 3 × 10^-7 C
Distance between the spheres, r = 30 cm = 0.3 m
Electrostatic force between the spheres is given by the relation,
F = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r^{2}}\)
where, ε₀ = Permittivity of free space
F = \(\frac{9 \times 10^{9} \times 2 \times 10^{-7} \times 3 \times 10^{-7}}{(0.3)^{2}}\)
= 6 × 10^-3 N
Hence, force between the two small charged spheres is 6 × 10^-3 N. The charges are of same nature. Hence, force between them will be repulsive.

Question 2.
The electrostatic force on a small sphere of charge
0.4 μC due to another small sphere of charge -0.8 μC in air is 0.2 N.
(a) What is the distance between the two spheres?
(b) What is the force on the second sphere due to the first?
Answer:
Electrostatic force on the first sphere, F = 0.2 N
Charge on this sphere, q₁ = 0.4 μC = 0.4 × 10^-6C
Charge on the second sphere, q₂ = -0.8 μC = -0.8 × 10^-6C

(a) Electrostatic force between the spheres is given by the relation,
F = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r^{2}}\)
where, ε₀ = Permittivity of free space
r² = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{F}\)
= \(=\frac{0.4 \times 10^{-6} \times 0.8 \times 10^{-6} \times 9 \times 10^{9}}{0.2}\)
= 16 × 9 × 10^-4 = 144 × 10^-4
= \(\sqrt{144 \times 10^{-4}}\) = 0.12 m
The distance between the two spheres is 0.12 m.

(b) Force on q₂ due to q₁= ?
We know that electrostatic forces always, appear in priors and follow Newton’s 3rd law of motion.
∴ \(\left|\vec{F}_{21}\right|\) = Force on q₂ due to q₁
= 0.2 N and it is attractive in nature
We now that,
F₂₁ = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r_{21}^{2}}\)

On substituting the values, we get
F₂₁ = 9 × 10⁹ × \(\frac{\left(0.4 \times 10^{-6}\right) \times\left(0.8 \times 10^{-6}\right)}{(0.12)^{2}}\)
= 0.2 N

Question 3.
Check that the ratio ke² / Gm_em_p is dimensionless. Look up a
table of physical constants and determine the value of this ratio. What does the ratio signify?
Answer:
The given ratio is \(\frac{k e^{2}}{G m_{e} m_{p}}\)
where, G = Gravitational constant
Its unit is Nm²kg^-2.
m_p and m_p = Masses of electron and proton
Their unit is kg.
e = Electric charge Its unit is C.
k = A constant = \(=\frac{1}{4 \pi \varepsilon_{0}}\)
Its unit is N m²C^-2.
Therefore, unit of the given ratio
\(\frac{k e^{2}}{G m_{e} m_{p}}\) = \(\frac{\left[\mathrm{Nm}^{2} \mathrm{C}^{-2}\right]\left[\mathrm{C}^{-2}\right]}{\left[\mathrm{Nm}^{2} \mathrm{~kg}^{-2}\right][\mathrm{kg}][\mathrm{kg}]}\) = M⁰L⁰T⁰
Hence, the given ratio is dimensionless.
e = 1.6 × 10^-19 C
G = 6.67 × 10^-11 N m²kg^-2
m_e = 9.1 × 10^-31 kg
m_p = 1.67 × 10^-27 kg
Hence, the numerical value of the given ratio is
\(\frac{k e^{2}}{G m_{e} m_{p}}\) = \(\frac{9 \times 10^{9} \times\left(1.6 \times 10^{-19}\right)^{2}}{6.67 \times 10^{-11} \times 9.1 \times 10^{-31} \times 1.67 \times 10^{-27}}\)
≈ 2.3 × 10³⁹
This is the ratio of electric force to the gravitational force between a proton and an electron, keeping distance between them constant.

Question 4.
(a) Explain the meaning of the statement ‘electric charge of a body is quantised’.
(b) Why can one ignore quantisation of electric charge when dealing with macroscopic i. e., large scale charges?
Answer:
(a) Electric charge of a body is quantised. This means that only integral (1, 2 …………,n) number of electrons can be transferred from one body to the other. Charges are not transferred in fraction. Hence, a body possesses total charge only in integral multiples of electric charge.

(b) In macroscopic or large scale charges, the charges used are huge as compared to the magnitude of electric charge. Hence, quantisation of electric charge is of no use on macroscopic scale. Therefore, it is ignored and it is considered that electric charge is continuous.

Question 5.
When a glass rod is rubbed with a silk cloth, charges appear on both. A similar phenomenon is observed with many other pairs of bodies. Explain how this observation is consistent with the law of conservation of charge.
Answer:
Rubbing produces charges of equal magnitude but of opposite nature on the two bodies because charges are created in pairs. This phenomenon of charging is called charging by friction. The net charge on the system of two rubbed bodies is zero. This is because equal amount of opposite charges annihilate each other. When a glass rod is rubbed with a silk cloth, opposite natured charges appear on both the bodies. This phenomenon is in consistence with the law of conservation of energy. A similar phenomenon is observed with many other pairs of bodies.

Question 6.
Four point charges q_A = 2 μC, q_B = -5 μC, q_C = 2 μC and q_D) = -5 μC are located at the comers of a square ABCD of side 10 cm. What is the force on a charge of 1 μC placed at the centre of the square?
Answer:
Consider the square ABCD of each side 10 cm and centre O. The charge of 1 μC is placed at O.
Now clearly, OA = OB =OC = OD
AB = BC – 10 cm = 0.1 m
AO = \(\frac{1}{2}\) AC = \(\frac{1}{2} \sqrt{A B^{2}+B C^{2}}\) = \(\frac{1}{2}\) × √2 AB
= \(\frac{1}{\sqrt{2}}\) × 0.1 m = OB = OC = OD

Here,q_A = 2μC, q_B = -5μC,q_C = 2 μC,q_D = -5μC
Clearly q_A = q_C = 2μC = 2 × 10^-6C
and q_B = q_D = -5 μC = -5 × 10^-6C
Since q_A = q_C, the charge of 1 μC will experience equal and opposite forces due to the charges q_A and q_C i. e., along OC and OA respectively. Their magnitudes are
F_A = F_C = \(\frac{1}{4 \pi \varepsilon_{0}} \times \frac{q_{A} \times 1 \mu \mathrm{C}}{A O^{2}}\)
\(\frac{9 \times 10^{9} \times 2 \times 10^{-6} \times 10^{-6}}{\left(\frac{1}{\sqrt{2}} \times 0.1\right)^{2}}\) = 3.6N
∴ \(\vec{F}_{A}=-\vec{F}_{C}\)
Similarly F_B = F_D, the charge of 1 μC will experience equal and opposite forces due to the charge q_B and q_D i. e., along OB and OD respectively, thus
\(\overrightarrow{F_{B}}=-\overrightarrow{F_{D}}\).
Thus the net force on the charge ofl μC due to the given arrangement of charges is zero i.e.,
\(\vec{F}=\vec{F}_{A}+\vec{F}_{B}+\vec{F}_{C}+\vec{F}_{D}\) = 0

Question 7.
(a) An electrostatic field line is a continuous curve. That is, a field line cannot have sudden breaks. Why not?
Explain why two field lines never cross each other at any point?
Answer:
(a) An electrostatic field line is a continuous curve because a charge experiences a continuous force when traced in an electrostatic field. The field line cannot have sudden breaks because the charge moves continuously and does not jump from one point to the other.

(b) If two field lines cross each other at a point, then electric field intensity will show two directions at that point. This is not possible. Hence, two field lines never cross each other.

Question 8.
Two point charges q_A = 3 μC and q_B = -3 μC are located 20 cm apart in vacuum.
(a) What is the electric field at the midpoint O of the line AB joining the two charges?
(b) If a negative test charge of magnitude 1.5 × 10^-9C is placed at this point, what is the force experienced by the test charge?
Answer:
(a) The situation is represented in the given figure. O is the mid-point of line AB.

Distance between the two charges, AB = 20 cm
∴ AO = OB =10 cm
Net electric field at point O = E
Magnitude of electric field at point 0 caused by + 3 μC charge,

[Since the values of E₁ and E₂ are same, the value is multiplied with 2]
= 5.4 × 10⁶ N/C along OB
Therefore, the electric field at mid-point O is 5.4 × 10⁶ NCT^-1 along OB.

(b) A test charge of amount 1.5 × 10^-9 C is placed at mid-point O.
According to question, q = -1.5 × 10^-9 C
Force experienced by the test charge = F
F = qE
= -1.5 × 10^-9 × 5.4 × 10⁶
= -8.1 × 10^-3 N
The force is directed along line QA. This is because the negative test charge is repelled by the charge placed at point B but attracted towards point A.

Question 9.
A system has two chargesg q_A = 2.5 × 10^-7C andq_A = -2.5 × 10^-7 located at points A : (0, 0, -15 cm) and B: (0, 0, +15 cm), respectively. What are the total charge and electric dipole moment of the system?
Answer:
Both the charges can be located in a coordinate frame of reference as shown in the given figure At A, amount of charge,
q_A =2.5 × 10^-7C
At B, amount of charge,
q_B = -2.5 × 10^-7C

Total charge of the system,
q = q_A + q_B
= 2.5 × 10^-7 C-2.5 × 10^-7C
= 0
Distance between two charges at points A and B,
d. =15 + 15 = 30 cm = 0.3 m
Electric dipole moment of the system is given by,
p = q_A × d = q_B × d.
= 2.5 × 10^-7 × 0.3
= 7.5 × 10^-8 Cm along positive z-axis
Therefore, the electric dipole moment of the system is 7.5 × 10^-8C m along positive z-axis.

Question 10.
An electric dipole with dipole moment 4 × 10^-9 C m is aligned at 30° with the direction of a uniform electric field of magnitude 5 × 10⁴NC^-1. Calculate the magnitude of the torque acting on the dipole.
Answer:
Electric dipole moment, p = 4 × 10^-9 C m
Angle made by p with a uniform electric field, 0 = 30°
Electric field, E = 5 × 10⁴NC^-1
Torque acting on the dipole is given by the relation,
τ = pE sinθ
= 4 × 10^-9 × 5 × 10⁴ × sin30
= 20 × 10^-5 \(\frac{1}{2}\)
= 10^-4 Nm
Therefore, the magnitude of the torque acting on the dipole is 10^-4 N m.

Question 11.
A polythene piece rubbed with wool is found to have a negative charge of 3 × 10^-7C.
(a) Estimate the number of electrons transferred (from which to which?)
(b) Is there a transfer of mass from wool to polythene?
Answer:
(a) When polythene is rubbed with wool, a number of electrons get transferred from wool to polythene. Hence, wool becomes positively charged and polythene becomes negatively charged.
Amount of charge on the polythene piece, q = -3 × 10^-7 C
Amount of charge on an electron, e = -1.6 × 10^-19C
Number of electrons transferred from wool to polythene = n
n can be calculated using the relation,
> q = ne
n = \(\frac{q}{e}\)
= \(\frac{-3 \times 10^{-7}}{-1.6 \times 10^{-19}}\)
= 1.87 × 10¹²
Therefore, the number of electrons transferred from wool to polythene is 1.87 × 10¹².

(b) Yes.
There is a transfer of mass taking place. This is because an electron has mass,
m_e = 9.1 × 10^-31 kg
Total mass transferred to polythene from wool,
m = m_e × n
= 9.1 × 10^-31 × 1.87 × 10¹²
= 1.706 × 10^-18 kg
Hence, a negligible amount of mass is transferred from wool to polythene.

Question 12.
(a) Two insulated charged copper spheres A and B have their centres separated by a distance of 50 cm. What is the mutual force of electrostatic repulsion if the charge on each is 6.5 × 10^-7 C ? The radii of A and B are negligible compared to the distance of separation.
(b) What is the force of repulsion if each sphere is charged double the above amount, and the distance between them is halved?
Answer:
(a) Charge on sphere A, q_A = Charge on sphere B, q_B = 6.5 × 10^-7 C
Distance between the spheres, r = 50 cm = 0.5 m
Force of repulsion between the two spheres,
F = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{A} q_{B}}{r^{2}}\)
∴ F = \(=\frac{9 \times 10^{9} \times\left(6.5 \times 10^{-7}\right)^{2}}{(0.5)^{2}}[latex]
= 1.52 × 10^-2 N
Therefore, the force between the two spheres is 1.52 × 10^{-2 N.}

(b) After doubling the charge, charge on sphere A, q_A = charge on sphere
B, q_B = 2 × 6.5 × 10^-7 C = 1.3 × 10<>-6 C
The distance between the spheres is halved
∴ r = [latex]\frac{0.5}{2}\) = 0.25 m
Force of repulsion between the two spheres,
F = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{A} q_{B}}{r^{2}}\)
∴ F = \(\frac{9 \times 10^{9} \times 1.3 \times 10^{-6} \times 1.3 \times 10^{-6}}{(0.25)^{2}}\)
= 16 × 1.52 × 10^-2 = 0.243 N Therefore, the force between the two spheres is 0.243 N.

Question 13.
Suppose the spheres A and B in exercise 1.12 have identical sizes. A third sphere of the same size but uncharged is brought in contact with the first, then brought in contact with the second, and finally removed from both. What is the new force of repulsion between A and B ?
Answer:
Distance between the spheres, A and B,r = 0.5 m
Initially, the charge on each sphere, q = 6.5 × 10 ^-7 C
When sphere A is touched with an uncharged sphere C, \(\frac{q}{2}[latex] amount of
charge from A will transfer to sphere C. Hence, charge on each of the spheres, A and C is [latex]\frac{q}{2}\).
When sphere C with charge \(\frac{q}{2}\) is brought in contact with sphere B with
charge q, total charges on the system will divide into two equal halves given as,
\(\frac{\frac{q}{2}+q}{2}=\frac{3 q}{4}\)
Each sphere will each half. Hence, charge on each of the spheres, C and B, is \(\frac{3 q}{4}\).
Force of repulsion between sphere A having charge \(\frac{q}{2}\) and sphere B having
charge \(\frac{3 q}{4}\)

= 5.703 × 10^-3 N
Therefore, the force of attraction between the two spheres is 5.703 × 10^-3 N.

Question 14.
Figure 1.33 shows tracks of three charged particles in a uniform electrostatic field. Give the signs of the three charges. Which particle has the highest charge to mass ratio?

Answer:
Opposite charges attract each other and same charges repel each other. It can be observed that particles 1 and 2 both move towards the positively charged plate and repel away from the negatively charged plate. Hence, these two particles are negatively charged. It can also be observed that particle 3 moves towards the negatively charged plate and repels away from the positively charged plate. Hence, particle 3 is positively charged. The charge to mass ratio (emf) is directly proportional to the displacement or amount of deflection for a given velocity. Since the deflection of particle 3 is the maximum, it has the highest charge to mass ratio.

Question 15.
Consider a uniform electric field E = 3 × 10³ î N/C. (a) What is the flux of this field through a square of 10 cm on a side whose plane is parallel to the yz plane? (b) What is the flux through the same square if the normal to its plane makes a 60° angle with the x-axis?
Answer:
Here, \(\overrightarrow{\vec{E}}\) = 3 × 10³ î NC^-1 i.e., the electric field acts along positive direction of x-axis.
Side of square = 10 cm
∴ Its surface area, ΔS = (10 cm)² = 10^-2 m²
or Δ\(\overrightarrow{\vec{S}}\) = 10^-2 î m²
as normal to the square is along x-axis.

(a) If Φ be the electric flux through the square, then

Φ = \(\vec{E} \cdot \Delta \vec{S}\)
= (3 × 10³î) .(10^-2)
= 3 × 10³ × 10^-2 î .î
= 3 × 10 = 30 Nm²C^-1

(b) Here, angle between normal to the square i.e., area vector and the electric field is 60°. i.e.,
θ = 60°
∴ Φ = \(\overrightarrow{\vec{E}}\). Δ \(\overrightarrow{\vec{S}}\) = E. Δ S cos60°
= 3 × 10³ × 10^-2 × \(\frac{1}{2}\)
= 15Nm²C^-1

Question 16.
What is the net flux of the uniform electric field of exercise 1.15 through a cube of side 20 cm oriented so that its faces are parallel to the coordinate planes?
Answer:
All the faces of a cube are parallel to the coordinate axes. Therefore, the number of field lines entering the cube is equal to the number of field lines piercing out of the cube. As a result, net flux through the cube is zero.

Question 17.
Careful measurement of the electric field at the surface of a black box indicates that the net outward flux through the surface of the box is 8.0 × 10³ N m² / C. (a) What is the net charge inside the box? (b) If the net outward flux through the surface of the box were zero, could you conclude that there were no charges inside the box? Why or Why not?
Answer:
(a) Net outward flux through the surface of the box Φ = 8.0 × 10³ N m² / C
For a body containing net charge q, flux is given by the relation,
Φ = \(\)
q = ε₀Φ)
= 8.854 × 10^-12 × 8.0 × 10³
(∵ ε₀ = 8.854 × 10^-12N^-1C²m^-2) = 7.08 × 10^-8
= 0.07 µC
Therefore, the net charge inside the box is 0.07 pC.

(b) No.
Net flux piercing out through a body depends on the net charge contained in the body. If net flux is zero, then it can be inferred that net charge inside the body is zero. The body may have equal amount of positive and negative charges.

Question 18.
A point charge +10 µC is a distance 5 cm directly above the centre of a square of side 10 cm, as shown in Fig. 1.34. What is the magnitude of the electric flux through the square? (Hint : Think of the square as one face of a cube with edge 10 cm.)

Answer:
The square can be considered as one face of a cube of edge 10 cm with a centre where charge q is placed. According to Gauss’s theorem for a cube, total electric flux is through all its six faces.
Φ total = \(\frac{q}{\varepsilon_{0}}\)

Hence, electric flux through one face of the cube i. e., through the square,
Φ = \(\frac{\phi_{\text {Total }}}{6}=\frac{1}{6} \frac{q}{\varepsilon_{0}}\)
ε₀ = 8.854 × 10^-12 N^-1C²m^-2
q = 10 µC =10 × 10^-6C
Φ = \(\frac{1}{6} \times \frac{10 \times 10^{-6}}{8.854 \times 10^{-12}}\)
= 1.88 × 10⁵ N m² C^-1
Therefore, electric flux through the square is 1.88 × 10⁵ N m² C^-1.

Question 19.
A point charge of 2.0 µC is at the centre of a cubic Gaussian surface 9.0 cm on edge. What is the net electric flux through the surface?
Answer:
Net electric flux (Φ _Net) through the cubic surface is given by,
Φ _Net = \(\frac{q}{\varepsilon_{0}}\)
ε₀ = 8.854 × 10^-12 N^-1C²m^-22 q q = Net charge contained inside the cube
= 20 µC = 2 × 10^-6C
∴ Φ _Net = \(\frac{2 \times 10^{-6}}{8.854 \times 10^{-12}}\)
∴ Φ _Net = \(\frac{2 \times 10^{-6}}{8.854 \times 10^{-12}}\)
= 2.26 × 10⁵ Nm²C^-1
The net electric flux through the surface is = 2.26 × 10⁵ Nm²C^-1

Question 20.
A point charge causes an electric flux of -1.0 × 10³ Nm² /C to pass through a spherical Gaussian surface of 10.0 cm radius centred on the charge, (a) If the radius of the Gaussian surface were doubled, how much flux would pass through the surface? (b) What is the value of the point charge?
Answer:
Electric flux, Φ = -1.0 × 10³ Nm²/C
Radius of the Gaussian surface,
r = 10.0 cm

(a) Electric flux piercing out through a surface depends on the net charge enclosed inside a body. It does not depend on the size of the body. If the radius of the Gaussian surface is doubled, then the flux passing through the surface remains the same i. e., -1.0 × 10³ 

(b) Electric flux is given by the relation,
Φ = \(\frac{q}{\varepsilon_{0}}\)
q = Φε₀
= -1.0 × 10³ × 8.854 × 10^-12
= -8.854 × 10^-9 C
= -8.854 nC
Therefore, the value of the point charge is -8.854 nC.

Question 21.
A conducting sphere of radius 10 cm has an unknown charge. If the electric field 20 cm from the centre of the sphere is 1.5 × 10³ N/C and points radially inward, what is the net charge on the sphere?
Answer:
Here R = radius of the conducting sphere = 10 cm = 0.10 m
r = distance of the point from centre of sphere = 20 cm = 0.20 m Clearly
r > R
E = electric field at a point at a distance of 20 cm from the sphere = 1.5 × 10³ NC ^-1acting inward.
q = net charge on the sphere = ?
Using the formula, E = \(\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q}{r^{2}}\) We get
q = 4πε₀Er² = \(\frac{1}{9 \times 10^{9}}\) × 1.5 × 10<>3 × (0.20)²
= 6.67 × 10^-9C =6.67 nC
Also as E acts in the inward direction, so charge on the sphere is negative.
q = -6.67 × 10^-9C -6.67nC

Question 22.
A uniformly charged conducting sphere of 2.4 m diameter has a surface charge density of 80.0 μC / m². (a) Find the charge on the sphere, (b) What is the total electric flux leaving the surface of the sphere?
Answer:
Diameter of the sphere, d = 2.4 m
Radius of the sphere, r = 1.2 m
Surface charge density, σ = 80.0 μC / m² = 80 × 10 ^-6C / m²

(a) Total charge on the surface of the sphere,
q = Charge density × Surface area = σ × 4πr²
= 80 × 10^-6 × 4 × 3.14 × (1.2)² = 1.447 × 10^-3 C
Therefore, the charge on the sphere is 1.447 × 10^-3 C.

(b) Total electric flux (Φ _Total) leaving out the surface of a sphere containing net charge q is given by the relation,
Φ _Total = \(\frac{q}{\varepsilon_{0}}\)
ε₀ = 8.854 × 10^-12 N^-1C²m^-2
q = 1.447 × 10^-3 C
Φ _Total = \(\frac{1.44 \times 10^{-3}}{8.854 \times 10^{-12}}\)
= 1.63 × 10⁸ NC^-1 m²
Therefore, the total electric flux leaving the surface of the sphere is 1.63 × 10⁸ NC^-1 m².

Question 23.
An infinite line charge produces a field of 9 × 10⁴ N/C^-1 at a distance of 2 cm. Calculate the linear charge density.
Answer:
Here E = electric field produced by infinite line charge = 9 × 10⁴ NC^-1.
r = distance of the point where E is produce = 2 cm = 0.02 m.
λ = linear charge density = ?

Question 24.
Two large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude 17.0 × 10^-22 C/m². What is E : (a) in the outer region of the first plate, (b) in the outer region of the second plate, and (c) between the plates?
Answer:
The situation is represented in the following figure:

A and B are two parallel plates close to each other. Outer region of plate A is labelled as I, outer region of plate B is labelled as III, and the region between the plates, A and B is labelled as II.

(a) Charge density of plate A,
σ = 17.0 × 10^-22 C/m²
Charge density of plate B,
σ = -17.0 × 10^-22 C/ m²
In the regions, I and III, electric field E is zero. This is because charge is not enclosed by the respective plates.

(b) Electric field E in region II is given by the relation,
E = \(\frac{\sigma}{\varepsilon_{0}}\)
where, ε₀ = Permittivity of free space
= 8.854 × 10^-12N^-1C²m^-2
E = \(\frac{17.0 \times 10^{-22}}{8.854 \times 10^{-12}}\)
= 1.92 × 10^-10 N/C
Therefore, electric field between the plates is 1.92 × 10^-10 N/C.

Question 25.
An oil drop of 12 excess electrons is held stationary under a constant electric field of 2.55 × 10⁴ NC^-1 in Millikan’s oil drop experiment. The density of the oil is 1.26 g cm^-3. Estimate the radius of the drop. (g = 9.81 ms^-2, e = 1.60 × 10^-9 C).
Answer:
Here, E = constant electric field = 2.55 × 10⁴ NC^-1, e = charge of an electron = 1.6 × 10^-19 C, n = no. of electrons = 12
If q = charge on the drop, then
q = ne = 12 × 1.6 × 10^-19 C = 19.2 × 10^-19 C
If F_e be the electrostatic force on the oil drop due to electric field, then
F_e = qE = 19.2 × 10^-19 × 2.55 × 10⁴ …………..(1)
Also let F_g = Force on the drop due to gravity, then
F_g = mg = \(\frac{4}{3}\) πr³ρg …………… (2)
Here ρ = density of oil = 1.26 g cm^-3
= 1.26 × 10^-3 kg(10^-2 m)^-3
= 1.26 × 10³ kg m^-3 g
g = 9.81 ms^-2
r = radius of the drop = ?
Putting these values in equation (2), we get

Question 26.
Which among the curves shown in Fig. 1.35 cannot possibly represent electrostatic field lines?


Answer:
(a) The field lines showed in (a) do not represent electrostatic field lines because field lines must be normal to the surface of the conductor.
(b) The field lines showed in (b) do not represent electrostatic field lines because the field lines cannot emerge from a negative charge and cannot terminate at a positive charge.
(c) The field lines showed in (c) represent electrostatic field lines. This is because the field lines emerge from the positive charges and repel each other.
(d) The field lines showed in (d) do not represent electrostatic field lines because the field Hnes should not intersect each other.
(e) The field lines showed in (e) do not represent electrostatic field lines because closed loops are not formed in the area between the field lines.

Question 27.
In a certain region of space, electric Held is along the z-direction throughout. The magnitude of electric field is, however, not constant but increases uniformly along the positive z-direction, at the rate of 10⁵ NC^-1 per metre. What are the force and torque experienced by a system having a total dipole moment equal to 10^-7 Cm in the negative z-direction?
Answer:
Dipole moment of the system, p = q × dl = -10^-7Cm
Rate of increase of electric field per unit length,
\(\frac{d E}{d l}\) = 10⁺⁵ NC^-1
Force (F) experienced by the system is given by the relation,
F = qE
F = q\(\frac{d E}{d l}\) × dl
= p × \(\frac{d E}{d l}\)
= -10^-7 × 10⁵ .
= -10^-2 N
The force is -10^-2 N in the negative z-direction i.e., opposite to the direction of electric field. Hence, the angle between electric field and dipole moment is 180°.
Torque (τ) is given by the relation,
τ = pEsin180°
= 0
Therefore, the torque experienced by the system is zero.

Question 28.
(a) A conductor A with a cavity as shown in Fig. 1.36 (a) is given a charge Q. Show that the entire charge must appear on the outer surface of the conductor.

(b) Another conductor B with charge q is inserted into the cavity keeping B insulated from A. Show that the total charge on the outside surface of A is Q q [Fig. 1.36 (b)].

(c) A sensitive instrument is to be shielded from the strong electrostatic fields in its environment. Suggest a possible way.

Answer:
(a) Let us consider a Gaussian surface that is lying wholly within a conductor and enclosing the cavity. The electric field intensity E inside the charged conductor is zero.
Let q is the charge inside the conductor and e 0 is the permittivity of free space.
According to Gauss’s law,
Flux, Φ = \(\vec{E} \cdot \overrightarrow{d s}\) = \(\frac{q}{\varepsilon_{0}}\)
Here, E = 0
\(\frac{q}{\varepsilon_{0}}\) = 0
∵ ε₀ ≠ 0
∴ q = 0
Therefore, charge inside the conductor is zero.
The entire charge Q appears on the outer surface of the conductor.

The outer surface of conductor A has a charge of amount Q. Another conductor B having charge +q is kept inside conductor A and it is insulated from A. Hence, a charge of amount -q will be induced in the inner surface of conductor A and + q is induced on the outer surface of conductor A. Therefore, total charge on the outer surface of conductor A is Q + q.

A sensitive instrument can be shielded from the strong electrostatic field in its environment by enclosing it fully inside a metallic surface. A closed metallic body acts as an electrostatic shield.

Question 29.
A hollow charged conductor has a tiny hole cut into its surface. Show that the electric field in the hole is (\(\)) n̂, where n̂ is the unit vector in the outward normal direction and a is the surface charge density near the hole.
Answer:
Let us consider a conductor with a cavity or a hole. Electric field inside the cavity is zero.

Let E is the electric field just outside the conductor, q is the electric charge, σ is the charge density, and ε₀ is the permittivity of free space.
Charge \(|q|=\vec{\sigma} \times \overrightarrow{d s}\)
According to Gauss’s law,
Flux Φ = \(\vec{E} \cdot \overrightarrow{d s}\) = \(\frac{|q|}{\varepsilon_{0}}\)
Eds = \(\frac{\vec{\sigma} \times \overrightarrow{d s}}{\varepsilon_{0}}\)
∴ E = \(\frac{\sigma}{\varepsilon_{0}} \hat{n}\)

Therefore, the electric field just outside the conductor is \(\frac{\sigma}{\varepsilon_{0}} \hat{n}\) . This field is

a superposition of field due to the cavity (\(\vec{E}\)) and the field due to the rest of the charged conductor (E). These fields are equal and opposite inside the conductor, and equal in magnitude and direction outside the conductor.
∴ E’ + E’ = E
E’ = \(=\frac{E}{2}=\frac{\sigma}{2 \varepsilon_{0}} \hat{n}\)
Therefore, the field due to the rest of the conductor is \(\frac{\sigma}{\varepsilon_{0}} \hat{n}\) .
Hence, proved.

Question 30.
Obtain the formula for the electric field due to a long thin wire of uniform linear charge density λ without using Gauss’s law. [Hint: Use Coulomb’s law directly and evaluate the necessary integral.]
Answer:
Take a long thin wire XY (as shown in the figure) of uniform linear charge density λ.

Consider a point A at a perpendicular distance l from the mid-point O of the wire, as shown in the following figure:

Let E be the electric field at point A due to the wire, XY.
Consider a small length element dx on the wire section with OZ = x
Let q be the charge on this piece.
∴ q = λ dx
Electric field due to the piece,
dE = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{\lambda d x}{(A Z)^{2}}\)
However, AZ = \(\sqrt{\left(l^{2}+x^{2}\right)}\)
∴ dE = \(\frac{\lambda d x}{4 \pi \varepsilon_{0}\left(l^{2}+x^{2}\right)}\)

The electric field is resolved into two rectangular components. dE cos θ is the perpendicular component and dE sin0 is the parallel component. When the whole wire is considered, the component dE sin0 is cancelled. Only the perpendicular component dE cosO affects point A.

Hence, effective electric field at point A due to the element dx is dE₁.
∴ dE₁ = \(\frac{\lambda d x \cos \theta}{4 \pi \varepsilon_{0}\left(x^{2}+l^{2}\right)}\) ……………. (1)
In Δ AZO, tanθ = \(\frac{x}{l}\)
x = ltanθ ……………. (2)

On differentiating equation (2), we obtain
\(\frac{d x}{d \theta}\) = l sin²θ
dx = lsin²θ dθ ……………… (3)

Question 31.
It is now believed that protons and neutrons (which constitute nuclei of ordinary matter) are themselves built out of more elementary units called quarks. A proton and a neutron consist of three quarks each. Two types of quarks, the so called ‘up* quark (denoted by u) of charge (+2/3)e, and the ‘down’ quark (denoted by d) of charge (-1/3) e, together with electrons build up ordinary matter. (Quarks of other types have also been found which give rise to different unusual varieties of matter.) Suggest a possible quark composition of a proton and neutron.
Answer:
A proton has three quarks. Let there be n up quarks in a proton, each having a charge of + \(\frac{2}{3}\) e.
Charge due to n up quarks = (\(\frac{2}{3}\)e)n
Number of down quarks in a proton = 3 – n
Each down quark has a charge of – \(\frac{1}{3}\) e.
Charge due to (3 – n) down quarks = (-\(\frac{1}{3}\)e) (3 – n)
Total charge on a proton = + e
e = (\(\frac{2}{3}\)e)n + (-\(\frac{1}{3}\)e) (3 – n)
e = (\(\frac{2 \text { ne }}{3}\)) – e + \(\frac{n e}{3}\)
2e = ne
n = 2
Number of up quarks in a proton, n = 2
Number of down quarks in a proton = 3 – n = 3 – 2 = 1
Therefore, a proton can be represented as ‘uud’.
A neutron also has three quarks. Let there be n up quarks in a neutron,
each having a charge of + \(\frac{2}{3}\) e.
Charge on a neutron due to n up quarks (+\(\frac{2}{3}\)e) n

Number of down quarks is 3 -n, each having a charge of (-\(\frac{1}{3}\))e
Charge on a neutron due to (3 – n) down quarks = (-\(\frac{1}{3}\)e) (3 – n)
Total charge on a neutron = 0
0 = (\(\frac{2}{3}\)e)n + (-\(\frac{1}{3}\)e) (3 – n)
0 = \(\frac{2}{3}\) en – e + \(\frac{n e}{3}\)
e = ne
n = 1
Number of up quarks in a neutron, n = 1
Number of down quarks in a neutron = 3 – n = 3 – 1 = 2
Therefore, a neutron can be represented as ‘udd’.

Question 32.
(a) Consider an arbitrary electrostatic field configuration. A small test charge isplaced at a null point (i. e., where E = 0) of the configuration. Shew that the equilibrium of the test charge is necessarily unstable.
(b) Verify this result for the simple configuration of two charges of the same magnitude and sign placed a certain distance apart.
Answer:
(a) An arbitrary electrostatic configuration consists of two charges of unequal charges of unequal magnitude and of same sign. e. g., consider a system of two fixed charges + ve and + e separated by a distance r placed at point A and B respectively. Let a test charge q0 be placed at a point C at a distance x from + 4 e. C is the point is resultant field or force on 90 is zero.

or 4(r – x)² = x² or 2(r – x) = ±x
∴ x = \(\frac{2 r}{3}\) or 2r
For equilibrium, the charge q0 can be either + ve or – ve.

Case I: If q0 is – ve, then it experiences equal attractive force due to both the charges. When it is displaced on either side along the line joining the two charges from its equilibrium position, the attractive force due to one charge gets increased while due to the other, it is decreased. As a result of this, charge -q0 no longer returns to its equilibrium position i.e., equilibrium of – ve charge is necessarily unstable.

Case II: If q0 is the + ve but displaced perpendicular to line joining the two charges, then resultant force tends to displace it further more i.e., it will not come back to its equilibrium position i. e., equilibrium will be unstable.

(b) Let the simple configuration consists of two equal charges +q at point A and B. As now the two charges are of same nature and have same magnitude hence their resultant \(\vec{E}\) will be zero at the mid-point O of the line joining them being equal and opposite and system will be unstable if the charge is slightly displaced, it executes S.H.M.

Question 33.
A particle of mass m and charge (~q) enters the region between the two charged plates initially moving along x-axis with speed vx (like particle 1 in Fig. 1.33). The length of plate is L and an uniform electric field E is maintained between the plates. Show that the vertical deflection of the particle at the far edge of the plate is q EL² (2m v²x).
Compare this motion with motion of a projectile in gravitational field discussed in section 4.10 of Class XI Textbook of Physics.
Answer:
Charge on a particle of mass m = -q
Velocity of the particle = v_x
Length of the plates = L
Magnitude of the uniform electric field between the plates = E
Mechanical force,F = Mass (m) x Acceleration (a)
a = \(\frac{F}{m}\)
However, electric force, F = qE
Therefore, acceleration, a = \(\frac{q E}{m}\) …………. (1)
Time taken by the particle to cross the field of length L is given by,
= \(\frac{\text { Length of the plate }}{\text { Velocity of the particle }}=\frac{L}{v_{x}}\) …………… (2)

Velocity of the particle vx In the vertical direction, initial velocity, u = 0
According to the third equation of motion, vertical deflection s of the particle can be obtained as,
s = ut + \(\frac{1}{2}\)at²
s = 0 + \(\frac{1}{2}\) (\(\frac{q E}{m}\))(\(\frac{L}{v_{x}}\))²
s = \(\frac{q E L^{2}}{2 m v_{x}^{2}}\) ……………. (3)

Hence, vertical deflection of the particle at the far edge of the plate is qEL² / (2m v_x²). This is similar to the motion of horizontal projectiles under gravity.

Question 34.
Suppose that the particle in Exercise in 1.33 is an electron projected with velocity v_x = 2.0 x 10⁶ ms^-1. If E between the plates separated by 0.5 cm is 9.1 x 10² N/C, where will the electron strike the upper plate? (|e| = 1.6 x 10^-19 C, me = 9.1 x 10^-31 kg.)
Answer:
Velocity of the particle, v_x = 2.0 x 10⁶ m/ s
Separation of the two plates, d = 0.5 cm = 0.005 m
Electric field between the two plates, E = 9.1 x 10² N / C
Charge on an electron, q = 1.6 x 10^-19 C
Mass of an electron, m_e = 9.1 x 10^-31 kg
Let the electron strike the upper plate at the end of plate L, when deflection is s. Therefore,

Therefore, the electron will strike the upper plate after travelling 1.6 cm.

Punjab State Board PSEB 12th Class Physics Book Solutions Chapter 14 Semiconductor Electronics: Materials, Devices, and Simple Circuits Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Physics Chapter 14 Semiconductor Electronics: Materials, Devices, and Simple Circuits

PSEB 12th Class Physics Guide Semiconductor Electronics: Materials, Devices, and Simple Circuits Textbook Questions and Answers

Question 1.
In an n-type silicon, which of the following statement is true:
(a) Electrons are majority carriers and trivalent atoms are the dopants.
(b) Electrons are minority carriers and pentavalent atoms are the dopants.
(c) Holes are minority carriers and pentavalent atoms are the dopants.
(d) Holes are majority carriers and trivalent atoms are the dopants.
Answer:
The correct statement is (c).
In an n-type silicon, the electrons are the majority carriers, while the holes are the minority carriers.
An n-type semiconductor is obtained when pentavalent atoms, such as phosphorus, are doped in silicon atoms.

Question 2.
Which of the statements given in Exercise 14.1 is true for p-type semiconductors.
Answer:
The correct statement is (d).
In a p-type semiconductor, the holes are majority carriers, while the electrons are the minority carriers.
A p-type semiconductor is obtained when trivalent atoms, such as aluminum, are doped in silicon atoms.

Question 3.
Carbon, silicon, and germanium have four valence electrons each.
These are characterized by valence and conduction bands separated by energy bandgap respectively equal to (E_g)_C, (E_g) _si, and (E_g)_Ge Which of the following statements is true?
(a) (E_g)_si<(E_g)_Ge<(E_g)_C
(b) (E_g)_C<(E_g)_Ge>(E_g)_Si
(c) (E_g)_C > (E_g)_Si > (E_g)_Ge
(d) (E_g)_C =(E_g)_Si = (E_g)_Ge
Answer:
The correct statement is (c).
Out of the three given elements, the energy band gap of carbon is the maximum and that of germanium is the least.
The energy band gap of these elements are related as (E_g)_C > (E_g)_Si > (E_g)_Ge.

Question 4.
In an unbiased p-n junction, holes diffuse from the p-region to n-region because
(a) free electrons in the n-region attract them.
(b) they move across the junction by the potential difference.
(c) hole concentration in p-region is more as compared to n-region.
(d) All of the above.
Answer:
The correct statement is (c).
The diffusion of charge carriers across a junction takes place from the region of higher concentration to the region of lower concentration. In this case, the p-region has greater concentration of holes than the n-region. Hence, in an unbiased p-n junction, holes diffuse from the p-region to the n-region.

Question 5.
When a forward bias is applied to a p-n junction, it
(a) raises the potential barrier,
(b) reduces the majority carrier current to zero,
(c) lowers the potential barrier.
(d) None of the above.
Answer:
The correct statement is (c).
When a forward bias is applied to a p-n junction, it lowers the value of potential barrier.
In the case of a forward bias, the potential barrier opposes the applied voltage.
Hence, the potential barrier across the junction gets reduced.

Question 6.
For transistor action which of the following statements are correct:
(a) Base, emitter and collector regions should have similar size and doping concentrations.
(b) The base region must be very thin and lightly doped.
(c) The emitter junction is forward biased and collector junction is reverse biased.
(d) Both the emitter junction as well as the collector junction are forward biased.
Answer:
The correct statements are (b) and (c).
For a transistor action, the junction must be lightly doped so that the base region is very thin.
Also, both the emitter junction must be forward-biased and collector junction should be reverse-biased.

Question 7.
For a transistor amplifier, the voltage gain
(a) remains constant for all frequencies.
(b) is high at high and low frequencies and constant in the middle-frequency range.
(c) is low at high and low frequencies and constant at mid frequencies.
(d) None of the above.
Answer:
The correct statement is (c).
The voltage gain of a transistor amplifier is constant at mid-frequency range only. It is low at high and low frequencies.

Question 8.
In half-wave rectification, what is the output frequency if the input frequency is 50 Hz.
What is the output frequency of a full-wave rectifier for the same input frequency.
Answer:
Input frequency = 50 Hz
For a half-wave rectifier, the output frequency is equal to the input frequency.
∴ Output frequency = 50 Hz
For a full-wave rectifier, the output frequency is twice the input frequency
∴ Output frequency = 2 x 50 = 100 Hz

Question 9.
For a CE-transistor amplifier, the audio signal voltage across the collected resistance of 2 kΩ is 2V.
Suppose the current amplification factor of the transistor is 100, find the input signal voltage and base current, if the base resistance is 1 kΩ.
Answer:
Given, R_c = 2 kΩ, R_B = 1 kΩ,
V₀ = 2V, input voltage V_i = ?
β = \(\frac{I_{C}}{I_{B}}\) = 100
V₀=I_CR_C= 2V
i_c = \(\frac{2 V}{R_{C}}=\frac{2 \mathrm{~V}}{2 \times 10^{3} \Omega}\) = 1.0^-3 A.

Base current,
I_B = \(\frac{I_{C}}{\beta}=\frac{10^{-3}}{100}\) = 10 x 10^-6 A = 10 μA
Base current, R_B = \(\frac{V_{B B}}{I_{B}}\)
Input Voltage, V_i = R_B x I_B
= 1 x 10³ x 10 x 10^-6
= 0.01 V

Question 10.
Two amplifiers are connected one after the other in series (cascaded). The first amplifier has a voltage gain of 10 and the second has a voltage gain of 20. If the input signal is 0.01 volt, calculate the output ac signal.
Answer:
Voltage gain of the first amplifier, V₁ = 10
Voltage gain of the second amplifier; V₂ = 20
Input signal voltage, V_i = 0.01V
Output AC signal voltage = V₀
The total voltage gain of a two-stage cascaded amplifier is given by the product of voltage gains of both the stages, Le.,
V = V₁ x V₂=10 x 20 =200
We have the relation
V₀ =V x V_i= 200 x 0.01 = 2 V
Therefore, the output AC signal of the given amplifier is 2 V.

Question 11.
A p-n photodiode is fabricated from a semiconductor with bandgap of 2.8 eV. Can it detect a wavelength of 6000 nm?
Answer:
Energy band gap of the given photodiode, E_g = 2.8 eV
Wavelength, λ = 6000 nm= 6000 x 10^-9m
The energy of a signal is given by the relation
E = \(\frac{h c}{\lambda}\)
where, h = Planck’s constant = 6.63 x 10^-34 Js
c = Speed of light = 3 x 10⁸ m/s
E = \(\frac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{6000 \times 10^{-9}}\) = 3.313 x 10^-20 J
But 1.6 x 10^-19 J = 1 eV
E = \(\frac{3.313 \times 10^{-20}}{1.6 \times 10^{-19}}\) = 0.207 eV

Additional Exercises

Question 12.
The number of silicon atoms per m³ is 5 x 10²⁸.
This is doped simultaneously with 5 x 10²² atoms per m³ of Arsenic and 5 x 10²⁰ per m³ atoms of Indium.
Calculate the number of electrons and holes. Given that n_i= 1.5 x 10¹⁶m^-3. Is the material n-type or p-type?
Answer:
Arsenic is n-type impurity and indium is p-type impurity.
Number of electrons, n_e = n_D – n_A
= 5 x 10²² – 5 x 10²⁰ = 4.95 x10²² m^-3
Also, n_i = n_en_h
Given, n_i =1.5 x 10¹⁶ m^-3
Number of holes, n_h=\(\frac{n_{i}^{2}}{n_{e}}\) = \(\frac{\left(1.5 \times 10^{16}\right)^{2}}{4.95 \times 10^{22}} \)
⇒ n_h =4.54 x 10⁹ m^-3
As n_e > n_h. so the material is an n-type semiconductor.

Question 13.
In an intrinsic semiconductor, the energy gap E_g is 1.2 eV. Its hole mobility is much smaller than electron mobility and independent of temperature. What is the ratio between conductivity at 600K and that at 300K?  Assume that the temperature dependence of intrinsic carrier concentration n_i is given by n_i = n₀ exp\(\left[-\frac{E_{g}}{2 k_{B} T}\right]\) where n₀ is a constant.
Answer:
Energy gap of the given intrinsic semiconductor, E = 1.2 eV
The temperature dependence of the intrinsic carrier-concentration is written as
n_i = n₀ exp\(\left[-\frac{E_{g}}{2 k_{B} T}\right]\)

where, k_B = Boltzmann constant = 8.62 x 10^-5eV/K
T = Temperature, n₀ = Constant
Initial temperature, T₁ = 300 K
The intrinsic carrier-concentration at this temperature can be written as
n_i1 =n₀exp \(\left[-\frac{E_{g}}{2 k_{B} \times 300}\right]\)
………………………….. (1)
Final temperature, T₂ = 600 K
The intrinsic carrier-concentration at this temperature can be written as
n_i1 = n₀exp \(\left[-\frac{E_{g}}{2 k_{B} \times 600}\right]\)
………………………………… (2)

The ratio between the conductivities at 600 K and at 300 K is equal to the ratio between the respective intrinsic carrier- concentrations at these temperatures.

Therefore, the ratio between the conductivities is 1.09 x 10⁵.

Question 14.
In a p.n junction diode, the current I can be expressed as
I = I₀exp\(\left(\frac{\mathrm{eV}}{2 k_{B} T}-1\right)\) where I₀ is called the reverse saturation current, V is the voltage across the diode and is positive for forward bias and negative for reverse bias, and I is the current through the diode, k_B is the Boltzmann constant (8.6 x 10^-5 eV/K) and T is the absolute temperature. if for a given diode I₀ = 5 x 10^-12 A and T = 300K, then
(a) What will be the forward current at a forward voltage of 0.6V?
(b) What will be the increase in the current if the voltage across the diode is increased to 0.7 V?
(c) What is the dynamic resistance?
(d) What will be the current if reverse bias voltage changes from 1V to 2 V?
Answer:
Given, I₀ = 5 x 10^-12 A, T = 300 K
k_B =8.6 x 10^-5 eV/K
= 8.6 x 10^-5 x 1.6 x 10^-19J/K
(a) Given, voltage V = 0.6 V
∴ \(\frac{e V}{k_{B} T}=\frac{1.6 \times 10^{-19} \times 0.6}{8.6 \times 10^{-5} \times 1.6 \times 10^{-19} \times 300}\) = 23.26
The current I through a junction diode is given by

(b) Given, voltage V = 0.7 V
∴ \( \frac{e V}{k_{B} T}=\frac{1.6 \times 10^{-19} \times 0.7}{8.6 \times 10^{-5} \times 1.6 \times 10^{-19} \times 300}\) = 27.14
Now,

Change in current ΔI = 3.035 — 0.063 = 2.9 A
(c) ΔI =2.9 A, voltage ΔV=0.7—0.6=0.1 V
Dynamic resistance R_d =\(\frac{\Delta V}{\Delta I}=\frac{0.1}{2.9}\) = 0.0336 Ω
(d) As the voltage changes from 1 V to 2 V, the current I will be almost
equal to I₀ = 5 x 10^-12 A.
It is due to that the diode possesses practically infinite resistance in the reverse bias.

Question 15.
You are given the two circuits as shown in Fig. 14.44. Show that
circuit (a) acts as OR gate while the circuit (b) acts as AND gate.

Answer:
(a) A and B are the inputs and Y is the output of the given circuit. The left half of the given figure acts as the NOR Gate, while the right half acts as the NOT Gate. This is shown in the following figure

Hence, the output of the NOR Gate = \(\overline{A+B}\)
This will be the input for the NOT Gate. Its output will be \(\overline{\overline{A+B}}\) = A+B
∴ Y = A + B
Hence, this circuit functions as an OR Gate.

(b) A and B are the inputs and Y is the output of the given circuit. It can be observed from the following figure that the inputs of the right half NOR Gate are the outputs of the two NOT Gates.

Hence, the output of the given circuit can be written as
Y = \(\overline{\bar{A}+\bar{B}}=\overline{\bar{A}} \cdot \overline{\bar{B}}= \) = A.B
Hence, the circuit functions as an AND Gate.

Question 16.
Write the truth table for a NAND gate connected as given in Fig. 14.45. Hence identify the exact logic operation carried out by this circuit.

Answer:
A acts as the two inputs of the NAND gate and Y is the output, as shown in the following figure

Hence, the output can be written as
Y =\(\overline{A \cdot A}=\bar{A}+\bar{A}=\bar{A}\) ……………………… (1)
The truth table for equation (1) can be drawn as

A	Y = \(\bar{A}\)
0	1
1	0

This circuit functions as a NOT gate. The symbol for this logic circuit is shown as

Question 17.
You are given two circuits as shown in Fig. 14.46, which consist of NAND gates. Identify the logic operation carried out by the two circuits.

Answer:
In both the given circuits, A and B are the inputs and Y is the output
(a) The output of the left NAND gate will be A. B, as shown in the following figure

Hence, the output of the combination of the two NAND gates is given as
Y= \(\overline{(\overline{A \cdot B}) \cdot(\overline{A \cdot B})}=\overline{\overline{A B}}+\overline{\overline{A B}}\) =AB
Hence, this circuit functions as an AND gate.

(b) \(\bar{A}\) is the output of the upper half of the NAND gate and B is the output of the lower half of the NAND gate, as shown in the following figure

Hence, the output of the combination of theNAND gates will be given as
Y = \(\bar{A} \cdot \bar{B}=\overline{\bar{A}}+\overline{\bar{B}}\) =A + B
Hence, this circuit functions as an OR gate.

Question 18.
Write the truth table for circuit given in Fig 14.47 below consisting of NOR gates and identify the logic operation (OR, AND, NOT) which this circuit is performing.

(Hint: A = 0, B = 1 then A and B inputs of second NOR gate will be 0 and hence Y = 1. Similarly, work out the values of Y for other combinations of A and B. Compare with the truth table of OR, AND, NOT gates and find the correct one.)
Answer:
A and B are the mputs of the given circuit The output of the first NOR gate ’ is \(\overline{A+B}\) .
It can be observed from the following figure that the inputs of the second NOR gate become the out put of the first one

Hence, the output of the combination is given as
Y= \(\overline{\overline{A+B}+\overline{A+B}}\)
= \(\overline{\bar{A}+\bar{B}}+\overline{\bar{A} \cdot \bar{B}}\)
= \(\overline{\bar{A} \cdot \bar{B}}=\overline{\bar{A}}+\overline{\bar{B}}\) = A+B
The truth table for this operation is given as

A	B	Y(= A+B)
0	0	0
0	1	1
1	0	1
1	1	1

This is the truth table of an OR gate. Hence, this circuit functions as an OR gate.

Question 19.
Write the truth table for the circuits given in Fig.14.48 consisting of NOR gates only. Identify the logic operations (OR, AND, NOT) performed by the two circuits.

Answer:
(a) A acts as the two inputs of the NOR gate and Y is the output, as shown in the following figure.
Hence, the output of the circuit is \(\overline{A+A}\)

The truth table for the same is given as

A	Y = \(\bar{A}\)
0	1
1	0

This is the truth table of a NOT gate. Hence, this circuit functions as a NOT gate.

(b) A and B are the inputs and Y is the output of the given circuit. By using the result obtained in solution
(a), we can infer that the outputs of the
first two NOR gates are \(\bar{A}\) and \(\bar{B}\), as shown in the following figure

\(\bar{A}\) and \(\bar{B}\) are the inputs for the last NOR gate.
Hence, the output for the circuit can be written as
Y = \(\overline{\bar{A}+\bar{B}}=\overline{\bar{A}} \cdot \overline{\bar{B}}\) = A.B
The truth table for the same can be written as

A	B	Y(=A.B)
o	o	o
o	1	o
1	0	0
1	1	1

This is the truth table of an ANL) gate. Hence, this circuit functions as an AND gate.

Punjab State Board PSEB 12th Class Biology Book Solutions Chapter 11 Biotechnology: Principles and Processes Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Biology Chapter 11 Biotechnology: Principles and Processes

PSEB 12th Class Biology Guide Biotechnology: Principles and Processes Textbook Questions and Answers
Question 1.
Can you list 10 recombinant proteins which are used in medical ; practice? Find out where they are used as therapeutics (use the internet).
Answer:

Recombinant proteins	Therapeutic uses
(a) Insulin	Used for diabetes mellitus
(b) OKT-3	Therapeutic antibody, used for reversal
(c) DNase	Treatment of cystic fibrosis
(d) Reo Pro	Prevention of blood clots
(e) Blood clotting factor VIII	Treatment of haemophilia A
(f) Blood clotting factor IX	Treatment of haemophilia B
(g) Tissue plasminogen activator	For acute myocardial infarction
(h) Interferon alpha (INF alpha)	Used for hepatitis C
(i) Interferon beta (INF beta)	Used for multiple sclerosis
(j) Interferon gamma (INF gamma)	Used for granulomatous disease

Question 2.
Make a chart (with diagrammatic representation) showing a restriction enzyme, the substrate DNA on which it acts, the site at which it cuts DNA and the product it produces.
Answer:

Question 3.
From what you have learnt, can you tell whether enzymes are bigger or DNA is bigger in molecular size? How did you know?
Answer:
The molecular size of DNA molecules is more than that of enzymes. It is because an enzyme (protein) is synthesised from a segment of DNA called the gene.

Question 4.
What would be the molar concentration of human DNA in a human cell? Consult your teacher.
Answer:
The molar concentration of human DNA in a human diploid cell is as follows:
Total number of chromosomes × 6.023 × 10²³
= 46 × 6.023 × 10²³
= 2.77 × 1018moles

Question 5.
Do eukaryotic cells have restriction endonucleases? Justify your answer.
Answer:
No. Eukaryotic cells do not have restriction endonucleases. All the restriction endonucleases have been isolated from the various strains of bacteria and they are also named according to the genus and species of prokaryotes. The first letter of the enzyme comes from the genus and the second two letters come from the species of the prokaryotic cell from which they have been isolated. For example, EcoRI comes from Escherichia coliRY 13. In EcoRI, the letter ‘R’ is derived from the name of the strain. Roman numbers following the names indicate the order in which the enzymes were isolated from that strain of bacteria.

Question 6.
Besides better aeration and mixing properties, what other advantages do stirred tank bioreactors have over shake flasks?
Answer:
Shake flasks are used for growing microbes and mixing the desired materials on a small scale in the laboratory. However, the large-scale production of a desired biotechnological product requires large stirred tank bioreactors.

Besides better aeration and mixing properties, bioreactors have the following advantages:

• It has an oxygen delivery system.
• It has a foam control, temperature and pH control system.
• Small volumes of culture can be withdrawn periodically.

Question 7.
Collect 5 examples of palindromic DNA sequences by consulting your teacher. Better try to create a palindromic sequence by following base-pair rules.
Answer:
Some palindromic DNA sequences and the restriction enzymes which act on them are as follows :

• 5′-AGCT-3′ Alul (Arthrobacter luteus)
  3′-TCGA-5′
• 5′-GAATTC-3′ EcoRI (Escherichia coli)
  3′-CTTAAG-5′
• 5′-AAGCTT-3′ Hindlil (Haemophilus influenzae)
  3′-TTCGAA-5′
• 5′-GTCGAC-3′ Sail (Streptomyces albus)
  3′-CAGCTG-5′
• 5′-CTGCAG-3′ PstI (Providencia stuartii)
  3′-GACGTC-5′

Question 8.
Can you recall meiosis and indicate at what stage a recombinant DNA is made?
Answer:
A recombinant DNA is made in the pachytene stage of prophase I by f crossing over.

Question 9.
Can you think and answer how a reporter enzyme can be used to
monitor transformation of host cells by foreign DNA in addition to a selectable marker?
Answer:
Reporter enzyme can differentiate recombinants from non-recombinants on the basis of their ability to produce a specific colour in the presence of a chromogenic substrate. DNA is inserted within the coding sequence of the enzyme p-galactosidase. This results into inactivation of the enzyme which is referred to as insertional inactivation.

The presence of a chromogenic substrate gives blue-coloured colonies if the plasmid in the bacteria does not have an insert. The presence of the insert results in insertional inactivation of α-galactosidase and the colonies do not produce any colour. These are identified as recombinant colonies.

Question 10.
Describe briefly the following:
(a) Origin of replication
(b) Bioreactors
(c) Downstream processing
Answer:
(a) Origin of Replication: This is a sequence from where replication starts and any piece of DNA when linked to this sequence can be made to replicate within the host cells. This sequence is also responsible for controlling the copy number of the linked DNA. So, if one wants to recover many copies of the target DNA it should be cloned in a vector whose origin supports a high copy number.

(b) Bioreactors: Bioreactors are vessels in which raw materials are biologically converted into specific products, individual enzymes etc. using microbial plant, animal or human cells. A bioreactor provides the optimal conditions for achieving the desired product by providing optimum growth conditions (temperature, pH, substrate, salts, vitamins, oxygen). The most commonly used bioreactors are of stirring type. A biogas plant is a good example of a bioreactor.

(c) Downstream Processing: After completion of the biosynthetic stage, the product is subjected through a series of processes before it is ready for marketing as a finished product. The processes include separation and purification, which are collectively referred to as downstream processing. The product has to be formulated with suitable preservatives. Such formulation has to undergo thorough clinical trials as in the case of drugs. Strict quality control testing for each product is also required. Downstream processing and quality control testing vary from product to product.

Question 11.
Explain briefly
(a) PCR
(b) Restriction enzymes and DNA
(c) Chitinase
Answer:
(a) PCR: PCR stands for Polymerase Chain Reaction. In this reaction multiple copies of the gene (or DNA) of interest is synthesised in vitro using two sets of primers and the enzyme DNA polymerase. The enzyme extends the primers using the nucleotides provided in the reaction and the genomic DNA as template. The segment of DNA can be amplified to approximately billion times if the process of replication of DNA is repeated many times.

(b) Restriction Enzymes and DNA: Restriction enzymes are synthesised by microbes as a defence mechanism and are specifically endonucleases which cleave the double-stranded DNA with the desired genes. This activity occurs at a limited number of sites depending on the number of recognition sequences in DNA. Lysing enzymes, synthesising enzymes (DNA polymerase and reverse transcriptase) and ligases are also tools of genetic engineering.

(c) Chitinase: During the isolation of DNA in the processes of recombinant DNA technology, the fungal cell is heated with an enzyme called chitinase. The chitinase enzyme dissolves the chitin membrane to open the cell for release of DNA along with other macromolecules such as RNA, proteins, polysaccharides and lipids.

Question 12.
Discuss with your teacher and find out how to distinguish between
(a) Plasmid DNA and Chromosomal DNA
(b) RNA and DNA
(c) Exonuclease and Endonuclease
Answer:
(a)

Plasmid DNA	Chromosomal DNA
Plasmid DNA is the naked double-stranded DNA which forms a circle with no free ends. It is associated with few proteins but contains RNA polymerase enzyme. They are smaller than the host chromosomes and can be easily separated.	Chromosomal DNA is a double-stranded linear DNA molecule associated with large proteins. This DNA exists in relaxed and supercoiled forms and provides a template for replication and transcription. It has free ends represented as 3′-5′.

(b)

DNA	RNA
(i) It is mainly confined to the nucleus. A small quantity occurs in mitochondria and chloroplasts.	It mainly occurs in the cytoplasm. A small quantity is found in the nucleus.
(ii) Its quantity is constant in each cell of a species.	Its quantity varies in different cells.
(iii) It contains deoxyribose sugar.	It contains ribose sugar.
(iv) Its pyrimidines are adenine and thymine.	Its pyrimidines are adenine and uracil.
(v) The amount of adenine is equal to the amount of thymine. Also, the amount of cytosine is equal to the amount of guanine.	Adenine and uracil are not necessarily in equal amounts, nor are cytosine and guanine necessarily in equal amounts.
(vi) It can replicate itself.	It cannot replicate itself. It is formed by DNA. Some RNA viruses (paramyxo virus) can produce RNA from an RNA template.

(c) Exonucleases are nucleases which cut off the nucleotides from the 5′ or 3′ ends of a DNA molecule, whereas endonucleases are nucleases which cleave the DNA duplex at any point except at the ends.

Punjab State Board PSEB 12th Class Biology Book Solutions Chapter 10 Microbes in Human Welfare Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Biology Chapter 10 Microbes in Human Welfare

PSEB 12th Class Biology Guide Microbes in Human Welfare Textbook Questions and Answers

Question 1.
Bacteria cannot be seen with the naked eyes, but these can be seen with the help of a microscope. If you have to carry a sample from your home to your biology laboratory to demonstrate the presence of microbes under a microscope, which sample would you carry and why?
Answer:
Curd can be used as a sample for the study of microbes. Curd contains numerous lactic acid bacteria (LAB) or Lactobacillus. These bacteria produce acids that coagulate and digest milk proteins. A small drop of curd contains millions of bacteria, which can be easily observed under a microscope.

Question 2.
Give examples to prove that microbes release gases during metabolism.
Answer:
The examples of microbes that release gases during metabolism are as follows :
(a) Bacteria and fungi carry out the process of fermentation and during this process, they release carbon dioxide. Fermentation is the process of converting a complex organic substance into a simpler substance with the action of bacteria or yeast. Fermentation of sugar produces alcohol with the release of carbon dioxide and very little energy.

(b) The dough used for making idli and dosa gives a puffed appearance. This is because of the action of bacteria which releases carbon dioxide. This CO₂ released from the dough gets trapped in the dough, thereby giving it a puffed appearance.

Question 3.
In which food would you find lactic acid bacteria? Mention some of their useful applications.
Answer:
Lactic acid bacteria can be found in curd. It is this bacterium that promotes the formation of milk into curd. The bacterium multiplies and increases its number, which converts the milk into curd. They also increase the content of vitamin B₁₂ in curd.
Lactic acid bacteria are also found in our stomach where it keeps a check on the disease-causing micro-organisms.

Question 4.
Name some traditional Indian foods made of wheat, rice and Bengal gram (or their products) which involve use of microbes.
Answer:

1. Wheat Product: Bread, cake etc.
2. Rice Product: Idli, dosa etc.
3. Bengal Gram Product: Dhokla, khandvi etc.

Question 5.
In which way have microbes played a m^jor role in controlling diseases caused by harmful bacteria?
Answer:
Several micro-organisms are used for preparing medicines. Antibiotics are medicines produced by certain micro-organisms to kill other disease-causing micro-organisms. These medicines are commonly obtained from bacteria and fungi. They either kill or stop the growth of disease-causing micro-organisms. Streptomycin, tetracycline, and penicillin are common antibiotics. Penicillium notatum produces chemical penicillin, which checks the growth of Staphylococci bacteria in the body. Antibiotics are designed to destroy bacteria by weakening their cell walls. As a result of this weakening, certain immune cells such as the white blood cells enter the bacterial cell and cause cell lysis. Cell lysis is the process of destroying cells such as blood cells and bacteria.

Question 6.
Name any two species of fungus, which are used in the production of the antibiotics.
Answer:
Antibiotics are medicines that are produced by certain micro-organisms to kill other disease-causing micro-organisms. These medicines are commonly obtained from bacteria and fungi.
The species of fungus used in the production of antibiotics are as follows:

Antibiotic	Fungus source
1. Penicillin	Penicillium notatum
2. Cephalosporin	Cephalosporium acremonium

Question 7.
What is sewage? In which way can sewage be harmful to us?
Answer:
Sewage is the municipal waste matter that is carried away in sewers and drains. It includes both liquid and solid wastes, rich in organic matter and microbes. Many of these microbes are pathogenic and can cause several water borne diseases. Sewage water is a major cause of polluting drinking water. Hence, it is essential that sewage water is properly collected, treated, and disposed. If untreated sewage is disposed into rivers and streams, it will pollute the water bodies.

Question 8.
What is the key difference between primary and secondary sewage treatment?
Answer:

Primary sewage treatment	Secondary sewage treatment
1. It is a mechanical process involving the removal of coarse solid materials.	It is a biological process involving the action of microbes.
2. It is inexpensive and relatively less complicated.	It is a very expensive and complicated process.

Question 9.
Do you think microbes can also be used as source of energy? If yes, how?
Answer:
Yes, microbes can be used as a source of energy. Bacteria such as Methane bacterium is used for the generation of gobar gas or biogas.

The generation of biogas is an anaerobic process in a biogas plant, which consists of a concrete tank (10-15 feet deep) with sufficient outlets and inlets. The dung is mixed with water to form the slurry and thrown into the tank. The digester of the tank is filled with numerous anaerobic methane-producing bacteria, which produce biogas from the slurry. Biogas can be removed through the pipe which is then used as a source of energy, while the spent slurry is removed from the outlet and is used as a fertiliser.

Question 10.
Microbes can be used to decrease the use of chemical fertilisers and pesticides. Explain how this can be accomplished.
Answer:
Microbes play an important role in organic farming, which is done without the use of chemical fertilisers and pesticides. Bio-fertilisers are living organisms which help increase the fertility of soil. It involves the ’ selection of beneficial micro-organisms that help in improving plant growth through the supply of plant nutrients. Bio-fertilisers are introduced in seeds, roots, or soil to mobilise the availability of nutrients. Thus, they are extremely beneficial in enriching the soil with organic nutrients. Many species of bacteria and cyanobacteria have the ability to fix free atmospheric nitrogen. Rhizobium is a symbiotic bacteria found in the root nodules of leguminous plants. Azpirillum and Azotobacter are free living nitrogen-fixing bacteria whereas Anabaena, Nostoc and Oscillatoria are examples of nitrogen-fixing cyanobacteria. Bio-fertilisers are cost effective and eco-friendly.

Microbes can also act as bio-pesticides to control insect pests in plants.
An example of bio-pesticides is Bacillus thuringiensis, which produces a toxin that kills the insect pests. Dried bacterial spores are mixed in water and sprayed in agricultural fields. When larvae of insects feed on crops, these bacterial spores enter the gut of the larvae and release r toxins, thereby it. Similarly, Trichoderma are free living fungi. They live in the roots of higher plants and protect them from various pathogens.

Baculoviruses is another bio-pesticide that is used as a biological control I agent against insects and other arthropods.

Question 11.
Three water samples namely river water, untreated sewage water and secondary effluent discharged from a sewage treatment plant were subjected to BOD test. The samples were labelled A, B and C; but the laboratory attendant did not note which was which. The BOD values of the three samples A, B and C were recorded as 20mg/L, 8mg/L and 400mg/L, respectively. Which sample of the water is most polluted? Can you assign the correct label to each assuming the river water is relatively clean?
Answer:
Biological oxygen demand (BOD) is the method of determining the amount of oxygen required by micro-organisms to decompose the waste present in the water supply. If the quantity of organic wastes in the water supply is high, then the number of decomposing bacteria present in the water will also be high. As a result, the BOD value will increase. Therefore, it can be concluded that if the water supply is more polluted, then it will have a higher BOD value. Out of the above three samples, sample C is the most polluted since it has the maximum BOD value of 400 mg/L.

After untreated sewage water, secondary effluent discharge from a sewage treatment plant is most polluted. Thus, sample A is secondary effluent discharge from a sewage treatment plant and has the BOD value of 20 mg/L, while sample B is river water and has the BOD value of 8 mg/L.
Hence, the correct label for each sample is:

Label	BOD value	Sample
A.	20 mg/L	Secondary effluent discharge from a sewage treatment plant
B.	8 mg/L	River water
C.	400 mg/L	Untreated sewage water

Question 12.
Find out the name of the microbes from which Cyclosporin A (an immunosuppressive drug) and Statins (blood cholesterol lowering agents) are obtained.
Answer:

Drug	Function	Microbe
1. Cyclosporin-A	Immuno suppressive drug	Trichoderma polysporum
2. Statin	Blood cholesterol lowering agent	Monascus purpureus

Question 13.
Find out the role of microbes in the following and discuss it with your teacher.
(a) Single cell protein (SCP)
(b) Soil
Answer:
(a) Single Cell Protein (SCP): A single cell protein is a protein obtained from certain microbes, which forms an alternate source of proteins in animal feeds. The microbes involved in the preparation of single cell proteins are algae, yeast, or bacteria. These microbes are grown on an industrial scale to obtain the desired protein. For example, Spirulina can be grown on waste materials obtained from molasses, sewage, and animal manures. It serves as a rich supplement of dietary nutrients such as proteins, carbohydrate, fats, minerals, and vitamins. Similarly, micro-organisms such as Methylophilus and methylotrophus have a large rate of biomass production. Their growth can produce a large amount of proteins.

(b) Soil: Microbes play an important role in maintaining soil fertility. They help in the formation of nutrient-rich humus by the process of decomposition. Many species of bacteria and cyanobacteria have the ability to fix atmospheric nitrogen into usable form. Rhizobium is a symbiotic bacteria found in the root nodules of leguminous plants. Azospirillum and Azotobacter are free living nitrogen-fixing bacteria, whereas Anabaena, Nostoc, and Oscillatoria are examples of nitrogen-fixing cyanobacteria.

Question 14.
Arrange the following in the decreasing order (most important first) of their importance, for the welfare of human society. Give reasons for your answer.
Biogas, Citric acid, Penicillin and Curd
Answer:
The order of arrangement of products according to their decreasing importance is :
Penicillin > Biogas > Citric acid > Curd
Penicillin is the most important product for the welfare of human society. It is an antibiotic, which is used for controlling various bacterial diseases. The second most important product is biogas. It is aneco-friendly source of energy. The next important product is citric acid, which is used as a food preservative. The least important product is curd, a food item obtained by the action of Lactobacillus bacteria on milk.

Question 15.
How do biofertilisers enrich the fertility of the soil?
Answer:
Bio-fertilisers are living organisms which help in increasing the fertility of soil. It involves the selection of beneficial micro-organisms that help in improving plant growth through the supply of plant nutrients. These are introduced to seeds, roots, or soil to mobilise the availability of nutrients by their biological activity. Thus, they are extremely beneficial jf in enriching the soil with organic nutrients. Many species of bacteria and cyanobacteria have the ability to fix free atmospheric nitrogen. Rhizobium is a symbiotic bacteria found in the root nodules of leguminous plants. Azospirillum and Azotobacter are free living nitrogen-fixing bacteria, whereas Anabaena, Nostoc, and Oscillatoria are examples of nitrogen-fixing cyanobacteria. Bio-fertilisers are cost effective and eco-friendly.

Punjab State Board PSEB 12th Class Biology Book Solutions Chapter 9 Strategies for Enhancement in Food Production Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Biology Chapter 9 Strategies for Enhancement in Food Production

PSEB 12th Class Biology Guide Strategies for Enhancement in Food Production Textbook Questions and Answers

Question 1.
Explain in brief the role of animal husbandry in human welfare.
Answer:
Animal husbandry deals with the scientific management of livestock. It includes various aspects such as feeding, breeding, and control diseases to raise the population of animal livestock. Animal husbandry usually includes animals such as cattle, pig, sheep, poultry, honeybee, silkworm and fish which are useful for humans in various ways. These animals are managed for the production of commercially important products such as milk, meat, wool, egg, honey, silk, etc. The increase in human population has increased the demand of these products. Hence, it is necessary to improve the management of livestock scientifically.

Question 2.
If your family owned a dairy farm, what measures would you undertake to improve the quality and quantity of milk production?
Answer:
Dairy farm management deals with processes which aim at improving the quality and quantity of milk production. Milk production is primarily dependent on choosing improved cattle breeds, provision of proper feed for cattle, maintaining proper shelter facilities, and regular cleaning of cattle.

Choosing improved cattle breeds is an important factor of cattle management. Hybrid cattle breeds are produced for improved productivity. Therefore, it is essential that hybrid cattle breeds should have a combination of various desirable genes such as high milk production and high resistance to diseases. Cattle should also be given healthy and nutritious food consisting of roughage, fibre concentrates, and high levels of proteins and other nutrients.

Cattle should be housed in proper cattle-houses and should be kept in well ventilated roofs to prevent them from harsh weather conditions such as heat, cold, and rain. Regular baths and proper brushing should be ensured to control diseases. Also, time-to-time check ups by a veterinary doctor for symptoms of various diseases should be undertaken.

Question 3.
What is meant by the term ‘breed’? What are the objectives of animal breeding?
Answer:
A breed is a special variety of animals within a species. It is similar in most characters such as general appearance, size, configuration, and features with other members of the same species. Jersey and Brown
Swiss are examples of foreign breeds of cattle. These two varieties of cattle have the ability to produce abundant quantities of milk. This milk is very nutritious with high protein content.
Objectives of animal breeding are as follows:

• To increase thd yield of animals.
• To improve the desirable qualities of the animal produce.
• To produce disease-resistant varieties of animals.

Question 4.
Name the methods employed in animal breeding. According to you which of the methods is best? Why?
Answer:
Animal breeding is the method of mating closely related individuals. There are several methods employed in animal breeding, which can be classified into the following categories:

(A) Natural Methods of Breeding Include Inbreeding and Out-breeding : Breeding between animals of the same breed is known as inbreeding, while breeding between animals of different breeds is known as out-breeding. Out-breeding of animals is of three types:
(a) Out-crossing: In this type of out-breeding, the mating of animals occurs within the same breed. Thus, they have no common ancestors up to the last 4-5 generations.

(b) Cross-breeding: In this type of out-breeding, the mating occurs between different breeds of the same species, thereby producing a hybrid.

(c) Interspecific hybridisation: In this type of out-breeding, the mating occurs between different species.

(B) Artificial Methods of Breeding Include Modern Techniques of Breeding : It involves controlled breeding experiments, which are of two types:
(a) Artificial insemination : It is a process of introducing the semen (collected from the male) into the oviduct or the uterus of the female body by the breeder. This method of breeding helps the breeder overcome certain problems faced in abnormal mating.

(b) Multiple ovulation embryo technology (MOET) : It is a technique for cattle improvement in which super-ovulation is induced by a hormone injection. Then, fertilisation is achieved by artificial insemination and early embryos are collected. Each of these embryos are then transplanted into the surrogate mother for further development of the embryo.

The best method to carry out animal breeding is the artificial method of breeding, which includes artificial insemination and MOET technology. These technologies are scientific in nature. They help overcome problems of normal mating and have a high success rate of crossing between mature males and females. Also, it ensures the production of hybrids with the desired qualities. This method is highly economical as a small amount of semen from the male can be used to inseminate several cattle.

Question 5.
What is apiculture? How is it important in our lives?
Answer:
Apiculture is the practise of bee-keeping for the production of various products such as honey, bee’s wax, etc. Honey is a highly nutritious food source and is used as an indigenous system of medicines. It is
useful in the treatment of many disorders such as cold, flu, and 1 dysentery. Other commercial products obtained from honey bees include bee’s wax and bee pollen. Bee’s wax is used for making cosmetics, polishes, and is even used in several medicinal preparations. Therefore, to meet the increasing demand of honey, people have started practicing bee-keeping on a large scale. It has become an f income generating activity for farmers since it requires a low investment and is labour intensive.

Question 6.
Discuss the role of fishery in enhancement of food production.
Answer:
Fishery is an industry which deals with catching, processing, and marketing of fishes and other aquatic animals that have a high economic value. Some commercially important aquatic animals are prawns, crabs, oysters, lobsters, and octopus. Fisheries play an important role in the Indian economy. This is because a large part of the Indian population is dependent on fishes as a source of food, which is both cheap and high in animal protein. Fishery is an employment generating industry especially for people staying in the coastal areas. Both fresh water fishes (such as Catla, Rohu, etc.) and marine fishes (such as tuna, mackerel, pomfret, etc.) are of high economic value.

Question 7.
Briefly describe various steps involved in plant breeding.
Answer:
Plant breeding is the process in which two genetically dissimilar varieties are purposely crossed to produce a new hybrid variety. As a result, characteristics from both parents can be obtained in the hybrid plant variety. Thus, it involves the production of a new variety with the desired characteristics such as resistance to diseases, climatic adaptability, and better productivity. The various steps involved in plant breeding are as follows:

(a) Collection of Genetic Variability: Genetic variability from various wild relatives of the cultivated species are collected to maintain the genetic diversity of a species. The entire collection of the diverse alleles of a gene in a crop is called the germplasm collection.

(b) Evaluation of Germplasm and Selection of Parents: The germplasm collected is then evaluated for the desirable genes. The selected plants with the desired genes are then used as parents in plant breeding experiments and are multiplied by the process of hybridisation.

(c) Cross-hybridisation between Selected Parents: The next step in plant breeding is to combine the desirable characters present in two different parents to produce hybrids. It is a tedious job as one has to ensure that the pollen grains collected from the male parent reach the stigma of the female parent.

(d) Selection of Superior Hybrids: The progenies of the hybrids having the desired characteristics are selected through scientific evaluation. The selected progenies are then self-pollinated for several generations to ensure homozygosity.

(e) Testing, Release, and Commercialisation of New Cultivars: The selected progenies are evaluated for characters such as yield, resistance to diseases, performance, etc. by growing them in research fields for at least three growing seasons in different parts of the country. After thorough testing and evaluation, the selected varieties are given to the farmers for growing in fields for a large-scale production.

Question 8.
Explain what is meant by biofortification.
Answer:
Biofortification is a process of breeding crops with higher levels of vitamins, minerals, proteins, and fat content. This method is employed to improve public health. Breeding of crops with improved nutritional quality is undertaken to improve the content of proteins, oil, vitamins, minerals, and micro-nutrients in crops. It is also undertaken to upgrade the quality of oil and proteins. An example of this is a wheat variety known as Atlas 66, which has high protein content in comparison to the existing wheat. In addition, there are several other improved varieties of crop plants such as rice, carrots, spinach etc. which have more nutritious value and more nutrients than the existing varieties.

Question 9.
Which part of the plant is best suited for making virus-free plants and why?
Answer:
Apical and axillary meristems of plants is used for making virus-free plants. In a diseased plant, only this region is not infected by the virus as compared to the rest of the plant region. Hence, the scientists remove axillary and apical meristems of the diseased plant and grow it in vitro to obtain a disease-free and healthy plant.
Virus-free plants of banana, sugarcane, and potato have been obtained using this method by scientists.

Question 10.
What is the major advantage of producing plants by micropropagation?
Answer:
Micropropagation is a method of producing new plants in a short duration using plant tissue culture.
Some major advantages of micropropagation are as follows:

• Micropropagation helps in the propagation of a large number of plants in a short span of time.
• The plants produced are identical to the mother plant.
• It leads to the production of healthier plantlets, which exhibit better disease-resisting powers.

Question 11.
Find out what the various components of the medium used for propagation of an explant in vitro are?
Answer:
The major components of medium used for propagation of explants in vitro are carbon sources such as sucrose, inorganic salts, vitamins, amino acids, water, agar-agar, and certain growth hormones such as auxins, gibberellins and cytokinins etc.

Question 12.
Name any five hybrid varieties of crop plants which have been developed in India.
Answer:
The five hybrid varieties of crop plants which have been developed in India are as follow:

Crop plant	Hybrid variety
Wheat	Sonalika and Kalyan Sona
Rice	Jaya and Ratna
Cauliflower	Pusa Shubhra and Pusa Snowball K-1
Cowpea	Pusa Komal
Mustard	Pusa Swarnim

Punjab State Board PSEB 12th Class Biology Book Solutions Chapter 8 Human Health and Disease Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Biology Chapter 8 Human Health and Disease

PSEB 12th Class Biology Guide Human Health and Disease Textbook Questions and Answers

Question 1.
What are the various public health measures, which you would suggest as safeguard against infectious diseases?
Answer:
Public health measures are preventive measures which are taken to check the spread of various infectious diseases. These measures should be taken to reduce the contact with infectious agents.
Some of these methods are as follows:
1. Maintenance of Personal and Public Hygiene: It is one of the most important methods of preventing infectious diseases. This measure includes maintaining a clean body, consumption of healthy and nutritious food, drinking clean water, etc. Public hygiene includes proper disposal of waste material, excreta, periodic cleaning, and disinfection of water reservoirs.

2. Isolation: To prevent the spread of air-borne diseases such as pneumonia, chicken pox, tuberculosis, etc., it is essential to keep the infected person in isolation to reduce the chances of spreading these diseases.

3. Vaccination: Vaccination is the protection of the body from communicable diseases by administering some agent that mimics the microbe inside the body. It helps in providing passive immunisation to the body. Several vaccines are available against many diseases such as tetanus, polio, measles, mumps, etc.

4. Vector Eradication: Various diseases such as malaria, filariasis, dengue, and chikungunya spread through vectors. Thus, these diseases can be prevented by providing a clean environment and by preventing the breeding of mosquitoes. This can be achieved by not allowing water to stagnate around residential areas. Also, measures like regular cleaning of coolers, use of mosquito nets and insecticides such as malathion in drains, ponds, etc. can be undertaken to ensure a healthy environment. Introducing fish such as Gambusia in ponds also controls the breeding of mosquito larvae in stagnant water.

Question 2.
In which way has the study of biology helped us to control infectious diseases?
Answer:
Various advancements that have occurred in the field of biology have helped us gain a better understanding to fight against various infectious diseases. Biology has helped us study the life cycle of various parasites, pathogens, and vectors along with the modes of transmission of various diseases and the measures for controlling them. Vaccination programmes against several infectious diseases such as small pox, chicken pox, tuberculosis, etc. have helped to eradicate these diseases. Biotechnology has helped in the preparation of newer and safer drugs and vaccines. Antibiotics have also played an important role in treating infectious diseases.

Question 3.
How does the transmission of each of the following diseases take * place?
(a) Amoebiasis
(b) Malaria
(c) Ascariasis
(d) Pneumonia
Answer:

Disease	Causative organism	Mode of transmission
a. Amoebiasis	Entamoeba histolytica	It is a vector-borne disease that spreads by the means of contaminated food and water. The vector involved in the transmission of this disease is the housefly.
b. Malaria	Plasmodium sp.	It is a vector-borne disease that spreads by the biting of the female Anopheles mosquito.
c. Ascariasis	Ascaris lumbricoides	It spreads via contaminated food and water.
d. Pneumonia	Streptococcus pneumoniae	It spreads by the sputum of an infected person.

Question 4.
What measure would you take to prevent water-borne diseases?
Answer:
Water-borne diseases such as cholera, typhoid, hepatitis B, etc. spread by drinking contaminated water. These water-borne diseases can be prevented by ensuring proper disposal of sewage, excreta, periodic cleaning. Also, measures such as disinfecting community water reservoirs, boiling drinking water, etc. should be observed.

Question 5.
Discuss with your teacher what does ‘a suitable gene’ means, in the context of DNA vaccines.
Answer:
‘A suitable gene’ refers to a specific DNA segment which can be injected into the cells of the host body to produce specific proteins. This protein kills the specific disease-causing organism in the host body and provides immunity.

Question 6.
Name the primary and secondary lymphoid organs.
Answer:

• Primary lymphoid organs include the bone marrow and the thymus.
• Secondary lymphoid organs include the spleen, lymph nodes, tonsils, Peyer’s patches of small intestine, and appendix.

Question 7.
The following are some well-known abbreviations, which have been used in this chapter. Expand each one to its full form:
(a) MALT
(b) CMI
(c) AIDS
(d) NACO
(e) HIV
Answer:
(a) MALT: Mucosa-Associated Lymphoid Tissue
(b) CMI: Cell-Mediated Immunity
(c) AIDS: Acquired Immuno Deficiency Syndrome
(d) NACO: National AIDS Control Organisation
(e) HIV: Human Immuno Deficiency Virus

Question 8.
Differentiate the following and give examples of each:
(a) Innate and acquired immunity
(b) Active and passive immunity
Answer:
(a) Innate and acquired immunity

Innate immunity	Acquired immunity
1. It is a non-pathogen specific type of defense mechanism.	It is a pathogen specific type of defense mechanism.
2. It is inherited from parents and protects the individual since birth.	It is acquired after the birth of an individual.
3. It operates by providing barriers against the entry of foreign infectious agents.	It operates by producing primary and secondary responses, which are mediated by B-lymphocytes and T-lymphocytes.
4. It does not have a specific memory.	It is characterised by an immunological memory.

(b) Active and passive immunity

Active immunity	Passive immunity
1. It is a type of acquired immunity in which the body produces its own antibodies against disease-causing antigens.	It is a type of acquired immunity in which readymade antibodies are transferred from one individual to another.
2. It has a long lasting effect.	It does not have long lasting effect.
3. It is slow. It takes time in producing antibodies and giving responses.	It is fast. It provides immediate relief.
4. Injecting microbes through vaccination inside the body is an example of active immunity.	Transfer of antibodies present in the mother’s milk to the infant is an example of passive immunity.

Question 9.
Draw a well-labelled diagram of an antibody molecule.
Answer:

Question 10.
What are the various routes by which transmission of human i immuno-deficiency virus takes place?
Answer:
AIDS (Acquired Immuno-Deficiency Syndrome) is caused by the Human I Immuno-deficiency Virus (HIV).
It has the following modes of transmission:

• Unprotected sexual contact with an infected person.
• Transfusion of blood from an infected person to a healthy person.
• Sharing infected needles and syringes.
• From an infected mother to a child through the placenta.

Question 11.
What is the mechanism by which the AIDS virus causes . deficiency of immune system of the infected person?
Answer:
AIDS (Acquired Immuno-Deficiency Syndrome) is caused by the Human immuno-deficiency virus (HIV) via sexual or blood-blood contact. After entering the human body, the HIV virus attacks and enters the macrophages. Inside the macrophages, the RNA of the virus replicates ’ with the help of enzyme reverse transcriptase and gives rise to viral
DNA. Then, this viral DNA incorporates into the host DNA and directs the synthesis of virus particles. At the same time, HIV enters helper T-lymphocytes. It replicates and produces viral progeny there. These newly formed progeny viruses get released into the blood, attacking p other healthy helper T-lymphocytes in the body. As a result, the number of T-lymphocytes in the body of an infected person decreases progressively, thereby decreasing the immunity of a person.

Question 12.
How is a cancerous cell different from a normal cell?
Answer:

Normal cell	Cancerous cell
1. Normal cells show the property of contact inhibition. Therefore, when these cells come into contact with other cells, they stop dividing.	Cancerous cells lack the property of contact inhibition. Therefore, they continue to divide, thereby forming a mass of cells or tumor.
2. They undergo differentiation after attaining a specific growth.	They do not undergo differentiation.
3. These cells remain confined at a particular location.	These cells do not remain confined at a particular location. They move into neighbouring tissues and disturb its function.

Question 13.
Explain what is meant by metastasis.
Answer:
The property of metastasis is exhibited by malignant tumors. It is the pathological process of spreading cancerous cells to the different parts of the body. These cells divide uncontrollably, forming a mass of cells called tumor. From the tumor, some cells get sloughed off and enter into the blood stream. From the blood stream, these cells reach distant parts of the body and therefore, initiate the formation of new tumors by dividing actively.

Question 14.
List the harmful effects caused by alcohol/drug abuse.
Answer:
Alcohol and drugs have several adverse effects on the individual, his family, and the society.
A. Effects of Alcohol
Effects on the Individual: Alcohol has an adverse effect on the body of an individual. When an individual consumes excess alcohol, it causes damage to the liver and the nervous system. As a result, other symptoms such as depression, fatigue, aggression, loss of weight and appetite may also be observed in the individual. Sometimes, extreme levels of alcohol consumption may also lead to heart failure, resulting coma and death. Also, it is advisable for pregnant women to avoid alcohol as it may inhibit normal growth of the baby.

Effects on the Family: Consumption of excess alcohol by any family member can have devastating effects on the family. It leads to several domestic problems such as quarrels, frustrations, insecurity, etc. Effects on the Society:

• Rash behaviour
• Malicious mischief and violence
• Deteriorating social network
• Loss of interest in social and other activities

B. Effects of Drugs
Effects on the Individual: Drugs have an adverse effect on the central nervous system of an individual. This leads to the malfunctioning of several other organs of the body such as the kidney, liver, etc. The spread of HIV is most common in these individuals as they share common needles while injecting drugs in their body. Drugs have long-term side effects on both males and females. These side effects include increased aggressiveness, mood swings, and depression.

Effects on the Family and Society: A person addicted to drugs creates problems for his family and society. A person dependant on drugs becomes frustrated, irritated, and anti-social.

Question 15.
Do you think that friends can influence one to take alcohol/ drugs? If yes, how may one protect himself/herself from such an influence?
Answer:
Yes, friends can influence one to take drugs and alcohol. A person cart take the following steps for protecting himself/herself against alcohol/ drug abuse:
(a) Increase your willpower to stay away from alcohol and drugs. One should not experiment with alcohol for curiosity and fun.

• Avoid the company of friends who take drugs.
• Seek help from parents and peers. ‘
• Take proper knowledge and counselling about drug abuse. Devote your energy in other extra-curricular activities.
• Seek immediate professional and medical help from psychologists and psychiatrists if symptoms of depression and frustration become apparent.

Question 16.
Why is that once a person starts taking alcohol or drugs, it is difficult to get rid of this habit? Discuss it with your teacher. Ans. Drug and alcohol consumption has an inherent addictive nature associated with euphoria and a temporary feeling of well-being. Repeated intake of drugs increases the tolerance level of the body’s receptors, leading to more consumption of drugs.

A. Effects of Alcohol
Effects on the Individual: Alcohol has an adverse effect on the body of an individual. When an individual consumes excess alcohol, it causes damage to the liver and the nervous system. As a result, other symptoms such as depression, fatigue, aggression, loss of weight and appetite may al“so be observed in the individual. Sometimes, extreme levels of alcohol consumption may also lead to heart failure, resulting coma and death. Also, it is advisable for pregnant women to avoid alcohol as it may inhibit normal growth of the baby.

Effects on the Family: Consumption of excess alcohol by any family member can have devastating effects on the family. It leads to several domestic problems such as quarrels, frustrations, insecurity, etc. Effects on the Society:

• Rash behaviour
• Malicious mischief and violence
• Deteriorating social network
• Loss of interest in social and other activities

B. Effects of Drugs
Effects on the Individual: Drugs have an adverse effect on the central nervous system of an individual. This leads to the malfunctioning of several other organs of the body such as the kidney, liver, etc. The spread of HIV is most common in these individuals as they share common needles while injecting drugs in their body. Drugs have long-term side effects on both males and females. These side effects include increased aggressiveness, mood swings, and depression.

Effects on the Family and Society: A person addicted to drugs creates problems for his family and society. A person dependant on drugs becomes frustrated, irritated, and anti-social.

Question 15.
Do you think that friends can influence one to take alcohol/ drugs? If yes, how may one protect himself/herself from such an influence?
Answer:
Yes, friends can influence one to take drugs and alcohol. A person cart take the following steps for protecting himself/herself against alcohol/ drug abuse:

• Increase your willpower to stay away from alcohol and drugs. One should not experiment with alcohol for curiosity and fun.
• Avoid the company of friends who take drugs.
• Seek help from parents and peers.
• Take proper knowledge and counselling about drug abuse. Devote your energy in other extra-curricular activities.
• Seek immediate professional and medical help from psychologists and psychiatrists if symptoms of depression and frustration become apparent.

Question 16.
Why is that once a person starts taking alcohol or drugs, it is difficult to get rid of this habit? Discuss it with your teacher.
Answer:
Drug and alcohol consumption has an inherent addictive nature associated with euphoria and a temporary feeling of well-being. Repeated intake of drugs increases the tolerance’ level of the body’s receptors, leading to more consumption of drugs.

Question 17.
In your view what motivates youngsters to take to alcohol or drugs and how can this be avoided?
Answer:
Many factors are responsible for motivating youngsters towards alcohol or drugs. Curiosity, need for adventure and excitement, experimentation are the initial causes of motivation. Some youngsters start consuming drugs and alcohol in order to overcome negative emotions (such as stress, pressure, depression, frustration) and to excel in various fields. Several mediums like television, internet, newspaper, movies etc. are also responsible for promoting the idea of alcohol to the younger generation. Amongst these factors, reasons such as unstable and unsupportive family structures and peer pressure can also lead an individual to be dependant on drugs and alcohol.

Preventive measures against addiction of alcohol and drugs are as follows:

• Parents should motivate and try to increase the willpower of their child.
• Parents should educate their children about the ill-effects of alcohol. They should provide them with proper knowledge and counselling regarding the consequences of addiction to alcohol.
• It is the responsibility of the parent to discourage a child from experimenting with alcohol. Youngsters should be kept away from the company of friends who consume drugs.
• Children should be encouraged to devote their energy in other extra¬curricular and recreational activities.
• Proper professional and medical help should be provided to a child if sudden symptoms of depression and frustration are observed.

Punjab State Board PSEB 12th Class Physics Book Solutions Chapter 15 Communication Systems Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Physics Chapter 15 Communication Systems

PSEB 12th Class Physics Guide Communication Textbook Questions and Answers

Question 1.
Which of the frequencies will be suitable for beyond-the-horizon communication using sky waves?
(a) 10 kHz
(b) 10 MHz
(C) 1 GHz
(d) 1000 GHz
Answer:
(b) 10 MHz.
For beyond-the-horizon communication, it is necessary for the signal waves to travel a large distance. 10 kHz signals cannot be radiated efficiently because of the antenna size. The high-energy signal waves (1 GHz – 1000 GHz) penetrate the ionosphere. 10 MHz frequencies get reflected easily from the ionosphere. Hence, signal waves of such frequencies are suitable for beyond-the-horizon communication.

Question 2.
Frequencies in the UHF range normally propagate by means of:
(a) Ground waves
(b) Sky waves
(c) Surface waves
(d) Space waves
Answer:
(d) Space waves
Owing to its high frequency, an ultra-high frequency (UHF) wave can neither travel along the trajectory of the ground nor can it get reflected by the ionosphere. The signals having UHF are propagated through line-of-sight communication, which is nothing but space wave propagation.

Question 3.
Digital signals
(i) do not provide a continuous set of values,
(ii) represent values as discrete steps,
(iii) can utilize binary system, and
(iv) can utilize decimal as well as binary systems.
Which of the above statements are true?
(a) (i) and (ii) only
(b) (ii) and (iii) only
(c) (i), (ii) and (iii) but not (iv)
(d) All of (i), (ii), (iii) and (iv)
Answer:
(c) A digital signal uses the binary (0 and 1) system for transferring message signals. Such a system cannot utilize the decimal system (which corresponds to analogue signals). Digital signals represent discontinuous values.

Question 4.
Is it necessary for a transmitting antenna to be at the same height as that of the receiving antenna for line-of-sight communication? A TV transmitting antenna is 81 m tall. How much service area can it cover if the receiving antenna is at the ground level?
Answer:
Line-of-sight communication means that there is no physical obstruction between the transmitter and the receiver.
In such communications, it is not necessary for the transmitting and receiving antennas to be at the same height.
Height of the given antenna, h = 81 m
Radius of earth, R = 6.4 x 10⁶ m

For range, d = 2Rh, the service area of the antenna is given by the relation
A = πd² = π(2Rh)
= 3.14 x 2 x 6.4 x 10⁶ x 81
= 3255.55 x 10⁶ m²
= 3255.55 ~ 3256 km².

Question 5.
A carrier wave of peak voltage 12 V is used to transmit a message signal.
What should be the peak voltage of the modulating signal in order to have a modulation index of 75%?
Answer:
Amplitude of the carrier wave, A_c =12,
Modulation index, m = 75% = 0.75
Amplitude of the modulating wave = A_m

Using the relation for modulation index,
m = \(\frac{A_{m}}{A_{c}}\)
∴ A_m =mA_c
= 0.75 x 12 = 9 V
Hence, amplitude of the modulating wave is 9 V.

Question 6.
A modulating signal is a square wave, as shown in Fig. 15.14.
The carrier wave is given by c(t) = 2 sin (8πt) volts.

(i) Sketch the amplitude modulated waveform.
(ii) What is the modulation index?
Answer:
Given, the equation of carrier wave
c(t) = 2sin(8πt) ……………………………… (i)
(i) According to the diagram.
Amplitude of modulating signal, A_m = 1V
Amplitude of carrier wave,
A_c = 2V [By eq.(1)]
T_m = 1s (From diagram)
From eq.(1) ω_m = \(\frac{2 \pi}{T_{m}}=\frac{2 \pi}{1}\) = 2π rad/s ………………. (2)
c(t) = 2sin8πt = Ac sinω_c t
ω_c =8π
So,
From Eq.(2)
So, ω_c = 4ω_m
Amplitude of modulated wave
A = A_m +A_c =2+1 =3V
The sketch of the amplitude modulated waveform is shown below :
For carrier signal, ω = 8π,T = \(\frac{2 \pi}{\omega}=\frac{2}{8}=\frac{1}{4}\) = 0.25s

(ii) Modulation index, µ = \(\frac{A_{m}}{A_{c}}=\frac{1}{2}\) = 0.5

Question 7.
For an amplitude modulated wave, the maximum amplitude is found to be 10 V while the minimum amplitude is found to be 2 V. Determine the modulation index, p.
What would be the value of p if the minimum amplitude is zero volts?
Answer:
Maximum amplitude, A_max = 10 V
Minimum amplitude, A_min = 2 V
Modulation index µ, is given by the relation
µ = \(\frac{A_{\max }-A_{\min }}{A_{\max }+A_{\min }}\)
= \(\frac{10-2}{10+2}=\frac{8}{12} \) = 0.67
If A_min=0,
Then µ = \(\frac{A_{\max }}{A_{\max }}=\frac{10}{10}\) = 1
Hence, µ = 1, if the minimum amplitude is zero volts.

Question 8.
Due to economic reasons, only the upper sideband of an AM wave is transmitted, but at the receiving station, there is a facility for generating the carrier. Show that if a device is available which can multiply two signals, then it is possible to recover the modulating signal at the receiver station.
Answer:
Let ω_c be the angular frequency of carrier waves and com by the angular frequency of signal waves.
Let the signal received at the receiving station be
e = E₁ cos(ω_c +ω_m )t
Let the instantaneous voltage of carrier wave
e_c = E_c cosω_c t
is available at receiving station.
Multiplying these two signals, we get
e x e_c = E₁E_c coscω_c t cos(ω_c+ω_m)t

Now, at the receiving end as the signal passes through filter, it will pass the high frequency (2ω_c + ω_m) but obstruct the frequency ω_m. So, we can \(\frac{E_{1} E_{c}}{2} \cos \omega_{m_{s}} t\) record the modulating signal frequency ω_m.

Punjab State Board PSEB 12th Class Biology Book Solutions Chapter 7 Evolution Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Biology Chapter 7 Evolution

PSEB 12th Class Biology Guide Evolution Textbook Questions and Answers

Question 1.
Explain antibiotic resistance observed in bacteria in light of Darwinian selection theory.
Answer:
Darwinian selection theory states that individuals with favourable variations are better adapted than individuals with less favourable variation. It means that nature selects the individuals with useful variation as these individuals are better evolved to survive in the existing environment. An example of such selection is antibiotic resistance in bacteria. When bacterial population was grown on an agar plate containing antibiotic penicillin, the colonies that were sensitive to penicillin died, whereas one or few bacterial colonies that were resistant to penicillin survived.

This is because these bacteria had undergone chance mutation, which resulted in the evolution of a gene that made them resistant to penicillin drug. Hence, the resistant bacteria multiplied quickly as compared to non-resistant (sensitive) bacteria, thereby increasing their number. Hence, the advantage of an individual over other helps in the struggle for existence.

Question 2.
Find out from newspapers and popular science articles any new fossil discoveries or controversies about evolution.
Answer:
Fossils of dinosaurs have revealed the evolution of reptiles in Jurassic period. As a result of this, evolution of other animals such as birds and mammals has also been discovered. However, two unusual fossils recently unearthed in China have ignited a controversy over the evolution of birds. Confuciusomis is one such genus of primitive birds that were crow sized and lived during the Creataceous period in China.

Question 3.
Attempt giving a clear definition of the term species.
Answer:
Species can be defined as a group of organisms, which have the capability to interbreed in order to produce fertile offspring.

Question 4.
Try to trace the various components of human evolution (hint: brain size and function, skeletal structure, dietary preference, etc.)
Answer:
The various components of human evolution are as follows:
(i) Brain capacity
(ii) Posture
(iii) Food/dietary preference and other important features

Question 5.
Find out through internet and popular science articles whether animals other than man has self-consciousness.
Answer:
There are many animals other than humans, which have self-consciousness. An example of an animal being self-conscious is dolphins. They are highly intelligent. They have a sense of self and they also recognise others among themselves and others. They communicate with each other by whistles, tail-slapping, and other body movements.

Not only dolphins, there are certain other animals such as crow, parrot, chimpanzee, gorilla, orangutan, etc., which exhibit self-consciousness.

Question 6.
List 10 modern-day animals and using the internet resources link it to a corresponding ancient fossil. Name both.
Answer:
The modern-day animals and their ancient fossils are listed in the following table:

Animal	Fossil
1. Man	Ramapithecus
2. Horse	Eohippus
3. Dog	Leptocyon
4. amel	Protylopus
5. Elephant	Moerithers
6. Whale	Protocetus
7. Fish	Arandaspis
8. Tetrapods	Icthyostega
9. Bat	Archaeonycteris
10. Giraffe	Palaeotragus

Question 7.
Practise drawing various animals and plants.
Answer:
Ask your teachers and parents to suggest the names of plants and animals and practise drawing them. You can also take help from your book to find the names of plants and animals.

Question 8.
Describe one example of adaptive radiation.
Answer:
Adaptive radiation is an evolutionary process that produces new species from a single, rapidly diversifying lineage. This process occurs due to natural selection. An example of adaptive radiation is Darwin finches, found in Galapagos Island. A large variety of finches is present in Galapagos Island that arose from a single species, which reached this land accidentally. As a result, many new species have evolved, diverged, and adapted to occupy new habitats. These finches have developed different eating habits and different types of beaks to suit their feeding habits. The insectivorous, blood sucking, and other species of finches with varied dietary habits have evolved from a single seed eating finch ancestor.

Question 9.
Can we call human evolution as adaptive radiation?
Answer:
No, human evolution cannot be called adaptive radiation. This is because adaptive radiation is an evolutionary process that produces new species from a single, rapidly diversifying lineage, which is not the case with human evolution. Human evolution is a gradual process that took place slowly in time. It represents an example of anagenesis.

Question 10.
Using various resources such as your school Library or the internet and discussions with your teacher, trace the evolutionary stages of any one animal, say horse.
Answer:
The evolution of horse started with Eohippus during Eocene period. It involved the following evolutionary stages:

1. Gradual increase in body size
2. Elongation of head and neck region
3. Increase in the length of limbs and feet
4. Gradual reduction of lateral digits
5. Enlargement of third functional toe
6. Strengthening of the back
7. Development of brain and sensory organs
8. Increase in the complexity of teeth for feeding on grass

The evolution of horse is represented as follows:

Eohippus: It had a short head and neck. It had four functional toes and a splint of 1 and 5 on each hind limb and a splint of 1 and 3 in each forelimb. The molars were short crowned that were adapted for grinding the plant diet.

Mesohippus: It was slightly taller than Eohippus. It had three toes in each foot.

Merychippus: It had the size of approximately 100 cm. Although it still had three toes in each foot, but it could run on one toe. The side toe did not touch the ground. The molars were adapted for chewing the grass.

Pliohippus: It resembled the modern horse and was around 108 cm tall. It had a single functional toe with splint of 2nd and 4th in each limb.

Equus: Pliohippus gave rise to Equus or the modem horse with one toe in each foot. They have incisors for cutting grass and molars for grinding food.