Punjab State Board PSEB 8th Class Science Book Solutions Chapter 1 फसल उत्पादन एवं प्रबंध Textbook Exercise Questions and Answers.
PSEB Solutions for Class 8 Science Chapter 1 फसल उत्पादन एवं प्रबंध
PSEB 8th Class Science Guide फसल उत्पादन एवं प्रबंध Textbook Questions and Answers
अभ्यास
प्रश्न 1.
उचित शब्द छांटकर रिक्त स्थानों की पूर्ति कीजिए-
तैरने, जल, फसल, पोषक, तैयारी।
(क) एक स्थान पर एक ही प्रकार के बड़ी मात्रा में उगाए गए पौधों को …………………… कहते हैं।
उत्तर-
फसल
(ख) फसल उगाने से पहले प्रथम चरण मिट्टी की …………………….. होती है।
उत्तर-
तैयारी
(ग) क्षतिग्रस्त बीज जल की सतह पर ……………………… लगेंगे।
उत्तर-
तैरने
(घ) फसल उगाने के लिए पर्याप्त सूर्य का प्रकाश एवं मिट्टी से ……………………… तथा …………………….. आवश्यक हैं।
उत्तर-
जल, पोषक।

प्रश्न 2.
‘कॉलम A’ में दिए गए शब्दों का मिलान कॉलम B से कीजिए।
| कॉलम A |
कॉलम B |
| (i) खरीफ़ फसल |
(a) मवेशियों का चारा |
| (ii) रबी फसल |
(b) यूरिया एवं सुपर फॉस्फेट |
| (iii) रासायनिक उर्वरक |
(c) पशु अपशिष्ट, गोबर, मूत्र एवं पादप अवशेष |
| (iv) कार्बनिक खाद |
(d) गेहूं, चना, मटर |
|
(e) धान एवं मक्का । |
उत्तर-
| कॉलम A |
कॉलम B |
| (i) खरीफ़ फसल |
(e) धान एवं मक्का |
| (ii) रबी फसल |
(d) गेहूँ, चना, मटर |
| (iii) रासायनिक उर्वरक |
(b) यूरिया एवं सुपर फॉस्फेट |
| (iv) कार्बनिक खाद |
(c) मवेशियों का चारा। |
प्रश्न 3.
निम्न के दो-दो उदाहरण दीजिए-
(क) खरीफ़ फसल
(ख) रबी फसल।
उत्तर-
(क) खरीफ़ फसल-
- धान
- मक्का
(ख) रबी फसल-
- गेहूँ
- चना।
प्रश्न 4.
निम्न पर अपने शब्दों में एक-एक पैराग्राफ लिखिए-
(क) मिट्टी तैयार करना
(ख) बुआई
(ग) निराई
(घ) थ्रेशिंग।
उत्तर-
(क) मिट्टी तैयार करना – मिट्टी को पलटना और पोला बनाना ताकि इसमें पौधे वृद्धि कर सकें और साँस ले सकें। इससे सूक्ष्मजीवों की वृद्धि भी उचित होती है। इस प्रक्रिया को जुताई कहते हैं।
जुते हुए खेत में सूखी मिट्टी के बड़े-बड़े ढेलों को पाटल की सहायता से तोड़ते हैं। मिट्टी का पानी और वायु द्वारा अपरदन रोकने के लिए मिट्टी को समतल करना भी ज़रूरी है।
(ख) बुआई – खेत में बीज बोने की विधि को बुआई कहते हैं। यह फसल उत्पादन का महत्त्वपूर्ण चरण है। बोने से पहले अच्छी गुणवत्ता वाले स्वस्थ बीजों का चयन किया जाता है। बीजों को हाथों द्वारा या सीड-ड्रिल द्वारा खेतों में बोया जाता है।
(ग) निराई – यह खेतों में से अवांछित पौधे (खरपतवार) हटाने की विधि है। यह विधि बहुत आवश्यक है क्योंकि खरपतवार जल, पोषक, स्थान और प्रकाश के लिए फसल से स्पर्धा रखती है।
खरपतवार पौधों को हाथ से जड़ सहित उखाड़ कर अथवा भूमि के निकट से काट कर हटाया जाता है। खरपतवार हटाने का सर्वोत्तम समय उनमें पुष्प एवं बीज बनने से पहले का होता है। यह कार्य खुरपी या हैरो से करते हैं। कुछ रसायनों का उपयोग खरपतवार नियंत्रण के लिए किया जाता है, जिन्हें खरपतवारनाशी कहते हैं। इनका उपयोग जल में घोल कर फसल पर छिड़काव द्वारा किया जाता है।
उदाहरण-2-4 D
(घ) श्रेशिंग – कटी हुई फसल में से अनाज को भूसे से अलग करने की विधि को थ्रेशिंग कहते हैं। श्रेशिंग के लिए पशुओं का अत्यधिक उपयोग किया जाता है। बड़े-बड़े खेतों में थ्रेशर या कंबाइन मशीन उपयोग में लाई जाती है। कंबाइन कटाई और थ्रेशिंग दोनों कार्य करती है।
प्रश्न 5.
स्पष्ट कीजिए कि उर्वरक खाद से किस प्रकार भिन्न है?
उत्तर-
उर्वरक और खाद में भिन्नता
| उर्वरक (Fertilizers) |
GIG (Manures) |
| (1) एक अकार्बनिक लवण है। |
(1) एक कार्बनिक पदार्थ है। |
| (2) इसका उत्पादन फैक्ट्रियों में होता है। |
(2) इसे खेतों में गोबर, अपशिष्ट के अपघटन से बनाया जाता है। |
| (3) इससे मिट्टी में हयूमस की वृद्धि नहीं होती। |
(3) इसमें ह्यूमस प्रचुर मात्रा में होती है। |
| (4) इसमें पादप पोषक प्रचुर मात्रा में होते हैं। |
(4) इसमें पादप पोषक की मात्रा अल्प होती है। |
प्रश्न 6.
सिंचाई किसे कहते हैं ? जल संरक्षित करने वाली सिंचाई की दो विधियों का वर्णन कीजिए।
उत्तर-
सिंचाई – विभिन्न अंतराल पर खेत में नियमित जल देना सिंचाई कहलाता है। सिंचाई का समय एवं बारंबारता फसलों, मिट्टी एवं ऋतु में भिन्न होता है।
सिंचाई की आधुनिक विधियों द्वारा जल का उपयोग मितव्ययता से होता है । जल संरक्षित करने वाली मुख्य विधियां हैं-
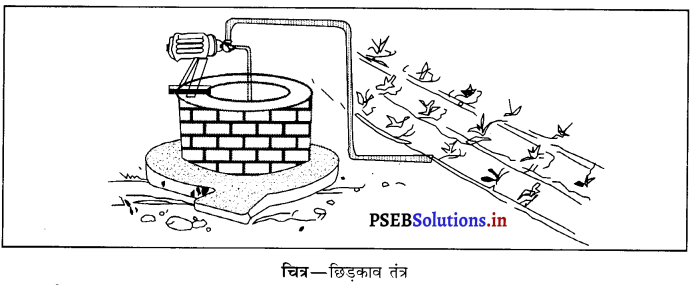
(i) छिड़काव तंत्र (Sprinkler System) – इस विधि का उपयोग असमतल भूमि जहां जल की मात्रा कम होती है, पर किया जाता है। सारे खेत में उर्ध्व पाइपों का जाल बिछा होता है, जिनके ऊपरी सिरों पर घूमने वाले नोजल लगे रहते हैं। यह पाइप निश्चित दूरी पर मुख्य पाइप से जुड़े होते हैं। पंप की सहायता से भेजा गया जल मुख्य पाइप से होता हुआ नोज़ल से वर्षा के रूप में पौधों पर गिरता है। यह छिड़काव रेतली (Sands) मिट्टी के लिए उपयोगी है।
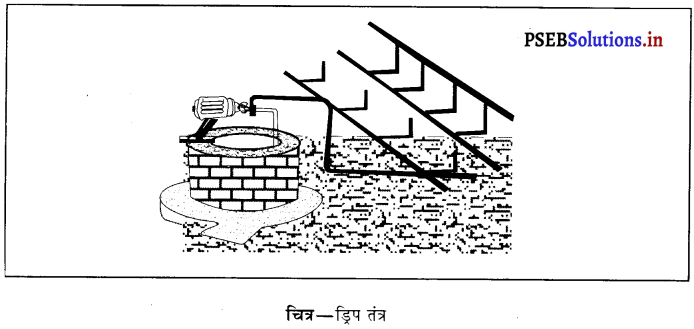
(ii) ड्रिप-तंत्र (Drip System) – इस विधि में पौधों की जड़ों पर जल बूंद-बूंद करके गिरता है, इसलिए इसे ड्रिप-तंत्र कहते हैं। फलदार पौधों, बगीचों और वृक्षों को जल देने की यह सर्वोत्तम विधि है।
ड्रिप तंत्र में एक मुख्य नली होती है जिसकी सहायक नलियां होती हैं । इन सहायक नलियों के सिरे पर विशेष नोजल लगी होती है। इनसे जड़ों को बूंद-बूंद पानी मिलता है और पानी व्यर्थ नहीं जाता। यह विधि जल की कमी वाले क्षेत्रों के लिए वरदान है।

प्रश्न 7.
यदि गेहूँ को खरीफ ऋतु में उगाया जाए तो क्या होगा? चर्चा कीजिए।
उत्तर-
गेहूँ एक रबी फसल है अर्थात् यह सर्दी की ऋतु में होती है और इसे कम तापमान और कम पानी की आवश्यकता होती है। यदि गेहूँ को खरीफ या वर्षा ऋतु में बोया जाएगा तो इसे अधिक पानी मिलने से गेहूँ की फसल मर जाएगी या अस्वस्थ पौधे उगेंगे।
प्रश्न 8.
खेत में लगातार फसल उगाने से मिट्टी पर क्या प्रभाव पड़ता है ? व्याख्या कीजिए।
उत्तर-
फसल के अच्छे उत्पादन के लिए खेतों में खाद व उर्वरकों का अत्यधिक उपयोग किया जाता है। खाद और उर्वरकों में नाइट्रोजन, फॉस्फोरस, पोटाशियम आदि पोषक तत्त्व भरपूर होते हैं, परंतु यह मिट्टी की प्रकृति बदल देते हैं। मिट्टी क्षारीय अथवा अम्लीय बन सकती है।
प्रश्न 9.
खरपतवार क्या हैं? हम उनका नियंत्रण कैसे कर सकते हैं ?
उत्तर-
खरपतवार – उपज के साथ उगे हुए अवांछित पौधे खरपतवार कहलाते हैं। खरपतवार हटाने को निराई कहते हैं। खरपतवार को हटाने और उनकी वृद्धि को नियंत्रण करने की विधियां निम्नलिखित हैं-
- जताई – मिट्टी को पलटना और पोला करना जुताई कहलाता है। जुताई हल से की जाती है। इससे खरपतवार उखड़ जाती और मिट्टी में मिल जाती है।
- उखाड़ना – इस विधि में खरपतवार को भौतिक रूप से हाथों द्वारा उखाड़कर अथवा मिट्टी के समीप से काटकर अलग किया जाता है। इसके लिए खुरपा या हैरो उपयोग में लाए जाते हैं।
- रासायनिक विधि – इस विधि में कुछ रासायनिक पदार्थ, जिन्हें खरपतवार-नाशक कहते हैं, उपज पर छिड़के जाते हैं। उदाहरण-2-4 D.
प्रश्न 10.
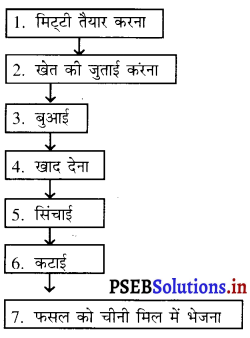
निम्न बॉक्स को सही क्रम से इस प्रकार लगाइए कि गन्ने की फसल उगाने का रेखाचित्र तैयार हो जाए।
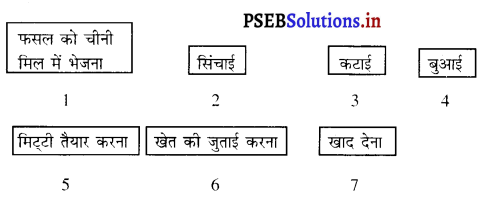
उत्तर-

प्रश्न 11.
नीचे दिए गए संकेतों की सहायता से पहेली को पूरा कीजिए-
ऊपर से नीचे की ओर
1. सिंचाई का एक पारंपरिक तरीका।
2. बड़े पैमाने पर पालतू पशुओं की उचित देखभाल करना।
3. फसल जिन्हें वर्षा ऋतु में बोया जाता है।
6. फसल पक जाने के बाद काटना।
बाईं से दाईं ओर
1. शीत ऋतु में उगाई जाने वाली फसलें।
4. एक ही किस्म के पौधे जो बड़े पैमाने पर उंगाए जाते हैं।
5. रासायनिक पदार्थ जो पौधों को पोषक प्रदान करते हैं।
7. खरपतवार हटाने की प्रक्रिया।
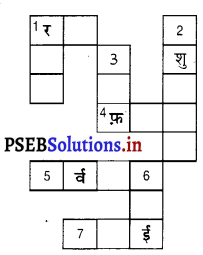
उत्तर-

PSEB Solutions for Class 8 Science फसल उत्पादन एवं प्रबंध Important Questions and Answers
TYPE-I
अति लघु उत्तरात्मक प्रश्न
प्रश्न 1.
रिक्त स्थान भरो-
(1) पौधे को खेत के टुकड़े में ……………………… किया जाता है।
उत्तर-
रोपित
(2) बीज बोने के लिए ……………………. का उपयोग किया जाता है।
उत्तर-
सीड-ड्रिल
(3) सिंचाई के लिए ……………………… उपयोग में आता है।
उत्तर-
रहट
(4) …………………………. कटाई के काम आती है।
उत्तर-
दरांती
(5) ………………………. रसायन खरपतवार को नष्ट करते हैं।
उत्तर-
खरपतवार-नाशक
(6) खेतों को पानी देने की विधि को ……………………….. कहते हैं।
उत्तर-
सिंचाई

(7) जब पौधे मुरझाने लगते हैं, तो ………………………. की आवश्यकता होती है।
उत्तर-
सिंचाई
(8) पौधों का मुरझाना ……………………. के अभाव से होता है।
उत्तर-
पानी
(9) वह भूमि जहां फसल उगाई जाती है, ……………………. कहलाती है।
उत्तर-
कृषि भूमि/खेत
(10) पानी मिट्टी के छिद्रों में से नीचे की ओर ……………………….. है।
उत्तर-
रिसता।
प्रश्न 2.
कृषि को परिभाषित करें।
उत्तर-
कृषि (Agriculture) – खेतों में फसलों के उगाने की प्रक्रिया को कृषि कहते हैं।
प्रश्न 3.
मुख्य खाद्य (Staple Food) क्या है ?
उत्तर-
मुख्य खाद्य (Staple Food) – वे खाद्य पदार्थ जो हमारे आहार का मुख्य अंश हैं, मुख्य खाद्य (Staple food) कहलाते हैं।
जैसे – गेहूँ और चावल। यह बड़े-बड़े खेतों में अत्यधिक मात्रा में उगाए जाते हैं क्योंकि इनका अत्यधिक उपयोग होता है।
प्रश्न 4.
पौधे की उचित वृद्धि के लिए कौन-से कारक आवश्यक हैं ?
उत्तर-
पौधे की उचित वृद्धि के लिए कारक-
- वायु
- सूर्य का प्रकाश
- जल एवं पोषक तत्त्व।
प्रश्न 5.
एक उपज पकने में प्रायः कितना समय लेती है ?
उत्तर-
एक उपज को पकने में प्राय: 3-4 मास लगते हैं।

प्रश्न 6.
कटाई ऋतु से संबंधित त्योहारों के नाम लिखिए।
उत्तर-
कटाई ऋतु से संबंधित त्योहार-
- पोंगल
- बैसाखी
- होली
- दीवाली
- नबान्या
- बीहूं।
प्रश्न 7.
खरपतवार-नाशक (Weedicides) क्या हैं ?
उत्तर-
खरपतवार-नाशक – वे रासायनिक पदार्थ जो खरपतवार को हटाने और उनकी वृद्धि को नियंत्रित करने के लिए खेत पर छिड़के जाते हैं, खरपतवार-नाशक कहलाते हैं।
प्रश्न 8.
पशुपालन (Animal Husbandry) क्या है ?
उत्तर-
पशुपालन – पालतू पशुओं के लिए भोजन, आवास और उचित देखभाल के अध्ययन को पशुपालन कहते हैं।
प्रश्न 9.
फसल (Crop) क्या है ?
उत्तर-
फसल (Crop) – एक ही किस्म के पौधे एक स्थान पर उगाने को फसल कहते हैं।
प्रश्न 10.
देश की दो मुख्य फसलों के नाम लिखो।
उत्तर-
गेहूँ, चावल।

प्रश्न 11.
उत्पाद (Produce) क्या है ?
उत्तर-
उत्पाद – खेतों अथवा जल में फसल को उगाने के पश्चात् जो पदार्थ मिलते हैं, उन्हें उत्पाद कहते हैं।
प्रश्न 12.
ऋतुओं के आधार पर उपज कैसे वर्गीकृत की जाती है ?
उत्तर-
उपज का वर्गीकरण है- रबी और खरीफ उपज।
प्रश्न 13.
खरीफ फसल किस मानसून पर निर्भर करती है ?
उत्तर-
दक्षिण-पश्चिम मानसून।
प्रश्न 14.
खरीफ फसल (Kharif Crop) क्या है ?
उत्तर-
खरीफ फसल – जून-अक्तूबर में उगाई जाने वाली फसल, खरीफ फसल है। जैसे- धान, मक्का।
प्रश्न 15.
रबी फसल (Rabi Crop) क्या है ?
उत्तर-
रबी फसल – नवंबर-अप्रैल में उगाई जाने वाली फसल, रबी फसल है। यह मानसून पर निर्भर नहीं करती।
उदाहरण – गेहूँ, फलीदार पौधे जैसे-चना (Gram)।
प्रश्न 16.
कृषि पद्धतियां (Agricultural Practices) क्या हैं ?
उत्तर-
कृषि पद्धतियां – फसल उगाने के लिए सामयिक अवधि में किसान द्वारा किए गए क्रिया-कलाप, कृषि पद्धतियां कहलाते हैं।

प्रश्न 17.
कृषि औज़ार (Impliments) क्या हैं?
उत्तर-
कृषि औज़ार- कृषि पद्धतियों में उपयोग आने वाले औज़ार, कृषि औज़ार कहलाते हैं।
प्रश्न 18.
पौधे मिट्टी में से क्या ग्रहण करते हैं ?
उत्तर-
जल और खनिज।
प्रश्न 19.
फसल उगाने से पहले जुताई क्यों आवश्यक है?
उत्तर-
जुताई से मिट्टी पोली होती है। इसमें वायु का फैलाव हो जाता है और नमी रखने की क्षमता बढ़ती है।
प्रश्न 20.
भूमि को समतल करने के लिए कौन-सा औज़ार उपयोग में आता है ?
उत्तर-
पाटल।
प्रश्न 21.
बीजों द्वारा उगने वाली तीन फसलों के नाम लिखो।
उत्तर-
गेहूँ, मक्का, जौ।
प्रश्न 22.
पौधे के कायिक भागों से उगने वाली दो फसलों के नाम लिखो।
उत्तर-
आलू, गन्ना।

प्रश्न 23.
मिट्टी में अधिक गहराई पर बीजे गए बीज क्यों नहीं पनपते ?
उत्तर-
क्योंकि गहराई में नमी और वायु उपलब्ध नहीं होती।
प्रश्न 24.
बुआई क्या है?
उत्तर-
बुआई – हाथों द्वारा बीजों को खेत में छिड़कना बुआई कहलाता है।
प्रश्न 25.
बुआई के लिए सीड-ड्रिल कैसे मददगार है ?
उत्तर-
सीड-ड्रिल से बीज उचित गहराई में बोए जाते हैं।
प्रश्न 26.
पौधशाला (Nursery) क्या है ?
उत्तर-
पौधशाला – एक छोटे क्षेत्र में बीजों से उगाए छोटे पौधों को उखाड़कर खेतों में रोपित करते हैं। इस क्षेत्र को पौधशाला कहते हैं।
प्रश्न 27.
बुआई के समय किस फसल के लिए खड़ा पानी आवश्यक है ?
उत्तर-
धान।
प्रश्न 28.
सिंचाई (Irrigation) की परिभाषा लिखें।
उत्तर-
सिंचाई – उचित समय अंतराल पर पौधों का पानी देने की प्रक्रिया सिंचाई कहलाती है।
प्रश्न 29.
फसल को अधिक पानी देने से क्या हानि होती है ?
उत्तर-
अधिक पानी से मिट्टी में वायु की मात्रा कम हो जाती है, जिससे जड़ें नष्ट हो जाती हैं।
प्रश्न 30.
जल मग्नता (Water logging) का क्या कारण है?
उत्तर-
अधिक सिंचाई।

प्रश्न 31.
पतन क्या है?
उत्तर-
पतन – वर्षा के साथ तेज़ हवाओं से उपज का गिरना पतन कहलाता है।
प्रश्न 32.
खेत खाली छोड़ना (Field Fallowing) क्या है ?
उत्तर-
खेत पर उपज न बोना खेत खाली छोड़ना कहलाता है।
प्रश्न 33.
जैविक खाद (Organic Manure) क्या है ?
उत्तर-
जैविक खाद – पौधों और पशु अपशिष्ट से प्राप्त जैविक पदार्थ, जैविक खाद कहलाता है।
प्रश्न 34.
फसल-चक्रण (Crop Rotation) कैसे किया जाता है ?
उत्तर-
फसल चक्रण – मिट्टी के पोषक तत्त्वों की पूर्ति के लिए एक फसल के बाद दूसरी अन्य फसल को उगाया जाता है।
प्रश्न 35.
किस फसल को नाइट्रोजन उर्वरक की आवश्यकता नहीं होती और क्यों?
उत्तर-
फलीदार पौधों को नाइट्रोजन उर्वरक की आवश्यकता नहीं होती क्योंकि उनकी जड़ों में उपस्थित बैक्टीरिया वायु की नाइट्रोजन को स्थिर कर सकते हैं।
प्रश्न 36.
दो फलीदार पौधों के नाम लिखिए।
उत्तर-
बरसीम और चना।

प्रश्न 37.
खरपतवार (Weeds) क्या है ?
उत्तर-
खरपतवार – उपज के अतिरिक्त सभी पौधे जो अवांछित हैं खरपतवार कहलाते हैं।
प्रश्न 38.
निराई (Weeding) क्या है ?
उत्तर-
खरपतवार हटाने की प्रक्रिया निराई है।
प्रश्न 39.
निराई क्यों आवश्यक है ?
उत्तर-
खरपतवार मिट्टी से पोषक तत्त्व ग्रहण करती है। यह पौधे जल और प्रकाश की स्पर्धा से फसल की वृद्धि रोकते हैं।
प्रश्न 40.
खरपतवारी नाशकों के स्थान पर कौन-से रसायन उपयोग में आ रहे हैं ?
उत्तर-
शाकनाशी (Herbicides)।
प्रश्न 41.
कीट (Pests) क्या हैं ?
उत्तर-
कीट – फसलों को नष्ट करने वाले जीव, कीट कहलाते हैं।
प्रश्न 42.
कीटनाशक (Pesticides) क्या हैं ?
उत्तर-
कीटनाशक – कीटों को नष्ट करने वाले रसायन कीटनाशक हैं।

प्रश्न 43.
किन्हीं दो कीटों के नाम लिखो।
उत्तर-
टिड्डी (Locust), घास का टिड्डा (Grass hopper)।
प्रश्न 44.
कटाई (Harvesting) क्या है ?
उत्तर-
कटाई – पकी हुई फसल को काटना, कटाई कहलाता है।
प्रश्न 45.
उपज उत्पादन से क्या अभिप्राय है ?
उत्तर-
उपज उत्पादन – कटी हुई फसल के दानों की मात्रा उपज उत्पादन है।
प्रश्न 46.
कंबाइन (Combine) क्या है ?
उत्तर-
कंबाइन – मशीनी कटाई यंत्र कंबाइन कहलाते हैं। इनसे कटाई और श्रेशिंग साथ-साथ और आसानी से हो जाती हैं।
प्रश्न 47.
भंडारण में नमी क्यों नियंत्रित की जाती है ?
उत्तर-
कवक की वृद्धि रोकने के लिए।
प्रश्न 48.
उपज-उत्पाद (Crop Yield) क्या है ?
उत्तर-
उपज-
उत्पाद – अनाज के बीजों की कुल मात्रा को उपज उत्पाद कहते हैं।

प्रश्न 49.
जुताई के लिए उपयुक्त होने वाले औज़ारों के नाम लिखिए।
उत्तर-
हल, कुदाली, कल्टीवेटर।
प्रश्न 50.
कल्टीवेटर (Cultivator) से क्या लाभ है ?
उत्तर-
इससे समय और बल कम लगता है।
प्रश्न 51.
उर्वरक की अधिक मात्रा से क्या हानि होती है ?
उत्तर-
भूमि की उपजाऊ शक्ति कम होती है। ये जल प्रदूषण का भी कारण बनते हैं।
प्रश्न 52.
सिंचाई के विभिन्न साधन क्या हैं ?
उत्तर-
कुएँ, ट्यूबवैल, तालाब, झीलें, नदियाँ, बाँध और नहरें।
प्रश्न 53.
सिंचाई के परंपरागत साधन कौन-कौन से हैं ?
उत्तर-
- मोट (घिरनी),
- चेन पंप,
- ढेकली,
- रहट।
प्रश्न 54.
घर में भंडारण समय किस पौधे की पत्तियाँ उपयोग में लाई जाती हैं ?
उत्तर-
नीम की पत्तियाँ ।
प्रश्न 55.
अनाज का उचित भंडारण क्यों आवश्यक है ?
उत्तर-
कीटों और सूक्ष्मजीवों के हमले से बचाने के लिए अनाज का उचित भंडारण आवश्यक है।
प्रश्न 56.
फ़सल कटाई के लिए हम कौन-सा कृषि औज़ार प्रयोग करते हैं ?
उत्तर-
दरांती, हार्वेस्टर ।

प्रश्न 57.
हमें भोजन की आवश्यकता क्यों होती है ?
उत्तर-
हमें ऊर्जा के लिए, वृद्धि के लिए, जीवन प्रक्रियाओं के लिए भोजन की आवश्यकता होती है।
प्रश्न 58.
खराब बीज की जाँच कैसे की जाती है ?
उत्तर-
खराब बीज हल्के होते हैं तथा पानी पर तैरते रहते हैं।
प्रश्न 59.
नर्सरी द्वारा उगाई जाने वाली फसलों के नाम दें।
उत्तर-
धानी, टमाटर आदि।
प्रश्न 60.
कुछ उर्वरकों के नाम लिखें।
उत्तर-
यूरिया, सुपर फास्फेट आदि।
प्रश्न 61.
नाइट्रोजन स्थिरीकरण किसे कहते हैं ?
उत्तर-
नाइट्रोजन स्थिरीकरण-दाल वाले पौधों की जड़ों में सूक्ष्मजीव (जीवाणु) द्वारा वायुमंडल की नाइट्रोजन को नाइट्रेट में बदलने की प्रक्रिया को नाइट्रोजन स्थिरीकरण कहते हैं।
TYPE-II
लघु उत्तरात्मक प्रश्न
प्रश्न 1.
बीज बोने से पहले मिट्टी को पलटा और पोला क्यों किया जाता है ?
उत्तर-
बीज बोने से पहले मिट्टी को पलटा और पोला करने के कारण हैं-
- इससे जड़ें आसानी से गहराई तक फैल सकती हैं।
- जड़ें आसानी से श्वास ले सकती हैं।
- पौधा मज़बूती से मिट्टी में खड़ा रह सकता है।
- कृमियों और सूक्ष्मजीवों की वृद्धि में सहायक है।

प्रश्न 2.
बुआई (Broadcasting) और रोपण (Transplanting) क्या है ?
उत्तर-
बुआई (Broadcasting) – मिट्टी की तैयारी के बाद बीज बोया जाता है। वीज बोने की क्रिया को बुआई कहते हैं। बीज बोने के दो तरीके हैं
हाथों दवारा अथवा सीड-ड्रिल दवारा।
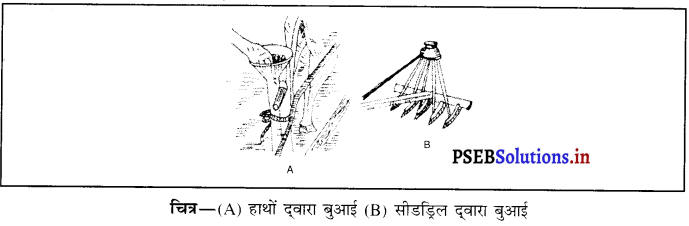
रोपण (Transplanting) – इस क्रिया द्वारा पौधशाला से पौध लेकर उसे पानी और खनिज युक्त उचित स्थान पर रोपित किया जाता है।
प्रश्न 3.
कीटनाशक (Insecticides) क्या है ? संक्षिप्त वर्णन करो।
उत्तर-
कीटनाशक – कुछ विशेष रसायन जो कीट और हानिकारक सूक्ष्मजीव और उनके लारवा को नष्ट करते हैं, परंतु पौधे पर कोई प्रभाव नहीं डालते, कीटनाशक कहलाते हैं।
प्रश्न 4.
कटी हुई फसल अथवा अनाज को नमी से क्यों बचाना चाहिए ?
उत्तर-
नमी से कवक और पीड़कों की वृद्धि में बढ़ौतरी होती है। कुछ सूक्ष्मजीव ज़हरीले भी होते हैं। इसलिए अनाज को सुखाकर उसका भंडारण करना चाहिए।
प्रश्न 5.
किसान फसल चक्रण कैसे करता है ?
उत्तर-
फसल चक्रण-फसल चक्रण से अभिप्राय है प्रति वर्ष फसल का बदलना अर्थात् एक फसल के बाद दूसरी फसल को उगाना ताकि कीट पीड़क न पनप सकें।
एक ही फसल बार-बार उगाने से मिट्टी के विशेष पोषक तत्त्व खत्म हो जाते हैं। इस समस्या से बचने के लिए दो विभिन्न किस्मों को एक-के बाद उगाना चाहिए। उदाहरण के लिए मक्का और गेहूँ, मूंगफली के साथ बदल-बदल कर उगाई जाती है। मूंगफली के पौधे की जड़ें नाइट्रोजन को स्थिर कर मिट्टी के पोषक तत्त्वों की पूर्ति करती हैं। यह पोषक तत्त्व गेहूँ के लिए लाभकारी होते हैं। फसल चक्रण से मिट्टी की उपजाऊ शक्ति बनी रहती है।
प्रश्न 6.
खेत में पीड़कों की रोकथाम कैसे की जाती है ? ।
उत्तर-
पीड़कों की रोकथाम – पीड़क सजीव हैं, जो फसल के रोग फैलाते हैं अथवा फसल नष्ट करते हैं। इनकी रोकथाम के लिए Mira पीड़कनाशक जैसे मैलाथिओन, डाइसिस्टोन, बी० एच० सी० आदि का उपयोग किया जाता है। इनका फसल पर छिड़काव करते हैं जिससे पीड़क मर जाते हैं और पौधों और मनुष्य पर इनका कुप्रभाव नहीं पड़ता।

प्रश्न 7.
खेत में अधिक पानी से क्या हानि होती है ?
उत्तर-
खेत में अधिक पानी से हानि-
- फसल नष्ट हो सकती है।
- लगातार जल मग्नता से मिट्टी में लवणों की मात्रा में वृद्धि हो सकती है। जिससे मिट्टी की प्रकृति सदा के लिए नष्ट हो सकती है।
अधिक पानी को उचित नालियों द्वारा निकाल देना चाहिए।
प्रश्न 8.
फल, सब्ज़ियों अथवा अनाज को उपयोग में लाने से पहले क्यों धोना चाहिए ?
उत्तर-
खेत से प्राप्त फल, सब्जियाँ, अनाज उपयोग में लाने से पहले इसलिए धोए जाते हैं क्योंकि इन पर पीड़कनाशकों की तह हो सकती है जो हानिकारक हो सकती है।

प्रश्न 9.
खेत को खाली छोड़ने से (Field Fallow) से क्या अभिप्राय है ?
उत्तर-
कुछ खेतों को कम-से-कम एक ऋतु के लिए बिना फसल छोड़ा जाता है ताकि पोषक तत्त्वों की प्राकृतिक रूप से आपूर्ति हो सके। इस क्रिया को खेत खाली छोड़ना कहते हैं।
इससे ह्यूमस की वृद्धि बढ़ती है जिससे सूक्ष्मजीवों की भी वृद्धि होती है। इसके साथ पोषक तत्त्वों की भी आपूर्ति होती है।
प्रश्न 10.
भंडारित अनाज कैसे नष्ट होता है ?
उत्तर-
चूहे, कीट आदि भंडारित अनाज को नष्ट करते हैं। अनुमानित 25% अनाज चूहों द्वारा नष्ट हो जाता है। कीट और कवक भी अनाज को नष्ट करते हैं। इन ग्रसित अनाजों के सेवन से कई रोग उत्पन्न हो सकते हैं।
प्रश्न 11.
खरपतवार (Weeds) क्या हैं ? इन्हें कैसे दूर किया जाता है ?
उत्तर-
खरपतवार (Weeds) – खेत में उपज के साथ उगने वाले अवांछित पौधे ही खरपतवार कहलाते हैं। खरपतवार को हटाने के लिए खुरपे एवं हैरो (Harrow) का उपयोग किया जाता है।

प्रश्न 12.
हैरो (Harrow) की बनावट बताएँ। इसका मुख्य उपयोग क्या है ?
उत्तर-
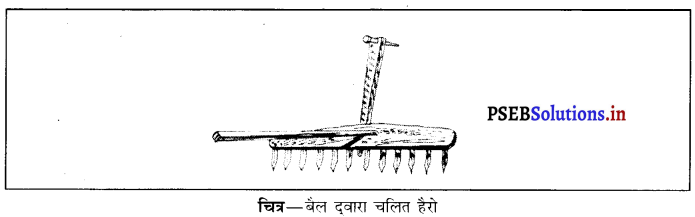
हैरो की बनावट – इसमें नोक वाली लोहे की छड़ या लकड़ी का तख्ता होता है। यह खेत में से हल की तरह खरपतवार को उखाड़ फेंकता है। .
चित्र-बैल द्वारा चलित हैरो उपयोग-यह खरपतवार को उखाड़ने के काम आता है।
प्रश्न 13.
बीज बोने या उपज उगाने से पहले मिट्टी पर हल क्यों चलाया जाता है ?
उत्तर-
बीज बोने से पहले मिट्टी पर हल चलाने के निम्नलिखित कारण हैं-
- हल चलाने से मिट्टी गहराई तक हिल जाती है। इससे आंशिक या पूर्ण मिट्टी पलटी जा सकती है।
- हल चलाने से पहली उपज के अवशेष बाहर निकल जाते हैं और मिट्टी पोली हो जाती है।
- बार-बार हल चलाने से खरपतवार हट जाती है।
- हानिकारक सूक्ष्मजीव नष्ट हो जाते हैं।
- हल चलाने से मिट्टी छिद्र युक्त हो जाती है।
- हल चलाने से मिट्टी नर्म, साफ और उपज उगाने हेतु योग्य बन जाती है।
प्रश्न 14.
खेतों में खाद क्यों डाली जाती है ?
उत्तर-
पौधे पोषक मिट्टी में से ग्रहण करते हैं। यदि फसल लगातार उगाई जाएगी तो मिट्टी के पोषक तत्त्वों में कमी आ जाएगी। इस कमी की पूर्ति के लिए खादें खेत में डाली जाती हैं।
प्रश्न 15.
कटाई (Harvesting) और थ्रेशिंग (Threshing) क्या है ?
उत्तर-
कटाई (Harvesting) – उपज के पकने पर उसे काटा जाता है, इस क्रिया को कटाई कहते हैं। अधिकतर फसलें दराँती या बड़ी कंबाइनों (Combines) से काटी जाती हैं।

थ्रेशिंग (Threshing) – भूसे से अनाज के दानों को पृथक् करने की विधि, थ्रेशिंग कहलाती है। बड़े पैमाने पर जंतुओं को थ्रेशिंग के लिए उपयोग में लाया जाता है।

प्रश्न 16.
ऋतुओं के आधार पर पौधों का वर्गीकरण क्या है ? प्रत्येक किस्म के उदाहरण दीजिए।
उत्तर-
ऋतुओं के आधार पर पौधे दो भागों में वर्गीकृत होते हैं-
(i) खरीफ फसल
(ii) रबी फसल।
(i) खरीफ फसल – मानसून ऋतु में उगने वाली फसल, खरीफ फसल कहलाती है। उदाहरण-मक्का, बाजरा और कपास आदि।
(ii) रबी फसल – शरद ऋतु में उगाई जाने वाली फसल, रबी फसल कहलाती है।
उदाहरण – गेहूँ, चना और सरसों आदि।
प्रश्न 17.
मिश्रित उपज (Mixed Cropping) क्या है ?
उत्तर-
मिश्रित उपज – समय और ऊर्जा की बचत हेतु दो फसलों को एक साथ उगाने की प्रक्रिया मिश्रित उपज कहलाती है।
उदाहरण – कपास के साथ मूंगफली की फसल उगाना।
प्रश्न 18.
मिट्टी में बीज उचित गहराई पर क्यों डालने चाहिएं ?
उत्तर-
मिट्टी में बीज उचित गहराई पर डालने चाहिएं क्योंकि यदि वह अधिक गहराई पर होंगे तो वे पनप नहीं सकेंगे अथवा यदि वे कम गहराई पर होंगे तो पक्षियों एवं जीवों द्वारा खा लिए जाएंगे।
प्रश्न 19.
फसल को कैसे भंडारित किया जाता है ?
उत्तर-
फसल का भंडारण बड़े गोदामों में भारतीय खाद्य निगम (Food Corporation of India) और राज्य गोदाम निगम (State Warehousing Corporation) जैसी संस्थाओं द्वारा किया जाता है।
प्रश्न 20.
उर्वरक की परिभाषा लिखें।
उत्तर-
उर्वरक – मानव निर्मित रसायन जिनमें नाइट्रोजन, फास्फोरस और पोटाशियम अर्थात् जैविक पोषक तत्त्व से भरपूर होता है, उर्वरक कहलाते हैं।
प्रश्न 21.
जैविक खाद का उपयोग क्यों करना चाहिए ?
उत्तर-
जैविक खाद के उपयोग से मिट्टी को कोई हानि नहीं पहुँचती परंतु पोषक तत्त्वों की पूर्ति हो जाती है। यह खाद उर्वरकों से बेहतर है। सब्जियां और फल जो जैविक खाद से वृद्धि करते हैं, खाने के लिए सुरक्षित होते हैं। जबकि सब्जियां और फल उर्वरकों द्वारा वृद्धि करने में सहायक हो सकते हैं।
प्रश्न 22.
आपको कुछ बीज बोने के लिए दिए गए हैं। आप किन कारकों को ध्यान में रखोगे ?
उत्तर-
हमें बीज बोते समय निम्न बातों पर ध्यान देना चाहिए-
- उचित गहराई पर बोना।
- नियमित सिंचाई।
- उचित समय पर खाद देना।
- खरपतवार को न उगने देना।
- पीड़कनाशी का छिड़काव ।
- उचित प्रकाश का प्रबंध।
प्रश्न 23.
रासायनिक उर्वरकों का उपयोग कम क्यों करना चाहिए ?
उत्तर-
रासायनिक उर्वरक. हानिकारक हो सकते हैं क्योंकि-
- मिट्टी की प्राकृतिक उपजाऊ शक्ति नष्ट करते हैं।
- मिट्टी की रसायन प्रकृति बदल देते हैं।
- रसायन मिट्टी में रिस कर उपज में शोषित हो जाते हैं और भोजन श्रृंखला में पहुँच कर पौधों और जानवरों को नष्ट करते हैं।
प्रश्न 24.
हम अनाज कैसे भंडारित करते हैं ? शीत भंडारण (Cold Storage) क्या है ?
उत्तर-
अनाज भंडारण की विधियां-
- किसान धातु अथवा मिट्टी के छोटे डिब्बों में अनाज का भंडारण करता है। इन्हें अनाज घर (Granaries) कहते हैं।
- सूखे अनाज को उचित हवादार सीमेंट के कमरों में स्थानांतरित किया जाता है। इन्हें गोदाम कहते हैं।
- कुछ फलों और सब्जियों को निम्न ताप पर भंडारित किया जाता है। इसे शीत भंडारण कहते हैं।

प्रश्न 25.
एक क्षेत्र में उपज उगाने की मूल आवश्यकताएँ क्या हैं ?
उत्तर-
एक क्षेत्र में उपज उगाने की मूल आवश्यकताएँ-
- उचित किस्म की मिट्टी
- खाद का उपयोग
- सिंचाई
- बीजों की उत्तम किस्में
- कृषि औजार
- उपज के रोगों की रोकथाम के लिए रसायन।
प्रश्न 26.
सभी फसलें एक ही ऋतु में क्यों नहीं उगती हैं ?
उत्तर-
सभी फसलें एक ही ऋतु में नहीं उगती क्योंकि प्रत्येक फसल की वृद्धि के लिए विशेष प्रकार की मिट्टी _ और पर्यावरणीय परिस्थितियाँ जैसे प्रकाश, ताप और वाय चाहिए।
प्रश्न 27.
क्या सभी फसलों को समान खाद और उर्वरक की आवश्यकता होती है ?
उत्तर-
नहीं, प्रत्येक फसल की वृद्धि के लिए विशेष प्रकार की खाद तथा उर्वरक की ज़रूरत होती है। धान की फसल के लिए जैविक खाद (Farmyard Manure) उत्तम है। मूंगफली की फसल को कोई खाद व उर्वरक नहीं चाहिए क्योंकि इसकी जड़ों में ग्रंथिकाएँ (Nodules) होती हैं, जिनमें नाइट्रोजन स्थिर करने वाले बैक्टीरिया होते हैं। यह वायुमंडलीय नाइट्रोजन को स्थिर करके नाइट्राइट और नाइट्रेट में परिवर्तित कर देते हैं। गेहूँ की फसल के लिए हरी खाद (Green Malure) और जैविक खाद (Farmyard Manure) का मिश्रण उपयोग में लाया जाता है।
प्रश्न 28.
कीटनाशकों तथा खरपतवार नाशकों में दो अन्तर बताओ।
उत्तर-
कीटनाशकों और खरपतवार नाशकों में अन्तर-
| कीटनाशक (Insecticides) |
खरपतवार नाशक (Weedicides) |
| (i) यह रसायन उपज को नुकसान पहँचा रहे कीटों का नाश करती है। |
(i) यह रसायन उपज के साथ उगे अवांछित पौधों (खरपतवारों) का नाश करती है। |
| (ii) यह रसायन मानवीय शरीर पर प्रभाव डालते हैं। उदाहरण D.D.T. |
(ii) यह रसायन मानवीय शरीर पर प्रभाव डालते हैं और भोजन श्रृंखला में भी सम्मिलित हो जाते हैं। उदाहरण 2-+ D, बूटाकलौर |
प्रश्न 29.
पनीरी लगाने से क्या भाव है ?
उत्तर-
पनीरी लगाना-धान, मिर्च, टमाटर तथा गोभी आदि ऐसी फसलें हैं जिनको सीधे ही खेत में नहीं लगाया जाता। इनके बीजों को एक छोटे-से भू-खण्ड में बीज कर जो पनीरी तैयार की जाती है, उसे पनीरी (Seedling) कहते हैं।
जब पनीरी अच्छी तरह तैयार हो जाती है तो भू-खण्ड में से उखाड़कर खेतों में एक विशेष दूरी पर लगा दिया जाता है। इस विधि को पनीरी लगाना कहते हैं।
प्रश्न 30.
सिंचाई के पारंपरिक तरीकों का चित्रों द्वारा वर्णन करो।
उत्तर-
सिंचाई के पारंपरिक तरीके
(a) मोट
(b) चेन पंप
(c) ढेकली
(d) रहट।
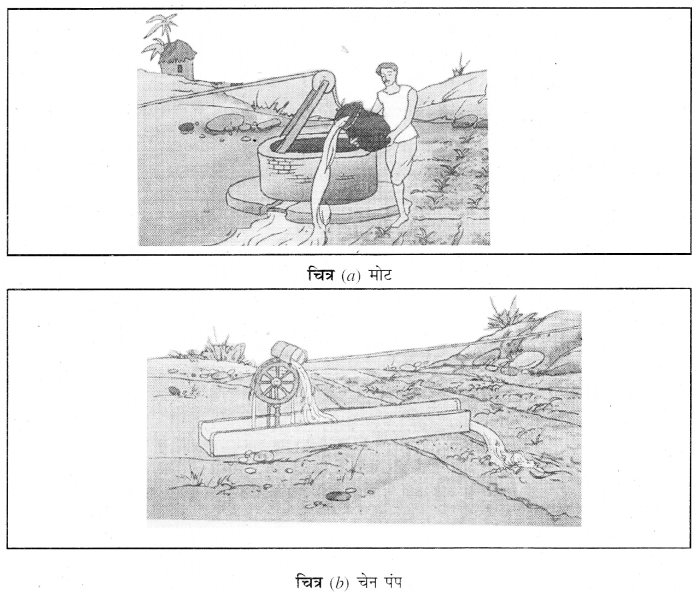
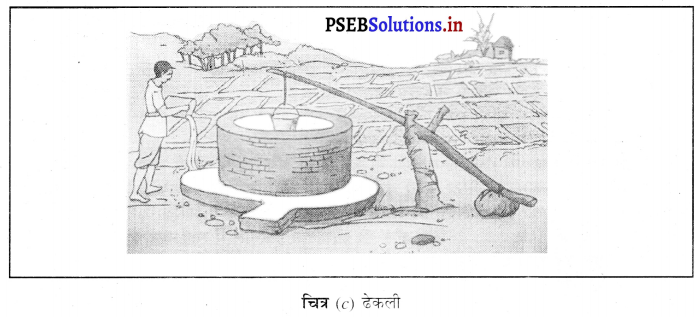

पानी खींचने के लिए प्रायः पंपों का उपयोग किया जाता है। डीज़ल, बायोगैस, विद्युत् और सौर ऊर्जा से पंप चलाए जाते हैं। पंपों की विभिन्न शक्ति होती है। उनका चयन क्षेत्र की आवश्यकता के आधार पर किया जाता है।

TYPE-III
दीर्घ उत्तरात्मक प्रश्न
प्रश्न 1.
मुख्य कृषि पद्धतियों का वर्णन करें।
उत्तर-
मुख्य कृषि पद्धतियाँ-
- हल चलाना – इससे मिट्टी पोली और पतली हो जाती है। यह लकड़ी या लोहे के बने होते हैं। हल चलाने के बाद मिट्टी समतल की जाती है ताकि हवा और पानी से मिट्टी उड़ न सके।
- बुआई – मिट्टी की तैयारी के बाद खेतों में बीज हाथों अथवा सीड-ड्रिल द्वारा डाला जाता है। इसे बुआई __ कहते हैं।
- सिंचाई – फसली पौधे मिट्टी में से जड़ों द्वारा जल ग्रहण करते हैं। पौधे की वृद्धि के लिए पानी आवश्यक है। सिंचाई के विभिन्न ढंगों जैसे-पानी चक्की, छिड़काव, ट्यूवबैल, दोलित टोकरियों आदि का उपयोग किया जाता है।
- खाद डालना – प्रत्येक फसल मिट्टी में से काफ़ी मात्रा में पोषक अवशोषित करती है। इन पोषकों की पूर्ति के लिए खाद डालना आवश्यक है।
- निराई – खेतों में फसल के साथ कई अन्य पौधे भी उग जाते हैं। यह फसल के साथ जल, प्रकाश और पोषकों की स्पर्धा रखते हैं। अतः इनका खेतों में से हटाना अति आवश्यक है। इस क्रिया को निराई कहते हैं।
- फसल की सुरक्षा – कीट, कवक, बैक्टीरिया, चूहे आदि फसल को नुकसान पहुंचाते हैं। कीटनाशी और खरपतवारनाशी का उपयोग करके इन्हें नष्ट किया जाता है।
- कटाई और भंडारण – जब फसल तैयार हो जाती है तो उचित समय पर इसे काटा जाता है। फसलों की कटाई हाथों से, दराँती से अथवा हारवेस्टर से की जाती है। अनाज को भूसे से अलग किया जाता है और अनाज का भंडारण बड़े-बड़े भंडार ग्रहों में किया जाता है। अनाज में नमी की मात्रा 14% से अधिक नहीं होनी चाहिए।
प्रश्न 2.
फसल की उपज बढ़ाने के लिए कौन-सी पद्धतियाँ इस्तेमाल में लाई जाती हैं ?
उत्तर-
फसल की उपज बढ़ाने की पद्धतियाँ हैं-
(i) मिट्टी में उर्वरकों का मिलाना
(ii) चयनित बीजों का उपयोग
(iii) खरपतवार नियंत्रण
(iv) पौधों के रोगों का नियंत्रण।
(i) उर्वरक (Fertilizers) – यह रासायनिक पदार्थ, खेतों में मिट्टी की उपजाऊ शक्ति बढ़ाने के लिए डाले जाते हैं। यह पोषक तत्त्वों की आपूर्ति करके फसल की उपज बढ़ाने में सहायक होते हैं।
(ii) चयनित बीजों का उपयोग (Selective Breeding) – रोग निरोधक बीजों का निर्माण किया जाता है। उच्च किस्म के बीजों के नियमित उपयोग से फसल में वृद्धि होती है।
(iii) खरपतवार नियंत्रण (Weed Control) – खरपतवार-नाशकों के उपयोग से खरपतवार को नष्ट किया जाता है।
(iv) पौधों के रोगों का नियंत्रण (Control of Plant Diseases) – फसल को कीटों, कवक, जंतुओं और रोगों से बचाना चाहिए। फसल की उपज के लिए यह अति आवश्यक प्रक्रम है। कीटों को नष्ट करने के लिए कीटनाशी का उपयोग करना चाहिए।
प्रश्न 3.
उर्वरक क्या है ? मिश्रित उर्वरक क्या है ? किसान खेतों में उर्वरक क्यों डालते हैं ? हमें उर्वरक कैसे भंडारित करने चाहिएं ?
उत्तर-
उर्वरक – खेत अथवा मिट्टी की उपजाऊ शक्ति कायम रखने के लिए उपयोग किए जाने वाले रसायन, उर्वरक कहलाते हैं।
मिश्रित उर्वरक-उर्वरक जो एक साथ कई पोषक तत्त्वों की आपूर्ति करें, मिश्रित उर्वरक कहलाते हैं ; जैसे-
(i) NPK में नाइट्रोजन, फास्फोरस और पोटाशियम है।
(ii) CAN – कैल्शियम, अमोनियम नाइट्रेट का मिश्रित उर्वरक है।
उर्वरकों की महत्ता – खेतों में खनिज तत्त्व जैसे नाइट्रोजन, फास्फोरस और पोटाशियम की आपूर्ति के लिए रासायनिक उर्वरक और मिश्रित उर्वरक डाले जाते हैं। मिट्टी में तत्त्वों की कमी लगातार उपज उगाने से होती है। इसलिए किसान खेतों में उर्वरक डालते हैं।
उर्वरकों का भंडारण – कई उर्वरक नमी प्रिय होते हैं अर्थात् यह जल शोषित करते हैं। यदि उर्वरकों को नमी युक्त स्थानों पर भंडारित किया जाए तो यह खेतों में डालने योग्य नहीं रहते। कुछ उर्वरक थैलों को नष्ट कर देते हैं जिनमें वे रखे जाते हैं। इनका भंडारण शुष्क स्थानों पर होना चाहिए।
प्रश्न 4.
जुताई (Ploughing) के लिए कौन-कौन से औज़ार उपयुक्त होते हैं, वर्णन करो।
उत्तर-
जुताई (Ploughing) के लिए उपयोग में आने वाले औज़ार-हल, कुदाली (Hoe), कल्टीवेटर (Cultivator)।
(i) हल – इसका उपयोग मिट्टी के पलटने, उर्वरक डालने, खरपतवार हटाने, मिट्टी को छांटने आदि के लिए किया जाता है। यह लकड़ी से बना होता है और बैलों के एक जोड़े से खींचा जाता है।

इसमें लोहे की मज़बूत तिकोनी पत्ती होती है, जिसे फाल कहते हैं। हल का मुख्य भाग लंबी लकड़ी का बना होता है जिसे हल शैफ्ट कहते हैं। इसके एक सिरे पर हैंडल होता है तथा दूसरा सिरा जोत के डंडे से जुड़ा होता है जिसे बैलों की गरदन के ऊपर रखा जाता है। एक जोड़ी बैल एवं एक आदमी इसे सरलता से चला सकता है।
(ii) कुदाली (Hoe) – यह एक सरल औज़ार है जिसका उपयोग खरपतवार निकालने और मिट्टी को पोला करने के लिए किया जाता है। इसमें लकड़ी अथवा लोहे की छड़ होती है जिसके सिरे पर लोहे की चौड़ी और मुड़ी प्लेट लगी होती है जो ब्लेड का कार्य करती है। इसका दूसरा सिरा पशुओं द्वारा खींचा जाता है।
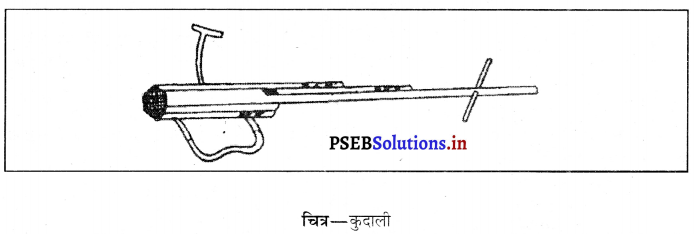
(iii) कल्टीवेटर (Cultivator) – आजकल जुताई ट्रैक्टरों द्वारा संचालित कल्टीवेटर से की जाती है। इनके उपयोग से श्रम और समय दोनों की बचत होती है।

![]()


![]()