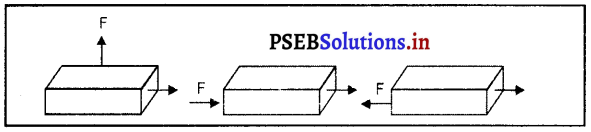
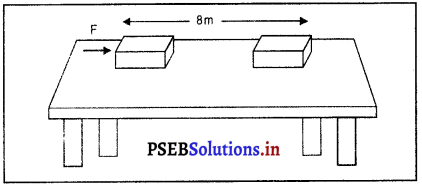
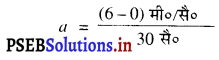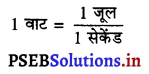Punjab State Board PSEB 9th Class Science Important Questions Chapter 8 गति Important Questions and Answers.
PSEB 9th Class Science Important Questions Chapter 8 गति
दीर्घ उत्तरात्मक प्रश्न (Long Answer Type Questions)
प्रश्न 1.
गणितीय विधि द्वारा गति के समीकरणों को स्थापित कीजिए।
उत्तर-
एक समान त्वरण के अंतर्गत गति के समीकरण – एक समान त्वरण के अंतर्गत सरल रेखीय गति करती हुई वस्तु के लिए गति के निम्न समीकरण हैं-
(i) ν = u + at
(ii) S = ut + \(\frac {1}{2}\)at2
(iii) v2 – u2 = 2aS
(i) गति का प्रथम समीकरण v = u + at
मान लो किसी गतिशील वस्तु का प्रारंभिक वेग u व एकसमान त्वरण है। मान लो 1 सेकंड में S दूरी चलने के पश्चात् वस्तु का वेग v हो जाता है।
1 सेकंड में वस्तु के वेग में वृद्धि = a
1 सेकंड में वस्तु के वेग में वृधि = a × t
अत: t सेकंड के पश्चात् वस्तु का वेग = वस्तु का प्रारंभिक वेग + 1 सेकंड में वस्तु के वेग में वृद्धि
अथवा V = u + at
(ii) गति का दूसरा समीकरण S = ut + \(\frac {1}{2}\)at2
मान लो किसी गतिशील वस्तु का प्रारंभिक वेग u , एक समान त्वरण a तथा 1 समय पश्चात् वस्तु का अंतिम वेग v हो जाता है, अतः
1 सेकंड में वस्तु के वेग में वृद्धि = a
गति के प्रारंभ होने के 1 सेकंड बाद वस्तु का वेग = (u + a)
गति समाप्त होने के 1 सेकंड पहले वस्तु का वेग = (v – a)
अतः वस्तु का औसत वेग = \(\frac{(u+a)+(v-a)}{2}\)
= \(\frac{(u+v)}{2}\)
इसी प्रकार, गति प्रारंभ होने के 2 सेकंड बाद वस्तु का वेग = (u + 2a)
गति समाप्त होने के 2 सेकंड पहले वस्तु का वेग = (v – 2a)
अतः वस्तु का औसत वेग = \(\frac{(u+2 a)+(v-2 a)}{2}\)
= \(\frac{(u+v)}{2}\)
इस प्रकार, त्वरण के नियत होने पर वस्तु का औसत वेग सदैव ही \(\frac {1}{2}\) (u + v) रहता है। अतः हम यह मान सकते हैं कि t सेकंड तक वस्तु औसत वेग \(\frac {1}{2}\)(u + v) से चलती है।
अतः t सेकंड में वस्तु द्वारा चली गई दूरी, S = वस्तु का औसत वेग × समय
= \(\frac {1}{2}\)(u + v) × t
परंतु गति के प्रथम समीकरण v = u + at से
∴ वस्तु द्वारा चली गई दूरी S = b[latex]\frac{u+(u+a t)}{2}[/latex] × t
= [latex]\frac{2 u t+a t^{2}}{2}[/latex]
S = u t + \(\frac {1}{2}\)at2
(iii) गति का तीसरा समीकरण – गति के प्रथम समीकरण v = u + at का दोनों ओर का वर्ग करने पर,
v2 = (u + at)2
= u2 + 2u at + a2t2
= u2 + 2a (ut + \(\frac {1}{2}\)at2)
परंतु गति की दूसरी समीकरण से, ut + = \(\frac {1}{2}\)at2 का मान रखने पर
v2 = u2 + 2aS
v2 – u2 = 2aS

प्रश्न 2.
एक समान त्वरण से गतिमान वस्तु के लिए, ग्राफ़ीय विधि से निम्नलिखित संबंध स्थापित कीजिए-
(i) v = u + at,
(ii) S = u t + \(\frac {1}{2}\)at2,
(iii) v2 = u2 + 2 aS.
उत्तर-
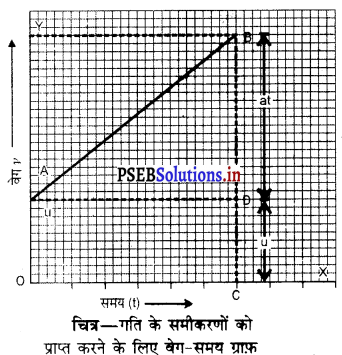
I. ग्राफ द्वारा गति के समीकरण स्थापित करना-मान लो कोई वस्तु प्रारंभिक वेग u तथा अचर त्वरण a से चलना प्रारंभ करती है तथा t समय पश्चात् वस्तु का वेग v हो जाता है। यदि समय को X-अक्ष पर तथा वेग को Y-अक्ष पर निरूपित किया जाए तो वस्तु का समय-वेग ग्राफ एक झुकी हुई सरल रेखा BA के रूप में प्राप्त होता है। इसकी सहायता से गति के समीकरणों को निम्नलिखित प्रकार से ज्ञात करते हैं-
BC = BD + DC
BD + OA (∵ DC = OA)
इसमें BC = v तथा OA = u रखने पर हम पाते हैं,
v = BD + u
या BD = v – u ………………….(1)
वेग समय ग्राफ़ से वस्तु के त्वरण को व्यक्त किया गया है।

OC = t, रखने पर हम पाते हैं,
a = BD
t …………….(2)
या BD = at
समीकरण (1) तथा (2) से हम पाते हैं।
V = u + at
II. समय-स्थिति संबंध
मान लें एक वस्तु एक समान त्वरण α से t समय में S दूरी तय की। चित्र में वस्तु द्वारा तय की गई दूरी, वेगसमय ग्राफ़ AB के नीचे घिरे क्षेत्र OABC द्वारा प्राप्त की जाती है।
इस प्रकार, वस्तु के द्वारा तय की गई दूरी S निम्न प्रकार से व्यक्त की जाती है,
S = OABC का क्षेत्रफल (जो एक समलंब है)
= आयत OADC का क्षेत्रफल + त्रिभुज ABD का क्षेत्रफल
= OA × OC + \(\frac {1}{2}\) (AD × BD)
OA = u, OC = AD = t और BD = at, मान रखने पर हम पाते हैं,
S = u × t + \(\frac {1}{2}\) (t × at)
या S. = ut + \(\frac {1}{2}\)at2
III. वेग-स्थिति संबंध
चित्र में प्रदर्शित वेग-समय ग्राफ़ से वस्तु द्वारा एक समान त्वरण a से 1 समय में तय की गई दूरी S को ग्राफ़ नीचे समलंब चतुर्भुज OABC द्वारा घेरे गए क्षेत्रफल द्वारा प्रदर्शित किया गया है। अर्थात्
S = समलंब OABC का क्षेत्रफल
= \(\frac{(\mathrm{OA}+\mathrm{BC}) \times \mathrm{OC}}{2}\)
OA = u, BC = v और OC = t रखने पर हम पाते हैं,
S = \(\frac{(u+v)_{t}}{2}\) ………………… (3)
वेग-समय संबंध से हम पाते हैं,
t = \(\frac{(v-u)}{a}\) ……………….. (4)
समीकरण (3) और समीकरण (4) से हम पाते हैं,
S = \(\frac{(v+u) \times(v-u)}{2 a}\)
या 2a S = v2 – u2
प्रश्न 3.
(क) दूरी-समय ग्राफ़ क्या है ?
(ख) इसकी ढाल क्या प्रदर्शित करती है ?
उत्तर-
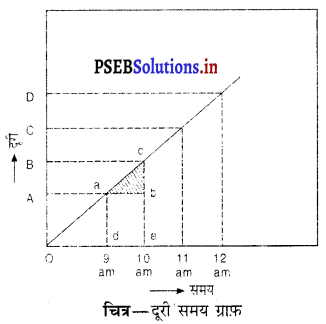
(क) समय-दूरी ग्राफ – यह किसी वस्तु द्वारा तय दूरी तथा लगे समय में रेखांकित ग्राफ है। यह सरल रेखीय हो भी सकता है और नहीं भी।
दूरी-समय का अर्थ – जब कोई वस्तु एक समान है चाल से गतिमान होती है तो यह समान-अंतरालों में से समान दूरी तय करती है। एक समान चाल से गतिमान वस्तु का दूरी-समय ग्राफ़ सदा सरल रेखीय होता है।
उदाहरण – समय-दूरी से यह देखा गया है कि 9 पू० दो० से 10 पृ० दो० तथा 10 पू० दो० से 11 पू० दो० के समय अंतरालों में क्रमश: AB तथा CD दूरी तय होती है।
यह भी देखा जा सकता है कि AB = CD
चित्र-दूरी समय ग्राफ़ अतः समान दूरी समान समय अंतरालों में तय की जाती है जिस कारण चाल एक समान है।
(ख) दूरी-समय ग्राफ की ढाल – मान लो a और c समय-दूरी ग्राफ पर निकटवर्ती बिंदु हैं। ad और ce दो लंब क्रमशः a और C से समय-अक्ष पर गिराओ। ab⊥ce खींचो। तब त्रिभुज abr में अनुपात \(\frac{b c}{a b}\) को ग्राफ की ढाल कहते हैं।
∴ रेखा की ढाल = \(\frac{b c}{a b}\)
फिर bc वस्तु द्वारा ab समय में तय हुई दूरी

अतः दूरी – समय ग्राफ की ढाल = चाल
दूरी – समय ग्राफ की ढाल वस्तु की चाल को दर्शाती है।

प्रश्न 4.
वेग-समय ग्राफ की सहायता से एक समान वेग से गतिशील वस्तु की दूरी कैसे ज्ञात करोगे ? उदाहरण सहित समझाओ।
उत्तर-
एक समान गति के लिए वेग – समय ग्राफ-एक समान गति के लिए किसी वस्तु का वेग-समय ग्राफ वह ग्राफ होता है जब कोई वस्तु स्थिर वेग से चल रही हो। ऐसी अवस्था में वेग-समय ग्राफ X अक्ष के समांतर होता है। चित्र में सरल रेखा द्वारा दर्शाया गया है ।
मान लो रमेश अपने मोटर साइकिल पर 40 km/h के स्थिर वेग से जा रहा है। इसका अर्थ है कि किसी भी समय अंतराल में उसका वेग 40 km/h पर स्थिर रहेगा। इसलिए वह पहले एक घंटे में 40 km., दूसरे घंटे के अंत में 80 km तथा तीसरे घंटे के अंत में 120 km दूरी तय करेगा। अगले प्रत्येक घंटे में उसकी दूरी इसी तरह बढ़ती जाएगी। ग्राफ की सहायता से हम किसी भी दिए समय में रमेश द्वारा तय की गई दूरी पता कर सकते हैं।
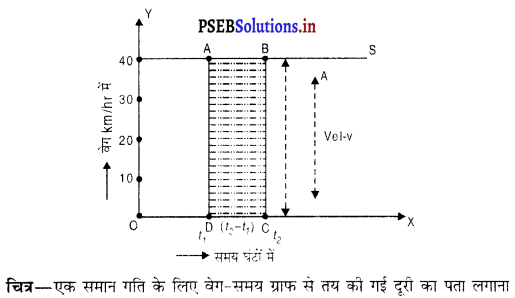
सरल रेखीय ग्राफ RS पर बिंदु A तथा B समय अंतरालों OD = t1 तथा OC = t2 पर रमेश की स्थिति दर्शाता है । समय मूल बिंदु 0 से मापा गया है। AD तथा BC बिंदु A तथा B से समय अक्ष पर लंब खींचे गए हैं। इस प्रकार ABCD एक आयत बन गई है ।
समय अंतराल (OC-OD) = (t2 – t1) में रमेश द्वारा तय की गई दूरी
S = आयत ABCD का क्षेत्रफल
= AD × DC
= वेग × समय अंतराल
S = v × (t2 – t1)
या S = 40 × (t2 – t1) km
प्रश्न 5.
एक समय प्रवेगित गति के लिए वेग-समय ग्राफ बनाओ तथा इस ग्राफ से आप वस्तु द्वारा तय की गई दूरी का पता कैसे करोगे ?
उत्तर-
एक समान प्रवेगित के लिए वेग-समय ग्राफ-जब कोई वस्तु स्थित वेगसे नहीं, परंतु लगातार बढ़ते हुए वेग के साथ चल रही हो, तो वह वस्तु प्रवेगित होती है तथा इसकी गति को प्रवेगित गति कहते हैं। इस अवस्था में वेग-समय (v – t) ग्राफ एक सरल रेखा OR होता है जो मूल बिंदु O से शुरू होता है तथा दोनों अक्षों से दूर जाता है ।
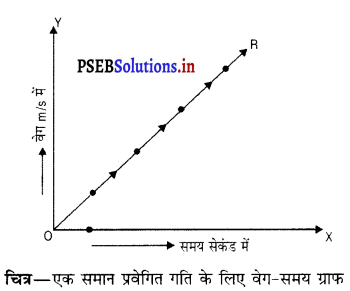
निम्न चित्र की सहायता से हम एक समान प्रवेगित गति के साथ चल रही वस्तु द्वारा तय की गई दूरी पता कर सकते हैं ।
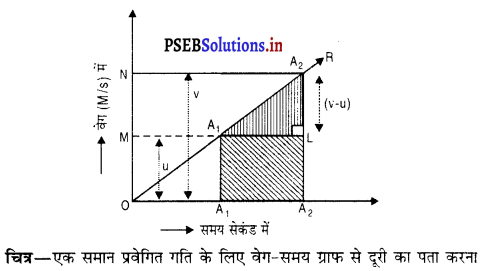
OR एक सरल रेखीय ग्राफ है। ग्राफ पर दो बिंदुओं A1 तथा A2 से समय-अक्ष पर A1, A4 तथा A2, A3 लंब खींचो : A2, A3 पर एक लंब AL खींचो। समलंब चतुर्भुज A1A2A3A4 का क्षेत्रफल वस्तु द्वारा तय की गई दूरी होगी।
समलंब चतुर्भुज A1A2A3A4 का क्षेत्रफल = \(\frac {1}{2}\)(A1A4 + A2A3) × A1L
S = \(\frac {1}{2}\)(u + v) × (t2 – t1)
तय की गई दूरी S = औसत वेग × समय अंतराल
प्रश्न 6.
निम्नलिखित के ग्राफ खींचकर उदाहरण द्वारा समझाए-
(i) एकसमान त्वरित गति
(ii) असमान त्वरित गति।
उत्तर-
(i) एकसमान त्वरित गति- यदि किसी वस्तु के वेग में समान समय अंतरालों में समान परिवर्तन होता है, तो वस्तु की गति एकसमान त्वरित गति कहलाती है। चित्र (a) में मुक्त रूप से गिरते हुए पत्थर का वेगसमय ग्राफ प्रदर्शित है। इसमें पत्थर का वेग प्रति सेकंड 9.8 मीटर/सेकंड बढ़ता जाता है, अर्थात् वस्तु की गति में त्वरण 9.8 मीटर/सेकंड है। यह ग्राफ एक झुकी हुई सरल रेखा के रूप में प्राप्त होता है, जो यह दर्शाता है कि वस्तु की गति एक समान त्वरित गति है ।
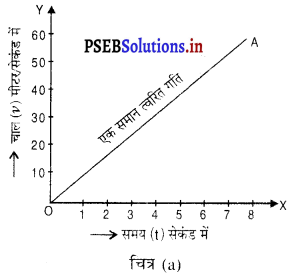
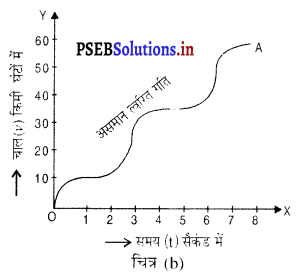
यदि किसी वस्तु के वेग समान समय अंतरालों में असमान परिवर्तन होते हैं, तब वस्तु की गति असमान त्वरित गति कहलाती है। चित्र में एक कार की गति का वेग-समय ग्राफ दिया गया है। इसमें कार का वेग घटता-बढ़ता है। वह ग्राफ टेढ़े-मेढ़े वक्र के रूप में प्राप्त होता है, जो यह दर्शाता है कि कार की गति, असमान त्वरित गति है।

प्रश्न 7.
(क) वृत्तीय गति क्या होती है ? समान चाल की वृत्तीय गति त्वरित गति क्यों होती है ?
(ख) कोणीय वेग की परिभाषा दो । इसकी इकाई क्या है ?
(ग) सरल रेखीय और कोणीय वेगों में संबंध स्थापित करो ।
उत्तर-
(क) वृत्तीय गति – यदि किसी गतिमान वस्तु का गमन पथ सरल रेखा न होकर एक वृत्त हो, तो उस वस्तु की गति को वृत्तीय गति कहते हैं।
वृत्तीय गति में चाल अचर होने पर भी प्रत्येक बिंदु दिशा में होने वाला निरंतर परिवर्तन वेग में परिवर्तन उत्पन्न करता है, जिससे वस्तु की गति त्वरित होती है ।
(ख) कोणीय वेग – प्रति इकाई समय में हुए कोणीय विस्थापन को कोणीय वेग कहते हैं।
यदि t समय में वस्तु θ कोण तय करती है, तो कोणीय वेग इस प्रकार दिया जा सकता है-

या ω =
यह ω (ओमेगा) वर्तुल वेग को दर्शाता है
ω = \(\frac{\theta}{t}\)
कोणीय वेग की इकाई – कोणीय वेग रेडियन प्रति सेकंड में मापा जाता है।
(ग) सरल रेखीय तथा कोणीय वेग में संबंध – मान लो एक वस्तु एक समान रेखीय वेग v से r अर्धव्यास वाले वृत्त में गतिमान है। मान लो सरल रेखा में : s दूरी t समय में तय की गई और इसके सापेक्ष कोण θ विस्थापित होता है।
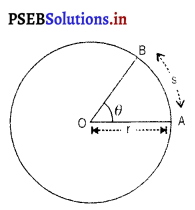
तब कोण (रेडियन में)
θ = \(\frac{\mathrm{s}}{t}\) …………………. (i)
परंतु सरल रेखीय दूरी = चाल × समय
s = v × t ………………… (ii)
(2) से s का यह मान समीकरण (t) में रखने पर,
θ = \(\frac{v \times t}{r}\)
या \(\frac{\theta}{t}=\frac{v}{r}\)
ω = \(\frac{v}{r}\) (∵ \(\frac{\theta}{r}\) = ω)
अर्थात् v = r ω
प्रश्न 8.
एक समान वक्रीय या वर्तुल गति क्या होती है ? एक समान वक्रीय गति प्रवेगित गति क्यों होती है ? व्यावहारिक क्रिया द्वारा समझाओ। इससे क्या निष्कर्ष निकलता है ?
उत्तर-
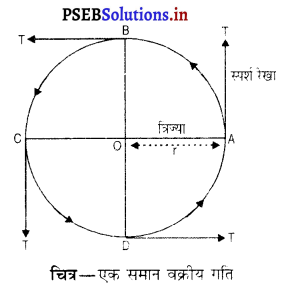
एक समान वर्तुल या वक्रीय गतिएक समान वक्रीय गति वह गति होती है जहां कि एक समान प्रवेगित गति, वेग की मात्रा में परिवर्तन के
स्पर्श रेखा कारण नहीं अपितु वेग की दिशा में परिवर्तन कारण होती है। जब कोई वस्तु वृत्ताकार पथ में घूमती है तो उस वृत्त की परिधि के प्रत्येक जिंदु पर गति की दिशा बदलती रहती है । दिखाए गए चित्र में बिंदु A, B, C, D वस्तु की चार स्थितियां दर्शायी गई हैं। CT तथा DT इन बिंदुओं पर गति की भिन्न-भिन्न दिशाएं हैं। अब क्योंकि गति की दिशा बदल रही है इसलिए वस्तु बदले हुए वेग से गति करती है । इसलिए यह गति एक समान प्रवेगित है।
महत्त्वपूर्ण निष्कर्ष – मान लो एक विद्यार्थी, अर्धव्यास = r वाले वृत्त की परिधि के साथ-साथ एक पूरा चक्कर ‘t’ सेकंड में लगाता है, तो उसका वेग,

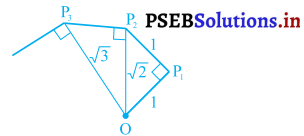
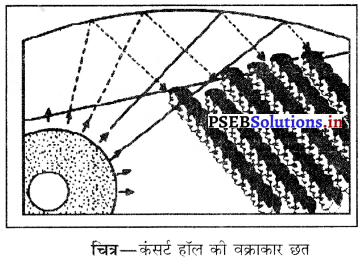
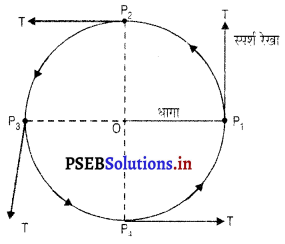
व्यावहारिक क्रिया – एक मीटर लंबा सूती या नायलॉन का धागा लो। इसके एक सिरे के साथ एक धातु का गोला बांधो तथा दूसरे सिरे को हाथ से पकड़ कर गोले को वृत्ताकार पथ में घुमाओ। जब गोला घूम रहा है तो इसकी चाल उस समय एक समान रहती है पर इसका वेग प्रत्येक बिंदु पर बदलता रहता है। वेग में परिवर्तन का कारण गोले की गति की दिशा में परिवर्तन है। गति की दिशा हमेशा वृत्ताकार पथ के स्पर्श रेखा के साथ होती है। स्पर्श रेखा वृत्त के अर्धव्यास के लंब रूप में होती है। चित्र में P1T तथा P2T क्रमशः P1 तथा P2 पर स्पर्श रेखाएं हैं जो इन बिंदुओं पर गोले की गति की दिशाएं दर्शाती हैं। यदि किसी भी समय गोले को छोड़ दिया जाए तो यह तीर की दिशाओं में जा गिरेगा।
लघु उत्तरात्मक प्रश्न (Short Answer Type Questions)
प्रश्न 1.
किसी वस्तु की विराम अवस्था तथा गति अवस्था को उदाहरण देते हुए स्पष्ट कीजिए।
उत्तर-
विराम अवस्था – यदि किसी वस्तु की स्थिति में समय के साथ कोई परिवर्तन नहीं होता है तो वह वस्तु विराम अवस्था में कहलाती है।
उदाहरण – मेज पर रखी हुई पुस्तक. पृथ्वी पर खड़े पेड़-पौधे तथा बिजली का खंभा आदि।
गति अवस्था- यदि किसी वस्तु की स्थिति में समय के साथ-साथ परिवर्तन हो रहा है तो वह वस्तु गति की अवस्था में कहलाती है।
उदाहरण – सड़क पर दौड़ती कार, वायु में उड़ता हुआ वायुयान आदि।

प्रश्न 2.
गति की विभिन्न किस्में कौन-कौन सी हैं ? उदाहरण देकर स्पष्ट कीजिए।
उत्तर-
गति की विभिन्न किस्मेंगति की तीन विभिन्न किस्में हैं-
- सरल रेखीय
- वर्तुल गति
- दोलन गति।
उदाहरण-
(1) मान लो एक प्रेक्षक ) पर है और वह एक कार स्थिति A में देखता है। कुछ देर बाद वह कार को स्थिति B पर देखता है। कार की इस स्थिति में परिवर्तन यह बतलाता है कि कार O के सापेक्ष गति में है।

(2) मान लो एक व्यक्ति धागे के एक सिरे पर बंधे पत्थर को घुमा रहा है । वह किसी क्षण पत्थर को A पर और फिर कुछ क्षण के बाद B पर देखता है। अतः O के सापेक्ष पत्थर की स्थिति बदलती है। अतः पत्थर O के सापेक्ष गति में है। यह वर्तुल या कोणीय गति का उदाहरण है।
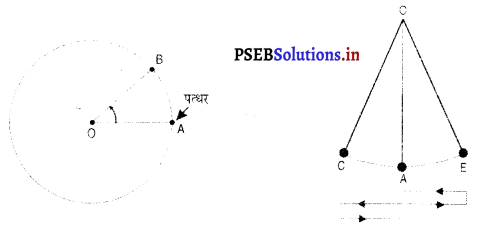
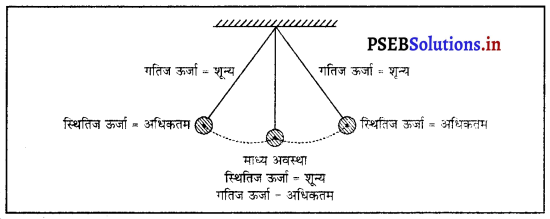
(3) मान लो धागे से बंधा पत्थर एक निश्चित बिंदु से नीचे लटक रहा है। यदि पत्थर को हम एक ओर ले जाकर छोड़ दें तो यह A के इर्द-गिर्द बार-बार उसी पथ पर गति करने लगेगा। इस तरह की गति को दोलन गति कहते हैं।
प्रश्न 3.
“विराम तथा गति सापेक्ष है।” इस कथन से क्या अभिप्राय है ?
उत्तर-
विराम तथा गति सापेक्ष- इसका अर्थ यह है कि यदि कोई वस्तु किसी अन्य वस्तु के सापेक्ष विराम अवस्था में है तो इसका यह अर्थ नहीं है कि वह संसार की अन्य सभी वस्तुओं के सापेक्ष विराम अवस्था में है। यह अन्य वस्तुओं के सापेक्ष गति में हो सकती है। अतः हम कहते हैं कि विराम और गति सापेक्ष हैं।
प्रश्न 4.
अदिश तथा सदिश राशियों को परिभाषित कीजिए।
उत्तर-
अदिश राशियां – जिन भौतिक राशियों को व्यक्त करने के लिए केवल परिमाण की आवश्यकता होती है, अदिश राशियां (scalar quantities) कहलाती हैं। जैसे-लंबाई, दूरी, द्रव्यमान, क्षेत्रफल, समय, चाल, कार्य, ऊर्जा, ताप, घनत्व, आयतन, विद्युत् धारा आदि।
किसी भी अदिश राशि को केवल एक संख्या द्वारा व्यक्त किया जा सकता है। जैसे-
अदिश राशियों को गणित के साधारण नियमों के अनुसार जोडा, घटाया, गणा एवं भाग किया जा सकता है।
सदिश राशियां – जिन भौतिक राशियों को व्यक्त करने के लिए परिमाण एवं दिशा दोनों की आवश्यकता होती है, वे सदिश राशियां (vector quantities)) कहलाती हैं। जैसे-विस्थापन, वेग, त्वरण, बल, संवेग, भार, विद्युत् क्षेत्र आदि।
किसी भी सदिश राशि को पूर्ण रूप से व्यक्त करने के लिए राशि के परिमाण के साथ-साथ उसकी दिशा का उल्लेख करना भी आवश्यक है।
प्रश्न 5.
सदिश और अदिश राशियों में अंतर बताइये।
उत्तर-
| सदिश |
अदिश |
| 1. सदिश राशियां वे भौतिक राशियां हैं जिनमें दिशा और परिमाण दोनों होते हैं, जैसे-विस्थापन, बल, वेग विस्थापन आदि। |
1. अदिश राशियां वे भौतिक राशियां हैं जिनमें केवल परिमाण होता है, जैसे द्रव्यमान, आयतन, दूरी आदि। |
| 2. इन्हें तीर के चिह्न से निरूपित किया जाता है। |
2. इन्हें किसी विशेष तरीके से निरूपित नहीं किया जाता। |
| 3. इनका संकलन त्रिभुज या समांतर चतुर्भुज के नियम द्वारा किया जा सकता है। |
3. इन्हें बीज गणितीय ढंग से संकलित किया जा सकता है। |
प्रश्न 6.
निम्नलिखित भौतिक राशियों को अदिश तथा सदिश में वर्गीकृत कीजिए-
दूरी, विस्थापन, घनत्व, बल, संवेग, वेग, त्वरण, चाल, समय, आयतन, ऊर्जा।
उत्तर-
अदिश राशियां – दूरी, घनत्व, चाल, आयतन, ऊर्जा, समय।
सदिश राशियां – विस्थापन, बल, संवेग, वेग, त्वरण।
उदाहरण – एक चल रही रेलगाड़ी में दो यात्रियों A तथा B पर विचार करें। दोनों यात्री एक-दूसरे तथा रेलगाड़ी के सापेक्ष विराम अवस्था में हैं। परंतु रेलगाड़ी के बाहर स्थित प्रेक्षकों के सापेक्ष उनकी स्थिति निरंतर बदल रही है। अतः वे बाहरी प्रेक्षकों के सापेक्ष गति में हैं। अतः विराम और गति सापेक्ष कथन हैं।

प्रश्न 7.
मूल बिंदु क्या है ? उदाहरण भी दो।
उत्तर-
मूल बिंदु – यह एक निश्चित बिंदु है, जिसके सापेक्ष किसी वस्तु की स्थिति का वर्णन किया जा सकता है।
वस्तु की स्थिति बताने के लिए हम मूल बिंदु से उसकी दूरी और दिशा बताते हैं। जैसे ही वस्तु गति करती है, मूल बिंदु के सापेक्ष इसकी गति और दिशा बदल सकती है।
उदाहरण-
(i) मान लो O एक निश्चित बिंदु है। इस बिंदु O से चल कर एक कार किसी समय P पर पहुंचती है। OP = 3 कि० मी० है। तब हम कहते हैं कि कार ने O के सापेक्ष 3 किलोमीटर दूरी तय की है। कार की स्थिति O के सापेक्ष ही परिभाषित की जा रही है ।
इसलिए O मूल बिंदु है।

(ii) एक तल में वस्तु की कोणीय गति के लिए भी वस्तु की दूरी और दिशा O मूल बिंदु के सापेक्ष ही बताई जाती है। यदि वस्तु P पर है तो यह कहा जाता है कि यह 30° पूर्व की ओर है।

प्रश्न 8.
दूरी तथा विस्थापन से क्या अभिप्राय है ?
उत्तर-
दूरी – किसी गतिमान वस्तु द्वारा किसी निश्चित समय में तय की गई मार्ग की लंबाई वस्तु द्वारा चली गई दूरी होती है। इसका मात्रक मीटर है। दूरी एक अदिश राशि है।
विस्थापन – किसी वस्तु की किसी निश्चित दिशा में स्थिति परिवर्तन को विस्थापन कहते हैं। यह अंतिम तथा प्रारंभिक स्थितियों के बीच की न्यूनतम दूरी होती है। विस्थापन सरल रेखीय तथा कोणीय हो सकता है। विस्थापन का मात्रक मीटर है तथा यह एक सदिश राशि है।
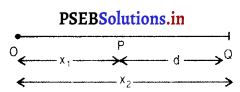
एक सरल रेखा में गतिशील वस्तु के लिए – मान लो एक वस्तु P से Q तक अपनी स्थिति बदलती है। यदि निश्चित बिंदु O से इसकी दूरी क्रमशः x1 और x2 है तो, विस्थापन ‘d’ इस तरह हो सकता है-
d = (x1 – x2) P से Q की दिशा में सरल रेखा में गति के लिए विस्थापन +ve तथा विपरीत दिशा में गति के लिए -ve चिह्नों द्वारा प्रदर्शित किया जा सकता है।
प्रश्न 9.
एक समान रेखीय गति और एक समान वृत्तीय गति में क्या अंतर है ?
उत्तर-
एक समान रेखीय गति – यदि कोई गतिमान वस्तु किसी सरल रेखीय पथ पर इस प्रकार गति करे कि उसके द्वारा समान समय में समान दूरी तय की जाए, तो वस्तु की गति एक समान रेखीय गति कहलाती है। इस प्रकार की गति में चाल का परिमाण समान रहता है तथा गति की दिशा भिन्न-भिन्न बिंदुओं पर परिवर्तित नहीं होती है। अत: एक समान रेखीय गति में वस्तु में त्वरण नहीं होता है।
एक समान वृत्तीय गति – जब कोई वस्तु इस प्रकार गति करती है कि उसका पथ वृत्ताकार हो तथा उसकी चाल एक समान हो, तो वस्तु की गति एक समान वृत्तीय गति कहलाती है।
यद्यपि वस्तु की चाल का परिमाण समान रहता है, परंतु गति की दिशा प्रत्येक बिंदु पर परिवर्तित होती रहती है। दिशा में यह परिवर्तन वस्तु में त्वरण उत्पन्न करता है।
प्रश्न 10.
दूरी तथा विस्थापन में अंतर बताओ।
उत्तर-
दूरी और विस्थापन में अंतर-
| दूरी |
विस्थापन |
| 1. गतिमान वस्तु द्वारा तय की गई कुल लंबाई को दूरी कहते हैं। |
1. निश्चित दिशा में गतिमान वस्तु की प्रारंभिक तथा अंतिम स्थितियों के बीच की दूरी को विस्थापन कहते हैं। |
| 2. दूरी एक अदिश राशि है। |
2. विस्थापन एक सदिश राशि है। |
| 3. दूरी को केवल इसके परिमाण (Magnitude) से ही वर्णित किया जा सकता है।
उदाहरण -एक पत्थर ‘h’ ऊंचाई तक फेंका गया जो वापिस आरंभिक स्थान पर पहुंच गया है।
पत्थर द्वारा तय हुई दूरी = h + h = 2h |
3. विस्थापन का वर्णन दो राशियों-दूरी तथा दिशा से ही किया जाता है। दूरी को ही विस्थापन का परिमाण कहते हैं।
पत्थर का विस्थापन = h – h = 0 (शून्य) |
प्रश्न 11.
चाल तथा वेग से क्या तात्पर्य है ? ये कैसी राशियां हैं ? इनके मात्रक भी लिखिए।
उत्तर-
चाल – किसी वस्तु द्वारा एक एकांक समय अंतराल में चली गई दूरी को उस वस्तु की चाल कहते हैं

इसका मात्रक मीटर/सेकंड (m/s) है तथा यह अदिश राशि है।
वेग-किसी वस्तु द्वारा एकांक समय में निश्चित दिशा में चली गई दूरी अर्थात् विस्थापन उस वस्तु का वेग कहलाता है। इसे v प्रदर्शित करते है; अत:

समय अंतराल इसका मात्रक मीटर/सेकंड (m/s) है। यह सदिश राशि है।

प्रश्न 12.
चाल और वेग में अंतर बताओ।
उत्तर-
चाल तथा वेग में अंतर-
| चाल |
वेग |
| 1. एकांक समय में तय की गई दूरी चाल कहलाती है। |
1. एकांक समय में किसी निश्चित दिशा में चली गई दूरी वेग कहलाता है। अथवा इकाई समय में हुआ विस्थापन कहलाता है। |
| 2. चाल का वर्णन करने के लिए केवल परिमाण की आवश्यकता होती है। अतः यह एक अदिश राशि है। |
2. वेग का वर्णन करने के लिए परिमाण तथा दिशा दोनों का ज्ञान होना आवश्यक है। अतः यह एक सदिश राशि है। |
| 3. चाल हमेशा धनात्मक होती है। |
3. वेग धनात्मक तथा ऋणात्मक दोनों प्रकार का हो सकता है। |
| 4. चाल को तीर युक्त सरल रेखा द्वारा प्रदर्शित नहीं किया जा सकता। |
4. वेग को एक तीर युक्त सरल रेखा द्वारा निरूपित किया जा सकता है। तीर की लंबाई वेग के परिमाण तथा तीर की दिशा वेग की दिशा को प्रदर्शित करती है। |
प्रश्न 13.
एकसमान वेग तथा परिवर्तनशील वेग से क्या अभिप्राय है ?
उत्तर-
एकसमान वेग – यदि कोई वस्तु समान समय अंतरालों में समान दूरी किसी विशेष दिशा में तय करे तो वस्तु को एकसमान वेग से गतिशील कहा जाता है।
परिवर्तनशील वेग – यदि कोई वस्तु किसी विशेष दिशा में समान समय-अंतरालों में असमान दूरी तय करे अथवा समान समय-अंतरालों में समान दूरी तय करे परंतु उसकी दिशा बदल जाए तो वस्तु के वेग को परिवर्तनशील वेग कहा जाता है।
प्रश्न 14.
औसत चाल तथा औसत वेग से क्या तात्पर्य है ?
उत्तर-
औसत चाल – किसी गतिमान वस्तु द्वारा एकांक समय में तय की गई औसत दूरी को उसकी औसत चाल कहते हैं। औसत चाल ज्ञात करने के लिए वस्तु द्वारा तय की गई कुल दूरी को कुल दूरी तय करने में लगे समय से भाग दिया जाता है।

तय करने में लगा समय यदि वस्तु की गति एकसमान है तो चाल तथा औसत चाल में कोई अंतर नहीं होता।
औसत वेग – किसी वस्तु द्वारा किसी समय में तय किए गए कुल विस्थापन तथा विस्थापन तय करने में लगे कुल समय का अनुपात, वस्तु का औसत वेग कहलाता है।

यदि वस्तु का वेग निश्चित दिशा में एकसमान दर से परिवर्तित हो रहा है तो

प्रश्न 15.
त्वरण किसे कहते हैं ? यह कैसी राशि है ? इसका मात्रक लिखिए।
उत्तर-
त्वरण – किसी गतिमान वस्तु के वेग-परिवर्तन की दर को उस वस्तु का त्वरण कहते हैं। इसे व से प्रदर्शित करते हैं। यह सदिश राशि है। इसका मात्रक मीटर/सेकंड है।

समय अंतराल यदि वस्तु का प्रारंभिक वेग u, समय t में वेग v हो जाता है तो
वस्तु का त्वरण (a) = \(\frac{v-u}{t}\)
प्रश्न 16.
धनात्मक तथा ऋणात्मक त्वरण से क्या तात्पर्य है ?
उत्तर-
धनात्मक तथा ऋणात्मक त्वरण – यदि किसी वस्तु के वेग का परिमाण (अर्थात् वस्तु की चाल) समय के साथ-साथ बढ़ रहा हो तो वस्तु का त्वरण धनात्मक होता है। यदि वस्तु के वेग का परिमाण समय के साथ-साथ घट रहा हो तो रस्तु का त्वरण ऋणात्मक होता है, इसे मंदन भी कहते हैं।

प्रश्न 17.
एकसमान त्वरण तथा असमान त्वरण का अर्थ उदाहरण देकर समझाइए।
उत्तर-
एकसमान त्वरण – यदि किसी वस्तु के वेग में समान समयान्तरालों में समान परिवर्तन हो रहा है, तो वस्तु का त्वरण, एकसमान त्वरण कहलाता है।
उदाहरण-वृत्तीय गति में।
असमान त्वरण – यदि किसी वस्तु के वेग में परिवर्तन एकसमान समयान्तरालों के लिए भिन्न-भिन्न हो तो वस्तु का त्वरण, असमान त्वरण कहलाता है। उदाहरण-भीड़ भरे बाज़ार में गाड़ी चलाते समय गाड़ी का त्वरण असमान रहता है।
प्रश्न 18.
ग्राफ किसे कहते हैं ? इसकी क्या उपयोगिता है ?
उत्तर-
दो भिन्न अक्षों पर किसी भौतिक राशि को दूसरी भौतिक राशि के सापेक्ष चित्रित करने को ग्राफ कहते हैं। ग्राफ़ की उपयोगिता आज के युग में अत्यधिक है। लगभग सभी क्षेत्रों में इसका तथा तुलनात्मक तथा विश्लेषणात्मक कार्यों के लिए सहायक सिद्ध होता है। इसके प्रमुख लाभ निम्नलिखित हैं-
- दो या दो से अधिक राशियों का तुलनात्मक अध्ययन अधिक सरलता और सुविधा से हो जाता है।
- विभिन्न राशियों के संबंधों को आसानी से दर्शाया जा सकता है।
- कम स्थान में विभिन्न आंकड़ों को प्रस्तुत किया जा सकता है।
- ग्राफ की ढाल से विभिन्न राशियों, सूचनाओं आदि को प्रकट किया जा सकता है।
प्रश्न 19.
आप किसी वस्तु के वेग के बारे में क्या कहेंगे यदि-
(i) समय-विस्थापन ग्राफ़ सरल रेखीय हो।
(ii) समय वेग ग्राफ़ सरल रेखीय हो।
उत्तर-
(i) वस्तु एक समान वेग से गतिशील है।
(ii) यदि ग्राफ समय-अक्ष के समानांतर एक सरल रेखा हो तो इसका अर्थ यह है कि वस्तु एकसमान वेग से गतिशील है। यदि समय-वेग ग्राफ सरल रेखीय हो परंतु समय-अक्ष के साथ कोण बनाती हो तो इसका अर्थ है कि वस्तु असमान त्वरण से गतिशील है।
प्रश्न 20.
निम्नलिखित स्थितियों में कौन-सी स्थिति संभव है तथा प्रत्येक का एक उदाहरण दीजिए-
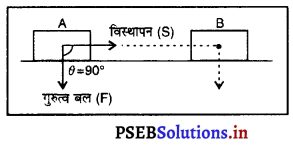
(a) कोई ऐसी वस्तु जिसका वेग शून्य है, परंतु उसका त्वरण स्थिर है।
(b) त्वरित गति में स्थिर वेग से चलती हुई कोई वस्तु।
(c) क्षैतिज दिशा में गति करती हुई कोई वस्तु, जिसका त्वरण ऊर्ध्वाधर दिशा में है।
उत्तर-
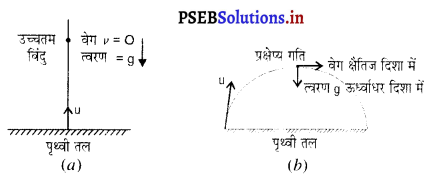
(a) पृथ्वी तल से ऊपर की ओर फेंकी गई वस्तु जब अपने पथ के उच्चतम बिंदु पर पहुंचती है तो उसका वेग शून्य होता है जबकि त्वरण अचर रहता है। [चित्र (a)]
(b) असंभव है। यदि वस्तु की गति त्वरित है तो वस्तु का वेग स्थिर नहीं रह सकता, या तो वेग का परिमाण बदलेगा अन्यथा दिशा बदलेगी। संभवतया दोनों भी परिवर्तित हो सकते हैं।
(c) प्रक्षेप्य गति में प्रक्षेप्य पथ के उच्चतम बिंदु पर वेग क्षैतिज दिशा में रहता है, जबकि त्वरण ऊर्ध्वाधर दिशा में रहता है। [चित्र (b)]
प्रश्न 21.
निम्नलिखित ग्राफ में किस प्रकार की गति प्रदर्शित है ?
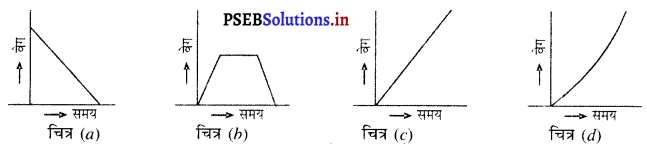
उत्तर-
(a) मंदित गति जो वस्तु को विराम अवस्था में ले आती है।
(b) परिवर्तनशील वेग। वस्तु विराम अवस्था से शुरू होती है और पहले भाग में एक समान त्वरण रखती है। दूसरे भाग में वस्तु एक समान वेग से चलती है। तीसरे भाग में वस्तु की गति मंदित होती है।
(c) विराम अवस्था से आरंभ होकर एक समान त्वरित गति।
(d) असमान त्वरित गति।

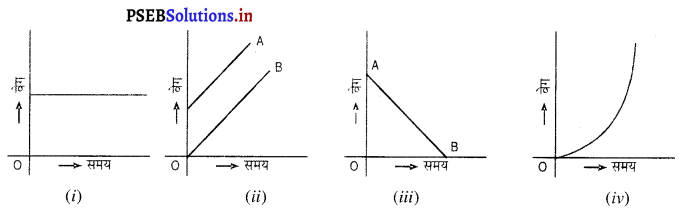
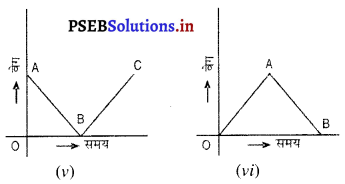
प्रश्न 22.
जिन कणों का निम्नलिखित वेग-समय ग्राफ हो उनके त्वरण पर टिप्पणी करो।
उत्तर-
(i) ढाल शून्य है ∴ त्वरण शून्य अर्थात् वेग अचर है।।
(ii) A और B दोनों की ढाल समान है और इसका त्वरण + ve है। त्वरण एक समान है।
(iii) यह मंदन की स्थिति है अर्थात् त्वरण ऋण है।
(iv) त्वरण परिवर्तनशील है, क्योंकि त्वरण (चक्र की ढाल) विभिन्न बिंदुओं पर भिन्न-भिन्न है।
(v) एक समान मंदन B पर एकसमान त्वरण में बदलता है।
(vi) एकसमान त्वरण A पर एक समान मंदन में बदलता है।
प्रश्न 23.
एक वस्तु एकसमान चाल (V) से गतिशील है। चाल-समय ग्राफ से t1 से t2 समय के मध्य उसके द्वारा तय की गई दूरी की आप किस प्रकार गणना करेंगे ?
उत्तर-
एक समान चाल (V) से चलने वाली वस्तु का चाल-समय ग्राफ अक्ष के समानांतर रेखा के रूप में होगा।
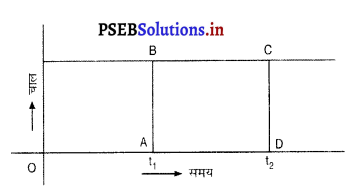
∴ दूरी = चाल × समय
= V(t2 – t2)
= AB × (OD – OA)
= AB × AD
∴ आयत ABCD का क्षेत्रफल ही तय की गई दूरी होगी।
प्रश्न 24.
असमान गति के चार उदाहरण दीजिए।
उत्तर-
- हवाई जहाज़ के द्वारा पट्टी (Run way) पर उतरते हुए या उड़ान भरते समय गति।
- किसी बस के द्वारा ब्रेक लगाने पर गति।
- ऊपर से नीचे की ओर गिरती वस्तु की गति।
- किसी पेंडुलम की दोलन गति।
प्रश्न 25.
एक धागे के सिरे पर पत्थर को बांधकर उसे एक सिरे से पकड़ कर स्थिर वेग से वृत्तीय पथ पर घुमाया गया। धागे को छोड़ देने से पत्थर की दिशा कौन-सी होगी ? इस आधार पर वस्तुओं की एक समान वृत्तीय गति के उदाहरण दीजिए।
उत्तर-
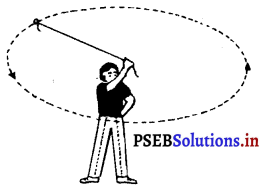
धागे को छोड़ देने पर इसकी दिशा वृत्तीय पथ की स्पर्श रेखा में होगी। जब धागे को छोड़ा जाता है तब पत्थर उसी दिशा में गति करता रहता है जिसमें गति कर रहा था।
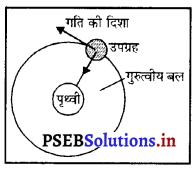
उदाहरण – चंद्रमा और पृथ्वी की गति, पृथ्वी के चारों ओर वृत्तीय कक्षा में घूमता हुआ उपग्रह।

प्रश्न 26.
दो रेलगाड़ियां उत्तर और दक्षिण दिशा में जा रही हैं। उत्तर दिशा में जाने वाली गाड़ी 60 कि०मी० प्रति घंटा और दक्षिण दिशा में जाने वाली गाड़ी 80 किमी प्रति घंटा है। एक घंटे बाद इसका विस्थापन कितना होगा।
उत्तर-
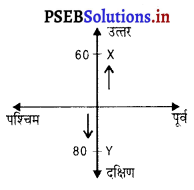
एक घंटे के बाद विस्थापन = OX + OY
= 60 + 80 = 140 कि०मी०
प्रश्न 27.
चलती रेलगाड़ी में बैठा एक व्यक्ति गेंद को लंबात्मक दिशा में ऊपर की ओर फेंकता है। गेंद किस प्रकार गति करती दिखाई देगी-
(क) रेलगाड़ी में बैठे व्यक्ति को।
(ख) रेलगाड़ी के बाहर बैठे व्यक्ति को।
उत्तर-
(क) रेलगाड़ी में बैठे व्यक्ति को गेंद एकसमान गति में दिखाई देगी। यह गति बिल्कुल वैसी है जैसे गेंद पृथ्वी की सतह पर फेंकी गई हो।
(ख) रेलगाड़ी के बाहर बैठे व्यक्ति को गेंद असमान गति में दिखाई देगी तथा इस गति का पथ पैराबोलिक होगा क्योंकि इस अवस्था में गेंद पर क्षैतिज तथा गुरुत्वीय वेग दोनों ही क्रिया कर रहे हैं।
प्रश्न 28.
निम्नलिखित कथनों में से कौन-सा वेग से और कौन-सा चाल से सम्बन्ध रखता है
(क) दूरी को तय करने की दर
(ख) विस्थापन को तय करने की दर।
उत्तर-
(क) दूरी को तय करने की दर को चाल कहते हैं। इसलिए इस कथन का संबंध चाल से है।
(ख) विस्थापन की दर को वेग कहते हैं। इसलिए इस कथन का संबंध वेग से है।
प्रश्न 29.
एक फुटबाल सीधी ऊपर की ओर फेंकी गई है। शीर्ष पर पहुंच कर इसका वेग और त्वरण क्या होगा ?
उत्तर-
ऊपर सीधी फेंकी गई फुटबाल का वेग धीरे-धीरे कम होगा और शिखर शीर्ष पर पहुंच कर इसका वेग शून्य हो जाएगा। परंतु इसका गुरुत्वीय प्रवेग, g = – 9.81 m/s2 के बराबर होगा।
प्रश्न 30.
क्या यह संभव है कि कोई व्यक्ति स्थिर (एक समान) चाल से चले, परंतु उसका वेग अस्थिर (असमान) हो। यदि हां, तो एक उदाहरण दो।
उत्तर-
हां, यह संभव हो सकता है, जब कोई व्यक्ति वृत्ताकार पथ पर स्थिर एक समान चाल से चलता है, तो उसकी वृत्ताकार पथ के प्रत्येक बिंदु पर दिशा बदलती रहती है। गति की यह दिशा उस बिंदु पर वृत्त के टेंजैट (स्पर्श रेखा) की दिशा में होती है। इसलिए दिशा बदलने के कारण वेग अस्थिर (असमान) होता है।
प्रश्न 31.
चित्र में किसी वस्तु की गति के लिए वेग-समय ग्राफ AB दर्शाता है। उस वस्तु का प्रारंभिक वेग और त्वरण ज्ञात करो।
उत्तर-
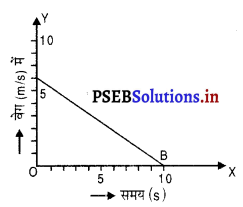
दिए गए वेग-समय ग्राफ से यह स्पष्ट है कि
वस्तु का आरंभिक वेग (u) = 7 m/s
अंतिम वेग (v) = 0
समय (t) = 10s
मान लो वस्तु का त्वरण a है
∴ a = \(\frac{v-u}{t}\)
= \(\frac{0-7}{10}\)
= – 0.7 m/s2

भौतिक राशियों के चिह्न एवं महत्त्वपूर्ण सूत्र (Symbols of Physical Quantities and Important Formula)
(क) भौतिक राशियों के चिह्न
समय = t
चाल = v
दूरी = S
आरंभिक वेग = u
अंतिम वेग = v
त्वरण = a
औसत वेग = Vav
(ख) महत्त्वपूर्ण सूत्र
यदि आरंभिक वेग u समय t पर वेग v तथा समरूप त्वरण a हो तो निम्न संबंध गति समीकरण कहलाते हैं-
v = v + at (समय t पर वेग)
S = ut + \(\frac {1}{2}\)at2 (समय अंतराल 1 में विस्थापन)
v2 = u2 + 2as (वेग-वर्ग संबंध)
(nवें इकाई, समयांतराल में विस्थापन) (Sn) = u + (2n – 1) (\(\frac{a}{2}\))
संख्यात्मक प्रश्न (Numerical Problems)
प्रश्न 1.
रीता साइकिल पर 3.2. कि०मी० दूरी तय करने में 20 मिनट लगाती है। उसका वेग कि०मी०/ मिनट, मीटर/मिनट और कि०मी०/घंटा में ज्ञात करो।
हल :
तय की गई कुल दूरी = 3.2 कि०मी०
= 3200 मीटर
कुल समय = 20 मिनट]

प्रश्न 2.
अहमद अपनी कार 45 कि०मी०/घंटा वेग से चला रहा है ? वह (I) एक मिनट (II) एक सेकंड में कितनी दूरी तय करेगा ?
हल :
कार का वेग = 45 कि०मी०/घंटा
कार 60 मिनट में दूरी तय कर रही है = 45 कि०मी०
कार 1 मिनट में दूरी तय करेगी = \(\frac{45}{60}\)
= \(\frac{3}{4}\) = 0.75 कि०मी०
= 750 मीटर
इसी प्रकार, कार 1 सेकंड में दूरी तय करेगी
= \(\frac{750}{60}\)
= 12.5 मीटर।
प्रश्न 3.
सौरभ विराम अवस्था से अपने साइकिल का 30 सेकंड में वेग 6 मीटर/सै० प्राप्त कर लेता है। ब्रेक लगाने से अगले 5 सेकंड में साइकिल का वेग 4 मीटर/सै० हो गया। दोनों अवस्थाओं में साइकिल का त्वरण ज्ञात करो।
हल :
u = 0, v = 6 मी०/सै०, t = 30 सै०
v = u + at
6 = 0 + a × 30
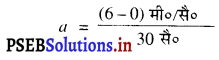
= 0.2 मी०/सै०2
(ii) = 6 मी०/सै०, v = 4 मी०/सै०, t = 4 सै०
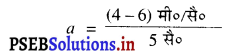
= 0.4 मी०/सै०2
मंदन = 0.4 मी०/सै०2
प्रश्न 4.
एक रेलगाड़ी विराम अवस्था से आरंभ होकर 5 मिनट में 72 कि० मी०/घंटा का वेग प्राप्त कर लेती है। समान त्वरण मानकर इसका त्वरण और तय की गई दूरी ज्ञात करो।
हल :
u = 0, t = 5 मिनट
v = 72 कि०मी०/घंटा,
v = \(\frac{72 \times 1000}{60 \times 60}\)
= 20 मी०/सै०
t = 5 × 60 = 300 सै०
परंतु a = \(\frac{v-u}{t}\)
= \(\frac{20-0}{300}=\frac{1}{15}\) = मी०/सै०2
∵ v2 = u2 + 2aS
= 0 + 2aS
S = \(\frac{v^{2}}{2 a}\)
= \(\frac{20 \times 20}{2 \times \frac{1}{15}}\) = 3000 मी०
= 3.0 कि०मी०।
प्रश्न 5.
एक कार समान त्वरण से 18 कि०/घंटा से 36 कि०/घंटा की गति 5 सेकंड में प्राप्त कर लेती है। इसका त्वरण और इस समय के बीच तय की गई दूरी ज्ञात करो।
हल :
u = 18 कि०मी०/घंटा, v = 36 कि०मी०/घंटा, t = 5 सै०
u = \(\frac{18 \times 1000}{60 \times 60}\)
= 5 मी०/सै०
v = \(\frac{36 \times 1000}{60 \times 60}\)
= 10 मी०/सै०
v = u + at
10 = 5 + a × 5
a = 1 मी०/सै०2
S = ut + \(\frac {1}{2}\)at2
= 5 × 5 + \(\frac {1}{2}\)(1) (5)2
= 25 + 12.5 = 37.5 मीटर।

प्रश्न 6.
एक पुलिस की गाड़ी हाइवे पर 30 कि०मी०/घंटे की चाल से दौड़ती हुई, उसी दिशा में चोरों की गाड़ी जो 192 कि०मी० प्रति घंटे की चाल से दौड़ रही है, पर गोली चलाते हैं। यदि गोली की चाल 150 मी०/ से० हो तो किस चाल से गोली चोरों की गाड़ी को लगेगी ?
हल :
गोली की छोड़ने की चाल = 150 मी०/से० = 540 कि०मी०/घंटा
∴ कुल चाल = 30 + 540 = 570 कि०मी०/घंटा
गोली की चाल चोरों की गाड़ी की सापेक्ष, जो उसी दिशा में चल रही है
= 570 – 192 = 378 कि०मी०/घंटा
= \(\frac{378 \times 1000}{60 \times 60}\) मी./से०
= 105 मी०/सेकंड।
प्रश्न 7.
एक रेलगाड़ी जो 50 मी० लंबी है, एक सीधे तथा समतल ट्रैक पर चलकर एक खंभे के पास 5 सेकंड में पहुंचती है।
(i) गाड़ी की चाल ज्ञात करो।
(ii) 450 मी० लंबे पुल को पार करने में गाड़ी कितना समय लगायेगी।
हल :
(i) जैसा कि गाड़ी खंभे को 5 सेकंड में तय करती है तो यह अपनी लंबाई के बराबर दूरी तय करती है। तब-

= 10 मी०/सेकंड
(ii) पुल को पार करने में गाड़ी द्वारा तय की गई दूरी
= पुल की लंबाई + गाड़ी की लंबाई
= 450 मी० + 50 मी० = 500 मी०
इसलिए पुल को पार करने में गाड़ी को लगा समय

= 50 सेकंड
प्रश्न 8.
एक मोटर गाड़ी 50 कि०मी०/घंटा की चाल से एक निश्चित दूरी की यात्रा तय करती है और 40 कि०मी०/घंटा की चाल से वापस लौटती है। संपूर्ण यात्रा के लिए इसकी औसत चाल की गणना कीजिए।
हल :
माना कि निश्चित दूरी = x कि०मी०
50 कि०मी०/घंटा की चाल से x कि०मी० दूरी जाने में लगा समय

प्रश्न 9.
10.00 a.m. पर एक गाड़ी 40 km/h की चाल से गति कर रही है तथा 10.02 a.m. पर 50 km/ h की चाल से गाड़ी का त्वरण ज्ञात कीजिए।
हल :

= \(\frac{10 \times 60}{2}\) कि०मी०/घंटा2
= 300 कि०मी०/घंटा2
प्रश्न 10.
एक रेलगाड़ी 90km लंबे मार्ग में से पहले 30 km की दूरी 30 km/h की एकसमान चाल से तय करती है। शेष 60 km मार्ग को रेलगाड़ी किस चाल से तय करे कि उसकी औसत चाल 60 km/h हो जाए ?
हल :
पहले 30 km तय करने में लगा समय = \(\frac{30 \mathrm{~km}}{30 \mathrm{kmh}^{-1}}\) = 1h
मान लो x km/h की चाल से अगले 60 km तय होते हैं
तो अगले 60 km तय करने में लगा समय = \(\frac{60}{x}\)h

x = 120
अतः चाल 120 kmh-1 होनी चाहिए।

प्रश्न 11.
एक रेलगाड़ी 0.52 घंटे के लिए 60 km/h की चाल से 0.24 घंटे में 30 km/h तथा उससे अगले 0.71 घंटों में 70 km/h की चाल से चलती है। रेलगाड़ी की औसत चाल ज्ञात कीजिए।
हल :
0.52h समय में तय हुई दूरी
S1 = 0.52 × 60
= 31.2 km
0.24 h समय में तय हुई दूरी
S2 = 0.24 × 30
= 7.2 km
0.71 h समय में तय हुई दूरी
S3 = 0.71 × 70
= 49.7 km
कुल तय की गई दूरी = S1 + S2 + S3
= 31.2 + 7.2 + 49.7
= 88.1 km
कुल समय = 0.52 + 0.24 + 0.71
= 1.47 h

= \(\frac{88.1 \mathrm{~km}}{1.47 \mathrm{~h}}\)
प्रश्न 12.
एक कार 30 कि०मी० की दूरी 60 कि०मी०/घंटा की एक समान चाल से तय करती है तथा अगले 30 कि०मी० की दूरी 40 कि०मी०/घंटा की एक समान चाल से तय करती है। कुल लिया गया समय ज्ञात करो।
हल :
एक समान चाल के लिए
S = ul
माना पहले 30km की दूरी तय करने में लगा समय = t1
30 km = (60 km/h)t1

= \(\frac {1}{2}\)h = 30
मिनट इसी प्रकार, अगले 30 कि०मी० की दूरी तय करने में लगा समय = t2
30 km = (40 कि०मी०/घंटा) × t2

= 3/4 h = 45 मिनट
कुल लगा समय = t1 + t2 = 30 मिनट + 45 मिनट = 75 मिनट।
= 1 घण्टा 15 मिनट ।
प्रश्न 13.
पृथ्वी की कोणीय चाल का परिकलन कीजिए जबकि पृथ्वी अपने अक्ष के चारों ओर घूर्णन करती है।
हल :
पृथ्वी अपने अक्ष के चारों ओर एक घूर्णन 24 घंटे में पूरा करती है, अर्थात् 24 × 3600 5 में।
कोणीय विस्थापन, θ = 2π rad
समय अंतराल, t = 24h = (24 × 60 × 60) से०
पृथ्वी का कोणीय वेग,
ω = \(\frac{\theta}{t}=\frac{2 \pi \mathrm{rad}}{24 \times 3600 \mathrm{~s}}\)
= \(\frac{\pi}{43200}\)rad/s
= \(\frac{3.14}{43200}\)rad/s
= 7.27 × 10-5 rad/s.
प्रश्न 14.
एक पिंड विराम अवस्था से 0.6 मी०/से०2 के त्वरण के साथ चलता है। 300 मीटर चलने के बाद इसका वेग क्या होगा ? इस दूरी को तय करने में इसे कितना समय लगा ?
हल :
u = 0, a = 0.6 मी०/से०2
S = 300 मी०, y = ?, t = ?
v2 = u2 + 2aS
v2 = 2 × 0.6 × 300 = 360
v = \(\sqrt{360}\) = 6 × \(\sqrt{10}\) मी०/से०
= 19 मी०/से० (लगभग)
S = ut + \(\frac {1}{2}\)at2
300 = \(\frac {1}{2}\) × 0.6 × t2
t2 = \(\frac{300}{0.3}\)
\(\frac{3000}{3}\) = 1000
t = \(\sqrt{1000}\) = 31.5 सेकंड (लगभग)
प्रश्न 15.
15 मी०/से० की गणना कि०मी०/घंटा में करो।
हल :

= 54 कि०मी०/घंटा।

प्रश्न 16.
एक वस्तु 2 m/s के वेग से 5s तक चलती है। अगले 5s में एक समान त्वरण के कारण इसका वेग बढ़ कर 10 m/s हो जाता है। इसके बाद इस वस्तु का वेग एक समान रूप से कम होता है और वस्तु 10s में विराम की अवस्था में आ जाती है, तो
(a) इस वस्तु की गति के लिए वेग-समय तथा दूरी-समय ग्राफ खींचिए।
(b) ग्राफ में वह भाग दिखाइए, जहाँ गति एक समान है तथा जहाँ असमान है।
(c) ग्राफ से वस्तु द्वारा प्रारंभ से 25 तथा 12s बाद, तथा अंतिम 10s में तय की गई दूरी ज्ञात कीजिए।
उत्तर-
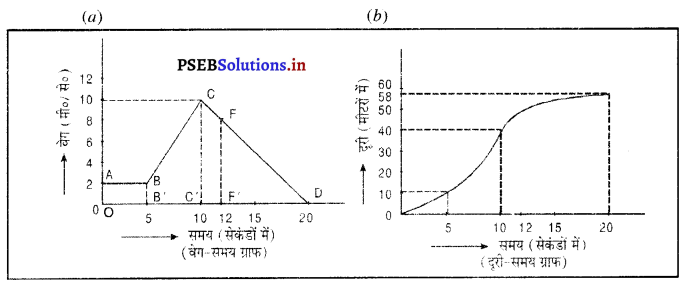
(c) एकसमान गति = BC तथा CD
असमान गति = OB
2 सेकंड में तय की गई दूरी = OA × OE’ = 2 × 2 = 4 मी०
12 सेकंड में तय की गई दूरी = 12 से० के बाद दूरी = ABCFF’ का क्षेत्रफल
= OABB+ BBCC’ का क्षेत्रफल + CC FF’ क्षेत्रफल
= (5 × 2) + \(\frac {1}{2}\)(2 +10) × 5 + \(\frac {1}{2}\)(10 + 8) × 2
= 10 + 30 + 18
= 58 मी०
अंतिम 10 से० में तय की गई दूरी = \(\sqrt{(10)^{2}+(10)^{2}}\)
= \(\sqrt{100+100}\) = \(\sqrt{200}\)
= \(\sqrt{100 \times 2}\) = 10√2 मीटर
प्रश्न 17.
चीता सबसे तेज़ दौड़ने वाला स्थल जंतु है और 500 मीटर से कम दूरी के लिए इसका सर्वोच्च वेग 100 km/h तक हो सकता है। यदि चीता अपने शिकार को 100m की दूरी पर देखता है तो उस तक पहुँचने में चीता कम-से-कम कितना समय लेगा यदि इस दौरान उसका औसत वेग 90kh/h हो।
हल :
औसत वेग = 90 कि०मी०/घंटा
= \(\frac{90 \times 1000}{60 \times 60}\) = 25 मी०/से०
चीते के द्वारा 25 मीटर दूरी तय की गई = 1 से०
चीते के द्वारा 1000 मीटर दूरी तय की गई = \(\frac{1}{25}\) × 100 = 4 सेकंड
अत: चीता 4 सेकंड में अपना शिकार पकड़ लेगा।
प्रश्न 18.
आजकल सभी बसों और कारों में स्पीडोमीटर लगे होते हैं जो किसी क्षण पर उनका वेग दिखाते हैं। ओडोमीटर नामक यंत्र वाहन द्वारा तय की गई दूरी मापता है। यदि किसी वाहन के आडोमीटर की माप यात्रा के प्रारंभ में 1048km और 40 मिनट बाद 1096 km थी, तो वाहन का औसत वेग परिकलित कीजिए। क्या वाहन की गतिशील स्थिति में स्पीडोमीटर की माप यही वेग प्रदर्शित करेगी ? अपने उत्तर के लिए कारण बताइए।
हल :
वाहन के द्वारा कुल तय की गई दूरी = 1096 – 1048
=48 कि०मी० समय = 40 मिनट

= 1.2 कि०मी०/मिनट
= 1.2 × 60
= 72 कि०मी०/घंटा
स्पीडोमीटर वाहन का वेग 72 कि०मी०/घंटा नहीं दर्शाएगा क्योंकि यह उसका औसत वेग है। भीड़ भरी सड़कों, चढ़ाई, उतराई आदि के कारण वाहन का वेग बढ़ता-घटता रहता है। वह सदा समान वेग से सड़क पर नहीं चलता।
प्रश्न 19.
कोई धावक 100 मीटर की दौड़ में भाग लेते हुए, पहले सेकंड में 4 मीटर, अगले 4 सेकंड में 30 मीटर व उससे अगले 4 सेकंड में 52 मीटर की दूरी तय करता है और वह दौड़ 10 सेकंड में पूरी कर लेता है तो,
(a) धावक के औसत वेग की गणना कीजिए।
(b) किस समय अंतराल में धावक का औसत वेग अधिकतम है ? इस वेग को उपयुक्त मात्रक में व्यक्त कीजिए।
(c) किस समय अंतराल में त्वरण अधिकतम होगा ?
(d) इस दौड़ में धावक की गति के लिए दूरी-समय ग्राफ बनाइए।
(e) ग्राफ की सहायता से धावक द्वारा 6 s के अंत तक तय की गई दूरी ज्ञात कीजिए।
हल :
(a)
कुल दूरी = 100 मीटर
कुल समय = 10 सेकंड

= 10 मी०/सेकंड


∴ दूसरे और तीसरे अंतराल में त्वरण अधिकतम होगा।
(d) दूरी समय ग्राफ
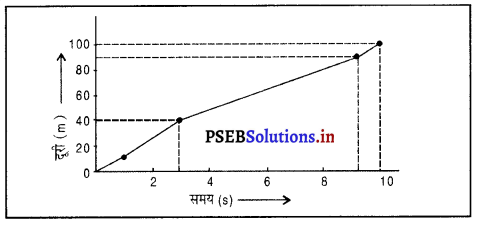
(e) 5 सेकंड के पश्चात् धावक द्वारा तय दूरी = \(\frac{34}{5}\) = 6.8 मी०/से०
6 सेकंड के अंत तक धावक द्वारा तय की गई दूरी = 40 मी०/से०

प्रश्न 20.
कोई पत्थर ऊर्ध्वाधर दिशा में ऊपर की और 5 m/s के वेग से फेंका गया है। इसका त्वरण ऊर्ध्वाधर नीचे की ओर 10 m/s2 हो तो, पत्थर द्वारा प्राप्त अधिकतम ऊँचाई ज्ञात कीजिए। इस उच्चतम ऊँचाई तक पहुँचने में पत्थर को कितना समय लगेगा ?
हल :
u = 5 मी०/से०, v = 0, a = 10 मी०/से०2
h = ?
t = ?
v2 = u2 + 2gh
(0)2 = (5)2 + 2 (-10) × h
0 = 25 – 20h
-20h = -25
h = \(\frac{25}{20}\)
= \(\frac{5}{4}\) = 1.2 मीटर
अब v = u + at
0 = 5 – 10t
t = \(\frac{-5}{-10}=\frac{1}{2}\) = 0.5 सेकंड
प्रश्न 21.
यात्रा शुरू होते समय कार का ओडोमीटर 2000 km प्रदर्शित करता है और यात्रा समाप्ति पर 2400 km प्रदर्शित करता है। यदि इस यात्रा में 8 h लगते हैं, तो कार की औसत चाल को km h-1 और ms-1 में ज्ञात करें।
हल :
कार के द्वारा तय की गई दूरी S = 2400 km – 2000 km = 400 km
दूरी तय करने में लगा कुल समय t = 8 h
कार की औसत चाल v = \(\frac{S}{t}\)
= \(\frac{400 \mathrm{~km}}{8 \mathrm{~h}}\) = 50km h-1
= 50 \(\frac{\mathrm{km}}{\mathrm{h}} \times \frac{1000 \mathrm{~m}}{1 \mathrm{~km}} \times \frac{1 \mathrm{~h}}{3600 \mathrm{~s}}\)
= 13.9 ms-1
कार की औसत चाल 50 km h-1 अथवा 13.9 ms-1 है।
प्रश्न 22.
ऊषा 90 m लंबे तालाब में तैरती है। वह एक सिरे से दूसरे सिरे तक सरल रेखीय पथ पर जाती है तथा वापस आती है। इस दौरान वह कुल 180 m की दूरी 1 मिनट में तय करती है। ऊषा की औसत चाल और औसत वेग को ज्ञात कीजिए।
हल:
ऊषा द्वारा 2 मिनट में तय की गई कुल दूरी (90 m + 90 m) = 180 m है।
1 मिनट में ऊष्मा का विस्थापन = 90 + (-90) = 90 – 90 = 0 m (∵ आरंभिक और अंतिम स्थिति एक ही है।)

= 0 ms-1
अतः ऊषा की औसत चाल 3 ms-1 है औसत वेग 0 ms-1 है।
प्रश्न 23.
विरामावस्था से राहुल अपनी साइकिल को चलाना शुरू करता है और 30 s में 6 ms-1 का वेग प्राप्त करता है। वह इस प्रकार से ब्रेक लगाता है कि साइकिल का वेग अगले 5 s से कम होकर 4 ms-1 हो जाता है। दोनों स्थितियों में साइकिल के त्वरण की गणना करें।
हल :
पहली स्थिति में
प्रारंभिक वेग, = 0;
अंतिम वेग, ‘ = 6 ms-1;
समय, t = 30s
∴ a = \(\frac{v-u}{t}\)
u, v और t का दिया हुआ मान ऊपर दिए गए समीकरण में रखने पर,
a = \(\frac{6 m s^{-1}-0 m s^{-1}}{30 s}\)
= 0.2 ms-2
दूसरी अवस्था में,
प्रारंभिक वेग, u = 6 ms-1;
अंतिम वेग v = 4 ms-1;
समय t = 5s;
तब a = \(\frac{4 m s^{-1}-6 m s^{-1}}{5 s}\)
= – 0.4 ms-2
साइकिल का त्वरण पहली स्थिति में 0.2 ms-2 है और दूसरी स्थिति में -0.4 ms-2 है।
प्रश्न 24.
किसी कार पर ब्रेक लगाने पर वह गति के विपरीत दिशा में 6 ms-2 का त्वरण उत्पन्न करती है। यदि कार ब्रेक लगाए जाने के बाद रुकने में 2 s का समय लेती है तो उतने समय में तय की गई दूरी की गणना करें।
हल :
दिया गया है,
a = -6 ms-2, t = 2S तथा v = 0 ms-1
v = u + at
0 = u + (-6 ms-2) × 2S
या u = 12 ms-1
S = ut + \(\frac {1}{2}\)at2
= (12 ms-1) × (2s) + \(\frac {1}{2}\) (6 ms-2) × (2s)2
= 24 m – 12 m
= 12 m
∴ कार रुकने के पहले 12 m की दूरी तय करेगी।
क्या अब आप इस महत्त्व को समझ सकते हैं कि चालक सड़क पर गाड़ी चलाते समय दूसरी गाड़ी से दूरी क्या बना कर रखते हैं ?

प्रश्न 25.
(i) घड़ी की सेकंडों वाली सुई
(ii) घड़ी की मिनटों वाली सुई
(iii) घड़ी की घंटों वाली सुई का कोणीय वेग ज्ञात करो।
हल :
(i) घड़ी की सेकंड वाली सुई 1 सेकंड में एक चक्र पूरा करती है। इसे समय अंतराल कहते हैं।
θ = 2π रेडियन, t = 1 मिनट = 60s
ω = \(\frac{\theta}{t}\)
= \(\frac{2 \pi}{60}\) rad. s-1
= \(\frac{\pi}{30}\) rad s-1
(ii) मिनटों की सुई के लिए θ = 2π rad.
t = 1h = 60 × 60s
∴ ω = \(\frac{\theta}{t}\)
= \(\frac{2 \pi}{60 \times 60}\)
= \(\frac{\pi}{1800}\) rad s-1
(iii) घंटों की सुई के लिए t = 12 h
∴ ω = \(\frac{\theta}{t}\)
= \(\frac{2 \pi}{12 \times 60 \times 60}\)
= \(\frac{\pi}{21600}\) rad s-1
प्रश्न 26.
एक रेडियन कितने डिग्री के बराबर है ?
हल :
रेडियन और डिग्री में संबंध-
पूरे वृत्त द्वारा केंद्र पर स्थापित कोण = \(\frac{2 \pi r}{r}\) = 2π रेडियन और केंद्र पर स्थापित कुल कोण = 360°
∵ 2π rad = 360°
π rad = 180°
1 rad = \(\frac{180}{\pi}\)
= \(\frac{180}{22 / 7}\)
= \(\frac{180 \times 7}{22}\) = 57.3
1 rad = 57.3°
प्रश्न 27.
किसी कार का वेग 18 मीटर/से० है। इसको कि०मी०/घंटा में व्यक्त कीजिए।
हल :
कार का वेग = 18 मीटर/से०
\(\frac{18}{1000}\) × 60 × 60
= 64.8 कि०मी०/घंटा
प्रश्न 28.
मान लीजिए आप एक 9m लंबे कमरे में 1.5 किलोमीटर प्रति घंटा के वेग से चल रहे हैं। इस वेग को m/s के मात्रक में लिखिए। इस कमरे के एक सिरे से दूसरे सिरे तक जाने में आपको कितना समय लगेगा ?
हल :
वेग = \(\frac{3}{2}\) कि०मी०/घंटा
= \(\frac{3}{2} \times \frac{1000}{60 \times 60}\)
= \(\frac{5}{12}\) मी०/से०
= 0.42 मी०/से० (m/s)
\(\frac{5}{12}\) मी० की दूरी तय होने में समय लगाती है = 1/से०
9 मी० की दूरी तय होने में समय लगेगा = \(\frac{1 \times 9 \times 12}{5}\)
= \(\frac{108}{5}\) सेकंड
= 21.65 से०
∴ कमरे के एक ओर से दूसरी ओर जाने में लगा समय = 21.65 से०
प्रश्न 29.
किसी वृत्ताकार साइकिल ट्रैक की परिधि 314 मीटर है, AB इसका एक व्यास है। यदि कोई साइकिल सवार इस वृत्ताकार पथ पर A से B तक 15.7 मीटर प्रति सेकंड के स्थिर वेग से साइकिल चलाता है तो साइकिल सवार के लिए ज्ञात कीजिए-
(a) उसके द्वारा तय की गई दूरी।
(b) उसका विस्थापन, यदि AB उत्तर-दक्षिण दिशा में हो।
(c) उसका औसत वेग।
हल :
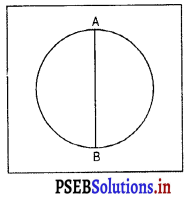
व्यास = AB
परिधि = 314 m.
चाल = 15.7 m/s.
15.7 मी० तय करने में लगा समय = 1 से०
314 मी० तय करने में लगा समय = \(\frac{1 \times 314}{15.7}\)
= 20 से०
(a) साइकिल सवार के द्वारा तय की गई दूरी = 2πr = 314 मीटर
r = \(\frac{314}{2 \times 3.14}\)
= \(\frac{314 \times 100}{2 \times 314}\)
= 50 मी०
(b) विस्थापन = शून्य
∵ अंतिम स्थिति तथा प्रारंभिक स्थिति समान है।
(c) 
औसत वेग = \(\frac{314}{20}\)
= 15.7 मीटर/से०

अति लघु उत्तरात्मक प्रश्न (Very Short Answer Type Questions)
प्रश्न 1.
गति किसे कहते हैं ?
उत्तर-
गति – जब कोई वस्तु समय के साथ अपनी स्थिति में परिवर्तन करती है तो उसे गति में कहते हैं।
प्रश्न 2.
नियंत्रित गति का मानव के लिए एक उपयोग लिखिए।
उत्तर-
पानी के द्वारा विद्युत् उत्पादन।
प्रश्न 3.
वस्तु की दूरी को जानने के लिए किस बात की आवश्यकता नहीं होती ?
उत्तर-
गति की दिशा की।
प्रश्न 4.
वस्तु का विस्थापन क्या है ?
उत्तर-
विस्थापन – वस्तु का प्रारंभिक और अंतिम स्थिति के बीच की न्यूनतम दूरी को वस्तु का विस्थापन कहते हैं।
प्रश्न 5.
दो विभिन्न भौतिक राशियां कौन-सी हैं ?
उत्तर-
दूरी और विस्थापन।
प्रश्न 6.
गाड़ियों की गति को कौन-सा यंत्र प्रदर्शित करता है ?
उत्तर-
ओडोमीटर।

प्रश्न 7.
एक समान गति किसे कहते हैं ?
उत्तर-
एक समान गति – जब कोई वस्तु समान समयांतराल में समान दूरी तय करती है तो उस की गति को एक समान गति कहते हैं।
प्रश्न 8.
असमान गति के दो उदाहरण दीजिए।
उत्तर-
सड़क पर जा रही कार, पार्क में व्यायाम कर रहा एक व्यक्ति।
प्रश्न 9.
चाल किसे कहते हैं ?
उत्तर-
चाल – वस्तु द्वारा इकाई समय में तय की गई दूरी को चाल कहते हैं।
प्रश्न 10.
चाल का मात्रक क्या है ?
उत्तर-
चाल का मात्रक मीटर प्रति सेकंड (ms-1) है। यह सेंटीमीटर प्रति सेकंड (cms-1) तथा किलोमीटर प्रति घंटा (km h-1) भी हो सकता है।
प्रश्न 11.
औसत चाल को किस प्रकार प्राप्त किया जाता है ?
उत्तर-
औसत चाल – वस्तु की औसत चाल को उसके द्वारा तय की गई कुल दूरी को कुल समयावधि से भाग देकर प्राप्त किया जाता है।

प्रश्न 12.
वेग किसे कहते हैं ?
उत्तर-
वेग – एक निश्चित दिशा में चाल को वेग कहते है।
अथवा
एक निश्चित दिशा में इकाई समय में वस्तु द्वारा तय की गई दूरी।

प्रश्न 13.
त्वरण किसे कहते हैं ?
उत्तर-
त्वरण – किसी वस्तु के प्रति इकाई समय में वेग परिवर्तन की माप को त्वरण कहते हैं।

प्रश्न 14.
त्वरण का मात्रक क्या है ?
उत्तर-
ms-2
प्रश्न 15.
ग्राफ़ से क्या अभिप्राय है ?
उत्तर-
ग्राफ़ – एक भौतिक राशि से दूसरी भौतिक राशि के सापेक्ष परिवर्तन को दो विभिन्न अक्षों पर चित्रित करना ग्राफ़ कहलाता है।
प्रश्न 16.
दूरी-समय ग्राफ़ क्या है ?
उत्तर-
किसी वस्तु की स्थिति को समय के साथ प्रदर्शित करना दूरी-समय ग्राफ़ कहलाता है।
प्रश्न 17.
एकसमान चाल के लिए समय के साथ तय की गई दूरी का ग्राफ़ कैसा होता है ?
उत्तर-
एक सरल रेखा।
प्रश्न 18.
दूरी-समय ग्राफ़ से क्या जाना जा सकता है ?
उत्तर-
वस्तु की चाल।

प्रश्न 19.
एकसमान त्वरित गतियों के लिए वेग-समय ग्राफ़ कैसा होता है ?
उत्तर-
एक सीधी रेखा।
प्रश्न 20.
त्वरित गति का एक उदाहरण दीजिए।
उत्तर-
एक वृत्तीय पथ पर दौड़ता हुआ एक एथलीट।
प्रश्न 21.
किसी एथलीट को षट्कोणीय पथ के अनुदिश दौड़ते हुए एक चक्कर पूरा करने में कितनी बार अपनी दिशा बदलनी पड़ेगी ?
उत्तर-
छ: बार।
प्रश्न 22.
यदि एक एथलीट r त्रिज्या वाले वृत्तीय पथ का एक चक्कर लगाने के लिए ‘t’ सेकंड समय लेता है तो उसका वेग (v) क्या होगा ?
उत्तर-
v\(\frac{2 \pi r}{t}\)
प्रश्न 23.
एकसमान वृत्तीय गति किसे कहते हैं ?
उत्तर-
जब एक वस्तु वृत्तीय रास्ते पर एकसमान चाल से चलती है जब उसकी गति को एकसमान वत्तीय गति कहते हैं।
प्रश्न 24.
वृत्तीय गति के दो उदाहरण दीजिए।
उत्तर-
- किसी वाहन के पहिए की गति ।
- रम्पी के सिरे पर बँधा पत्थर जो समतल वृत्त में गतिमान हो।

प्रश्न 25.
यदि कोई वस्तु एक वृत्तीय पथ पर एक समान चाल से गति कर रही हो तो उसकी गति किस प्रकार की होगी ?
उत्तर-
एक असमान और त्वरित गति।
प्रश्न 26.
एक वस्तु त्रिज्या r के वृत्तीय पथ पर चल रही है। एक चक्कर लगाने में इसका विस्थापन और दूरी क्या है ?
उत्तर-
विस्थापन – 0 (शून्य)
दूरी = 2πr.
प्रश्न 27.
एक क्रिकेट खिलाड़ी गेंद को ऊपर उछालता है और उसी स्थिति में पुनः कैच कर लेता है। गेंद का कुल विस्थापन कितना है ?
उत्तर-
कुल विस्थापन शून्य है।
प्रश्न 28.
दूरी समय ग्राफ़ में ढाल क्या बताती है ?
उत्तर-
वस्तु की चाल बताती है।
प्रश्न 29.
कोई वस्तु सूर्य के इर्द-गिर्द अचर चाल से वृत्ताकार परिपथ में घूम रही है। इसकी गति त्वरित है या नहीं ?
उत्तर-
वस्तु की गति की दिशा निरंतर बदल रही है अतः वेग भी निरंतर बदल रहा है। गति त्वरित है।
प्रश्न 30.
घड़ी की सेकंड वाली सुई के सिरे की गति कैसी है ?
उत्तर-
वृत्ताकार।

प्रश्न 31.
यदि कोई ट्रक 2 घंटे में 100 km की दूरी तय करे तो उसकी औसत चाल क्या होगी ?
उत्तर-

प्रश्न 32.
प्रकाश की चाल 3 × 108 m/s है। यह km/h में कितनी होगी ?
उत्तर-
प्रकाश की चाल 3 × 108 m/s
= \(\frac{3 \times 10^{8} \times 3600}{1000}\) km/h
= 1.8 × 109 km/h
प्रश्न 33.
यदि किसी वाहन की चाल 3 घंटे में 0 से 60 km/h हो जाए तो उसका त्वरण कितना होगा?
उत्तर-
त्वरण = \(\frac{(60-0) \mathrm{km} / \mathrm{h}}{3 \mathrm{~h}}\) = 20 km/h2
प्रश्न 34.
गीता प्रातः 7.00 बजे स्कूल गई और दोपहर 1.30 बजे वापस घर लौट आई। उसका विस्थापन ज्ञात कीजिए।
उत्तर-
शून्य।
प्रश्न 35.
सुधीर 300 मीटर की दूरी को 15 सेकंड में पूरा करता है। उसका वेग कितना होगा ?
उत्तर-

प्रश्न 36.
आपकी साइकिल 20 सेकंड 5 m/s की चाल प्राप्त करती है। साइकिल का त्वरण क्या होगा ?
उत्तर-
त्वरण (a) = \(\frac{v-u}{t}=\frac{5-0}{20}=\frac{5}{20}=\frac{1}{4}\) = 25m/s2

प्रश्न 37.
किसी गतिशील वस्तु का एक समय अंतराल में विस्थापन शून्य है। क्या उस वस्तु के दवाग तय की गई दूरी भी शून्य होगी ? स्पष्ट कीजिए।
उत्तर-
नहीं। यद्यपि गतिशील वस्तु पुनः अपने प्रारंभिक स्थल पर वापस लौट आती है तथापि उसके दवारा जय की गई दूरी शून्य नहीं होगी।
प्रश्न 38.
पृथ्वी और चंद्रमा की गति किस प्रकार की गति के उदाहरण हैं ?
उत्तर-
एकसमान वृत्तीय गति के उदाहरण।
प्रश्न 39.
विस्थापन को आप किस प्रकार की राशि मानते हैं-स्केलर या वैक्टर ?
उत्तर-
वैक्टर राशि।
प्रश्न 40.
दूरी किस प्रकार की राशि है-स्केलर या वैक्टर ?
उत्तर-
स्कलेर राशि।
प्रश्न 41.
वायु में ध्वनि की चाल कितनी होती है ?
उत्तर-
346 m/s-1
प्रश्न 42.
असमान चाल से चलने वाले वाहन का दूरी-समय ग्राफ़ का आकार कैसा होगा ?
उत्तर-
वक्र रेखा आकार का।

प्रश्न 43.
वृत्तीय गति किसे कहते हैं ?
उत्तर-
वृत्तीय गति – जब कोई वस्तु वृत्ताकार पथ पर गति करती है तो वस्तु की गति वृत्तीय गति कहलाती है।
प्रश्न 44.
कोणीय वेग क्या होता है ?
उत्तर-
कोणीय वेग – वृत्तीय पथ पर गति करती हुई वस्तु का कोणीय विस्थापन तय करने की दर उस वस्तु का कोणीय वेग कहलाता है। उसे ω ( ओमेगा) से दर्शाते हैं।
प्रश्न 45.
यदि कोई वस्तु 25 मीटर प्रति सेकंड के एकसमान वेग से गति कर रही है, तो 5 सेकंड के पश्चात् उस वस्तु का वेग क्या होगा ?
उत्तर-
5 सेकंड के बाद भी वस्तु का वेग 25 मीटर/सेकंड ही रहेगा क्योंकि वह वस्तु एकसमान वेग से गतिशील है।
प्रश्न 46.
दो साइकिल सवार विपरीत दिशाओं में चलते हुए एक घंटे में एकसमान दूरी S तय करते हैं। यदि साइकिल सवार उत्तर-दक्षिण दिशा में चल रहे हों तो एक घंटे में उनके द्वारा कितना विस्थापन होगा ?
उत्तर-
उनका विस्थापन = S + S = 2S
प्रश्न 47.
नीचे के ग्राफ़ में चाल का मान (Value) बताइए।
उत्तर-
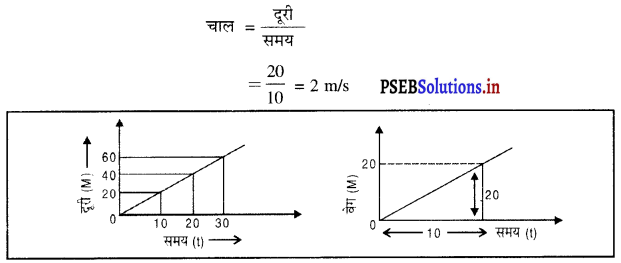
प्रश्न 48.
हमारी आँख झपकने की चाल क्या है ? इसके लिए आपको आँख की पुतली का आकार तथा उस समय का अनुमान लगाना होगा जितनी देर आँख पलक झपकने के दौरान बन्द रहती है ?
उत्तर-
10-1 ms-1
संकेत : आँख के गोलक का आकार लगभग ≈10-2m है। आँख जितनी देर के लिए बन्द रहती है ≈10-1s ।
चाल = \(\frac{10^{-2} \mathrm{~m}}{10^{-1} \mathrm{~s}}\) = 10-1 ms -1

प्रश्न 49.
एक वस्तु त्रिज्या r के वृत्तीय पथ पर चल रही है। एक चक्कर लगाने में इसका विस्थापन क्या है और तय की गई दूरी क्या है ?
उत्तर-
विस्थापन = 0 (शून्य)
दूरी = 2πr
प्रश्न 50.
साथ दिए ग्राफ़ में दूरी-समय आरेख में बताओ किसकी चाल अधिक है?
उत्तर-
B की चाल A की अपेक्षा अधिक है।
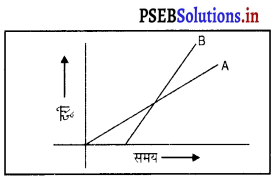
प्रश्न 51.
एक कण r अर्धव्यास के वृत्तीय पथ पर गतिशील है। कण के द्वारा आधी परिक्रमा में तय की गई दूरी क्या है ? उसका विस्थापन कितना होगा ?
उत्तर
दूरी = πr
विस्थापन = 2r
![]()