PSEB 11th Class Maths Solutions Chapter 12 Introduction to Three Dimensional Geometry Ex 12.2

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 12 Introduction to Three Dimensional Geometry Ex 12.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 12 Introduction to Three Dimensional Geometry Ex 12.2

Question 1.
Find the distance between the following pairs of points :
(i) (2, 3, 5) and (4, 3, 1)
(ii) (- 3, 7, 2) and (2, 4, – 1)
(iii) (- 1, 3, – 4) and (1, – 3, 4)
(iv) (2, – 1, 3) and (- 2, 1, 3).
Answer.
The distance between point P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) is given by
PQ = \(\)
(i) Distance between points (2, 3, 5) and (4, 3, 1)
= \(\sqrt{(4-2)^{2}+(3-3)^{2}+(1-5)^{2}}=\sqrt{(2)^{2}+(0)^{2}+(-4)^{2}}\)
= \(\sqrt{4+16}=\sqrt{20}=2 \sqrt{5}\)

(ii) Distance between points (- 3, 7, 2) and (2, 4, – 1)
= \(\sqrt{(2+3)^{2}+(4-7)^{2}+(-1-2)^{2}}=\sqrt{(5)^{2}+(-3)^{2}+(-3)^{2}}\)
= \(\sqrt{25+9+9}=\sqrt{43}\)

(iii) Distance between points ( – 1, 3, – 4) and (1, – 3, 4)
= \(\sqrt{(1+1)^{2}+(-3-3)^{2}+(4+4)^{2}}\)
= \(\sqrt{(2)^{2}+(-6)^{2}+(8)^{2}}\)
= \(\sqrt{4+36+64}=\sqrt{104}=2 \sqrt{26}\)

(iv) Distance between points (2, -1, 3) and (-2, 1, 3)
= \(\sqrt{(-2-2)^{2}+(1+1)^{2}+(3-3)^{2}}\)
= \(\sqrt{(-4)^{2}+(2)^{2}+(0)^{2}}\)
= \(\sqrt{16+4}=\sqrt{20}=2 \sqrt{5}\)

Question 2.
Show that the point (- 2, 3, 5), (1, 2, 3) and (7,0, – 1) are collinear.
Answer.
Let points (- 2, 3, 5), (1, 2, 3) and (7, 0, – 1) be denoted by P, Q, and R respectively.
Points P, Q, and R are collinear if they lie on a line.

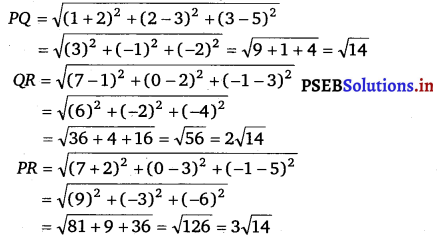
Here, PQ + QP = \(\sqrt{14}+2 \sqrt{14}=3 \sqrt{14}\) = PR
Hence, points P (- 2, 3, 5), Q(1, 2, 3), and P (7, 0, – 1) are collinear.

Question 3.
Verify the following:
(i) (0, 7, – 10), (1, 6, – 6) and (4, 9, – 6) are the vertices of an isosceles triangle.
(ii) (0, 7, 10), (- 1, 6, 6) and (- 4, 9, 6) are the vertices of a right angled triangle.
(iii) (- 1, 2, 1), (1, – 2, 5), (4, – 7, 8) and (2, – 3, 4) are the vertices of a parallelogram.
Answer.
(i) Let points (0, 7, – 10), (1, 6, – 6) and (4, 9, – 6) be denoted by A, B and C respectively.

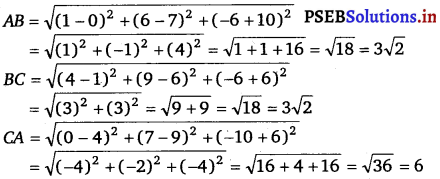
Here, AB = BC ≠ CA.
Thus, the given points are the vertices of an isosceles triangle.

(ii) Let (0, 7, 10), (- 1, 6, 6) and (- 4, 9, 6) be denoted by A, B, and C respectively.

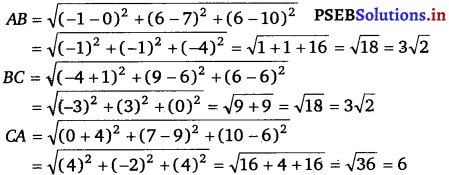
Now, AB² + BC² = (3√2)² + (3√2)²
= 18 + 18 = 36 = AC²
Hence, the given points are the vertices of a right-angled triangle.

(iii) Let points (- 1, 2, 1), (1, – 2, 5), (4, – 7, 8) and (2, – 3, 4) be denoted by A, B, C and D respectively.

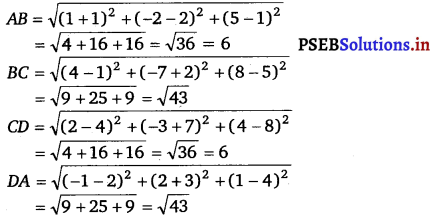
Now, AB = CD = 6, BC = AD = √43.
Hence, the opposite sides of quadrilateral ABCD, whose vertices are taken in order, are equal.
Therefore, ABCD is a parallelogram.
Hence, the given points are the vertices of a parallelogram.

Question 4.
Find the equation of the set of points which are equidistant from the points (1, 2, 3) and (3, 2, – 1).
Answer.
Let P(x, y, z) be the point that is equidistant from points A(l, 2, 3) and B(3, 2, -1).
Accordingly, PA = PB
⇒ PA² = PB²
⇒ (x – 1)² + (y – 2)² + (z – 3)² = (x – 3)² + (y – 2)² + (z + 1)²
x² – 2x + 1 + y² – 4y + 4 + z² – 6z + 9 = x² – 6x + 9 + y² – 4y + 4 + z² + 2z +1
⇒ – 2x – 4y – 6z + 14 = – 6x – 4y + 2z + 14
⇒ – 2x – 6z + 6x – 2z = 0
⇒ 4x – 8z = 0
⇒ x – 2z = 0
Thus, the required equation is x – 2z = 0.

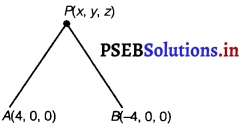
Question 5.
Find the equation of the set of points P, the sum of whose distances from A (4, 0, 0) and B (- 4, 0, 0) is equal to 10.
Answer.
We have, a point P(x, y, z) such that, PA + PB = 0

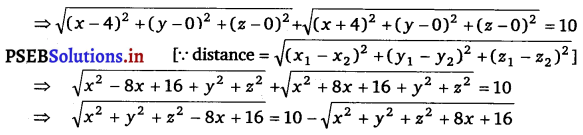
On squaring both sides, we get
x² + y² + z² – 8x + 16 = 100 + x² + y² + z² + 8x + 16 – 20 \(\sqrt{x^{2}+y^{2}+z^{2}+8 x+16}\)
⇒ – 16x – 100 = – 20 \(\sqrt{x^{2}+y^{2}+z^{2}+8 x+16}\)
⇒ 4x + 25 = 5 \(\sqrt{x^{2}+y^{2}+z^{2}+8 x+16}\) [dividing both sides by -4]
Again squaring on both sides, we get
16x² + 200x + 625 = 25 (x² + y² + z² + 8x +16)
⇒ 16x² + 200x + 625 = 25x² + 25y² + 25z² +200x + 400
⇒ 9x² + 25y² + 25z² – 225 = 0.