Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 12 Introduction to Three Dimensional Geometry Ex 12.3 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 11 Maths Chapter 12 Introduction to Three Dimensional Geometry Ex 12.3
Question 1.
Find the coordinates of the point which divides the line segment joining the points (- 2, 3, 5) and (1, – 4, 6) in the ratio (i) 2 : 3 internally,
(ii) 2 : 3 externally.
Answer.
Let P(x, y, z) be any point which divides the line segment joining points A(- 2, 3, 5) and B(1, – 4, 6) in the ratio 2 : 3 internally.
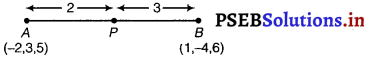
Here, the ratio is 2 : 3
m = 2, n = 3
The coordinates of point P = \(\left[\left(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}, \frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}, \frac{m_{1} z_{2}+m_{2} z_{1}}{m_{1}+m_{2}}\right)\right]\)
= \(\left[\frac{2 \times 1+3 \times(-2)}{2+3}, \frac{2(-4)+3(3)}{2+3}, \frac{2(6)+3(5)}{2+3}\right]\)
= \(\left(\frac{2-6}{5}, \frac{-8+9}{5}, \frac{12+15}{5}\right)=\left(\frac{-4}{5}, \frac{1}{5}, \frac{27}{5}\right)\)
(ii) Let P(x, y, z) be any point which divides the line segment joining points A(- 2, 3, 5) and 8(1, – 4, 6) in the ratio 2 : 3 externally.
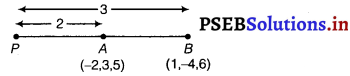
Here, the ratio is 2 : 3
∴ m = 2, n = 3
The coordinates of point P = \(\left[\left(\frac{m_{1} x_{2}-m_{2} x_{1}}{m_{1}-m_{2}}, \frac{m_{1} y_{2}-m_{2} y_{1}}{m_{1}-m_{2}}, \frac{m_{1} z_{2}-m_{2} z_{1}}{m_{1}-m_{2}}\right)\right]\)
= \(\left[\frac{2(1)+(-3)(-2)}{2+(-3)}, \frac{2(-4)+(-3) \times 3}{2+(-3)}, \frac{2(6)+(-3)(5)}{2+(-3)}\right]\)
= \(\left(\frac{2+6}{2-3}, \frac{-8-9}{2-3}, \frac{12-15}{2-3}\right)=\left(\frac{8}{-1}, \frac{-17}{-1}, \frac{-3}{-1}\right)\)
= (- 8, 17, 3).
![]()
Qiestion 2.
Given that P (3, 2, -4), Q (5, 4, – 6) and R (9, 8, – 10) are coimear. Find the ratio in which Q divides PR.
Answer.
Let point Q(5, 4, -6) divide the line segment joining point P (3, 2, – 4) and R (9, 8, – 10) in the ratio k : 1.
Therefore, by section formula:
(5, 4, – 6) = \(\left(\frac{k(9)+3}{k+1}, \frac{k(8)+2}{k+1}, \frac{k(-10)-4}{k+1}\right)\)
⇒ \(\frac{9 k+3}{k+1}\) = 5
⇒ 9k + 3 = 5k + 5
⇒ 4k = 2
⇒ k = \(\frac{2}{4}=\frac{1}{2}\).
Thus, point Q divides PR in the ratio 1 : 2.
Qiestion 3.
Find the ratio in which the YZ-plane divides the line segment formed by joining the points (- 2, 4, 7) and (3, – 5, 8).
Answer.
Let the YZ plane divide the line segment joining points (- 2, 4, 7) and (3, – 5, 8) in the ratio k: 1.
Hence, by section formula, the coordinates of point of intersection are given by
\(\left(\frac{k(3)-2}{k+1}, \frac{k(-5)+4}{k+1}, \frac{k(8)+7}{k+1}\right)\)
On the YZ plane, the x-coordinate of any point is zero.
⇒ \(\frac{3 k-2}{k+1}\) = 0
⇒ 3k – 2 = 0
⇒ k = \(\frac{2}{3}\)
Thus, the YZ plane divides the line segment formed by joining the given points in the ratio 2 : 3.
![]()
Qiestion 4.
Using section formula, show that the points A (2, – 3, 4), B(- 1, 2, 1) and C(0, \(\frac{1}{3}\), 2) are collinear.
Answer.
Let C(0, \(\frac{1}{3}\), 2) divides the join of A(2, – 3, 4) and B(- 1, 2,1) in the ratio k : 1.
Then, coordinates of C are \(\left(\frac{-k+2}{k+1}, \frac{2 k-3}{k+1}, \frac{k+4}{k+1}\right)\) ………………. (i)
[using internal ratio formula]
But coordinates of C are (0, \(\frac{1}{3}\), 2) ………………(ii) [given]
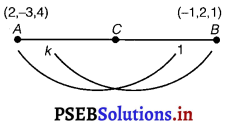
\(\frac{-k+2}{k+1}\) = 0
⇒ – k + 2 = 0
⇒ k = 2
\(\frac{2 k-3}{k+1}=\frac{1}{3}\)
⇒ 6k – 9 = k + 1
⇒ k = 2
\(\frac{k+4}{k+1}\) = 2
⇒ k + 4 = 2k + 2
⇒ k = 2
From each of these equations, we get k = 2
Since, each of these equations give same value of k.
Therefore, the given points are collinear and C divides AB internally in the ratio 2 : 1.
![]()
Question 5.
Find the coordinates of the points which trisect the line segment joining the points P(4,2, -6) and Q (10, -16, 6).
Answer.
Let R and S be two points which trisect the joining of P and Q.
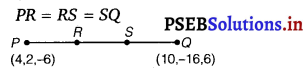
Point R divides the join of PQ in the ratio 1 : 2.
∴ Coordinates of R are \(\left[\frac{1(10)+2(4)}{1+2}, \frac{1(-16)+2(2)}{1+2}, \frac{1(6)+2(-6)}{1+2}\right]\)
= \(\left(\frac{10+8}{3}, \frac{-16+4}{3}, \frac{6-12}{3}\right)\)
= \(\left(\frac{18}{3}, \frac{-12}{3}, \frac{-6}{3}\right)\)
= (6, – 4, – 2).
Also, point S divides the join of PQ in the rano 2 : 1
∴ Coordinates of S are \(\left[\frac{2(10)+1(4)}{1+2}, \frac{2(-16)+1(2)}{1+2}, \frac{2(6)+1(-6)}{1+2}\right]\)
= \(\left(\frac{20+4}{3}, \frac{-32+2}{3}, \frac{12-6}{3}\right)\)
= \(\left(\frac{24}{3}, \frac{-30}{3}, \frac{6}{3}\right)\)
= (8, – 10, 2).
