PSEB 11th Class Maths Solutions Chapter 12 Introduction to Three Dimensional Geometry Miscellaneous Exercise

by

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 12 Introduction to Three Dimensional Geometry Miscellaneous Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 12 Introduction to Three Dimensional Geometry Miscellaneous Exercise

Question 1.
Three vertices of a parallelogram ABCD are A (3,- 1, 2), B(1, 2, – 4) and C (- 1, 1, 2). Find the coordinates of the fourth vertex.
Answer.
The three vertices of a parallelogramABCD are given as A (3,- 1, 2), B (1, 2, – 4) and C (- 1, 1, 2).
Let the coordinates of the fourth vertex be D(x, y, z).

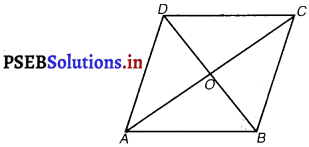
PSEB 11th Class Maths Solutions Chapter 12 Introduction to Three Dimensional Geometry Miscellaneous Exercise 1

We know that the diagonals of a parallelogram bisect each other.
Therefore, in parallelogram ABCD, AC and BD bisect each other.
∴ Mid-point of AC = Mid-point of BD
\(\left(\frac{3-1}{2}, \frac{-1+1}{2}, \frac{2+2}{2}\right)=\left(\frac{x+1}{2}, \frac{y+2}{2}, \frac{z-4}{2}\right)\)
(1, 0, 2) = \(\left(\frac{x+1}{2}, \frac{y+2}{2}, \frac{z-4}{2}\right)\)
\(\frac{x+1}{2}\) = 1, \(\frac{y+2}{2}\) = 0, and \(\frac{z-4}{2}\) = 2
x = 1 ,y = – 2, and z = 8
Thus, the coordinates of the fourth vertex are (1, – 2, 8).

Question 2.
Find the lengths of the medians of the trisìngle with vertices A (0, 0, 6), B (0, 4, 0) and C (6, 0, 0).
Answer.
ABC is a thangle with vertices A (0, 0, 6), B (0, 4, 0) and C (6, 0, 0).

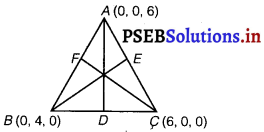
PSEB 11th Class Maths Solutions Chapter 12 Introduction to Three Dimensional Geometry Miscellaneous Exercise 2

[∵ Coordinates of mid-points = \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}, \frac{z_{1}+z_{2}}{2}\right)\)]

Let points D, E and F are the mid-points of BC, AC and AB, respectively.
So, AD, BE and CF will be the medians of the triangle.
Coordinates of point D = \(\left(\frac{0+6}{2}, \frac{4+0}{2}, \frac{0+0}{2}\right)\) = (3, 2, 0)

Coordinates of point E = \(\left(\frac{0+6}{2}, \frac{0+0}{2}, \frac{6+0}{2}\right)\) = (3, 0, 3)

Coordinates of point F = \(\left(\frac{0+0}{2}, \frac{0+4}{2}, \frac{6+0}{2}\right)\) = (0, 2, 3)

Thus, the coordinates of the fourth vertex are (1, – 2, 8).

Now, length of median
AD = Distance between points A and D
AD = \(\sqrt{(0-3)^{2}+(0-2)^{2}+(6-0)^{2}}\)
[∵ distance = \(\sqrt{\left(x_{1}-x_{2}\right)^{2}+\left(y_{1}-y_{2}\right)^{2}+\left(z_{1}-z_{2}\right)^{2}}\)]
= \(\sqrt{9+4+36}\)
= √49 = 7

similarly, BE = \(\sqrt{(0-3)^{2}+(4-0)^{2}+(0+3)^{2}}\)
= \(\sqrt{9+16+9}\) = √34

and CF = \(\sqrt{(6-0)^{2}+(0-2)^{2}+(0-3)^{2}}\)
= \(\sqrt{36+4+9}\) = √49 = 7
Hence, length of the median are 7, √34 and 7.

Question 3.
If the origin is the centroid of the triangle PQR with vertices P (2a, 2, 6), Q (- 4, 3b, -10) and R (8, 14, 2c), then find the values of a, b and c.
Answer.

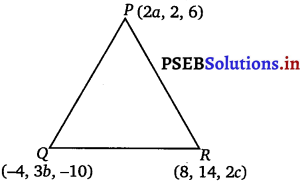
PSEB 11th Class Maths Solutions Chapter 12 Introduction to Three Dimensional Geometry Miscellaneous Exercise 3

It is known that the coordinates of the centroid of the triangle, whose vertices are (x1, y1, z1), (x2, y2, z2) and (x3, y3, z3),are \(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}, \frac{z_{1}+z_{2}+z_{3}}{3}\right)\)

Therefore, coordinates of the centroid of ∆PQR = \(\left(\frac{2 a-4+8}{3}, \frac{2+3 b+14}{3}, \frac{6-10+2 c}{3}\right)\)

= \(\left(\frac{2 a+4}{3}, \frac{3 b+16}{3}, \frac{2 c-4}{3}\right)\)

It is given that the origin is the centroid of ∆PQR.
∴ (0, 0, 0) = \(\left(\frac{2 a+4}{3}, \frac{3 b+16}{3}, \frac{2 c-4}{3}\right)\)

\(\frac{2 a+4}{3}\) = 0, \(\frac{3 b+16}{3}\) = 0 and \(\frac{2 c-4}{3}\) = 0

a = – 2, b = – \(\frac{16}{3}\) and c = 2.

Thus, the respective values of a, b and c are – 2, – \(\frac{16}{3}\) and 2.

Question 4.
Find the coorlinsites of a point on y-axis which are at a distance of 5√2 from point P(3, – 2, 5).
Answer.
If a point is on the y-axis, then x-coordinate and the z-coordinate of the point are zero.
Let A (0, b, 0) be the point on the y-axis at a distance of 5√2 from point P (3, – 2, 5).
Accordingly, AP = 5√2
∴ AP2 = 50
(3 – 0)2 + (- 2 – b)2 + (5 – 0)2 = 50
⇒ 9 + 4 + b2 + 4b + 25 = 50
⇒ b2 + 4b – 12 = 0
⇒ b2 + 6b – 2b – 12 = 0
⇒ (b + 6) (b – 2) = 0
⇒ b = – 6 o r2.
Thus, the coordinates of the required points are (0, 2, 0) and (0, – 6, 0).

Question 5.
A point R with x-coordinnte 4 lies on the line segment joining the points P (2, – 3, 4) and Q(8, 0, 10). Find the coordinates of the point R.
[Hint : Suppose R divides PQ in the ratio k : 1. The co-ordinates of the point R are given by, \(\left(\frac{8 k+2}{k+1}, \frac{-3}{k+1}, \frac{10 k+4}{k+1}\right)\)]
Answer.
Let the coordinates of R be (4, y, z) and R divides PQ in ratio k : 1
∴ Coordinate of R is \(\left(\frac{8 k+2}{k+1}, \frac{-3}{k+1}, \frac{10 k+4}{k+1}\right)\).
[∵ using internal ratio formula]

PSEB 11th Class Maths Solutions Chapter 12 Introduction to Three Dimensional Geometry Miscellaneous Exercise 4

But x – coordinate of R is 4.
So, \(\frac{8 k+2}{k+1}\) = 4
⇒ 8k + 2 = 4k + 4
⇒ 4k = 2
⇒ k = \(\frac{1}{2}\)

img 5

Hence, coordinates of R are (4, – 2, 6).

Question 6.
If A and B be the points (3, 4, 5) and (- 1, 3, – 7), respectively, find the equation of the set of points P such that PA2 + PB2 = k2, where k is a constant.
Answer.
The coordinates of points A and B are given as (3, 4, 5) and Q (- 1, 3, – 7) respectively.
Let the coordinates of point P be (x, y, z).
On using distance formula, we obtain .
PA2 = (x – 3)2 + (y – 4)2 + (z – 5)2
= x2 + 9 – 6x + y2 +16 – 8y + z2 + 25 – 10z
= x2 – 6x + y2 – 8y + z2 – 10z + 50
PB2 = (x + 1)2 + (y – 3)2 + (z + 7)2
= x2 + 2x +1 + y2 – 6y + 9 + z2 + 14z + 49
= x2 + 2x + y2 – 6y + z2 + 14z + 59
Now, if PA2 + PB2 = k2, then
(x2 – 6x + y2 – 8y + z2 – 10z + 50) + (x2 + 2x + y2 – 6y + z2 + 14z + 59) = k2
⇒ 2x2 + 2y2 + 2z2 – 4x – 14y + 4z +109 = k2
⇒ 2(x2 + y2 + z2 – 2x – 7y + 2z) = k2 – 109
⇒ x2 + y2 + z2 – 2x – 7y + 2z = \(\frac{k^{2}-109}{2}\)
Thus, the required equation is x2 + y2 + z2 – 2x + 7y + 2z = \(\frac{k^{2}-109}{2}\).

Leave a Comment