PSEB 11th Class Maths Solutions Chapter 13 Limits and Derivatives Ex 13.2

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 13 Limits and Derivatives Ex 13.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 13 Limits and Derivatives Ex 13.2

Question 1.
Find the derivative of x² – 2 at x = 10.
Answer.
We have, f(x) = x² – 2
By using first principle of derivative,
f'(10) = \(\lim _{h \rightarrow 0} \frac{f(10+h)-f(10)}{h}\)

= \(\lim _{h \rightarrow 0} \frac{\left[(10+h)^{2}-2\right]-\left[(10)^{2}-2\right]}{h}\)

= \(\lim _{h \rightarrow 0} \frac{100+20 h+h^{2}-2-100+2}{h}\)

= \(\lim _{h \rightarrow 0} \frac{h^{2}+20 h}{h}\)

= \(\lim _{h \rightarrow 0}\) (h + 20) = 20.

Question 2.
Find the derivative of 99x at x = 100.
Answer.
Let f(x) = 99x. Accordingly,
f'(100) = \(\lim _{h \rightarrow 0} \frac{f(100+h)-f(100)}{h}\)

= \(\lim _{h \rightarrow 0} \frac{99(100+h)-99(100)}{h}\)

= \(\lim _{h \rightarrow 0} \frac{99 \times 100+99 h-99 \times 100}{h}\)

= \(\lim _{h \rightarrow 0} \frac{99 h}{h}\)

= \(\lim _{h \rightarrow 0}\) (99) = 99
Thus, the derivative of 99x at x = 100 is 99.

Question 3.
Find the derivative of x at x = 1.
Answer.
Let f(x) = x. Accordingly,
f(1) = \(\lim _{h \rightarrow 0} \frac{f(1+h)-f(1)}{h}\)

= \(\lim _{h \rightarrow 0} \frac{(1+h)-1}{h}=\lim _{h \rightarrow 0} \frac{h}{h}=\lim _{h \rightarrow 0}(1)\) = 1.
Thus, the derivative of x at x = 1 is 1.

Question 4.
Find the derivative of the following functions from first principle.
(i) x³ – 27
(ii) (x – 1) (x – 2)
(iii) \(\frac{1}{x^{2}}\)
(iv) \(\frac{x+1}{x-1}\)
Answer.
(i) We have, f(x) = x³ – 27
By using first principle of derivative,

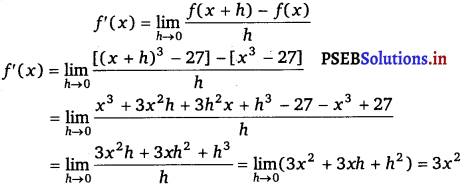
(ii) We have, f(x) = (x – 1) (x – 2) = x² – 3x + 2
By first principle of derivative, we have

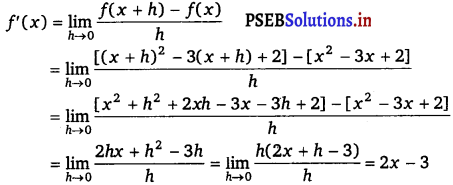
(iii) Let f(x) = \(\frac{1}{x^{2}}\).
Accordingly, from the first, principle,

(iv) Let f(x) = \(\frac{x+1}{x-1}\)
Accordingly, from the first principle,

Question 5.
For the function f(x) = \(\). Prove that f'(1) = 100 f'(0).
Answer.

At x = 0, f'(0) = 1
At x = 1, f'(1) = 1⁹⁹ + 1⁹⁸ + ………….. + 1 + 1
= [1 + 1 + 1 + …………… + 1 + 1]_{100 terms}
= 1 × 100 = 100.

Question 6.
Find the derivative of xⁿ + ax^{n – 1} + a² x^{n – 2} + ………….. + a^{n – 1} x + aⁿ for some fixed real number a.
Answer.
Let f(x) = xⁿ + ax^{n – 1} + a² x^{n – 2} + ………….. + a^{n – 1} x + aⁿ
On differentiating both sides, we get
f'(x) = nx^{n – 1} + a(n – 1)x^{n – 2} + a² (n – 2)x^{n – 3} + …………. + a^{n – 1} . 1 + 0
On putting x = a both sides, we get
f'(a) = na^{n – 1} + a (n – 1) x^{n – 2} + a² (n – 2) a^{n – 3} + ……………. + a^{n – 1}
= n a^{n – 1} + (n – 1) a^{n – 1} + (n – 2) a^{n – 1} + ……………. + a^{n – 1}
= a^{n – 1} [n + (n – 1) + (n – 2) + ………….. + 1]
[∵ sum of n natural numbers = \(\frac{n(n+1)}{2}\)]
= \(a^{n-1} \frac{n(n+1)}{2}\).

Question 7.
For some constants a and b, find the derivative of
(i) (x – a) (x – b)
(ii)(ax +b)
(iii) \(\frac{x-a}{x-b}\)
Ans.
(i) Let f(x) = (x – a) (x – b)
f(x)= x² – (a + b) x + ab
∴ f'(x) = \(\frac{d}{d x}\) [x² – (a + b) x + ab]
= \(\frac{d}{d x}\) (x²) – (a + b) \(\frac{d}{d x}\)(x) + \(\frac{d}{d x}\) (ab)
On using theorem \(\frac{d}{d x}\) (xⁿ) = nx^{n – 1}, we obtain
f'(x) = 2x – (a + b) + 0 = 2x – a – b.

(ii) Let f(x) = (ax² + b)²
f(x) = a²x⁴ + 2abx² + b²
∴ f'(x) = \(\frac{d}{d x}\) (a²x⁴ + 2abx² + b²)
= a² \(\frac{d}{d x}\) (x⁴) + 2ab \(\frac{d}{d x}\) (x²) + \(\frac{d}{d x}\) (b²)
On using theorem \(\frac{d}{d x}\) (xⁿ) = nx^{n – 1}, we obtain
f’(x) = a² (4x³) + 2ab (2x) + b2(O) = 4a2x3 + 4abx= 4ax (ax2 + b).

(iii) Let f(x) = \(\frac{x-a}{x-b}\)

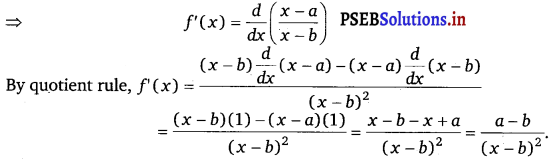
Question 8.
Find the derivative of \(\frac{x^{n}-a^{n}}{x-a}\) for some constant a.
Answer.

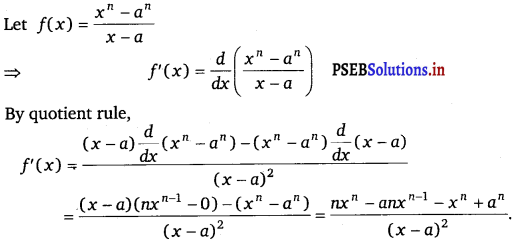
Question 9.
Find the derivative of
(i) 2x – \(\frac{3}{4}\)
(ii) (5x³ + 3x – 1) (x – 1)
(iii) x^{– 3} (5 + 3x)
(iv) x⁵ (3 – 6x^{– 9})
(v) x^-4 (3 – 4x^{– 5})
(vi) \(\frac{2}{x+1}-\frac{x^{2}}{3 x-1}\)
Answer.
(i) Let f(x) = 2x – \(\frac{3}{4}\)
f'(x) = \(\frac{d}{d x}\left(2 x-\frac{3}{4}\right)\)

= \(2 \frac{d}{d x}(x)-\frac{d}{d x}\left(\frac{3}{4}\right)\)

= 2 – 0 = 2

(ii) Let f(x) = (5x³ + 3x – 1) (x – 1)
By Leibnitz product rule,
f(x) = (5x³ + 3x – 1) \(\frac{d}{d x}\) (x -1) + (x – 1) \(\frac{d}{d x}\) (5x³ + 3x – 1)
= (5x³ + 3x – 1) (1) + (x – 1) (53x² + 3 – 0)
= (5x³ +3x – 1) +(x – 1) (15x² + 3)
= 5x³ + 3x – 1 + 15x³3 + 3x – 15x² – 3
= 20x³ – 15x² + 6x – 4.

(iii) Let f(x) = x^{– 3} (5 + 3x) .
By Leibnitz product rule,
f(x) = x^{– 3} \(\frac{d}{d x}\) (5 + 3x) + (5 + 3x) \(\frac{d}{d x}\) (x^{– 3})
= x^{– 3} (0 + 3) + (5 + 3x) (- 3x^{– 3 – 1})
= x^{– 3} (3) + (5 + 3x) (- 3x^{– 4})
= – 3x^{– 3} (2 + \(\frac{5}{x}\))
= \(\frac{-3 x^{-3}}{x}\) (2x + 5)
= \(=\frac{-3}{x^{4}}\) (5 + 2x)

(iv) Let f(x) = x⁵ (3 – 6x^-9)
By Leibnitz product rule,
f'(x) = \(x^{5} \frac{d}{d x}\left(3-6 x^{-9}\right)+\left(3-6 x^{-9}\right) \frac{d}{d x}\left(x^{5}\right)\)
= x⁵ {0 – 6 (- 9) x^{– 9 – 1}} + (3 – 6x^{– 9}) (5x⁴)
= x⁵ (54x^{– 10}) + 15x⁴ – 30x^{– 5}
= 54x^{– 5} + 15x⁴ – 30x^{– 5}
= 24x^{– 5} + 15x⁴
= 15x⁴ + \(\frac{24}{x^{5}}\)

(v) Let f(x) = x^{– 4} (3 – 4x^{– 5})
By Leibnitz product rule,
f’(x) = x^{– 4} \(\frac{d}{d x}\) (3 – 4x^{– 5}) + (3 – 4x^{– 5}) \(\frac{d}{d x}\) (x^{– 4})
= x^{– 4} {0 – 4 (- 5) x^{– 5 – 1}} + (3 – 4x^{– 5}) (- 4)x^{– 4 – 1}
= x^{– 4} (20 x^{– 6}) + (3 – 4x^{– 5}) (- 4 x^{– 5})
= 20x^{– 10} – 12x^{– 5} + 16x^{– 10}
= 36x^{– 10} – 12x^{– 5}
= \(-\frac{12}{x^{5}}+\frac{36}{x^{10}}\).

(vi)

Question 10.
Find the derivative of cos x from first principle.
Answer.
Let f(x) = cos x.
Accordingly, from the first principle, /'(*) = Um /(* +10-/00 = ^ COSUM 111 <mx

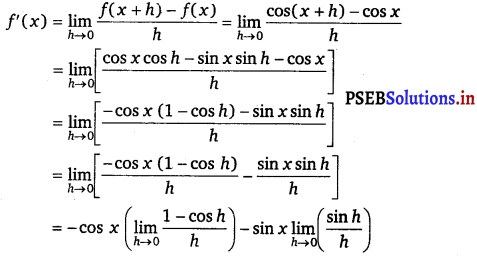
= – cos x (0) – sin x(1)
[∵ \(\lim _{h \rightarrow 0} \frac{1-\cos h}{h}\) = 0 and \(\lim _{h \rightarrow 0} \frac{\sin h}{h}\) = 1]
= – sin x
∴ f'(x) = – sin x

Question 11.
Find the derivative of the following functions:
(i) sin x cos x
(ii) sec x
(iii) 5 sec x + 4 cos x
(iv) cosec x
(v) 3 cot x + 5 cosec x
(vi) 5 sin x – 6 cos x+7
(vii) 2 tan x – 7 sec x
Answer.
(i) Let f(x) = sin x cos x.
Accordingly, from the first principle,

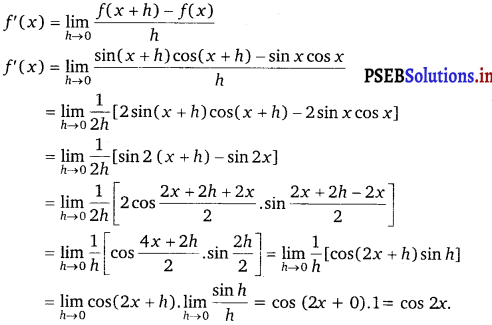
(ii) Let (x) = sec x.
Accordingly, from the first principle.

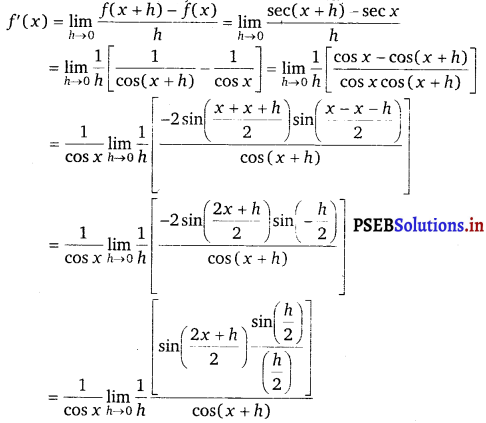
= \(\frac{1}{\cos x} \lim _{\frac{h}{2} \rightarrow 0} \frac{\sin \left(\frac{h}{2}\right)}{\left(\frac{h}{2}\right)} \lim _{h \rightarrow 0} \frac{\sin \left(\frac{2 x+h}{2}\right)}{\cos (x+h)}\)

= \(\frac{1}{\cos x} \cdot 1 \cdot \frac{\sin x}{\cos x}\)

= sec x tan x.

(iii) Let f(x) = 5 sec x + 4 cos x.
Accordingly, from the first principle,

= \(\frac{5}{\cos x}\left[\lim _{h \rightarrow 0} \frac{\sin \left(\frac{2 x+h}{2}\right)}{\cos (x+h)} \lim _{\frac{h}{2} \rightarrow 0} \frac{\sin \left(\frac{h}{2}\right)}{\frac{h}{2}}\right]\) -4 sin x

= \(\frac{5}{\cos x} \cdot \frac{\sin x}{\cos x} \cdot 1\) – 4 sin x

= 5 sec x tan x – 4 sin x

(iv) Let f(x) = cosec x
Accordingly, from the first principle,

(v) Let f(x) = 3cot x – 5 cosec x
Accordingly, from the first principle,

(vi) Let f(x) = 5sin x – 6cos x + 7.
Accordingly, from the first principle,
f’(x) = \(\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\)
= \(\lim _{h \rightarrow 0} \frac{1}{h}\) [5 sin (x + h) – 6 cos (x + h) + 7 – 5 sin x + 6 cos x – 7]

= \(\lim _{h \rightarrow 0} \frac{1}{h}\) [5 {sin (x + h) – sin x) – 6 {cos (x + h) – cos x}]

= 5 \(\lim _{h \rightarrow 0} \frac{1}{h}\) [sin(x + h) – sin x] – 6 \(\lim _{h \rightarrow 0} \frac{1}{h}\) [cos(x + h) – cos x]

= \(5 \lim _{h \rightarrow 0} \frac{1}{h}\left[2 \cos \left(\frac{x+h+x}{2}\right) \sin \left(\frac{x+h-x}{2}\right)\right]\) – 6 \(\lim _{h \rightarrow 0} \frac{\cos x \cos h-\sin x \sin h-\cos x}{h}\)

= 5 \(\lim _{h \rightarrow 0} \frac{1}{h}\left[2 \cos \left(\frac{(2 x+h)}{2}\right) \sin \frac{h}{2}\right]\) – 6 \(\lim _{h \rightarrow 0} \frac{1}{h}\left[\frac{-\cos x(1-\cos h)-\sin x \sin h}{h}\right]\)

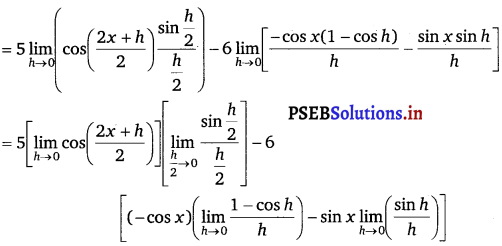
= 5 cos x . 1 – 6 [(- cos x) . (0) – sin x . 1]
= 5 cos x + 6 sin x

(vi) Let f(x) = 2 tan x – 7 sec x
Accordingly, from the first principle,

= \(\) \(\)

= \(\)

= 2 sec² x – 7 sec x tan x.