PSEB 11th Class Maths Solutions Chapter 15 Statistics Ex 15.2

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 15 Statistics Ex 15.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 15 Statistics Ex 15.2

Question 1.
Find the mean and variance for the data 6, 7, 10, 12, 13, 4, 8, 12.
Answer.
The given data is 6, 7, 10, 12, 13, 4, 8, 12

Mean \(\bar{x}=\frac{\sum_{i=1}^{8} x_{i}}{n}\)

= \(\frac{6+7+10+12+13+4+8+12}{8}=\frac{72}{8}\) = 9.

The following table is obtained.

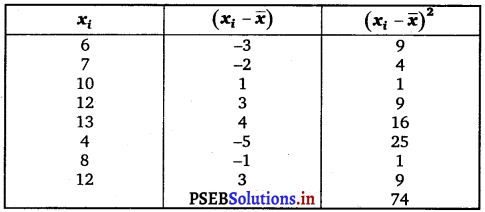
Variance (σ²) = \(\frac{1}{n} \sum_{i=1}^{8}\left(x_{1}-\bar{x}\right)^{2}\)

= \(\frac{1}{8}\) × 74 = 9.25.

Question 2.
Find the mean and variance for the first n natural numbers.
Answer.
The mean of first n natural numbers is calculated as follows.

Mean = \(\frac{\text { Sum of all observations }}{\text { Number of observations }}\)

Mean = \(\frac{\frac{n(n+1)}{2}}{n}=\frac{n+1}{2}\)

Question 3.
Find the mean and variance for the first 10 multiples of 3.
Answer.
The first 10 multiples of 3 are 3, 6, 9, 12, 15, 18, 21, 24, 27, 30
Here, number of observations, n = 10
Mean, \(\bar{x}=\frac{\sum_{i=1}^{10} x_{i}}{10}=\frac{165}{10}\) = 16.5
The following table is obtained.

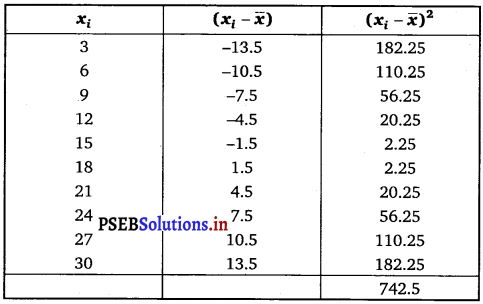
Variance (σ²) = \(\frac{1}{n} \sum_{i=1}^{10}\left(x_{1}-\bar{x}\right)^{2}\)
= \(\frac{1}{10}\) × 742.5 = 74.25.

Question 4.
Find the mean and variance for the data

Answer.
The data is obtained in tabular form as follows.

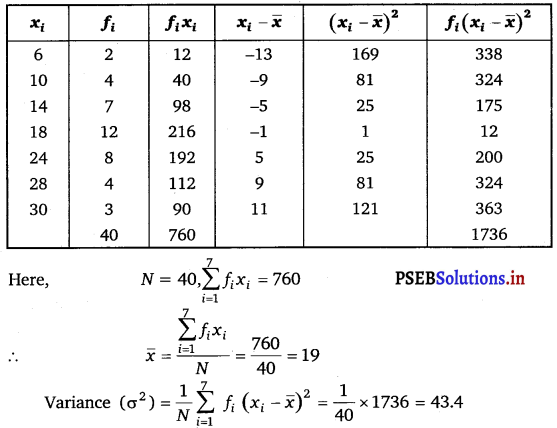
Question 5.
Find the mean and variance for the data

Answer.

Question 6.
Find the mean and standerd deviation using short-cut method.

Answer.
The data is obtained in tabular form as follows.

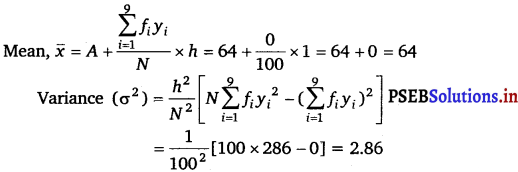
Question 7.
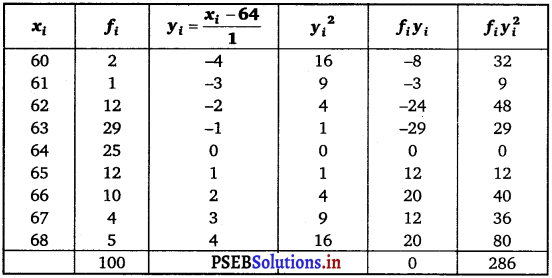
Find the mean and variance for the following frequency distribution.

Answer.

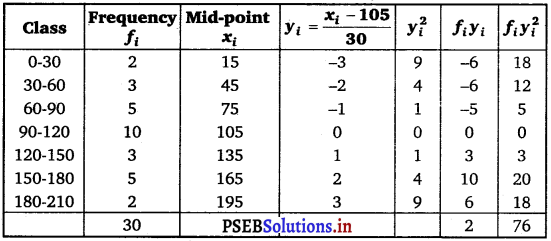
Mean, \(\bar{x}\) = A + \(\frac{\sum_{i=1}^{7} f_{i} y_{i}}{N}\) × h
= 105 + \(\frac{2}{30}\) × 30
= 105 + 2 = 107

Variance (σ²) = \(\frac{h^{2}}{N^{2}}\left[N \sum_{i=1}^{7} f_{i} y_{i}^{2}-\left(\sum_{i=1}^{7} f_{i} y_{i}\right)^{2}\right]\)

= \(\frac{(30)^{2}}{(30)^{2}}\) [30 × 76 – (2)²]
= 2280 – 4 = 2276.

Question 8.
Find the mean and variance for the following frequency distribution.

Answer.

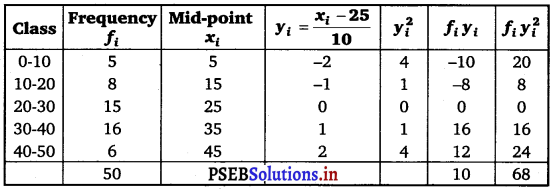
Mean, \(\bar{x}\) = A + \(\frac{\sum_{i=1}^{5} f_{i} y_{i}}{N}\) × h
= 25 + \(\frac{10}{50}\) × 10
= 25 + 2 = 27

Variance (σ²) = \(\frac{h^{2}}{N^{2}}\left[N \sum_{i=1}^{5} f_{i} y_{i}^{2}-\left(\sum_{i=1}^{5} f_{i} y_{i}\right)^{2}\right]\)

= \(\frac{(10)^{2}}{(50)^{2}}\) [50 × 68 – (10)²]

= \(\frac{1}{25}\) [3400 – 100]

= \(\frac{3300}{25}\) = 132.

Question 9.
Find the mean, variance and standard deviation using short-cut method.

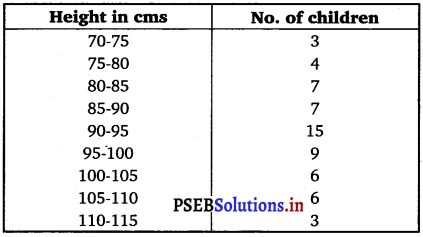
Answer.

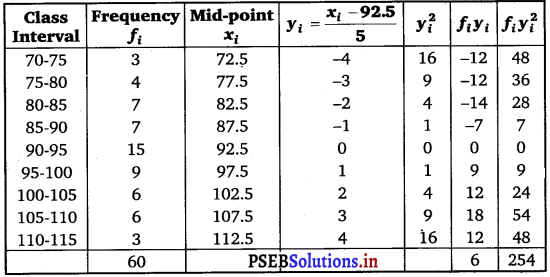
Mean, \(\bar{x}\) = A + \(\frac{\sum_{i=1}^{5} f_{i} y_{i}}{N}\) × h
= 92.5 + \(\frac{6}{60}\) × 5
= 92.5 + 0.5 = 93

Variance (σ²) = \(\frac{h^{2}}{N^{2}}\left[N \sum_{i=1}^{9} f_{i} y_{i}^{2}-\left(\sum_{i=1}^{9} f_{i} y_{i}\right)^{2}\right]\)

= \(\frac{(5)^{2}}{(60)^{2}}\) [60 × 254 – (6)²]

= \(\frac{25}{3600}\) (15204) = 105.58

∴ Standard deviation (σ) = \(\sqrt{105.58}\) = 10.27.

Question 10.
The diameters of circles (in mm) drawn in a design are given below:

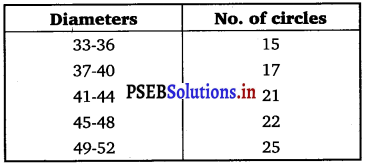
Answer.

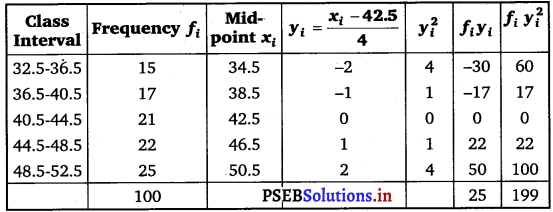
Here, N = 100, h = 4
Let the assumed mean, A, be 42.5

Mean, \(\) = A + \(\frac{\sum_{i=1}^{5} f_{i} y_{i}}{N}\) × h
= 42.5 + \(\frac{25}{100}\) × 4 = 43.5

Variance (σ²) = \(\frac{h^{2}}{N^{2}}\left[N \sum_{i=1}^{5} f_{i} y_{i}^{2}-\left(\sum_{i=1}^{5} f_{i} y_{i}\right)^{2}\right]\)

= \(\frac{16}{10000}\) [100 × 199 – (25)²]
= \(\frac{16}{10000}\) [19900 – 625]
= \(\frac{16}{10000}\) × 19275 = 30.84
∴ Standard deviation (σ) = 5.55.